Abstract
In this work, we present a simple decomposition scheme of the Kohn-Sham optimized orbitals which is able to provide a reduced basis set, made of localized polycentric orbitals, specifically designed for Quantum Monte Carlo. The decomposition follows a standard Density functional theory (DFT) calculation and is based on atomic connectivity and shell structure. The new orbitals are used to construct a compact correlated wave function of the Slater–Jastrow form which is optimized at the Variational Monte Carlo level and then used as the trial wave function for a final Diffusion Monte Carlo accurate energy calculation. We are able, in this way, to capture the basic information on the real system brought by the Kohn-Sham orbitals and use it for the calculation of the ground state energy within a strictly variational method. Here, we show test calculations performed on some small selected systems to assess the validity of the proposed approach in a molecular fragmentation, in the calculation of a barrier height of a chemical reaction and in the determination of intermolecular potentials. The final Diffusion Monte Carlo energies are in very good agreement with the best literature data within chemical accuracy.
PACS:
31.15.E-
1. Introduction
Density functional theory (DFT) is a quantum-mechanical approach mainly developed for the study of the electronic structure of many body systems like atoms, molecules and solids. The Thomas-Fermi [1,2] statistical method laid the foundations of DFT but only with the Hohenberg-Kohn [3] theorems was this new method put on a firm theoretical footing. This approach is completely different from standard quantum-mechanical methodologies based on the calculation of an N particle wave function. In DFT, the basic quantity is the electron density, namely a much simpler function of only the position of a point in a three-dimensional space. For this reason, DFT was initially the most popular for the treatment of solids where, in principle, one has to deal with an infinite number of electrons. After important work on N-representability of density functions (see Levy [4]) and the generation of a plethora of valuable approximated energy density functionals, DFT is nowadays one of the most used techniques also for the study of molecules and molecular aggregates. Following DFT, the total electronic density is thus the fundamental variable on which any ground-state n-body property depends. In order to better understand this relation, which is also extremely important to improve the existing energy density functionals, a deep analysis of the density itself as well as of the related functions and derivatives is requested. In this context, we should mention the study of Bader and co-workers [5], mainly based on gradient and Laplacian of the density, and the electron localization function introduced by Becke and Edgecombe [6].
In this work, we focus on how one can get useful information on a real molecular system by starting from the electronic density. Although we use the basic knowledge of working with N-electron wave functions, we seek to define a route capable of bringing directly from the density to the construction of the wave function and then to the computation of an accurate energy. By decomposing the Kohn–Sham orbitals, which are the building blocks of the density, we use the concept of pairs together with the information on shell structure and connectivity to build an accurate correlated wave function whose nodal (Fermionic) structure is able to provide a very good energy through a diffusion Quantum Monte Carlo (QMC) calculation.
2. Theory
The first theorem of Hohenberg-Kohn [3] shows that there is a one-to-one correspondence between the electron density and the external potential for a non-degenerate ground state of a system of electrons. The immediate consequence of this statement is that the corresponding energy is a functional of the electron density and that the N-electron wave function itself depends only on such a density. However, despite the enormous progress done in the last twenty years, the exact form of the energy functional is still unknown. In the practical implementation of DFT, the Kohn-Sham (KS) approach [7] takes a role of primary importance. In the Kohn-Sham theory, such a density is constructed from the orbitals of an independent particle model. Provided the so-called exchange-correlation energy functional is known, a set of one-particle equations can be derived and solved within a standard Self-Consistent-Field (SCF) framework. These building blocks, namely the KS orbitals, thus bring information from the real system. In the spirit of building the N-electron wave function from the exact density, we start from KS orbitals and define a route which leads to an accurate variational energy through the construction of a correlated well-defined wave function. To this end, we use the QMC method in both variational (VMC) and diffusional (DMC) versions.
The QMC is a robust method and is one of the most accurate to compute the electronic energy of the ground state of a molecular system [8,9]. In the last two decades, the interest in QMC has grown considerably [10,11]. In QMC, a common way to build a many-body wave function to describe a system of electrons is by employing a spin-free Slater-Jastrow (SJ) form of the type.
where Φ is given by
in which and are the Slater determinants written in terms of occupied orbitals of spin-up and spin-down electrons, respectively, and are the mixing coefficients. The Jastrow factor is, instead, a function which depends explicitly on interparticle distances and is capable of treating the short range Coulomb correlation. This type of wave function is, in general, compact and is able to introduce a very large fraction of dynamical correlation through the Jastrow factor.
It is well known that KS orbitals are better than the Hartree-Fock ones in QMC calculations with a single determinant Slater–Jastrow wave function [12]. This is already evidence that KS orbitals bring information on electron correlation. To get more information, we go here beyond the single determinant form in QMC. A very compact and many determinant SJ wave function can be obtained in a Jastrow-Linear Generalized Valence Bond of order n (J-LGVBn) framework [13]. These wave functions are inspired by the generalized valence bond (GVB) approach and are constructed with localized orbitals (bonding, anti-bonding, lone-pair, and diffuse lone-pair functions with nodes). The use of localized orbitals allows the definition of a coupling scheme between electron pairs, which progressively includes new classes of excitations in the determinantal component. The resulting forms are rather compact and have a number of determinants that grows linearly with respect to the size of the molecule. The highest class of excitations included is indicated by n. In order to get localized bonding or pair functions and corresponding anti-bonding orbitals, KS orbitals must undergo a decomposition scheme, which involves a localization followed by a further generation of partner orbitals by taking account of connectivity and atomic shell structure.
Let us start from the density written in terms of KS orbitals in a more general spin unrestricted form, namely
where σ is the one electron spin state. We can separately transform the and sets to derive localized orbitals for α and β spins. This operation can be performed with any suitable localization technique through a unitary transformation within each of the two sets. By writing
We still have
The localized orbitals , depending on the nature of the electronic system, can be localized on one center (lone pair), two centers (bond) or, in some particular case, on three or more centers. If we consider the more frequent case of a bond function between two atoms, A and B say, we can identify in the corresponding localized orbital a contribution coming from each atom. Thus, we can write, regardless of normalization,
which allows us to define a new linearly independent orbital of anti-bonding type in the form
that can be used as the starting partner orbital of in the J-LGVBn wave function. This part of the decomposition is dictated by connectivity. For a three-center (A-B-C) localized function recognized as
a possible, but not unique, definition of appropriate partner orbitals can be the following
and
A further decomposition can be invoked resorting to shell structure. Atomic-like functions so far derived are essentially generalized hybrid orbitals with a well defined orientation in space depending on chemical sorrounding. These orbitals have atomic basis set components of s-, p-, d-, f-type and so on. We can split these generalized hybrids in several oriented atomic hybrids by acting on the separate shell components without changing the orientation. For instance, a typical orbital will generate two hybrids of the same type, namely and , if there are two shells in the atomic basis set. Thus, if we can write
We can use the components to define directly partner orbitals for lone pair , if this is already obtained from the localization of KS orbitals, or external orbitals of the type
to improve the J-LGVBn orbitals at the VMC optimization of the QMC wave function. In order to avoid linear dependencies, localized KS orbitals, partner and external orbitals, to be used at VMC level and coming from the double decomposition scheme above, are orthogonalized. This orthogonalization is performed in two steps, (i) the first step is a hierarchical orthogonalization of partner and external orbitals with respect to KS localized orbitals, namely
and (ii) the second step by a symmetric (Löwdin) orthogonalization, namely
where is the overlap matrix after the step (i). Step (ii) allows the cancellation of all linear dependencies from the set of new orbitals. In this process, the localized KS orbitals are not modified in order to start from a J-LGVB0 wave function of good quality. Finally, once the aforementioned polycentric basis set has been prepared, we pass to the VMC calculation and perform the optimization at J-LGVB0, J-LGVB1 and J-LGVB2 levels. All the orbitals of the complementary space spanned by the starting atomic orbital basis set have been removed. The number of variational parameters is then greatly reduced. The determinantal functions of the SJ form of the three cases considered here are defined as follows
and
where is the LGVB0 form, namely a determinant made by assigning all electrons to the localized KS orbitals. Here, N is the number of valence electrons, are, more generally, bond orbitals and antibonding orbitals and where the arrow indicates a single or double substitution of a bonding orbital with the corresponding antibonding. In the computing of excited functions, all the electrons are coupled to give the same spin state of . Excited functions are, in fact, configuration state functions (CSF). More details for the construction of J-LGVBn wave functions can be found in the source paper [13]. During the VMC step, orbitals, determinant coefficients and Jastrow factor parameters are optimized. More precisely, following Fracchia et al. [13], we optimize orbitals and Jastrow factor of J-LGVB0 wave function, orbitals, determinant coefficients and Jastrow factor of the J-LGVB1 one, while we keep the J-LGVB1 orbitals in the optimization of determinant coefficients and Jastrow factor at the J-LGVB2 level of calculation. The resulting wave functions are used as trial wave function in the last DMC energy calculations. It is important to remark that a single determinant SJ wave function involves for the energy evaluation a scaling with the number of electrons similar to that of DFT, namely between and even if with a proportionality constant approximately a few thousand times larger. The use of multi determinant wave functions normally worsens this behavior but the J-LGVBn functions involve a number of determinants which grows linearly with the size of the molecules. Moreover, although not attempted in this work, the use of the present decomposition scheme should lead to a number of orbital parameters linearly dependent with the number of electrons if the mixing of the orbitals is allowed only between orbitals localized in the same region. This latter approximation is well founded and finds a logical application in calculations performed on large molecules.
In the next section, we show test results following this approach on a molecular fragmentation, in a hydrogen transfer reaction and in the calculation of a weak intermolecular potential.
3. Results and Discussion
By way of example, we tested the KS decomposition scheme proposed here in some prototypical process for which the accurate calculation of the potential energy surface (PES) must be performed through high quality quantum chemistry methods. We chose the fragmentation of hydrazine as an example of a homolytic bond breaking, a hydrogen transfer reaction and the formation of a weak van der Waals complex such as the methane dimer.
3.1. Computational Details
The KS orbitals have been optimized using the GAMESS-US package [14] with the hybrid Perdew-Burke-Ernzerhof functional PBE0 [15,16]. We have chosen the PBE0 functional because it derives from an improvement of the original PBE functional which has been classified as possibly variationally valid [17]. For the localization, we adopted the Edmiston-Ruedenberg method [18] implemented in GAMESS. The QMC calculations, instead, were performed with the CHAMP program [19]. In all calculations, we employed the Burkatzki-Filippi-Dolg (BFD) pseudopotentials [20,21] and the VTZ basis set specifically developed for these pseudopotentials. For the hydrogen transfer and the methane dimer formation, we added a set of diffuse functions taken from all-electron standard aug-cc-pVDZ basis set [22]. The pseudopotentials are treated beyond the locality approximation using the T-move approach [23]. The Jastrow factors contain electron-nuclear, electron-electron, and electron-electron-nuclear terms [24]. For the optimization of all parameters in our SJ wave functions, we used the iterative linear method developed by Umrigar et al. [25]. Here, we used a time step of 0.05 a.u. in all the DMC fixed-node calculations and also of 0.01 a.u. for the methane dimer. Finally, we used Gaussian 09 package [26] for standard quantum chemistry calculations on the methane dimer.
3.2. Fragmentation of Hydrazine
The fragmentation of hydrazine,
is a homolytic bond breaking in which the number of electronic pairs is not conserved. For this reason, the computational method must be capable of providing a good estimate of the correlation energy and must be size extensive. The J-LGVBn wave functions, already with n = 2, are able to provide a good estimate of the corresponding reaction energy [13]. Fracchia et al. used the full variational space spanned by the VTZ basis set in the global optimization of the J-LGVB2 wave function. This means to use all the 128 atomic orbitals of the hydrazine basis set. In this work, the KS decomposition scheme described in the previous section leads to a basis set made of 36 polycentric orbitals with a significant reduction of the number of parameters for the VMC optimization. In Table 1, we show the comparison between the VMC and DMC electronic energies of hydrazine calculated in this work and the corresponding values calculated by Fracchia et al. [13] with the full atomic basis set. The variational energy loss ranges from 0.0029 to 0.0031 Hartree at VMC level and from 0.0003 to 0.0007 Hartree with DMC. Resulting fragmentation energies are shown, instead, in Table 2. In this Table, we report also, for comparison purposes, Fracchia et al. theoretical results [13] and the experimental value [27,28]. As shown by Fracchia et al. [13], the level 2 of J-LGVBn theory is enough to approach the limiting value corresponding to the maximum level, namely 10. Moreover, DMC is needed to achieve chemical accuracy. Results obtained with the present approach are in close agreement with those of the previous QMC calculation showing that our decomposition scheme of KS orbitals is a valid alternative to standard J-LGVBn approach. We remind readers that standard J-LGVBn theory subsumes the use of the full atomic basis set and a Multi-Configuration SCF (MCSCF) preliminary calculation for the VMC setup. Finally, we note that our J-LGVB2 DMC fragmentation energy differs only by 0.5 kcal/mol from the experimental value. For a comparison with DFT calculations, we remind readers that Fracchia et al. [13] found that, for some of the most used functionals, the discrepancies with the experiment range from 1.5 to more than 4 kcal/mol.

Table 1.
Comparison between variational Monte Carlo (VMC) and diffusion Monte Carlo (DMC) electronic energies (Hartree) of hydrazine computed with the full atomic basis set [13] and with the reduced basis set obtained from KS orbital decomposition presented in this work. The wave function form is indicated by the level n of the Jastrow-Linear Generalized Valence Bond (J-LGVBn) theory [13]. Statistical error is about 0.0001 Hartree.
| J-LGVBn | VMC [13] | VMC (This Work) | DMC [13] | DMC (This Work) |
|---|---|---|---|---|
| 0 | −22.2438 | −22.2406 | −22.2724 | –22.2721 |
| 1 | −22.2538 | −22.2509 | −22.2762 | –22.2755 |
| 2 | −22.2565 | −22.2534 | −22.2777 | –22.2771 |

Table 2.
Fragmentation energy (kcal/mol) of hydrazine computed at various level of calculation and comparison with experimental data. Statistical error is about 0.1 kcal/mol. The experimental (exp) reference is active thermochemical tables (ATcT) [27] data corrected for zero-point energy, spin-orbit interaction, and Born–Oppenheimer approximation [28].
| J-LGVBn | VMC [13] | DMC [13] | VMC (This Work) | DMC (This Work) | Exp [27] |
|---|---|---|---|---|---|
| 0 | 67.3 | 70.8 | 65.4 | 71.6 | – |
| 1 | 69.5 | 71.8 | 69.3 | 72.3 | – |
| 2 | 70.8 | 72.4 | 70.3 | 72.9 | – |
| 10 | 71.1 | 72.8 | – | – | – |
| exp | – | – | – | – | 73.39 |
3.3. Barrier Height in a Prototypical Hydrogen Transfer Reaction
The hydrogen transfer reaction
plays an important role in atmospheric chemistry and is included in the HTB38/04 database [29], a reference database for computed reaction and activation energies. This reference is based on a semi-experimental recipe in which kinetic and thermodynamic data are combined with results from dynamical simulations and quantum mechanical calculations.
For this reaction, DFT gives poor results on barrier heights apart for the hybrid meta-functional MPWB1K [30] which is able to provide forward and reverse barrier heights within a deviation of 2 kcal/mol. In Table 3, we report our calculations and we compare our results with the previous work of Fracchia et al. [31] and with literature reference data. Fracchia et al. used 148 atomic orbitals for the basis set while, here, we have 39 basis functions from KS orbital decomposition. The two sets of J-LGVBn data are in agreement with each other with small differences between 0 and 0.5 kcal/mol. In addition, in this case, J-LGVB2 is the level of calculation closest to reference values. Our J-LGVB2 calculation is in good agreement (within chemical accuracy) with the Coupled Cluster method with the Single Double and the perturbative Triple (CCSD(T))/aug-cc-pvTZ results while showing a discrepancy with the best reference of 1.6 and 1.5 kcal/mol with forward and reverse barrier heights, respectively. For the reaction energy, the agreement is instead very good. This fact suggests that there could be a small inaccuracy in the description of three electrons localized on a molecular subunit made of three nuclei, as it happens here when the hydrogen is in the middle between the two molecules. This will be investigated in future work.

Table 3.
Barrier heights and reaction energies (kcal/mol) for the hydrogen transfer at various level of calculation and comparison with literature data. Statistical error is about 0.1 kcal/mol.
| Forward Reaction Barrier Height | |||
|---|---|---|---|
| Method | DMC [31] | DMC (This Work) | Literature |
| J-LGVB0 | 15.3 | 14.8 | – |
| J-LGVB1 | 14.9 | 14.5 | – |
| J-LGVB2 | 14.6 | 14.3 | – |
| CCSD(T)/aug-cc-pvQZ [31] | – | – | 14.19 |
| DFT(MPWB1K) [30,32] | – | – | 13.15 |
| best reference [29,33] | – | – | 12.7 |
| Reverse Reaction Barrier Height | |||
| J-LGVB0 | 5.2 | 4.9 | – |
| J-LGVB1 | 4.7 | 4.7 | – |
| J-LGVB2 | 4.6 | 4.7 | – |
| CCSD(T)/aug-cc-pvQZ [31] | – | – | 3.86 |
| DFT(MPWB1K) [30,32] | – | – | 5.04 |
| reference [29,33] | – | – | 3.2 |
| Reaction Energy | |||
| J-LGVB0 | 10.1 | 9.9 | – |
| J-LGVB1 | 10.2 | 9.8 | – |
| J-LGVB2 | 10.0 | 9.6 | – |
| CCSD(T)/aug-cc-pvQZ [31] | – | – | 10.33 |
| DFT(MPWB1K) [30,32] | – | – | 8.12 |
| reference [29,33] | – | – | 9.5 |
3.4. Methane Dimer Intermolecular Potential
The accurate calculation of interaction energies of weakly bound van der Waals complexes is a challenge for both QMC and DFT for different reasons. The "gold standard" for these type of calculations is the CCSD(T) excitations extrapolated in the limit of the Complete Basis Set (CBS). Such an approach can be used to establish a benchmark for relatively small systems, but it has an unfavorable scaling with the size of the intermolecular complex. Both QMC and DFT have a better scaling but present some difficulties to be overcome. QMC, provided a trial wave function with the right nodes is given, should give, at the DMC level, the exact total energy within the statistical error. The two main points are, in fact, the form of the wave function and the length of the simulation. While the form of the wave function with standard quantum chemistry methods must account for the dynamical correlation energy to provide good interaction potentials, it is not yet clear which more compact and simplified functional forms should account for the correct nodes. The second point is related to the statistical error. For weak interaction energies, it is mandatory to have an error on the total energy of the order of 0.00001 Hartree (sub chemical accuracy). Such a precision in a standard QMC calculation can be achieved only by very long simulations or by highly parallelized calculations. In this regard, it is important to remind readers that, in order to reduce an error by a factor of 10, one has to perform a simulation 100 times longer. DFT presents, instead, the well known problem of the evaluation of the dispersion energy. Dispersion energy is a contribution to non local intermolecular correlation energy. Although many proposed functionals afford some possible solutions to this problem, an exact treatment of the dispersion energy in the framework of DFT has not yet been provided.
The computation of the intermolecular potential of methane dimer is a good test case to check the reliability of the present approach in this context. In this case, the size of the system is small enough to guarantee a good analysis of the wave function for the DMC step and to compute energies with relatively small statistical errors. We have analyzed eight structures whose geometries are displayed in Figure 1. By starting from the 228 atomic orbitals of the aug-VTZ basis set, we have generated, through the PBE0 KS orbital decomposition described in this work, a basis set made of 48 two center orbitals, namely six along each C-H bond. A schematic representation of these orbitals is given in Figure 2. Finally, we have performed DMC energy calculations as done for the two examples above. In these QMC computations, we have not included the e-e-n three-body Jastrow term. We have checked the importance of this term on a selected structure, and we noticed that the corresponding effect on the interaction energy is negligible. A summary of all VMC and DMC calculations performed on the methane dimer is given in the Supplementary Information (Tables S1–S11). Here, we report the more significant results of this study.
For the DMC calculation, we have produced two sets of results for different values of time step, namely 0.05 and 0.01 a.u. In this way, we can have an estimate of the finite time step error on the intermolecular potential. In the previous two cases, Fracchia et al. [13] made a similar test and concluded that the value of 0.05 a.u. was accurate enough for the evaluation of energy differences like reaction energy and barrier height. Here, instead, the interaction potential is a much smaller quantity and consequently a smaller time step could be necessary. The resulting DMC interaction energies are displayed in Figure 3 for the eight structures and for two levels of calculation J-LGVB0 and J-LGVB1. The J-LGVB2 case gives results comparable with the J-LGVB1 level with the higher time step (see Tables S9–S11 of Supplementary Information). This is in line with what was expected considering that, for the methane dimer, the interaction energy is very small and the convergence, with the level of the J-LGVBn theory, should be very fast. In this Figure, the points are connected by lines in order to help the reader in the assignment of the corresponding level of computation. Although the differences between different geometries are, in some cases, of the same order of magnitude of the statistical error, the difference in the relative stability is quite evident. In this plot, we have added the patterns of analogous calculations performed at the second order Möller-Plessett (MP2) perturbation theory with a standard aug-cc-pvTZ basis set with and without countepoise correction [34]. In this model system and with such a basis set, MP2 overestimates the attraction while the so-called basis set superposition error (BSSE) coming from the use of counterpoise method tends to overestimate the necessary correction to the potential. This suggests that, in our plot, the best estimate of interaction energy should give a broken line between the two of the corrected and uncorrected MP2 calculations. For the smaller time step values, this happens only for the J-LGVB1 case. From the comparison of the two time step sets of data, it is evident that, in order to achieve the subchemical accuracy, one has to resort to a time step of 0.01 a.u. or smaller.
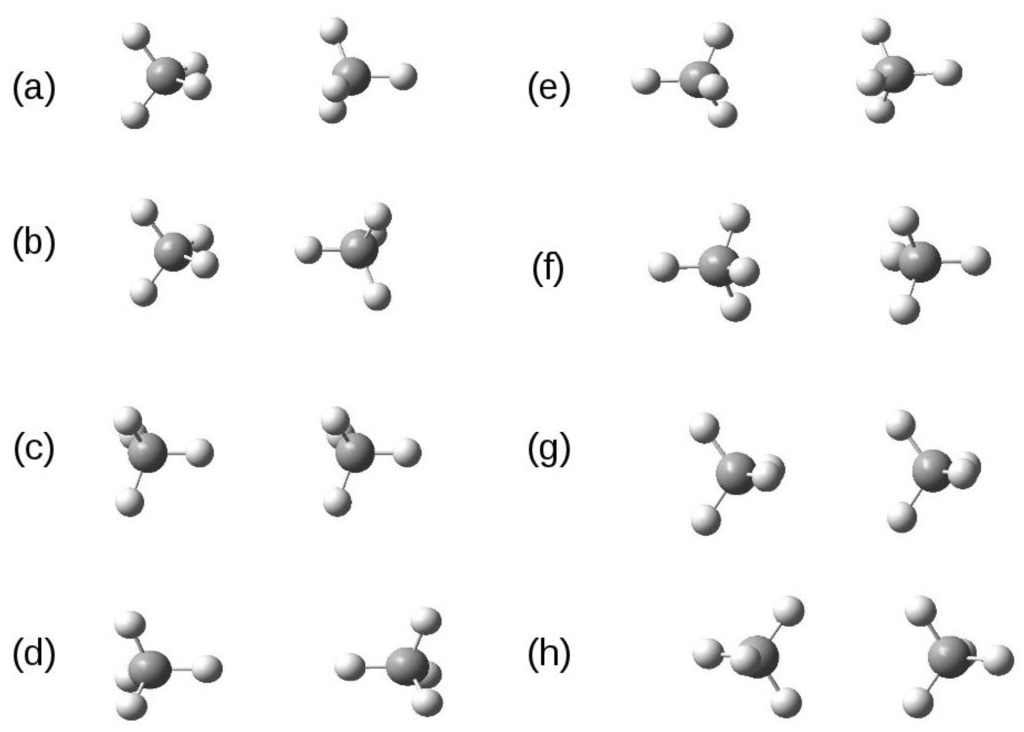
Figure 1.
Methane dimer structures considered in this work.
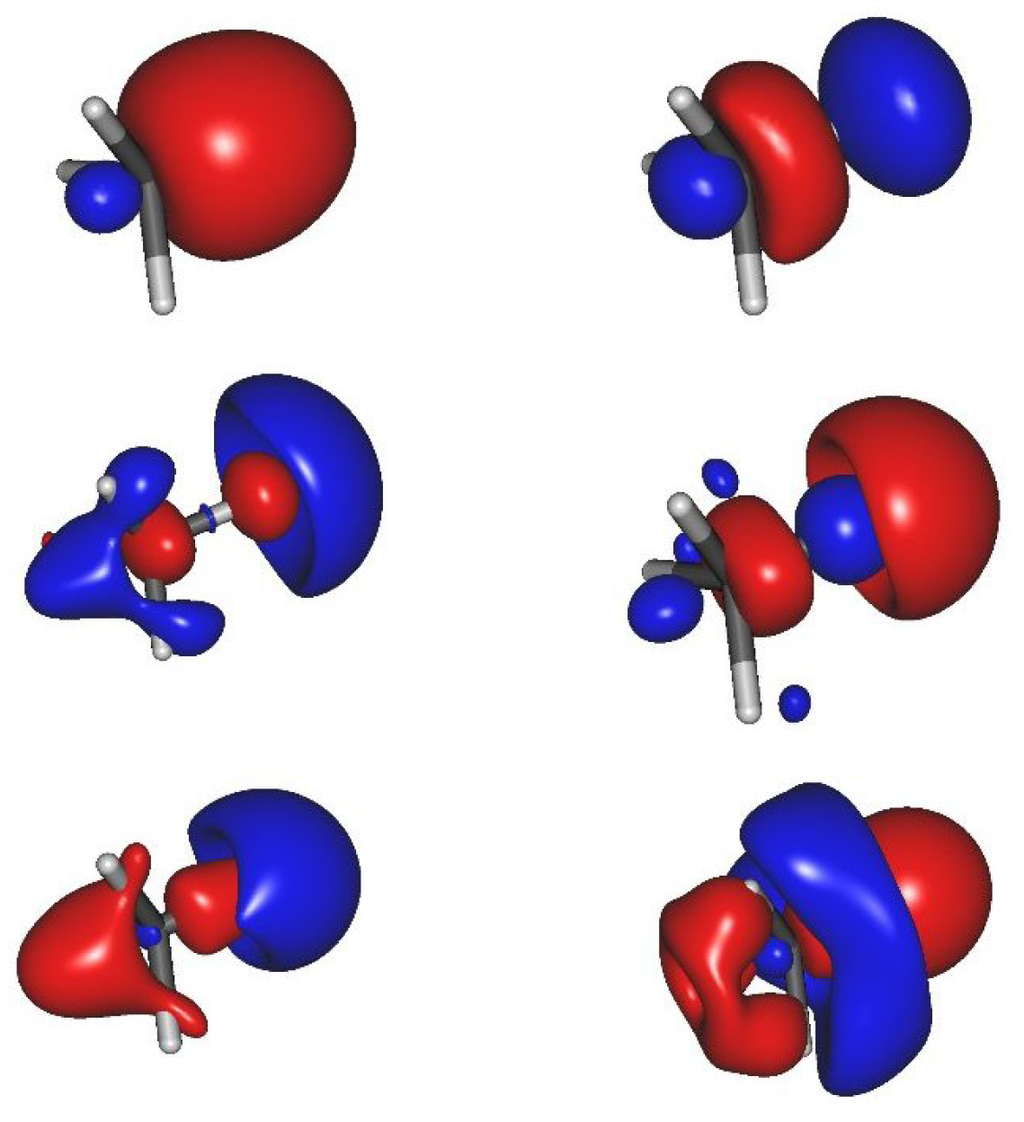
Figure 2.
Two center (C–H) localized basis set orbitals of methane.
The literature benchmark data from a CCSD(T)/CBS [35] estimate of the methane dimer PES predicts the (f) structure as the most stable with a value of −0.53 kcal/mol as interaction energy, corresponding to −0.00084 Hartree. Here, at DMC/J-LGVB1 level, we find −0.58 ± 0.04 kcal/mol with the highest time step and −0.51 ± 0.04 kcal/mol in the other case. The agreement is very good in both cases. In a recent work, Dubecký et al. [36] proposed a simplified protocol for the evaluation of intermolecular potential energies following a DMC calculation. Their protocol is based on a single-determinant SJ wave function made with B3LYP orbitals computed with an aug-VTZ basis set and with an optimized elaborated Jastrow factor. They analyzed several complexes with an average error on the binding energies of about 0.1–0.2 kcal/mol. For the methane dimer in the minimal energy configuration, they computed an interaction energy of −0.44 ± 0.05 kcal/mol. Here, we go beyond the single-determinant SJ wave function allowing a larger flexibility in the description of the position of nodes and, moreover, we optimize the orbitals at VMC level. Our J-LGVB1 wave function seems to be the more accurate in determining the interaction energy, the J-LVB0 being slightly more attractive. Some explanation for the bahavior of all these DMC calculations can be given by considering that the Pauli repulsion is related to antisymmetry, so the change of the nodal structure could affect the intermolecular potential. Moreover, dispersion energy also depends on isolated molecule polarizabilities and such response properties depend strongly on correlation energy as well. At present, it is very difficult to quantify these effects, but we think that our results on the methane dimer can offer some interesting ideas for future developments.
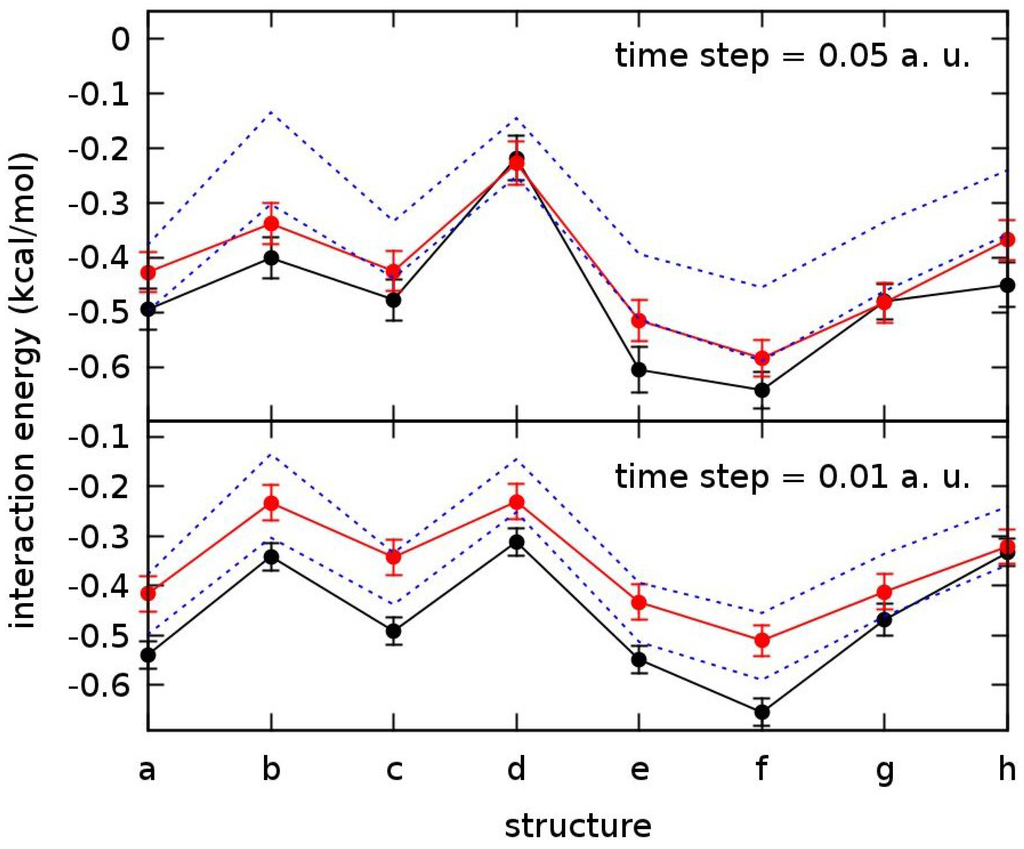
Figure 3.
DMC interaction energies for the methane dimer structures considered in this work calculated at J-LGVB0 (black) and J-LGVB1 (red) levels of the theory. Dashed lines correspond to counterpoise corrected (upper) and uncorrected (lower) MP2/aug-cc-pvTZ data plotted for comparison.
Finally, in Figure 4 we show results from some DFT calculations. More precisely, we report PBE0 interaction energies obtained with the same basis set and pseudopotential used for QMC and with the ωB97XD functional [37] with the standard aug-cc-pvTZ basis set. As we can see, PBE0, which is a good hybrid functional for many purposes, here clearly suffers of the lack of a good description of dispersion energy. ωB97XD, instead, is a range-separated hybrid functional with the inclusion of empirical dispersion. Results with this functional for the methane dimer seem to be good, at least for these eight structures. For comparison purposes, we have included in this Figure also the minimal energy from CCSD(T)/CBS literature reference [35] and from QMC calculation of Dubecký et al. [36].
At this point, because the quality of a PES cannot be checked on a single geometry, we have attempted the calculation of the second virial coefficient from the computed interaction energies of the eight dimer configurations. In order to build a PES with these few data, we have fitted the DMC interaction energies with scaled Hartree-Fock (HF) and second order Möller-Plessett (MP) corresponding values, namely we have written
where α and β are linear fitting parameters. The HF interaction energy is dominated by Pauli repulsion, the quadrupole-quadrupole electrostatic interaction being much smaller in magnitude at the most stable geometries. The second order MP intermolecular energy is instead always attractive, being the main contribution to the dispersion energy. By performing an MP2/aug-cc-pvTZ all electron calculation, our fit leads to and . This is an interesting result which tells us that electron correlation affects both Pauli repulsion and London interaction (dispersion energy) with a resulting modulation of the MP2 PES. With the purpose of computing the second virial coefficient, we have fitted the modified PES with the following analytical form
where is the damping function
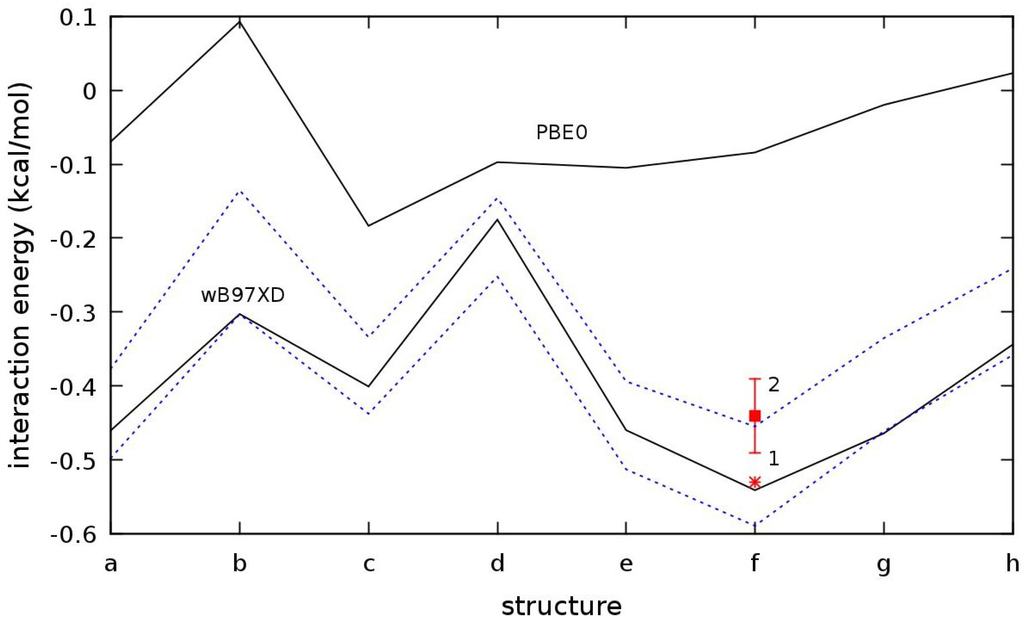
Figure 4.
PBE0 and ωB97XD KS DFT interaction energies for the methane dimer structures considered in this work. Dashed lines correspond to counterpoise corrected (upper) and uncorrected (lower) MP2/aug-cc-pvTZ data plotted for comparison. Isolated points refer to the minimum energy configuration literature benchmark CCSD(T)/CBS (1) [35] and of the QMC calculation of Dubecký et al. [36] (2).
The second virial coefficient measures the first correction from the ideality of a real gas in the equation of state
where here ρ is the molar density of the gas. depends on the intermolecular potential and has the following expression [35]
where U is the intermolecular potential written in terms of the relative coordinates of the two methane molecules and corresponding to above and is the Avogadro’s number. The expression above does not include the quantum correction which is always positive and decreases very rapidly with the temperature; it is about 20 cm/mol at 100 K and about 2 cm/mol at 200 K [35]. can be accurately measured at room temperature and, hence, it provides a reliable reference to test a computed intermolecular potential. In this work, we have computed the intregral of Equation (23) by a one-dimensional grid along the C-C distance and by a Monte Carlo integration over all the other variables related to the relative orientations. In Figure 5, we compare our computed value from J-LGVB1 DMC calculation with the time step 0.01 a.u. at different temperatures with some experimental data and with the corresponding value computed from unmodified MP2 PES. From this comparison, we can see that the modified PES has a better agreement with experimental data [38,39,40,41,42,43] than that obtained directly from MP2 calculation. We believe that this result is promising for future development of this approach, although we must recognize that our extrapolated PES is based on only very few points computed at the highest level of calculation. On the other hand, the full calculation of a DMC PES is still not practicable, and our approach could be a suggestion for, at least, a preliminary study of a complex system like that made of interacting molecules.
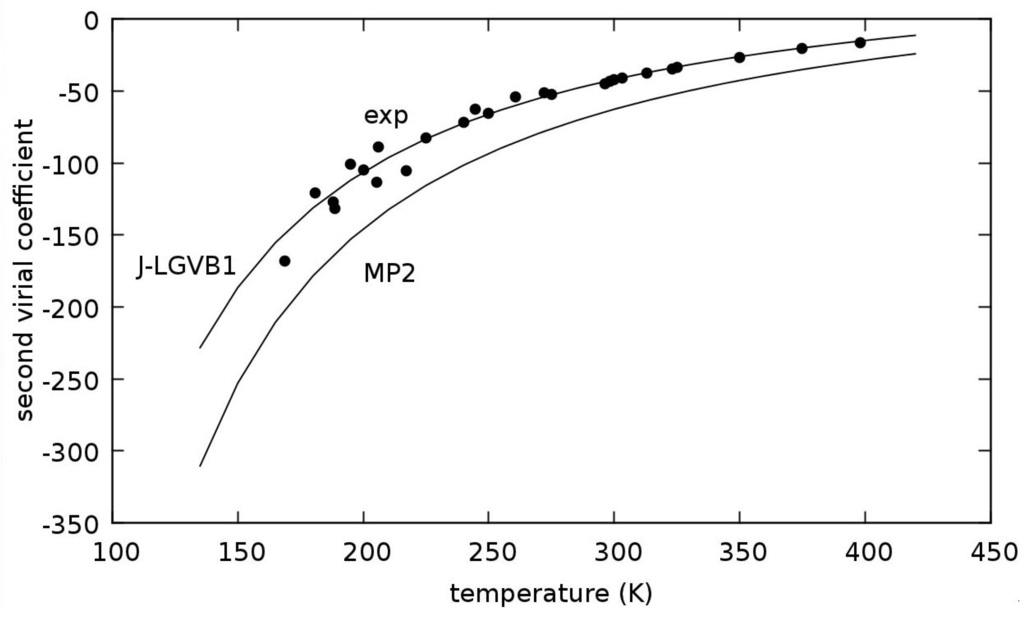
Figure 5.
Second virial coefficient (cm/mol) of methane as a function of temperature. Comparison between calculated (this work, solid line, and experimental values (circle, [38,39,40,41,42,43]).
4. Conclusions
A procedure to decompose the KS optimized orbitals with the aim of generating a new basis set specifically designed for QMC calculations is given. The proposed scheme preserves the initial KS orbitals in a localized form and adds new partner and external orbitals, also localized, which are capable of bringing information on electron correlation. The decomposition technique resorts to concepts that are commonly used in the analysis of the density like electron pair, connectivity and shell structure. By starting from an accurate electron density, the procedure allows the construction of a correlated wave function that is further optimized within a step of VMC computation. The functional form used in this context is taken from the J-LGVBn approach of Fracchia et al. [13]: it is compact, size-extensive and displays a better flexibility than that of a single determinant SJ wave function on Fermionic nodal structure. Finally, DMC is used to compute the energy. The method has been tested on some simple process namely, the fragmentation of hydrazine, the hydrogen transfer reaction between ammonia and OH radical and the formation the methane dimer.
For the reaction energy of the fragmentation of hydrazine, the previous result of Fracchia et al. [13] is reproduced as well as the experimental value within chemical accuracy [27]. The main achievement with respect to previous work is the great reduction of the number of variational parameters due to the information brought by the new basis set derived from KS orbitals. We pass from the 128 atomic orbitals of the full starting basis set to the new set made of only 36 localized orbitals.
For the hydrogen transfer, again the reaction energy of all best references, included Fracchia et al. calculations [31], is here reproduced within chemical accuracy. The two barrier heights, forward and reverse processes, show instead a slightly bigger deviation, namely 1.5 kcal/mol, but are in better agreement with high quality CCSD (T)/aug-cc-pvQZ calculations [31]. Probably, some improvement of our approach is needed for a better description of the localization of three electrons on three centers as found in the transition state of this reaction. In addition, in this case, we use only 39 localized basis functions instead of 148 atomic orbitals of the starting basis set.
Finally, for the methane dimer intermolecular complex, we have analyzed eight structures. We have been able to recover the intermolecular interaction energy within 0.1 kcal/mol of previous QMC [36] calculation and within statistical error of the literature benchmark CCSD (T)/CBS [35] data. We used 48 essentially two-center orbitals instead of the full basis set of 228 atomic orbitals. The data obtained with the J-LGVB1 wave function at the DMC level of calculation have been utilized to extrapolate a PES from standard MP2/aug-cc-pvTZ computation. The modified PES comes from a different mixing of HF and second order MP2 contributions based on a fit of DMC interaction energies. Both repulsive and attractive forces resulted as weakened in this transformation of the PES. The resulting PES has been further elaborated in order to be used through an analytical expression in the calculation of the second virial coefficient of gaseous methane. A plot is given with the dependence on the temperature. The agreement with corresponding experimental data [38,39,40,41,42,43] is much better then with the starting MP2 unmodified PES.
As a final remark, it is interesting to notice that, in the present approach, the electron density remains essentially the same in passing from KS to QMC. Of course, this is not rigorous but we can expect that, at least, both KS and QMC are able to provide a density better than HF and closer to the exact one. Under this assumption, if we look at the VMC model wave function as a partially interacting example of a link between the independent particle model of KS and the fully interacting case represented by DMC, we can argue that this point could have some relation with adiabatic connection. This point will be a matter of further study.
Supplementary Files
Supplementary File 1Acknowledgments
The authors acknowledge financial support from the University of Pisa (Fondi di Ateneo and PRA_2016_46).
Author Contributions
Claudio Amovilli conceived and supervised the work and wrote the paper. Franca Maria Floris and Andrea Grisafi performed calculations and contributed to the analysis of data and to the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fermi, E. Un metodo statistico per la determinazione di alcune proprietà dell’atomo. Rend. Accad. Lincei 1927, 6, 602–607. [Google Scholar]
- Thomas, L.H. The calculation of atomic fields. Proc. Camb. Philos. Soc. 1927, 23, 542–548. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Levy, M. Universal variational functionals of electron densities, first order density matrices and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; MacDougall, P.J.; Lau, C.D.H. Bonded and nonbonded charge concentrations and their relation to molecular geometry and reactivity. J. Am. Chem. Soc. 1984, 106, 1594–1605. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Reynolds, P.J.; Ceperley, D.M.; Alder, B.J.; Lester, W.A., Jr. Fixed-node quantum Monte Carlo for molecules. J. Chem. Phys. 1982, 77, 5593–5603. [Google Scholar] [CrossRef]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33–83. [Google Scholar] [CrossRef]
- Lüchow, A. Quantum Monte Carlo methods. WIREs Comput. Mol. Sci. 2011, 1, 388–402. [Google Scholar] [CrossRef]
- Austin, B.M.; Zubarev, D.Y.; Lester, W.A., Jr. Quantum Monte Carlo and Related Approaches. Chem. Rev. 2012, 112, 263–288. [Google Scholar] [CrossRef] [PubMed]
- Benedek, N.A.; Snook, I.K.; Towler, M.D.; Needs, R.J. Quantum Monte Carlo calculations of the dissociation energy of the water dimer. J. Chem. Phys. 2006, 125, 104302. [Google Scholar] [CrossRef] [PubMed]
- Fracchia, F.; Filippi, C.; Amovilli, C. Size-Extensive Wave Functions for Quantum Monte Carlo: A Linear Scaling Generalized Valence Bond Approach. J. Chem. Theory Comput. 2012, 8, 1943–1951. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Amovilli, C.; March, N.H.; Bogar, F.; Gal, T. Use of ab initio methods to classify four existing energy density functionals according to their possible variational validity. Phys. Lett. A 2009, 373, 3158–3160. [Google Scholar] [CrossRef]
- Edmiston, C.; Ruedenberg, K. Localized Atomic and Molecular Orbitals. Rev. Mod. Phys. 1963, 35, 457–465. [Google Scholar] [CrossRef]
- CHAMP is a Quantum Monte Carlo Program Package. Available online: http://pages.physics.cornell.edu/cyrus/champ.html (accessed on 5 February 2016).
- Burkatzki, M.; Filippi, C.; Dolg, M. Energy-consistent pseudopotentials for quantum Monte Carlo calculations. J. Chem. Phys. 2007, 126, 234105. [Google Scholar] [CrossRef] [PubMed]
- Dolg, M.; Filippi, C.; (University of Twente, Enschede, The Netherlands). Private communication, 2012.
- Kendall, R.; Dunning, T., Jr.; Harrison, R. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Casula, M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B 2006, 74, 161102. [Google Scholar] [CrossRef]
- Filippi, C.; Umrigar, C.J. Multiconfiguration wave functions for quantum Monte Carlo calculations of first-row diatomic molecules. J. Chem. Phys. 1996, 105, 213–226. [Google Scholar] [CrossRef]
- Umrigar, C.J.; Toulouse, J.; Filippi, C.; Sorella, S.; Hennig, R.G. Alleviation of the fermion-sign problem by optimization of many-body wave functions. Phys. Rev. Lett. 2007, 98, 110201. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.gaussian.com/ (accessed on 5 February 2016).
- Ruscic, B.; Pinzon, R.; Morton, M.; von Laszevski, G.; Bittner, S.; Nijsure, S.; Amin, K.; Minkoff, M.; Wagner, A. Introduction to Active Thermochemical Tables: Several “Key” Enthalpies of Formation Revisited. J. Phys. Chem. A 2004, 108, 9979–9997. [Google Scholar] [CrossRef]
- Karton, A.; Daon, S.; Martin, J.M. W4-11: A high-confidence benchmark dataset for computational thermochemistry derived from first-principles W4 data. Chem. Phys. Lett. 2011, 510, 165–178. [Google Scholar] [CrossRef]
- Zhao, Y.; Lynch, B.; Truhlar, D. Multi-coefficient extrapolated density functional theory for thermochemistry and thermochemical kinetics. Phys. Chem. Chem. Phys. 2005, 7, 43–52. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Hybrid Meta Density Functional Theory Methods for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions: The MPW1B95 and MPWB1K Models and Comparative Assessments for Hydrogen Bonding and van der Waals Interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
- Fracchia, F.; Filippi, C.; Amovilli, C. Barrier Heights in Quantum Monte Carlo with Linear-Scaling Generalized-Valence-Bond Wave Functions. J. Chem. Theory Comput. 2013, 9, 3453–3462. [Google Scholar] [CrossRef] [PubMed]
- Minnesota Database Collection. Available online: http://t1.chem.umn.edu/misc/database_group/database_therm_bh (accessed on 5 February 2016).
- Lynch, B.; Truhlar, D. What Are the Best Affordable Multi-Coefficient Strategies for Calculating Transition State Geometries and Barrier Heights? J. Phys. Chem. A 2002, 106, 842–846. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Hellmann, R.; Bich, E.; Vogel, E. Ab initio intermolecular potential energy surface and second pressure virial coefficients of methane. J. Chem. Phys. 2008, 128, 214303. [Google Scholar] [CrossRef] [PubMed]
- Dubecký, M.; Derian, R.; Jurečka, P.; Mitas, L.; Hobza, P.; Otyepka, M. Quantum Monte Carlo for Noncovalent Interactions: Analysis of Protocols and Simplified Scheme Attaining Benchmark Accuracy. Phys. Chem. Chem. Phys. 2014, 16, 20915–20923. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Kerl, K. Interferometric Determination of Mean Polarizabilities and Second Density Virial Coefficients of Methane Between 128 K and 890 K. Int. J. Phys. Chem. Ber. Bunsen-Ges. 1991, 95, 36–42. [Google Scholar]
- Trusler, J.P.M. The Speed of Sound in (0.8CH4 + 0.2C2H6) (G) at Temperatures between 200 K and 375 K and Amount-of-Substance Densities up to 5 Mol/dm3. J. Chem. Therm. 1994, 26, 751–763. [Google Scholar] [CrossRef]
- Ramazanova, A.E. Volumetric Properties and Virial Coefficients of (Water + Methane). J. Chem. Therm. 1993, 25, 249–259. [Google Scholar]
- Renner, C.A. Excess Second Virial Coefficients for Binary Mixtures of Carbon Dioxide with Methane, Ethane and Propane. J. Chem. Eng. Data 1990, 35, 314–317. [Google Scholar]
- Katayama, T. The Interaction Second Virial Coefficients for Seven Binary Systems Containing Carbon Dioxide, Methane, Ethylene, Ethane and Propylene at 25 °C. J. Chem. Eng. Jpn. 1981, 14, 71–72. [Google Scholar]
- Katayama, T. Interaction Second Virial Coefficients for Six Binary Systems Containing Carbon Dioxide, Methane, Ethylene and Propylene at 125 °C. J. Chem. Eng. Jpn. 1982, 15, 85–90. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).