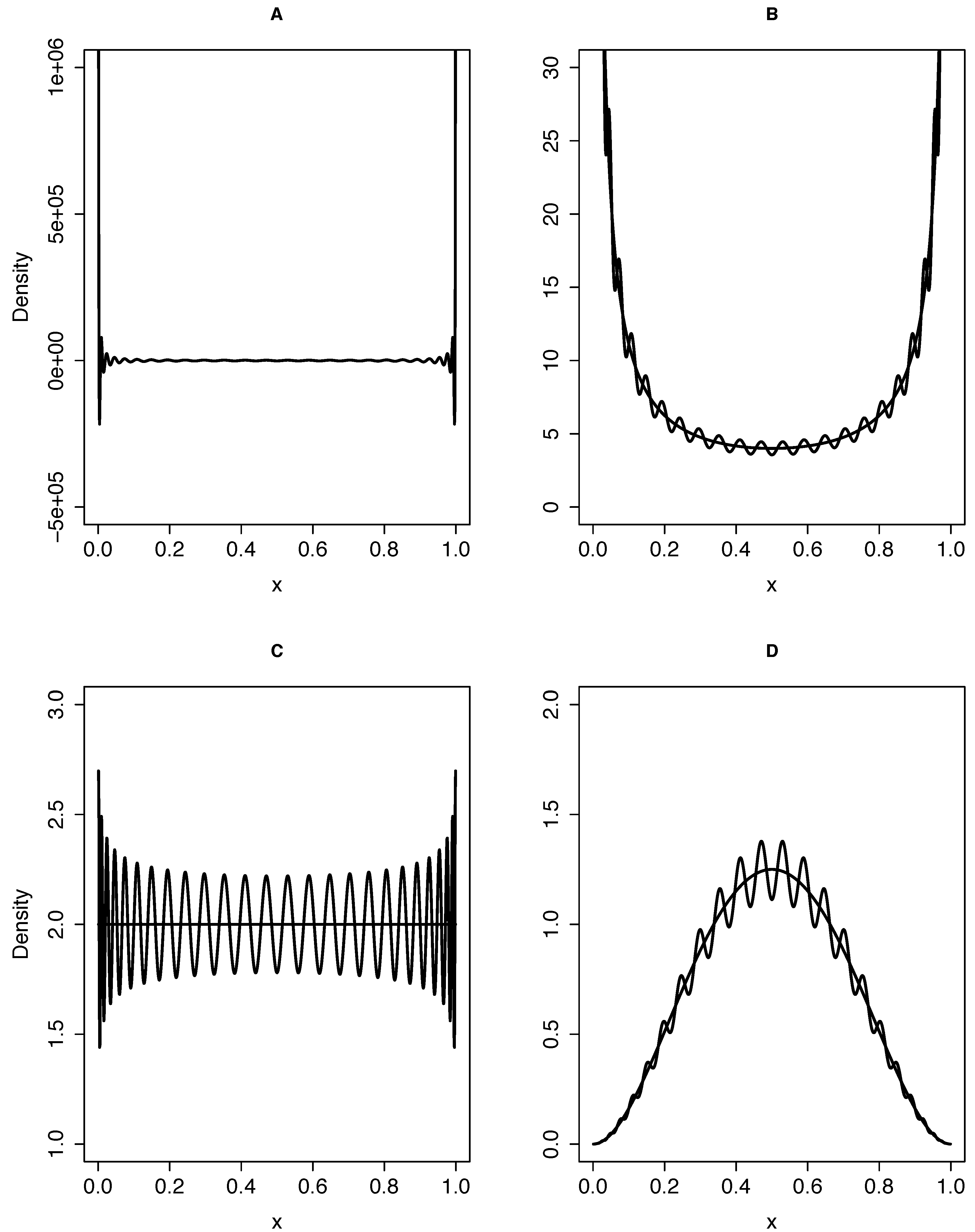
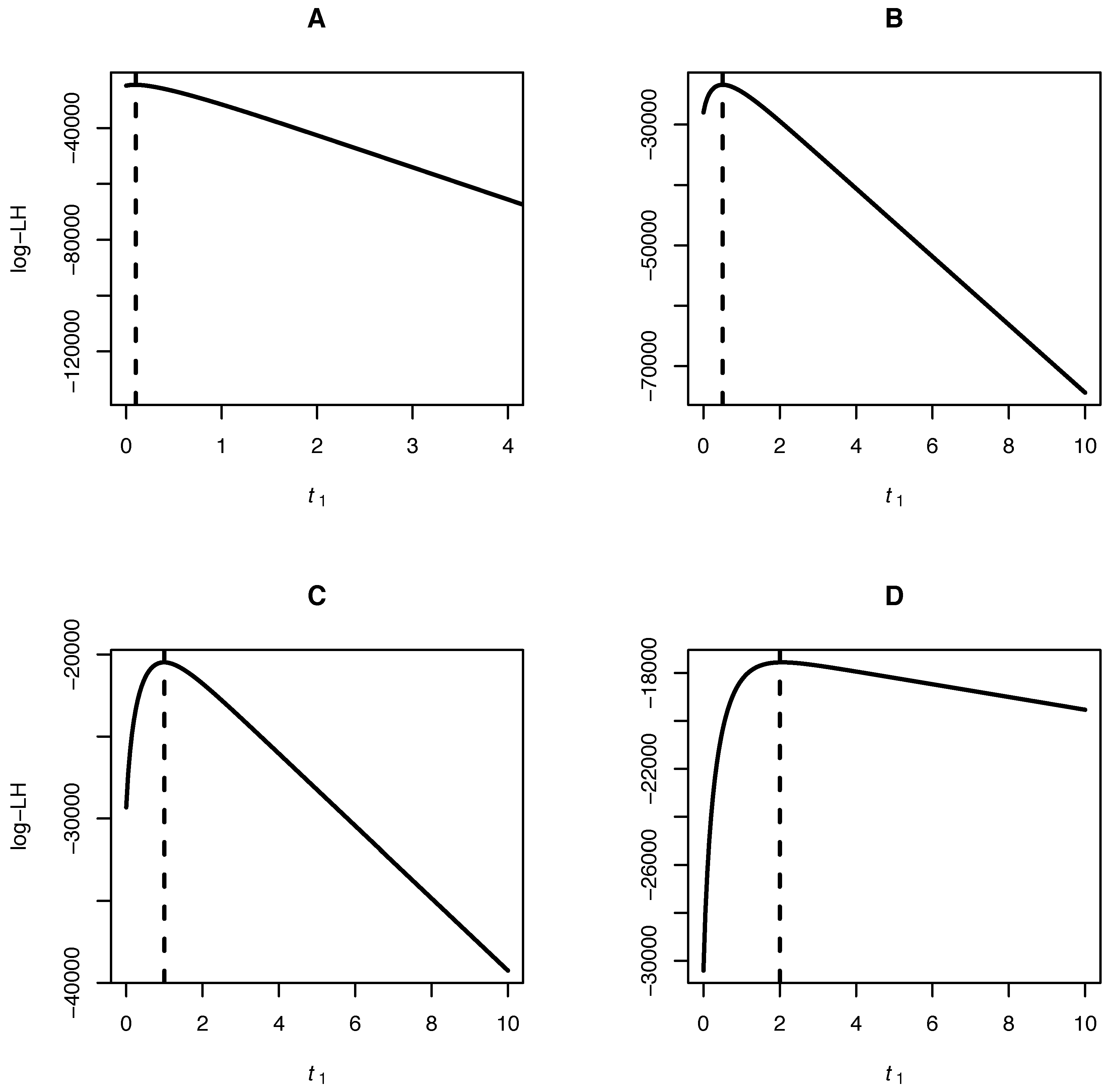
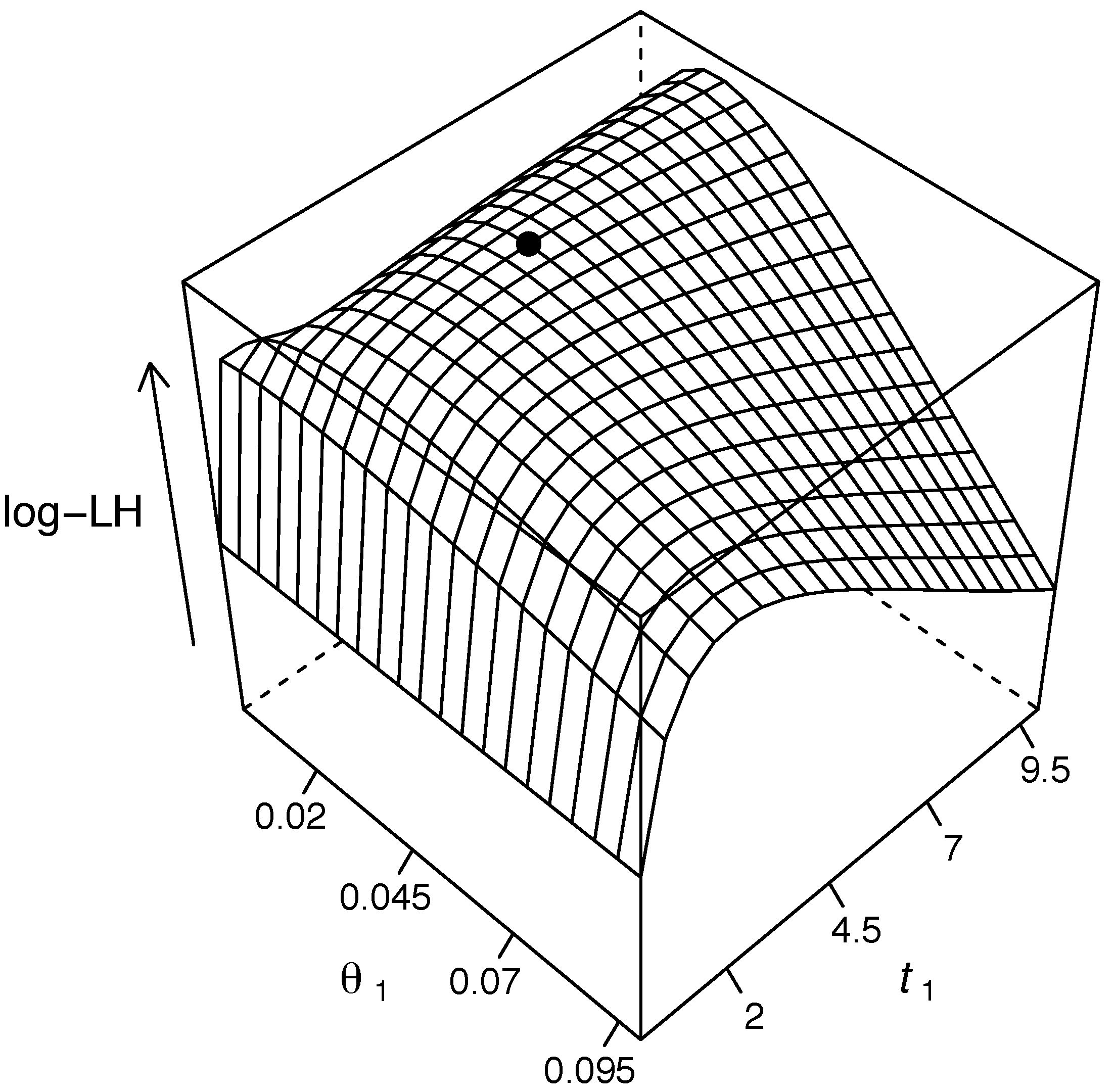
1. Introduction
Evolutionary forces, e.g., mutation, selection and genetic drift, shape DNA sequence information. Typically, the evolutionary processes that have influenced the data reach back millions of generations or years. Mathematical theory that describes these processes has been available for more than 80 years (e.g., [
1,
2]), yet inference of population genetic parameters using probabilistic models is difficult, and only few analytical maximum-likelihood estimators are available; those based on diffusion theory, so far, assume independence among sites and are briefly reviewed in Vogl [
3] and in the theory section below.
A DNA molecule is a string (or strand) of nucleotides (or sites) that usually pairs with a complementary strand to form a double-stranded chromosome. Pairing of sites is accomplished by hydrogen bonds between the complementary base pairs adenine (A) and thymine (T), on the one hand, and cytosine (C) and guanine (G), on the other. An assortment of chromosomes forms a genome, which is specific for a species. The main functional units of genomes are genes that often code for proteins. Proteins provide structure, catalyze metabolism or mediate physiological pathways in all living organisms. While the single-celled Bacteria and Archaea generally have compact genomes, genes of the more complex eukaryotic organisms are often interrupted by non-coding introns. Introns are spliced out, i.e., eliminated, during maturation of the messenger RNA, which is then translated into the chain of amino acids that makes up proteins.
A point mutation at a certain nucleotide or site creates a new genetic variant, i.e., an allele. Mutation is not strand-specific, but may be biased towards A or T (A/T) over C or G (C/G) or vice versa, because mutation rates between these two allelic classes may vary. Genome-wide sequence data may be made bi-allelic (binary), by considering A/T nucleotides as Allele 0 and C/G nucleotides as Allele 1. This simplifies mathematical analysis, such that maximum-likelihood inference becomes possible. Mutations introduce new variants into the genome and, thus, increase genomic variation. Conversely, stochastic fluctuations of the allelic proportion due to finite population sizes, i.e., random genetic drift, eventually cause fixation of an allelic type, thus eliminating variation. An equilibrium between mutation and drift may establish with time.
Recently, relatively inexpensive, high throughput DNA sequencing methods have made available population data from whole genomes (in multicellular organisms typically comprising sites), at least for humans and model species, such as fruit flies of the genus Drosophila. These data provide the basis for inference of population genetic forces, such as random genetic drift, the mutation rate scaled by the population size, directional selection and the time of the split between two populations.
In this article, we focus on inferring population genetic parameters using a mutation-drift model of the allelic proportion x. For mathematical convenience, genomic sites are classified as binary with respect to their nucleotide (C/G vs. A/T). A total of L sites are classified into categories, depending on the count y of Allele 1 (C/G) among M aligned genomic sequences. Together, these counts form a site frequency spectrum (SFS) of size with . Joint SFS may be constructed considering the allelic states of sites within a single population at two different time points or two related populations at a single time point.
The solution of the diffusion equation describing the evolution of
x conditional on mutation and drift parameters has previously been represented as a series expansion of orthogonal polynomials (e.g., [
5,
6,
7,
8,
9]). In this article, we extend the mathematical theory to a boundary-mutation model [
4], which describes the evolution of
x when the scaled mutation rate
θ is small,
i.e., on the order
or smaller [
10]. Using this model, a method for the inference of
θ and the time of split
t is derived and applied to both simulated and empirical
Drosophila population data. The empirical data are joint SFS of short introns, as the nucleotide composition of this site class is considered to not be affected by selection, but only by the joint forces of mutation and drift [
11,
12,
13]. Therefore, the study of these sites likely provides an accurate estimate of the population demography and the genome-wide scaled mutation rate. The joint SFS from a sample of six individuals from the Malawian
D. melanogaster population [
14] and the
D. sechellia reference sequence (Release 1.0; [
15]) is used to infer mutation and drift parameters.
1.1. Inference with a Single Site Frequency Spectrum Assuming Equilibrium
Assume that a sample of L genomic loci or sites is available for M haploid individuals. The sample space of the allelic count for each locus l is then copies of Allele 1, with . In regions of high recombination rates relative to mutation rates, sites may be assumed to be independently and identically distributed, such that the probabilities given the model parameters of all L sites can be multiplied. In this case, the theory developed below can be considered maximum likelihood. In regions of relatively low recombination rates, estimators are still consistent and may be considered a composite likelihood. For notational convenience, the index l is often dropped in the following.
1.2. Inference Based on the Beta Equilibrium Distribution
In a classical study, Wright [
2] proposed a model for the evolution of a bi-allelic locus under the influence of the population genetic forces: mutation, directional selection and drift. He also derived the equilibrium distribution of the allelic proportion, conditional on the scaled mutation rate, the mutation bias and the scaled strength of directional selection. In the absence of selection, the equilibrium distribution of the population allelic proportion
x of Allele 1 is a beta:
where
α is the mutation bias towards Allele 1 and
and
θ the overall scaled mutation rate,
i.e., the product of the per-generation mutation rate
μ and the effective population number or size
N.
Conditional on
x, the distribution of the allelic count
y is assumed to be binomial. Especially with genome-wide samples, the allelic proportions at particular sites are not interesting and “integrated out”, which leads to the beta-binomial distribution of the allelic count:
Given a sample of
L independent loci for
M individuals for each locus and a common
α and
θ, let
represent the counts of sites with
y alleles of Type 1. Set
. The likelihood is then:
For arbitrarily large values of
θ, only iterative algorithms have been derived to obtain maximum likelihood estimates of
α and
θ [
3], even in the simple case without selection. Note that this model corresponds to the canonical model of the empirical Bayes method, and maximizing this marginal likelihood corresponds to a parametric empirical Bayes approach [
16].
In the limit of small
θ, the beta-binomial compound distribution (2) can be expanded into a Taylor series in
θ at
, up to first order. The “folded” site frequency spectrum (folded SFS) is derived from the general site frequency spectrum by lumping the samples
with
, such that the state space becomes
per locus. For a polymorphic sample of such a folded SFS, the Taylor series expansion in
θ of the beta-binomial compound distribution has been derived by RoyChoudhury and Wakeley [
17]. In the general situation with
, the series expansion of the beta-binomial compound distribution leads to the general “RoyChoudhury–Wakeley” distribution [
3]:
With this first order expansion of the beta-binomial in
θ, approximate maximum likelihood (ML) estimators of
α and
θ and their posterior distributions can be obtained easily [
3]. In particular, the approximate ML estimator for the scaled mutation rate is:
where
and
,
i.e., the sum over all polymorphic sites in the sample, while the approximate ML estimator for
α is:
If the boundary mutation model is assumed, these estimators are maximum likelihood, rather than approximations in the limit of small-scaled mutation rates
θ [
4].
1.3. Inference Based on the Assumptions of Equilibrium and Rare Mutations
The estimator
of Formula (5) is a variant of the well-known Ewens–Watterson estimator of the scaled mutation rate [
18,
19],
. The latter was originally derived assuming the infinite sites model [
20,
21], which in turn was based on a model with irreversible mutation [
2]. With the infinite sites model, infinitely many sites may be hit by mutation at a finite rate, such that each site is hit only once [
19,
21]. Furthermore, it is usually assumed that the ancestral and derived allelic states can be inferred with outgroup information,
i.e., with information from closely-related species or populations (e.g., [
12,
13,
22,
23,
24]). Then, segregating mutations are assumed to only arise once from the ancestral background. Alleles at a site are thus not defined as having bases A/T
versus C/G, but as being ancestral
versus derived. Note that the factor of two difference between
of Formula (5) and the Ewens–Watterson estimator reflects that mutations arise from both boundaries in the former and only one boundary in the latter. Obviously, the mutation bias cannot be inferred with polarization. Yet, irrespective of whether or not data are polarized, a polymorphic site is scored as polymorphic.
The Ewens–Watterson estimator is generally unbiased. If sites are unlinked, it can be shown that it is also the maximum likelihood estimator of
θ and, thus, a sufficient statistic (e.g., [
3]). Ewens [
18] neglected to show this explicitly, while he earlier showed that the estimator for the corresponding infinite alleles model is maximum likelihood [
25]. Furthermore, it can been shown that the estimators are unbiased (e.g., [
3,
18]). Note that if assumptions are met,
corresponds to the “expected heterozygosity”,
i.e., the expected proportion of polymorphism in a sample of size
.
Similar to the infinite sites model, applications of the Poisson random field (PRF) model to population genetics generally assume small mutation rates. The PRF theory is often based on irreversible mutation models and, like the infinite sites model of Kimura [
21], usually assumes the presence of directional selection. For an equilibrium distribution to exist, an inexhaustible and unvarying supply of sites must be assumed. Furthermore, the ancestral state of all sites must be known without errors and conditioned on. This is because, as discussed above, the rates of mutation from A/T to C/G generally differ, and the force of directional selection is reversed if an A/T mutates to a C/G or
vice versa. The above assumptions are not met with real datasets: genomes are finite, and inference of the ancestral state is error-prone. Nevertheless, if appropriate outgroup information is available and quasi-equilibrium is assumed, the approach is sensible [
26,
27,
28,
29].
While RoyChoudhury and Wakeley [
17] also use the PRF approach, they do not assume outgroup information, but rather start from a Taylor series expansion in
θ of the equilibrium beta distribution Equation (
1). As shown above (Equation (5)), the estimator RoyChoudhury and Wakeley [
17] derived is essentially identical to the Ewens–Watterson estimator of
θ. Starting from a Moran model that only allows for mutations from the boundaries, Vogl and Clemente [
10] derive a generalization of the estimator also for the case with directional selection, without assuming outgroup information. Vogl and Bergman [
4] derive ML estimators for all three parameters: mutation bias
α, scaled mutation rate
θ and scaled selection strength
γ, with the same assumptions, but base the analysis on a diffusion model.
2. Mathematical Theory and Algorithms
The Ewens–Watterson estimator
[
18,
19] or its varieties are sufficient statistics for the analysis of site frequency spectra assuming the infinite sites model, equilibrium and unlinked sites. With real datasets, however, changes in demography or mutation parameters usually invalidate the equilibrium assumption. Moreover, the approach to equilibrium is dominated by the scaled mutation rate
θ. Since
θ is often on the order of
per unit of diffusion time, which is scaled in
N generations, it takes on the order of
generations to reach equilibrium. This is on the order of
generations. Even with the short-lived fruit flies, equilibrium is thus usually not reached before a change in population demography, the selection regime or the mutation bias. For probabilistic analysis of datasets that have not yet reached equilibrium, calculation of transition probabilities or densities is necessary. This is also necessary for joint site frequency spectra, where samples are drawn from a single population at two different time points or two closely-related populations at a single time point, which we will present in this article.
Consider a population of haploid population size
, where
t is time. The dynamics are governed by only two population genetic forces: mutation and drift. Generally, the diffusion limit,
i.e.,
, is considered such that, at each time point only two quantities matter: the scaled mutation rate
and the mutation bias
. Let
denote the proportion of the first allelic type, which in our case may be identified with the proportion of C/G at this site in the population at time
t. Assume now that the parameters
,
and
are piecewise constant and consider only a single such epoch of constant parameters. Usually, the following forward operator is obtained [
3,
30]:
The corresponding forward diffusion or Kolmogorov equation is:
where
is the transition density of the allelic proportion
x at any time
t. To solve this equation, Song and Steinrücken [
7] employ a series expansion with the modified Jacobi polynomials:
where
are the classical Jacobi polynomials [
31]. Note that Song and Steinrücken [
7] primarily analyze the backward diffusion equation (but also use the forward diffusion equation in the section: “Empirical Transition Densities and Stationary Distributions”). However, the relationship between the adjoint backward and forward diffusion equations is such that adaption of the theory concerning the backward equation to the forward equation is minimal (compare [
9]).
2.1. The Boundary-Mutation Model
Further in the text, we will follow Vogl and Bergman [
4] and model mutations as only affecting the boundaries. Then,
must be interpreted as a generalized probability measure that integrates to one over the unit interval, but may contain point masses at the boundaries (compare [
32]). Within the polymorphic region,
, the dynamics are purely governed by drift, such that the diffusion generator is:
and the corresponding Kolmogorov forward (or forward diffusion) equation is:
Mutations are assumed to arise at the boundaries and correspond to a transition from to , for a mutation from A/T to C/G, or from to , for a mutation from C/G to A/T.
The Wright–Fisher model is most familiar to population geneticists. With this model, the transition between subsequent generations due to drift is modeled via binomial sampling, such that transitions between distant states are possible. The slightly less familiar Moran model only allows transitions between neighboring states, which simplifies the math. This simplification pertains also to the boundaries [
4]. With the boundary-mutation model, mutations are assumed to arise only at the boundaries; a transition from
to
corresponds to a mutation from a monomorphic state with only A/T to a polymorphic state with a single C/G in the population; conversely, a transition from
to
corresponds to a mutation from C/G to A/T. The reverse transitions from the polymorphic region to the boundaries at
and
are caused by drift. In particular, the flow from
towards zero is proportional to drift times the probability mass at
, and similarly at the other boundary.
With a change from the Moran to the diffusion model, the formulas for the flow towards the boundaries due to drift are:
where the sign of the flow represents the direction. Conversely, the mutational flow from the boundaries to the interior is given by:
2.2. Modified Gegenbauer Polynomials
We will first analyze the situation without mutations,
i.e.,
. With pure drift, the transition density
can be expanded into a series of Gegenbauer polynomials (e.g., [
5,
7,
8,
9,
33]). Define:
where the
are the modified Gegenbauer polynomials of Song and Steinrücken [
7], and the
correspond to the classical ultraspherical or Gegenbauer polynomials with
([
31], Chapter 22), also used by Kimura [
5] and Tran
et al. [
8]. The forward and backward diffusion generators are adjoint, such that the modified Gegenbauer polynomials from Song and Steinrücken [
7] can also be used to solve the forward diffusion equation. Multiplication of the weight function
and
in (14) transforms a solution of the backward equation into that of the forward equation (compare [
9]).
The first two polynomials are
and
; the recurrence relation to calculate all other polynomials is [
7]:
The
solve the differential equation:
with:
The
are orthogonal with the weight function:
and the proportionality constant:
A function
defined within
can be represented by an expansion of the
. The coefficients
can be calculated using:
2.2.1. Solution of the Pure Drift Forward Equation with Gegenbauer Polynomials
Substituting
, where
is a function pertaining to the temporal part of the transition density, into the diffusion Equation (11) leads to:
For each
i, we have:
which can be rearranged to:
Observing Equation (16), we obtain the eigenvalue equations:
As stated above, the
solve the spatial differential Equation in (24) for each
i, while
solves the temporally homogeneous, linear differential Equation in (24). The
depend on the starting conditions and can be obtained from Formula (20). Since any function in
can be represented by
,
solves the diffusion Equation (11) for any starting condition.
Integrating (16) from zero to one for the symmetric eigenvectors with even
i, we obtain:
Note that, for odd i, we have , such that , , and . Equation (26) is therefore trivially true for odd i.
Following Kimura [
5], we substitute
into the differential Equation (11) and integrate from zero to one observing Equation (26):
As in the temporal part of Formula (24), substituting
solves the system of differential equations:
For even i, the flow out at the boundaries zero and one per unit time is symmetric and corresponds to what is present just inside the boundaries, i.e., and . The rate of loss is the eigenvalue .
Now, multiply
with
x and integrate again from zero to one:
Thus,
will eventually drift to Boundary 1, and conversely
to Boundary 0. This is expected, since drift is symmetric, such that the probability of eventual fixation is equal to the proportion
x, for the boundary at one, and
, for the boundary at zero (see also [
30], Chapter 4.3). As in the temporal part of Formula (24), substituting
solves the system of differential Equations (28).
The solution of the diagonal system of differential Equations (28) thus fulfills Equation (11) for all t, as well as the boundary conditions at both zero and one (12).
The above results suggest augmenting the
with the boundary terms:
Furthermore, the result (30) shows that the boundary terms derived above correspond to those defined by Tran
et al. [
8].
We therefore define the following set of orthogonal polynomials augmented with boundary terms:
where
is the Dirac delta function (compare Tran
et al. [
8], who arrive at the corresponding set of augmented eigenfunctions). With this definition of eigenfunctions, the probability mass that leaves the polymorphic region for each
i at
and
is added to the monomorphic boundaries at
and
. The integral over the closed interval between zero and one thus remains unity for all times. In
Appendix A.1, we show that these augmented orthogonal polynomials can also be obtained by a Taylor series expansion of the general eigensystem solving the diffusion Equation (11) using the modified Jacobi polynomials
.
2.2.2. Starting and Prior Distributions
We base the following description on the theory of hierarchical Bayesian models and the empirical Bayes method [
16] that we also employed earlier [
3,
4]. In a frequentist context, one would rather use the context of marginal likelihoods.
Traditionally, a Dirac delta function at a certain position
p has been used as a starting condition [
33]. With a site frequency spectrum, however, the joint density of the population allelic proportion
x and the observed allelic count
y in a sample of size
must be used as starting density. Most naturally, the conditional distribution of the data
y given the allelic proportion
x is modeled as a binomial:
With the pure drift model, we are generally interested in the polymorphic region, since probability mass at a boundary remains there due to the absence of mutations.
For “integrating out” the population allelic proportions
x, a prior distribution for
x must be assumed. With small-scaled mutation rates, an “improper prior” proportional to
within
and
is appropriate, as this is proportional to the equilibrium distribution (see also
SubSection 2.3.4 and
Section 2.3.5 below). Note that this prior corresponds to the inverse of the weight function. Thus, the inner product (20) to calculate the initial coefficients becomes:
where the limit notation indicates that the integration includes only the polymorphic region,
i.e., no point masses at the boundaries.
We can thus specify a general algorithm that also includes the boundaries.
2.2.3. Algorithm 1: Allelic Proportions x with Pure Drift for All Times t, Conditional on Initial Values
A measure
between zero and one, which may have point masses
and
at Boundaries 0 and 1, is represented by an expansion of the
up to
. The coefficients
are calculated according to Equation (34). The expansion of
times the prior, up to the order
n, is then:
The solution of Equation (28) for all
t conditional on the initial distribution can be represented by a series expansion up to
n:
with
.
Note that the contain the boundary terms that balance the probability masses at zero and one. This is obvious if the initial probability measure does not contain point masses at the boundaries, i.e., if .
2.3. Modified Gegenbauer Polynomials and the Boundary-Mutation Model
In this subsection, we will use the expansion in orthogonal polynomials with boundary terms to model both mutation and drift.
2.3.1. Mutation and Drift: Slowly Evolving Dynamics
For the slowly evolving dynamics at the boundaries, we augment the system with two eigenfunctions. Starting from the system for general
θ, which can be expanded in a series of modified Jacobi polynomials (see Equation (9) in Song and Steinrücken [
7]), we note that the eigenfunction for
does not change with time,
i.e.,
. The eigenfunction for
has the eigenvalue
(compare: [
7]) and reflects the slow change in allele frequencies through mutation. Expressing the Jacobi polynomials as beta distributions and taking the limit
, such that only probability masses at the boundaries remain, the first two eigenvectors become:
(see
Appendix A.1). Obviously, these two eigenfunctions are unaffected by the dynamics in the polymorphic region inside
.
These two eigenvectors have no probability mass within the polymorphic region, such that only eigenvectors with
have nonzero probability masses in the polymorphic region. Hence, the model separates two spatial regions: the monomorphic boundaries and the polymorphic interior. As
while the
for all eigenvalues with
, two different temporal regions can also be distinguished, in addition to the two spatial regions. Thus, evolution is modeled as a two-time process, where the slow dynamics captured by the eigenfunctions
and
are evolving independently from the polymorphic region, while the fast dynamics in the polymorphic region are in quasi-equilibrium with the slow dynamics at the boundaries. Generally, we are thus looking at a system of differential equations that for the slowly evolving part of the system is:
Initially at
, the boundary values are
and
. The solution over time is
, such that the boundary values will slowly, at a rate of
θ, approach the equilibrium values:
If does not integrate to one, i.e., , modifications are trivial. Note that and correspond to the probability mass currently at the boundaries plus the part of the probability mass within the polymorphic region that is expected to be fixed by drift (i.e., without any further mutations) at the respective boundaries. They would only be identical to the probability mass currently at the boundaries if there were no probability mass in the polymorphic region.
2.3.2. Mutation and Drift: Quickly Evolving Dynamics
The slowly evolving part of the system is given in (39). For the quickly evolving part, note that, from Equation (13), mutation moves probability mass from the boundary at zero
to
and from
to
, respectively. We can model this with a Dirac delta function at
and
:
with
and
as above. Combined with the pure drift diffusion Equation (11), we thus obtain the following diffusion equation within the interval between
and
:
Equation (41) is an extension of Equation (21) to mutations from the boundaries.
2.3.3. Mutation and Drift: Slowly and Quickly Evolving Dynamics
Theorem 1. Starting from a generalized probability measure within the unit interval (Equation (11)), with the boundary Conditions (12) and (13), and letting , the following function provides the general solution for all times of the Kolmogorov forward equation of boundary-mutation drift diffusion:with the previously-defined eigenfunctions (Equations (37) and (32)); the are given by a system of linear inhomogenous first order differential equations:The starting values, for , are given by the initial probability masses at the boundaries and by the expansion of the initial density in the interior into the eigenvectors. Proof. The slowly evolving part of the system is given in (39). The coefficients for expanding the delta function in (40) are (compare Equation (20)) for the boundary at zero:
and similarly for the boundary at one. Substituting the Gegenbauer expansion into Equation (41), we obtain:
For each
i, we have:
which can be rearranged to:
Observing Equation (16), we obtain eigenvalue equations corresponding to those in (24):
Compared to the case without mutation, the spatial part is unchanged, while the temporal part becomes a system of linear inhomogenous first order differential equations:
All other considerations correspond to the case without mutation. □
Note that, substituting
and
, Equation (49) can also be written as:
with constants:
Furthermore, note that we assumed that the probability measure integrates to one over the closed interval between zero and one, i.e., . If this is not the case, the constants and must be multiplied by .
2.3.4. Boundary-Mutation-Drift Equilibrium Distribution
In earlier work [
4], we show that the equilibrium solution of the boundary-mutation model is the measure:
where the interior region is bounded by
and
and
stands for boundary-mutation equilibrium.
integrates to one over the unit interval, irrespective of
N. However, note that for large
N, it integrates to more than one inside the interval
, while assuming negative values at the boundaries. In this limit, it therefore must be considered an “improper distribution” [
4,
34].
In
Appendix A.2, we show that, with time, Solution (43) converges to the BME (Equation (52)).
2.3.5. Prior Distribution
With the BME as prior and a binomial likelihood
with
, the coefficients of the joint distribution
become:
where the limit notation indicates that the integration includes only the polymorphic region. Note that already Ewens used the same limit for inference [
18,
25]. For polymorphic data,
i.e.,
, this function is a polynomial and, thus, can be represented accurately as a series of Gegenbauer polynomials as long as
. The boundary terms can also be derived easily because the probability of drifting to boundary one corresponds to the current proportion
x (and to
to the boundary zero), such that:
where the limit notation is not used for brevity.
For monomorphic
y,
i.e.,
or
, the
for the probability mass in the interior are also given by Equation (53) with
. The corresponding boundary terms are:
and analogously for
.
2.3.6. Algorithm 2: Allelic Proportions x with Boundary-Mutations and Drift for All Times t, Conditional on Initial Values
The interior of a joint distribution is represented as a Gegenbauer series (53).
The slowly evolving part of the system consists of the dynamics at the boundaries. Set the boundary terms at to and as in Equations (54) and (55). With time, the boundary terms and then change slowly at the rate of θ according to the exponential function in Equation (39).
Set
. The solution of Equation (41) for all
t conditional on
can be represented by a series expansion up to
n:
with:
and constants analogous to (51):
Equation (57) is a solution to (50), as can be shown by substitution.
4. Discussion
Most population genetic models, e.g., the Wright–Fisher and Moran models and the corresponding (forward) Wright–Fisher or Moran diffusion models, do not restrict the number of mutations segregating in a population at a given site and time. By contrast, most population genetic methods that allow for analytical maximum likelihood estimators assume that variation at a specific site originates from only a single mutation, such that no more than two alleles can be present at any given site and time. This assumption is made for the Ewens–Watterson estimators of the scaled mutation rate [
18,
19] and the Poisson random field (PRF) models [
26,
27,
28,
29]. These approaches thus implicitly assume low scaled mutation rates. Usually, it is also assumed that the ancestral state of a site is known. Both of these assumptions are made explicit with the infinite sites model. When introducing the infinite sites model, Kimura [
20,
21] assumed selection against the mutant allelic variant, such that only the favored ancestral allele would exist in the monomorphic state, while a mutant allele is eventually lost from the population by the joint action of adverse selection and drift. Kimura based the mathematics on a model of irreversible mutation [
2].
In later developments of the infinite sites model [
18,
19], the assumption of selection was dropped. Without selection, sites may become monomorphic for all possible allelic states (usually two states are assumed, such that the model is bi-allelic). In practical applications, the ancestral state has to be inferred via “outgroup” information. For this inference, which is also called “polarization”, data from an extant closely related population or species,
i.e., an “outgroup”, are used (e.g., [
12,
13,
22,
23,
24]). Polarization can only be successful if the outgroup is related closely enough to the focal population, such that double mutations are improbable, but distantly enough, such that allelic polymorphism is not shared with the focal population. These biological assumptions are rather restrictive.
With unrestricted mutations,
i.e., with the assumptions of the Wright–Fisher diffusion or the Moran models, allelic proportions in a population converge to a beta equilibrium distribution. For a sample of moderate size, a beta-binomial equilibrium distribution is obtained. It seems that RoyChoudhury and Wakeley [
17] were the first to expand the beta-binomial equilibrium distribution into a Taylor series up to first order in the scaled mutation rate
θ to derive the sample distribution of a bi-allelic locus. With this approach, polarization is not necessary. Rather, DNA sequence data can be made binary by grouping together sites with the bases adenine (A) and thymine (T) to A/T and cytosine (C) and guanine (G) to C/G. In spite of this difference of the original infinite sites model, the sample distribution of polymorphic sites is a variant of the infinite sites model [
18], and the maximum likelihood estimator of the scaled mutation rate derived from this distribution is a variant of the Ewens–Watterson estimator. Based on the Moran model, Vogl and Clemente [
10] arrived at the same distribution of polymorphic sites if mutations only occur at the monomorphic boundaries. A Moran model with mutations only at the boundaries approximates a Moran model with mutations at any allelic state sufficiently well if the scaled mutation rate
θ is below 0.1 [
10]. Obviously, the critical assumption that allows for analytical derivation of the maximum likelihood estimator is not that the ancestral state is known, but rather that only a single mutation segregates. Indeed, without selection equivalence of the estimators derived from the Taylor series expansion in
θ of the general mutation model, estimators assuming the boundary mutation model can be shown [
4]. In the latter case, the ML estimators can be considered exact. Note that mutation bias has generally been ignored when analyzing DNA sequence data. In contrast to the usual infinite sites model, which assumes that ancestral and derived states can be inferred, a mutation bias
α creating an imbalance between A/T and C/G sites can be modeled naturally with our approach. As deviations in the A/T:C/G ratio from 1:1 are generally observed and as inference of ancestral states is difficult, such theory is practically useful. Vogl [
3] derived a maximum likelihood estimator for not only the scaled mutation rate
θ, but also the mutation bias
α.
Computation-intensive, probabilistic methods for estimating population genetic parameters, such as the ones implemented in the LAMARC software package [
38], are suitable for the analysis of populations governed by non-equilibrium dynamics. Our method also considers non-equilibrium population dynamics, such as changes in the effective size of the population, the mutation rate and mutation bias between different time points, but poses less computational burden. This is achieved by extending the boundary mutation model [
4] to joint site frequency spectra and using modified Gegenbauer polynomials to solve the transition density
of the allelic proportion
x at any time
t. If these model assumptions hold, the method also provides maximum likelihood estimates.
Gutenkunst
et al. [
39] estimate migration rates, selection coefficients and split times from joint site frequency spectra in their program
by approximating the diffusion process using a numerical grid of population proportions
x. Influx of mutations is modeled by “injecting
ϕ density at low frequency in each population (at a rate proportional to the total mutation flux
θ)”. This presumably corresponds to the boundary mutation model, but seems to assume influx in equal proportions from the boundaries. Furthermore, this method is directed towards evaluating population sizes, growth rates and migration rates from joint site frequency spectra, rather than scaled mutation rates. The difference in mutation rates of the different allelic classes,
i.e., mutation bias, is not taken into account.
With mutations arising only at the boundaries, evolution of the allelic proportion
x separates into a slowly evolving part, where the proportions of alleles at the boundaries change at a rate of
θ, while the interior dynamics adjust relatively quickly to the slowly evolving boundary proportions. This process leads to a system of inhomogeneous linear differential equations. With this theory, changes in the parameters,
i.e., the scaled mutation rate
θ or the mutation bias
α, do not necessitate a recalculation of the eigensystem, unlike the approach described in Song and Steinrücken [
7]. Thus, our approach speeds up computation, such that more complicated population genetic scenarios may be modeled, e.g., growing or shrinking population sizes that are commonly observed in nature. Since the equilibrium is reached at the rate of the scaled mutation rate
θ, natural populations are rarely in equilibrium, and non-equilibrium dynamics need to be considered when inferring population genetic parameters.
We note that Evans
et al. [
40] also arrived at a system of inhomogeneous linear differential equations assuming the infinite sites model as defined above. Furthermore, they assume directional selection. Their analysis is based on iteration of moments, rather than on orthogonal polynomials, which leads to a recursive inhomogeneous system of differential equations. Nevertheless, the similarities between their and our approaches are readily apparent. In a follow-up study, Zivkovic
et al. [
41] apply their algorithm to human and fruit fly data.
So far, we have only discussed approaches based on the Kolmogorov (or diffusion) forward or backward equations. Another approach successfully employed for analyzing joint site frequency spectra is based on Kingman’s coalescence [
42,
43]. With the coalescence, the starting point is the sample. Inference proceeds by summing and integrating over the sample’s genealogical history. It is also possible to derive the beta-binomial equilibrium distribution with the coalescent. In more complicated cases, one or the other of the two approaches may be more suited. Generally, the coalescence seems preferable if the sample distribution can be derived fairly easily compared to the population distribution. This is the case for the infinite sites model without recombination, where only the coalescence approach has been used to derive joint site frequency spectra, as far as we are aware. Recently, Chen [
44,
45] and Kamm
et al. [
46] improved the computational efficiency of the coalescence approach to joint site frequency spectra. We note that changes in the mutation bias, as incorporated into our approach, have not yet been incorporated into the coalescence approach.
Our algorithm allows for inference of the mutation bias α, the scaled mutation rate θ and the time separating the samples of joint site frequency spectra. A fruit fly dataset consisting of a joint site frequency spectrum of two Drosophila species is analyzed to illustrate the method.
5. Conclusions
In this article, we present a method for inferring population genetic parameters from joint site frequency spectra,
i.e., from allelic frequencies at two (or more) time points. The parameters inferred are the time between the samples
t and the mutation rate
θ, scaled by the (effective) population size
N. In contrast to earlier approaches [
7,
47,
48], we assume a small mutation rate
θ, such that only a mutation of single origin may segregate per site at any given time point in a sample. This assumption simplifies the mathematical treatment because, unlike with earlier approaches, changes in the parameters do not lead to a change in the eigensystem. Rather, the spatial expansion in orthogonal polynomials, specifically in Gegenbauer polynomials, remains unaffected. Compared to the case without mutations,
i.e., to the pure drift model, the temporal part changes from a system of homogeneous to one of inhomogenous linear differential equations. In effect, the system separates into the slowly evolving boundaries, which change at a rate of the scaled mutation rate
θ, and a fast evolving interior polymorphic region, which changes at the rate of drift, conditional on the dynamics at the boundaries. We show that the eigenvectors can be derived from the general Jacobi polynomials by a Taylor series expansion. Furthermore, the equilibrium distribution corresponds to the Taylor series expansion of the equilibrium distribution for general
θ. Due to the underlying boundary mutation model, parameter estimation is computationally efficient, and the method can be expanded to accommodate analysis of more complex population genetic scenarios.