Abstract
The real and imaginary parts of the complex refractive index of SixNyHz have been calculated from first principles. Optical spectra for reflectivity, absorption coefficient, energy-loss function (ELF), and refractive index were obtained. The results for Si3N4 are in agreement with the available theoretical and experimental results. To understand the electron energy loss mechanism in Si-rich silicon nitride, the influence of the Si/N ratio, the positions of the access Si atoms, and H in and on the surface of the ELF have been investigated. It has been found that all defects, such as dangling bonds in the bulk and surfaces, increase the intensity of the ELF in the low energy range (below 10 eV). H in the bulk and on the surface has a healing effect, which can reduce the intensity of the loss peaks by saturating the dangling bonds. Electronic structure analysis has confirmed the origin of the changes in the ELF. It has demonstrated that the changes in ELF are not only affected by the composition but also by the microstructures of the materials. The results can be used to tailor the optical properties, in this case the ELF of Si-rich Si3N4, which is essential for secondary electron emission applications.
1. Introduction
Silicon nitrides are commonly used for high-temperature and high-endurance applications due to their excellent mechanical strength and wear resistance [1]. The recent progress of micro electro-mechanical systems (MEMS) technology in the semiconductor industry has led to significant advancements in the development of silicon-nitride based microelectronic technology, including as an insulator [2,3], as a diffusion barrier to prevent diffusion of impurities, as a masking material for KOH etching [4], and for masking to prevent oxidation as used in the LOCOS process [5]. Meanwhile, the advantages of smaller, less costly systems have provided opportunities for researchers to develop versatile MEMS devices. One of these MEMS based devices is a novel photon detector with a goal of ps temporal resolution proposed by H. van der Graaf [6] at NIKHEF, Amsterdam. The photon detector (called Tipsy) being developed has the potential to revolutionize photon detection with its superb temporal resolution. This device relies on a stacked set of curved, miniature, thin (in order of 10 nm) silicon nitride free standing membranes for generating secondary electrons, replacing the traditional gain dynodes in a photo multiplier tube. The main challenge of realizing Tipsy is sufficient secondary electron yield (SEY) at relative low primary electron energy. For operation, a yield of 4 secondary electrons must be achieved at 500 eV.
MEMS based silicon nitride is expected to be a promising secondary electron emission material for Tipsy for four reasons: (1) Silicon nitride has a wide band gap (5.1 eV [7]), where high SEY can be expected. (2) There is one experimental report of SEY of 2.9 at reflective mode at primary energy of 350 eV for LPCVD silicon nitride thin films [8]. (3) Mechanically stable and ultrathin (in order of 10 nm) silicon nitride films can be realized through MEMS technology [9]. For such thin systems, the SEY from above (reflection mode) and from below (transmission mode) the film is expected to be equally high. (4) Various surface treatments may induce negative electron affinity on silicon nitride surfaces, such as H termination or alkali metal oxide termination, according to our previous prediction by DFT calculations [10,11].
Despite the potential advantages of silicon nitride as a secondary electron emission material, there are few reports in the literature on their secondary electron emission properties. Furthermore, there are few systematic studies on the electron energy loss mechanism in silicon nitride. Within the research group of H. van der Graaf [6], recent efforts have been made in this matter by using a Monte Carlo code based on the Geant4 platform of CERN [12], which is developed by Bosch and Kieft [13]. This code is one of few with a good description of low-energy (<50 eV) interactions of electrons with matter. For the modelling of inelastic scattering (electron scattering with energy loss) events, dielectric function theory is applied to calculate the inelastic mean free path. Dielectric function theory allows derivation of differential cross-sections for electron–atom interaction from optical data.
The advantage of using the dielectric function theory is that optical data are readily available for a wide range of materials, and in broad energy ranges. However, despite the fact that there were several reports in the literature for Si3N4, the data have generally been limited to the evaluation of the index of refraction in the visible region and the infrared measurements. The results of these experiments have been used mainly for structural and chemical evaluation purposes [14]. Other studies also indicate the presence of chemically bound hydrogen in the film. Thus, the stoichiometry of an arbitrary film can be more accurately indicated by SixNyHz. Thus the refractive index and other optical properties will be a function of x, y and z. To study secondary electron emission property of silicon rich silicon nitride, a complete set of optical data (ELF) in a wide energy range is necessary.
The purpose of this paper is to use density functional theory (DFT) to perform a systematic investigation of the optical properties of Si-rich silicon nitride in a wide energy range (from infrared to ultraviolet). The real and imaginary parts of the complex refractive index have been calculated. Optical spectra for reflectivity, absorption coefficient, energy-loss function (ELF), and refractive index are obtained, and the results for pure β-Si3N4 are validated against available theoretical and experimental results. The materials have been studied in the form of SixNyHz (modified based on the β-Si3N4), so that the effect of the Si/N ratio, of the position of the access Si, and of the H in the bulk and on the surfaces can be taken into account. Furthermore, density of states (DOS) analysis has revealed that the change in the ELF has a direct link to the electronic structure of the materials. This work opens a window into the application in the fields of secondary electron emission by providing insight into the dielectric and optical properties of Si-rich silicon nitride.
2. Computational Methods and Structural Models
Geometry optimization and electronic structure calculations were performed before the optical spectrum calculations. All calculations were performed using DFT as implemented in the Vienna Ab-Initio Simulation Package (VASP) [15,16]. The Kohn-Sham equations were solved using a basis of Projector Augmented Wave functions with a plane-wave energy cut-off of 400 eV [17,18]. The electron-exchange correlation energy is described by using the functional of Perdew, Burke, and Ernzerhof (PBE) based within the generalized gradient approximation (GGA) [19]. Detailed computational setups, lattice parameters of bulk β-Si3N4, and their validation by comparing with the literature [20,21,22,23,24] are described in our previous study [10].
To model Si-rich silicon nitride in the form of SixNyHx, modifications of the used unit cell have been made based on that of β-Si3N4. For example, Si13N15 has been modelled by replacing one N atom with one Si atom in a unit cell with 28 atoms; Si7N7 has been modelled by replacing one N with one Si atom in the unit cell with 14 atoms. For Si7N7, two different distributions of the access Si have been included: Si distributed homogenously or forming a cluster (four N atoms next to each other are replaced by four Si atoms) in the unit cell. To study the influence of the H in the bulk Si-rich silicon nitride on the ELF, three types of H in the bulk in Si7N7, namel, H forming bonding with only Si, only N, and both Si and H, respectively. Geometric and electronic structures of clean and H terminated (100) and (110) β-Si3N4 surfaces have been documented in our previous study [10] and details will not be shown here again.
For optical calculations, the static dielectric tensor of β-Si3N4 has been calculated using density functional perturbation theory including local field effects. They are 4.21 (parallel to a and b) and 4.29 (parallel to c). This is in good agreement with previous theoretical values of 4.19 and 4.26 from Cai et al. [25] and of 4.24 and 4.32 from Watts [26].
The frequency dependent dielectric function has been calculated with the independent particle approximation (IPA). The implementation in VASP is the calculation of the response function in the framework of the PAW method. Details are given in references [27,28]. In crystals of high symmetry, the nomenclature of the isotropic medium can still be applied along high symmetry directions. Thus, in the hexagonal unit cells β-Si3N4, the components of the dielectric tensor parallel to a, b and c-axes are inspected.
VASP calculates the frequency dependent dielectric matrix after the electronic ground state has been determined. The imaginary part is determined by a summation over empty states using the equation:
where the indices c and v refer to conduction and valence band states respectively, and µck is the cell periodic part of the wave functions at the k-point k. The real part of the dielectric tensor is obtained by the usual Kramers-Kronig transformation,
where the P denotes the principle value. The main optical spectra, such as the reflectivity R(ω), absorption coefficient I(ω), energy-loss spectrum L(ω), and refractive index n(ω), all can be obtained from the dynamical dielectric response functions ε(ω). The explicit expressions are given by
and
3. Results AND Discussion
3.1. Validation of β-Si3N4
Figure 1 shows the imaginary and real part of the frequency dependent dielectric tensor as a function of photon energy in the energy range of 0–60 eV with components parallel to (a, b) and c-axes. The imaginary part of the frequency dependent dielectric tensor represents the absorption spectrum of a material. β-Si3N4 is transparent in the energy range from 0.0 to about 5.0 eV and is featured by main absorption peaks between 8.5 eV and 10.5 eV, which continuously slopes down with increasing photon energies. It has slightly anisotropic characteristics parallel to the c-axis due to the hexagonal unit cells. The main optical spectra, i.e., the reflectivity, adsorption coefficient, energy-loss function (ELF), and refractive index can be calculated from the frequency dependent dielectric tensor shown in Figure 1. Due to the lack of experimental data for other spectra, only the refractive index and ELF have been plotted and compared with experimental references in Figure 2 and Figure 3, respectively.
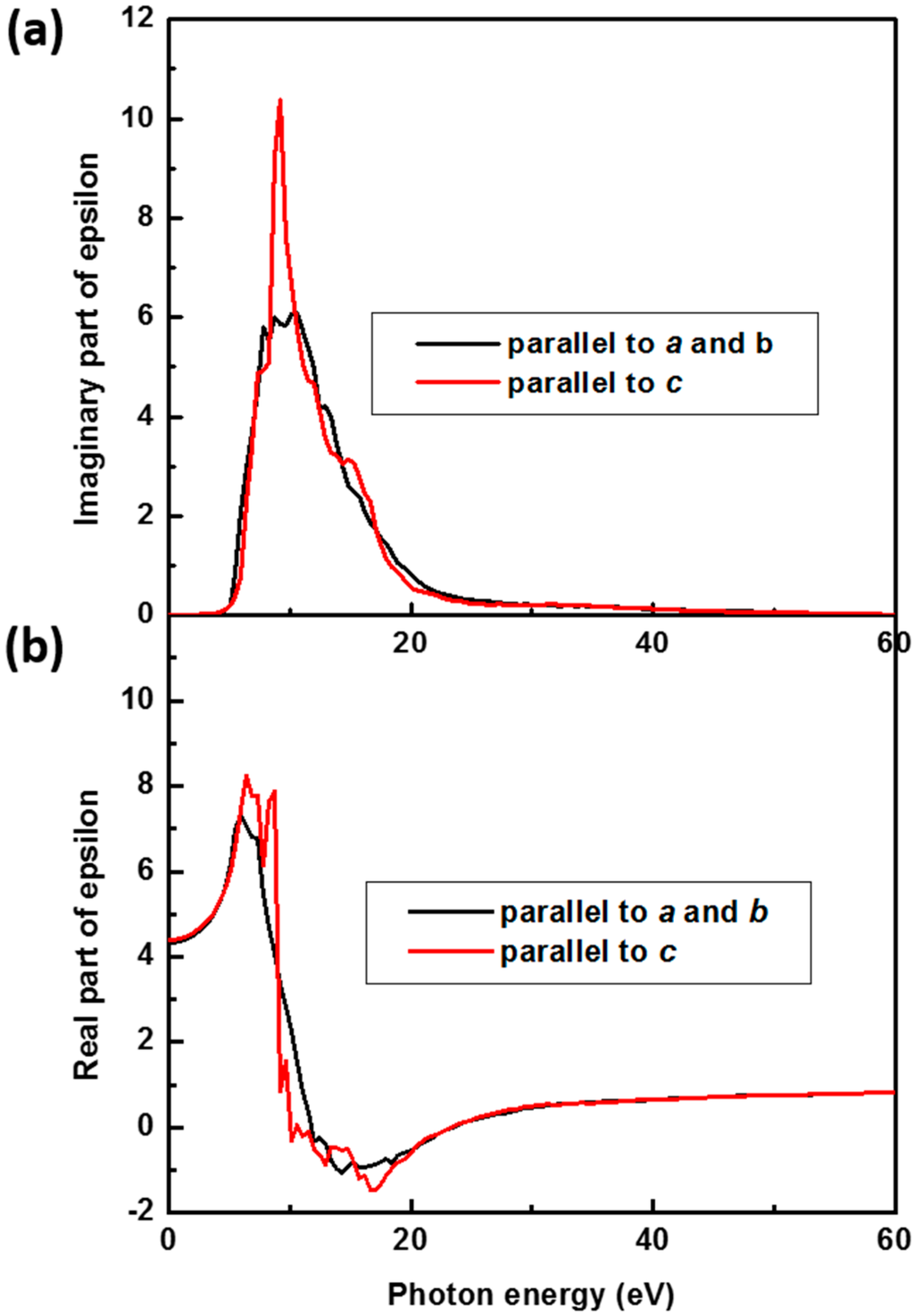
Figure 1.
The frequency dependent dielectric function ε(ω) = ε1(ω) + iε2(ω) of β-Si3N4 as a function of the photon energy. (a) and (b) represent our calculated imaginary and real parts of dielectric function ε(ω), respectively. The black and red lines are polarization parallel to (a, b) and c-axes, respectively.
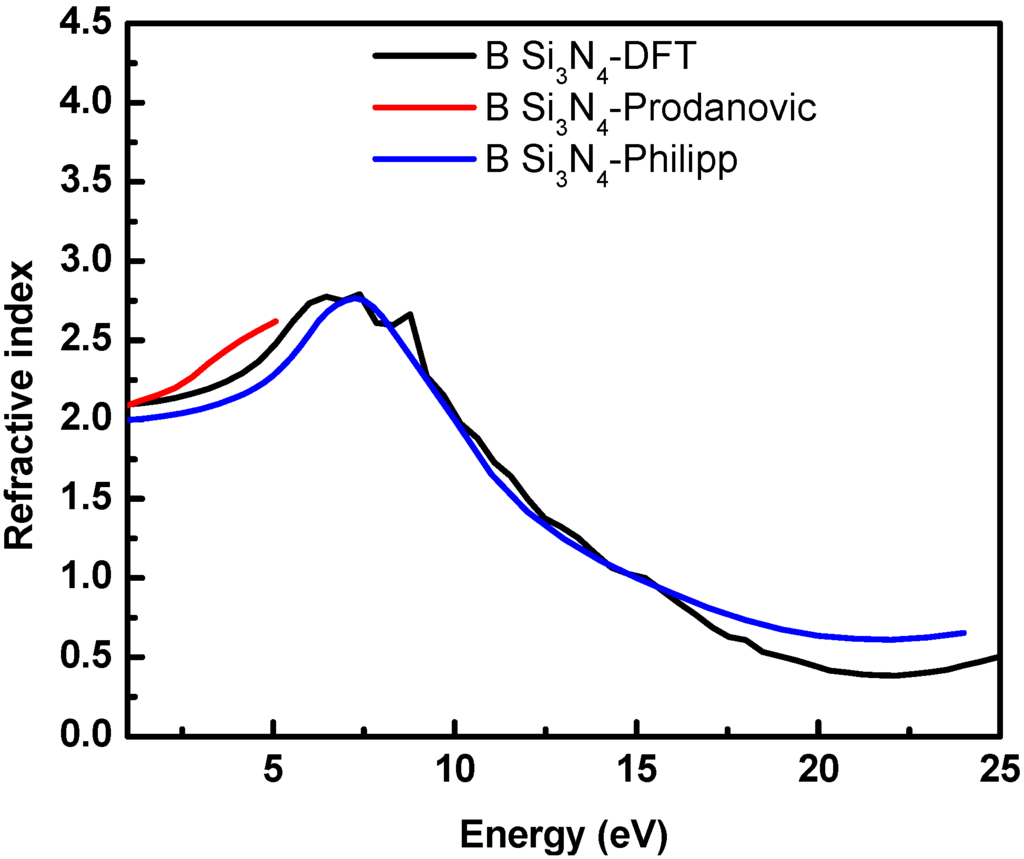
Figure 2.
A comparison of the refractive index as a function of photon energy. The black curve represents the DFT results for β-Si3N4, and the red and blue lines are optical measurements for amorphous Si3N4. The blue line is reproduced from Philipp [29]. The red line was obtained by spectroscopic ellipsometry by Prodanović [30].
For the refractive index (see Figure 2), the calculated curve is nicely positioned in the middle of the two experimental curves within the available energy range. The discrepancy between experimental and theoretical data is smaller than the discrepancy between the experimental data (due to the differences in the preparations of the samples, the measurement techniques and the derivation of the data). For the ELF (see Figure 3), the agreement is also very good except two main differences between the DFT and experimental plots: (i) there is a kink at the peak just above 20 eV in the experimental curve, which is very likely caused by combining different sets of optical data from different sources due to lack of experimental data in a wide energy range from the same work [14] (three sets of data, i.e., <1 eV, 1–24 eV and > 26 eV); (ii) The peaks below 0.3 eV seen in experimental curve is absent in the one obtained from DFT. The latter can be explained by the fact that the optical spectra are directly calculated from inter-band transitions, whereas the phonon modes at very low energies are not included. As shown by Monte Carlo studies carried out by the same authors, the secondary electron emission properties of β-Si3N4 is barely affected by the inclusion of this part of the ELF [31].
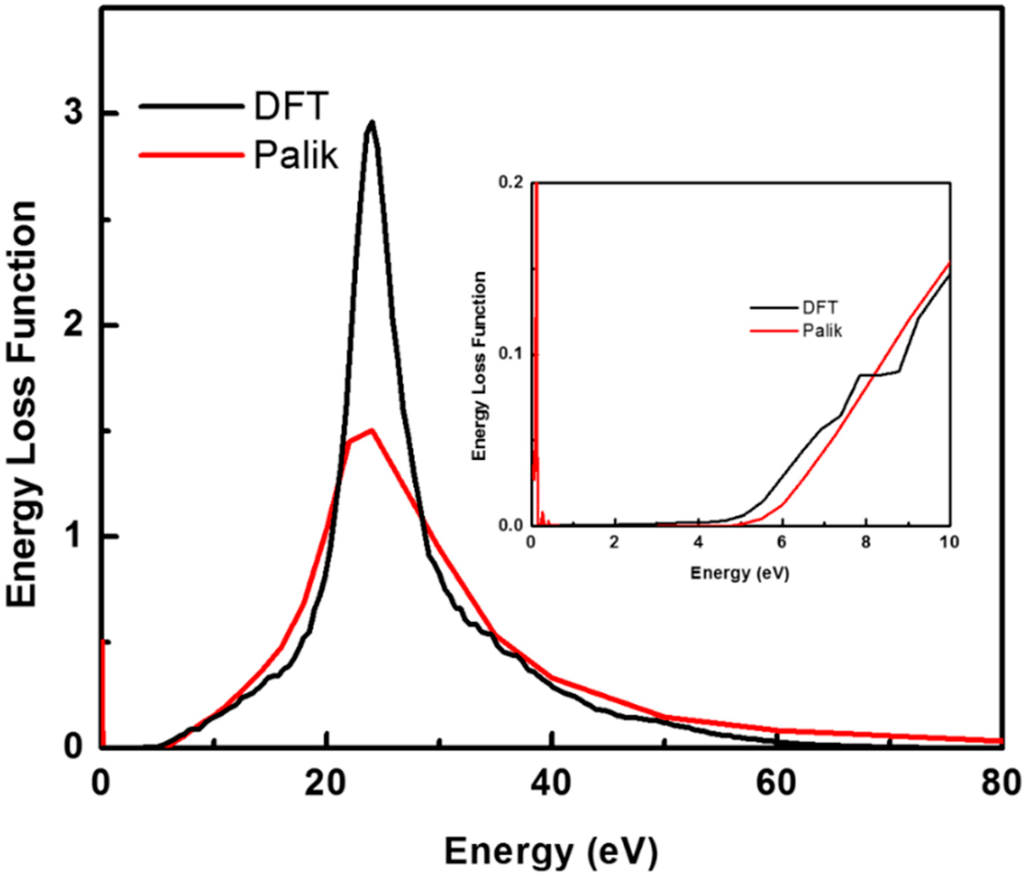
Figure 3.
A comparison of the energy loss spectrum as a function of photon energy. The black curve represents the DFT results for β-Si3N4, and the red curve represents the curve derived from the combination of a few sets of optical data from handbook of Palik [14] by Bosch and Kieft [13].
3.2. SixNy—The Influence of the Si/N Ratio and Si Positions
Figure 4 illustrates the calculated ELF of Si-rich silicon nitride in comparison with those of β-Si3N4 and Si. The studied forms of Si-rich silicon nitride are Si13N15 (one N atom is replaced by one Si in a unit cell with 28 atoms), Si7N7 (one N atom is replaced by one Si atom in the unit cell with 14 atoms), and Si7N7 cluster (the four N atoms are replaced by four Si atoms forming a Si cluster inside the unit cell with 56 atoms). Compared to that of β-Si3N4, the ELF of the Si-rich silicon nitride exhibits three main features:
- (1)
- The general shape and the position of the main peaks are similar, where the ELF increases from low energy and peaks at about 23 to 27 eV and slopes down at higher energy.
- (2)
- The main peaks of the Si-rich silicon nitride have shifted slightly to lower energy (at about 1–2 eV). Therefore, the magnitude of the ELF at low energies side of the slope is larger than that of β-Si3N4.
- (3)
- Extra energy loss peaks appear below 5 eV. The increase in the magnitude of the ELF and number of peaks are larger for Si7N7 than for Si13N15.
For the influence of the Si position, one should compare the ELF of the Si7N7 and Si7N7 cluster. Compared with the ELF of Si7N7, that of Si7N7 cluster exhibits more Si character which can be summarized as follows:
- (1)
- The position of the main peak of Si7N7 cluster is significantly sharper and is in a position at about 5 eV lower, and which is closer to that of Si.
- (2)
- The positions of the adsorption peaks below 10 eV can be seen as a combination of those of Si, Si3N4, and Si7N7, but the peaks are in general smaller and broader (below 1 eV and at about 7 eV).
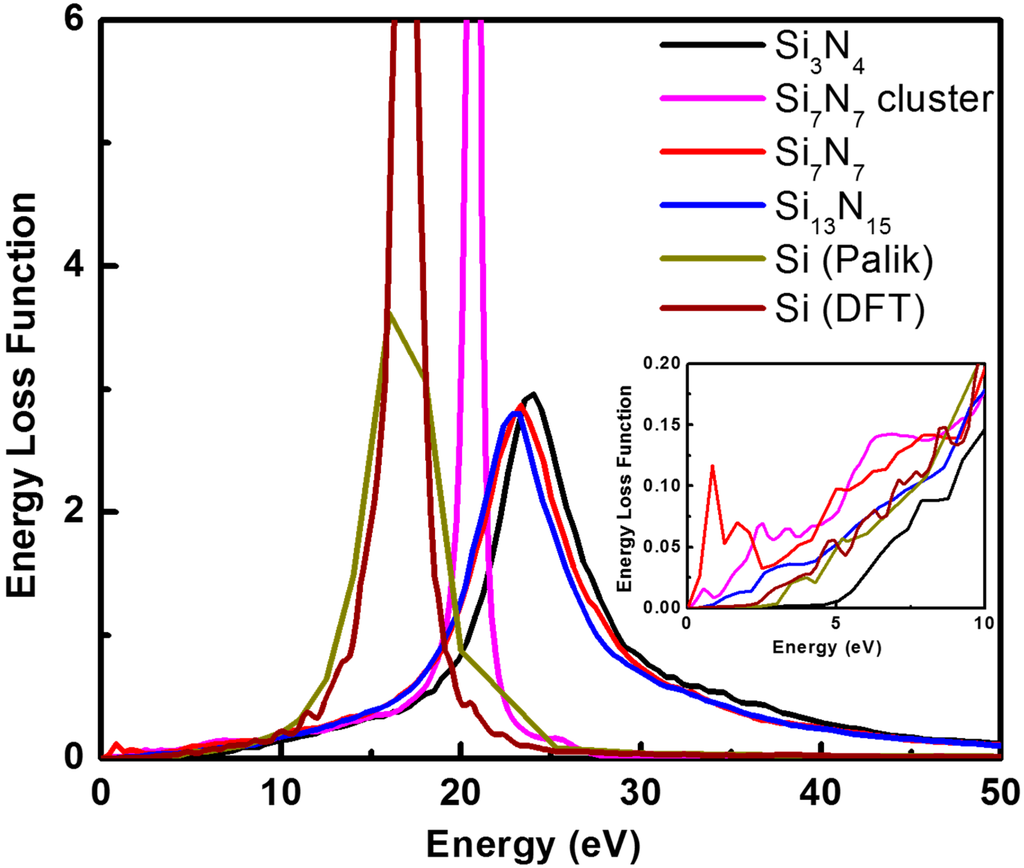
Figure 4.
Energy loss function of Si-rich silicon nitride SixNy with comparison with β-Si3N4 and Si derived from experimental reference [14] by Bosch and Kieft [13] and DFT results.
Since the optical spectra are directly calculated from interband transitions, a comparison of the electronic structures should be useful to understand the changes in the ELF. Shown from the density of states (DOS) in Figure 5, the excess Si in Si-rich silicon nitride SixNy has introduced (i) extra electronic states in the band gap just above the Fermi level which can be assigned to the unsaturated Si bonds; (ii) broader Si nonbonding feature in the range of 5–10 eV at conduction band. This observation is similar to a recent finding of Hintzsche [32] for amorphous SixNyHz. For the Si7N7 cluster, the intensity of the unsaturated Si feature is much smaller and the overall DOS plot is shifted to lower energy.
To summarize Figure 4 and Figure 5 together, the extra energy loss peaks at Si7N7 below 5 eV are due to the introduction of the electronic states at the band gap originating from the unsaturated Si atom. For the Si7N7 cluster case, the ELF can be seen as a combination of Si and Si3N4 and Si-rich Si3N4. Based on this calculated result, one can conclude that the optical properties of the Si-rich silicon nitride not only are determined by the composition of the materials, but are also determined by the microstructure at an atomic level.
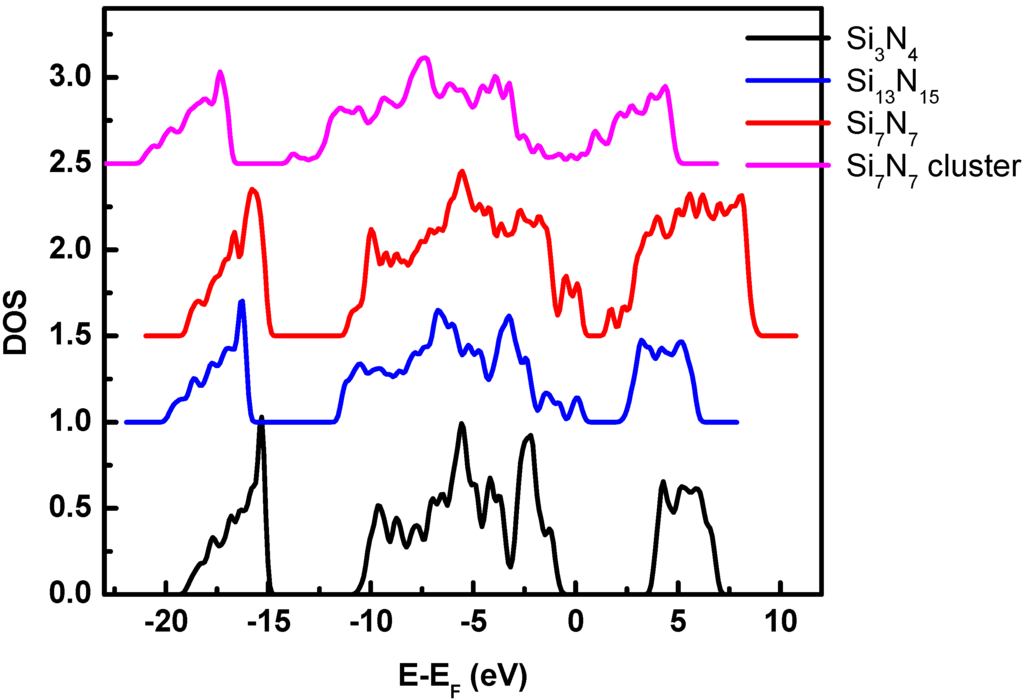
Figure 5.
Density of states (DOS) of Si-rich silicon nitride (SixNy), compared to β-Si3N4.
3.3. SixNyHz—H in Bulk Si-Rich Silicon Nitride
Figure 6 and Figure 7 summarize the ELF and DOS of SixNyHz in the form of Si7N7H1-2 in comparison with Si7N7. Three possibilities have been studied. They are one H forming bond with the dangling bond of the access Si, one H with N, and two H with both Si and N, respectively. The main peaks of the ELF of Si7N7H1-2 are located at almost the same energies as that of Si7N7. The main differences can be found in the energy range below 5 eV. The sharp peak located at about 1 eV for Si7N7 is now absent for all three, where the H has directly or indirectly saturated the defects in the Si-rich silicon nitride. This function of H in curing defects is the largest when bonded with Si, the smallest when bonded with N, and logically intermediate for a combination of the two.
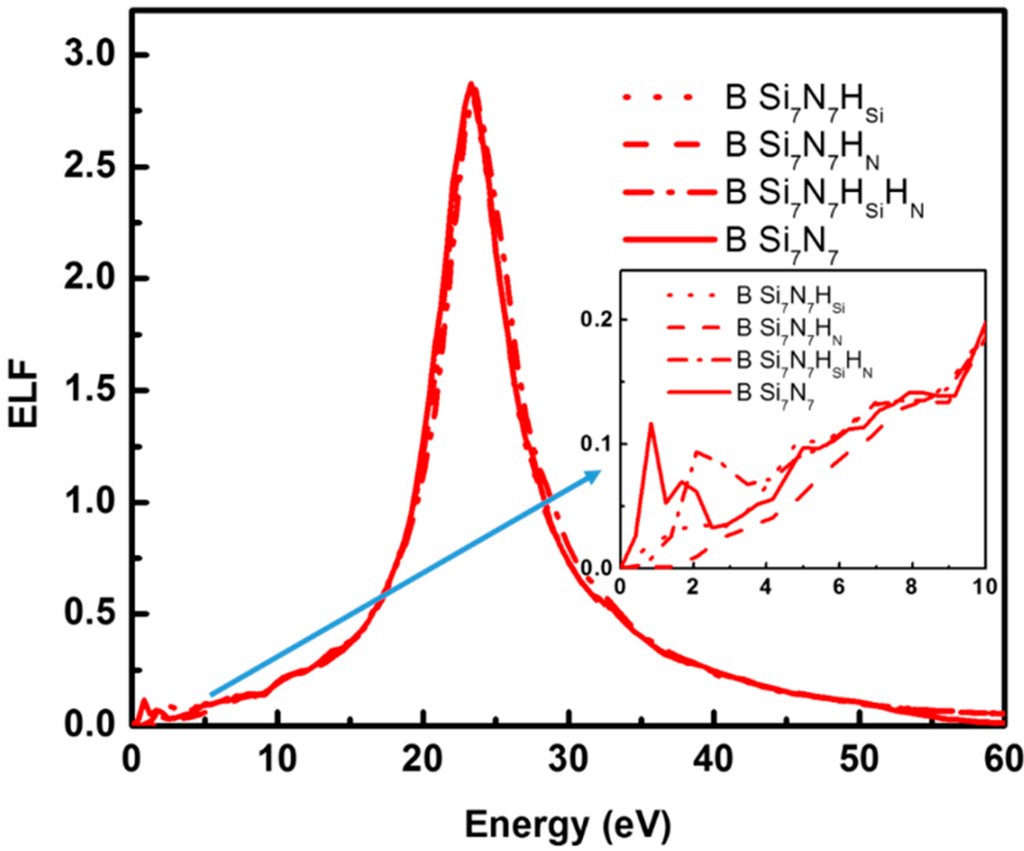
Figure 6.
Energy loss function of H in Si-rich silicon nitride Si7N7H1-2 in comparison with Si7N7. Si7N7HSi, Si7N7HN, and Si7N7HNHSi represent H forming bonds with unsaturated Si atoms, N atoms, and the combination of the two, respectively.
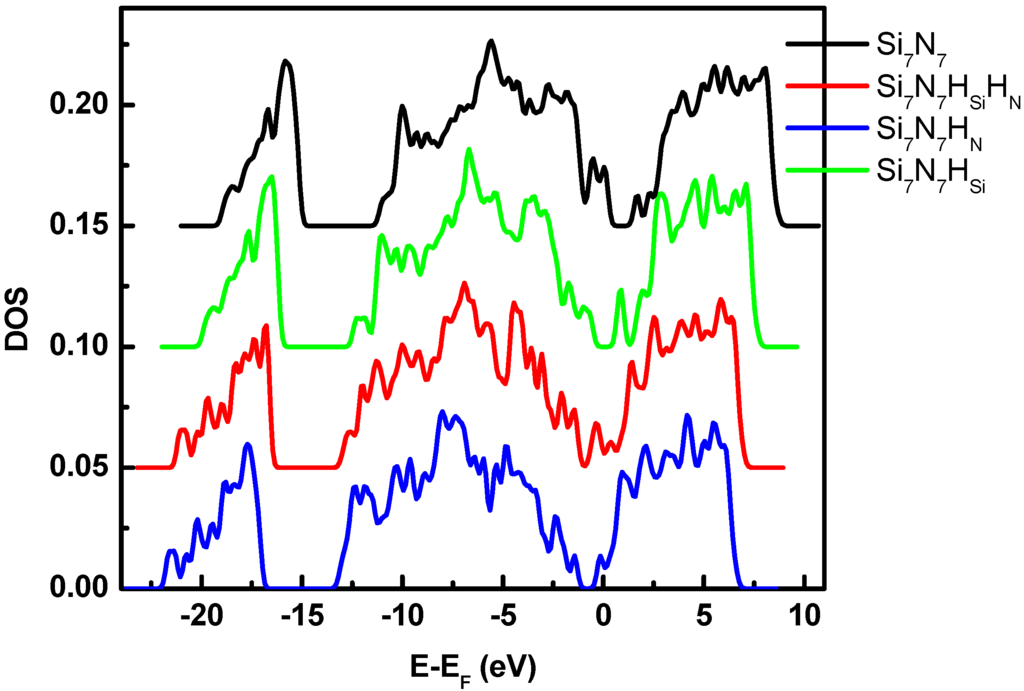
Figure 7.
Density of States (DOS) of Si-rich silicon nitride (Si7N7H1-2) in comparison with Si7N7.
3.4. SixNyHz—H Termination on the Surfaces of Si3N4
3.4.1. Surface vs. Bulk
The effect of surface defects has been studied by comparing bulk β-Si3N4 with two surfaces: (100) and (110). Compared with bulk β-Si3N4, the main peaks of the ELFs (see Figure 8) of both surfaces have shifted energies which are about 3 to 5 eV lower. Similarly with defects in the bulk, the defects introduced by surfaces also lead to adsorption peaks at about 3 eV. However the peaks in the system with surface defects are much lower and broader that the ones observed in the system with bulk defects. This is because in both β-Si3N4 with surfaces and Si-rich silicon nitride, defects (unsaturated bonds) occur and these introduce extra electronic states as seen in the DOS (see Figure 9). However, the defects on the surface are more often self-cured in the sense that the atoms on the surfaces tend to relocate to such positions to saturate the dangling bonds. In the bulk there is limited volume to allow the atoms to do so.
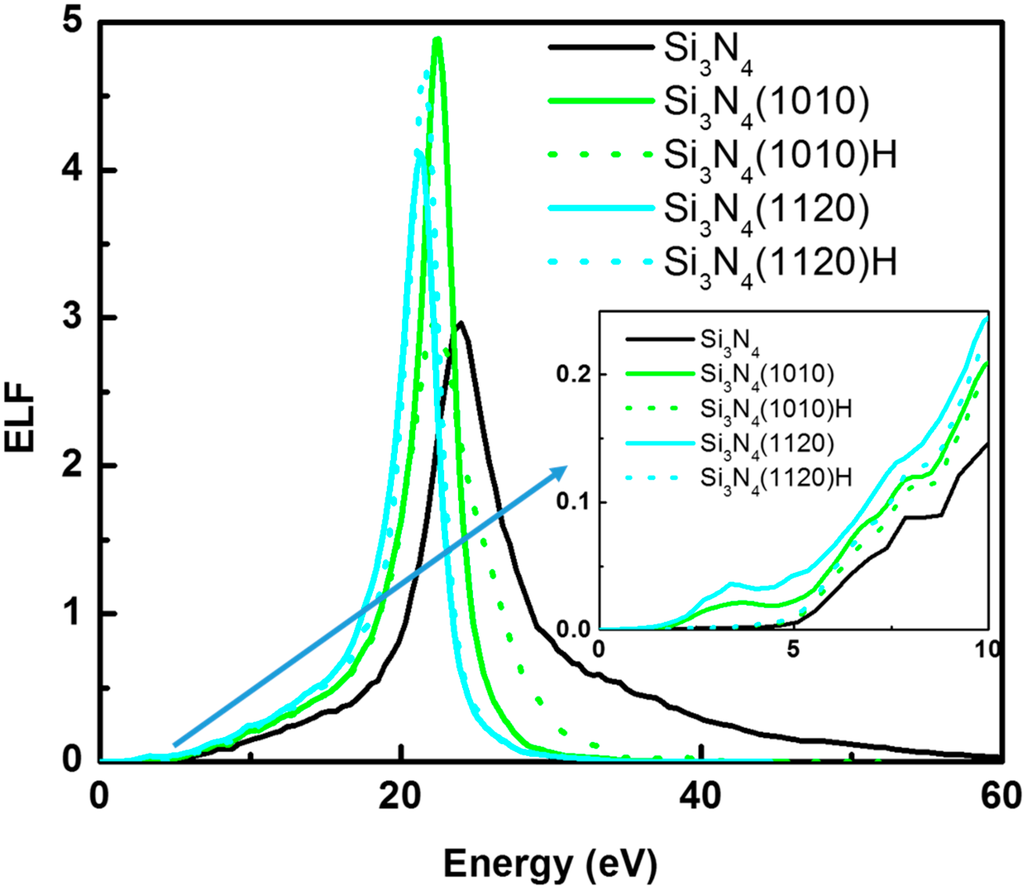
Figure 8.
Energy loss function of surfaces with and without H termination in comparison with bulk β-Si3N4.
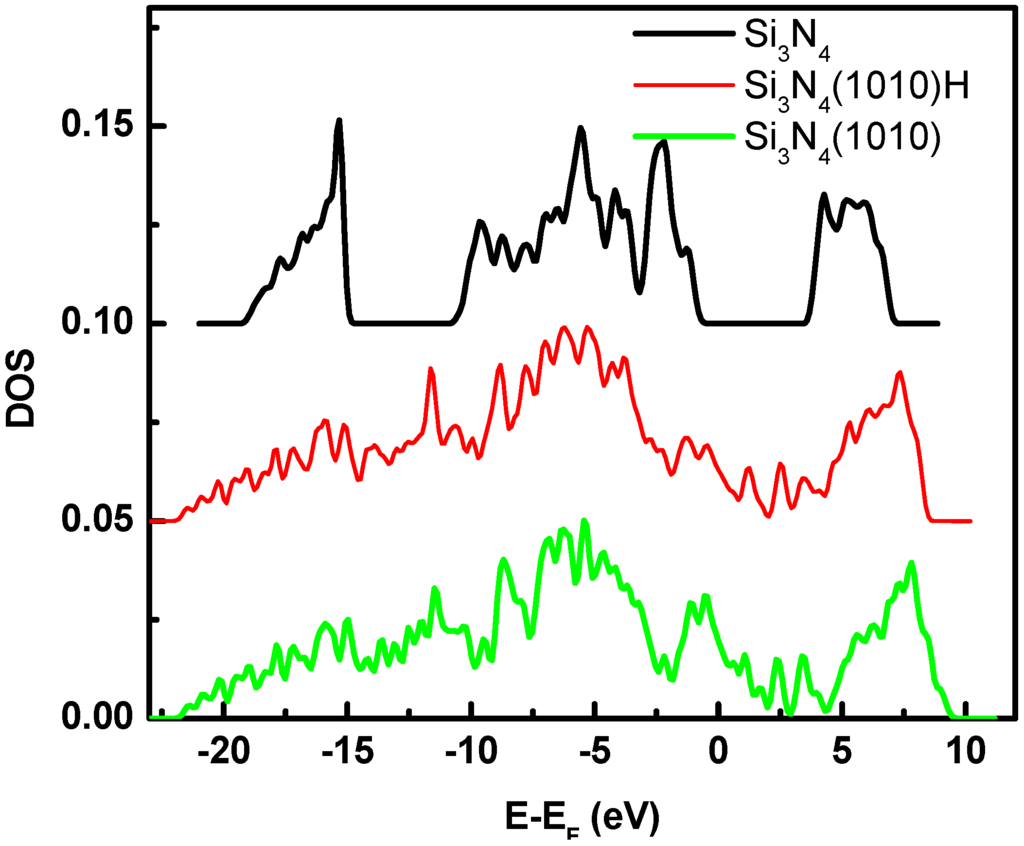
Figure 9.
Density of states (DOS) of surfaces with and without H termination in comparison with bulk β-Si3N4.
3.4.2. Clean Surface vs. H Termination
Again, similar to H in the bulk, H termination on the surfaces reduces the defect effect by saturating the dangling Si and N bonds. This can be seen in the slightly smoother ELF and DOS plots, in particular in the energy range of 0–5 eV.
Monte Carlo simulations using the calculated ELF have been performed to evaluate the influences of the material parameters (such as Si/N ratio, surface defects, H terminations, and electron affinity) on the secondary electron yield (SEY) of thin Si-rich silicon nitride films. The results indicate that the SEY is extremely sensitive to the ELF in low energies, especially below 10 eV. The highest SEY is obtained using the ELF of the bulk β-Si3N4. This is mainly due to the large band gap, where the secondary electrons are more likely to escape to the surface without losing energy from interacting with impurities. As expected, the access Si in silicon rich silicon nitride and surfaces both cause decrease in the SEY. Whereas H adsorption in the bulk and H termination on the surface both have reduced the effect caused by the defects. Details of the electron transport mechanism and SEY results will be published in a separate paper [31]. In combination with Monte Carlo simulations, the significance of this work is to provide a guideline for tuning the material parameters to achieve favorable secondary electron emission properties.
4. Summary
The optical properties of SixNyHz have been studied using DFT, with a focus on the energy loss spectrum. Defects in the bulk (due to the excess Si) and on the surface, and the influence of hydrogen in the bulk, hydrogen termination on the surfaces have been investigated. Extra energy loss peaks have been found in the energy range lower than 10 eV in all the studied systems compared with β-Si3N4. The origins of these energy loss peaks have been identified in their corresponding electronic structures. It is concluded that the changes in ELF are not only affected by the composition but also by the microstructures of the materials. The excess Si in the bulk in Si-rich silicon nitride leads to a major increase both in the magnitude and the number of adsorption peaks in ELF, whereas those caused by surface defects are much milder. H in the bulk of Si-rich silicon nitride and H termination on surfaces has a healing effect by saturating the dangling bonds and therefore reducing the number and flattening the sharpness of the adsorption peaks. The results can be used as reference data for tuning the optical properties via controlling the composition and microstructures for secondary electron emission applications.
Acknowledgments
This work is funded by the European Research Council (320764) (ERC-Advanced 2013 MEMBrane).
Author Contributions
Shu Xia Tao and Harry van der Graaf conceived and designed the experiments; Shu Xia Tao performed the DFT simulations; Violeta Prodanović performed optical measurements. All the authors have contributed to the data analysis and preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Riley, F.L. Silicon nitride and related materials. J. Am. Ceram. Soc. 2000, 83, 245–265. [Google Scholar] [CrossRef]
- Hezel, R.; Schroner, R. Plasma Si nitride—A promising dielectric to achieve high quality silicon MIS/IL solar cells. J. Appl. Phys. 1981, 52, 3076–3079. [Google Scholar] [CrossRef]
- Eitan, B.; Pavan, P.; Bloom, I.; Aloni, E.; Frommer, A.; Finzi, D. A novel localized trapping, 2-bit nonvolatile memory cell. IEEE Electron Device Lett. 2000, 21, 543–545. [Google Scholar] [CrossRef]
- Seidel, H.; Csepregi, L.; Heuberger, A.; Baumgärtel, H. Anisotropic etching of crystalline silicon in alkaline solutions II, influence of dopants. J. Electrochem. Soc. 1990, 137, 3626–3632. [Google Scholar] [CrossRef]
- Kooi, E.; van Lierop, J.G.; Appels, J.A. Formation of silicon nitride at a Si–SiO2 interface during local oxidation of silicon and during heat-treatment of oxidized silicon in NH3 gas. J. Electrochem. Soc. 1976, 123, 1117–1120. [Google Scholar] [CrossRef]
- Bilevych, Y.; Brunner, S.E.; Chan, H.W.; Charbon, E.; van der Graaf, H.; Hagen, C.W.; Nützel, G.; Pinto, S.D.; Prodanović, V.; Rotman, D.; et al. Potential Applications of Electron Emission Membranes in Medicine. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2015, in press. [Google Scholar] [CrossRef]
- Goodman, A.M. Photoemission of electrons and holes into silicon nitride. Appl. Phys. Lett. 1968, 13, 275–277. [Google Scholar] [CrossRef]
- Fijol, J.J.; Then, A.M.; Tasker, G.W. Secondary electron yield of SiO2 and Si3N4 thin films for continuous dynode electron multipliers. Appl. Surf. Sci. 1991, 464, 48–49. [Google Scholar] [CrossRef]
- Creemer, J.F.; Helveg, S.; Kooyman, P.J.; Molenbroek, A.M.; Zandbergen, H.W.; Sarro, P.M. A MEMS reactor for atomic-scale microscopy of nanomaterials under industrially relevant conditions. J. Microelectromech. Syst. 2010, 19, 254–264. [Google Scholar] [CrossRef]
- Tao, S.X.; Theulings, A.; Smedley, J.; van der Graaf, H. Ab initio study of electron affinity of hydrogen terminated β-Si3N4. Diam. Relat. Mater. 2015, 53, 52–57. [Google Scholar] [CrossRef]
- Tao, S.X.; Theulings, A.; Smedley, J.; van der Graaf, H. DFT study of electron affinity of alkali metal termination on clean and oxygenated β-Si3N4. Diam. Relat. Mater. 2015, 58, 214–220. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Available online: http://www.sciencedirect.com/science/article/pii/S0168900203013688 (accessed on 7 December 2015).
- Kieft, E.; Bosch, E. Refinement of Monte Carlo simulations of electron-specimen interaction in low-voltage SEM. J. Phys. D Appl. Phys. 2008, 41, 215310. [Google Scholar] [CrossRef]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids III; Academic Press: New York, NY, USA, 1998.
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. J. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Boulay, D.D.; Ishizawa, N.; Atake, T.; Streltsov, V.; Furuya, K.; Munakatae, F. Synchrotron X-ray and ab initio studies of β-Si3N4. Acta Crystallogr. B 2004, 60, 388–405. [Google Scholar] [CrossRef] [PubMed]
- Belkada, R.; Kohyama, M.; Shibayanagi, T.; Naka, M. Relative stability of P63/m and P63 structures of β-Si3N4. Phys. Rev. B 2002, 65, 092104. [Google Scholar] [CrossRef]
- Villars, P.; Calvert, L.D. Pearson’s Handbook of Crystallographic Data for Intermetallic Phases; ASM International: Russell Township, OH, USA, 1985; Volume 3. [Google Scholar]
- Idrobo, J.C.; Iddir, H.; Ögüt, S.; Ziegler, A.; Browning, N.D.; Ritchie, R.O. Ab initio structural energetics of β-Si3N4 surfaces. Phys. Rev. B 2005, 72, 241301. [Google Scholar] [CrossRef]
- Bermudez, V.M. Theoretical study of the electronic structure of the Si3N4 (0001) surface. Surf. Sci. 2005, 579, 11–20. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Zhang, L.T.; Zeng, Q.F.; Cheng, L.F.; Xu, Y.D. First-principles study of vibrational and dielectric properties of β-Si3N4. Phys. Rev. B 2006, 74, 174301. [Google Scholar] [CrossRef]
- Thomas, W. Properties of Silicon Nitride—An Ab-Initio Study of the Crystalline Phases and Amorphous Silicon-Nitrogen Alloys. Master’s Thesis, University of Vienna, Vienna, Austria, 2011. [Google Scholar]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector augmented-wave methodology. Phys. Rev. B 2006, 73, 45112. [Google Scholar] [CrossRef]
- Harl, J. The Linear Response Function in Density Functional Theory: Optical Spectra and Improved Description of the Electron Correlation. Ph.D. Thesis, University of Vienna, Vienna, Austria, 31 October 2008. [Google Scholar]
- Philipp, H.R. Optical Properties of Silicon Nitride. J. Electrochein. Soc. 1973, 120, 295–300. [Google Scholar] [CrossRef]
- Prodanovic, V.; Chan, H.W.; Smedley, J.; Theulings, A.; Tao, S.X.; van der Graaf, H.; Sarro, P.M. Optimization of Silicon-rich Silicon Nitride Films for Electron Multiplication in Timed Photon Counters. Procedia Eng. 2015, 120, 1111–1114. [Google Scholar] [CrossRef]
- Theulings, A.; Tao, S.X.; van der Graaf, H. Monte Carlo simulation of low energy photon-electron interaction and transportation in silicon rich silicon nitride. In preparation.
- Hintzsche, L.E.; Fang, C.M.; Marsman, M.; Jordan, G.; Lamers, M.W.P.E.; Weeber, A.W.; Kresse, G. Defects and defect healing in amorphous Si3N4-xHy: An ab initio density functional theory study. PRB 2013, 88, 155204. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).