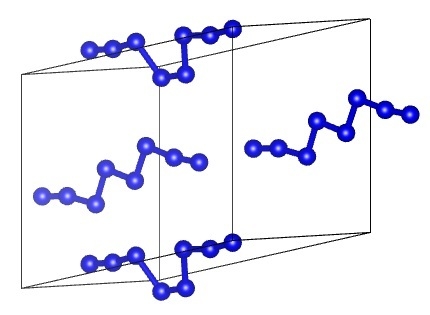
A Comparative Density Functional Theory and Density Functional Tight Binding Study of Phases of Nitrogen Including a High Energy Density Material N8
Abstract
:1. Introduction
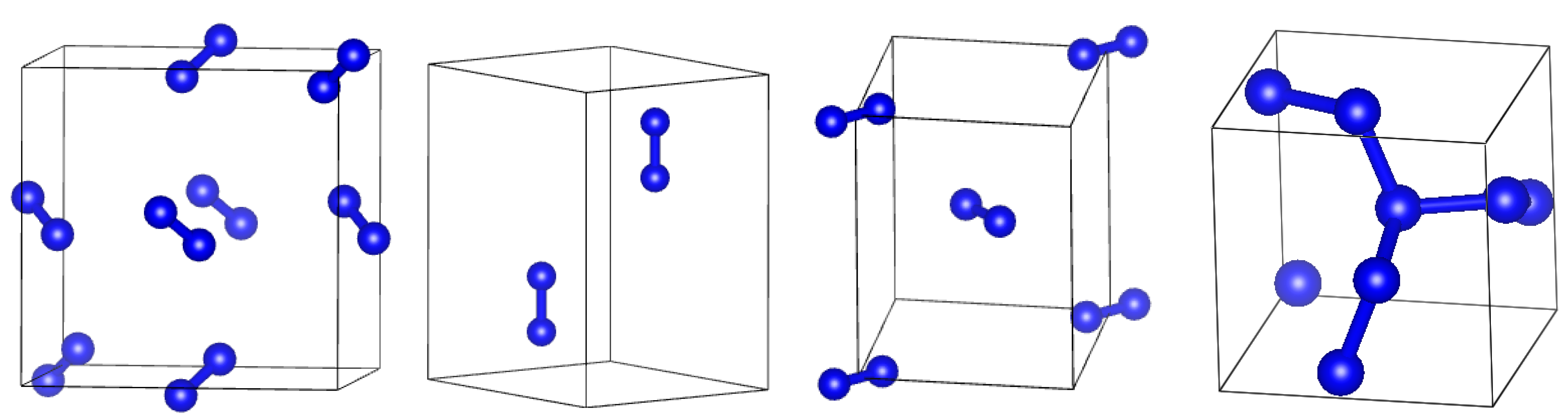
2. Methods
2.1. DFT Simulations
2.2. DFTB Simulations
3. Results
3.1. Tuning of DFT Parameters
| Method/Phase | α | β | γ | cg | N8 |
|---|---|---|---|---|---|
| DFT-D | −270.59 | 0.01 | 0.00 | 1.41 | 0.84 |
| DFTB-D (3ob-2-1) | −65.46 | 0.00 | 0.00 | Unstable | 1.05 |
| DFTB-D (matsci-0-3) | −67.96 | −0.01 | 0.00 | −0.55 | −0.05 |
| DFTB-D (pbc-0-3) | −66.61 | 0.00 | 0.01 | 1.68 | 1.07 |
| Reference | −8.32 | 0.01 | 0.00 | 1.41 | 0.88 |
| Phase/Method | DFT-D | DFTB-D | Reference Values | ||
|---|---|---|---|---|---|
| 3-ob-2-1 | matsci-0-3 | pbc-0-3 | |||
| α, a | 5.49 | 5.54 | 5.54 | 5.52 | 5.49–5.87 a,b |
| β, a | 3.85 | 3.59 | 3.59 | 3.55 | 4.04–4.05 b |
| c | 7.03 | 7.65 | 7.70 | 7.70 | 6.60–6.67 b |
| γ, a | 4.03 | 4.04 | 4.04 | 4.03 | 3.96–4.06 b |
| c | 5.16 | 5.17 | 5.17 | 5.15 | 5.11–5.34 b |
| cg, a | 3.82 | unstable | 3.61 | 3.73 | 3.75–3.79 c |
| N8, a | 10.66 | 10.92 | 10.46 | 10.40 | 10.59–10.83 d |
| b | 4.53 | 4.17 | 4.16 | 4.12 | 4.40–4.67 d |
| c | 6.83 | 7.55 | 7.71 | 7.76 | 6.42–7.05 d |
| α | 86.5 | 105.0 | 102.7 | 101.9 | 88.4–91.5 d |
| β | 80.5 | 89.1 | 88.9 | 88.5 | 81.7–84.9 d |
| γ | 48.2 | 54.3 | 50.1 | 49.7 | 44.1–47.4 d |
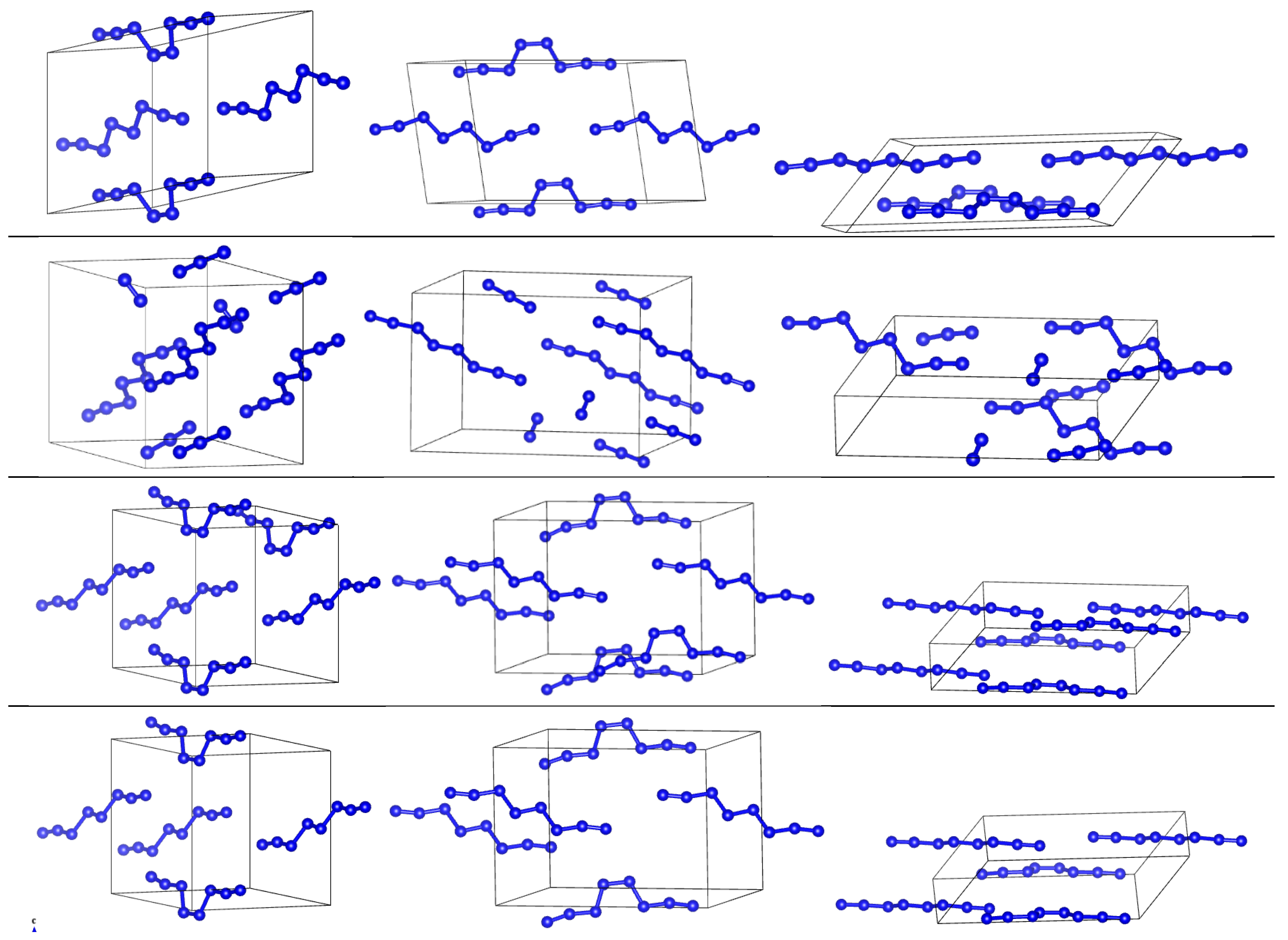
3.2. Comparison of DFT-D and DFTB-D Models of Different Phases of Nitrogen
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
Basis (SIESTA format)
Pseudopotential header (.psf format)
References
- Fried, L.E.; Manaa, M.R.; Pagoria, P.F.; Simpson, R.L. Design and synthesis of energetic materials. Annu. Rev. Mater. Res. 2001, 31, 291–321. [Google Scholar] [CrossRef]
- Tsyshevsky, R.V.; Pagoria, P.; Kukla, M.M. Computational design of novel energetic materials: Dinitro-bistriazolo-tetrazine. J. Phys. Chem. C 2015, 119, 8512–8521. [Google Scholar] [CrossRef]
- Ramesh Babu, K.; Vaitheeswaran, G. Structural and vibrational properties of nitrogen-rich energetic material guanidinium 2-methyl-5-nitraminotetrazolate. Chem. Phys. Lett. 2014, 592, 132–137. [Google Scholar] [CrossRef]
- Hirshberg, B.; Denekamp, C. First principles prediction of an insensitive high energy density material. Phys. Chem. Chem. Phys. 2013, 15, 17681–17688. [Google Scholar] [CrossRef] [PubMed]
- Fendt, T.; Fischer, N.; Klapotke, T.M.; Stierstorfer, J. N-rich salts of 2-methyl-5-nitraminotetrazole: Secondary explosives with low sensitivities. Inorg. Chem. 2011, 50, 1447–1458. [Google Scholar] [CrossRef] [PubMed]
- Appalakondaiah, S.; Vaitheeswaran, G.; Lebègue, S. Structural, elastic, optical properties and quasiparticle band structure of solid cyanuric triazide. Chem. Phys. Lett. 2014, 605, 10–15. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, W.; Xiao, H. An ab initio molecular dynamics study of thermal decomposition of 3,6-di(azido)-1,2,4,5-tetrazine. Phys. Chem. Chem. Phys. 2014, 16, 21620–21628. [Google Scholar] [CrossRef] [PubMed]
- Rice, B.M.; Larentzos, J.P.; Byrd, E.F.C.; Weingarten, N.S. Parameterizing complex reactive force fields using multiple objective evolutionary strategies (MOES): Part 2: Transferability of ReaxFF models to C−H−N−O energetic materials. J. Chem. Theory Comput. 2015, 11, 392–405. [Google Scholar] [CrossRef]
- Tsyshevsky, R.V.; Pagoria, P.; Zhang, M.; Racoveanu, A.; DeHope, A.; Parrish, D.; Kuklja, M.M. Searching for low-sensitivity cast-melt high-energy-density materials: Synthesis, characterization, and decomposition kinetics of 3,4-bis(4-nitro-1,2,5-oxadiazol-3-yl)-1,2,5-oxadiazole-2-oxide. Phys. Chem. C 2015, 119, 3509–3521. [Google Scholar] [CrossRef]
- Agrawal, J.P. High. Energy Materials: Propellants, Explosives and Pyrotechnics; Wiley-VCH Verlag: Weinheim, Germany, 2010. [Google Scholar]
- Pitzer, K.S. Repulsive forces in relation to bond energies, distances and other properties. J. Am. Chem. Soc. 1948, 70, 2140–2145. [Google Scholar] [CrossRef]
- Mailhiot, C.; Yang, L.H.; McMahan, A.K. Polymeric nitrogen. Phys. Rev. B 1992, 46, 14419–14435. [Google Scholar] [CrossRef]
- Barbee, T.W. Metastability of atomic phases of nitrogen. Phys. Rev. B 1993, 48, 9327–9330. [Google Scholar] [CrossRef]
- Mitas, L.; Martin, R.M. Quantum Monte Carlo of nitrogen: Atom, dimer, atomic, and molecular solids. Phys. Rev. Lett. 1994, 72, 2438–2441. [Google Scholar] [CrossRef] [PubMed]
- Alemany, M.M.G.; Martins, J.L. Density-functional study of nonmolecular phases of nitrogen: Metastable phase at low pressure. Phys. Rev. B 2003, 68, 024110. [Google Scholar] [CrossRef]
- Eremets, M.I.; Gavriliuk, A.G.; Trojan, I.A.; Dzivenko, D.A.; Boehler, R. Single-bonded cubic form of nitrogen. Nat. Mater. 2004, 2, 558–563. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Gerber, R.B. Formation of novel rare-gas molecules in low-temperature matrices. Annu. Rev. Phys. Chem. 2004, 55, 55–78. [Google Scholar] [CrossRef] [PubMed]
- Vij, A.; Pavlovich, J.G.; Wilson, W.W.; Vij, V.; Christie, K.O. Experimental detection of the pentaazacyclopentadienide (pentazolate) anion, cyclo-N5(-). Angew. Chem. Int. Ed. 2002, 41, 3051–3054. [Google Scholar] [CrossRef]
- Cacace, F.; de Patris, G.; Troiani, A. Experimental detection of tetranitrogen. Science 2002, 295, 480–481. [Google Scholar] [CrossRef] [PubMed]
- Östmark, H.; Wallin, S.; Brinck, T.; Carlqvist, P.; Claridge, R.; Hedlund, E.; Yudina, L. Detection of pentazolate anion (cyclo-N5-) from laser ionization and decomposition of solid p-dimethylaminophenylpentazole. Chem. Phys. Lett. 2003, 379, 539–546. [Google Scholar] [CrossRef]
- Samartzis, P.C.; Lin, J.-J.; Ching, T.-T.; Chaudhuri, C.; Lee, Y.T.; Lee, S.-H.; Wodtke, A.M. Two photoionization thresholds of N3 produced by ClN3 photodissociation at 248 nm: Further evidence for cyclic N3. J. Chem. Phys. 2005, 123, 051101. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; Wodtke, A.M.; Goncher, S.J.; Robinson, J.C.; Sveum, N.E.; Neumark, D.M. Photofragment translation spectroscopy of ClN3 at 248 nm: Determination of the primary and secondary dissociation pathways. J. Chem. Phys. 2005, 123, 104305. [Google Scholar] [CrossRef] [PubMed]
- Hirshberg, B.; Gerber, R.B.; Krylov, A.I. Calculations predict a stable molecular crystal of N8. Nat. Chem. 2014, 6, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M. SCC-DFTB: What is the proper degree of self-consistency? J. Phys. Chem. A 2007, 111, 5614–5621. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Seifert, G. Density functional tight binding. Phil. Trans. R. Soc. A 2014, 372, 20120483. [Google Scholar] [CrossRef] [PubMed]
- Gaus, M.; Goez, A.; Elstner, M. Parametrization and benchmark of DFTB3 for organic molecules. J. Chem. Theory Comput. 2013, 9, 338–354. [Google Scholar] [CrossRef]
- Gaus, M.; Lu, X.; M. Elstner, M.; Cui, Q. Parameterization of DFTB3/3OB for sulfur and phosphorus for chemical and biological applications. J. Chem. Theory Comput. 2014, 10, 1518–1537. [Google Scholar] [CrossRef] [PubMed]
- Lukose, B.; Kuc, A.; Frenzel, J.; Heine, T. On the reticular construction concept of covalent organic frameworks. Beilstein J. Nanotechnol. 2010, 1, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Gemming, S.; Enyashin, A.N.; Frenzel, J.; Seifert, G. Adsorption of nucleotides on the rutile (110) surface. Int. J. Mat. Res. 2010, 101, 758–764. [Google Scholar] [CrossRef]
- Koehler, C.; Frauenheim, T. Molecular dynamics simulations of CFx (x = 2, 3) molecules at Si3N4 and SiO2 surfaces. Surf. Sci. 2006, 600, 453–460. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Dale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter. 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhoff, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Zhechkov, L.; Heine, T.; Patchkovskii, S.; Seifert, G.; Duarte, H.A. An efficient a posteriori treatment for dispersion interaction in density-functional-based tight binding. J. Chem. Theory Comput. 2005, 1, 841–847. [Google Scholar] [CrossRef]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules; Springer Science: New York, NY, USA, 1979. [Google Scholar]
- Chen, X.-Q.; Fu, C.L.; Podloucky, R. Bonding and strength of solid nitrogen in the cubic gauche (cg-N) structure. Phys. Rev. B 2008, 77, 064103. [Google Scholar] [CrossRef]
- Zhao, J. First-principles study of atomic nitrogen solid with cubic gauche structure. Phys. Lett. A 2007, 360, 645–648. [Google Scholar] [CrossRef]
- Eremets, M.I.; Trojan, I.A.; Gavriliuk, A.G.; Medvedev, S.A. Synthesis of High-Nitrogen Energetic Material. In Static Compression of Energetic Materials; Peiris, S.M., Piermarini, G.J., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 75–97. [Google Scholar]
- Malyi, O.I.; Sopiha, K.; Kulish, V.; Tan, T.L.; Manzhos, S.; Persson, C. A computational study of Na behavior on graphene. Appl. Surf. Sci. 2015, 333, 235–243. [Google Scholar] [CrossRef]
- The Materials Project. Available online: https://www.materialsproject.org (accessed on 10 November 2015).
- Young, D.A. Phase Diagrams of the Elements; California University: Livermore, CA, USA, 1975. [Google Scholar]
- Schuch, A.F.; Mills, R.L. Crystal structures of the three modifications of nitrogen 14 and nitrogen 15 at high pressure. J. Chem. Phys. 1970, 52, 6000–6008. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capel, N.; Bharania, D.; Manzhos, S. A Comparative Density Functional Theory and Density Functional Tight Binding Study of Phases of Nitrogen Including a High Energy Density Material N8. Computation 2015, 3, 574-585. https://doi.org/10.3390/computation3040574
Capel N, Bharania D, Manzhos S. A Comparative Density Functional Theory and Density Functional Tight Binding Study of Phases of Nitrogen Including a High Energy Density Material N8. Computation. 2015; 3(4):574-585. https://doi.org/10.3390/computation3040574
Chicago/Turabian StyleCapel, Nicholas, Devang Bharania, and Sergei Manzhos. 2015. "A Comparative Density Functional Theory and Density Functional Tight Binding Study of Phases of Nitrogen Including a High Energy Density Material N8" Computation 3, no. 4: 574-585. https://doi.org/10.3390/computation3040574
APA StyleCapel, N., Bharania, D., & Manzhos, S. (2015). A Comparative Density Functional Theory and Density Functional Tight Binding Study of Phases of Nitrogen Including a High Energy Density Material N8. Computation, 3(4), 574-585. https://doi.org/10.3390/computation3040574