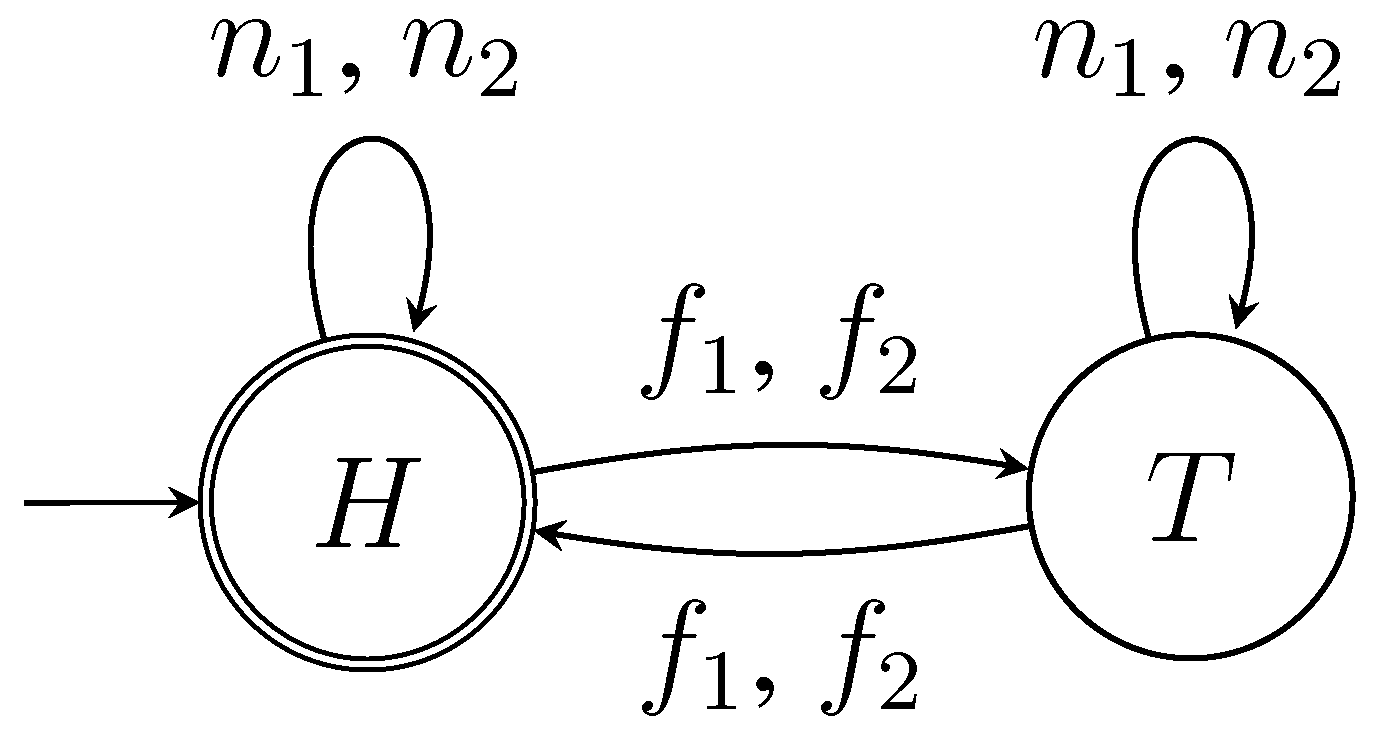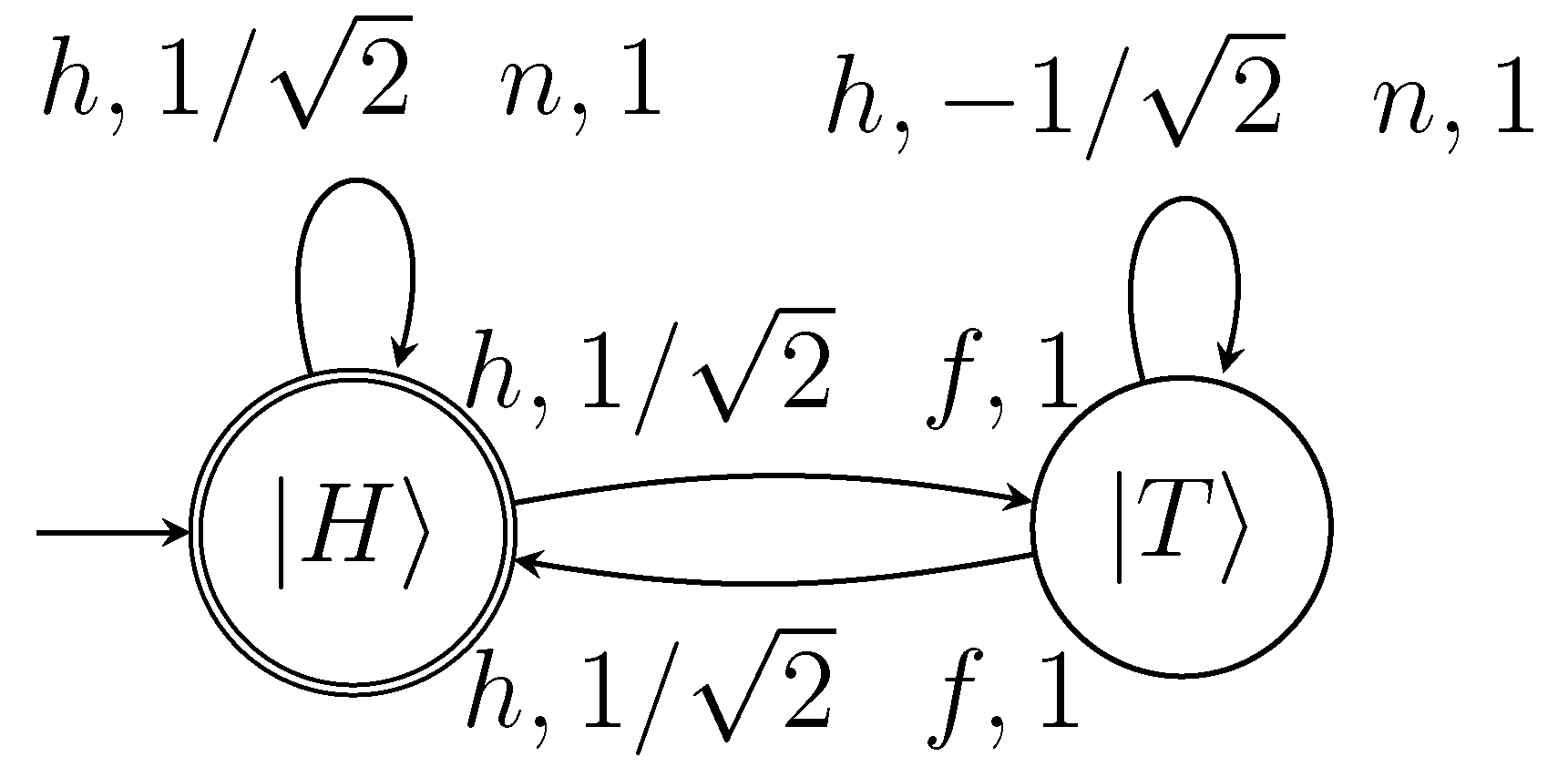Dominant Strategies of Quantum Games on Quantum Periodic Automata

Abstract

Game theory and its quantum extension apply in numerous fields that affect people’s social, political, and economical life. Physical limits imposed by the current technology used in computing architectures (e.g., circuit size) give rise to the need for novel mechanisms, such as quantum inspired computation. Elements from quantum computation and mechanics combined with game-theoretic aspects of computing could open new pathways towards the future technological era. This paper associates dominant strategies of repeated quantum games with quantum automata that recognize infinite periodic inputs. As a reference, we used the PQ-PENNY quantum game where the quantum strategy outplays the choice of pure or mixed strategy with probability 1 and therefore the associated quantum automaton accepts with probability 1. We also propose a novel game played on the evolution of an automaton, where players’ actions and strategies are also associated with periodic quantum automata.

1. Introduction

Game Theory has numerous applications, both in theory and practice. J. von Neumann, one of the greatest mathematicians of the 20th century, is considered the pioneer in the creation of the game theory. Game theoretic reasoning is widely used in politics, military, law, social sciences and biology. It is a useful tool for explaining and predicting behaviour in a wide range of situations. After all, a game is “...a purely imaginary idealization of a social interaction” [1]. In such models, it is important for deliberate decisions to be included in the game theory analysis, because people may act rational or instinctively. Systems regarding security, politics and economics are related to these models, e.g., political crisis is often treated like contest between two persons. Quantum game theory examines the application of quantum techniques in classical games, such as the Prisoners’ Dilemma, coin flipping, etc.

Quantum computing, a field that has been developed quite recently, was introduced by Richard Feynman in the 1980s, as he pointed out that the efficient simulation of an actual quantum system using a classical computer is not possible [2,3], since there would be an exponential slowdown when simulating actual quantum processes. Combining the above observation with the fact that Moore’s law is reaching its limits, it is becoming more and more obvious that we need to search for novel technologies and computation models [4,5]. Quantum computing, a concept that perceives the computing process as a natural phenomenon, could be one potential substitute or an addition to the standard computation methods.

Quantum computing stretches the use of quantum mechanics methods and models of computation. For works on the advantages of quantum computing over the classical one in terms of complexity theory examples can be found in [6,7]. A quantum system follows the laws of quantum mechanics. Transitions among the quantum states are stated through the application of unitary matrices (we explain what a unitary matrix is in the next sections). Instead of the bit as the basic unit of computation, quantum computing systems use qubits. Notable works that followed in the next years after the famous works of Feynman were the ones from Deutsch, and Deutsch and Jozsa in [8,9] and Shor [10].

Especially Shor’s work on the the problem of factoring integers in polynomial time by proposing a quantum algorithm drew the attention of the computing community because of the significance of this problem in various fields of computer science, including cryptography, algorithms and many more. Another important milestone was the algorithm of Grover that proposed a novel quantum algorithm for searching an unsorted array in $O\left(N^{1/2}\right)$, whereas any classical one needs $O\left(N\right)$ [11]. Furthermore, a famous work from Simon in [12] exhibited the power of quantum computation over the classic one, discussing for example quantum Turing machines. Quantum mechanics and the use of quantum-inspired computing technologies could offer an increase in computational capabilities and efficiency, since the quantum world has an inherently probabilistic nature, and non-classical phenomena, such as superposition and entanglement, occur.

This works addresses a game-theoretic problem using an automata-like approach. Finite automata (deterministic or not) are simple models of computation. In this paper, our contribution includes a variant of finite automata with quantum infinite evolution (quantum infinite automata). One can regard quantum automata as a quantum system with finitely many particles, where the application of a unitary operator is a symbol of its alphabet. We note that the notion of quantum automata was introduced in 1997 by Kondacs and Watrous [13], and independently by Moore and Crutchfield [14]. There are two prevailing approaches regarding the measurement of quantum automata, the measure-once (MO) and the measure-many (MM) approach. Measure-once automata are quantum automata for which the measurement takes place only once, after reading the last symbol of the input word. On the contrary, the measure-many approach involves measurements of the quantum automaton after the reading of each symbol.

Our paper is organised as follows. The next Section presents related works and the most basic literature on the preliminary concepts, specifically on quantum games, quantum computation, and automata theory concerning this study. Then, Section 3 covers the background, which includes definitions and the formalism we use in game theory, the mathematical concepts needed, ω-computability, and quantum computation. In this section, the definition and a brief description of the PQ-PENNY quantum game is offered along with the definition of the periodic infinite quantum automaton. Then we proceed to Section 4 that contains the main part of this study with the results of our work, which are briefly discussed in the last section. Subsection 4.1 involves the formulation of a novel game that shares similar properties, as far as the association with periodic quantum automata is concerned.

This work contributes to the algorithmic game theory by proposing a methodology that associates winning strategies of some quantum games with quantum automata on infinite periodic inputs. We present a method to translate actions into quantum inputs as unitary matrices with periodic behaviour inspired by the automata of related works and then we use the well-known PQ-PENNY quantum game as a case study, showing the corresponding automaton with the appropriate transition “weights”. We showcase generated automata that correspond to the always-winning strategies and depict the complex evolution matrices for the choice of each player every time. We also propose a novel game, the Provider vs. Measurer, where players’ actions and strategies in the quantum version are also associated with periodic quantum automata.

2. Related Works

Numerous works investigate the connection of games with economy, security and cryptography [15], social relations and so on. Quantum computation is well explained in [16], whereas [17] provides an elegant introduction to the concept of quantum game theory, along with a review of the related literature. Quantum automata have met a remarkable growth during the last decade. On one hand, it seems that they possess some interesting and useful properties (e.g., they are usually space-efficient), but on the other hand, many aspects and variants of quantum automata are still unexplored. Adequate literature on quantum automata, and their various variants that have already been proposed, can be found in [18,19,20,21].

A first attempt to combine automata receiving infinite words with quantum behaviour was described in [22]. The reader can consult the work of [23] on the necessary mathematical background for our study. The study of finite state machines that work with infinite inputs begun in the ’60s by various scientists such as Büchi, Rabin, McNaughton and others. An elegant summary of these works is presented in [24,25] by Thomas et al. Applications of finite automata in game theory can be traced back to 1985, when Neyman in [26] studied the results of using finite automata to bind the complexity of strategies available to players. Rubinstein in [27] studied a variation of the repeated prisoners’ dilemma, in which each player is required to play the game using a Moore machine (a type of finite state transducer). Extending the aforementioned work, Rubinstein and Abreu examined infinitely repeated games, using Nash equilibrium as a solution concept, in which players seek to maximize their profit and minimize the complexity of their strategies [28].

Infinite games and their connection with automata are reviewed and studied in [29], where the authors propose the use of automata for solutions of games with complex winning conditions. The works of [24,30,31] are also oriented to the connection of infinite automata and games. Another popular application of automata in game theory is their combination with evolutionary processes such as genetic algorithms. In [32] the authors examined Abreu-Rubinstein style systems, replacing the solution concept of Nash equilibrium with that of the evolutionarily stable strategy, concluding that such automata are efficient in the sense that they maximize the sum of the payoffs. Ho in [33] showed how computing complexity costs affects the resulting strategies. A recent work by Ambainis and Yakaryilmaz in [34] presents a detailed review, covering the full spectrum of the various variants of quantum automata that have been proposed. [35] contains the association of parrondo games with a variant of automata (quantum lattice gas automata). Parrondo games and quantum algorithms are discussed in [36], as well. Finally, the authors in [37] investigated the use of probabilistic automata, evolved by a genetic algorithm, to model adaptive behaviour in prisoners’ dilemma.

A seminal study in the field of quantum game theory is the one presented in [38] where the authors examined the application of quantum techniques in a Prisoners’ dilemma game and ended up with three very interesting conclusions, namely, that whenever both players resort to quantum strategies there is no longer a dilemma, that there exists a Nash equilibrium pair for quantum strategies that always gives reward, and that there exists a particular “miracle move” that always gives reward when played against any classical one. However, the aforementioned work of Eisert et al. in [38] was debated by other investigations, such as Benjamin and Hayden in [39] and Zhang in [40]. The above works noted that players in [38] were restricted and therefore the Nash equilibria that turn up are not right.

Landsburg in [41] studied mixed-strategy Nash equilibria in quantum games, showing that up to a natural definition of equivalence, all Nash equilibria in a set of games called “generic games” have a simple form. Zhang in [40] examined the twofold advantages of quantum strategies proposing a new complexity measure called correlation complexity. In the same work, it was also proposed a novel model, that is now widely considered as the correct one for studying quantum games in strategic form. The concept of correlation complexity is also discussed in [42] by Jain et al., a work that extended the [40], whereas in [43] there is the extension to the multipartite case. Quantum games are also studied in [44] with focus on the illustration of the relationship among quantum mechanics notions and Nash equilibria. They, also, investigate the entropy of such games and their minimal value under specific Nash equilibria.

3. Preliminary Concepts and Definitions

Before proceeding to the main parts of this work, we provide the most important background notions and definitions. In the next subsections we offer the appropriate material covering parts of game theory, ω-computability (mainly ω-automata), and formalism of quantum computing.

3.1. Game Theory

The number of players is denoted by n. Players are labeled with numbers 1 to n, forming the set N = {1, 2, ..., n}. In our work we focus on 2-player games.

The simplest mathematical description of a game is the strategic form. According to it, a two-person zero-sum game is a triplet (X, Y, A), where

• X is a nonempty set denoting the strategies of Player 1,
• Y is a nonempty set for the strategies of Player 2, and
• A is a real-valued function defined on $X\times Y$.

Games involve strategies executed with two kinds of actions, pure and mixed. We refer to elements of sets X or Y as pure strategies, whereas the choice of pure strategies at random comprises a mixed strategy. A two-person zero-sum game is said to be a finite game if both strategy sets X and Y are finite [45].

3.2. Mathematical Background

Σ defines the alphabet, ${\Sigma }^{*}$ is the set of all finite strings over the Σ, and ${\Sigma }^{\omega }$ denotes the set of all strings with infinite length. If U is a $n\times n$ square matrix $\overline{U}$ denotes its conjugate, and $U^{†}$ its transpose and conjugate. The set of complex numbers and real numbers are denoted with $\mathbb{C}$ and $\mathbb{R}$, respectively. ${\mathbb{C}}^{n\times n}$ stands for the set of all $n\times n$ complex matrices.

The possible outcomes of measuring a quantum system are the eigenvalues of the chosen observable. Transitions that define the evolution of a quantum system (and therefore a quantum automaton) are described by complex coefficients whose squared norm is in the closed set [0,1]. In addition, the sum of these norms is always equal to 1. The conjugate of z is $\overline{z}=a-ib$. The polar form of a complex number $z=a+ib$ is expressed as $z=\left|z\right|(cos\psi +isin\psi )$. Lastly, a n-dimensional vector space ${\mathbb{C}}_n$ with the inner product $〈x|y〉$ is called a Hilbert space ${\mathcal{H}}_n$ [23].

3.3. ω-Computability and ω-Automata

An ω-automaton is an extension of the non-deterministic finite automaton reading infinite words [25]. Along with determining final states, we impose an acceptance condition under which we accept/reject the infinite input. An ω-automaton is a tuple (Q, Σ, δ, $q_0$, F, Acc) where Q is a finite set of states, Σ is the finite alphabet, δ : Q × Σ → P(Q) is the transition function (P(Q) defines the powerset of the set Q), $q_0$ is the initial state, F is the set of final states and Acc determines the acceptance condition. The powerset of the set of states as a range of the transition function refers to the non-deterministic version of ω-automata, while in the case of deterministic ones the range is simply a state of the set Q. The most common acceptance conditions are these of Büchi, Streett, Rabin, and Muller [25].

3.4. Quantum Computing

There are two types of quantum states: pure and mixed states. A pure state is a state represented by a single vector $\left|\psi \right.〉$ over a complex Hilbert space. A mixed state is a statistical distribution of pure states expressed in the form of density matrices. Each state $q_i$ of the set Q with $\left|Q\right|=n$ is represented by a vector $e_i=(0,\dots ,1,\dots ,0)$. Each of the quantum states is a superposition of the form ${\displaystyle \sum _{i=1}^n}{c}_i{e}_i$, where n is the number of states, $c_i\in \mathbb{C}$ are the coefficients and $e_i$ denotes the (pure) basis state corresponding to i. Each symbol ${\sigma }_i$ of the finite alphabet Σ is associated with a unitary matrix $U_{{\sigma }_i}$ and each observable is associated with an Hermitian matrix $\mathcal{O}$. Transitions among states are achieved through the application of unitary operators of the form $U_{{\sigma }_i}$. In Dirac formalism, each state of the machine is a superposition of basis states $\left|{\psi }_i\right.〉$. Each state has the form $\left|\psi \right.〉$=$c_1\left|{\psi }_2\right.〉+c_2\left|{\psi }_2\right.〉+\dots +c_n\left|{\psi }_n\right.〉$, where we have that $|c_1{|}^2+|c_2{|}^2+\dots +{\left|c_n\right|}^2=1$.

3.5. Periodic Quantum Automata for Infinite Inputs

Here we summarize the definition of the quantum automata for infinite periodic words from [46].

Definition 1. 

A simple m-periodic, 1-way quantum ω-automaton with periodic measurements is a tuple (Q, Σ, $U_{\delta }$, $q_0$, m, ${\pi }_0$, F, P, Acc), where Q is a finite set of states, Σ; is the input alphabet, $U_{\alpha }$ : Q × Σ →${\mathbb{C}}_{[0,1]}$ is the $n\times n$ unitary matrix that describes the transitions among the states for each symbol $\alpha \in \Sigma$, $q_0$ ∈ Q is the (pure) initial state, m ∈ $\mathbb{N}$ defines the measurement period, ${\pi }_0$ is the vector of the initial pure state $q_0$, F ∈ Q is the set of final states,P is the set [$P_0$, $P_1$, …, $P_n$] of the projection matrices of states, and Acc is the almost-sure periodic quantum acceptance condition.

In order to achieve the periodic functionality, the transition matrix for every symbol must have the form of $U_{\varphi }$ = i $\left(\begin{array}{cc}cos\left(\varphi \right)& sin\left(\varphi \right)\\ -sin\left(\varphi \right)& cos\left(\varphi \right)\end{array}\right)$. The angle ϕ in the transition matrix defines the period (if m is the period of the transition, then $\varphi =\pi /m$). After m applications of the transition matrix U, the state of the system is $U^m\left|\psi \right.〉$. Automaton starts at its initial pure state $q_0$, either the $1\left|q_0\right.〉+0\left|q_1\right.〉$ or the $0\left|q_0\right.〉+1\left|q_1\right.〉$. Transitions among the states are expressed with complex amplitude.

4. Mapping Dominating Quantum Strategies to Quantum Periodic Automata

In this work we present a novel way to formally establish a dominating quantum strategy in certain games. Specifically, we refer to zero-sum games and we use the well-known game called PQ-PENNY played by two players (the formal definition of the PQ-PENNY can be accessed in [47]). We have already provided the necessary notions and definitions regarding game theory and their algorithmic description. We have also described the functionality and the behaviour of the quantum periodic automata for infinite inputs as they are described in [46].

In short, we observed that when playing this game infinitely often and in sequential mode, the produced sequence describing the strategy that guarantees a win for the first player, is actually a periodic word of period 3. This is a result of the choice of both players, having in mind that actually the second player is doomed to a losing strike, regardless of his chosen actions. We remind the reader that the second player is able to act through pure or mixed strategies and not quantum ones.

The work of Meyer [47] is mainly focused on the description of the PQ-PENNY game. It demonstrates the superiority of choosing a quantum strategy over a classical (or even probabilistic) one. In Meyer’s work, the chosen game has finite sequences of rounds. On the other hand, as it will be shown in the next sections, our work is devoted to the analysis of the infinite version, where repeated rounds are examined in a more extensive form. Moreover, in the Subsection 4.1 we propose another game, where the association with the same automata appears.

A novel quantum variant of finite automata receiving infinite inputs was introduced in [46] by Giannakis et al. The key point of this work was the periodic measurement mode on the input, since any realisable quantum system has to undergo measurement(s) in order to obtain a tangible result. Contrary to the finite inputs where the choice of measurement number in most cases is either one (after the reading of the whole input) or many (after the reading of each symbol), the field of infinite inputs is still largely unexplored. In [46] the authors use a periodic mode of measuring the quantum system, using a constant period of m∈$\mathbb{N}$. In the case of a quantum game, we show in this work that this period can be specified by the number of actions that take place in the game. Even Meyer in [35] associated games with a variant of automata for specific forms of games (i.e., parrondo games, games with the property that alternating plays of losing games can result to a win).

The actions in the standard PQ-PENNY game are usually finite, but they can be extended to become infinite if we allow the game to be played infinitely many times in a consecutive manner. In this case, we refer to the game as a repeated game (see [47,48]). Although the expressiveness of this automata type is restricted to periodic inputs, they can be used as acceptors for repeated games, where the dominating strategy is always selected. The fact that in many games a winning strategy is present, regardless of the opponent’s action(s), assumes an underlying sequence of chosen actions that are characterised by a period depending on the minimum actions that are necessary for the simple (not repeated) game.

The procedure for transforming the actions chosen by the players to input strings is simple. In the PQ-PENNY game each player has two choices, he either flips the coin or he leaves it untouched. Therefore, we can call these flip ($F_a$) and no-flip ($N_a$) for this player (player a). In the case of pure actions, his strategy will be either $F_a{F}_a$, $F_a{N}_a$, $N_a{N}_a$, or $N_a{F}_a$. The modeling of the action chosen by the second player follows a similar approach.

In order to be consistent with the use of unitary matrices for the quantum evolution of the game, we use the matrix-like approach for each symbol of the automaton (or, equivalently, each action). Therefore, the pure actions for the players are of the form $F_a=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$ and $N_a=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$. One can easily observe that $F_a$ is the first of the Pauli matrices (${\sigma }_1$ or ${\sigma }_x$), whereas $N_a$ is the unit matrix. In the case of mixed strategies, the above matrices have the form of $F_a=\left(\begin{array}{cc}1-p& p\\ p& 1-p\end{array}\right)$ and $N_a=\left(\begin{array}{cc}p& 1-p\\ 1-p& p\end{array}\right)$ where p is a probability. Similarly, we can define the matrices for the second player.

If we allow the players to use solely pure strategies, we would obtain a state machine where the input alphabet is the actions, the initial state is the Head (according to the definition of PQ-PENNY game in [47]), and the terminating state is also the Head (to define the win of player 1, we can alter this in case we want to “accept” movements that give player 2 the win). We remind the reader that in the case of the PQ-PENNY game with pure actions, there is no Nash equilibrium.

If we denote each action of each player with a corresponding symbol, we will have:

• $f_1$ and $n_1$ for the flipping and no-flipping by player 1, and similarly
• $f_2$ and $n_2$ for the choices of the second player.

The automaton below (in Figure 1) accepts words that end in state H. Thus, sequences of the choices made by the players in the simple version of the game (e.g., $n_1{n}_2{n}_1$, $n_1{f}_2{f}_1$, etc.) are the input of the automaton. Those that provide victory for the first player are the accepting runs by this finite automaton.

Figure 1. A simple example of a DFA (i.e., Deterministic Finite Automaton) that accepts sequences of moves of the simple coin game.

Figure 1. A simple example of a DFA (i.e., Deterministic Finite Automaton) that accepts sequences of moves of the simple coin game.

If we consider the repeated version of the game (still with pure actions) with infinite horizon, we have to declare the acceptance condition under which the automaton accepts/rejects. Nevertheless, we have already declared that player 1 (Q in the original work of Meyers in [48]) is capable of using quantum strategy. Therefore, the evolution matrices for his choice is described by the matrix $U_{h_a}=\left(\begin{array}{cc}a& b\\ b& -a\end{array}\right)$. Observe that this quantum transition matrix defines clockwise rotation [46].

The dominating sequence of moves is the successive application of a unitary matrix by player 1 that is equivalent to the Hadamard transform (the Hadamard transform is expressed with the unitary matrix $H={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$). This choice is expressed by the symbol h in the automaton’s alphabet. The second player can perform either a flip or a no-flip, which are associated with the symbols f and n, respectfully. These two symbols have their corresponding transition matrices, but contrary to the quantum unitary matrix of h, we have simple deterministic matrices.

Figure 2. A simple example of the quantum periodic automaton accepting the infinite sequence of movements in PQ-PENNY game (see [47] for details). The measurement period is $m=3$ (it is equal to the number of movements to complete a simple game).

Figure 2. A simple example of the quantum periodic automaton accepting the infinite sequence of movements in PQ-PENNY game (see [47] for details). The measurement period is $m=3$ (it is equal to the number of movements to complete a simple game).

Consequently, for a simple game we have the strings $hfh$ and $hnh$ that both result in the winning of player 1. Since we observe that this is a dominant strategy, repeated executions of the game do not affect the plan of player 1 that guarantees him a victory with probability equal to 1. Below we show how the associated automaton for the dominant strategy is. Figure 2 depicts the previously described sequence of moves, translated into strings of infinite length. We assume as an accepting state the Head state, that is we accept games that offer the win to the first player (Q in Meyers).

4.1. Provider vs. Measurer: Another Example Game

In this subsection we depict another game and we then associate its actions with a finite automaton. Afterwards, we proceed with the quantum version of the game, where the association corresponds to periodic quantum automata.

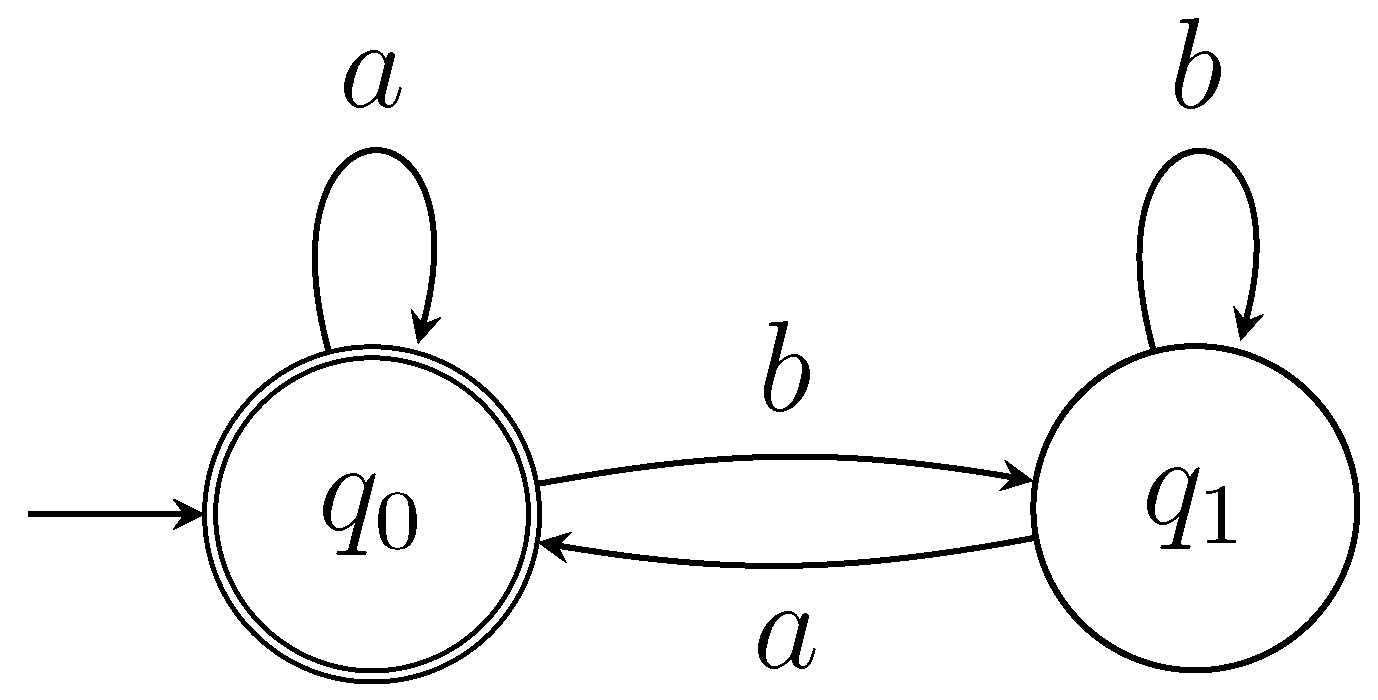
The game has the following set-up. There are two players playing a game over the evolution of a simple deterministic automaton. The basic version is a game played over a two-state automaton (states $q_0$ and $q_1$) with an alphabet consisting of two symbols ($\Sigma =\{a,b\}$). We declare that $q_0$ state is the winning final state for Player 1 and $q_1$ the winning one for Player 2. The automaton is described in Figure 3 and it has the simple transition matrix shown in Table 1.

Figure 3. The automaton that corresponds to Player 1. In the case of Player 2, the accepting state is the state $q_1$.

Figure 3. The automaton that corresponds to Player 1. In the case of Player 2, the accepting state is the state $q_1$.

Table 1. Transition matrix of the automaton of Figure 3.

	$q_0$	$q_1$
$q_0$	a	b
$q_1$	a	b

Table 1. Transition matrix of the automaton of Figure 3.

	$q_0$	$q_1$
$q_0$	a	b
$q_1$	a	b

Player 1 chooses at each timestep a symbol and runs it on the automaton. He keeps reading symbols until Player 2 decides to stop the procedure (after having read sufficiently enough symbols). Player 2 has no knowledge about either the read symbols or the current state. Then, the payoff for each player depends on two parameters: the current state after the stop command called by Player 2 and the number of bs read until the pause. At first, a player gains 2 if the final state is the one corresponding to him. Secondly, Player 1 gains 1 if the number of read bs in the input string is greater than the number of as until the stop command. In the other case (if $\left|b\right|\le \left|a\right|$, where $\left|b\right|$ denotes the number of the occurrences of the symbol b in the final string), Player 2 gains the 1 “points”. Therefore we have the below payoff matrix shown in Table 2.

Player 2 is not allowed to observe the read input symbols until he decides to stop the procedure. He is only aware of the total length of the input word, and he is informed each time Player 1 pushes a letter to the automaton. He chooses the time to ask blindly. On the other hand, Player 1 chooses one of the two symbols not knowing when Player 2 is about to stop the procedure in order to compute the gain and loss of both the players (see the above payoff matrix in Table 2). Every reading of a b symbol gets his win in stake since the automaton transits to state 2, which is the winning state for Player 2. But if he insists on reading only the symbol a, he guarantees a (1, 1) result for himself, since the pause of Player 2 will occur on having the current automaton’s state to be the $q_0$, but the number of bs will be 0 and therefore smaller than the number of as ($\left|b\right|<\left|a\right|$).

Table 2. The game’s payoff matrix. The state in the columns denote the automaton’s state after reading the final symbol when Player 2 stops the procedure.

	$\left|b\right|\le \left|a\right|$	$\left|b\right|>\left|a\right|$
$q_0$	(1, 1)	(2, 0)
$q_1$	(0, 2)	(1, 1)

Table 2. The game’s payoff matrix. The state in the columns denote the automaton’s state after reading the final symbol when Player 2 stops the procedure.

	$\left|b\right|\le \left|a\right|$	$\left|b\right|>\left|a\right|$
$q_0$	(1, 1)	(2, 0)
$q_1$	(0, 2)	(1, 1)

The rational strategy for both the players under simple deterministic actions would lead to one of the two situations with payoff 1 for both the players, i.e., (1, 1). Player 1 would constantly choose b, that would drive the automaton on state $q_1$, whereas if he chooses the option of constantly remaining in $q_0$, the state $q_0$ as a result is guaranteed. Therefore, in order to avoid risking a loss by a margin of two, Player 1 will chose one of the above strategies. Any other strategy reduces the possibility of winning.

Imagine players as war opponents, where the two states of the automaton resemble the two war camps of each player/opponent. Player 1 is the leading opponent and he has the choices of either attacking or defending. When in attack, he resides in the opponent’s camp, whereas defending means he is in his own camp (state $q_0$ in the automaton). Player 1 aims at attacking more frequently than defending, while he hopes that when Player 2 stops, he will be found in his own war camp (state $q_0$). The strategy of Player 1 involves infinite choices of attacks and defences, the procedure halts when Player 2 calls for a stop.

If you transfer the game setup of the previously described game in the quantum world, we observe a different behaviour, under specific circumstances. At first, Player 2 in the quantum variant is not actually stopping the evolution but rather, he measures the current state. That is the reason he is called the “measurer”. Player 1 still chooses the symbols in each timestep. But since we talk about quantum systems, symbols are operators expressed by unitary matrices.

Since the underlying automaton is now operating as a quantum system, well-known properties from the quantum world arise. The state of the automaton after the read of each symbol/operator is now a superposition of states rather than the simple pure states $q_0$ and $q_1$. Player 1 decides to associate each symbol to specific unitary matrices in order to maximize the probabilities to win. Therefore, he associates a quantum operator, similar to those of periodic quantum automata, to the symbol a in order to control the state after providing this symbol to the automaton. In the case of b, he associates it with a specific matrix that actually does not alter the quantum state, similarly to the actions of Piccard in the PQ-PENNY game.

For example, he chooses the matrix $U_1$ = i $\left(\begin{array}{cc}cos\left(\varphi \right)& sin\left(\varphi \right)\\ -sin\left(\varphi \right)& cos\left(\varphi \right)\end{array}\right)$ with $\varphi =\pi /m$, $m=2$ for the a and the $U_2$ = i $\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)$ with $\varphi =\pi /m$, $m=1$ for the b. That is, for the symbol a the transition is periodic with period $m=2$, and for the b with period $m=2$. Thus, Player 1 chooses the for the first 2 inputs the symbol a (as stated before, Player 2 stops the procedure after the automaton has consumed sufficiently enough symbols), and then he consequently applies the matrix $U_1$, i.e., the symbol b that guarantees that the states is not changing. Therefore, the quantum version of the game, offers strategies that can be described as inputs in quantum periodic automata, after the proper translation of the input symbols to quantum, unitary matrices. An example quantum strategy for Player 1 would be the $w=aabbbbbbbbbbbb\dots bbbb$, then Player 2 stops the procedure, and Player 1 wins 2 points, while Player 2 gains 0.

5. Conclusions

Traces of game theory are found in many aspects of research. Therefore game theory, and especially its quantum variants could be useful in the proper design of efficient and fairer structures that will affect the people in a direct manner. This remark enhances the research on algorithmic quantum game theory, in order to find suitable models.

In this work we proposed the association of dominant strategies of some quantum games with a variant of quantum automata. We examined the repeated version of the game in infinite horizon and therefore the corresponding automata had to be modified to express this reality. Thus, the association was achieved using quantum automata that run on infinite periodic words. Specifically, we used the PQ-PENNY quantum game as a model to demonstrate our approach. We also provided a novel game, designed on the evolution of an automaton, where the above result still holds.

Quantum automata on periodic infinite inputs have recently been proposed as an extension to the classic ω-automata, solving the problem of the measurement timing by using periodic timesteps. As we displayed in Section 4, the connection between (infinite) sequences of chosen actions formed by dominant strategies and the evolution of such automata is straightforward, by exploiting the fact that a dominant strategy hides a periodic part that simulates the winning choices of quantum actions. These quantum actions are expressed by unitary matrices.

The fact that there appears a connection among automata-like models of computation and algorithmic aspects of quantum games seems an appealing observation and could be found useful in the computation process and modeling of systems that involve traces of specific quantum games. The expressive power and the simplicity of automata variants can be found crucial in the analysis and description of more complex entities and environments, such as games (in this case quantum games). Besides, there is a need for a better exploration of quantum strategies in games, since in some cases they seem to offer advantages over the classical ones (e.g., see the work of [49]).

Regarding the results of this work, there are some questions that have arisen. More research is required on other variants of quantum games, besides zero-sum games of two players. Moreover, it would be interesting to analyse repeated games that deal with voting protocols and voting procedures that exploit the advantages of quantum computation and quantum strategies.