On Roof Geometry for Urban Wind Energy Exploitation in High-Rise Buildings
Abstract
:1. Introduction
2. Turbulence Modeling and Computational Tools Validation
2.1. Governing Equations, Turbulence Modeling and Computational Settings
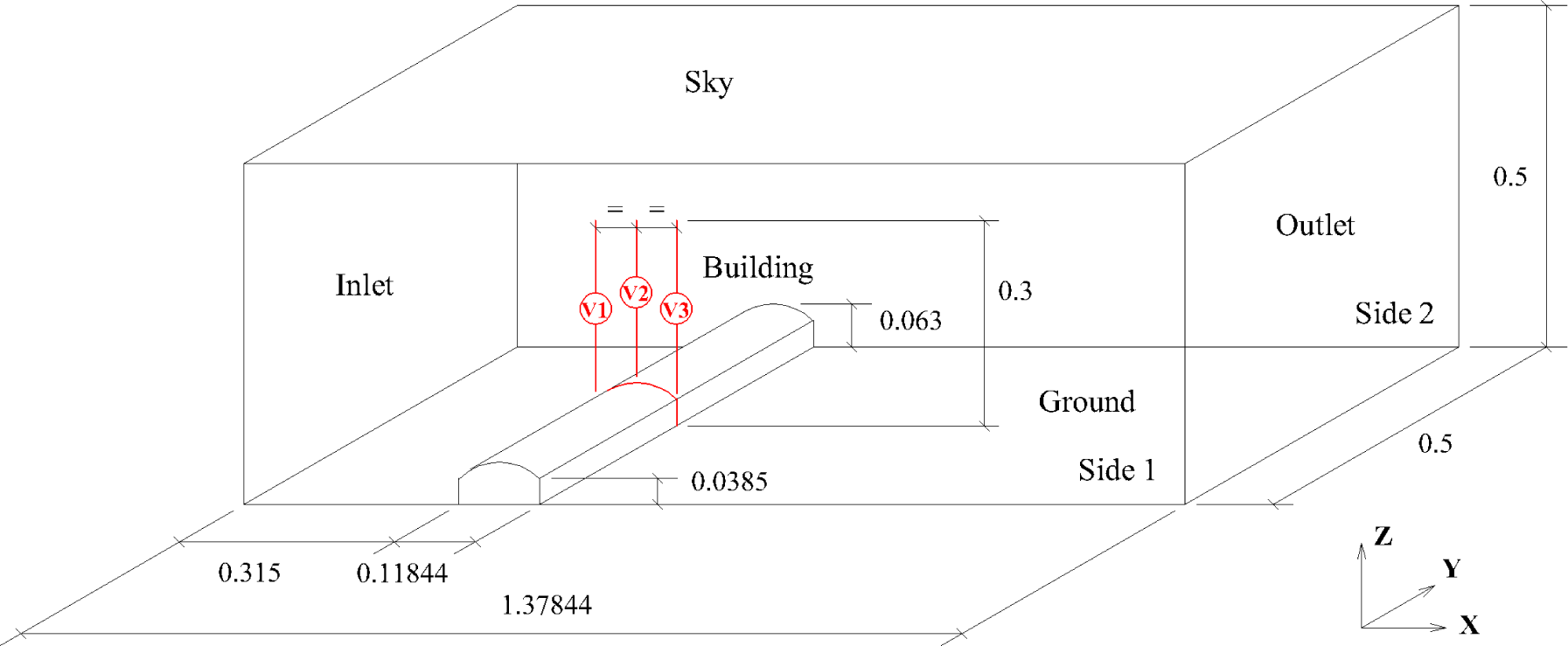
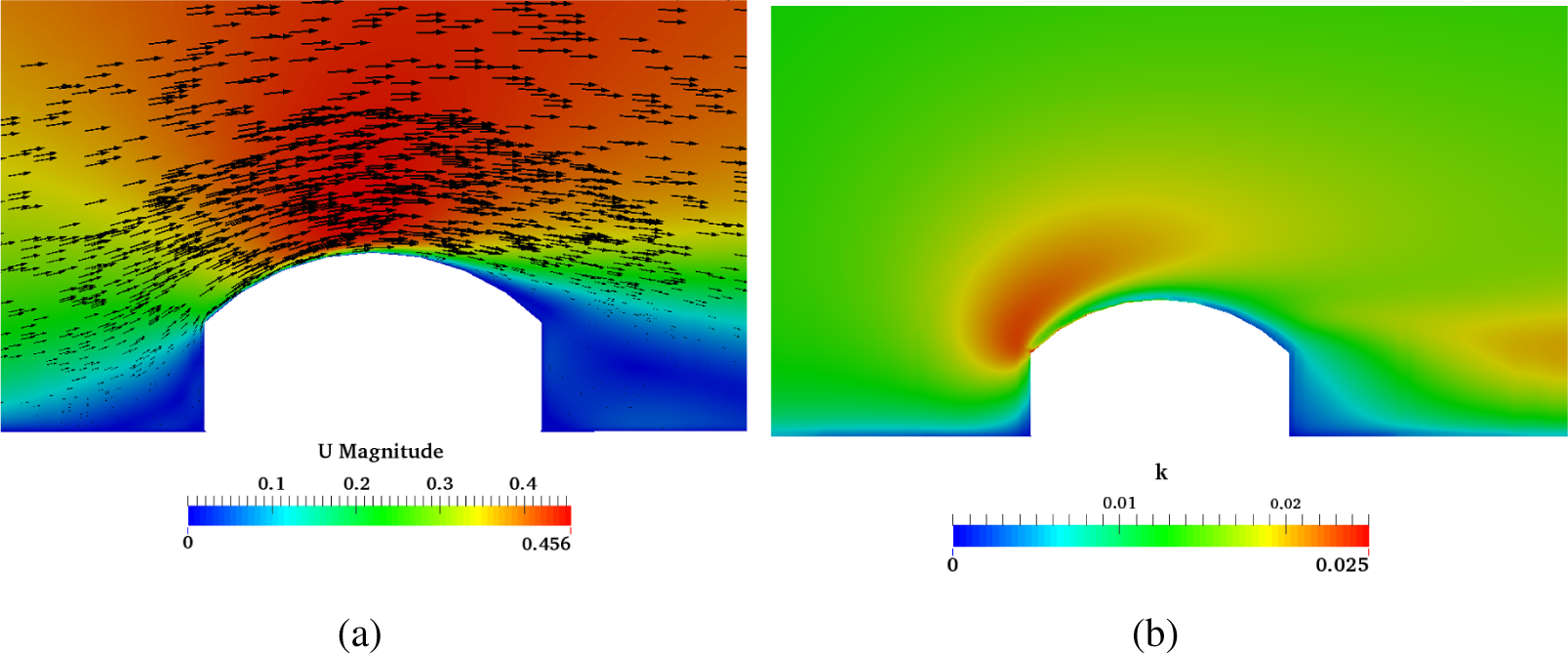
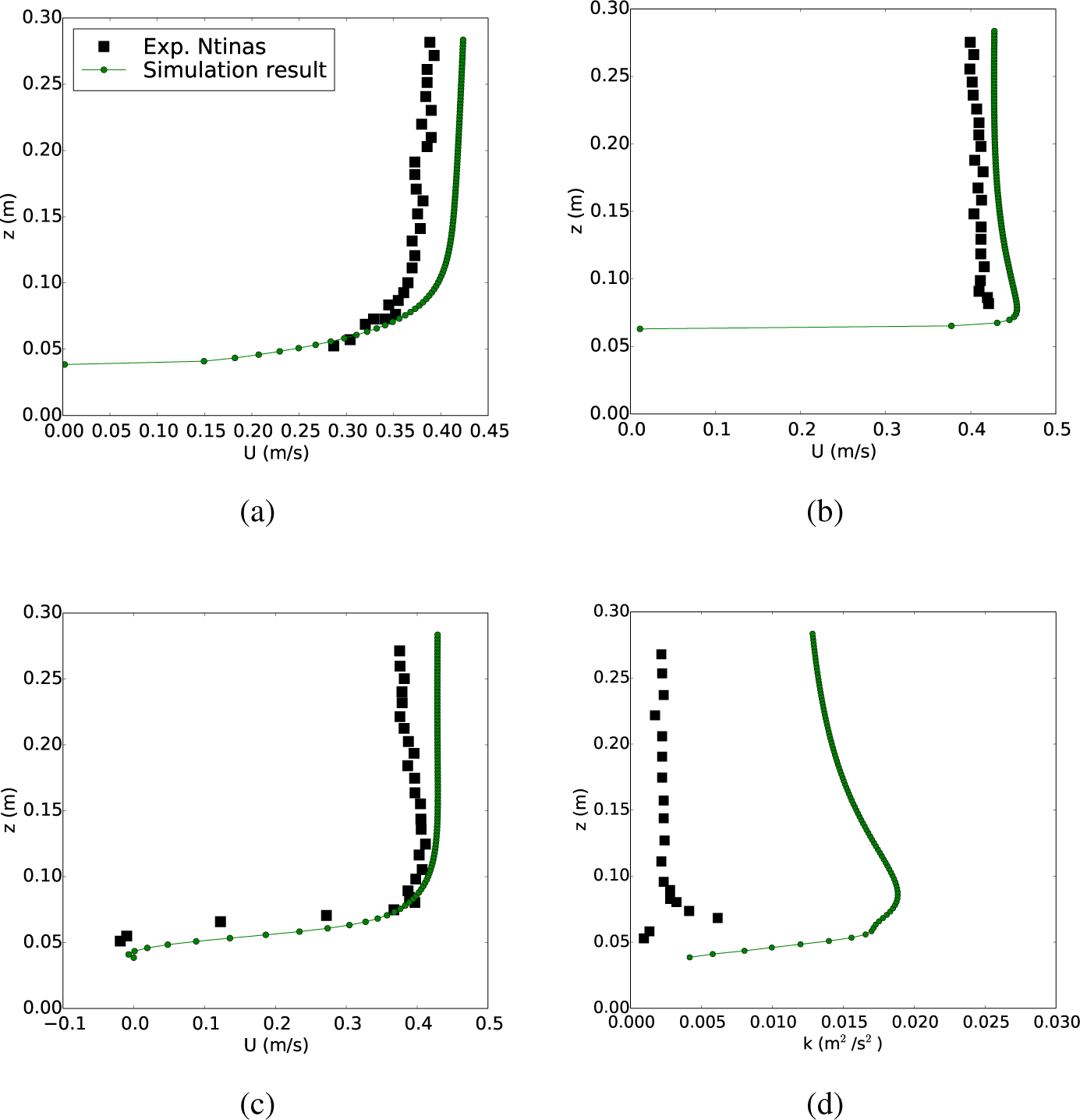
2.2. Additional Validation of Numerical Schemes Using a Curved Roof Model in Wind Tunnel
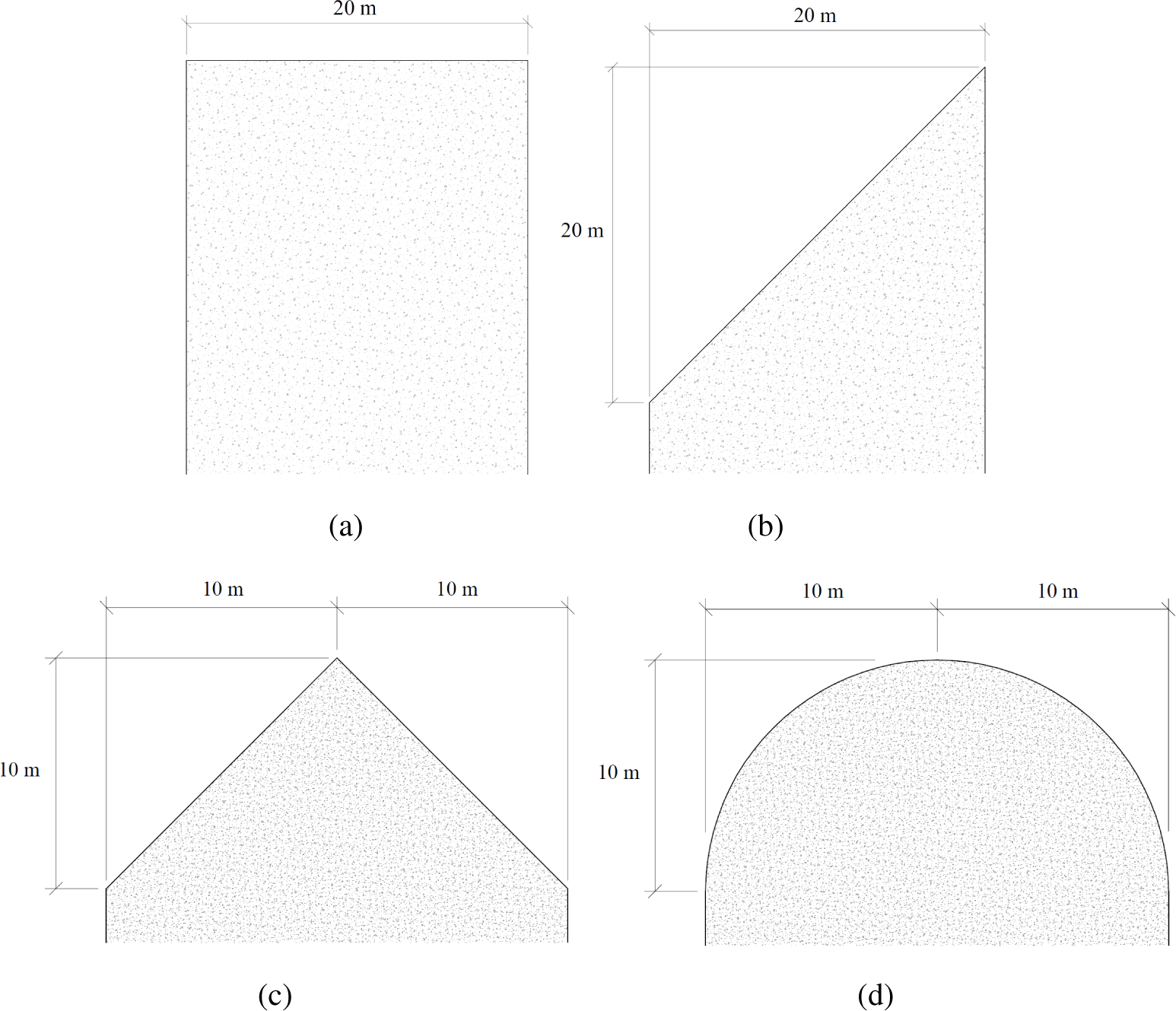
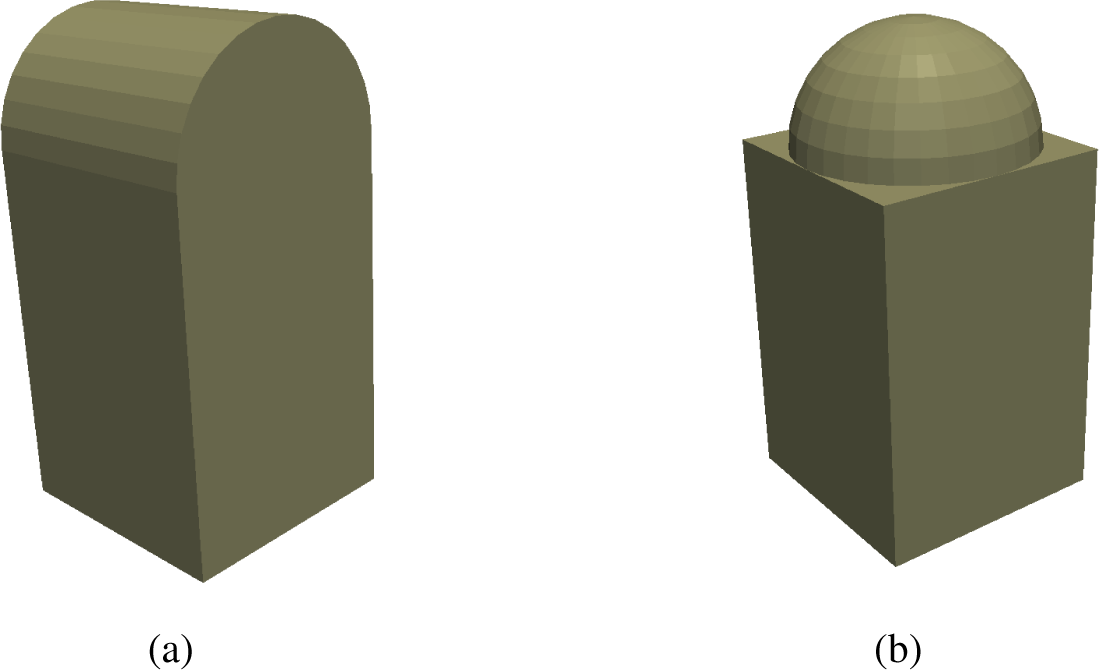
3. State-of-the-Art Roof Shapes
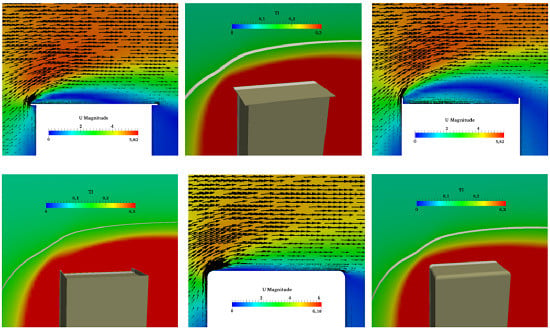
4. Influence of the Roof Edge Shape on the Wind Flow
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Greek | |
|---|---|
| κ | Von Karman constant (-) |
| ε | Turbulence dissipation (m2/s3) |
| ρ | Fluid density (kg/m3) |
| σk | Kinetic energy Prandtl number (-) |
| σε | Dissipation Prandtl number (-) |
| ν | Kinematic viscosity (m2/s) |
| νt | Kinematic eddy viscosity (m2/s) |
| Latin | |
|---|---|
| AD | Absolute maximum admissible deviation from the experimental data |
| C | Calculated |
| Cε1 | Closure constant k − ε model (-) |
| Cε2 | Closure constant k − ε model (-) |
| Cµ | Model coefficient turbulence model (-) |
| CAD | Computer-aided design |
| CFD | Computational fluid dynamics |
| DIC | Diagonal incomplete-Cholesky |
| DILU | Diagonal incomplete LU |
| EU | European Union |
| EXPi | Experimental value |
| fV | fixed value |
| GAMG | Generalized geometric-algebraic multi-grid |
| H | Building height (m) |
| HAWT | Horizontal axis wind turbine |
| HRk | Hit rate for k (%) |
| HRU | Hit rate for U (%) |
| iP | Inlet profile |
| k | Turbulent kinetic energy (m2/s2) |
| LU | Lower upper (factorization) |
| M | Millions |
| n | Total number of points compared (-) |
| PBiCG | Preconditioned bi-conjugate gradient |
| Pk | Production of k (m2/s) |
| RANS | Reynolds Averaged Navier-Stokes equations |
| RD | Relative maximum admissible deviation from the experimental data |
| Re | Reynolds number (-) |
| SIMi | Simulation value |
| S | Modulus of the rate of strain tensor (-) |
| SKE | Standard kε turbulence model |
| sl | Slip |
| sP | Symmetry plane |
| STL | Stereolithography |
| T | Turbulence velocity time scale (s) |
| TD | Turbulence velocity time scale adopted for the Durbin turbulence model (s) |
| TSKE | Turbulence velocity time scale adopted for the SKE turbulence model (s) |
| TI | Turbulence intensity (-) |
| U | Streamwise velocity (m/s) |
| U∗ | Frictional velocity (m/s) |
Reynolds stresses (m2/s2) | |
| Uref | Reference velocity (m/s) |
| VAWT | Vertical axis wind turbine |
| wF | Wall function |
| XR | Recirculation (or reattachment) distance on the roof |
| y+ | Non-dimensional wall distance (-) |
| z | Height (m) |
| z0 | Roughness height (m) |
| zref | Reference height (m) |
| zG | zeroGradient |
References
- European Commission. Horizon 2020 Programme. Available online: http://ec.europa.eu/programmes/horizon2020/ accessed on 6 April 2015.
- Walker, S.L. Building mounted wind turbines and their suitability for the urban scale—A review of methods of estimating urban wind resource. Energy Build 2011, 43, 1852–1862. [Google Scholar]
- Banks, D.; Cochran, B.; Denoon, R.; Wood, G. Harvesting wind power from tall buildings, Proceedings of the CTBUH 8th World Congress, Dubai, United Arab Emirates, 3–5 March 2008; The Council on Tall Buildings and Urban Habitat: Chicago, IL, USA; pp. 320–327.
- Chicco, G.; Mancarella, P. Distributed multi-generation: A comprehensive view. Renew. Sustain. Energy Rev 2009, 13, 535–551. [Google Scholar]
- COST Action TU1304, WINd Energy Technology Reconsideration to Enhance the Concept of Smart Cities (WINERCOST). Available online: http://www.cost.eu/domains_actions/tud/Actions/TU1304 accessed on 6 April 2015.
- Toja-Silva, F.; Colmenar-Santos, A.; Castro-Gil, M. Urban wind energy exploitation systems: Behavior under multidirectional flow conditions—Opportunities and challenges. Renew. Sustain. Energy Rev 2013, 24, 364–378. [Google Scholar]
- European Commission. Communication from the Commission of 13 November 2008—Energy Efficiency: Delivering the 20% Target (COM/2008/0772). Available online: http://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:52008DC0772 accessed on 6 April 2015.
- European Union. Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Available online: http://eur-lex.europa.eu/legal-content/EN/ALL/;ELX_SESSIONID=pYTKJQJVCnsLtvvTQYwvq2mhVggH4bGvfhbnzbBflyJph87tlv7p!1397879892?uri=CELEX:32010L0031 accessed on 6 April 2015.
- Cooper, R.C. Decision Support for Urban Wind Energy Extraction. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 2007. [Google Scholar]
- Ledo, L.; Kosasih, P.B.; Cooper, P. Roof mounting site analysis for micro-wind turbines. Renew. Energy 2011, 36, 1379–1391. [Google Scholar]
- Lu, L.; Ip, K.Y. Investigation on the feasibility and enhancement methods of wind power utilization in high-rise buildings of Hong Kong. Renew. Sustain. Energy Rev 2009, 13, 450–461. [Google Scholar]
- Balduzzi, F.; Bianchini, A.; Ferrari, L. Microeolic turbines in the built environment: Influence of the installation site on the potential energy yield. Renew. Energy 2012, 45, 163–174. [Google Scholar]
- Tabrizi, A.B.; Whale, J.; Lyons, T.; Urmee, T. Performance and safety of rooftop wind turbines: Use of CFD to gain insight into inflow conditions. Renew. Energy 2014, 67, 242–251. [Google Scholar]
- Abohela, I. Effect of Roof Shape, Wind Direction, Building Height and Urban Configuration on the Energy Yield and Positioning of Roof Mounted Wind Turbines. In Ph.D. Thesis; Newcastle University: Newcastle, UK, 2012. [Google Scholar]
- Craighead, G. High-rise building definition, development, and use. In High-Rise Cecurity and Fire Life Safety, 3rd ed; Butterworth-Heinemann: Boston, MA, USA, 2009; Chapter 1. [Google Scholar]
- Cheng, Y.; Lien, F.S.; Yee, E.; Sinclair, R. A comparison of Large Eddy Simulations with a standard k − ε Reynolds-Averaged Navier-Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes. J. Wind Eng. Ind. Aerodyn 2003, 91, 1301–1328. [Google Scholar]
- Durbin, P.A. On the k − ε stagnation point anomaly. Int. J. Heat Fluid Flow 1996, 17, 89–90. [Google Scholar]
- Toja-Silva, F.; Peralta, C.; Lopez-Garcia, O.; Navarro, J.; Cruz, I. Roof region dependent wind potential assessment with different RANS turbulence models. J. Wind Eng. Ind. Aerodyn 2015, 142, 258–271. [Google Scholar]
- Meng, T.; Hibi, K. Turbulent measurements of the flow field around a high-rise building. J. Wind Eng 1998, 76, 55–64, In Japanese. [Google Scholar]
- Crespo, A.; Manuel, F.; Moreno, D.; Fraga, E.; Hernandez, J. Numerical analysis of wind turbine wakes, Proceedings of Delphi Workshop on Wind Energy Applications, Delphi, Greece, 20–22 May 1985; pp. 15–25.
- Panofsky, H.; Dutton, J. Atmospheric Turbulence; Wiley: New York, NY, USA, 1984. [Google Scholar]
- OpenFOAM. Available online: http://www.openfoam.com accessed on 6 April 2015.
- Architectural Institute of Japan. Guidebook for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. Available online: http://www.aij.or.jp/jpn/publish/cfdguide/index_e.htm accessed on 7 April 2015.
- Ntinas, G.K.; Zhang, G.; Fragos, V.P.; Bochtis, D.D.; Nikita-Martzopoulou, C. Airflow patterns around obstacles with arched and pitched roofs: Wind tunnel measurements and direct simulation. Eur. J. Mech. B Fluid 2014, 43, 216–229. [Google Scholar]
- Richards, P.J.; Hoxey, R.P. Appropriate boundary conditions for computational wind engineering models using the k − ε turbulence model. J. Wind Eng. Ind. Aerodyn 1993, 46–47, 145–153. [Google Scholar]
- Parente, A.; Gorlé, C.; van Beeck, J.; Benocci, C. A comprehensive modeling approach for the neutral atmospheric boundary layer: Consistent inflow conditions, wall function and turbulence model. Bound. Lay. Meteorol 2011, 140, 411–428. [Google Scholar]
- Santiago, J.L.; Martilli, A.; Martín, F. CFD simulation of airflow over a regular array of cubes. Part I: Three-dimensional simulation of the flow and validation with wind-tunnel measurements. Bound. Lay. Meteorol 2007, 122, 609–634. [Google Scholar]
- Tominaga, Y. Flow around a high-rise building using steady and unsteady RANS CFD: Effect of large-scale fluctuations on the velocity statistics. J. Wind Eng. Ind. Aerodyn 2015, 142, 93–103. [Google Scholar]
- Gousseau, P.; Blocken, B.; van Heijst, G.J.F. Quality assessment of Large-Eddy Simulation of wind flow around a high-rise building: Validation and solution verification. Comput. Fluid 2013, 79, 120–133. [Google Scholar]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment; COST Action 732; COST Office: Brussels, Belgium, 2007. [Google Scholar]
- Hall, R.C. Evaluation of Modeling Uncertainty. CFD Modeling of Near-Field Atmospheric Dispersion, European Commission Directorate—General XII Science, Research and Development Contract EV5V-CT94-0531; WS Atkins Consultants Ltd: Surrey, UK, 1997.
- Cowan, I.R.; Castro, I.P.; Robins, A.G. Numerical considerations for simulations of flow and dispersion around buildings. J. Wind Eng. Ind. Aerodyn 1997, 67–68, 535–545. [Google Scholar]
- Scaperdas, A.; Gilham, S. Thematic Area 4: Best practice advice for civil construction and HVAC. QNET-CFD Netw. Newslett 2004, 2, 28–33. [Google Scholar]
- Bartzis, J.G.; Vlachogiannis, D.; Sfetsos, A. Thematic area 5: Best practice advice for environmental flows. QNET-CFD Netw. Newslett 2004, 2, 34–39. [Google Scholar]
- SnappyHexMesh, OpenFOAM Wiki. Available online: http://www.openfoamwiki.net/index.php/SnappyHexMesh accessed on 6 April 2015.
- SnappyHexMeshDict, SnappyWiki. Available online: https://sites.google.com/site/snappywiki/snappyhexmesh/snappyhexmeshdict accessed on 6 April 2015.
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ 2007, 41, 238–252. [Google Scholar]
- O’Sullivan, J.P.; Archer, R.A.; Flay, R.G.J. Consistent boundary conditions for flows within the atmospheric boundary layer. J. Wind Eng. Ind. Aerodyn 2011, 99, 65–77. [Google Scholar]
- Van Hooff, T.; Blocken, B. On the effect of wind direction and urban surroundings on natural ventilation of a large semi-enclosed stadium. Comput. Fluid 2010, 39, 1146–1155. [Google Scholar]
- Pierik, J.T.G.; Dekker, J.W.M.; Braam, H.; Bulder, B.H.; Winkelaar, D.; Larsen, G.C.; Morfiadakis, E.; Chaviaropoulos, P.; Derrick, A.; Molly, J.P.; et al. European wind turbine standards II (EWTS-II). In Wind Energy for the Next Millennium. Proceedings; James and James Science Publishers: London, UK, 1999. [Google Scholar]
- Toja-Silva, F.; Peralta, C.; Lopez-Garcia, O.; Navarro, J.; Cruz, I. Effect of roof-mounted solar panels on the wind energy exploitation on high-rise buildings. J. Wind Eng. Ind. Aerodyn 2015. under review. [Google Scholar]
- Dayan, E. Wind energy in buildings: Power generation from wind in the urban environment—Where it is needed most. Refocus 2006, 7, 33–38. [Google Scholar]
- Balduzzi, F.; Bianchini, A.; Carnevale, E.A.; Ferrari, L.; Magnani, S. Feasibility analysis of a Darrieus vertical-axis wind turbine installation in the rooftop of a building. Appl. Energy 2012, 97, 921–929. [Google Scholar]
- Mertens, S. Wind energy in the built environment. In Concentrator Effects of Buildings; Multi-Science: Brentwood, UK, 2006. [Google Scholar]
- Bianchi, S.; Bianchini, A.; Ferrara, G.; Ferrari, L. Small wind turbines in the built environment: Influence of flow inclination on the potential energy yield. J. Turbomach 2014, 136, 1–9. [Google Scholar]
- Wood, D. Small Wind Turbines: Analysis, Design, and Application; Springer: London, UK, 2011. [Google Scholar]
- Pedersen, T.F.; Gjerding, T.; Ingham, P.; Enevoldsen, P.; Hansen, J.K.; Jørgensen, H.K. Wind Turbine Power Performance Verification in Complex Terrain and Wind Farms; Technical Report Risø-R-1330(EN); Risø Laboratory—DTU: Roskilde, Denmark, 2002. [Google Scholar]
- Tsalicoglou, C.; Barber, S.; Chokani, N.; Abhari, R.S. Effect of flow inclination on wind turbine performance. J. Eng. Gas Turbines Power 2012, 134. [Google Scholar] [CrossRef]
















| U | k | ε | νt | p | |
|---|---|---|---|---|---|
| Inlet | iP | iP | iP | C | zG |
| Outlet | zG | zG | zG | C | fV zero |
| Ground | fV zero | kqRwF | epsilon wF | nutkrough wF | zG |
| Building | fV zero | kqR wF | epsilon wF | nutk wF | zG |
| Sky | sl | sl | sl | C | zG |
| Sides | sP | sP | sP | sP | sP |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toja-Silva, F.; Peralta, C.; Lopez-Garcia, O.; Navarro, J.; Cruz, I. On Roof Geometry for Urban Wind Energy Exploitation in High-Rise Buildings. Computation 2015, 3, 299-325. https://doi.org/10.3390/computation3020299
Toja-Silva F, Peralta C, Lopez-Garcia O, Navarro J, Cruz I. On Roof Geometry for Urban Wind Energy Exploitation in High-Rise Buildings. Computation. 2015; 3(2):299-325. https://doi.org/10.3390/computation3020299
Chicago/Turabian StyleToja-Silva, Francisco, Carlos Peralta, Oscar Lopez-Garcia, Jorge Navarro, and Ignacio Cruz. 2015. "On Roof Geometry for Urban Wind Energy Exploitation in High-Rise Buildings" Computation 3, no. 2: 299-325. https://doi.org/10.3390/computation3020299
APA StyleToja-Silva, F., Peralta, C., Lopez-Garcia, O., Navarro, J., & Cruz, I. (2015). On Roof Geometry for Urban Wind Energy Exploitation in High-Rise Buildings. Computation, 3(2), 299-325. https://doi.org/10.3390/computation3020299