Universal Dimensions of Meaning Derived from Semantic Relations among Words and Senses: Mereological Completeness vs. Ontological Generality

Abstract

A key to semantic analysis is a precise and practically useful definition of meaning that is general for all domains of knowledge. We previously introduced the notion of weak semantic map: a metric space allocating concepts along their most general (universal) semantic characteristics while at the same time ignoring other, domain-specific aspects of their meanings. Here we address questions of the number, quality, and mutual independence of the weak semantic dimensions. Specifically, we employ semantic relationships not previously used for weak semantic mapping, such as holonymy/meronymy (“is-part/member-of”), and we compare maps constructed from word senses to those constructed from words. We show that the “completeness” dimension derived from the holonym/meronym relation is independent of, and practically orthogonal to, the “abstractness” dimension derived from the hypernym-hyponym (“is-a”) relation, while both dimensions are orthogonal to the maps derived from synonymy and antonymy. Interestingly, the choice of using relations among words vs. senses implies a non-trivial trade-off between rich and unambiguous information due to homonymy and polysemy. The practical utility of the new and prior dimensions is illustrated by the automated evaluation of different kinds of documents. Residual analysis of available linguistic resources, such as WordNet, suggests that the number of universal semantic dimensions representable in natural language may be finite. Their complete characterization, as well as the extension of results to non-linguistic materials, remains an open challenge.

1. Introduction

Many modern applications in cognitive sciences rely on semantic maps, also called (semantic) cognitive maps or semantic spaces [1,2,3,4]. These are continuous manifolds with semantics attributed to their elements and with semantic relations among those elements captured by geometry. For example, the popular approach to represent semantic dissimilarity as geometric distance, despite earlier criticism [5] proved useful (e.g., [6]). A disadvantage in this case is the difficult interpretation of the map’s emergent global semantic dimensions.

We have recently introduced the alternative approach of weak semantic mapping [7], in which words or concepts are allocated in space based on semantic relationships such as synonymy and antonymy. In this case, the principal spatial components of the distribution (defining the axes of the map) have consistent semantics that can be approximately characterized as valence, arousal, freedom, and richness, thus providing metrics related to affective spaces [8] and feature maps (e.g., [9]). Weak semantic maps are unique in two key aspects: (i) the semantic characteristics captured by weak semantic mapping apply to all domains of knowledge, i.e., they are “universal”; (ii) the geometry of the map only captures the universal aspects of semantics, while remaining independent of other, domain-specific semantic aspects. As a result, in contrast with “strong” maps based on the dissimilarity metric, a weak semantic map may allocate semantically unrelated elements next to each other, if they share the values of universal semantic characteristics. In other words, zero distance does not imply synonymy.

An example of a universal semantic dimension is the notion of “good vs. bad” (valence, or positivity): arguably, this notion applies to all domains of human knowledge, even to very abstract domains, if we agree to interpret the meaning of good-bad broadly. Another example of a universal dimension is “calming vs. exciting” (arousal). To show that these two dimensions are not reducible to one, we notice that every domain presents examples of double-dissociations, i.e., four distinct meanings that are (i) good and exciting; (ii) bad and exciting; (iii) good and calming; or (iv) bad and calming. For instance, in the academic context of grant proposal submission, one possible quadruplet would be: (i) official announcement of an expected funding opportunity; (ii) shortening of the deadline from two weeks to one; (iii) success in submission of the proposal two minutes before the deadline; or (iv) cancelation of the opportunity by the agency before the deadline.

In contrast, the pair “good” and “positive” does not represent two independent universal semantic dimensions. While examples of contrasting semantics can be found in some domains, as in the medical sense of “tested positive” vs. “good health”, it would be difficult or impossible to contrast these two notions in many or most domains. Thus, the antonym pairs “good-bad” and “positive-negative” likely characterize one and the same universal semantic dimension. Naturally, there exist a great variety of non-universal semantic dimensions (e.g., “political correctness”), which make sense within a limited domain only and may be impossible to extend to all domains in a consistent manner.

We have recently demonstrated that not all universal semantic dimensions can be exemplified by antonym pairs: e.g., the dimension of “abstractness”, or ontological generality, which can be derived from the hypernym-hyponym (“is-a”) relation [10]. The question of additional, as of yet unknown universal semantic dimensions is still open. More generally, it is not yet known whether the dimensionality of the weak semantic map of natural language is finite or infinite, and, if finite, whether it is low or high. On the one hand, the unlimited number of possible expressions in natural language whose semantics are not reducible to each other may suggest infinite (or very high) dimensionality. On the other hand, if all possible semantics expressible in natural language are constructed from a limited set of semantic primes [11,12], the number of universal, domain-independent semantic characteristics may well be finite and small. In this context it is desirable to identify the largest possible set of linearly independent semantic dimensions that apply to virtually all domains of human knowledge.

In the present work we continue the study of weak semantic mapping by identifying another universal semantic dimension: (mereological) “completeness”, derived from the holonym-meronym (“is-part/member-of”) relation. In particular, we demonstrate that “completeness” can be geometrically separated from “abstractness” as well as from the previously identified antonym-based dimensions of valence, arousal, freedom, and richness. Moreover, we investigate the fine structure of “completeness” by analyzing the distinction between partonymy (e.g., “the thumb is a part of the hand”) and member meronymy or “memberonymy” (e.g., “blue is a member of the color set”). Furthermore, we compare the results of semantic mapping based on word senses and their relations with those obtained with the previous approach utilizing words and their relations.

2. Materials and Methods

The methodology used here was described in detail in our previous works [7,10] and is only briefly summarized in this report. Specifically, the optimization method used for construction of the maps of abstractness and completeness is inspired by statistical mechanics and based on a functional introduced previously [10]. The numerical validation of this method is presented in Section 2.4.

2.1. Data Sources and Preparation: Semantic Relations, Words, and Senses

The datasets used in this study for weak semantic map construction were extracted from the publicly available database WordNet 3.1 [13]. We also re-analyze our previously published results of semantic map construction based on the Microsoft Word 2007 Thesaurus (a component in the commercially available Microsoft Office (Microsoft Office 2007 Professional for Windows, Microsoft Corporation, Redmond, WA, USA)).

The basic process of weak semantic mapping starts with extracting the graph structure of a thesaurus (e.g., a dictionary), where the graph nodes are in the simplest case words and the graph edges are given by a semantic relation of interest. For example, using the hypernymy/hyponymy (“is-a”) relationship in WordNet [13], two word nodes would be connected by a (directional) edge if one of a word is a hypernym or hyponym of the other. In general, not all words of the thesaurus will be connected together, and our approach only considers the largest connected graph, which we call the “core”.

All words of the core are then allocated on a metric space using a statistical optimization procedure based on energy minimization [7,10]. The details of the energy functional and of the space depend on the characteristics of the semantic relation: synonymy and antonymy are symmetric (and opposite in sign) and yield a multi-dimensional space with four independent coordinates approximately corresponding to valence, arousal, freedom, and richness [7]. Hypernymy and hyponymy are anti-symmetric (and complementary) and yield a uni-dimensional space whose single coordinate measures the ontological generality (or abstractness) of words [10].

A new element introduced here is the use of word senses available in WordNet [13], as opposed to words, as graph nodes. Word senses are unique meanings associated with words or idioms (typically a number of senses per word), each defined by the maximal collection of words that share the same joint sense (a “synset”). Thus, there is usually a many-to-many relationship between words and senses: the word “palm” for example has distinct senses as the tree, the side of a hand, and the honorary recognition; the latter sense is defined as the collection of the words “award, honor, palm, praise, and tribute”. Senses also specify an individual part of speech, while one and the same word may correspond to a noun, an adjective, and a verb (e.g., “fine”). WordNet [13] provides semantic relationships among senses as well as words, and also attributes a single-word tag to each sense, which allows direct comparison of the maps obtained with words and with senses.

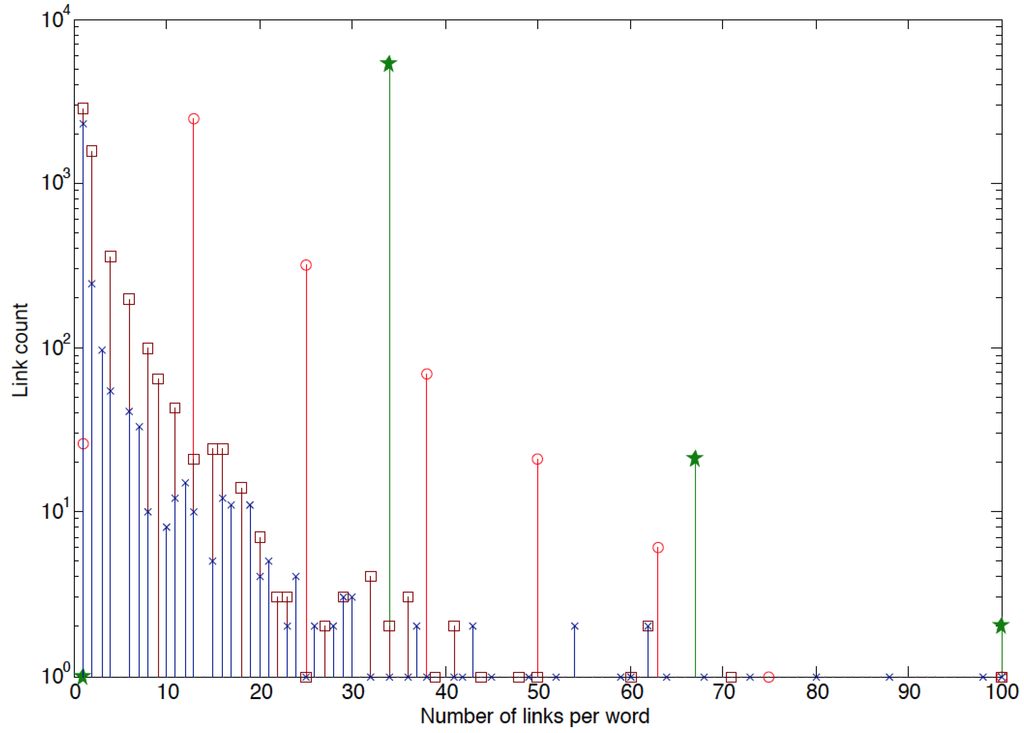
Figure 1. Statistics of graphs of holonym-meronym relations. The represented links are: brown (squares), memberonyms to whole; blue (crosses), partonyms to whole; green (stars), memberonyms to member; red (circles), partonyms to member.

Figure 1. Statistics of graphs of holonym-meronym relations. The represented links are: brown (squares), memberonyms to whole; blue (crosses), partonyms to whole; green (stars), memberonyms to member; red (circles), partonyms to member.

In this work we attempted to extract semantic map from all other semantic relations available in WordNet [13]: holonymy and meronymy, as well as their varieties (partonymy, memberonymy, and substance meronymy); varieties of hypernymy-hyponymy (conceptual hyponymy: e.g., action is an event; and instance hyponymy: e.g., Earth is a planet); troponymy, which is similar to hypernymy, except it applies to verbs (“walking is a kind of moving”, i.e., moving is a hypernym of walking); as well as causality and entailment (e.g., “to arrive at” entails “to travel/go/move”). All of these relationships are (like hypernymy/hyponymy) anti-symmetric, e.g., dog is a hyponym of animal and animal is hypernym of dog. In general, for graphs of these sorts, links in one direction far outnumber the links in the opposite direction (e.g., for member meronymy and partonymy, see Figure 1). Relations of this sort can in principle be mapped using the energy functional devised for abstractness (see also Section 2.4).

2.2. Data Statistics and Usability

Definitions and essential statistical parameters of the datasets that we used in this study, as well as of previously constructed maps, are summarized in Table 1. The first important observation is that not all datasets and relations are amenable to weak semantic mapping. Specifically, our approach as explained above requires the maximal component of the graph (the “core”) to be of sufficient size for statistical optimization. In WordNet [13], the causality/entailment relations among verb senses and the substance meronymy relation among nouns are too sparse for this purpose, and the same holds for conceptual and instance hypernymy/hyponymy. The situation is even more extreme for the antonymy/synonymy relations among senses: by definition, there cannot be any synonyms among distinct senses, since synonyms are part of the same synset by construction. Similarly, each sense in WordNet typically has at most one antonym. Thus the synonym-antonym graph turns out to be a collection of disjoined antonyms pairs. In contrast, the hyponym-hypernym and holonym-meronym relations define sufficiently large cores to construct and compare maps starting from either words or senses.

To measure and compare semantic map quality, we recorded the number of “inconsistencies” (last column in Table 1), understood as a pair of words (or senses) with values whose difference has a sign opposite to that expected from the nature of the link between those same words (or senses) in the original graph. For example, on the map of abstractness derived from the hypernym-hyponym relations among words in WordNet, the value of “condition” and “shampoo” is 2.6 and 0.15 respectively, while “condition” is listed as a variety of “shampoo”, in addition to the more general meaning of this term. Similarly, an “inconsistency” of the map constructed from synonym-antonym relations is counted when two synonyms have opposite signs of valence (the first principal component of the distribution) or two antonyms have the same signs of valence. An example in the map constructed from Microsoft Word English dictionary is the case of two synonyms, “difference” (negative valence) and “distinction” (positive valence).

In order to compare semantic maps obtained with different relationships or datasets, it is necessary to ascertain the extent of dataset overlap (Table 2). For example, the 15,783 words in the MS Word synonym/antonym core and the 20,477 words in the WordNet synonym/antonym core have an intersection of 5926 words (analyzed in detail in [7]); in contrast, the 7621 senses in the core of WordNet troponymy have practically no overlap with the 2927 senses in the core of WordNet [13] partonymy, which is understandable given that these relations imply distinct parts of speech (verbs and nouns, respectively).

Table 1. Parameters of the weak semantic maps constructed or attempted to date: datasets highlighted in blue correspond to previously published maps that are re-analyzed here; green highlights correspond to new maps introduced in this work; yellow highlights indicate datasets analyzed here but deemed unsuitable for weak semantic mapping; datasets without color highlights are previously published maps that are not re-analyzed here (besides Table 2), but are included for the sake of comprehensiveness. Source abbreviations: WordNet 3.1 [13] (WN3), Microsoft Word 2007 (Microsoft Corporation, Redmond, WA, USA) English Thesaurus (MWE), French (MWF), and German (MWG). Semantic relations abbreviations: synonymy-antonymy (s-a), antonymy (ant), hypernymy-hyponymy (hyp), conceptual hyponymy (conc), instance hyponymy (inst), holonymy-meronymy (h-m), causality-entailment (c/e), troponymy (trop), memberonymy (mem), partonymy (part), substance meronymy (subs).

Dataset label	Source	Elements: words or senses	Parts of speech	Relation(s) defining the graph	Graph kind: core (the main component) or all components	Map dimensionality	Number of nodes	Number of edges	Percentage of inconsistencies (in first map dimension only)
Ms	MWE	words	all	s-a	Core	4	15,783	100,244	0.30
Fr	MWF	words	all	s-a	Core	4	65,721	543,369	1.33
De	MWG	words	all	s-a	Core	4	93,887	1,071,753	0.24
Wn	WN3	words	all	s-a	Core	4	20,477	89,783	3.35
-	WN3	senses	adject	Ant	All	N/A	14,565	18,185	N/A
A	WN3	words	all	Hyp	Core	1	124,408	347,691	6.2
Aa	WN3	senses	nouns	Hyp	Core	1	82,192	84,505	0.62
-	WN3	senses	nouns	Conc	All	N/A	7621	7629	N/A
-	WN3	senses	nouns	Inst	All	N/A	8656	8589	N/A
C	WN3	words	all	h-m	Core	1	8453	20,729	25.6
Cc	WN3	senses	nouns	h-m	Core	1	11,455	11,566	0.22
Cm	WN3	senses	nouns	Mem	Core	1	5312	5324	0.26
Cp	WN3	senses	nouns	Part	Core	1	2927	3459	0.35
-	WN3	senses	nouns	Subs	All	N/A	1173	797	N/A
-	WN3	senses	verbs	c/e	All	N/A	1004	629	N/A
Vt	WN3	senses	verbs	Trop	Core	1	7621	7629	0.52

Table 1. Parameters of the weak semantic maps constructed or attempted to date: datasets highlighted in blue correspond to previously published maps that are re-analyzed here; green highlights correspond to new maps introduced in this work; yellow highlights indicate datasets analyzed here but deemed unsuitable for weak semantic mapping; datasets without color highlights are previously published maps that are not re-analyzed here (besides Table 2), but are included for the sake of comprehensiveness. Source abbreviations: WordNet 3.1 [13] (WN3), Microsoft Word 2007 (Microsoft Corporation, Redmond, WA, USA) English Thesaurus (MWE), French (MWF), and German (MWG). Semantic relations abbreviations: synonymy-antonymy (s-a), antonymy (ant), hypernymy-hyponymy (hyp), conceptual hyponymy (conc), instance hyponymy (inst), holonymy-meronymy (h-m), causality-entailment (c/e), troponymy (trop), memberonymy (mem), partonymy (part), substance meronymy (subs).

Dataset label	Source	Elements: words or senses	Parts of speech	Relation(s) defining the graph	Graph kind: core (the main component) or all components	Map dimensionality	Number of nodes	Number of edges	Percentage of inconsistencies (in first map dimension only)
Ms	MWE	words	all	s-a	Core	4	15,783	100,244	0.30
Fr	MWF	words	all	s-a	Core	4	65,721	543,369	1.33
De	MWG	words	all	s-a	Core	4	93,887	1,071,753	0.24
Wn	WN3	words	all	s-a	Core	4	20,477	89,783	3.35
-	WN3	senses	adject	Ant	All	N/A	14,565	18,185	N/A
A	WN3	words	all	Hyp	Core	1	124,408	347,691	6.2
Aa	WN3	senses	nouns	Hyp	Core	1	82,192	84,505	0.62
-	WN3	senses	nouns	Conc	All	N/A	7621	7629	N/A
-	WN3	senses	nouns	Inst	All	N/A	8656	8589	N/A
C	WN3	words	all	h-m	Core	1	8453	20,729	25.6
Cc	WN3	senses	nouns	h-m	Core	1	11,455	11,566	0.22
Cm	WN3	senses	nouns	Mem	Core	1	5312	5324	0.26
Cp	WN3	senses	nouns	Part	Core	1	2927	3459	0.35
-	WN3	senses	nouns	Subs	All	N/A	1173	797	N/A
-	WN3	senses	verbs	c/e	All	N/A	1004	629	N/A
Vt	WN3	senses	verbs	Trop	Core	1	7621	7629	0.52

Table 2. Numerical relations among datasets defined in Table 1. The number in each cell is the number of common nodes of the two graphs. Diagonal elements show the total numbers of nodes in each graph, which are also given in Table 1.

	Ms	Fr	De	Wn	A	Aa	C	Cc	Cm	Cp	Vt
Ms	15,783	4,704	5,290	5,926	5,556	3,044	714	63	18	1	1,153
Fr		65,721	7,335	5,038	7,339	4,979	1,372	145	45	0	1,737
De			93,887	5,238	6,172	3,978	1,198	114	29	1	1,476
Wn				20,477	4,750	2,680	854	94	29	2	1,017
A					124,408	29,580	5,552	2,789	1,222	5	4,208
Aa						82,192	4,548	10,903	5,248	2,747	1,978
C							8,453	886	133	3	784
Cc								11,455	5,248	6	131
Cm									5,312	4	44
Cp										2,927	1
Vt											7,621

Table 2. Numerical relations among datasets defined in Table 1. The number in each cell is the number of common nodes of the two graphs. Diagonal elements show the total numbers of nodes in each graph, which are also given in Table 1.

	Ms	Fr	De	Wn	A	Aa	C	Cc	Cm	Cp	Vt
Ms	15,783	4,704	5,290	5,926	5,556	3,044	714	63	18	1	1,153
Fr		65,721	7,335	5,038	7,339	4,979	1,372	145	45	0	1,737
De			93,887	5,238	6,172	3,978	1,198	114	29	1	1,476
Wn				20,477	4,750	2,680	854	94	29	2	1,017
A					124,408	29,580	5,552	2,789	1,222	5	4,208
Aa						82,192	4,548	10,903	5,248	2,747	1,978
C							8,453	886	133	3	784
Cc								11,455	5,248	6	131
Cm									5,312	4	44
Cp										2,927	1
Vt											7,621

2.3. Document Analysis

The text documents used for analysis of abstractness, completeness, valence, and arousal at a document level were recent articles from the Journal of Neuroscience. Two article categories were selected for this analysis: 165 brief communications and 143 mini-reviews, randomly sampled within the period from 2000 and 2013. The header (including the abstract) and the list of references at the end of each article were removed. From the text body, only words identified on the map were taken into consideration.

2.4. Validation of the Method

Here we present a methodological validation of weak semantic mapping for anti-symmetric relations (e.g., holonymy/meronymy) using a simple numerical experiment. The test material is the set of natural numbers from 1 to N = 10,000. 2 to 4 random connections are originated from each number (therefore, each number has on average 6 connections). Connection targets are randomly distributed. Polarity is determined by the actual order of connected numbers. One connected cluster is formed including all numbers. Reconstruction is based on the following formula:

(1)

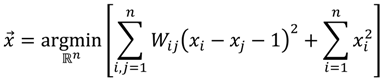
Results are represented by the distributions (Figure 2A,B). Results with increased numbers of connections (2–8 originated, 10 per number on average) visibly improve (Figure 2C,D).

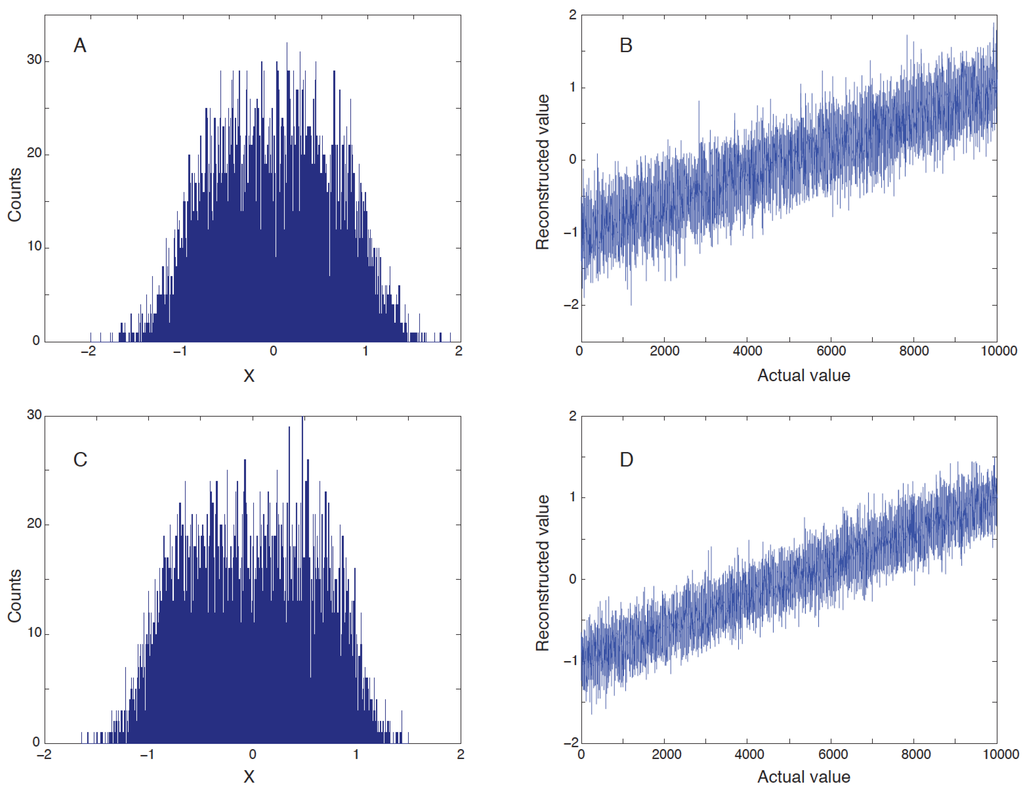
Figure 2. Validation of the method by reconstruction of the order of numbers. (A) Histogram. N = 10,000, 2–4 connections, 1000 bins; (B) Reconstructed order of numbers. N = 10,000, 2–4 connections. Results with increased numbers of connections; (C) Histogram. N = 10,000, 2–8 connections (10 on average), 1000 bins; (D) Reconstructed order of numbers. N = 10,000, 2–8 connections (10 on average).

Figure 2. Validation of the method by reconstruction of the order of numbers. (A) Histogram. N = 10,000, 2–4 connections, 1000 bins; (B) Reconstructed order of numbers. N = 10,000, 2–4 connections. Results with increased numbers of connections; (C) Histogram. N = 10,000, 2–8 connections (10 on average), 1000 bins; (D) Reconstructed order of numbers. N = 10,000, 2–8 connections (10 on average).

3. Results

3.1. Mereological Completeness

Our initial attempt to construct a map of mereological completeness, or “wholeness”, based on WordNet [13] holonym-meronym relations among words essentially failed: the quality of the sorted list was poor in the sense that the word order had little to do with the notion of completeness. For example, the terms artery, arm, and car appeared in the top 20 positions of the sorted list, whereas the terms vein, shoulder, and ship appeared in the bottom 20 positions. Examination of the “core” graph and of the very high proportion of map inconsistencies (more than a quarter: Table 1) suggested that this negative result was ultimately due to word polysemy.

The quality of the completeness map improved dramatically when using holonymy/meronymy relations among senses, as suggested by a reduction of more than two orders of magnitude in the fraction of inconsistencies in the core (down to less than a quarter percent: Table 1). In this case, the single word-tags of senses are meaningfully ordered in one dimension, as illustrated by the two ends of the corresponding sorted list (Table 3).

Table 3. Words sorted by completeness based on senses: two ends of the list.

Top of the List		Bottom of the List
4.56	Angiospermae	−2.97	paper_nautilus
4.43	Dicotyledones	−2.94	Crayfish
4.31	Monocotyledones	−2.91	whisk_fern
4.23	Spermatophyta	−2.89	blue_crab
4.17	Rosidae	−2.88	Platypus
4.05	World	−2.85	Octopus
3.99	Reptilia	−2.82	linolenic_acid
3.97	Dilleniidae	−2.82	horseshoe_crab
3.94	Asteridae	−2.78	Asian_horseshoe_crab
3.88	Eutheria	−2.71	Mastoidale
3.79	Caryophyllidae	−2.71	Bluepoint
3.75	Plantae	−2.69	sea_lamprey
3.74	Vertebrata	−2.69	Echidna
3.70	Commelinidae	−2.68	passion_fruit
3.67	Rodentia	−2.68	Echidna
3.67	Mammalia	−2.64	palm_oil
3.62	Liliidae	−2.61	Mescaline
3.62	Arecidae	−2.61	Swordfish
3.52	Aves	−2.60	guinea_hen
3.52	Magnoliidae	−2.57	Scrubbird

Table 3. Words sorted by completeness based on senses: two ends of the list.

Top of the List		Bottom of the List
4.56	Angiospermae	−2.97	paper_nautilus
4.43	Dicotyledones	−2.94	Crayfish
4.31	Monocotyledones	−2.91	whisk_fern
4.23	Spermatophyta	−2.89	blue_crab
4.17	Rosidae	−2.88	Platypus
4.05	World	−2.85	Octopus
3.99	Reptilia	−2.82	linolenic_acid
3.97	Dilleniidae	−2.82	horseshoe_crab
3.94	Asteridae	−2.78	Asian_horseshoe_crab
3.88	Eutheria	−2.71	Mastoidale
3.79	Caryophyllidae	−2.71	Bluepoint
3.75	Plantae	−2.69	sea_lamprey
3.74	Vertebrata	−2.69	Echidna
3.70	Commelinidae	−2.68	passion_fruit
3.67	Rodentia	−2.68	Echidna
3.67	Mammalia	−2.64	palm_oil
3.62	Liliidae	−2.61	Mescaline
3.62	Arecidae	−2.61	Swordfish
3.52	Aves	−2.60	guinea_hen
3.52	Magnoliidae	−2.57	Scrubbird

Interestingly, the histogram of the sense-based completeness values resembles a bimodal distribution suggesting the presence of two components (Figure 3A). We thus analyzed separately the graphs of member meronymy or memberonymy (Figure 3B) and part meronymy or partonymy (Figure 3C).

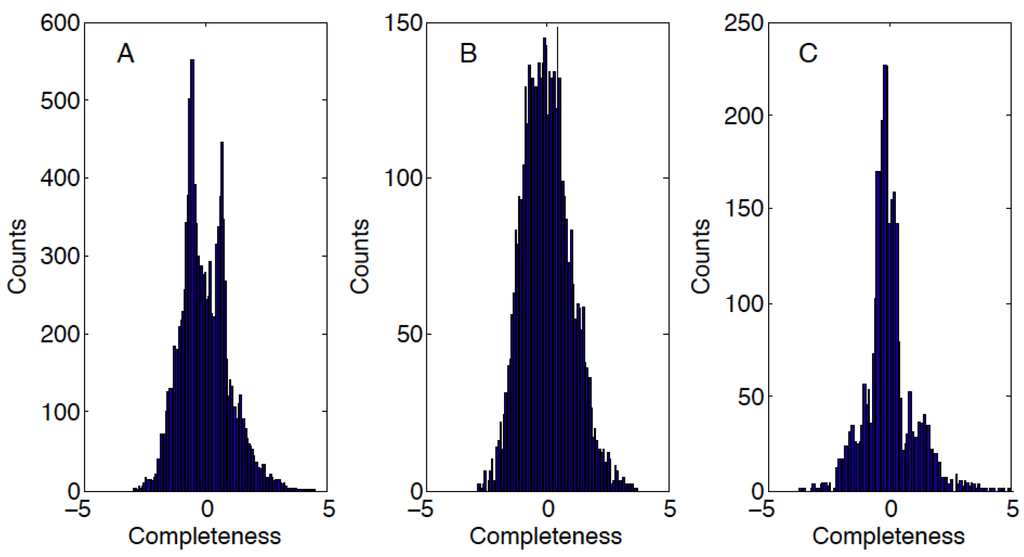
Figure 3. Sense-based mereological completeness map constructed from (A) the overall noun holonymy/meronymy relation; (B) noun member meronymy; and (C) noun partonymy.

Figure 3. Sense-based mereological completeness map constructed from (A) the overall noun holonymy/meronymy relation; (B) noun member meronymy; and (C) noun partonymy.

The beginning and end of the member meronymy sorted lists were extremely similar to those of the overall completeness map (Table 3). For example, one extreme included 6 out of 20 words in common as well as several others of the same kind (Squamata, Animalia, Insecta, Passeriformes, Crustacea, Chordata, etc.). Similarly, the opposite extreme had paper_nautilus and horseshoe_crab in common and many other similar terms (grey_whale, opossum_shrimp, sea_hare, tropical_prawn, sand_cricket, etc.). Such a stark correspondence is consistent with the intersections of the cores reported in Table 2: more than 98.8% of the senses in the memberonymy core appear in the overall meronymy core against a mere 0.2% of the senses in the partonymy core. Together, these results suggest that memberonyms dominate the meronymy relation.

At the same time, and for the same reason, the sense-based completeness map obtained from noun partonymy is largely complementary to that obtained from member meronymy. Specifically, the overlap of the two cores is limited to only four senses (Table 2). Therefore, based on these data, the two kinds of completeness cannot even be tested for statistical independence, because the two parts of the dictionary are essentially disjoint. Nevertheless, the partonymy-based map appears to be meaningful on its own, as illustrated by the term listed at the beginning and the end of the distribution (Table 4). Note that the term “world” appeared at the top of the list in the completeness map built based on the overall meronymy relation.

Table 4. Two ends of the sorted list of partonyms.

Top of the List		Bottom of the List
5.72	northern_hemisphere	−3.69	Papeete
5.60	western_hemisphere	−3.59	Fingals_Cave
5.37	West	−3.49	Grand_Canal
5.17	America	−3.15	Saipan
4.95	eastern_hemisphere	−3.13	Pago_Pago
4.72	southern_hemisphere	−3.04	Apia
4.51	Latin_America	−3.04	Vatican
4.31	Caucasia	−2.95	Alhambra
4.17	North_America	−2.93	Funafuti
3.99	Eurasia	−2.84	Port_Louis
3.79	Laurasia	−2.76	Ur
3.73	Strait_of_Gibraltar	−2.76	Belmont_Park
3.71	South	−2.73	Kaaba
3.69	United_States	−2.71	Greater_Sunda_Islands
3.57	Corn_Belt	−2.69	Lesser_Sunda_Islands
3.53	West	−2.66	Malabo
3.52	South_America	−2.63	Pearl_Harbor
3.50	Midwest	−2.61	Kingstown
3.44	Middle_East	−2.61	Tijuana
3.44	Austronesia	−2.57	Valletta

Table 4. Two ends of the sorted list of partonyms.

Top of the List		Bottom of the List
5.72	northern_hemisphere	−3.69	Papeete
5.60	western_hemisphere	−3.59	Fingals_Cave
5.37	West	−3.49	Grand_Canal
5.17	America	−3.15	Saipan
4.95	eastern_hemisphere	−3.13	Pago_Pago
4.72	southern_hemisphere	−3.04	Apia
4.51	Latin_America	−3.04	Vatican
4.31	Caucasia	−2.95	Alhambra
4.17	North_America	−2.93	Funafuti
3.99	Eurasia	−2.84	Port_Louis
3.79	Laurasia	−2.76	Ur
3.73	Strait_of_Gibraltar	−2.76	Belmont_Park
3.71	South	−2.73	Kaaba
3.69	United_States	−2.71	Greater_Sunda_Islands
3.57	Corn_Belt	−2.69	Lesser_Sunda_Islands
3.53	West	−2.66	Malabo
3.52	South_America	−2.63	Pearl_Harbor
3.50	Midwest	−2.61	Kingstown
3.44	Middle_East	−2.61	Tijuana
3.44	Austronesia	−2.57	Valletta

Strikingly, the sense-based completeness map has minimal if any overlap with the antonym/synonym word-based map of value, arousal, freedom, and richness constructed with either WordNet [13] or Microsoft Word (Microsoft Office 2007 Professional for Windows, Microsoft Corporation, Redmond, WA, USA) (Table 2). Words with holonyms or meronyms seemingly have no antonyms. Thus, the completeness dimension is by default independent of the antonym-based “sentiment” metrics (at any rate, the Pearson coefficients computed on the 63 common words with the MSE map indicated no statistically significant correlation after multiple-testing correction). In contrast, the completeness map overlaps substantially with the abstractness dimension, as discussed below.

3.2. Abstractness Based on Senses and Verb Troponymy

Switching from words to senses substantially improved the quality of semantic mapping for mereological completeness. The attempted map based on words yielded inconsistent values of the emergent coordinate, with similar words (e.g., vein and artery) found on opposite sides of the distribution. Adoption of senses eliminated the obstacle of polysemy and resulted in a coherent semantic map of completeness as well as a finer distinction between member meronymy and partonymy. At the same time, the requirement of a sizeable connected graph of relations as a starting point for this approach makes weak semantic mapping based on senses untenable in some cases, such as for synonym-antonym relations.

In recent work, we reported the construction of a semantic map of ontological generality (“abstractness”) based on words [10]. Might the quality of such a map be improved by switching from words to senses in this case? The graph of noun hypernym/hyponyms relations among word senses is of sufficient size for semantic mapping (Table 1), and the overlap between the two corpora is substantial enough (Table 2) for allowing a direct comparison between the two approaches. We thus constructed a sense-based noun abstractness map (Figure 4).

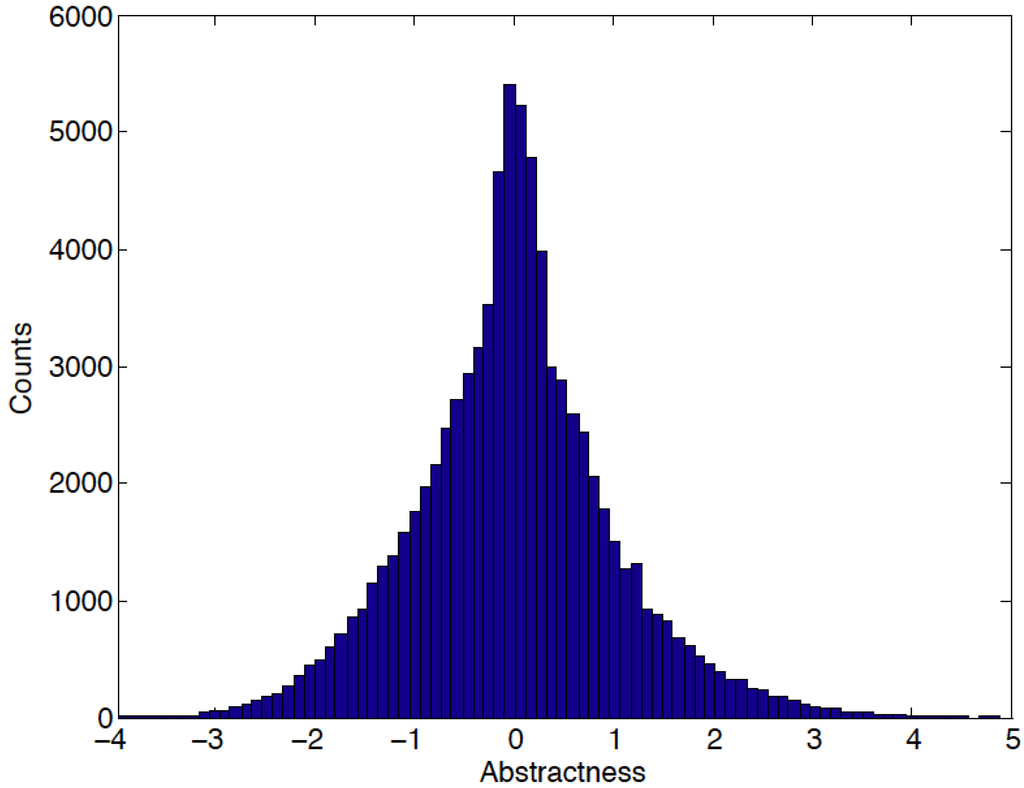
Figure 4. Histogram distribution of sense-based noun abstractness.

Figure 4. Histogram distribution of sense-based noun abstractness.

Results of examination of the two ends of the sorted list of sense nouns are consistent with the expectation of high semantic quality of the map (Table 5), similar to that reported for word-based abstractness. The word-based abstractness map had been previously shown to be practically orthogonal to the synonym/antonym-based dimensions [10]. Similarly, the independence between sense-based abstractness and the four principal components of the MSE synonym/antonym map is supported by negligible values of Pearson correlation coefficients: R = 0.031 with “valence”, 0.0069 with “arousal”, −0.0093 with “freedom”, and 0.0195 with “richness”.

Using word senses instead of words reduces the fraction of inconsistencies on the abstractness map 10-fold (Table 1), suggesting that the switch to sense-based relationship may be advantageous in this case. At the same time, direct comparison between the word-based and sense-based abstractness maps reveals a more complex story. While the correlation between the two maps (R = 0.61) is statistically very significant (p < 10–99), the residual scatter indicates a considerable variance between the two coordinates (Figure 5).

Table 5. Sorted lists of sense-based noun abstractness.

Top of the list		Bottom of the list
4.56	entity	−2.97	cortina
4.43	abstraction	−2.94	attic fan
4.31	psychological feature	−2.91	riding mower
4.23	physical entity	−2.89	venture capitalism
4.17	process	−2.88	axle bar
4.05	communication	−2.85	sneak preview
3.99	instrumentality	−2.82	Loewi
3.97	cognition	−2.82	glorification
3.94	attribute	−2.78	secateurs
3.88	event	−2.71	purification
3.79	artifact	−2.71	shrift
3.75	act	−2.69	Chabad
3.74	aquatic bird	−2.69	index fund
3.70	whole	−2.68	Amish
3.67	social event	−2.68	iron cage
3.67	vertebrate	−2.64	foresight
3.62	way	−2.61	epanodos
3.62	relation	−2.61	rehabilitation
3.52	placental	−2.60	justification
3.52	basic cognitive process	−2.57	flip-flop

Table 5. Sorted lists of sense-based noun abstractness.

Top of the list		Bottom of the list
4.56	entity	−2.97	cortina
4.43	abstraction	−2.94	attic fan
4.31	psychological feature	−2.91	riding mower
4.23	physical entity	−2.89	venture capitalism
4.17	process	−2.88	axle bar
4.05	communication	−2.85	sneak preview
3.99	instrumentality	−2.82	Loewi
3.97	cognition	−2.82	glorification
3.94	attribute	−2.78	secateurs
3.88	event	−2.71	purification
3.79	artifact	−2.71	shrift
3.75	act	−2.69	Chabad
3.74	aquatic bird	−2.69	index fund
3.70	whole	−2.68	Amish
3.67	social event	−2.68	iron cage
3.67	vertebrate	−2.64	foresight
3.62	way	−2.61	epanodos
3.62	relation	−2.61	rehabilitation
3.52	placental	−2.60	justification
3.52	basic cognitive process	−2.57	flip-flop

It is thus reasonable to ask which of the two coordinates (word-based or sense-based) provides a better quantification of the meaning of ontological generality when their values are mutually discordant. To answer this question, we sorted the points in the scatter plot of Figure 5 by their distance from the linear fit (the red line). At least for these “outliers” with the most divergent values between the two maps (Table 6), the notion of abstractness overall appears to better conform to the map constructed from words than to the map constructed from senses. Comparison of the node degrees of the outliers on the two maps suggests that the inconsistent assignments may be due to the corresponding graph being sparser. For example, the ontological generality of the concepts “theropod” and “think” appear to be more aligned with the values in X (word-based) than in Y (sense-based), and the corresponding graph degrees are also greater in X than in Y. The node degree in the graph of words is generally greater compared to the graph of senses, but the cases of low or similar degree in the graph of words compared to the degree in the graph of senses seem to correspond to a greater error in X (abstractness coordinate on the map of words) than in Y (abstractness coordinate on the map of senses). For instance, the abstractness of the concept “entity”, with the same degree in X and Y, is better captured by the value in the sense-based map than in the word-based map.

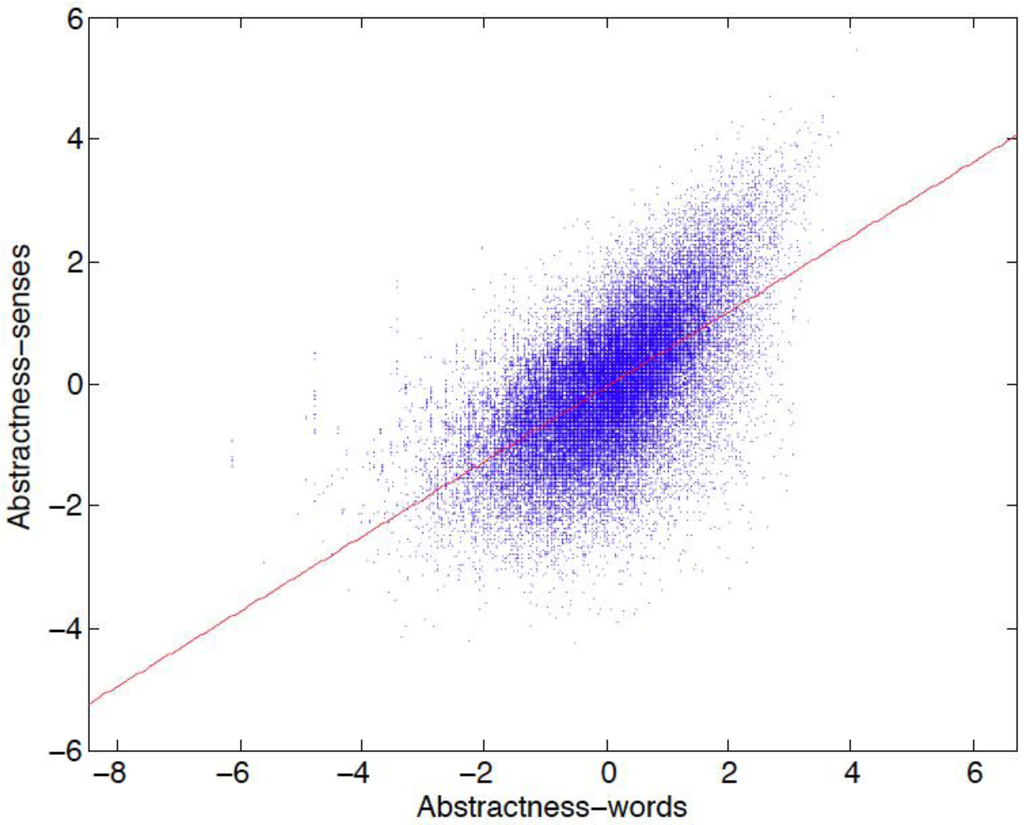
Figure 5. Relation among the two maps of abstractness. The red line shows the linear fit (y = 0.61x – 0.052).

Figure 5. Relation among the two maps of abstractness. The red line shows the linear fit (y = 0.61x – 0.052).

Table 6. “Outliers”: words sorted by the difference of scaled coordinates in Figure 5 (the distribution is “sliced” by lines parallel to the red line in Figure 5). Two ends of the list are shown in the left and right columns. X and Y are map coordinates on the map constructed from words and from senses respectively; dx and dy are the corresponding degrees of graph nodes.

Top of the list					Bottom of the list
X	Y	dx	dy		X	Y	dx	dy
−3.41	1.68	18	11	Theropod	2.02	−3.36	31	1	Interrupt
4.61	6.38	3	3	Entity	2.30	−2.92	18	1	Melody
−2.04	2.25	14	8	Ornithischian	2.39	−2.69	37	1	Sensation
−2.04	2.19	6	3	Saurischian	2.00	−2.86	87	1	Divide
−4.78	0.51	5	3	Ornithomimid	0.46	−3.78	2	1	Foresight
−4.78	0.50	10	7	Maniraptor	1.56	−3.08	46	1	Meal
−4.78	0.50	2	2	Ankylosaur	0.70	−3.59	51	1	Pile
−4.78	0.40	4	2	Ceratosaur	0.17	−3.89	12	1	Glorification
−3.41	1.07	8	5	Hadrosaur	0.48	−3.69	2	1	Floodgate
2.66	4.69	55	20	Attribute	2.65	−2.34	79	1	Think
0.89	3.57	1	1	Otherworld	0.90	−3.38	1	1	Countertransference
2.07	4.27	13	6	Diapsid	−0.51	−4.23	2	1	Cortina
−0.47	2.68	24	12	Elapid	1.43	−3.02	13	1	Doormat
1.45	3.84	36	10	Primate	1.45	−2.97	9	1	Spirituality
1.56	3.90	3	2	Saurian	1.24	−3.08	7	1	Insemination
−3.41	0.86	8	5	Ceratopsian	1.83	−2.70	50	1	Example
−0.67	2.53	14	8	Dinosaur	2.36	−2.36	22	1	Impedimenta
0.44	3.18	25	3	Monkey	0.86	−3.21	8	1	Stooper
1.83	4.02	3	3	Waterfowl	2.34	−2.26	13	1	Assignation
−2.17	1.54	9	3	Dichromacy	−0.15	−3.75	14	1	Rehabilitation

Table 6. “Outliers”: words sorted by the difference of scaled coordinates in Figure 5 (the distribution is “sliced” by lines parallel to the red line in Figure 5). Two ends of the list are shown in the left and right columns. X and Y are map coordinates on the map constructed from words and from senses respectively; dx and dy are the corresponding degrees of graph nodes.

Top of the list					Bottom of the list
X	Y	dx	dy		X	Y	dx	dy
−3.41	1.68	18	11	Theropod	2.02	−3.36	31	1	Interrupt
4.61	6.38	3	3	Entity	2.30	−2.92	18	1	Melody
−2.04	2.25	14	8	Ornithischian	2.39	−2.69	37	1	Sensation
−2.04	2.19	6	3	Saurischian	2.00	−2.86	87	1	Divide
−4.78	0.51	5	3	Ornithomimid	0.46	−3.78	2	1	Foresight
−4.78	0.50	10	7	Maniraptor	1.56	−3.08	46	1	Meal
−4.78	0.50	2	2	Ankylosaur	0.70	−3.59	51	1	Pile
−4.78	0.40	4	2	Ceratosaur	0.17	−3.89	12	1	Glorification
−3.41	1.07	8	5	Hadrosaur	0.48	−3.69	2	1	Floodgate
2.66	4.69	55	20	Attribute	2.65	−2.34	79	1	Think
0.89	3.57	1	1	Otherworld	0.90	−3.38	1	1	Countertransference
2.07	4.27	13	6	Diapsid	−0.51	−4.23	2	1	Cortina
−0.47	2.68	24	12	Elapid	1.43	−3.02	13	1	Doormat
1.45	3.84	36	10	Primate	1.45	−2.97	9	1	Spirituality
1.56	3.90	3	2	Saurian	1.24	−3.08	7	1	Insemination
−3.41	0.86	8	5	Ceratopsian	1.83	−2.70	50	1	Example
−0.67	2.53	14	8	Dinosaur	2.36	−2.36	22	1	Impedimenta
0.44	3.18	25	3	Monkey	0.86	−3.21	8	1	Stooper
1.83	4.02	3	3	Waterfowl	2.34	−2.26	13	1	Assignation
−2.17	1.54	9	3	Dichromacy	−0.15	−3.75	14	1	Rehabilitation

These results indicate some usefulness of polysemy for mapping abstractness. More precisely, these examples demonstrate a tradeoff between homonymy and graph connectivity. In fact, when both maps are combined, the quality improves further, at least judging by the tails of the lists sorted by the orthogonal to the red line slicing of Figure 5: (Entity, Cognition, Vertebrate, Ability, Mammal, Concept, Trait, Artifact, Thinking, Message, Attribute, Happening, Equipment, Reptile, Assets, know-how, Non-accomplishment, Emotion, Food, Placental) from one end; and (Velociraptor, Oviraptorid, Utahraptor, Dromaeosaur, Coelophysis, Deinonychus, Struthiomimus, Deinocheirus, Regain, Apatosaur, Barosaur, Tritanopia, Tetartanopia, Plasmablast, Pachycephalosaur, Fructose, Gerund, Secateurs, Triceratops, Psittacosaur) from the opposite end. However, the pool of terms mapped in this case is limited to the subset that is common to both maps.

It should be remarked that, because senses represent unique meanings, their semantic relationships yield segregated maps for different parts of speech. In particular, the sense-based abstractness map analyzed above refers selectively to nouns. In contrast, the word-based abstractness map [10] includes both nouns and verbs. We thus also constructed a sense-based verb abstractness map, from the verb “is-a” (troponymy) relationship (e.g., punching “is-a” kind of hitting). The total numbers of nodes and edges in the verb troponymy graph are respectively 13,563 and 13,256, resulting in 7621 verbs in the core. The two ends of the sorted list confirmed the expected ontological generality ranking for verbs (Table 7).

The sense-based verb abstractness map was also uni-dimensional and its comparison with the word-based map (Figure 6) paralleled the analysis reported above for sense-based noun abstractness.

Table 7. Two ends of the sense list of sorted by troponymy.

X	Top of the list	X	Bottom of the list
4.01	Transfer	−3.71	talk_shop
3.89	Take	−3.64	Refocus
3.40	Touch	−3.62	Embargo
3.30	Connect	−3.60	Gore
3.29	Make	−3.39	Rat
3.20	Interact	−3.36	Ligate
3.18	Communicate	−3.28	Descant
3.14	Cause	−3.21	Ferret
3.12	Move	−3.17	Tug
3.11	Give	−3.05	Din
3.07	Tell	−3.04	Distend
3.07	change_shape	−3.04	Rise
3.07	Inform	−3.01	Evangelize
3.05	create_by_mental_act	−3.00	Caponize
2.99	Get	−2.96	Tampon
2.99	Change	−2.93	trouble_oneself
2.98	Pass	−2.91	Slant
2.96	create_from_raw_material	−2.90	slam-dunk
2.85	change_magnitude	−2.90	Pooch
2.81	Travel	−2.89	Streamline

Table 7. Two ends of the sense list of sorted by troponymy.

X	Top of the list	X	Bottom of the list
4.01	Transfer	−3.71	talk_shop
3.89	Take	−3.64	Refocus
3.40	Touch	−3.62	Embargo
3.30	Connect	−3.60	Gore
3.29	Make	−3.39	Rat
3.20	Interact	−3.36	Ligate
3.18	Communicate	−3.28	Descant
3.14	Cause	−3.21	Ferret
3.12	Move	−3.17	Tug
3.11	Give	−3.05	Din
3.07	Tell	−3.04	Distend
3.07	change_shape	−3.04	Rise
3.07	Inform	−3.01	Evangelize
3.05	create_by_mental_act	−3.00	Caponize
2.99	Get	−2.96	Tampon
2.99	Change	−2.93	trouble_oneself
2.98	Pass	−2.91	Slant
2.96	create_from_raw_material	−2.90	slam-dunk
2.85	change_magnitude	−2.90	Pooch
2.81	Travel	−2.89	Streamline

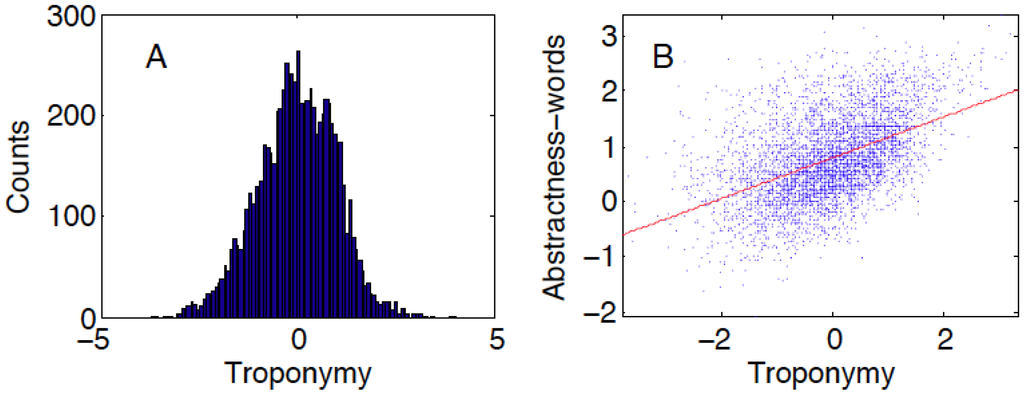
Figure 6. (A) Verb troponymy map constructed from word senses based on WordNet 3.1 [13], represented by a histogram; (B) Troponymy of verb senses vs. abstractness of words. Red line shows linear fits (y = 0.37x + 0.8).

Figure 6. (A) Verb troponymy map constructed from word senses based on WordNet 3.1 [13], represented by a histogram; (B) Troponymy of verb senses vs. abstractness of words. Red line shows linear fits (y = 0.37x + 0.8).

Completeness and abstractness turn out to be essentially independent semantic coordinates. Examples of words that discriminate the two dimensions, partially borrowed from the sorted lists, include: Northern hemisphere (whole, concrete), world (whole, abstract), part (part, abstract), whisker (part, concrete). The size of the overlap of two cores (10,903 words) allows quantification of the linear independence of abstractness and completeness with good statistical significance (Figure 7A; R² < 0.013). The same appear to apply to the relationship between abstractness and the two distinct kinds of completeness corresponding to member meronymy and partonymy, respectively (Figure 7B,C). However, it appears that memberonymy is more similar to abstractness, compared to partonymy (Table 3, Table 4 and Table 5, respectively).

Figure 7. (A) Abstractness and completeness dimensions are linearly independent semantic dimensions, with the Pearson correlation R = 0.113; (B,C) Memberonymy and partonymy separated.

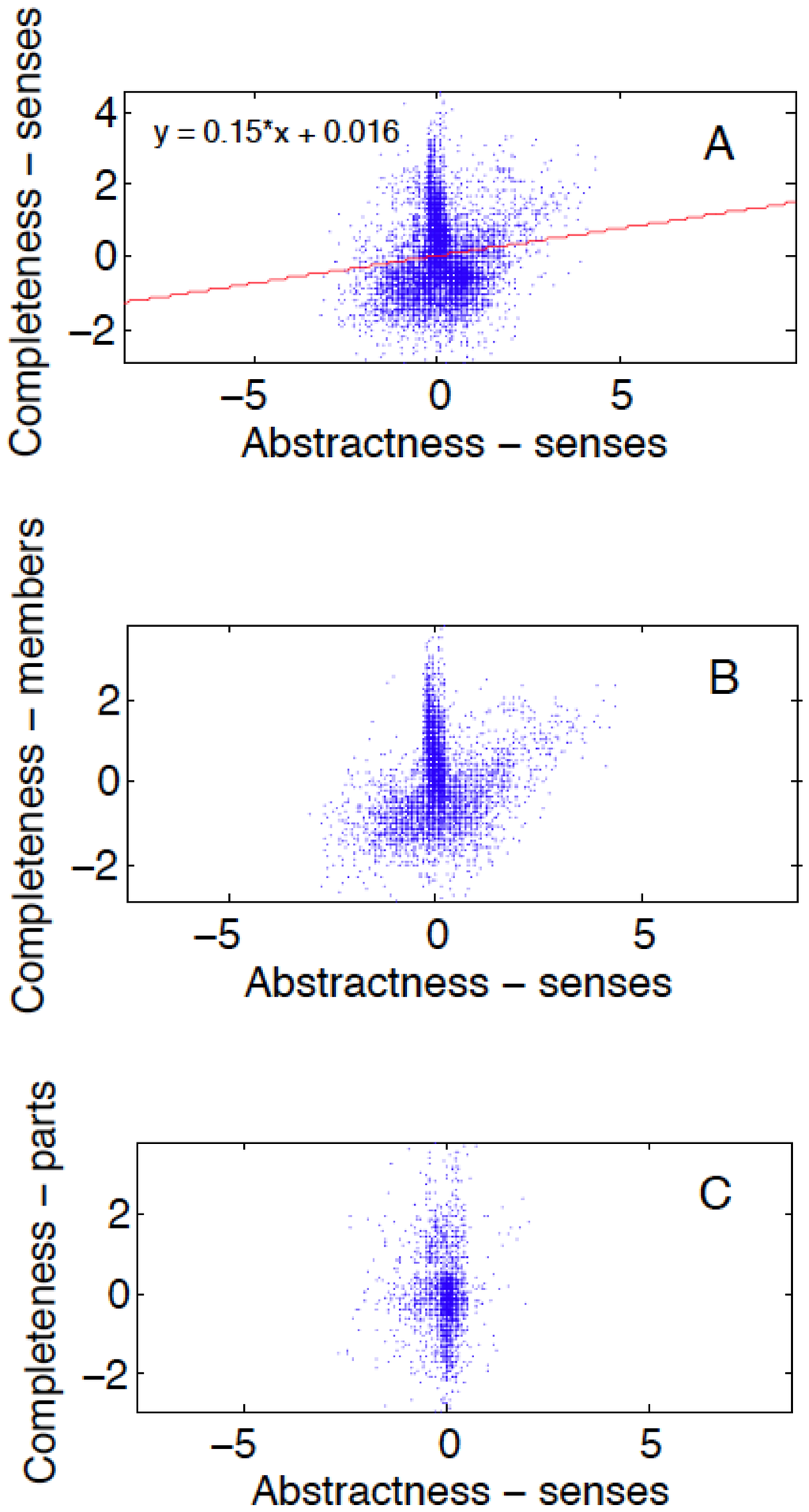
Figure 7. (A) Abstractness and completeness dimensions are linearly independent semantic dimensions, with the Pearson correlation R = 0.113; (B,C) Memberonymy and partonymy separated.

3.3. Analysis of Text Corpora

Lastly, we utilized the map data to compute the mean values of abstractness, completeness, valence, and arousal of two categories of recent articles from the Journal of Neuroscience: mini-reviews and brief communications (Figure 8). On average, relative to brief communications, mini-reviews tend to be more exciting, more positive, at a more general level, and more comprehensive. Interestingly, the strongest effect size was observed in the new “completeness” dimension (note the equal scales in all three panels of Figure 8). This suggests that newly identified semantic dimensions may be directly reducible to practical applications.

Figure 8. Semantic measures of documents from the Journal of Neuroscience. Filled ovals show the means with standard errors. Blue: Brief communications; Red: Mini-reviews. The numbers of words for the two types of documents for each measure are, respectively: Valence, 33,971 and 35,787; Arousal, 33,971 and 35,787; Freedom, 33,971 and 35,787; Richness, 33,971 and 35,787; Abstractness, 40,255 and 38,156; Completeness, 1453 and 1717. The largest differences between the two kinds of documents are in Completeness, Abstractness, and Valence.

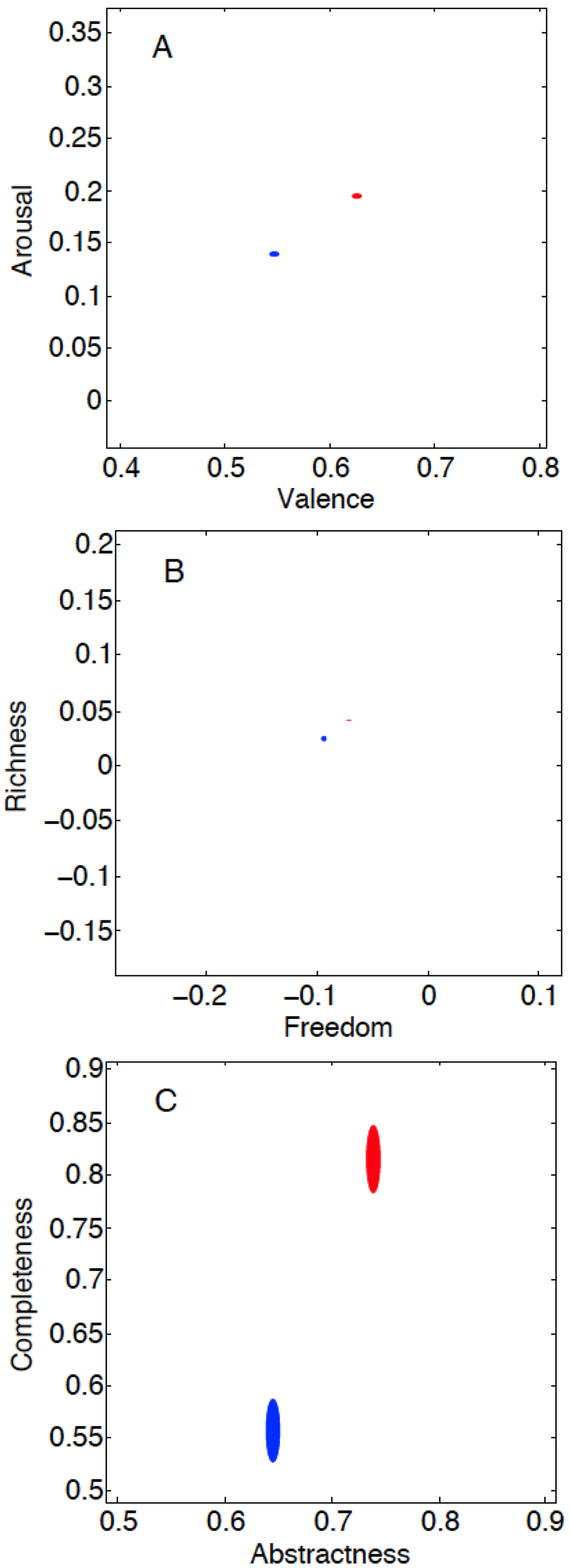
Figure 8. Semantic measures of documents from the Journal of Neuroscience. Filled ovals show the means with standard errors. Blue: Brief communications; Red: Mini-reviews. The numbers of words for the two types of documents for each measure are, respectively: Valence, 33,971 and 35,787; Arousal, 33,971 and 35,787; Freedom, 33,971 and 35,787; Richness, 33,971 and 35,787; Abstractness, 40,255 and 38,156; Completeness, 1453 and 1717. The largest differences between the two kinds of documents are in Completeness, Abstractness, and Valence.

4. Discussion

The key to semantic analysis is in a precise and practically useful definition of semantics that are general for all domains of knowledge. In this work we presented a new semantic dimension (mereological completeness) and a corresponding weak semantic map constructed from WordNet data [13]. We found the new dimension to be independent of the previously described abstractness dimension. The quality was acceptable only when completeness was computed for word senses, and not for words. This is in contrast with abstractness, where maps constructed from words and word senses are only quantitatively different. Dimensions of completeness and abstractness were shown to be practically orthogonal to each other, as well as to the weak semantic map dimensions of valence, arousal, freedom, and richness previously computed from synonym/antonym relations [7].

A weak semantic map [14] is a metric space that separately allocates representations along general semantic characteristics that are common for all domains of knowledge, while at the same time ignoring other, domain-specific semantic aspects. In contrast, usage of dissimilarity metrics defines, from this perspective, “strong” (or traditional) semantic maps. In a weak semantic map, the universal semantic characteristics become space dimensions, and their scales determine the metrics on the map. This notion generalizes several old, widely used models of continuous affective spaces, including Osgood’s semantic differential [4], the Circumplex model [15], PAD (pleasure, arousal, dominance: [9]), and EPA (evaluation, potency, arousal: [8]), but also more recent proposals (e.g., [16]), as well as discrete ontological hierarchies, such as WordNet, and continuous semantic spaces constructed computationally for representation of knowledge. Examples include, e.g., ConceptNet [17], which also utilizes is-part/member-of relationships, and SenticNet [18,19,20]. In particular, SenticSpace is known to be used for knowledge visualization and reasoning, and sentic medoids [21] are known to be used for defining semantic relatedness of concepts according to the semantic features they share.

This work addressed questions of the number, quality, consistency, correlation and mutual independence of the universal semantic dimensions by extending previous studies in two main directions. (1) We used semantic relations that were not previously used for weak semantic map construction, such as holonymy and meronymy; (2) We investigated the results of map construction based on word senses as opposed to words. In particular, we showed that the “completeness” dimension derived from holonyms and meronyms is independent of, and practically orthogonal to, the dimension of “abstractness” derived from hypernym-hyponym relations, while both dimensions are orthogonal to the synonym-antonym-derived maps. Moreover, we demonstrated that switching from words to senses can dramatically improve the map quality in some cases (such as for the new dimension of mereological completeness), but it prevents weak semantic mapping altogether in others (e.g., using the synonym/antonym relations). Therefore, while introducing some noise, polysemy may also be useful for weak semantic mapping. Specifically, there is a trade-off between the broad coverage of more densely connected word graphs and the “clean” meanings (and therefore sparser relations) of unique senses. New and old semantic dimensions were also evaluated for sets of documents. Groups of documents of different kinds were clearly separated from each other on the map. We anticipate applications of this method to sentiment analysis of text [22]. Therefore, our future continuation of this research will integrate related recent approaches [23,24,25].

Finally, our numerical results allow us to speculate that the number of independent universal semantic dimensions, at least those represented in natural language, is finite. This idea is supported by neuroimaging reports suggesting that only a finite, relatively small number of neural characteristics globally discriminate semantics in the brain [26]. It is also consistent with studies in linguistics [11,12] attempting to reduce a large number of semantics representable with natural language to a small set of semantic primes. Complete characterization of the minimal set of universal semantic dimensions, as well as their extension to non-linguistic materials, remains an important open challenge, the solution of which will have broader impacts on the scientific study of human mind [27].

5. Conclusions

A semantic map is an abstract metric space with semantics associated to its elements: i.e., a mapping from semantics to points in space. Two kinds of semantic maps can be distinguished [14]:

i. A strong semantic map, in which the distance is a measure of dissimilarity between two elements, although globally the map coordinates may not be associated with definite or easily interpretable meanings, and

ii. A weak semantic map, in which any direction globally corresponds to a movement toward a definite meaning (e.g., more positive, or more exciting, or more abstract), but pairs of unrelated concepts can be found next to each other.

Examples of (i) are numerous and popular (e.g., [6]). These spaces are usually characterized by a large dimensionality. Examples of (ii) are relatively limited in several senses: in the numbers of models, in their dimensionality, in the semantics of dimensions, in the domains of application, and in popularity (e.g., affective spaces that are used in models of emotions). Among examples of (ii) are our weak semantic maps [7,10], whose dimensions emerge from semantic relations among words and not from human data or any semantics given a priori. While related approaches are being developed in parallel [17,18,19,20,21], our method brought to existence new constructs that have no analogs in the number, quality, and semantics of emergent dimensions (e.g., the dimension of “freedom”).

The present work addressed the important issue of the fundamentally limitated number and kinds of semantic dimensions in a weak map. The results clearly demonstrated again, after [10], that weak semantic maps are not limited to separation of synonym-antonym pairs. Instead, new dimensions can be added to the weak map that were previously not obvious. Therefore, the question of their maximal number is nontrivial. An equally important step in our understanding of the weak map was to determine the extent to which independently constructed dimensions may nonetheless be strongly correlated: e.g., meronymy and troponymy.

In summary, the present work addressed questions of the number, quality, and mutual independence of the weak semantic dimensions. Specifically,

1. We employed semantic relationships not previously used for weak semantic mapping, such as holonymy/meronymy (“is-part/member-of”).

2. We compared maps constructed from word senses to those constructed from words.

3. We showed that the “completeness” dimension derived from the holonym/meronym relation is independent of, and practically orthogonal to, the “abstractness” dimension previously derived from the hypernym-hyponym (“is-a”) relation [10], as well as to the dimensions derived from synonymy and antonymy [7].

4. We found that the choice of using relations among words vs. senses implies a non-trivial trade-off between rich and unambiguous information due to homonymy and polysemy.

5. We demonstrated the practical utility of the new and prior dimensions by the automated evaluation of the content of a set of documents.

6. Our residual analysis of available linguistic resources, such as WordNet [13], together with related studies [12], suggests that the number of universal semantic dimensions representable in natural language may be finite and precisely defined, in contrast with the infinite number of all possible meanings.

7. The precise value of this number, the complete characterization of all weak semantic dimensions, as well as the extension of results to non-linguistic materials [28] constitute an open challenge.

Future outcomes of the continuation of this study can be expected to impact the design of human-compatible agents and robots, and to produce a large variety of academic applications.