Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper–Water Nanofluid
Abstract
1. Introduction
2. Computational Methods
2.1. Problem Statement and Boundary Conditions
2.2. Computational Formations and Assumptions
3. Grid Independence and Code Validation
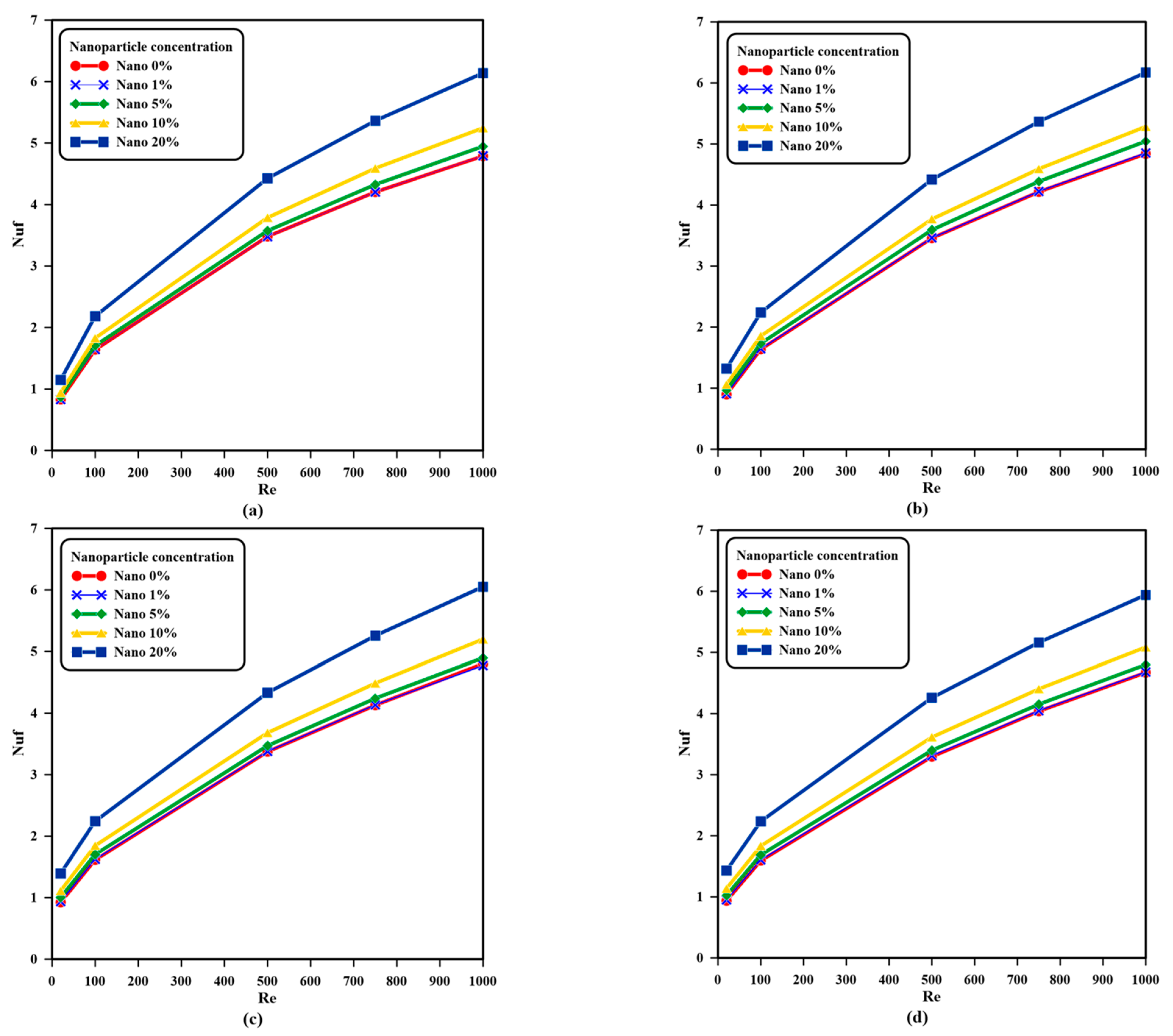
4. Results and Discussions
4.1. Non-Corrugated Vertical Left Sidewall
4.2. Corrugated Vertical Left Sidewall
5. Conclusions
- The streamlines intensified and the convection heat flow rose with an increasing number and increasing aspect ratios of the inlet and outlet vents, especially when the latter was increased to ;
- The fluid-phase temperature of the metal foam compared to the solid-phase temperature decreased when the volume fraction of the nanofluid particles increased;
- The number for the fluid phase of the copper metal foam near the hot left sidewall increased when the nanoparticle concentration volume ratio increased by at and , and by at and , while the solid-phase number decreased by at and , and by at and when the nanoparticle volume fraction increased from to ;
- The Nusselt number for the two phases of metal foam greatly intensified with the amplification of the number compared with an increase in the inflow and outflow vent aspect ratio; at , the fluid-phase Nusselt number rose by at and by at , whereas the solid-phase Nusselt number increased by at and by at when the Reynolds number was augmented from to ;
- As the corrugation ratio increased from to , the penetration of fluid towards the cavity’s left sidewall pockets became hard and small re-circulation zones were established within those pockets;
- For the corrugated hot wall, the numbers of the two metal foam phases increased with an increase in the number; at , , , and , it was determined that the fluid-phase and solid-phase Nusselt numbers increased by and , respectively, as the Reynolds number increased in the range of ;
- For the corrugated hot wall, the number of the two phases decreased with an increase in the aspect ratio; when , , , and , it was determined that the fluid-phase and solid-phase Nusselt numbers decreased by and , respectively, as the opening aspect ratio increased from to ;
- The fluid-phase number near the corrugated left sidewall increased and the solid-phase number decreased with an increase in the nanoparticle volume fraction; the fluid-phase Nusselt number rose by at and , and by at and , whereas the solid-phase Nusselt number decreased by at and , and by at and when the nanoparticle volume fraction was increased from to ;
- The fluid- and solid-phase Nusselt numbers for the corrugated wall were higher than those for the non-corrugated wall, irrespective of the number of corrugations or the corrugation ratio;
- By augmenting the corrugation ratio from to at , , and , the fluid- and solid-phase Nusselt number values decreased by and , respectively.
- Increasing the corrugation number from to led to a reduction in the Nusselt number value; at , , and , the fluid and solid Nusselt number values decreased by and , respectively;
- Corrugation is a good option for enhancing thermal performance. For instance, corrugations and a can be utilized to corrugate walls and achieve a high Reynolds number in solar air heaters, solar dryers, green building heating, and electronic cooling in order to achieve a noteworthy heat transfer enhancement without exaggerated flow resistance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Latin Symbols | |
| specific surface area () | |
| Forchheimer coefficient | |
| heat capacitance | |
| inlet and outlet vent width () | |
| Darcy number | |
| acceleration due to gravity () | |
| Grashof number | |
| interfacial heat transfer coefficient | |
| height () | |
| thermal conductivity | |
| permeability () | |
| length () | |
| normal direction | |
| number of corrugation waves | |
| Nusselt number | |
| pressure () | |
| dimensionless pressure | |
| Prandtl number | |
| Rayleigh number | |
| Reynolds number | |
| coordinate along non-corrugated and corrugated left wall | |
| surface length of thermal region () | |
| temperature () | |
| cold fluid inlet temperature () | |
| hot temperature () | |
| , | velocity components () |
| cold fluid inlet velocity () | |
| , | dimensionless velocity components |
| , | Cartesian coordinates () |
| , | dimensionless coordinates |
| Greek Symbols | |
| thermal diffusivity () | |
| volumetric thermal expansion coefficient () | |
| dynamic viscosity () | |
| density () | |
| porosity | |
| nanoparticle volume fraction | |
| dimensionless temperature | |
| Subscripts | |
| water base fluid | |
| nanofluid | |
| nanoparticles | |
| porous solid matrix |
References
- Saeidi, S.M.; Khodadadi, J.M. Forced Convection in a Square Cavity with Inlet and Outlet Ports. Int. J. Heat Mass Transf. 2006, 49, 1896–1906. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Shahi, M.; Talebi, F. Effect of Inlet and Outlet Location on the Mixed Convective Cooling inside the Ventilated Cavity Subjected to an External Nanofluid. Int. Commun. Heat Mass Transf. 2010, 37, 1158–1173. [Google Scholar] [CrossRef]
- Ismael, M.A.; Jasim, H.F. Role of the Fluid-Structure Interaction in Mixed Convection in a Vented Cavity. Int. J. Mech. Sci. 2018, 135, 190–202. [Google Scholar] [CrossRef]
- Abdulwahed, A.S.; Ali, L.F. Numerical Investigation of Natural Convection in a Square Enclosure Partially Filled with Horizontal Layers of a Porous Medium. Heat Transf. 2023, 52, 874–889. [Google Scholar] [CrossRef]
- Alkinani, I.H.; Ali, L.F. Natural Convection in Annulus between Two Concentric Cylinders Partially Filled with Metal Foam Distributed with New Suggested Design. IOP Conf. Ser. Earth Environ. Sci. 2022, 961, 012032. [Google Scholar] [CrossRef]
- Mussa, M.A. Numerical Simulation of Natural Convection in a Rhombic Enclosure with Heated Sidewall Coated with Metal Foam. Diyala J. Eng. Sci. 2024, 17, 77–90. [Google Scholar] [CrossRef]
- Zachi, F.J.; Ali, L.F. Experimental Study of Natural Convection Heat Transfer on an Enclosure Partially Filled Porous Medium Heated from below by Constant Heat Flux. AIP Conf. Proc. 2023, 2651, 050002. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Ghalambaz, M.; Chamkha, A.J.; Izadi, M. Numerical Study on Natural Convection of Ag–MgO Hybrid/Water Nanofluid inside a Porous Enclosure: A Local Thermal Non-Equilibrium Model. Powder Technol. 2020, 367, 443–455. [Google Scholar] [CrossRef]
- Ali, L.F.; Humaidi, A.J. Offset Temperature and Amplitude–Frequency Effect on Convection Heat Transfer in Partially Gradient Porous Cavity with Different Outlet Port Locations. Processes 2025, 13, 2279. [Google Scholar] [CrossRef]
- Saidi, M.; Karimi, G. Free Convection Cooling in Modified L-Shape Enclosures Using Copper-Water Nanofluid. Energy 2014, 70, 251–271. [Google Scholar] [CrossRef]
- Saleem, K.B.; Marafie, A.H.; Al-Farhany, K.; Hussam, W.K.; Sheard, G.J. Natural Convection Heat Transfer in a Nanofluid Filled L-Shaped Enclosure with Time-Periodic Temperature Boundary and Magnetic Field. Alex. Eng. J. 2023, 69, 177–191. [Google Scholar] [CrossRef]
- Almeshaal, M.A.; Maatki, C.; Kolsi, L.; Ghachem, K.; Chamkha, A. 3D Rayleigh-Bénard-Type Natural Convection in MWCNT-Nanofluid-Filled L-Shaped Enclosures with Consideration of Aggregation Effect. Math. Methods Appl. Sci. 2020, 1–17. [Google Scholar] [CrossRef]
- Jamy, R.H.; Chowdhury, S.; Chowdhury, F.K.; Saha, S. Analyzing Overall Thermal Behaviour of Conjugate MHD Free Convection in L-Shaped Chamber with a Thick Fin. Case Stud. Therm. Eng. 2023, 48, 103137. [Google Scholar] [CrossRef]
- Naseri Nia, S.; Rabiei, F.; Rashidi, M.M.; Kwang, T.M. Lattice Boltzmann Simulation of Natural Convection Heat Transfer of a Nanofluid in a L-Shape Enclosure with a Baffle. Results Phys. 2020, 19, 103413. [Google Scholar] [CrossRef]
- Ma, Y.; Tang, H.; Wang, C. Enhancement of Natural Convection of a Nanofluid by Stress-Free Patches in an L-Shaped Enclosure. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 2153–2180. [Google Scholar] [CrossRef]
- Massoudi, M.D.; Ben Hamida, M.B. Free Convection and Thermal Radiation of a Nanofluid inside an Inclined L-Shaped Microelectronic Module under the Lorentz Forces’ Impact. Heat Transf. 2021, 50, 2849–2873. [Google Scholar] [CrossRef]
- Jain, S.; Bhargava, R.; Gupta, P. Numerical Simulation of Natural Convection MHD Flow in a Wavy L-Shaped Cavity with Line Heat Source Using Hybrid EFGM/FEM. Heat Transf. 2022, 51, 7030–7055. [Google Scholar] [CrossRef]
- Moghimi, S.M.; Domairry, G.; Bararnia, H.; Soleimani, S.; Ghasemi, E. Numerical Study of Natural Convection in an Inclined L-Shaped Porous Enclosure. Adv. Theor. Appl. Mech. 2012, 5, 237–245. [Google Scholar]
- Mojumder, S.; Saha, S.; Rizwanur Rahman, M.; Rahman, M.M.; Rabbi, K.M.; Ibrahim, T.A. Numerical Study on Mixed Convection Heat Transfer in a Porous L-Shaped Cavity. Eng. Sci. Technol. Int. J. 2017, 20, 272–282. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Numerical Simulation for Impact of Coulomb Force on Nanofluid Heat Transfer in a Porous Enclosure in Presence of Thermal Radiation. Int. J. Heat Mass Transf. 2018, 118, 823–831. [Google Scholar] [CrossRef]
- Moria, H. Natural Convection in an L-Shape Cavity Equipped with Heating Blocks and Porous Layers. Int. Commun. Heat Mass Transf. 2021, 126, 105375. [Google Scholar] [CrossRef]
- Al-Damook, A.; Azzawi, I.D.J. Magnetohydrodynamic Natural Convection of Water in an L-Shaped Container Filled With an Aluminum Metal Foam. J. Heat Transf. 2023, 145, 022601. [Google Scholar] [CrossRef]
- Yeasmin, S.; Billah, M.M.; Molla, M.Z.; Hoque, K.E. Numerical Analysis of Unsteady Mixed Convection Heat Transfer Characteristics of Nanofluids Confined within a Porous Lid-Driven L-Shaped Cavity. Int. J. Thermofluids 2022, 16, 100218. [Google Scholar] [CrossRef]
- Azzawi, I.D.J.; Khalil, W.H.; Al-damook, A. Multiobjective Optimization of Free Convection through a Nonuniform Cabinet Filled with Porous Media. Heat Transf. 2023, 52, 3300–3316. [Google Scholar] [CrossRef]
- Alawee, W.H.; Al-Sumaily, G.F.; Dhahad, H.A.; Thompson, M.C. Numerical Analysis of Non-Darcian Mixed Convection Flows in a Ventilated Enclosure Filled with a Fluid-Saturated Porous Medium. Therm. Sci. Eng. Prog. 2021, 24, 100922. [Google Scholar] [CrossRef]
- Mahmud, S.; Pop, I. Mixed Convection in a Square Vented Enclosure Filled with a Porous Medium. Int. J. Heat Mass Transf. 2006, 49, 2190–2206. [Google Scholar] [CrossRef]
- Bhuiyan, A.A.; Banna, M.H.; Barna, S.F.; Amin, M.R.; Sadrul Islam, A.K.M. Numerical Modelling of Thermal Characteristics in a Microstructure Filled Porous Cavity with Mixed Convection. Int. J. Heat Mass Transf. 2016, 93, 464–476. [Google Scholar] [CrossRef]
- Ali, L.F. Natural and Mixed Convection in Square Vented Enclosure Filled with Metal Foam. J. Eng. 2015, 21, 60–79. [Google Scholar] [CrossRef]
- Shi, Y.S.; Liu, D.; Wang, Y.; Zhao, F.Y.; Li, Y.X. Forced Flow Structure and Mixed Convection in a Ventilated Porous Enclosure with a Local Contaminant Source. Int. J. Heat Mass Transf. 2019, 131, 973–983. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Moattar, F.; Karbassi, A.; Sheremet, M.A.; Pop, I. Triple-Diffusive Mixed Convection in a Porous Open Cavity. Transp. Porous Media 2017, 116, 473–491. [Google Scholar] [CrossRef]
- Behzadi, T.; Shirvan, K.M.; Mirzakhanlari, S.; Sheikhrobat, A.A. Numerical Simulation on Effect of Porous Medium on Mixed Convection Heat Transfer in a Ventilated Square Cavity. Procedia Eng. 2015, 127, 221–228. [Google Scholar] [CrossRef]
- Ghazanfarian, J.; Abbassi, A. Mixed Convection in a Square Cavity Filled with a Porous Medium and Different Exit Port Position. J. Porous Media 2007, 10, 701–718. [Google Scholar] [CrossRef]
- Ataei-Dadavi, I.; Chakkingal, M.; Kenjeres, S.; Kleijn, C.R.; Tummers, M.J. Experiments on Mixed Convection in a Vented Differentially Side-Heated Cavity Filled with a Coarse Porous Medium. Int. J. Heat Mass Transf. 2020, 149, 119238. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Ishak, A. Double-Diffusive Mixed Convection in a Porous Open Cavity Filled with a Nanofluid Using Buongiorno’s Model. Transp. Porous Media 2015, 109, 131–145. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Roşca, N.C.; Roşca, A.V.; Pop, I. Mixed Convection Heat Transfer in a Square Porous Cavity Filled with a Nanofluid with Suction/Injection Effect. Comput. Math. Appl. 2018, 76, 2665–2677. [Google Scholar] [CrossRef]
- Ullah, N.; Nadeem, S.; Saleem, A. Finite Element Analysis of Convective Nanofluid Equipped in Enclosure Having Both Inlet and Outlet Zones. J. Taiwan Inst. Chem. Eng. 2020, 113, 428–441. [Google Scholar] [CrossRef]
- Ahmed, S.E. Caputo Fractional Convective Flow in an Inclined Wavy Vented Cavity Filled with a Porous Medium Using Al2O3-Cu Hybrid Nanofluids. Int. Commun. Heat Mass Transf. 2020, 116, 104690. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Mamourian, M.; Ellahi, R. Numerical Investigation and Optimization of Mixed Convection in Ventilated Square Cavity Filled with Nanofluid of Different Inlet and Outlet Port. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2053–2069. [Google Scholar] [CrossRef]
- Bahlaoui, A.; Raji, A.; Hasnaoui, M.; Näimi, M. Mixed Convection in a Nanofluid-Filled Vented Rectangular Cavity: Suction and Injection Heat Performance. Comput. Therm. Sci. 2014, 6, 129–142. [Google Scholar] [CrossRef]
- Kherroubi, S.; Benkahla, Y.K.; Labsi, N.; Ragui, K.; Bensaci, A.; Boutra, A.; Ouyahia, S.E.; Benzema, M. Two- and Three-Dimensional Comparative Study of Heat Transfer and Pressure Drop Characteristics of Nanofluids Flow through a Ventilated Cubic Cavity (Part I: Newtonian Nanofluids). J. Therm. Anal. Calorim. 2021, 144, 623–646. [Google Scholar] [CrossRef]
- Chummar, A.; Harish, R. Numerical Investigation of Forced Convective Heat Transfer of Nanofluids within an Enclosure. Mater Today Proc. 2022, 51, 1465–1472. [Google Scholar] [CrossRef]
- Arroub, I.; Bahlaoui, A.; Belhouideg, S.; Raji, A.; Hasnaoui, M. Combined Effects of Inclination Angle and Imposed Flow on Mixed Convective Cooling Inside a Vented Cavity Crossed by Nanofluids. Phys. Chem. Res. 2023, 11, 631–642. [Google Scholar] [CrossRef]
- Sourtiji, E.; Gorji-Bandpy, M.; Ganji, D.D.; Hosseinizadeh, S.F. Numerical Analysis of Mixed Convection Heat Transfer of Al2O3-Water Nanofluid in a Ventilated Cavity Considering Different Positions of the Outlet Port. Powder Technol. 2014, 262, 71–81. [Google Scholar] [CrossRef]
- Job, V.; Gunakala, S.R.; Rushi Kumar, B.; Sivaraj, R. Effects of Heat-Generating Component Size and Porous Layer Thickness on MHD Mixed Convection Flow of Ag-Water Nanofluid Through an L-Shaped Channel. In Applications of Fluid Dynamics; Lecture Notes in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 109–126. [Google Scholar] [CrossRef]
- Job, V.M.; Gunakala, S.R. Unsteady Hydromagnetic Mixed Convection Nanofluid Flows through an L-Shaped Channel with a Porous Inner Layer and Heat-Generating Components. Int. J. Heat Mass Transf. 2018, 120, 970–986. [Google Scholar] [CrossRef]
- Armaghani, T.; Rashad, A.M.; Vahidifar, O.; Mishra, S.R.; Chamkha, A.J. Effects of Discrete Heat Source Location on Heat Transfer and Entropy Generation of Nanofluid in an Open Inclined L-Shaped Cavity. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1363–1377. [Google Scholar] [CrossRef]
- Armaghani, T.; Ismael, M.A.; Chamkha, A.J.; Pop, I. Mixed Convection and Entropy Generation of an Ag-Water Nanofluid in an Inclined L-Shaped Channel. Energies 2019, 12, 1150. [Google Scholar] [CrossRef]
- Akkurt, N.; Shedd, T.; Memon, A.A.; Usman; Ali, M.R.; Bouye, M. Analysis of the Forced Convection via the Turbulence Transport of the Hybrid Mixture in Three-Dimensional L-Shaped Channel. Case Stud. Therm. Eng. 2023, 41, 102558. [Google Scholar] [CrossRef]
- Kherroubi, S.; Ragui, K.; Labsi, N.; Benkahla, Y.; Boutra, A.; El Ganaoui, M.; Liu, B.; Bennacer, R.; Morsli, S.; Darcherif, M. Three-Dimensional Numerical Study of Mixed Convection within a Ventilated Cavity (Shape ‘L’) Crossed by a Nanofluid under the Effect of a Magnetic Field. MATEC Web Conf. 2020, 307, 01027. [Google Scholar] [CrossRef]
- Ouri, H.; Selimefendigil, F.; Bouterra, M.; Omri, M.; Alshammari, B.M.; Kolsi, L. MHD Hybrid Nanofluid Convection and Phase Change Process in an L-Shaped Vented Cavity Equipped with an Inner Rotating Cylinder and PCM-Packed Bed System. Alex. Eng. J. 2023, 63, 563–582. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Constant Wall Heat Flux Boundary Conditions in Porous Media under Local Thermal Non-Equilibrium Conditions. Int. J. Heat Mass Transf. 2002, 45, 3071–3087. [Google Scholar] [CrossRef]
- Xu, H.J.; Gong, L.; Zhao, C.Y.; Yang, Y.H.; Xu, Z.G. Analytical Considerations of Local Thermal Non-Equilibrium Conditions for Thermal Transport in Metal Foams. Int. J. Therm. Sci. 2015, 95, 73–87. [Google Scholar] [CrossRef]
- Wang, B.; Hong, Y.; Hou, X.; Xu, Z.; Wang, P.; Fang, X.; Ruan, X. Numerical Configuration Design and Investigation of Heat Transfer Enhancement in Pipes Filled with Gradient Porous Materials. Energy Convers. Manag. 2015, 105, 206–215. [Google Scholar] [CrossRef]
- Ghashim, S.L. A Mathematical Analysis of Nanoparticles on Heat Transfer in a Circular Pipe. Case Stud. Therm. Eng. 2021, 28, 101524. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Abdulsahib, A.D. Study of Mixed Convection in Two Layers of Saturated Porous Medium and Nanofluid with Rotating Circular Cylinder. Prog. Nucl. Energy 2021, 135, 103723. [Google Scholar] [CrossRef]




















| No. of Elements | |||||||||
| No. of Elements | |||||||||
| Case | Correlation Expression | |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, L.F.; Togun, H.; Sadeq, A.M. Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper–Water Nanofluid. Computation 2025, 13, 218. https://doi.org/10.3390/computation13090218
Ali LF, Togun H, Sadeq AM. Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper–Water Nanofluid. Computation. 2025; 13(9):218. https://doi.org/10.3390/computation13090218
Chicago/Turabian StyleAli, Luma F., Hussein Togun, and Abdellatif M. Sadeq. 2025. "Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper–Water Nanofluid" Computation 13, no. 9: 218. https://doi.org/10.3390/computation13090218
APA StyleAli, L. F., Togun, H., & Sadeq, A. M. (2025). Effect of Heated Wall Corrugation on Thermal Performance in an L-Shaped Vented Cavity Crossed by Metal Foam Saturated with Copper–Water Nanofluid. Computation, 13(9), 218. https://doi.org/10.3390/computation13090218





