Matrix Factorization-Based Clustering for Sparse Data in Recommender Systems: A Comparative Study

Abstract

Clustering techniques significantly enhance recommender systems by improving predictive accuracy and interpretability, particularly in sparse, high-dimensional datasets. This research presents a comprehensive comparative analysis of traditional clustering methods such as K-means and Fuzzy C-Means (FCM) against advanced probabilistic clustering methodologies based on Non-negative Matrix Factorization (NMF), focusing specifically on Bayesian NMF. Experiments conducted using the widely recognized MovieLens 1M dataset reveal Bayesian NMF’s superior performance in terms of predictive accuracy, intra-cluster cohesion, and interpretability compared to classical methods. The study systematically evaluates the influence of key parameters such as overlap ($\alpha$) and evidence threshold ($\beta$) in Bayesian NMF, demonstrating that careful parameter tuning substantially improves recommendation quality. The results highlight the inherent trade-off between cluster cohesion and predictive accuracy, emphasizing the flexibility and robustness of probabilistic approaches in accurately modeling user preferences and behaviors. The paper concludes by proposing future directions, including the exploration of hybrid clustering methods, dynamic adaptation to evolving user preferences, and integration of contextual information, thereby fostering continued advances in personalized-recommendation research.

1. Introduction

Recommender Systems (RS) have become an indispensable component in many digital platforms, offering personalized content and improving user engagement by predicting user preferences. These systems play a critical role in industries ranging from e-commerce and digital streaming to social media and news aggregation. However, as these systems scale and encounter increasingly sparse and heterogeneous datasets, their predictive power and efficiency often suffer. The challenge lies not only in predicting user–item interactions accurately, but also in uncovering latent user behaviors and grouping similar users or items to enhance both interpretability and performance. This is where clustering becomes an essential methodological tool.

Clustering is a fundamental task in unsupervised machine learning and data mining that involves grouping similar data instances based on intrinsic properties, without prior labeling. In the context of RS, clustering is used to segment users or items into groups that share similar preferences or characteristics, enabling more efficient recommendations and improved model scalability. By organizing users into meaningful clusters, one can significantly reduce the dimensionality of the recommendation task and allow for more interpretable and computationally tractable models [1].

The challenge of clustering in RS is exacerbated by data sparsity—a common problem where users rate only a small fraction of available items, resulting in highly incomplete matrices. In traditional collaborative filtering systems, this leads to unreliable similarity computations and degraded performance of both memory-based and model-based methods [2]. Moreover, the very nature of user behavior is complex and multi-faceted; thus, forcing hard partitions, where each user belongs to a single cluster, may oversimplify user profiles and fail to capture important nuances.

In response to these limitations, various clustering techniques have been adapted or newly developed to enhance RS. Broadly, these techniques fall into two categories: hard clustering and soft clustering. Hard-clustering methods, such as k-means, assign each user or item exclusively to a single cluster. While simple and computationally efficient, such methods often fail to account for overlapping behaviors or preferences common among real-world users. Soft-clustering methods, such as Fuzzy C-Means [3], assign degrees of membership to multiple clusters, allowing for more flexible representations. These techniques are especially valuable in RS, where a user may enjoy content from multiple genres or contexts simultaneously.

The central premise of this study is that clustering is not merely an ancillary task in RS, but a core component that can significantly enhance prediction quality, model interpretability, and system scalability. Through clustering, RS can manage data sparsity, capture user heterogeneity, and offer more personalized and reliable recommendations. In particular, the Bayesian NMF model serves as a powerful tool that unifies clustering and prediction in a coherent probabilistic framework, offering both flexibility and rigor.

This paper presents a comparative study of clustering methods in RS, emphasizing the potential of Matrix Factorization techniques, especially probabilistic Bayesian NMF, for simultaneously improving clustering quality and recommendation performance. Drawing on theoretical background and empirical evidence from prior research [2,4,5], this study aims to demonstrate how clustering, when effectively integrated with latent-factor models, becomes a powerful mechanism for enhancing recommender systems in sparse-data environments.

The remainder of this paper is structured as follows: Section 2 reviews the relevant literature on clustering and recommendation techniques. Section 3 describes the methodology and experimental setup. Section 4 presents and analyzes the experimental results. Section 5 discusses the implications and significance of the findings. Finally, Section 6 concludes the paper and outlines directions for future work.

2. Related Works

Clustering is a pivotal unsupervised learning technique extensively applied in recommender systems (RS) to enhance user–item interactions and improve recommendation accuracy. Various methodologies have been proposed and investigated across the literature, generally categorized into two primary approaches: hierarchical and partitional clustering. Each approach has distinct advantages and challenges, particularly when handling sparse and high-dimensional datasets commonly encountered in RS.

Hierarchical clustering methods produce nested partitions through agglomerative or divisive strategies. Agglomerative clustering methods initiate each data point as an individual cluster, iteratively merging them based on similarity metrics until a specified clustering condition is achieved [1]. Conversely, divisive clustering methods start with all data points grouped together and iteratively split them based on dissimilarity. Hierarchical clustering techniques have been advantageous due to their ability to illustrate multi-level relationships among clusters; however, they often face scalability challenges with large datasets, a limitation particularly impactful in RS contexts [6].

Partitional clustering methods directly partition datasets into a predefined number of clusters, optimizing specific clustering criteria such as intra-cluster similarity and inter-cluster separation. K-means clustering is the quintessential partitional method extensively used in RS research. It partitions users or items into clusters based on minimizing intra-cluster distances to centroids, calculated typically as cluster means [7]. Despite its simplicity and computational advantages, K-means clustering significantly depends on the initialization of centroids, often resulting in suboptimal clustering due to convergence to local minima [1].

To mitigate centroid initialization sensitivity, various enhancements in the K-means algorithm have emerged. For instance, K-means++ introduces an intelligent centroid initialization strategy, considerably reducing computational iterations and improving clustering quality [8]. Other variations, like K-meansUserPower, specifically address the sparsity in user–item matrices by initializing centroids based on users with the highest interaction frequencies, leading to more robust clustering outcomes and higher predictive accuracy [6].

The traditional K-means clustering approach operates under the assumption that each data point belongs exclusively to a single cluster, known as hard clustering. Although straightforward, this assumption is frequently unrealistic in RS scenarios, where user preferences often span multiple categories or genres. Hence, soft-clustering methods, notably fuzzy clustering approaches, have gained significant attention. The Fuzzy C-Means (FCM) clustering method, introduced by Bezdek et al. [3], allows data points to belong to multiple clusters simultaneously, assigning membership grades to reflect their proximity to cluster centroids.

Nevertheless, FCM clustering encounters challenges, particularly in high-dimensional spaces characterized by significant data sparsity—typical conditions in RS. Specifically, FCM clustering performance deteriorates when dimensionality increases because membership computations become less meaningful due to distances converging in high-dimensional spaces [9].

Among the most promising advances in clustering for RS are model-based approaches that employ Matrix Factorization (MF). Traditional Matrix Factorization methods, such as Singular Value Decomposition (SVD) or Probabilistic Matrix Factorization (PMF), decompose the user–item interaction matrix into low-rank matrices that represent users and items in a shared latent space [10]. These latent representations can reveal underlying structures, such as genre preferences or user behavior patterns, that are not explicitly observable. Such techniques have been shown to outperform memory-based approaches in terms of scalability and predictive accuracy [2].

Matrix Factorization (MF)-based clustering methods factorize sparse user–item interaction matrices into lower-dimensional latent spaces [2]. Latent Semantic Analysis (LSA) and Probabilistic Latent Semantic Analysis (pLSA), initially developed within information retrieval contexts, have limitations such as arbitrary latent factors and susceptibility to overfitting [11,12,13]. Latent Dirichlet Allocation (LDA) addressed overfitting using Bayesian probabilistic modeling, although adapting these methods to RS remains challenging due to arbitrary data imputation [14].

Non-negative Matrix Factorization (NMF), introduced by Lee and Seung [15], emerged as an effective solution, enabling clear interpretability of latent factors. Bayesian probabilistic NMF further enhanced these advantages by explicitly modeling positive and negative voting behaviors, offering superior clustering interpretability and flexibility [4,5].

Recent evaluations comparing k-means, FCM, and various MF-based clustering techniques indicate that probabilistic Bayesian NMF outperforms other methods in terms of both prediction accuracy and clustering quality, especially when model parameters are carefully tuned [16]. The use of flexible parameterization, allowing a smooth transition between hard and soft clustering, is a major advantage of Bayesian NMF.

Evaluating clustering performance involves metrics such as intra-cluster cohesion and inter-cluster separation, with research predominantly emphasizing cohesion due to its correlation with recommendation accuracy improvements and computational feasibility [17,18].

In conclusion, clustering methodologies in recommender systems have evolved significantly, with Bayesian probabilistic NMF demonstrating particular effectiveness due to its interpretability, flexibility, and robust predictive capabilities in sparse-data environments.

3. Materials and Methods

In this study, we selected the widely recognized MovieLens 1M dataset as the experimental benchmark. This dataset was chosen not merely because of prior usage in earlier works, but because it provides an optimal balance of representativeness, reproducibility, and sparsity while remaining computationally tractable for clustering-based experiments. Larger-scale datasets tend to complicate fair comparison due to scalability constraints, whereas MovieLens 1M ensures reproducibility across the RS literature. Moreover, recent discussions [19] highlight the importance of reproducible datasets in avoiding memorization biases in recommender system evaluations.

3.1. Data Preparation

To mitigate potential sampling bias, the MovieLens 1M dataset was divided into 20 randomly generated subsets. Each of these datasets was further partitioned into two subsets: a training set, comprising 80% of the data, and a testing set, containing the remaining 20%. This partitioning was executed following a uniform random distribution to maintain unbiased representation. This stratified partitioning enhances robustness by ensuring that results are not overly dependent on a single train–test split, providing more generalizable insights. The procedure does not negatively bias clustering performance but strengthens statistical reliability.

The preprocessing pipeline was implemented following the methodology of Hernando [4], which provides a reproducible framework for handling sparsity in user–item matrices. The implementation of Bayesian NMF was developed using the CF4J framework https://cf4j.etsisi.upm.es/ (accessed on 1 July 2025), which offers reproducible libraries for collaborative filtering and Matrix Factorization algorithms. Building on this framework ensured consistency with prior works and reproducibility of the experimental setup.

3.2. Clustering Technique Evaluation

The clustering techniques analyzed in this research include classical methods such as K-means and Fuzzy C-Means (FCM), as well as advanced Matrix Factorization-based approaches (CMF), particularly Bayesian Non-negative Matrix Factorization (NMF). These methods were selected for their relevance, their demonstrated effectiveness in previous studies, and their ability to address the sparsity and high-dimensionality issues inherent to recommender systems.

K-means: A traditional partitional hard-clustering method characterized by its simplicity, computational efficiency, and sensitivity to centroid initialization. Equation (1) shows the objective function, and Equation (2) recalculates the new centroids.

$$J_{c-kmeans}=\sum _{j=1}^c\sum _{i=1}^n\left|\right|x_i-c_j{\left|\right|}^2$$

(1)

where

• n is the number of samples;
• c is the number of clusters;
• $c_j$ is the jth cluster;
• $x_i$ is the ith sample.

$$c_{j-kmeans}={\displaystyle \frac{{\sum }_{i=1}^n{x}_i}{{\sum }_{i=1}^n}}$$

(2)

Fuzzy C-Means (FCM): A soft-clustering method assigning membership degrees to multiple clusters, providing flexibility in capturing user preferences. Equation (3) shows the objective function, Equation (4) shows the membership function, and Equation (5) recalculates the new centroids.

$$J_{c-fcm}=\sum _{j=1}^c\sum _{i=1}^n{\mathcal{U}}_{ij}^a\left|\right|x_i-c_j{\left|\right|}^2$$

(3)

where

• n is the number of samples;
• c is the number of clusters;
• ${\mathcal{U}}_{ij}\in [0,1]$ represents the membership of the ith sample for the jth cluster;
• $c_j$ is the jth cluster;
• $x_i$ is the ith sample;
• $a\in {\mathbb{R}}^{+}$ y $a>=1$ is the overlapping coefficient. When $a=1$, the hard-clustering approach is used.

$${\mathcal{U}}_{ij}={\displaystyle \frac{1}{{\sum }_{k=1}^c{\left(\frac{\left|\right|x_i-c_i{\left|\right|}^2}{\left|\right|x_i-c_k{\left|\right|}^2}\right)}^{2(a-1)}}}$$

(4)

$$c_{j-fcm}={\displaystyle \frac{{\sum }_{i=1}^n\left({\mathcal{U}}_{ij}^a\right)x_i}{{\sum }_{i=1}^n\left({\mathcal{U}}_{ij}^a\right)}}$$

(5)

Non-negative Matrix Factorization (NMF): NMF is a factorization-based clustering technique characterized by its ability to generate easily interpretable clusters by decomposing the original user–item interaction matrix into non-negative latent-factor matrices. Unlike traditional factorization methods, NMF constrains the decomposed matrices to positive values, enhancing the interpretability of the latent factors as meaningful and interpretable memberships. NMF factorizes the user–item rating matrix R into two non-negative matrices, user factors P and item factors Q, represented as:

$$R\approx P\times Q^T$$

(6)

where

• $R\in {\mathbb{R}}^{n\times m}$ is the original sparse user–item rating matrix;
• $P\in {\mathbb{R}}^{n\times k}$ represents the user–factor matrix, indicating the degree of membership of users to latent clusters;
• $Q\in {\mathbb{R}}^{m\times k}$ represents the item–factor matrix, indicating the degree of membership of items to latent clusters;
• n and m are the number of users and items, respectively;
• k is the number of latent factors or clusters.

NNMF optimizes the following objective function to minimize the difference between the observed ratings and the estimated ratings:

$$\underset{P,Q}{min}\left|\right|R-P\times Q^T{\left|\right|}_F^2\mathrm{subject}\mathrm{to}P\ge 0,Q\ge 0$$

(7)

where $\left|\right|·{\left|\right|}_F$ represents the Frobenius norm, ensuring non-negativity constraints that provide clear interpretability and meaningful factorization.

Bayesian Non-negative Matrix Factorization (NMF): This is an advanced probabilistic clustering method that factorizes user–item matrices into interpretable latent factors, allowing adjustable clustering granularity through parameters $\alpha$ (overlap, Equation (8)) and $\beta$ (membership confidence, Equations (9) and (10)). Equation (11) shows the membership function.

$${\displaystyle {\gamma }_{u,k}=\alpha +\sum _{\left\{i\right|r_{u,i}\ne •\}}{\lambda }_{u,i,k}}$$

(8)

$${\displaystyle {ϵ}_{i,k}^{+}=\beta +\sum _{\left\{u\right|r_{u,i}\ne •\}}{\lambda }_{u,i,k}·r_{u,i}^{+}}$$

(9)

$${\displaystyle {ϵ}_{i,k}^{-}=\beta +\sum _{\left\{u\right|r_{u,i}\ne •\}}{\lambda }_{u,i,k}·r_{u,i}^{-}}$$

(10)

$${\displaystyle a_{u,k}=\frac{{\gamma }_{u,k}}{{\displaystyle \sum _{j=1\dots K}{\gamma }_{u,j}}}}$$

(11)

3.3. Evaluation Metrics

The evaluation of clustering quality within this research employs primarily intra-cluster metrics, focusing explicitly on cluster cohesion. The rationale for emphasizing intra-cluster cohesion is its direct correlation with the quality of recommendations generated by recommender systems. Lower intra-cluster distances typically indicate more homogeneous clusters, potentially translating into more accurate recommendations.

3.3.1. Hard-Clustering Metrics

In hard clustering, each user or item is strictly assigned to a single cluster. The objective function for hard clustering is the minimization of intra-cluster distance, calculated as the sum of distances between each data point and its assigned cluster centroid. Formally, the intra-cluster cohesion is given by

$$\mathrm{Intra}\text{-}\mathrm{cluster}=\sum _{k=1}^K\sum _{u=1}^n\left|\right|x_u-c_k{\left|\right|}^2$$

where

• n is the total number of users;
• K represents the total number of clusters;
• $c_k$ is the centroid of cluster k;
• $x_u$ denotes the uth user vector.

3.3.2. Soft-Clustering Metrics

In soft clustering, each user or item can belong simultaneously to multiple clusters, with varying degrees of membership. Hence, the intra-cluster cohesion for soft clustering accounts for these membership degrees by weighting distances accordingly:

$$\mathrm{Intra}\text{-}\mathrm{cluster}=\sum _{k=1}^K\sum _{u=1}^n{p}_{u,k}\left|\right|x_u-c_k{\left|\right|}^2$$

where

• $p_{u,k}$ denotes the membership probability of the uth user to the kth cluster;
• The other variables are consistent with the hard-clustering definition.

These metrics allow an accurate comparative analysis across different clustering methodologies, explicitly capturing their effectiveness in managing sparsity and dimensionality within recommender system contexts.

3.4. Implementation Details

All clustering methods were implemented and evaluated systematically to ensure fairness and reproducibility. For K-means clustering, multiple centroid initialization strategies, including random initialization and K-means++ [8], were employed. For FCM, the fuzziness coefficient was varied to examine its impact on clustering quality. For Bayesian NMF, parameters $\alpha$ and $\beta$ were systematically adjusted, allowing for a comprehensive evaluation of both soft- and hard-clustering capabilities under various levels of overlap and membership confidence.

This structured methodological approach ensures rigorous comparative insights into the performance, interpretability, and practical applicability of the evaluated clustering techniques within recommender systems.

4. Results

In this section, we present the comparative results of the evaluated clustering methodologies, namely K-means, Fuzzy C-Means (FCM), and Bayesian Non-negative Matrix Factorization (NMF). The analyses include assessments based on intra-cluster cohesion and predictive accuracy, leveraging visual and tabular representations from our experiments with the MovieLens 1M dataset.

4.1. Soft-Clustering Analysis

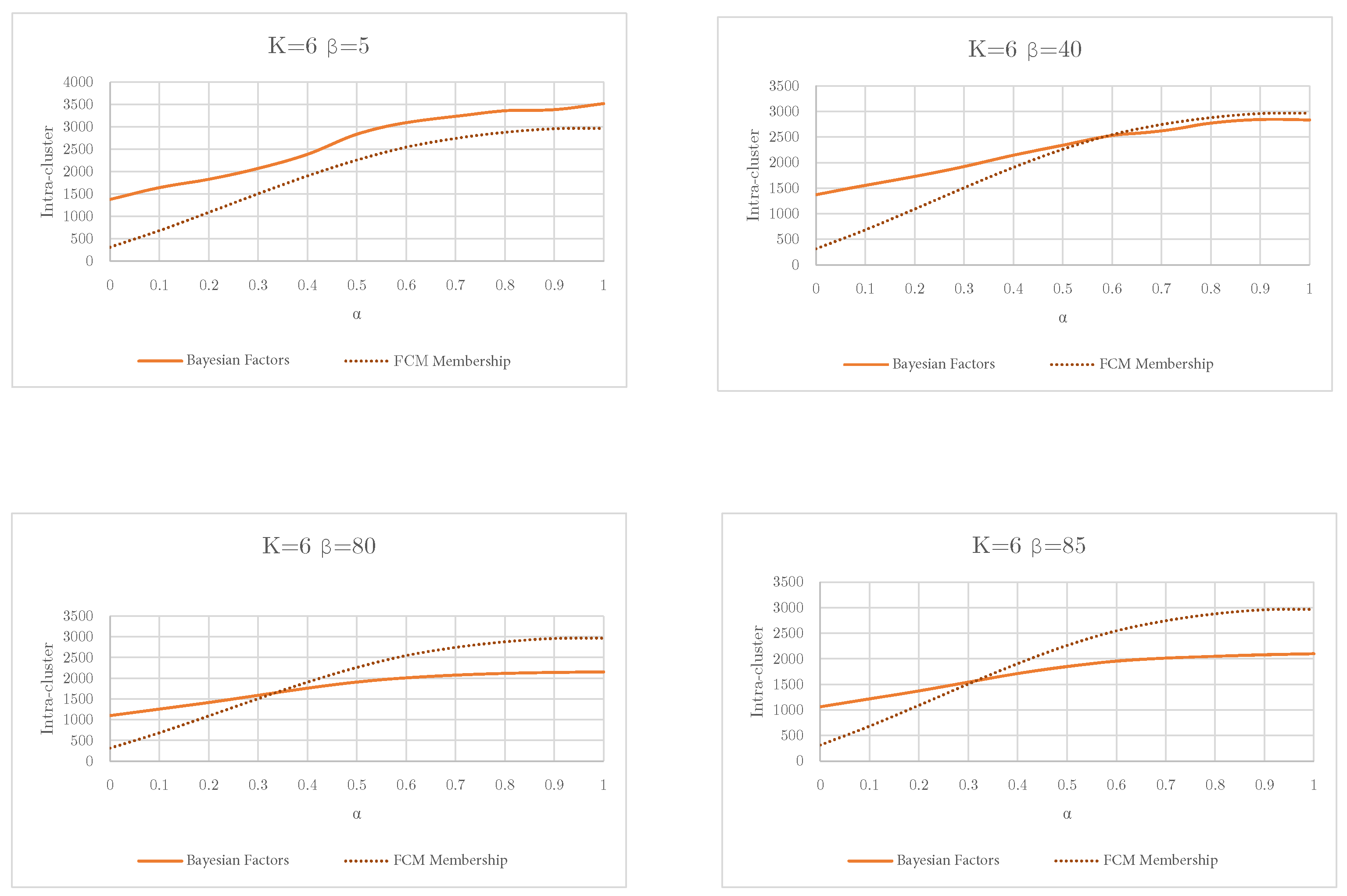
We first evaluated soft-clustering techniques, particularly focusing on Fuzzy C-Means and Bayesian NMF. Figure 1 presents intra-cluster cohesion for different parameter values of $\alpha$ and $\beta$ in Bayesian NMF compared to the membership values obtained from FCM. The intra-cluster cohesion is plotted against the overlap parameter $\alpha$, with varying levels of evidence parameter $\beta$. A general observation is that intra-cluster cohesion decreases as the overlap parameter $\alpha$ increases, indicating that clusters become less compact with greater overlap.

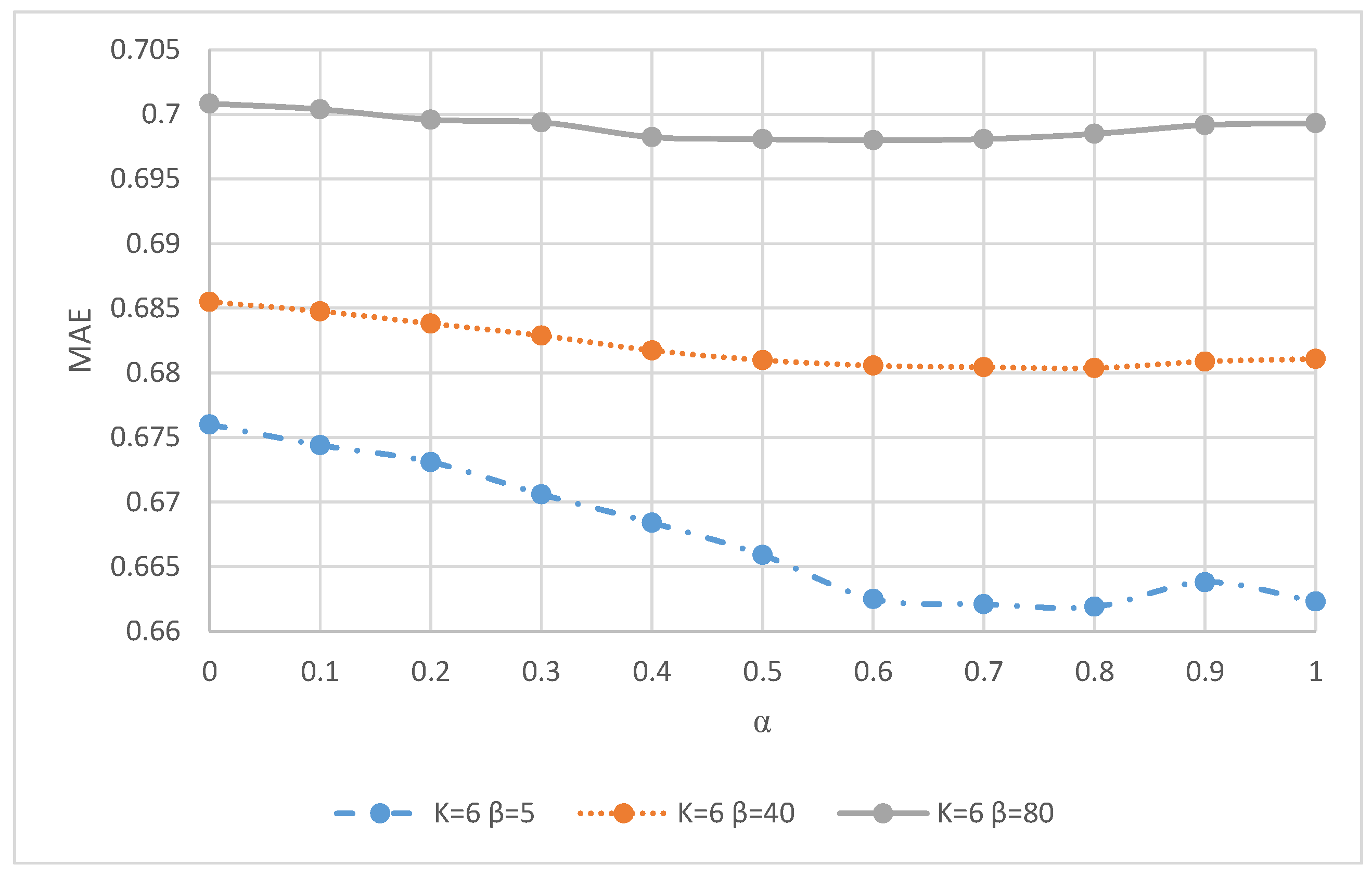
The corresponding predictive accuracy measured through the Mean Absolute Error (MAE) is illustrated in Figure 2. It demonstrates the influence of the $\beta$ parameter on prediction quality. Notably, higher $\beta$ values result in a significant improvement in predictive accuracy due to the stricter evidence threshold required for cluster membership, suggesting more reliable and robust cluster assignments.

The low MAE values observed in Figure 2 are attributable to Bayesian NMF’s probabilistic modeling and the use of high evidence thresholds ($\beta$ > 40), which enforce more reliable membership assignments. This leads to improved predictive performance and should not be interpreted as a limitation of the dataset structure.

4.2. Hard-Clustering Analysis

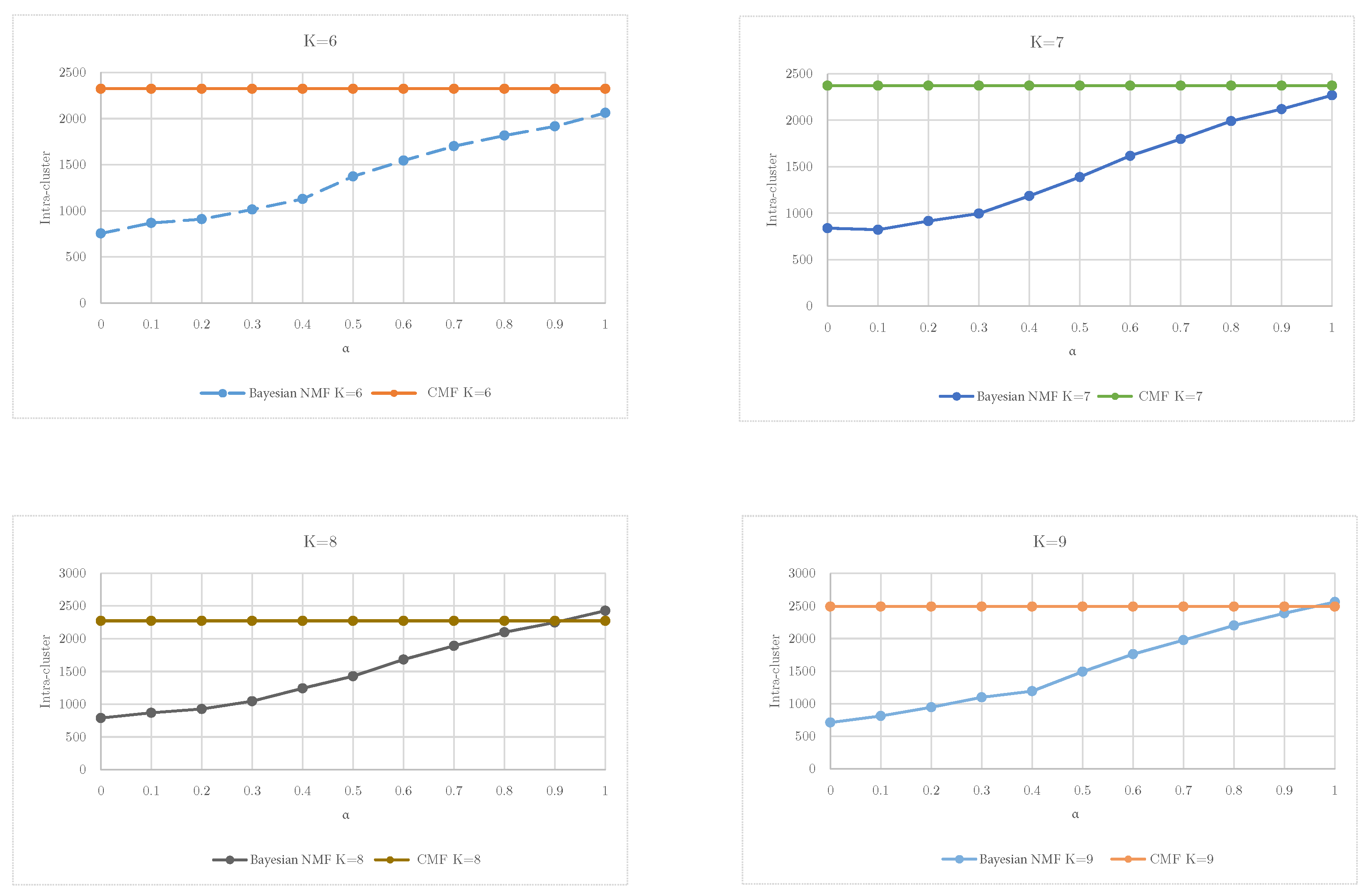
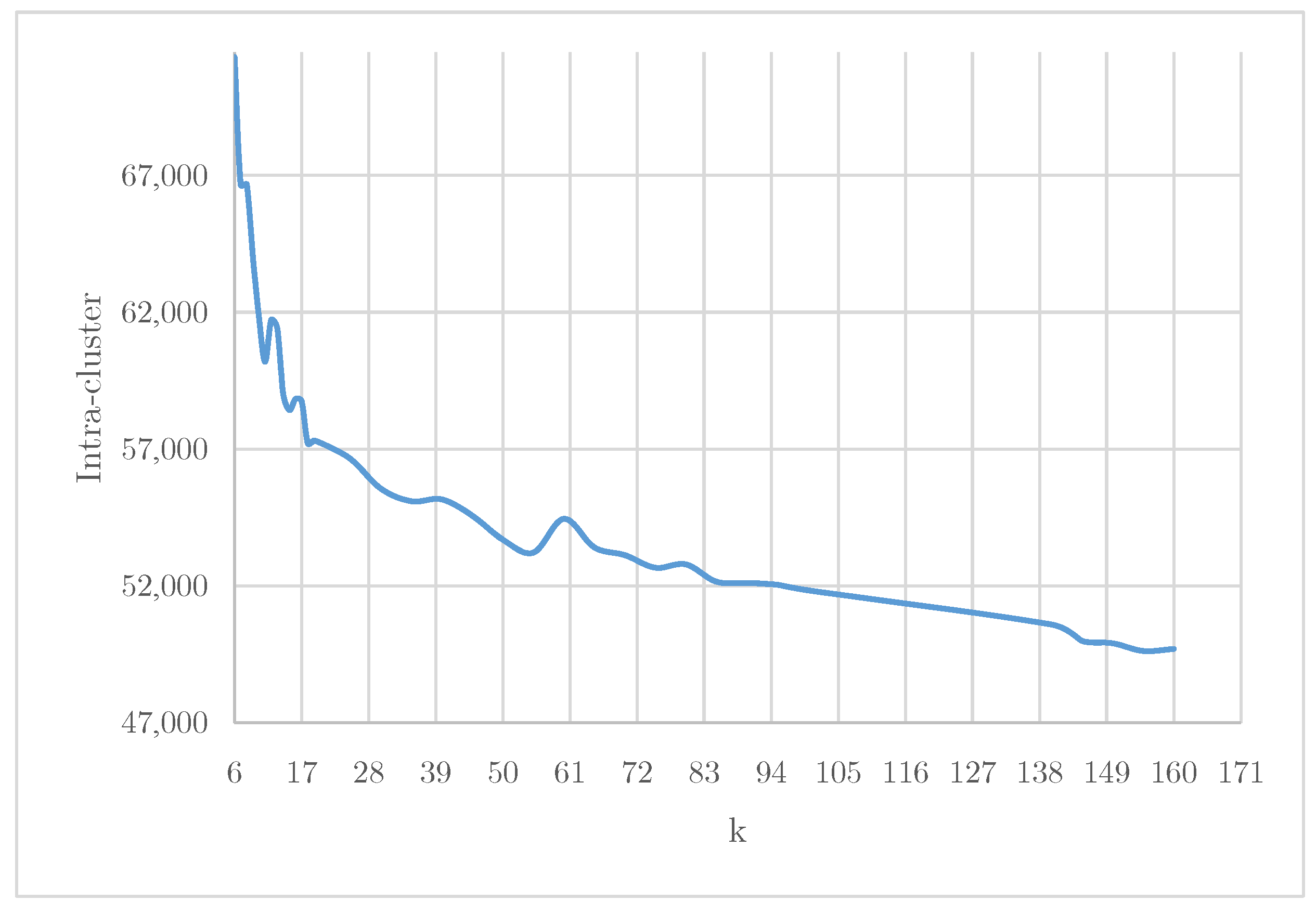
The evaluation of hard-clustering methods included comparisons between classical Matrix Factorization (CMF) and Bayesian NMF, specifically analyzing intra-cluster cohesion across varying numbers of clusters ($k=6,7,8,9$). The results are presented in Figure 3.

4.3. Comparative Performance: K-Means vs. NMF and FCM

The comparative analysis involving K-means, NMF with $\alpha =0$, and FCM with a fuzziness parameter of $a=1$, highlighted the relative strengths and limitations of each method. Bayesian NMF, even under hard-clustering conditions ($\alpha =0$), demonstrated superior clustering quality relative to both K-means and FCM. The flexibility and interpretability provided by the probabilistic framework of NMF emerged as critical factors contributing to its superior performance.

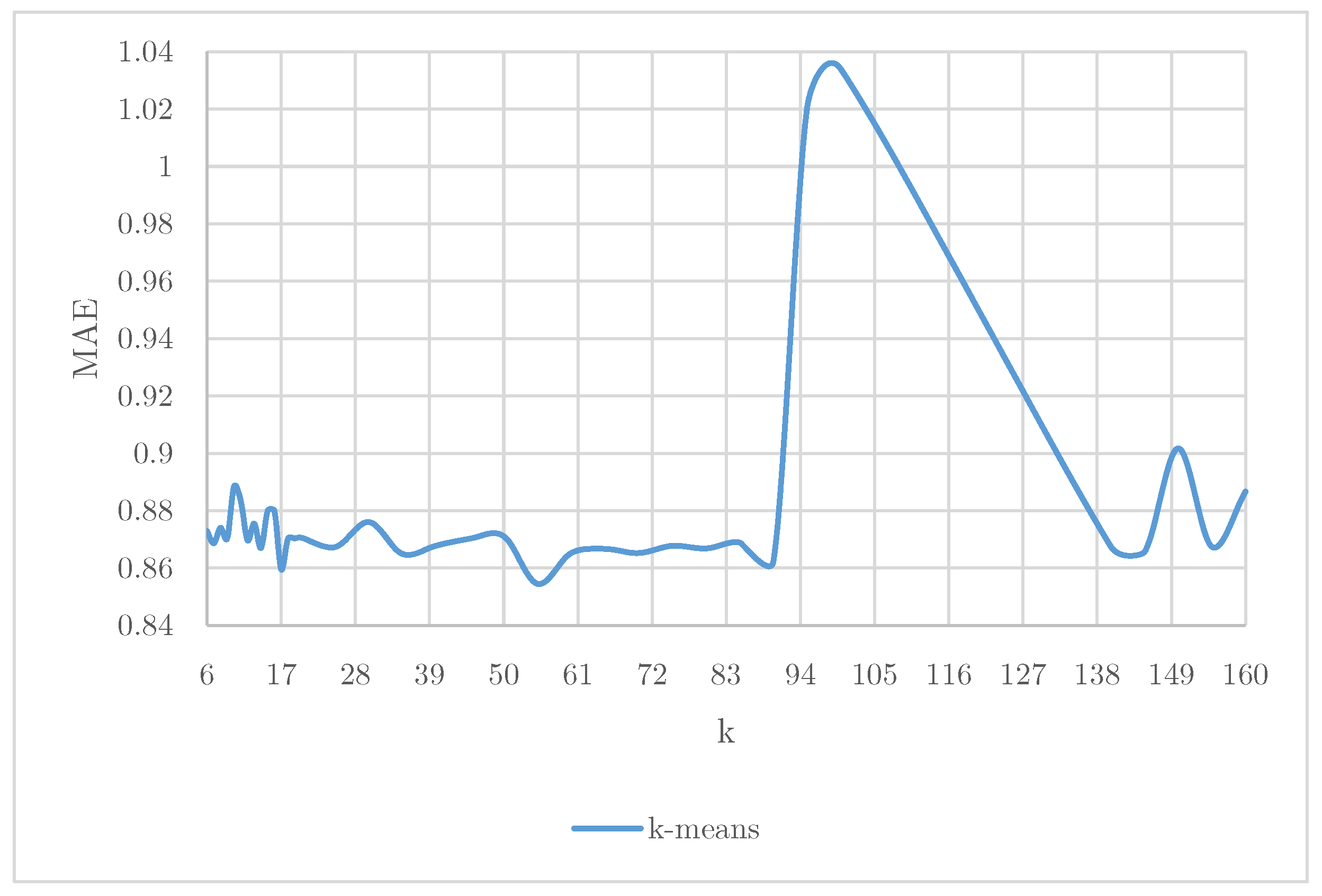
Further, Figure 4 compares predictive accuracy for different values of cluster numbers (k) in the K-means algorithm. The figure indicates that K-means does not achieve competitive predictive performance, maintaining relatively high MAE values across different cluster sizes. Figure 5 complements these results by displaying intra-cluster cohesion for various cluster numbers (k), illustrating that while intra-cluster cohesion improves with increasing k, the corresponding improvement in predictive accuracy remains limited.

4.4. Impact of Parameters on Clustering Quality

These experiments highlighted the importance of the overlap ($\alpha$) and evidence ($\beta$) parameters in Bayesian NMF. A key advantage of Bayesian NMF lies in its dual capacity for both hard and soft clustering within the same probabilistic framework. By adjusting $\alpha$, the model seamlessly transitions between exclusive partitions (hard clustering) and overlapping clusters (soft clustering), enabling more nuanced representations of user preferences compared to classical algorithms restricted to one regime.

Although parameters $\alpha$ and $\beta$ were varied systematically, future research should employ structured optimization strategies (e.g., grid search, Bayesian optimization) and statistical significance testing to establish the robustness of performance differences.

Higher overlap values ($\alpha$ between 0.5 and 1) consistently improved predictive accuracy but produced clusters with lower cohesion, reflecting realistic user behavior overlaps. Conversely, lower $\alpha$ values improved intra-cluster cohesion but resulted in inferior predictive accuracy.

The impact of $\beta$, particularly at high values ($\beta >40$), demonstrated substantial predictive improvement by enforcing rigorous evidence criteria for membership assignments, underscoring the value of careful parameter tuning in clustering-based recommender systems.

The analysis of membership evolution based on the overlap parameter ($\alpha$) is further detailed in

Table 1. Relationship between $a\left(FCMmembership\right)$ of Equation (3) and $\alpha$ of Bayesian NMF.

k	a	FCM Overlapping	$\mathit{\alpha }$	Bayesian Overlapping	k	a	FCM Overlapping	$\mathit{\alpha }$	Bayesian Overlapping
6	1.1	0.964	0	0.823	8	1.1	0.943	0	0.816
6	1.2	0.922	0.1	0.792	8	1.2	0.88	0.1	0.788
6	1.3	0.875	0.2	0.772	8	1.3	0.816	0.2	0.765
6	1.4	0.825	0.3	0.743	8	1.4	0.758	0.3	0.728
6	1.5	0.776	0.4	0.706	8	1.5	0.703	0.4	0.675
6	1.6	0.727	0.5	0.644	8	1.6	0.651	0.5	0.623
6	1.7	0.681	0.6	0.609	8	1.7	0.602	0.6	0.567
6	1.8	0.638	0.7	0.572	8	1.8	0.557	0.7	0.527
6	1.9	0.597	0.8	0.549	8	1.9	0.517	0.8	0.496
6	2	0.56	0.9	0.531	8	2	0.481	0.9	0.468
6	2.1	0.527	1	0.506	8	2.1	0.448	1	0.438
7	1.1	0.955	0	0.803	9	1.1	0.935	0	0.834
7	1.2	0.905	0.1	0.799	9	1.2	0.866	0.1	0.799
7	1.3	0.851	0.2	0.774	9	1.3	0.797	0.2	0.76
7	1.4	0.797	0.3	0.743	9	1.4	0.726	0.3	0.716
7	1.5	0.744	0.4	0.692	9	1.5	0.666	0.4	0.682
7	1.6	0.693	0.5	0.638	9	1.6	0.613	0.5	0.609
7	1.7	0.644	0.6	0.586	9	1.7	0.564	0.6	0.552
7	1.8	0.599	0.7	0.549	9	1.8	0.52	0.7	0.511
7	1.9	0.558	0.8	0.516	9	1.9	0.481	0.8	0.471
7	2	0.52	0.9	0.495	9	2	0.445	0.9	0.442
7	2.1	0.486	1	0.471	9	2.1	0.414	1	0.419

, highlighting critical insights into clustering behavior once the optimal number of clusters (k) was determined. Notably, the table demonstrates a clear inverse relationship between the overlap parameter ($\alpha$) and the fuzzy exponent parameter (a) across different cluster sizes ($k=6,7,8,9$). As the fuzzy exponent parameter (a) increases, cluster overlap consistently decreases, indicating that clusters become more exclusive and compact. Furthermore, the Bayesian model consistently yields lower overlapping values compared to FCM at identical exponent levels (a), particularly noticeable for larger values of k, underscoring Bayesian NMF’s robustness in defining well-separated clusters. These patterns indicate that optimal predictive performance is closely associated with moderate-to-high levels of cluster overlap, confirming Bayesian NMF’s ability to effectively model realistic user–item interactions characterized by multiple overlapping preferences, especially relevant in sparse recommendation scenarios.

4.5. Summary of Key Results

The summarized findings from our experiments using the MovieLens 1M dataset are as follows.

• Bayesian NMF provides significantly better clustering quality and predictive accuracy compared to traditional methods like K-means and classical CMF.
• Optimal predictive accuracy requires careful adjustment of parameters $\alpha$ and $\beta$, highlighting a balance between cluster overlap and evidence thresholds.
• Soft clustering (higher overlap) consistently improves predictive accuracy at the cost of cluster cohesion, whereas hard clustering improves cohesion at the expense of accuracy.

These findings underscore the importance of leveraging probabilistic clustering approaches, especially Bayesian NMF, to address the challenges posed by sparse, high-dimensional recommender system datasets.

5. Discussion

Our experimental results demonstrate that clustering techniques can significantly improve the performance of recommender systems, particularly under conditions of data sparsity. The comparative evaluation reveals that methods based on Matrix Factorization, when combined with clustering strategies, outperform baseline models in terms of both accuracy and scalability.

The scope of this study was limited to clustering quality. Although a detailed runtime analysis was not included, it is evident that Matrix Factorization-based approaches entail higher computational complexity than traditional algorithms, as they require dimensionality reduction followed by clustering. In our experiments, Bayesian NMF remained computationally feasible, converging within practical time frames. Future work will explicitly benchmark execution time and scalability on larger datasets.

Although this study employed MovieLens 1M as a controlled benchmark, we recognize that scalability and extreme sparsity remain open challenges in big data environments. Future research should extend Bayesian NMF to larger datasets such as Netflix Prize or Amazon Reviews and integrate recent approaches like dynamic multi-view clustering [20] or biclustering with ResNMTF [21], which are specifically designed to address sparsity in large-scale recommendation contexts.

An important observation is that clustering users or items prior to applying collaborative filtering reduces the dimensionality and noise in the data, leading to more personalized and reliable recommendations. However, the effectiveness of each clustering algorithm varies depending on the dataset characteristics and sparsity levels.

Furthermore, our results confirm that K-means clustering, although simple, remains competitive when used in conjunction with Matrix Factorization methods. On the other hand, hierarchical clustering tends to be more computationally expensive and sensitive to initial parameters, which may limit its applicability in large-scale systems.

While this research prioritizes methodological benchmarking, the implications are directly applicable to real RS applications: In e-commerce, Bayesian NMF clustering can enhance personalization by grouping users with overlapping purchasing patterns, thus improving product discovery and cross-selling strategies. In streaming services, the ability to model users with multiple overlapping preferences allows for more accurate content recommendations in multi-genre consumption scenarios. In educational platforms, clustering students with similar learning behaviors can support adaptive-learning pathways and targeted interventions. Furthermore, Bayesian NMF offers potential advantages in cold-start situations by assigning new users or items to probabilistic clusters based on partial information, thereby mitigating the lack of historical data. These applications underscore the practical relevance of probabilistic clustering in environments characterized by data sparsity and evolving user behaviors. Our experimental findings have direct implications for real-world recommender systems. For instance, the demonstrated ability of Bayesian NMF to handle sparse data and capture overlapping user preferences can be directly applied to e-commerce platforms for personalized product discovery, to streaming services for multi-genre content recommendation, and to educational systems for adaptive-learning support. These examples underscore that the methodological advances reported in this study provide actionable insights for practical RS deployments, bridging the gap between algorithmic evaluation and applied use cases.

These findings suggest that hybrid approaches that leverage the strengths of clustering and Matrix Factorization can offer robust solutions for real-world recommender systems. Future work should explore dynamic clustering models that adapt to evolving user behaviors and evaluate the impact of these techniques on real-time recommendation performance.

A limitation of this work is that we did not evaluate sensitivity to varying levels of sparsity or noisy ratings. Future experiments will systematically adjust sparsity levels and introduce synthetic noise to better assess the robustness of Bayesian NMF in real-world recommendation contexts.

6. Conclusions

This research provided a comprehensive comparative analysis of clustering techniques in recommender systems, specifically focusing on traditional methods like K-means and Fuzzy C-Means, as well as advanced Matrix Factorization-based approaches, notably Bayesian NMF. Our findings demonstrate significant advantages of Bayesian NMF over classical clustering methods, particularly regarding predictive accuracy, interpretability, and flexibility.

Bayesian NMF consistently outperformed traditional methods such as K-means and classical Matrix Factorization, offering superior clustering quality, indicated by lower intra-cluster distances and enhanced predictive performance measured through the Mean Absolute Error (MAE). The probabilistic interpretation of Bayesian NMF clusters significantly improves the model’s interpretability, an essential feature for recommender systems aiming for transparency and user trust.

Our experimental results highlighted the critical influence of parameters within Bayesian NMF. Specifically, the overlap parameter ($\alpha$) and the evidence parameter ($\beta$) emerged as key factors affecting both clustering cohesion and recommendation accuracy. Higher overlap values improved predictive accuracy by effectively modeling realistic user behaviors that span multiple clusters, albeit at the expense of cluster cohesion. Conversely, lower overlap values improved intra-cluster cohesion but negatively impacted predictive accuracy. Meanwhile, a high evidence threshold ($\beta >40$) substantially enhanced predictive accuracy, underscoring the necessity of rigorous parameter tuning for optimal clustering performance.

Despite these promising outcomes, several aspects warrant further investigation. Future research could explore hybrid clustering models integrating the strengths of Bayesian NMF with other advanced clustering or deep learning methodologies to further enhance recommendation accuracy and scalability. Additionally, applying these clustering techniques to more diverse and larger-scale datasets could provide deeper insights into their robustness and generalizability in real-world recommender systems.

Moreover, future work should examine dynamic clustering frameworks capable of adapting to temporal shifts in user preferences and behaviors, a critical aspect in rapidly evolving digital environments. Incorporating contextual data such as user demographics, temporal factors, and implicit feedback could also provide substantial gains in predictive accuracy and user experience.

Beyond summarizing our findings, this study opens avenues for future research. One promising direction is the integration of Bayesian NMF with neural recommender architectures, combining interpretability with the representational power of deep learning. Another avenue involves applying the method to streaming and real-time recommendation contexts, where user preferences evolve continuously and models must adapt dynamically. Incorporating contextual signals such as temporal dynamics, implicit feedback, and multi-modal information will further extend the applicability of Bayesian NMF in modern digital platforms. These perspectives highlight the potential of probabilistic clustering as a foundation for next-generation recommender systems. Future extensions of this work should incorporate systematic hyper-parameter tuning strategies combined with statistical validation, benchmarks with additional datasets, sensitivity analyses under varying sparsity conditions, and explicit reporting of random seed settings to further strengthen reproducibility.

Overall, Bayesian NMF emerges as a highly effective clustering technique for addressing the challenges of sparsity, interpretability, and predictive accuracy inherent to recommender systems, paving the way for continued advancements in personalized-recommendation research.