Fuzzy Lyapunov-Based Gain-Scheduled Control for Mars Entry Vehicles: A Computational Framework for Robust Non-Linear Trajectory Stabilization
Abstract
1. Introduction
- The development of a fuzzy parameter-varying framework tailored for Mars atmospheric entry, providing a novel approach to the computational modeling and control of non-linear aerospace systems.
- An accurate representation of complex aerodynamic interactions during entry through a sector-bounded approximation and fuzzy rule partitioning, enabling a tractable description of non-linear dynamics.
- An introduction of a refined stability analysis that departs from conventional quadratic Lyapunov functions by employing fuzzy Lyapunov function synthesis in combination with the Full-Block S-procedure.
- A reduction in conservatism in robust control design and the facilitation of gain-scheduled controller construction using linear matrix inequality (LMI) optimization.
2. Mathematical Modeling
3. System Stability Analysis
4. Controller Design
4.1. State-Feedback Controller
- .
 then the following states feedback controller can control the following system (System (8)):
then the following states feedback controller can control the following system (System (8)):4.2. Dynamical Output-Feedback Controller Design
 then System (18) is stabilized by the controller (Equation (19)), and the coefficient matrix of the controller is as follows:
then System (18) is stabilized by the controller (Equation (19)), and the coefficient matrix of the controller is as follows:4.3. Remarks
5. Numerical Illustration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
 and satisfies
and satisfies 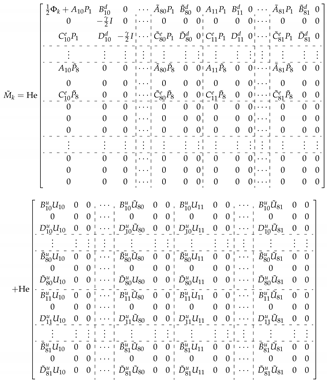 Thus,
Thus,- , where . As for , we have
References
- Ye, P.; Sun, Z.; Rao, Z.; Meng, L. Mission overview and key technologies of the first Mars probe of China. Sci.-China-Technol. Sci. 2017, 60, 649–657. [Google Scholar] [CrossRef]
- Goossens, S.; Sabaka, T.; Rao, Z. Probing Lateral Density Variations in the Crust from Gravity and Topography: Applications to the Moon and Mars. Planet. Sci. J. 2025, 6, 71. [Google Scholar] [CrossRef]
- Guinard, A.; Fienga, A.; Mémin, A.; Ganino, C. Coupled tidal tomography and thermal constraints for probing Mars viscosity profile. Icarus 2025, 425, 116318. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, B.; Li, T.; Zhang, H.; Xiang, C.; Fan, W.; Zhao, Z. Analysis of Aerodynamic Characteristics of Propeller Systems Based on Martian Atmospheric Environment. Drones 2023, 7, 397. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, Q.; Zhong, W. Comparison of the influence of Martian and Earth’s atmospheric environments on terahertz band electromagnetic waves. Int. J. Commun. Syst. 2021, 34, e4894. [Google Scholar]
- Zhang, J.; Guo, J.; Dobynde, M.; Wang, Y.; Wimmer-Schweingruber, R. From the Top of Martian Olympus to Deep Craters and Beneath: Mars Radiation Environment Under Different Atmospheric and Regolith Depths. J. Geophys.-Res.-Planets 2022, 127, e2021JE007157. [Google Scholar] [CrossRef]
- Tanaka, K.; Ohtake, H.; Wang, H.O. A Descriptor System Approach to Fuzzy Control System Design via Fuzzy Lyapunov Functions. IEEE Trans. Fuzzy Syst. 2007, 15, 333–341. [Google Scholar] [CrossRef]
- Li, J.; Zhou, S.; Xu, S. Fuzzy Control System Design via Fuzzy Lyapunov Functions. IEEE Trans. Syst. Man, Cybern. Part B (Cybern.) 2008, 38, 1657–1661. [Google Scholar] [CrossRef]
- Lam, H.K.; Lauber, J. Membership-function-dependent stability analysis of fuzzy-model- based control systems using fuzzy Lyapunov functions. Inf. Sci. 2013, 232, 253–266. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, F.; Ban, X. Dynamic output feedback control for continuous-time T-S fuzzy systems using fuzzy Lyapunov functions. IEEE Trans. Fuzzy Syst. 2016, 232, 1155–1167. [Google Scholar] [CrossRef]
- Zhang, H.; Ban, X.; Wu, F. Stability Analysis and Controller Design for a Novel Nonlinear System: Fuzzy Parameter Varying System. J. Intell. Fuzzy Syst. 2018, 34, 4387–4395. [Google Scholar] [CrossRef]
- Tang, R.; Yang, X.; Xiang, Z.; Qing, L. Finite-Time L2 Stabilization of Uncertain Delayed T-S Fuzzy Systems via Intermittent Control. IEEE Trans. Fuzzy Syst. 2024, 32, 116–125. [Google Scholar] [CrossRef]
- Liu, Q.; Long, X.; Li, T.; Chen, C. Attack Resilient Fault Tolerant Control for T-S Fuzzy Cyber-Physical Systems. IEEE Trans. Fuzzy Syst. 2024, 32, 2017–2028. [Google Scholar] [CrossRef]
- Collins, E. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach. Automatica 2003, 39, 2011–2013. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Nguyen, A.; Lauber, J.; Boada, M.; Boada, B. Event-Triggered Robust Path Tracking Control Considering Roll Stability Under Network-Induced Delays for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14743–14756. [Google Scholar] [CrossRef]
- Viadero-Monasterio., F.; Melendez-Useros, M.; Zhang, N.; Zhang, H.; Boada, B.; Boada, M. Motion Planning and Robust Output-Feedback Trajectory Tracking Control for Multiple Intelligent and Connected Vehicles in Unsignalized Intersections. IEEE Trans. Veh. Technol. 2025, 1–13. [Google Scholar] [CrossRef]
- Li, S.; Jiang, X. Review and Prospect of Guidance and Control for Mars Atmospheric Entry. Prog. Aerosp. Sci. 2014, 69, 40–57. [Google Scholar] [CrossRef]
- Tolson, R.; Willcockson, W.; Desai, P.; Thomas, P. Anomalistic Disturbance Torques During the Entry Phase of the Mars Exploration Rover Missions:A Telemetry and Mars-Surface Investigation. Prog. Aerosp. Sci. 2014, 125, 507. [Google Scholar]
- Xu, H.; Cui, H.; Tian, Y. Comparison of Two Robust Optimal Trajectory Design Methods for Mars Entry. ICIC Express Lett. 2015, 9, 2437–2443. [Google Scholar]
- Huang, Q.; Yang, C.; Zeng, Z.; Ye, Y.; Zhang, H. Trajectory Control of Mars Probe Based on Fuzzy Lyapunov Function. In Proceedings of the 2023 2nd Conference on Fully Actuated System Theory and Applications, Qingdao, China, 14–16 July 2023; pp. 1097–1102. [Google Scholar]
- Braun, R.; Manning, R. Mars Exploration Entry Descent and Landing Challenges. J. Spacecr. Rocket. 2007, 44, 310–323. [Google Scholar] [CrossRef]
- Huang, Y.; Li, H.; Zhang, J.; Du, X. Mars Atmospheric Entry Guidance Design by Sliding Mode Disturbance Observer-Based Control. Procedia Eng. 2015, 99, 1062–1075. [Google Scholar] [CrossRef][Green Version]
- Putnam, Z.; Braun, R. Precision Landing at Mars Using Discrete-Event Drag Modulation. J. Spacecr. Rocket. 2013, 51, 128–138. [Google Scholar] [CrossRef]
- Scherer, C. LPV Control and Full Block Multipliers. Automatica 2001, 37, 361–375. [Google Scholar] [CrossRef]
- Aubry, P.; Marrez, J.; Valibouze, A. Computing Real Solutions of Fuzzy Polynomial Systems. Fuzzy Sets Syst. 2020, 399, 55–76. [Google Scholar] [CrossRef]
- Li, Y.; Jian, C.; Su, H. Robust Memoryless H∞ Controller Design for Linear Time-Delay Systems with Norm-Bounded Time-Varying Uncertainty. Automatica 1996, 32, 1759–1762. [Google Scholar]
- Choi, H.; Chung, H. Memoryless H∞ Controller Design for Linear Systems with Delayed State and Control. Automatica 1995, 31, 917–919. [Google Scholar] [CrossRef]
- Pasquale, G.; Sturz, Y.; Valcher, M.; Smith, R. Extended Full Block S-Procedure for Distributed Control of Interconnected Systems. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; Volume 31, pp. 5628–5633. [Google Scholar]
- Ye, X.; Song, F.; Zhang, Z.; Zhang, R.; Zeng, Q. Semi-Aerodynamic Model-Aided Invariant Kalman Filtering for UAV Full-State Estimation. IEEE Sensors J. 2024, 24, 25920–25939. [Google Scholar]
- Wang, H.; Farid, Y.; Wang, L.; Garone, E.; Preumont, A. Hovering Flight of a Robotic Hummingbird: Dynamic Observer and Flight Tests. Actuators 2024, 13, 91. [Google Scholar] [CrossRef]
- Viadero-Monasterio, F.; Boada, B.; Boada, M.; Diaz, V. H∞ dynamic output feedback control for a networked control active suspension system under actuator faults. Mech. Syst. Signal Process. 2022, 162, 108050. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Guo, H.; Xi, L.; Liu, G.; Li, Y.; Hua, C. Distributed Output Feedback Prescribed Performance Control for High-Order Nonlinear Multi-Agent Systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 12730–12740. [Google Scholar] [CrossRef]



| Symbol | Description | Symbol | Description |
|---|---|---|---|
| e | evaluation output | subspaces consisted by real matrices | |
| d | external interference | atmospheric density of Mars | |
| subspaces of positive definite matrices | convex set about | ||
| vertex set of convex set | |||
| ⨂ | Kronecker product | element in |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Min, N.; Xie, S. Fuzzy Lyapunov-Based Gain-Scheduled Control for Mars Entry Vehicles: A Computational Framework for Robust Non-Linear Trajectory Stabilization. Computation 2025, 13, 205. https://doi.org/10.3390/computation13090205
Zhang H, Min N, Xie S. Fuzzy Lyapunov-Based Gain-Scheduled Control for Mars Entry Vehicles: A Computational Framework for Robust Non-Linear Trajectory Stabilization. Computation. 2025; 13(9):205. https://doi.org/10.3390/computation13090205
Chicago/Turabian StyleZhang, Hongyang, Na Min, and Shengkun Xie. 2025. "Fuzzy Lyapunov-Based Gain-Scheduled Control for Mars Entry Vehicles: A Computational Framework for Robust Non-Linear Trajectory Stabilization" Computation 13, no. 9: 205. https://doi.org/10.3390/computation13090205
APA StyleZhang, H., Min, N., & Xie, S. (2025). Fuzzy Lyapunov-Based Gain-Scheduled Control for Mars Entry Vehicles: A Computational Framework for Robust Non-Linear Trajectory Stabilization. Computation, 13(9), 205. https://doi.org/10.3390/computation13090205







