Abstract
Efficient simulation of multiphase, multicomponent fluid flow in heterogeneous reservoirs is critical for optimizing hydrocarbon recovery. In this study, we investigate advanced linearization techniques for fully implicit compositional reservoir simulations, a problem characterized by highly nonlinear governing equations that challenge both accuracy and computational efficiency. We implement four methods—finite backward difference (FDB), finite central difference (FDC), operator-based linearization (OBL), and residual accelerated Jacobian (RAJ)—within an MPI-based parallel framework and benchmark their performance against a legacy simulator across three test cases: (i) a five-component hydrocarbon gas field with CO2 injection, (ii) a ten-component gas field with CO2 injection, and (iii) a ten-component gas field case without injection. Key quantitative findings include: in the five-component case, OBL achieved convergence with only 770 nonlinear iterations (compared to 841–843 for other methods) and reduced operator computation time to 9.6 of total simulation time, highlighting its speed for simpler systems; in contrast, for the more complex ten-component injection, FDB proved most robust with 706 nonlinear iterations versus 723 for RAJ, while OBL failed to converge; in noninjection scenarios, RAJ effectively captured nonlinear dynamics with comparable iteration counts but lower overall computational expense. These results demonstrate that the optimal linearization strategy is context-dependent—OBL is advantageous for simpler problems requiring rapid solutions, whereas FDB and RAJ are preferable for complex systems demanding higher accuracy. The novelty of this work lies in integrating these advanced linearization schemes into a scalable, parallel simulation framework and providing a comprehensive, quantitative comparison that extends beyond previous efforts in reservoir simulation literature.
1. Introduction
Hydrocarbon reservoirs are characterized by significant heterogeneity in rock properties, permeability, and porosity, which can vary dramatically over short distances [1,2]. This variability complicates the prediction of fluid flow and phase behavior in porous media, as the multiphase and multicomponent systems require mathematical models that capture the complex interactions between fluid movement, heat transfer, and chemical reactions [3,4,5,6,7]. Accurately describing the thermodynamic state of such systems involves identifying a minimal set of independent variables, from which phase equilibrium and state functions are derived through constitutive relations and algebraic constraints [6,7,8,9]. Typically, solving equations involving multiple variables requires expressing one variable in terms of the others; this process is associated with finding the inverse of nonlinear functions [10,11,12]. This task is computationally intensive due to the nonlinearity and complexity of the governing equations. These governing equations consist of a set of partial differential equations (PDEs) coupled with algebraic constraint equations [10,13].
In reservoir simulation, governing PDEs are typically inherently nonlinear and require to be discretized over space and time to be solved numerically [14,15,16,17,18,19]. Traditional discretization schemes, including finite volume and finite-difference methods, and techniques like the two-point flux approximation (TPFA) provide structured approaches for domain partitioning. However, these methods often struggle in complex geological settings, particularly with unstructured grids and highly heterogeneous media, where convergence and accuracy can be compromised. The TPFA scheme requires the computational mesh to be K-orthogonal, which must have structured and homogeneous properties, where computational speed is a priority [20,21,22,23]. To overcome these limitations, advanced discretization techniques such as the multi-point flux approximation have been developed, offering more reliable numerical representations for pressure and phase behavior in heterogeneous reservoirs. Several studies have extended and refined the MPFA method [24,25,26,27]. offering proofs of convergence [26,28,29,30] and demonstrating its potential applications in reservoir simulation.
After discretizing the governing PDEs in space and time, the simulation domain is partitioned into manageable elements. This process transforms the problem into a system of nonlinear algebraic equations, where primary variables are updated at each time step, thereby increasing overall complexity [31]. Robust linearization is essential to convert these nonlinear systems into forms amenable to efficient iterative solution techniques. Although the Newton–Raphson method is widely used for its ability to handle strongly coupled equations, constructing the Jacobian matrix—which approximates the sensitivity of residuals to changes in primary variables—remains computationally demanding, especially in heterogeneous reservoir systems [6,32,33,34]. Iterative refinement of the Jacobian facilitates convergence, and several linearization techniques have been developed to enhance the performance of the Newton–Raphson method under challenging convergence conditions [35,36].
Modern reservoir simulation software emphasizes adaptability by offering multiple formulations for Jacobian construction, such as analytical differentiation, automatic differentiation (AD), and numerical differentiation [8,37,38,39]. Each method has distinct advantages and drawbacks: analytical differentiation yields precise derivatives but is labor-intensive and impractical for complex compositional models [40,41]; AD enhances robustness by leveraging the underlying mathematical structure, albeit at the cost of increased computational overhead [3,37,42]; and numerical differentiation, while simpler to implement and more adaptable to model changes, often encounters issues with conditional branches, high computational costs, and accuracy [43,44]. These limitations highlight the challenges in accurately representing multiphase, multicomponent fluid flow and phase behavior, which can lead to instability and reduced robustness across diverse simulation scenarios [45,46]. Thus, there is a critical need for advanced, computationally efficient linearization methods to reliably predict fluid behavior in compositional reservoir simulations.
In this work, we introduce and rigorously evaluate a suite of advanced numerical linearization methods for compositional reservoir simulation on structured grids. Specifically, we implement the finite backward difference (FDB), finite central difference (FDC), operator-based linearization, and residual accelerated Jacobian (RAJ) methods to accurately capture the nonlinear couplings inherent in multiphase, multicomponent flow while enabling efficient Jacobian computations [47,48]. The novelty of our approach lies in its integration within a unified, fully implicit, MPI-based parallel simulation framework, coupled with a comprehensive benchmarking against a commercial legacy simulator. We design three distinct test cases—a simplified five-component CO2 gas injection, a more complex ten-component CO2 gas injection, and a ten-component noninjection scenario—to elucidate the trade-offs in computational efficiency and convergence characteristics. Our results demonstrate that each technique uniquely addresses the challenges of multicomponent systems, providing robust and scalable solutions that significantly advance the state of the art in reservoir simulation.
2. Governing Equations
In this section, we present the governing equations that describe fluid flow and thermodynamic phase equilibrium in isothermal compositional reservoirs.
2.1. Fluid Flow Equations
We assume a compositional model for a multi-component, three-phase system consisting of water, oil, and gas in an isothermal system.
where is the porosity of the medium, is the concentration of component c in phase , is the phase molar density, is the phase saturation, is the Darcy velocity of the phase, is the source term of the phase, is the intrinsic permeability tensor, is the dynamic phase viscosity, is the phase pressure, is the vertical pressure gradient, is the vertical depth vector (positive downward), and is the phase relative permeability. The source term represents injection and represents (resident fluid) production. For simplicity, we use the Brooks–Corey model [17,49,50].
where is a Corey parameter, is the end-point relative permeability, is the normalized phase saturation, is the initial phase saturation and is the residual saturation for the other phase.
The Darcy velocity for phase reads as
2.2. Thermodynamic Equilibrium
The three-phase multicomponent system assumes that the hydrocarbon liquid and vapor phases are in thermodynamic equilibrium [51,52,53]. In multi-phase reservoir simulations, we assume hydrocarbon components remain undissolved in the water phase because hydrocarbons are nonpolar, while water is polar. As a result, water components exist only in the water phase. The mathematical expression for thermodynamic equilibrium is given by the following equation:
where is the fugacity of component c in phase and is the molar composition fraction of component c in phase , and p is the system pressure.
The following procedure is used to determine the phase behavior for the system at the equilibrium composition of each phase:
- The phase stability test: For the current p, pressure T, temperature, and components of mole fraction , this stability test is used to determine whether the system is in a single-phase or multi-phase state (e.g., vapor, liquid, or two-phase) and to identify the composition of each phase. It is necessary for any element (control volume) whose status is assumed to be in a single-phase state during the previous Newton iteration in our fully implicit approach.
- Flash calculation: Once the phase stability test suggests the instability (e.g., phase splitting), it indicates that the mixture should undergo a phase state change from single- to two-phase, which leads to a flash calculation. The flash calculation is carried out to determine the amount of composition of the resulting phases. The density is therefore calculated based on the convergence results of the flash calculations using an appropriate equation of state model.
2.3. Local Constraints
In addition to the physical and mathematical relationships required to close a system of equations, we require additional constraints. The purpose of these constraints is to maintain physical consistency, such as conserving mass and ensuring the sum of saturations and component fractions. In this work, the following local constraints are used to close the system:
where represents the molar fraction of component c in phase saturation constraint
where is the saturation of the phase capillary pressure relationship
where p is the system pressure and is the capillary pressure. The unknown variables in the governing equations are determined based on the natural variables formulation [17,54,55]. These variables include the phase pressure , phase saturation , and molar fractions of the components .
3. Nonlinear Solver
The nonlinear solver is designed to efficiently resolve the fully coupled system arising from the discretization of the governing equations presented in Section 2. In this work, we employ the backward Euler method for temporal discretization and the two-point flux approximation method for spatial discretization, which leads to a set of residual equations that capture the contributions from mass balance, Darcy flow, thermodynamic equilibrium, and the local constraints (Section 2.3) ensuring conservation of mass and saturation consistency. The discretized residual equation is derived from the governing equations; it is expressed as
- : transmissibility between cells i and k.
- : phase pressure potential between the neighboring at cell i.
These residuals are collectively expressed as
where represents the vector of primary unknowns, including pressures, saturations, component compositions, and any additional state variables required by the flash calculations.
To solve the nonlinear system, we apply the Newton–Raphson method, which involves linearizing the residual function around the current iterate . This linearization leads to the update equation
where is the increment to the solution and the Jacobian is defined by
The Jacobian matrix is of paramount importance because it contains the partial derivatives of the discretized forms of the governing equations with respect to the primary variables, thereby capturing the strong nonlinear couplings between fluid flow, phase behavior, and local constraints. An accurately assembled Jacobian ensures that the linearized system reliably reflects the underlying physics, allowing the Newton–Raphson method to achieve its convergence to the solution.
The residual vector is directly derived from the discretized forms of the governing equations, with each term representing a specific physical process: the mass balance equations enforce conservation of individual components, the Darcy flow equations account for momentum balance in each phase, and the thermodynamic and local constraints maintain phase equilibrium and composition integrity. After assembling the Jacobian and solving the linear system at each iteration, the updated solution is computed, and an adaptive damping strategy such as Appleyard chopping is employed to control the step size, thereby enhancing the robustness of the fully implicit approach in the presence of strong nonlinearities.
4. Linearization Schemes
Building upon the nonlinear solver described in Section 3, it is evident that the performance of the Newton–Raphson (NR) method critically depends on the accurate computation of the Jacobian matrix [56,57,58,59]. In compositional reservoir simulation, linearization is a crucial step when using the NR method to solve nonlinear systems of equations. One of the significant key components in this process is constructing the Jacobian matrix, which consists of the partial derivatives of the system’s residual with respect to the unknown variables. The efficiency and precision of the Jacobian estimation can greatly impact the convergence rate of the NR method. Several approaches are available for estimating the Jacobian matrix, including automatic differentiation (AD) [42,60,61,62,63,64] and the finite-difference method. In the pursuit of improving computational efficiency, accurately approximating the partial derivatives in the Jacobian is a fundamental challenge in numerical simulations. In this work, we explore several linearization methods aimed at achieving high-fidelity approximations of the Jacobian’s partial derivatives, thereby enhancing the overall convergence properties of the nonlinear solver. This discussion directly complements the previous section by providing the necessary tools and techniques to ensure that the linearization process effectively captures the complex couplings inherent in compositional reservoir models.
4.1. Finite Central Difference Scheme
The finite central difference (FDC) method approximates the derivative of a function at a point x using a symmetric difference quotient. Specifically, the derivative is approximated as
where h is a small perturbation. This approximation is derived from the Taylor series expansion of :
Subtracting the expansion for from that for cancels the even-order terms, yielding
Thus, the truncation error of this approximation is of order , which is superior to one-sided difference methods. The accuracy of the FDC method is highly sensitive to the choice of h. A larger h increases truncation errors, while a very small h can lead to significant round-off errors due to finite precision arithmetic. In our implementation, h is carefully selected to balance these errors, ensuring accurate and robust Jacobian approximations within the Newton–Raphson framework. This approach provides a computationally efficient means to approximate derivatives, thereby enhancing the stability and convergence of the overall nonlinear solver in compositional reservoir simulations.
4.2. Finite Backward Difference Scheme
The finite backward difference (FDB) method approximates the derivative of a function using values at the current point x and a different point , where h is a small numerical perturbation of the same state variable. The derivative is approximated as
This formulation follows from the Taylor series expansion of :
Rearranging the expansion provides an approximation with a truncation error of order . While the FDB method is straightforward and computationally efficient, its first-order accuracy implies that the error decreases linearly with h. Thus, choosing a sufficiently small value h minimizes truncation error; however, excessively small values h may lead to significant round-off errors. In our implementation, the FDB method is employed for Jacobian estimation within the Newton–Raphson framework, as illustrated in Algorithm 1.
| Algorithm 1 Newton–Raphson Method with OBL, FDC, FDB, and RAJ Methods |
|
4.3. Operator-Based Linearization Scheme
The operator-based linearization (OBL) method simplifies nonlinear physics. In implementation, OBL replaces repeated evaluations of complex physical properties through the use of pre-computed mathematical operators. These operators, which represent terms such as accumulation and flux, are also defined as functions of key state variables. Instead of recalculating these properties and their derivatives during each Newton iteration, OBL either precomputes them over a grid of possible states before the simulation begins or computes and stores the operator dynamically when new states are encountered. This approach reduces the computational complexity and time required for simulations involving nonlinear physics [65,66,67,68]. It achieves this by pre-computing or adaptively updating the operators [69,70,71]. Furthermore, the OBL often achieves better numerical stability than other methods that rely on derivatives, and it avoids the complexity, instability, and computational intensity of traditional differentiation. However, the OBL method may be less precise when applied to highly nonlinear equations with a large number of components. Algorithm 1 shows how the OBL method calculates the Jacobian matrix.
Following the OBL framework [67], the discretized governing equations are restructured in terms of operators, the state-based operators, which encapsulate nonlinear fluid and rock physical properties that are parametrized in space of primary variables and interpolated during the simulation, and space-based operators, which pertain to properties transformed spatially.
where
- is a state-dependent parameter,
- is a space-dependent parameter,
- ,
- ,
- ,
- .
The parameters and represent nonlinear unknowns at the current and previous timestep, respectively. The term acts as the source term, u well control variables and spatial coordinate. Initial volume, porosity, and phase density are denoted by V, , and phase density , respectively. The phase pressure potential between neighboring cells is represented by . Finally, and correspond to the space-dependent components of convective and diffusive transmissibility, respectively.
4.4. Residual Accelerated Jacobian Method
The residual accelerated Jacobian (RAJ) method is an adaptive numerical approach developed to improve the estimation of derivatives within reservoir simulations. In such simulations, the accurate computation of the Jacobian matrix is vital for the convergence of the Newton–Raphson method [48]. Unlike conventional finite-difference schemes that employ a fixed step size, the RAJ method adapts the step size in response to the local behavior of the residual function.
In practice, the RAJ method estimates the derivative at the current iterate using the finite backward difference formulation:
where denotes the function value at and is the dynamically adjusted step size. When the residual is large, indicating a significant deviation from the converged solution, is increased to maintain stability and ensure an accurate derivative estimation. Conversely, as the solution nears convergence and the residual diminishes, is reduced, thereby refining the approximation accuracy.
This adaptive mechanism enables the RAJ method to balance stability and precision, providing a robust Jacobian estimation that enhances the overall convergence performance of the Newton–Raphson solver. The computational procedure for the RAJ method is further detailed in Algorithm 1.
4.5. Implementation of Linearization Scheme
Advanced linearization techniques, incorporating the finite central difference (FDC), finite backward difference (FDB), operator-based linearization (OBL), and residual accelerate jacobian (RAJ) methods, are implemented in our in-house multiphase simulator [72,73,74,75,76,77,78,79,80,81]. This simulator is built on a message-passing interface (MPI) framework, allowing robust parallel computing and the efficient utilization of thousands of computational cores. It also incorporates advanced discretization schemes with a scalable MPI-based architecture and employs an unconditionally stable, fully implicit method to ensure a robust solution. Additionally, in our computational framework, the Newton–Raphson method is employed as a nonlinear solver due to its robustness in handling inherent nonlinear equations governing multiphase flow in porous media [82,83]. The approach relies on a carefully constructed Jacobian matrix, and its effectiveness is contingent upon a reliable linearization method, which significantly impacts the solver’s accuracy and convergence rate.
To improve simulation efficiency in the cases under consideration, we apply an iterative linear solver with an incomplete LU (Lower–Upper) preconditioner [84]. This preconditioner is used primarily to accelerate the convergence rate of iterative linear solvers [14], which is particularly important when handling the sparse matrices commonly encountered in computational reservoir simulation problems [85,86,87]. The linear solver is set at , ensuring high accuracy in the linear solution across all simulation results. For the nonlinear solver, we use a solver tolerance of with a maximum of 25 iterations per solution attempt. This balanced approach provides an accurate and computationally efficient solution for the complex nonlinear systems encountered in multiphase flow simulations. Our experience shows that the selected ILU solver tolerance in compositional model simulations optimally supports the Newton method’s convergence, ensuring a reliable and efficient approach for solving complex behavior multicomponent multiphase flow system.
5. Numerical Benchmark
In this section, we present a benchmark of numerical linearized methods with a commercial legacy simulator (LS) to evaluate the computational efficiency of four linearization methods for the compositional reservoir simulation. We run three simulation scenarios with varying total simulation times and fluid properties: first, gas injection into a five-component gas field; second, gas injection into a ten-component gas field; and third, depletion of a ten-component hydrocarbon gas field without gas injection. All scenarios are modeled using a 3D mesh based on the top five layers of the SPE10 model within a structured domain (comprising 66,000 cells). The well configuration, illustrated in Figure 1a, includes four producers located in the corners and a single central injector for the injection cases. The permeability and porosity distributions are displayed in Figure 1b,c.
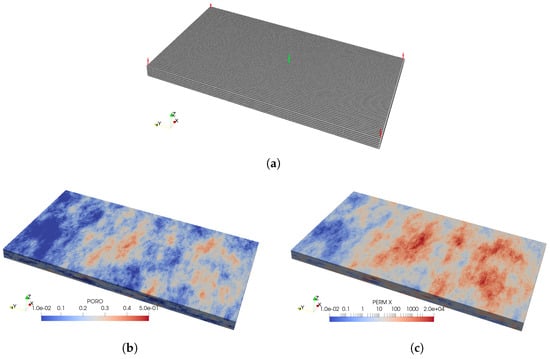
Figure 1.
The top five layers of the SPE10 model in the structure domain with producers are highlighted in red, and the injector is highlighted in lime, as displayed in (a). The variations in porosity and permeability are illustrated in the structured domain. (b) Porosity, (c) permeability.
5.1. Test 1: Analysis of Injection into Five-Component Gas Field
In this section, we injected into the center of the gas reservoir, with four producer wells located at the corners. The properties of the gas components and fluid system are listed in Table 1. The initial gas saturation was set at zero, with a pressure of 205 bar and a temperature of 373.65 K. The bottom hole pressure (BHP) was set to 213 bar for the injector and 200 bar for each producer. The total simulation time was 500 days, with a maximum time step of 1 day.

Table 1.
Five components of a gas reservoir and fluid properties of Test 1.
We benchmarked the performance of various numerical linearization methods, including finite backward difference (FDB), finite central difference (FDC), operator-based linearization (OBL), and residual accelerated Jacobian (RAJ) methods, integrated into the in-house multiphase simulator, against the widely used legacy simulator (LS). This comparison allowed us to assess the performance of each method in terms of computational efficiency. Figure 2a–c show the gas–oil ratio (GOR) and cumulative gas and oil production over time. The GOR is the ratio of gas produced per unit volume of oil from the well. The cumulative production phase volume (for both oil and gas) refers to the total amount of oil and gas produced over time, which is essential for assessing the overall success of the injection process. The cumulative injection phase volume gas measures the total volume that has been injected into the reservoir, which helps in evaluating the efficiency of the enhanced oil recovery (EOR) process and in estimating the input cost of injection, as shown in Figure 2d. The rate phase volume of oil represents the rate at which oil is produced from the four producer wells, depicted in Figure 2d, providing real-time insights into reservoir performance and the dynamics of the breakthrough.
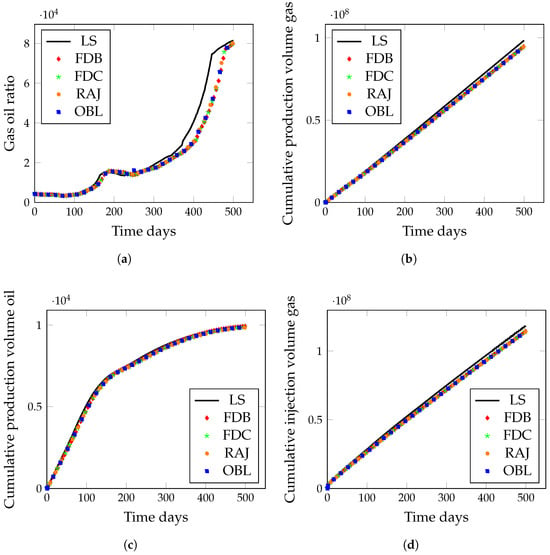
Figure 2.
A comparison of the (a) gas–oil ratio, (b) cumulative gas production, (c) cumulative oil production, and (d) cumulative gas injection results from different linearization methods against the legacy simulator.
The results show that the FDB, FDC, RAJ, and OBL methods achieve convergence solutions for the compositional reservoir simulations. Among these methods, the OBL is computationally efficient for simpler problems involving the five-component gas reservoir. Despite this, other methods, such as FDB, FDC, and RAJ, also demonstrate accuracy and stability. However, the OBL method proves to be the most computationally efficient for this case compared to the FDB, RAJ, and FDC methods due to its suitability for effectively modeling simpler problems.
In order to visualize the saturation distribution from the top and bottom views of the layers in the gas reservoir, we present the saturation maps at the four producer wells for three different simulation time periods, including 60, 140, and 250 days, as shown in Figure 3, Figure 4 and Figure 5. We aim to compare the accuracy of breakthrough times across different linearization methods, including the FDB and FDC, RAJ, and OBL methods. The results indicate that all methods better capture the saturation distribution patterns effectively at three different simulation times, suggesting that each method provides an accurate approximation of the breakthrough time. In general, the simulation performance data provide a clear assessment of the computational efficiency of linearization methods in capturing the complex flow dynamics of the five-component gas reservoir
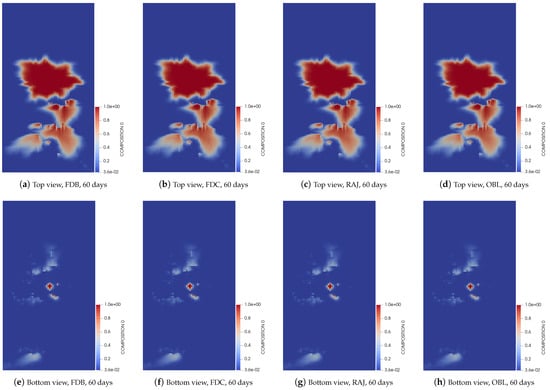
Figure 3.
Concentration of carbon dioxide gas distributions, presented as top and bottom views of layer after 60 days for different linearization methods.
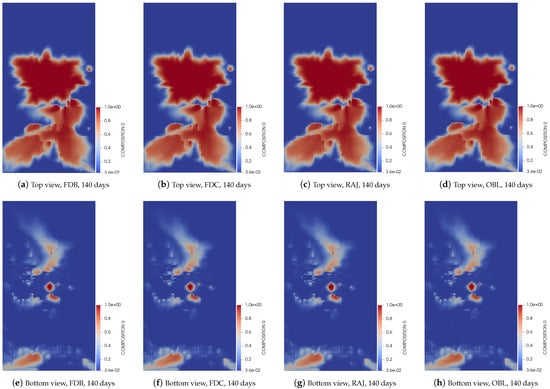
Figure 4.
The concentration of carbon dioxide gas distribution after 140 days is presented as top and bottom views of the layer for each numerical method.
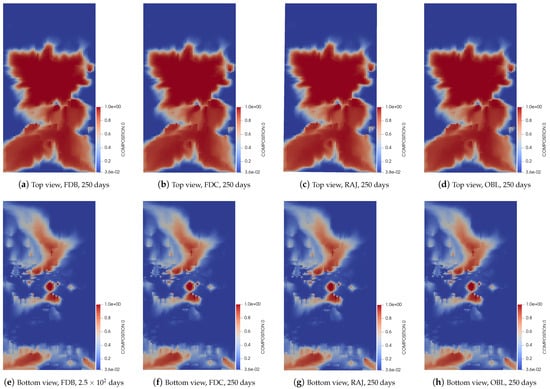
Figure 5.
Concentration of carbon dioxide gas distribution after 250 days, shown top and bottom views of the layer for each numerical method.
The simulation performance data for the five-component gas reservoir are shown in Table 2. Based on this simulation data, the OBL method is more efficient for a five-component gas reservoir. Thus, the OBL outperforms other methods by achieving fewer total nonlinear iterations without wasted iterations and significantly reducing the time spent on computing operators and nonlinear solving the most computationally intensive parts of the simulation. In contrast, FDB, FDC, and RAJ provide different balances between computational efficiency, but they remain accurate and adaptable. However, the OBL stands out by providing high computational efficiency to effectively handle the complex physics of a multicomponent multiphase gas reservoir, making it the preferred method for this type of simulation.

Table 2.
Case one: Simulation performance of a five-component gas reservoir.
5.2. An Analysis of Injection into a Ten-Component Gas Field (Test Two)
Similarly to test one, we injected into the center of a ten-component gas reservoir, where four producer wells are located at the corners. The properties of the ten components of the gas reservoir are shown in Table 3. This diverse mixture of gases represents a wide range of hydrocarbon chain lengths and properties, making the reservoir’s behavior complex. The presence of lighter hydrocarbons, such as methane, ethane, and propane, suggests a significant gaseous phase, while the heavier components, such as heptane, octane, and nonane, indicate potential for liquid hydrocarbon production under certain pressure and temperature conditions. However, all other simulation parameters remain consistent with those used in the previous test, such as temperature and pressure, total simulation time, the bottom-hole pressure (BHP) of the injector, and producer wells.

Table 3.
Ten-component gas reservoir properties of Test 2.
The simulation results presented in Figure 6 indicate that the RAJ method yields a numerical solution for ten components of a gas reservoir that closely match the FDB in terms of precision. This result shows that the RAJ method serves as a reliable alternative to the FDB, offering comparable accuracy with a difference in computational efficiency. However, the FDB method exhibits better computational efficiency, reducing simulation time. Given the computational demand of large simulations, this improved efficiency makes the FDB a more practical and scalable choice for this scenario. In contrast, the OBL method completely fails in this case due to the increased computational complexity and convergence difficulties associated with handling a larger number of components. The failure highlights the importance of selecting a robust and scalable linearization method for complex compositional simulations. Moreover, comparing the FDC is not feasible due to unrealistically long run times, as the central approach, along with a large number of components, requires the recurring calculation of the derivatives at each cell. Our simulator slightly over-predicts the amounts of oil produced at later times due to the differences in the approach to critical property calculations and flash heuristics in the LS simulator. Nonetheless, the overall trend of production is maintained. In fact, the amounts of oil produced are considered minimal since we have a gas reservoir in this case, and hence the weight of such differences is not of significance.
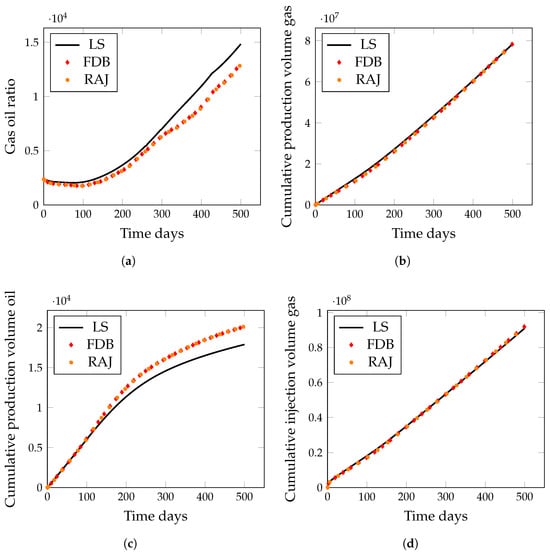
Figure 6.
A comparison of (a) gas–oil ratio, (b) Cumulative gas production, (c) Cumulative oil production, and (d) cumulative injection gas results from two different linearization methods against the legacy simulator.
In the second test, we follow the same trend as in test one to visualize the carbon dioxide gas saturation distribution pattern from the top and bottom views of the layers in the gas reservoir. The same saturation maps at varying simulation time shown in Figure 7, Figure 8 and Figure 9, are presented using two linearization methods. The primary difference in this test is the inclusion of ten components, while the first test involves a five-component version. This test evaluates the accuracy of these linearization methods in capturing the saturation distribution patterns at the same simulation times used in test one. The results show that all linearization methods accurately estimate the breakthrough time. Their computational efficiency in approximation of the multicomponent multiphase flow system is effectively determined through the simulation performance.
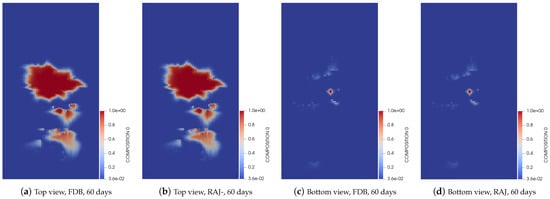
Figure 7.
Concentration carbon dioxide gas distribution after 60 days, showing top and bottom views of layer for FDB and RAJ methods.
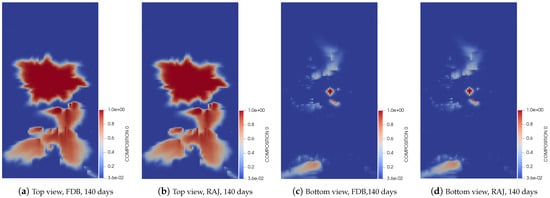
Figure 8.
Concentration carbon dioxide gas distribution after 140 days, display top and bottom views of layer for FDB and RAJ methods.
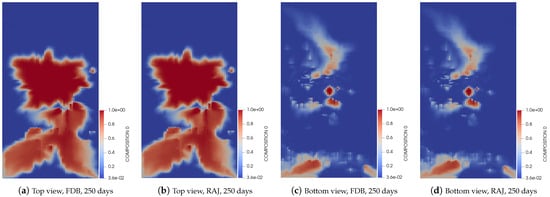
Figure 9.
Concentration carbon dioxide gas distribution after 250 days: depicted top and bottom views of layer for FDB and RAJ methods.
The simulation performance data of two different linearization methods are shown in Table 4. These performance data highlight that the FDB method is the fastest linearization technique among those tested for the ten-component gas reservoir. The FDB completes the simulation with fewer nonlinear and linear iterations and requires less time for both linear and nonlinear solvers compared to the RAJ method, demonstrating superior computational efficiency in this case.

Table 4.
Case two: Simulation performance of a ten-component gas reservoir.
5.3. Ten-Component Gas Reservoir with a Producer Well Without Gas Injection
In the third test case, we evaluated the three linearization techniques, including FDB, FDC, and RAJ, using a ten-component gas reservoir without gas injection, where four producing wells are placed at the corners. The properties of the fluid and ten components of the gas reservoir are depicted in Table 5. The initial pressure and temperature were set at 205 bar and 373.65 k, respectively. The BHP of the four producing wells was set at 200 bar. The total simulation time was 200 days, with a maximum time step of 1 day.

Table 5.
The fluid composition and operating conditions of Test 3.
The simulation results from the three linearization methods are shown in Figure 10. The physical results from the three different linearization techniques match nicely. The differences in gas–oil ratio (GOR) and cumulative gas production compared to the legacy simulator (LS) could be again influenced significantly by variations in how phase behavior is modeled. Even minor differences in how the EOS is implemented, parameterized, or coupled with the numerical solver can lead to discrepancies in the predicted gas liberation and oil shrinkage. Additionally, flash calculations used to compute phase compositions and amounts for a given pressure and temperature are sensitive to numerical tolerances and initialization schemes. Variations in the treatment of critical properties, binary interaction coefficients, or convergence criteria in these calculations can alter the equilibrium gas–liquid ratio, impacting both GOR and cumulative gas production trends. However, such differences are subtle and honor the overall trend of the physical results. Also, note that the OBL failed to converge in this case once again.
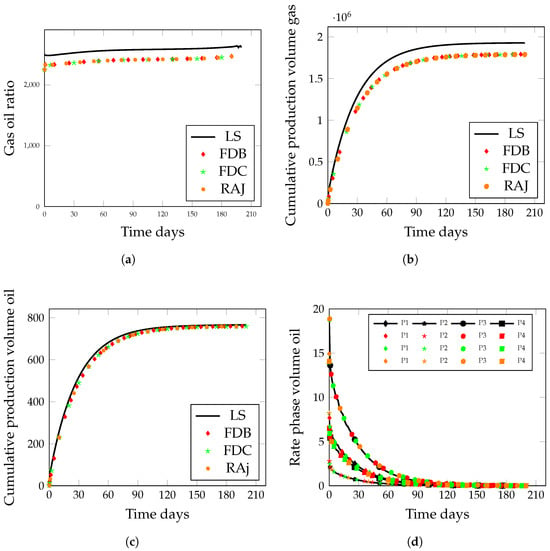
Figure 10.
A comparison of (a) gas–oil ratio, (b) cumulative production gas, (c) cumulative oil production, and (d) cumulative injection gas results from three distinct linearization methods against the legacy simulator.
The simulation performance of three distinct linearization methods is summarized in Table 6. The results show that the FDB requires a significantly higher total number of linear iterations compared to the FDC and RAJ; conversely, the FDC requires the lowest number of linear and nonlinear iterations compared to the FDB. Among the three, the RAJ demonstrates the lowest number of nonlinear iterations and spends a smaller amount of time on computing operators, highlighting its superior efficiency in this case. Although all three methods achieve similar accuracy, the RAJ offers the most computationally optimal performance by minimizing the most expensive computational operations, making it the preferred choice in this case.

Table 6.
Case three: Simulation performance of a ten-component gas reservoir producer well without gas injection.
6. Analysis of the Computational Tests
We investigate the simulation performance of three test cases in compositional reservoir simulation, focusing on the computational efficiency of several linearization methods, including finite backward difference (FDB), finite central difference (FDC), residual accelerated Jacobian (RAJ), and operator-based linearization (OBL). In the first test, we injected into a five-component gas reservoir. In the second test, we injected into the ten-component gas reservoir. Both tests were run with a simulation time of 500 days. In the third test, a ten-component gas reservoir was simulated without gas injection with a simulation time of 200 days. The analysis involved benchmarking these methods against a commercial legacy simulator (LS) to identify the most efficient approach to handling complex multicomponent reservoir dynamics. The following points were observed:
- In Test 1, the OBL demonstrates computational efficiency by significantly reducing operator computations and nonlinear solver time, making it ideally suited for simple problems such as a five-component gas reservoir. This efficiency allows for rapid decision-making in applications like real-time reservoir monitoring. However, it is noted that for a complex system with a large number of components existing in the gas reservoir, the OBL method completely fails to converge, thereby limiting its applicability in linearizing the complex nonlinear system. Meanwhile, the RAJ and FDC provide similar accuracy. Ultimately, OBL remains the most suitable choice for simpler problems or when rapid decisions are required due to its superior computational efficiency compared to other methods.
- In Test 2, the FDB exhibits high computational efficiency, making it a robust option for simulating a ten-component gas reservoir. The FDB, while robust, can be less efficient in simpler problems, especially in the first test scenario. For complex compositional and highly heterogeneous scenarios, where computational efficiency is crucial, the FDB offers more efficiency compared to other methods. Additionally, the OBL is not suitable for this case due to its limitations in handling complex models, particularly those involving a large number of components. Conversely, the FDC method is also less feasible due to its long-run simulation time as a central approach. Finally, the FDB demonstrates highly computational efficiency and is particularly well suited for a ten-component gas reservoir.
- In Test 3, in the third test without injection, the RAJ demonstrates higher computational efficiency compared to FDC and OBL methods, where it requires less time for operator computation and a nonlinear solver. The RAJ is efficient, but it might be a limitation when accuracy and stability are important factors. This trade-off between accuracy and speed must be highlighted when making operational decisions. However, real-time operations could be limited due to the time-sensitive nature of decisions that require rapid action, especially for the without gas injection scenarios.
The three test cases demonstrate that the different linearization methods are best suited for different scenarios for compositional reservoir simulations. In the first test, the OBL is computationally efficient for the five-component gas reservoir, making it ideal for handling simple problems. In contrast, in test two, the FDB, demonstrates its strength in handling more complex scenarios, ensuring computational efficiency despite the complexity of the system, involving a ten-component gas reservoir. In the third test, RAJ proves to be computationally efficient. Moreover, it is important to note that in all three tests, each method tends to overestimate fine gradient variations in the reservoir after approximately 350 days of simulation, especially for the GOR and cumulative productions. This overestimation is due to the variations in the treatment of critical properties and internal convergence criteria of flash calculations in each simulator. However, such differences do not affect the controlled comparison of the linearization techniques or specific scenarios.
7. Conclusions
In this work, we evaluate the various numerical linearization methods, including finite backward difference (FDB), finite central difference (FDC), operator-based linearization (OBL), and residual accelerated Jacobian (RAJ), for compositional reservoir simulation. To assess their effectiveness, we determine the computational efficiency of each method in estimating the behavior of complex multicomponent multiphase flows in the gas reservoir. The following conclusions can be drawn:
- The integration of advanced linearization methods into a fully implicit, parallel compositional reservoir simulation framework enables direct quantitative comparison. For example, in the five-component gas injection test, the operator-based linearization method achieved convergence in 770 nonlinear iterations compared to 841–843 iterations for other methods.
- The FDB method strikes a favorable balance between computational efficiency and accuracy in multicomponent systems. In the ten-component gas injection test, it completed simulations in 706 nonlinear iterations, demonstrating robust performance in complex scenarios.
- The FDC method delivers improved accuracy in smooth regions, although its increased derivative evaluations resulted in a higher overall computational cost.
- The OBL method significantly reduces computational overhead for simpler problems by leveraging precomputed or adaptively updated spatial operators. In the five-component test, its operator computation time accounted for only about 9.6% of the total simulation time.
- The RAJ method dynamically adjusts the derivative estimation step size based on local residuals, enhancing accuracy in regions with steep gradients. In the ten-component noninjection test, it achieved convergence with 521 nonlinear iterations.
Overall, the optimal linearization strategy is scenario-dependent: OBL is best suited for simpler problems requiring rapid convergence, FDB excels in complex injection scenarios, and RAJ is highly effective for accurately capturing nonlinear dynamics in noninjection cases. The novel contributions of this work include the scalable integration of multiple advanced linearization methods and the development of an adaptive residual accelerated Jacobian algorithm, thereby advancing the state-of-the-art in computational reservoir simulation. Future work will focus on improving the robustness of OBL for complex systems and extending numerical linearization methods to improve their applicability in compositional models, particularly within unstructured grids. This will involve developing linearization techniques that improve numerical stability and accuracy while maintaining computational efficiency in heterogeneous reservoirs.
Author Contributions
A.A. (Ali Asif) implemented the linearization schemes and constructed the simulation code, A.S.A. designed the numerical tests and carried out the simulations runs including formal analysis and interpretation. A.A. (Ahmad Abushaikha) supervised the overall work. All authors have read and agreed to the published version of the manuscript.
Funding
The publication was supported by the grant ARG 01-0502-230056 from Qatar National Research Fund.
Data Availability Statement
All data generated or analysed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Moshiri, M.; Manzari, M.T. Simulation of multi-component multi-phase fluid flow in two-dimensional anisotropic heterogeneous porous media using high-order control volume distributed methods. Comput. Math. Appl. 2019, 78, 3303–3328. [Google Scholar] [CrossRef]
- Pal, M.; Edwards, M.G. A family of multi-point flux approximation schemes for general element types in two and three dimensions with convergence performance. Int. J. Numer. Methods Fluids 2012, 69, 1797–1817. [Google Scholar] [CrossRef]
- Zhou, Y.; Tchelepi, H.A.; Mallison, B.T. Automatic differentiation framework for compositional simulation on unstructured grids with multi-point discretization schemes. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 21–23 February 2011; p. SPE-141592-MS. [Google Scholar]
- Alpak, F.O. A mimetic finite volume discretization method for reservoir simulation. SPE J. 2010, 15, 436–453. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhu, G.; Jin, Y.; Qu, M.; Lin, Q.; Zeng, L. Diffusion hysteresis in unsaturated porous media: A microfluidic study. J. Hydrol. 2024, 640, 131675. [Google Scholar] [CrossRef]
- Khait, M.; Voskov, D. Operator-based linearization for efficient modeling of geothermal processes. Geothermics 2018, 74, 7–18. [Google Scholar] [CrossRef]
- Deb, P.K.; Akter, F.; Imtiaz, S.A.; Hossain, M.E. Nonlinearity and solution techniques in reservoir simulation: A review. J. Nat. Gas Sci. Eng. 2017, 46, 845–864. [Google Scholar] [CrossRef]
- Cao, H. Development of Techniques for General Purpose Simulators; Stanford University: Stanford, CA, USA, 2002. [Google Scholar]
- Wang, Y.; Luther, J.; Jenny, D.; Immer, M.; Jenny, P. Space-Time Adaptive Conservative Finite Volume Scheme for Unsteady Compressible Flow. 2025. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5119570 (accessed on 5 March 2025).
- Farkas, E. Linearization techniques of reservoir-simulation equations: Fully implicit cases. SPE J. 1998, 3, 316–323. [Google Scholar] [CrossRef]
- Deucher, R.H.; Franc, J.; Møyner, O.; Tchelepi, H.A. Compositional reservoir simulation with a high-resolution compact stencil adaptive implicit method. J. Comput. Phys. 2025, 521, 113558. [Google Scholar] [CrossRef]
- Mohebbinia, S. Advanced equation of state modeling for compositional simulation of gas floods. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 18–20 February 2013. [Google Scholar]
- Rin, R. Implicit Coupling Framework for Multi-Physics Reservoir Simulation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2017. [Google Scholar]
- Baker, M.; Bowler, K.C.; Kenway, R. MIMD implementations of linear solvers for oil reservoir simulation. Parallel Comput. 1990, 16, 313–334. [Google Scholar] [CrossRef]
- Blair, P.; Weinaug, C. Solution of two-phase flow problems using implicit difference equations. Soc. Pet. Eng. J. 1969, 9, 417–424. [Google Scholar] [CrossRef]
- Aziz, K.; Wong, T. Considerations in the development of multipurpose reservoir simulation models. In Proceedings of the First and Second Forum on Reservoir Simulation, Alpbach, Austria, 4–8 September 1989; pp. 77–208. [Google Scholar]
- Abushaikha, A.S.; Voskov, D.V.; Tchelepi, H.A. Fully implicit mixed-hybrid finite-element discretization for general purpose subsurface reservoir simulation. J. Comput. Phys. 2017, 346, 514–538. [Google Scholar] [CrossRef]
- Yang, M.; Wang, D.; Dong, Z.; Zhang, Z.; Li, Y.; Du, D. Insight into the permeability effect on forced convective heat transfer characteristics in porous media based on the pore-scale numerical study. Int. Commun. Heat Mass Transf. 2025, 165, 109004. [Google Scholar] [CrossRef]
- Bosma, S.B.M. Algorithms and Discretization Schemes for Efficient Simulation of Multiphase Flow and Transport in Porous Media; Stanford University: Stanford, CA, USA, 2021. [Google Scholar]
- Settari, A.; Aziz, K. Use of irregular grid in reservoir simulation. Soc. Pet. Eng. J. 1972, 12, 103–114. [Google Scholar] [CrossRef]
- Sun, J.; Sun, R.; Qiao, P.; Tan, S.; Tian, R. Numerical Study of Bi-Stable Flow Phenomena in Square Tube Bundles Based on Refined Modelling Method. 2025. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5264819 (accessed on 25 May 2025).
- Chen, Y.; Voskov, D. Optimization of CO2 injection using multi-scale reconstruction of composition transport. Comput. Geosci. 2020, 24, 819–835. [Google Scholar] [CrossRef]
- Durlofsky, L.J. Accuracy of mixed and control volume finite element approximations to Darcy velocity and related quantities. Water Resour. Res. 1994, 30, 965–973. [Google Scholar] [CrossRef]
- Faille, I. A control volume method to solve an elliptic equation on a two-dimensional irregular mesh. Comput. Methods Appl. Mech. Eng. 1992, 100, 275–290. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Eigestad, G.T. Discretization on quadrilateral grids with improved monotonicity properties. J. Comput. Phys. 2005, 203, 744–760. [Google Scholar] [CrossRef]
- Wheeler, M.F.; Yotov, I. A multipoint flux mixed finite element method. SIAM J. Numer. Anal. 2006, 44, 2082–2106. [Google Scholar] [CrossRef]
- Contreras, F.R.; Lyra, P.R.; de Carvalho, D.K. A new multipoint flux approximation method with a quasi-local stencil (MPFA-QL) for the simulation of diffusion problems in anisotropic and heterogeneous media. Appl. Math. Model. 2019, 70, 659–676. [Google Scholar] [CrossRef]
- Klausen, R.A.; Winther, R. Convergence of multipoint flux approximations on quadrilateral grids. Numer. Methods Partial. Differ. Equ. Int. J. 2006, 22, 1438–1454. [Google Scholar] [CrossRef]
- Aavatsmark, I.; Eigestad, G.T.; Klausen, R.A. Numerical convergence of the MPFA O-method for general quadrilateral grids in two and three dimensions. In Compatible Spatial Discretizations; Springer: New York, NY, USA, 2006; pp. 1–21. [Google Scholar]
- Aavatsmark, I.; Eigestad, G.T.; Heimsund, B.O.; Mallison, B.T.; Nordbotten, J.M.; Øian, E. A new finite-volume approach to efficient discretization on challenging grids. SPE J. 2010, 15, 658–669. [Google Scholar] [CrossRef]
- Radu, F.A.; Nordbotten, J.M.; Pop, I.S.; Kumar, K. A robust linearization scheme for finite volume based discretizations for simulation of two-phase flow in porous media. J. Comput. Appl. Math. 2015, 289, 134–141. [Google Scholar] [CrossRef][Green Version]
- Lyu, X.; Khait, M.; Voskov, D. Operator-based linearization approach for modeling of multiphase flow with buoyancy and capillarity. SPE J. 2021, 26, 1858–1875. [Google Scholar] [CrossRef]
- Batycky, R.P.; Thiele, M.R.; Coats, K.; Grindheim, A.; Ponting, D. Reservoir simulation. Trans. AIME 1958, 213, 28. [Google Scholar]
- Lucia, A.; Voskov, D.; James, S.C.; Zaydullin, R.; Henley, H. Fully compositional and thermal reservoir simulations efficiently compare EOR techniques. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 5–7 November 2013; p. SPE-167184. [Google Scholar]
- Paniconi, C.; Putti, M. A comparison of Picard and Newton iteration in the numerical solution of multidimensional variably saturated flow problems. Water Resour. Res. 1994, 30, 3357–3374. [Google Scholar] [CrossRef]
- Castelletto, N.; White, J.A.; Tchelepi, H. Accuracy and convergence properties of the fixed-stress iterative solution of two-way coupled poromechanics. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1593–1618. [Google Scholar] [CrossRef]
- Younis, R.M. Modern Advances in Software and Solution Algorithms for Reservoir Simulation; Stanford University: Stanford, CA, USA, 2011. [Google Scholar]
- Wang, Z.; Herkersdorf, A. Software performance simulation strategies for high-level embedded system design. Perform. Eval. 2010, 67, 717–739. [Google Scholar] [CrossRef]
- Nardean, S.; Ferronato, M.; Abushaikha, A. Linear solvers for reservoir simulation problems: An overview and recent developments. Arch. Comput. Methods Eng. 2022, 29, 4341–4378. [Google Scholar] [CrossRef]
- Watts, J. Reservoir simulation: Past, present, and future. SPE Comput. Appl. 1997, 9, 171–176. [Google Scholar]
- Bartholomew-Biggs, M.; Brown, S.; Christianson, B.; Dixon, L. Automatic differentiation of algorithms. J. Comput. Appl. Math. 2000, 124, 171–190. [Google Scholar] [CrossRef]
- Voskov, D.V.; Tchelepi, H.A. Compositional nonlinear solver based on trust regions of the flux function along key tie-lines. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 21–23 February 2011; p. SPE-141743. [Google Scholar]
- Vanden, K.J.; Orkwis, P.D. Comparison of numerical and analytical Jacobians. AIAA J. 1996, 34, 1125–1129. [Google Scholar] [CrossRef]
- Mohajeri, S.; Eslahi, R.; Bakhtiari, M.; Alizadeh, A.; Madani, M.; Zeinali, M.; Rajabi, H.; Sharifi, E.; Mortezazadeh, E.; Mahdavifar, Y. A novel linear solver for simulating highly heterogeneous black oil reservoirs. J. Pet. Sci. Eng. 2020, 194, 107506. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Roy, C.J. Verification and Validation in Scientific Computing; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Khebzegga, O. Advanced Nonlinear Techniques for Compositional Reservoir Simulation; Stanford University: Stanford, CA, USA, 2020. [Google Scholar]
- Abd, A.S.; Asif, A.; Abushaikha, A. Performance analysis of linearization schemes for modelling multi-phase flow in porous media. Sci. Rep. 2024, 14, 15626. [Google Scholar] [CrossRef] [PubMed]
- Asif, A.; Abd, A.; Abushaikha, A. A Residual-Accelerated Jacobian Method for Rapid Convergence in Reservoir Simulation. In Proceedings of the ECMOR 2024—European Association of Geoscientists & Engineers, Oslo, Norway, 2–5 September 2024; Volume 2024, pp. 1–11. [Google Scholar]
- Brooks, R.; Corey, A. Hydraulic properties of porous media. In Civil Engineering Department; Hydrology Paper No. 3; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Sheng, Q.; Yang, H.; Chen, H.; Cheng, T.; Sun, S. Adaptive fully implicit and thermodynamically consistent modeling of multiphase flow in porous media on three dimensional grids. Comput. Fluids 2025, 298, 106673. [Google Scholar] [CrossRef]
- Iranshahr, A.; Voskov, D.; Tchelepi, H.A. A negative-flash tie-simplex approach for multiphase reservoir simulation. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 21–23 February 2011; p. SPE-141896. [Google Scholar]
- Li, Y. Robust and Accurate VT Flash Calculation and Efficient VT-Flash Based Compositional Flow Simulation. Ph.D. Thesis, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 2021. [Google Scholar]
- Michelsen, M.L. The isothermal flash problem. Part I. Stability. Fluid Phase Equilibria 1982, 9, 1–19. [Google Scholar] [CrossRef]
- Coats, K.H. An equation of state compositional model. Soc. Pet. Eng. J. 1980, 20, 363–376. [Google Scholar] [CrossRef]
- Voskov, D. An extended natural variable formulation for compositional simulation based on tie-line parameterization. Transp. Porous Media 2012, 92, 541–557. [Google Scholar] [CrossRef]
- Jiang, J.; Pan, H. Dissipation-based nonlinear solver for fully implicit compositional simulation. SPE J. 2022, 27, 1989–2014. [Google Scholar] [CrossRef]
- Chaabi, O.; Al-Kobaisi, M. Adaptive Nonlinear Elimination Preconditioning for Transport in Fractured Porous Media. arXiv 2025, arXiv:2504.18900. [Google Scholar]
- Riseth, A.N. Nonlinear Solver Techniques in Reservoir Simulation: A Review; Technical Report; Oxford University Mathematical Institute: Oxford, UK, 2015. [Google Scholar]
- Jiang, J.; Pan, H. Efficient dissipation-based nonlinear solver for multiphase flow in discrete fractured media. J. Comput. Phys. 2023, 479, 112006. [Google Scholar] [CrossRef]
- Neidinger, R.D. Introduction to automatic differentiation and MATLAB object-oriented programming. SIAM Rev. 2010, 52, 545–563. [Google Scholar] [CrossRef]
- Xu, Z.; Okuno, R. Numerical simulation of three-hydrocarbon-phase flow with robust phase identification. In Proceedings of the SPE Reservoir Simulation Conference, Houston, TX, USA, 23–25 February 2015; p. D021S005R001. [Google Scholar]
- Li, J. Sequential Fully Implicit Newton Method for Reservoir Simulation; Stanford University: Stanford, CA, USA, 2022. [Google Scholar]
- Griewank, A.; Walther, A. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Jiang, J.; Wen, X.H. Smooth Formulation for Three-Phase Black-Oil Simulation with Superior Nonlinear Convergence. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 28–30 March 2023; p. D021S009R003. [Google Scholar]
- Khait, M.; Voskov, D. Adaptive Parameterization for Solving of Thermal/Compositional Nonlinear Flow and Transport with Buoyancy. SPE J. 2018, 23, 522–534. [Google Scholar] [CrossRef]
- Khait, M.; Voskov, D. Operator-based linearization for non-isothermal multiphase compositional flow in porous media. In Proceedings of the ECMOR XV-15th European Conference on the Mathematics of Oil Recovery, Amsterdam, The Netherlands, 29 August–1 September 2016; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2016; p. cp-494. [Google Scholar]
- Voskov, D.V. Operator-based linearization approach for modeling of multiphase multi-component flow in porous media. J. Comput. Phys. 2017, 337, 275–288. [Google Scholar] [CrossRef]
- Iranshahr, A.; Voskov, D.V.; Tchelepi, H.A. Tie-simplex based compositional space parameterization: Continuity and generalization to multiphase systems. AIChE J. 2013, 59, 1684–1701. [Google Scholar] [CrossRef]
- Khait, M.; Voskov, D.; Konidala, G. Tie-simplex parametrization for operator-based linearization for non-isothermal multiphase compositional flow in porous. In Proceedings of the ECMOR XVI-16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3–6 September 2018; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2018; Volume 2018, pp. 1–16. [Google Scholar]
- Pour, K.M.; Voskov, D. Adaptive nonlinear solver for a discrete fracture model in operator-based linearization framework. In Proceedings of the ECMOR XVII—European Association of Geoscientists & Engineers, Online Event, 14–17 September 2020; Volume 2020, pp. 1–18. [Google Scholar]
- De Hoop, S.; Voskov, D.; Bertotti, G. Studying the effects of heterogeneity on dissolution processes using operator based linearization and high-resolution lidar data. In Proceedings of the ECMOR XVII—European Association of Geoscientists & Engineers, Edinburgh, UK, 14–17 September 2020; Volume 2020, pp. 1–13. [Google Scholar]
- Abushaikha, A.S. Numerical Methods for Modelling Fluid Flow in Highly Heterogeneous and Fractured Reservoirs. Ph.D. Thesis, Imperial College London, London, UK, 2013. [Google Scholar]
- Abd, A.S.; Zhang, N.; Abushaikha, A.S. Modeling the effects of capillary pressure with the presence of full tensor permeability and discrete fracture models using the mimetic finite difference method. Transp. Porous Media 2021, 137, 739–767. [Google Scholar] [CrossRef]
- Li, L.; Abushaikha, A. A fully-implicit parallel framework for complex reservoir simulation with mimetic finite difference discretization and operator-based linearization. Comput. Geosci. 2021, 26, 915–931. [Google Scholar] [CrossRef]
- Nardean, S.; Ferronato, M.; Abushaikha, A. A Novel and Efficient Preconditioner for Solving Lagrange Multipliers-Based Discretization Schemes for Reservoir Simulations. ECMOR XVII 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Abushaikha, A.S.; Terekhov, K.M. A fully implicit mimetic finite difference scheme for general purpose subsurface reservoir simulation with full tensor permeability. J. Comput. Phys. 2020, 406, 109194. [Google Scholar] [CrossRef]
- Zhang, N.; Abushaikha, A.S. An efficient mimetic finite difference method for multiphase flow in fractured reservoirs. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, London, UK, 3–6 June 2019; p. D021S001R011. [Google Scholar]
- Zhang, N.; Abushaikha, A.S. Fully Implicit Reservoir Simulation Using Mimetic Finite Difference Method in Fractured Carbonate Reservoirs. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 18 September 2019. [Google Scholar] [CrossRef]
- Hjeij, D.; Abushaikha, A. Comparing Advanced Discretization Methods for Complex Hydrocarbon Reservoirs. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 18 September 2019. [Google Scholar] [CrossRef]
- Hjeij, D.; Abushaikha, A. An Investigation of the Performance of the Mimetic Finite Difference Scheme for Modelling Fluid Flow in Anisotropic Hydrocarbon Reservoirs. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, London, UK, 5 June 2019. [Google Scholar] [CrossRef]
- Abushaikha, A.S.; Voskov, D.V.; Tchelepi, H.A. Fully Implicit Mixed Hybrid Finite-Element Formulation for General-Purpose Compositional Reservoir Simulation. In Proceedings of the SPE Reservoir Simulation Conference, Montgomery, TX, USA, 21 February 2017. [Google Scholar] [CrossRef]
- Akram, S.; Ann, Q.U. Newton raphson method. Int. J. Sci. Eng. Res. 2015, 6, 1748–1752. [Google Scholar]
- Ypma, T.J. Historical development of the Newton–Raphson method. SIAM Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef]
- Ma, S.; Saad, Y. Distributed ILU (0) and SOR Preconditioners for Unstructured Sparse Linear Systems; Citeseer; University of Minnesota: Minneapolis, MN, USA, 1994. [Google Scholar]
- Benzi, M. Preconditioning techniques for large linear systems: A survey. J. Comput. Phys. 2002, 182, 418–477. [Google Scholar] [CrossRef]
- Ries, M.; Trottenberg, U.; Winter, G. A note on MGR methods. Linear Algebra Its Appl. 1983, 49, 1–26. [Google Scholar] [CrossRef]
- Wu, W.; Li, X.; He, L.; Zhang, D. Accelerating the iterative linear solver for reservoir simulation on multicore architectures. In Proceedings of the 2014 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014; pp. 265–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).