Optimization of Rock-Cutting Tools: Improvements in Structural Design and Process Efficiency
Abstract
1. Introduction
2. Structural Innovations in Rock-Breaking Cutters
2.1. Conventional Cutter Design Limitations
2.1.1. Continuous Rock-Breaking Equipment and Types of Cutters
2.1.2. Rock-Breaking Mechanism and Mechanical Model
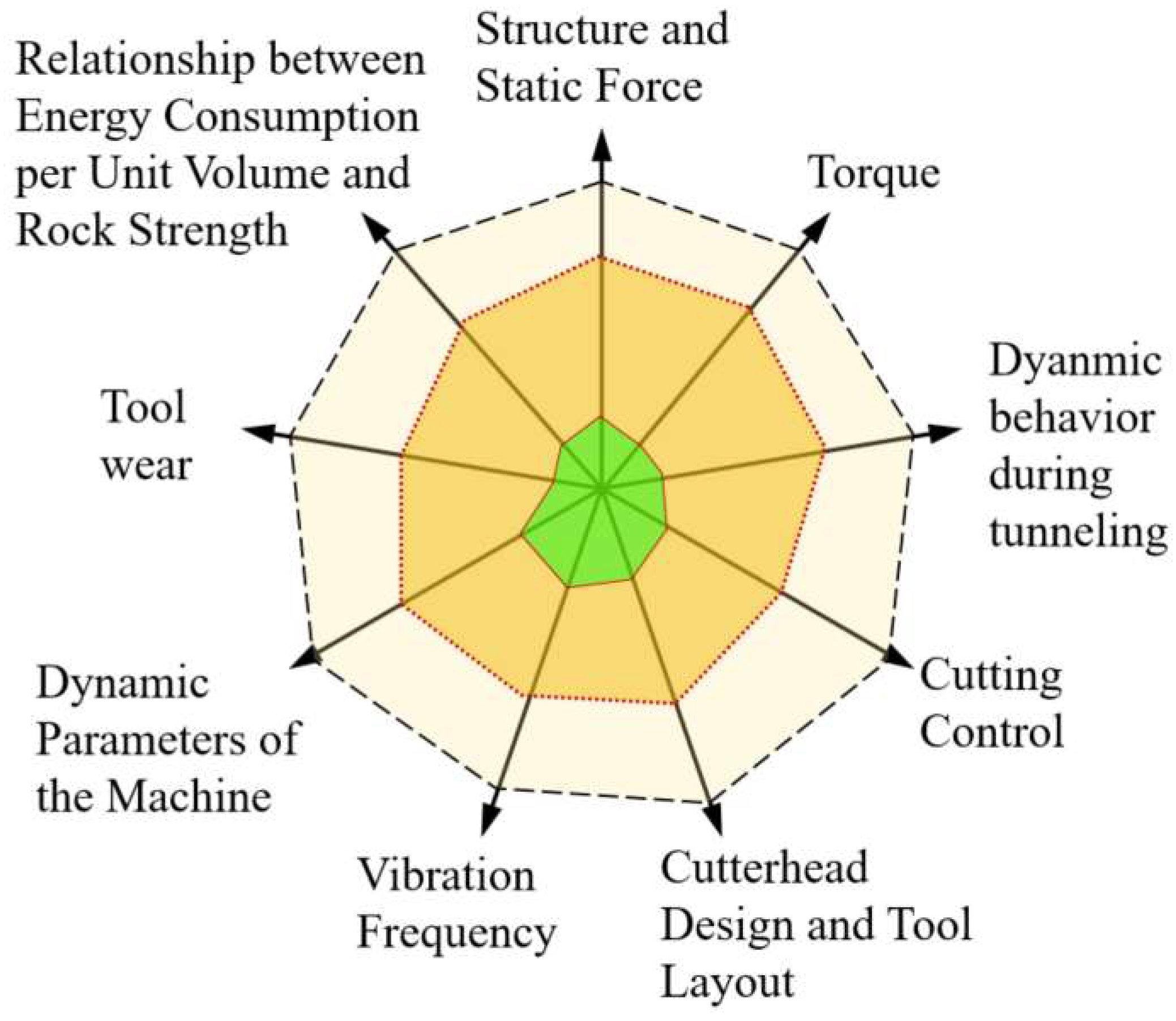
2.1.3. Optimization Objectives and Optimization Methods
| Authors and Year | Optimized Component | Optimization Objective(s) | Optimization Method | Performance Improvement |
|---|---|---|---|---|
| Park et al. (2018), Int. J. Rock Mech. Min. Sci. [5] | Point attack pick cutter and cutter holder assembly | Minimize specific energy; enhance structural stability; extend tool durability | Lab-scale linear cutting tests; finite element analysis; evaluated cut spacing, depth, skew angle, and attack angle | Achieved lower specific energy via optimized skew/attack angles. Positive skew angle linked to slower abrasion rates. |
| Sun et al. (2018), J. Cent. South Univ. [42] | Cutter layout (assembled radius layout of disk cutters) for TBMs | Optimize cutter layout for balanced forces/moments with coupling and non-interference. | Genetic algorithm; equal life and equal wear principles; comprehensive evaluation model | Assembled radius gap—reduced to 25.8 mm. Unbalanced radial force—decreased by 62.41%. |
| Palaniappan et al. (2019), Proc. MPES [43] | Conical cemented carbide pick | Reduce the wear rate; analyze cutting forces, cutting efficiency, and specific energy to find the best performance compromise | Coating the pick tip with aluminum titanium nitride; examining wear mechanisms via SEM and X-ray analysis | Hardness improvement: 22.47 GPa; wear rate reduction: 13.9–21.8%. |
| Kumar et al. (2020), Int. J. Rock Mech. Min. Sci. [44] | Operating parameters of surface miner (depth of cut, cutting speed, and pick temperature) | Minimum pick wear/consumption, higher production, and optimal cutting efficiency | Develop empirical models via Taguchi, MLR, and ANN to study temperature variations in cutting picks | Achieved optimized temperature at 95% confidence level. |
| Mahmoodzadeh et al. (2021), Autom. Constr. [45] | Prediction of TBM disk cutter life | Develop accurate machine learning models for cutter life prediction | GPR, SVR, DT, and KNN with 200 datasets; five-fold cross-validation | Most accurate model (GPR). |
| Fathipour-Azar (2023), Rock Mech. Rock Eng. [46] | Predictive model for mean cutting force (MCF) of conical picks | Establish quantitative correlation between rock strength, tool geometry, cutting data, and MCF | Fine-tune hyperparameters using grid search, random search, GA, PSO, and DE | Best model (DE-XGBoost). |
| Zhou et al. (2023), Acta Geotech. [24] | Predictive model for specific energy (SE) in roadheader excavation | Develop accurate SE prediction models considering rock properties, pick geometry, and operation parameters | Six ML algorithms (BPNN, Elman, ELM, KELM, RF, and SVR) optimized by sparrow search algorithm (SSA) | SSA-RF—training set: MAE = 0.7938, MAPE = 12.76%, R2 = 0.9632. |
| Liu et al. (2024), J. Cent. South Univ. [47] | Prediction model for mean cutting force (MCF) of conical picks | Accurately evaluate MCF for pick design and rock-cutting suitability | Hybrid models (boosting trees + Bayesian optimization (BO)) | Best model (BO-CatBoost): outperformed common ML models, especially in handling categorical features (θ with 6 angle types). |
| Wang et al. (2024), Simul. Model. Pract. Theor. [48] | Disk cutter arrangements and excavation parameters | Reduce cutter wear, minimize specific energy, and balance cutter force during rock-breaking | Enhanced bonding model | Penetration depth ≤ 5 mm; tip width > 20 mm; cutter spacing 80–95 mm. |
| Du et al. (2025), Rock Mech. Rock Eng. [49] | Working parameters of disk cutter | Rock-breaking mechanism of disk cutter to understand how parameters affect rock-breaking behavior | Brazilian tests; coupled FEM–DEM | Revealed shear–tension failure mechanism; quantified parameter–energy relationships. |
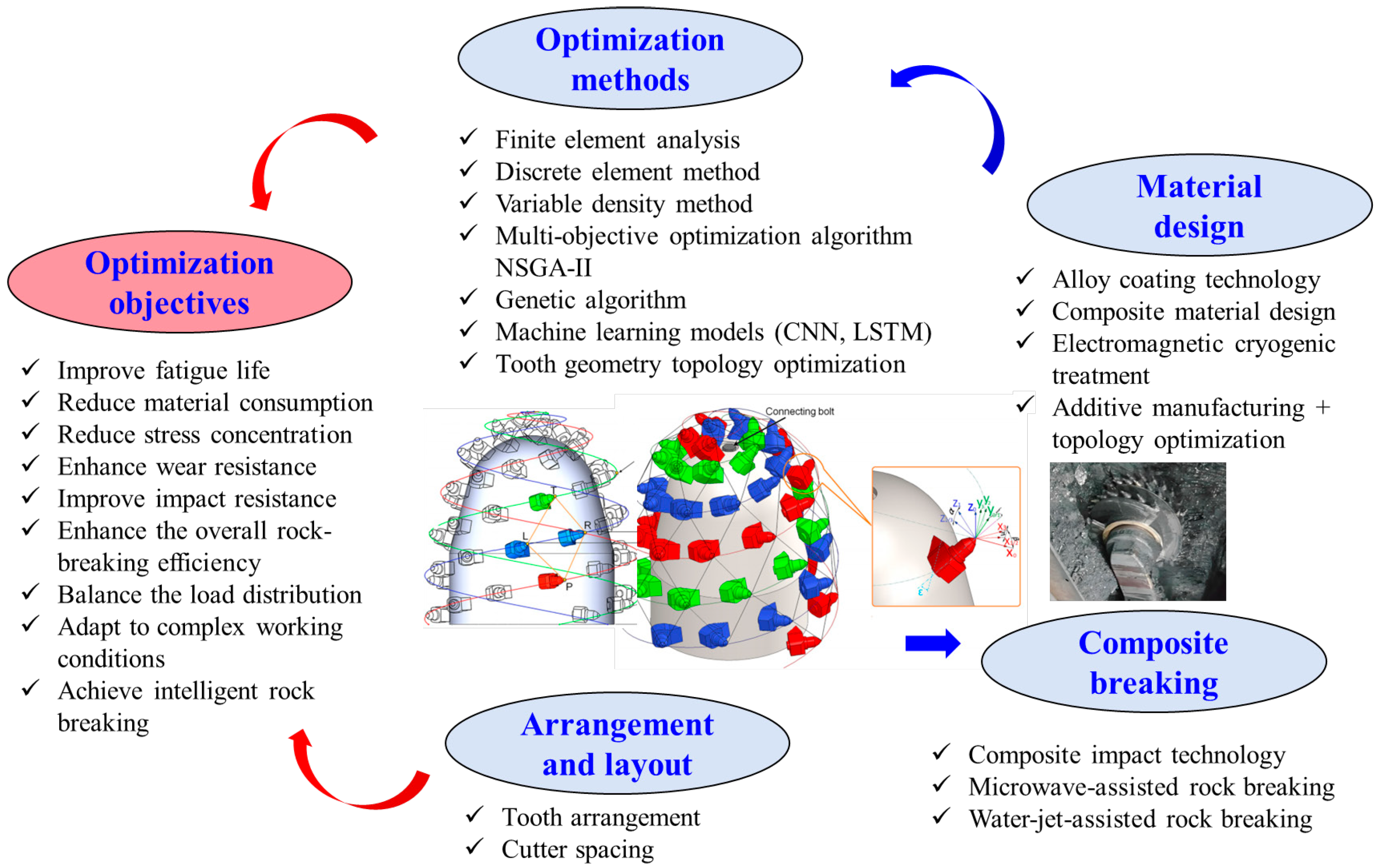
2.2. Issues for Topology Optimization for Rock-Cutting Tools
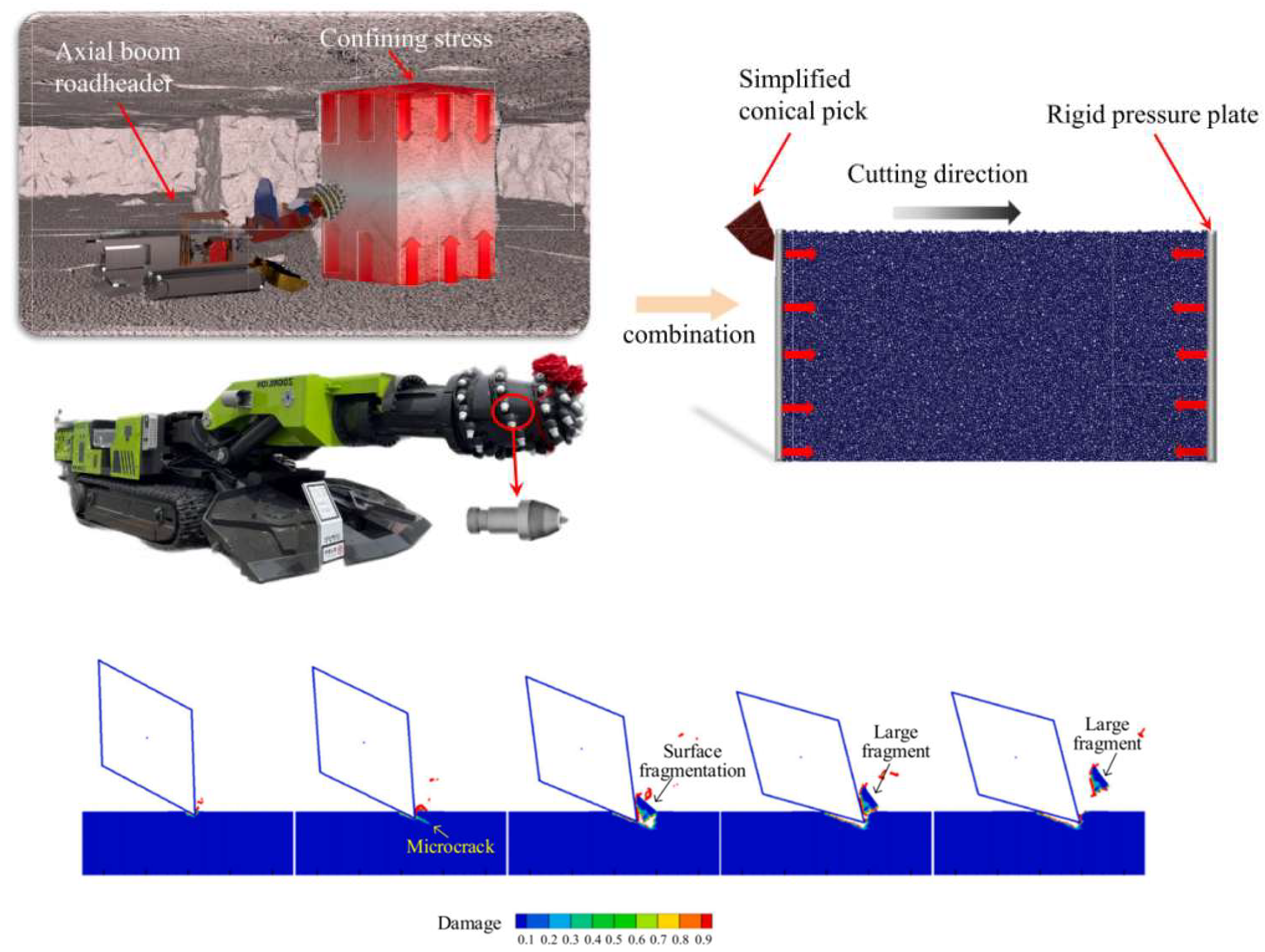
3. Numerical Modeling of Rock–Tool Interactions
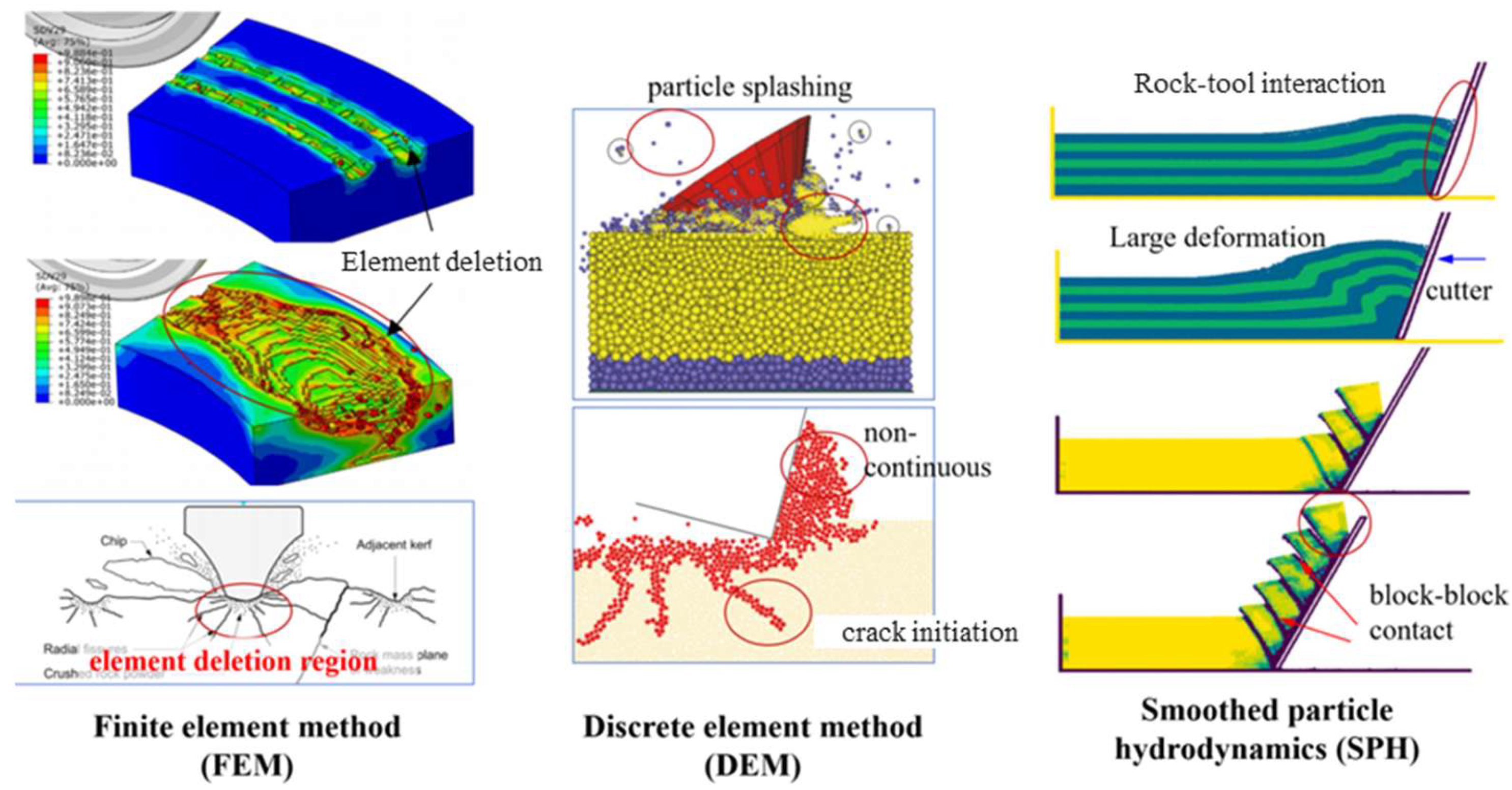
3.1. Numerical Simulation Techniques
3.2. Machine Learning (ML)-Enhanced Predictive Models
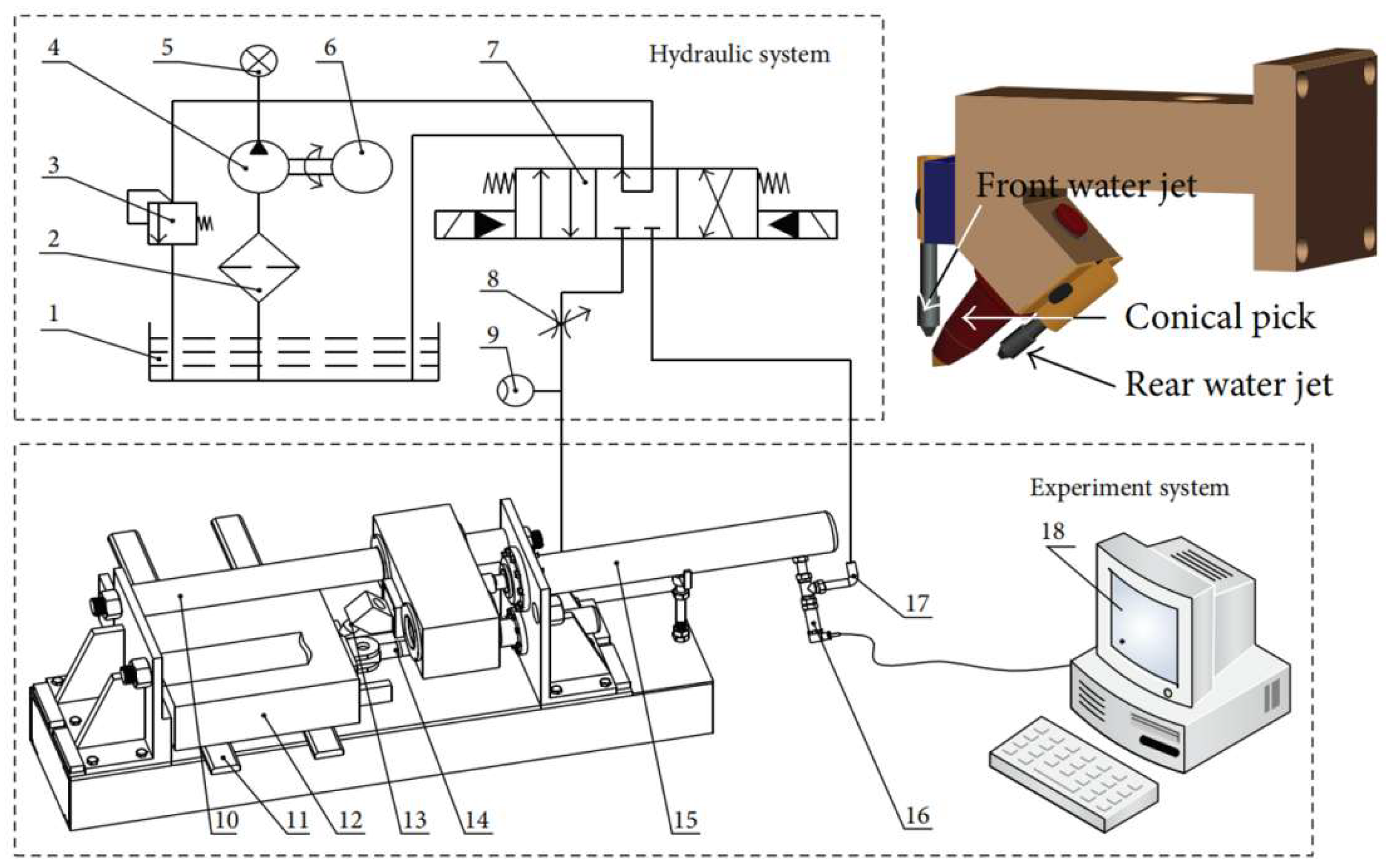
3.3. Experimental Validation
- (1)
- It provides a basis for the selection of tool materials and geometric optimization;
- (2)
- It quantifies the performance of tools under different rock conditions;
- (3)
- It verifies the accuracy of numerical models.
4. Cutting Process Optimization
4.1. Energy Efficiency and Specific Energy Reduction
4.2. Chip Formation and Debris Management
4.3. Sustainability and Scalability
4.4. Critical Challenges and Future Directions
5. Conclusions
- (1)
- The transformative potential of topology optimization in rock-cutting tools enables lightweight, high-strength structures that outperform empirical designs, resolving stress concentration, dynamic load adaptation, and wear resistance challenges.
- (2)
- Integration with advanced methods (DEM/SPH simulations and ML models) achieves the predictive optimization of rock–tool interactions, cutting forces, and tool lifespan.
- (3)
- Key innovations include multi-physics-coupled frameworks for dynamic loading, ML-enhanced predictive models, and sustainable recyclable designs.
- (4)
- Persisting challenges involve thermo-mechanical coupling effects, manufacturing feasibility of complex geometries, and scalability across heterogeneous rock conditions.
- (5)
- Depth-induced difficulties (elevated geostress, rockburst risks, and thermal/water hazards) necessitate intelligent monitoring and adaptive excavation strategies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, G.; Wang, W.; Jing, Z.; Zuo, L.; Wang, F.; Wei, Z. Mechanism and numerical analysis of cutting rock and soil by TBM cutting tools. Tunn. Undergr. Space Technol. 2018, 81, 428–437. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, D.; Wang, D.; Feng, C. A review of selected solutions on the evaluation of coal-rock cutting performances of shearer picks under complex geological conditions. Appl. Sci. 2022, 12, 12371. [Google Scholar] [CrossRef]
- Hamzaban, M.T.; Rostami, J.; Dahl, F. Wear of cutting tools in hard rock excavation process: A critical review of rock abrasiveness testing methods. Rock Mech. Rock Eng. 2023, 56, 1843–1882. [Google Scholar] [CrossRef]
- Deng, L.C.; Zhuang, Q.W.; Li, X.Z. Development and application of a full-scale mechanical rock-cutting platform for measuring the cutting performance of TBM cutter. Measurement 2022, 204, 112036. [Google Scholar] [CrossRef]
- Park, J.Y.; Kang, H.; Lee, J.W. A study on rock cutting efficiency and structural stability of a point attack pick cutter by lab-scale linear cutting machine testing and finite element analysis. Int. J. Rock Mech. Min. Sci. 2018, 103, 215–229. [Google Scholar] [CrossRef]
- Kang, H.; Cho, J.W.; Park, J.Y. A new linear cutting machine for assessing the rock-cutting performance of a pick cutter. Int. J. Rock Mech. Min. Sci. 2016, 88, 129–136. [Google Scholar] [CrossRef]
- Innaurato, N.; Oggeri, C.; Oreste, P. Laboratory tests to study the influence of rock stress confinement on the performances of TBM discs in tunnels. Int. J. Miner. Metall. Mater. 2011, 18, 253–259. [Google Scholar] [CrossRef]
- Li, T.; Wu, T.; Ding, X.; Chen, H.; Wang, L. Design of an internally cooled turning tool based on topology optimization and CFD simulation. Int. J. Adv. Manuf. Technol. 2017, 91, 1327–1337. [Google Scholar] [CrossRef]
- Langelaar, M. Topology optimization for multi-axis machining. Comput. Methods Appl. Mech. Eng. 2019, 351, 226–252. [Google Scholar] [CrossRef]
- Chan, T.C.; Reddy, S.V.V.S.; Ullah, A. Effect of spatial moving structure and topology optimization of the CNC turning machine tools. Int. J. Adv. Manuf. Technol. 2023, 129, 2969–2987. [Google Scholar] [CrossRef]
- Prathyusha, A.L.R.; Babu, G.R. A review on additive manufacturing and topology optimization process for weight reduction studies in various industrial applications. Mater. Today Proc. 2022, 62, 109–117. [Google Scholar] [CrossRef]
- Han, Y.; Xu, B.; Duan, Z.; Huang, X. Stress-based multi-material structural topology optimization considering graded interfaces. Comput. Methods Appl. Mech. Eng. 2022, 391, 114602. [Google Scholar] [CrossRef]
- Dong, Y.; Hussain, I.; He, S. Structural topology optimization of aircraft wing leading edge fabricated of multilayer composites. Aerosp. Sci. Technol. 2025, 159, 109993. [Google Scholar] [CrossRef]
- Xiong, F.; Zou, X.; Zhang, Z.; Shi, X. A systematic approach for multi-objective lightweight and stiffness optimization of a car body. Struct. Multidiscip. Optim. 2020, 62, 3229–3248. [Google Scholar] [CrossRef]
- Wu, N.; Li, S.; Zhang, B.; Wang, C.; Chen, B. The advances of topology optimization techniques in orthopedic implants: A review. Med. Biol. Eng. Comput. 2021, 59, 1673–1689. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, W.; Wang, L.; Bai, G.; Ma, G. Reinforcement design and structural performance for the topology optimized 3D printed concrete truss beams. Eng. Struct. 2025, 332, 120064. [Google Scholar] [CrossRef]
- Guibert, A.T.R.; Hyun, J.; Neofytou, A. Facilitating multidisciplinary collaboration through a versatile level-set topology optimization framework via COMSOL multiphysics. Struct. Multidiscip. Optim. 2024, 67, 159. [Google Scholar] [CrossRef]
- Costa, M.R.; Sohouli, A.; Suleman, A. Multi-scale and multi-material topology optimization of gradient lattice structures using surrogate models. Compos. Struct. 2022, 289, 115402. [Google Scholar] [CrossRef]
- Shin, S.; Shin, D.; Kang, N. Topology optimization via machine learning and deep learning: A review. J. Comput. Des. Eng. 2023, 10, 1736–1766. [Google Scholar] [CrossRef]
- Sun, S.; Rankouhi, B.; Thoma, D.J.; Cheadle, M.J.; Maples, G.D. Topology optimization, additive manufacturing and thermohydraulic testing of heat sinks. Int. J. Heat Mass Transf. 2024, 224, 125281. [Google Scholar] [CrossRef]
- Lin, S.Y.; Chang, C.H. Structure design improvement and stiffness reinforcement of a machine Tool through Topology optimization based on machining characteristics. Appl. Sci. 2023, 14, 61. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, C.; Li, Q.; Yue, H.; Zhang, J. Optimization of rock cutting process parameters with disc cutter for wear and cutting energy reduction based on the discrete element method. J. Clean. Prod. 2023, 391, 136160. [Google Scholar] [CrossRef]
- Hu, M.; Gao, T.; Dong, X.; Tan, Q.; Yi, C. Simulation of soil-tool interaction using smoothed particle hydrodynamics (SPH). Soil Tillage Res. 2023, 229, 105671. [Google Scholar] [CrossRef]
- Zhou, J.; Dai, Y.; Huang, S.; Armaghani, D.J.; Qiu, Y. Proposing several hybrid SSA—Machine learning techniques for estimating rock cuttability by conical pick with relieved cutting modes. Acta Geotech. 2023, 18, 1431–1446. [Google Scholar] [CrossRef]
- Kadkhodaei, M.H.; Ghasemi, E.; Hamidi, J.K.; Rostami, J. Evaluation of rock cutting performance of conical cutting tool based on commonly measured rock properties. Transp. Geotech. 2024, 48, 101318. [Google Scholar] [CrossRef]
- Cheluszka, P.; Mikuła, S.; Mikuła, J. Theoretical consideration of fatigue strengthening of conical picks for rock cutting. Tunn. Undergr. Space Technol. 2022, 125, 104481. [Google Scholar] [CrossRef]
- Li, J.; Gong, Y.; Zhao, S.; Sun, W.; Xu, Y. Material and processing optimization on disc cutter of tunnel boring machine for failure prevention. Eng. Fail. Anal. 2022, 138, 106363. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, J.; Zhou, Z.; Zhang, S.; Wang, S. Numerical investigation on the influence of cutting parameters on rock breakage using a conical pick. Eng. Fract. Mech. 2024, 312, 110607. [Google Scholar] [CrossRef]
- Rui, F.; Zhao, G.F.; Zheng, Y.; Gong, Q.; Zhao, X. Electromagnetic-thermo-mechanical coupled modelling of microwave-assisted TBM disc cutting. Tunn. Undergr. Space Technol. 2023, 138, 105171. [Google Scholar] [CrossRef]
- Krauze, K.; Mucha, K.; Wydro, T.; Pawlik, J.; Wróblewska, P. Mass and Volumetric Abrasive Wear Measurements of the Mining Conical Picks. Sustainability 2023, 15, 850. [Google Scholar] [CrossRef]
- Copur, H.; Balci, C.; Bilgin, N.; Tumac, D.; Avunduk, E. Predicting Cutting Performance of Chisel Tools By Using Physical And Mechanical Properties of Natural Stones. In Proceedings of the ISRM International Symposium—EUROCK 2012, Stockholm, Sweden, 28–31 May 2012. [Google Scholar]
- Yasar, S. A general semi-theoretical model for conical picks. Rock Mech. Rock Eng. 2020, 53, 2557–2579. [Google Scholar] [CrossRef]
- Liu, X.; Liu, S.; Li, L.; Cui, X. Experiment on conical pick cutting rock material assisted with front and rear water jet. Adv. Mater. Sci. Eng. 2015, 2015, 506579. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Wan, L.; Lu, Z.; Wang, H. Investigation of the influence of cutting parameters on conical pick cutting performance and rock damage. Machines 2022, 10, 1034. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, Q.; Liu, Q.; Liu, J.; Peng, X. Full-scale linear cutting tests to check and modify a widely used semi-theoretical model for disc cutter cutting force prediction. Acta Geotech. 2020, 15, 1481–1500. [Google Scholar] [CrossRef]
- Chinnasamy, M.; Rathanasamy, R.; Samanta, B.; Pal, S.; Palaniappan, S. Microstructure evolution, phase formation, mechanical and tribological response of deep cryogenically treated hard WC-6% Co cutting bits. J. Mater. Res. Technol. 2023, 27, 1293–1306. [Google Scholar] [CrossRef]
- Li, F.; Liu, W.; Gao, D.; Li, Y. Study on super impact resistant polycrystalline diamond compacts with homogeneous PCD/WC-Co interlayer. Int. J. Refract. Met. Hard Mater. 2024, 119, 106558. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, B.; Wang, B.; Wang, Y.; Cao, H. Application of Laser Cladding Technology on TBM Cutter Repairment and Enhancement. Indian Geotech. J. 2024, 55, 1374–1382. [Google Scholar] [CrossRef]
- Song, K.; Yang, H.; Xie, J.; Karekal, S. An optimization methodology of cutter-spacing for efficient mechanical breaking of jointed rock mass. Rock Mech. Rock Eng. 2022, 55, 3301–3316. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Q.; Liu, B.; Wang, D.; Wang, X. Development and in-situ application of a real-time cutting tool forces monitoring system in TBM tunnelling. Tunn. Undergr. Space Technol. 2022, 124, 104453. [Google Scholar] [CrossRef]
- Liu, S.; Cui, X.; Du, C.; Fu, L. Method to determine installing angle of conical point attack pick. J. Cent. South Univ. Technol. 2011, 18, 1994–2000. [Google Scholar] [CrossRef]
- Sun, H.; Guo, W.; Liu, J.; Song, L.; Liu, X. Layout design for disc cutters based on analysis of TBM cutter-head structure. J. Cent. South Univ. 2018, 25, 812–830. [Google Scholar] [CrossRef]
- Palaniappan, S.K.; Pal, S.K.; Chinnasamy, M. Efficiency of rock cutting and wear behavior of coated bits via lab-scale linear rock-cutting machine: Experimental approach. Int. J. Geomech. 2023, 23, 06022041. [Google Scholar] [CrossRef]
- Kumar, C.; Kumaraswamidhas, L.A.; Murthy, V.; Prakash, A. Experimental investigations on thermal behavior during pick-rock interaction and optimization of operating parameters of surface miner. Int. J. Rock Mech. Min. Sci. 2020, 133, 104360. [Google Scholar] [CrossRef]
- Arsalan, M.; Mokhtar, M.; Hawkar, H.; Sazan, N.; Hunar, F.; Ahmed, M.; Mohammad, K.; Hoger, M. Machine learning forecasting models of disc cutters life of tunnel boring machine. Autom. Constr. 2021, 128, 103779. [Google Scholar]
- Fathipour-Azar, H. Mean cutting force prediction of conical picks using ensemble learning paradigm. Rock Mech. Rock Eng. 2023, 56, 221–236. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Sun, J.; Yang, J.; Yang, B.; Li, D. Intelligent evaluation of mean cutting force of conical pick by boosting trees and Bayesian optimization. J. Cent. South Univ. 2024, 31, 3948–3964. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Li, Z.; Chao, Y.; Zhao, S.; Peng, K. Optimizing cutter wear in TBM operations through numerical analysis of enhanced rock-cutting interaction. Simul. Model. Pract. Theory 2024, 135, 102976. [Google Scholar] [CrossRef]
- Du, W.; Gao, J.; Zhang, C.; Ma, Q.; Zhang, J.; Cheng, A. A Numerical Study on the Rock Breakage Mechanism with TBM Disk Cutter in Calcareous Cemented Sand Pebble Stratum Using a Coupled FEM-DEM Method. Rock Mech. Rock Eng. 2025, 58, 2319–2347. [Google Scholar] [CrossRef]
- Fu, J.; Yin, X.; Liu, F.; Liu, H.; Cui, J. Investigation on thermal behavior of TBM disc cutter under different cooling conditions. Case Stud. Therm. Eng. 2023, 49, 103392. [Google Scholar] [CrossRef]
- Lu, Z.; Wan, L.; Zeng, Q.; Zhang, X.; Gao, K. The structural optimization of roadheader conical picks based on fatigue life. Int. J. Model. Simul. Sci. Comput. 2018, 9, 1850013. [Google Scholar] [CrossRef]
- Marji, M.; Hosseini Nasab, H.; Hossein Morshedi, A. Numerical modeling of crack propagation in rocks under TBM disc cutters. J. Mech. Mater. Struct. 2009, 4, 605–627. [Google Scholar] [CrossRef]
- Fang, Y.; Li, X.; Cao, Y.; Liu, H.; Guo, Y. Wear Characteristics and Optimization Measures of Disc Cutters During Large-Diameter Slurry Tunnel Boring Machine Advancing in Soil-Rock Composite Strata: A Case Study. Lubricants 2025, 13, 170. [Google Scholar] [CrossRef]
- Song, Y.; Yang, S.Q.; Li, K.S.; Yin, P.; Pan, P. Mechanical behavior and fracture evolution mechanism of composite rock under triaxial compression: Insights from three-dimensional DEM modeling. Rock Mech. Rock Eng. 2023, 56, 7673–7699. [Google Scholar] [CrossRef]
- Li, Y.-M.; Zhao, G.-F.; Jiao, Y.; Yan, C.; Wang, X. A benchmark study of different numerical methods for predicting rock failure. Int. J. Rock Mech. Min. Sci. 2023, 166, 105381. [Google Scholar] [CrossRef]
- Wang, S.; Shi, X.; Wu, Y. DEM-based 2D numerical simulation of the rock cutting process using a conical pick under confining stress. Comput. Geotech. 2024, 165, 105885. [Google Scholar] [CrossRef]
- Zhu, X.; Feng, C.; Cheng, P.; Wang, X.; Li, S. A novel three-dimensional hydraulic fracturing model based on continuum-discontinuum element method. Comput. Methods Appl. Mech. Eng. 2021, 383, 113887. [Google Scholar] [CrossRef]
- Yue, Z.; Zhou, J.; Feng, C.; Wang, X.; Peng, L. Coupling of material point and continuum discontinuum element methods for simulating blast-induced fractures in rock. Comput. Geotech. 2022, 144, 104629. [Google Scholar] [CrossRef]
- Gong, B.; Wang, S.; Sloan, S.W.; Sheng, D.; Tang, C. Modelling rock failure with a novel continuous to discontinuous method. Rock Mech. Rock Eng. 2019, 52, 3183–3195. [Google Scholar] [CrossRef]
- Geng, Q.; Wei, Z.; Ren, J. New rock material definition strategy for FEM simulation of the rock cutting process by TBM disc cutters. Tunn. Undergr. Space Technol. 2017, 65, 179–186. [Google Scholar] [CrossRef]
- Li, P.; Jiang, S.; Tang, D.; Xu, O. A PFC3D-based numerical simulation of cutting load for lunar rock simulant and experimental validation. Adv. Space Res. 2017, 59, 2583–2599. [Google Scholar] [CrossRef]
- Raymond, S.J.; Jones, B.D.; Williams, J.R. Modeling damage and plasticity in aggregates with the material point method (MPM). Comput. Part. Mech. 2019, 6, 371–382. [Google Scholar] [CrossRef]
- Wang, Y.; Bui, H.H.; Nguyen, G.D.; Ranjith, P.G. A new SPH-based continuum framework with an embedded fracture process zone for modelling rock fracture. Int. J. Solids Struct. 2019, 159, 40–57. [Google Scholar] [CrossRef]
- Tunsakul, J.; Jongpradist, P.; Kim, H.M.; Nanakorn, P. Evaluation of rock fracture patterns based on the element-free Galerkin method for stability assessment of a highly pressurized gas storage cavern. Acta Geotech. 2018, 13, 817–832. [Google Scholar] [CrossRef]
- Avunduk, E.; Tumaç, D.; Atalay, A.K. Prediction of roadheader performance by artificial neural network. Tunn. Undergr. Space Technol. 2014, 44, 3–9. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.; Fu, X.; Tiong, R.; Zhang, P. Digital twin enabled real-time advanced control of TBM operation using deep learning methods. Autom. Constr. 2024, 158, 105240. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Jing, H. Research on intelligent identification of rock types based on faster R-CNN method. IEEE Access 2020, 8, 21804–21812. [Google Scholar] [CrossRef]
- Mahmood, J.; Mustafa, G.; Ali, M. Accurate estimation of tool wear levels during milling, drilling and turning operations by designing novel hyperparameter tuned models based on LightGBM and stacking. Measurement 2022, 190, 110722. [Google Scholar] [CrossRef]
- Xie, Y.; Lian, K.; Liu, Q.; Zhang, C.; Liu, H. Digital twin for cutting tool: Modeling, application and service strategy. J. Manuf. Syst. 2021, 58, 305–312. [Google Scholar] [CrossRef]
- Niaki, S.A.; Haghighat, E.; Campbell, T.; Poursartip, A.; Vaziri, R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Comput. Methods Appl. Mech. Eng. 2021, 384, 113959. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, C.; Gao, Y.; Gao, S.; Guo, J. Microwave-Assisted Linear Cutting of Sandstone with a Conical Pick: Experimental Study. Rock Mech. Rock Eng. 2025, 58, 1021–1038. [Google Scholar] [CrossRef]
- Yu, R.; Dong, X.; Li, Z.; Fan, M. A coupled SPH–DEM model for erosion process of solid surface by abrasive water-jet impact. Comput. Part Mech. 2023, 10, 1093–1112. [Google Scholar] [CrossRef]
- Yu, R.; Dong, X.; Jing, Z.; Fan, M.; Li, Z. Meshfree modeling of brittle surface erosion by sharp-angled particle impact with Johnson–Holmquist-II (JH-2) model. Tribol. Int. 2023, 187, 108710. [Google Scholar] [CrossRef]
- Oggeri, C.; Fenoglio, T.M.; Vinai, R. Tunnel spoil classification and applicability of lime addition in weak formations for muck reuse. Tunn. Undergr. Space Technol. 2014, 44, 97–107. [Google Scholar] [CrossRef]
- Costamagna, E.; Oggeri, C.; Segarra, P.; Castedo, R.; Navarro, J. Assessment of contour profile quality in D&B tunnelling. Tunn. Undergr. Space Technol. 2018, 75, 67–80. [Google Scholar]
- Jihong, Z.H.U.; Han, Z.; Chuang, W.; Lu, Z.; Yuan, S. A review of topology optimization for additive manufacturing: Status and challenges. Chin. J. Aeronaut. 2021, 34, 91–110. [Google Scholar]
- Borda, F.; La Rosa, A.D.; Filice, L.; Gagliardi, F. Environmental impact of process constrained topology optimization design on automotive component’ life. Int. J. Mater. Form. 2023, 16, 48. [Google Scholar] [CrossRef]
- Li, H.; Yamada, T.; Jolivet, P.; Furuta, K.; Kondoh, T. Full-scale 3D structural topology optimization using adaptive mesh refinement based on the level-set method. Finite Elem. Anal. Des. 2021, 194, 103561. [Google Scholar] [CrossRef]

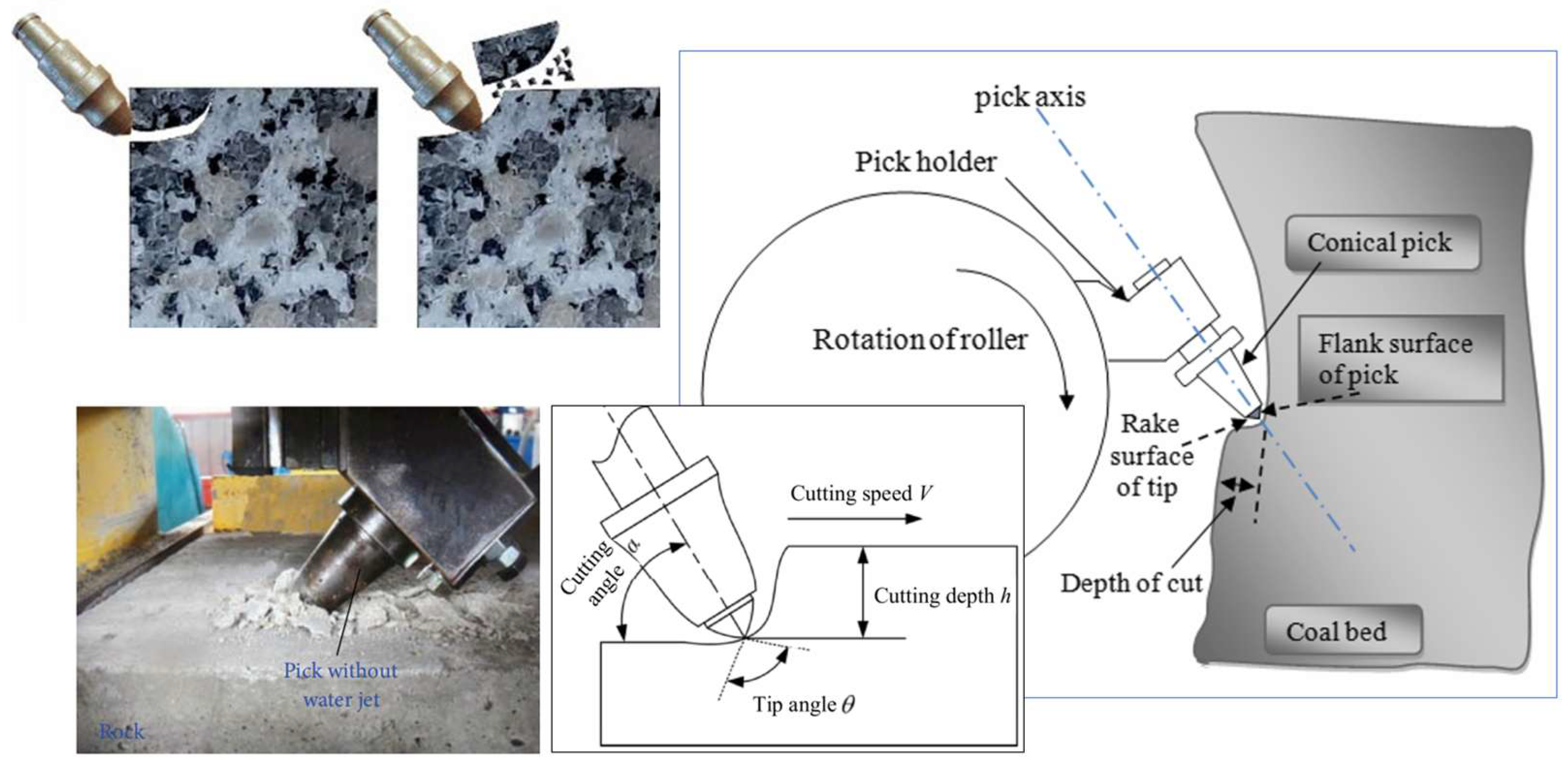
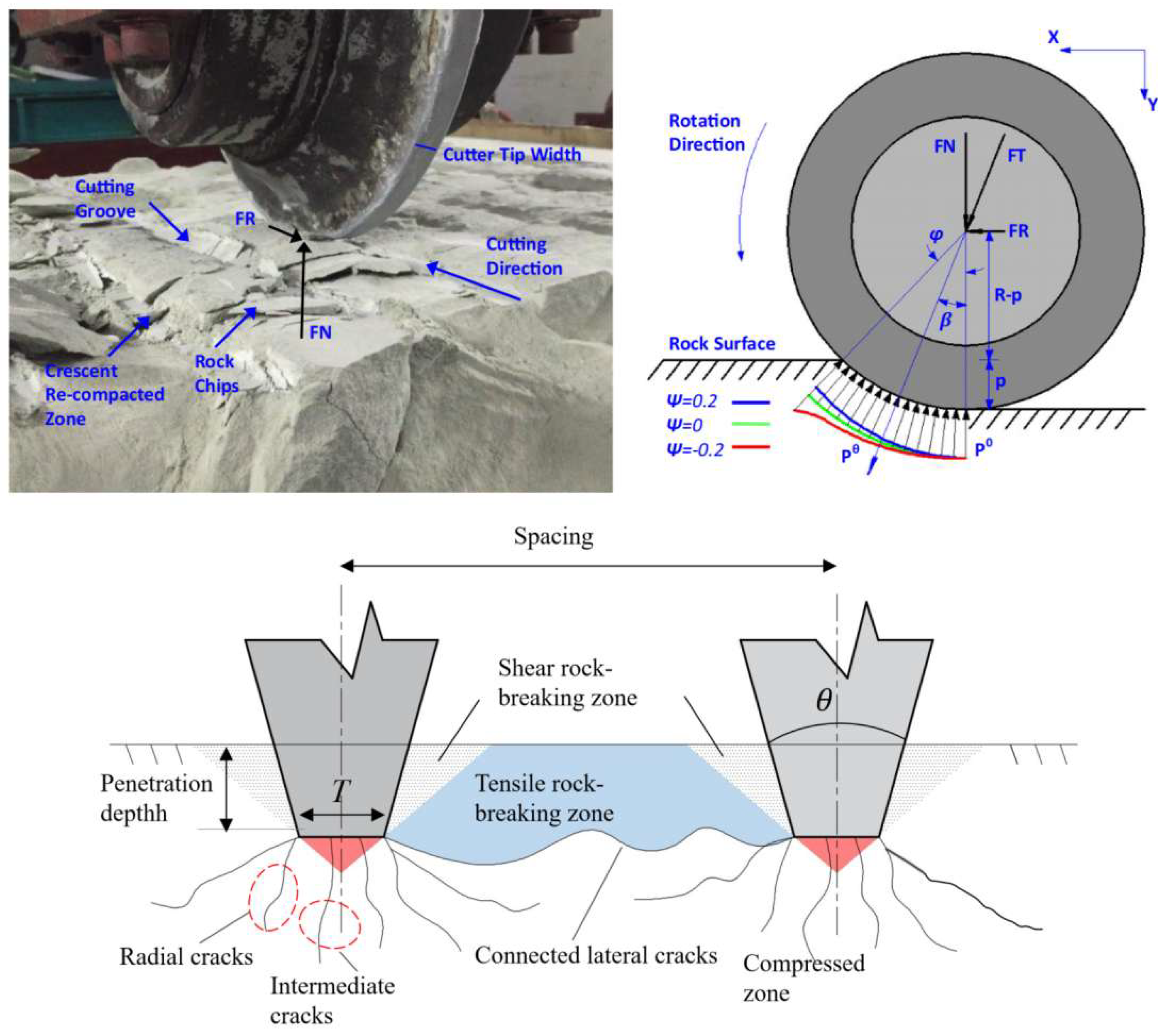




| Working Mode | Rock–Tool Interaction | Cutting Tool | Adaptability of Rock Strength |
|---|---|---|---|
| Drag/plowing | Continuous rotation | Cutter tooth | <40~60 MPa |
| Scraper | <60~80 MPa | ||
| Conical pick | <40~60 MPa | ||
| Rotation | Rolling | Disk cutter | <250 MPa |
| Unreal rolling | Roller cone cutter | <200 MPa | |
| Impact | Impact | Beaker hammer | <100 MPa |
| Step 1: Problem Definition and Physics-Based Modeling Input Parameters: Tool geometry (blade angle, edge length), material properties (hardness, elastic modulus), operating conditions (cutting speed, confining pressure). Output Targets: Stress field, temperature field, crack propagation path, tool wear rate, specific rock-breaking energy. Governing Equations: Rock Mechanics: Elastoplastic constitutive equations, as well as Drucker–Prager or Mohr–Coulomb failure criteria. Heat Transfer: Energy conservation equation with thermo-mechanical coupling terms. Tool–Rock Interaction: Frictional heating model, wear equations. Step 2: PINN Architecture Design Network Structure: Input Layer: Tool parameters (e.g., blade angle α, cutting depth d) and spatial coordinates (x, y, t). Hidden Layers: Multi-layer perceptron (activation: ReLU/Swish). Output Layer: Key physical quantities (stress σ, temperature T, damage factor D). Loss Function: Data Loss : mean square error of experimental or simulation data (such as the cutting tool forces ) Physics Loss : residual of the governing equation, the boundary condition. Step 3: Model Validation and Uncertainty Quantification Validation Metrics: Error between predictions and independent experimental data. Norm of physics equation residuals. Uncertainty Analysis: Monte Carlo dropout or Bayesian PINN to quantify robustness against input noise. Step 4: Tool Optimization Objective: Minimize specific energy or maximize tool life. Optimization Methods: Gradient-Based: Use PINN’s automatic differentiation to compute for gradient descent. Global Search: Genetic algorithms for multi-objective Pareto optimization (e.g., trade-off between energy consumption and wear rate). Experimental Validation: Verify optimized tool designs via experiments or high-fidelity simulations. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhang, Q.; Zhang, S.; Tian, Y.; Dong, X.; Song, X.; Wang, D. Optimization of Rock-Cutting Tools: Improvements in Structural Design and Process Efficiency. Computation 2025, 13, 152. https://doi.org/10.3390/computation13070152
Cao Y, Zhang Q, Zhang S, Tian Y, Dong X, Song X, Wang D. Optimization of Rock-Cutting Tools: Improvements in Structural Design and Process Efficiency. Computation. 2025; 13(7):152. https://doi.org/10.3390/computation13070152
Chicago/Turabian StyleCao, Yuecao, Qiang Zhang, Shucheng Zhang, Ying Tian, Xiangwei Dong, Xiaojun Song, and Dongxiang Wang. 2025. "Optimization of Rock-Cutting Tools: Improvements in Structural Design and Process Efficiency" Computation 13, no. 7: 152. https://doi.org/10.3390/computation13070152
APA StyleCao, Y., Zhang, Q., Zhang, S., Tian, Y., Dong, X., Song, X., & Wang, D. (2025). Optimization of Rock-Cutting Tools: Improvements in Structural Design and Process Efficiency. Computation, 13(7), 152. https://doi.org/10.3390/computation13070152







