Exploring the Chemical and Pharmaceutical Potential of Kapakahines A–G Using Conceptual Density Functional Theory-Based Computational Peptidology
Abstract
1. Introduction
2. Materials and Methods
2.1. Conceptual DFT Studies
2.2. Computational ADMET
3. Results and Discussion
3.1. Chemical Reactivity Properties
- Electronegativity
- Global Hardness
- Global Electrophilicity
- Global Hyperhardness
- Global Softness
- Nucleophilicity
- Electroaccepting Power
- Electrodonating Power
- Net Electrophilicity
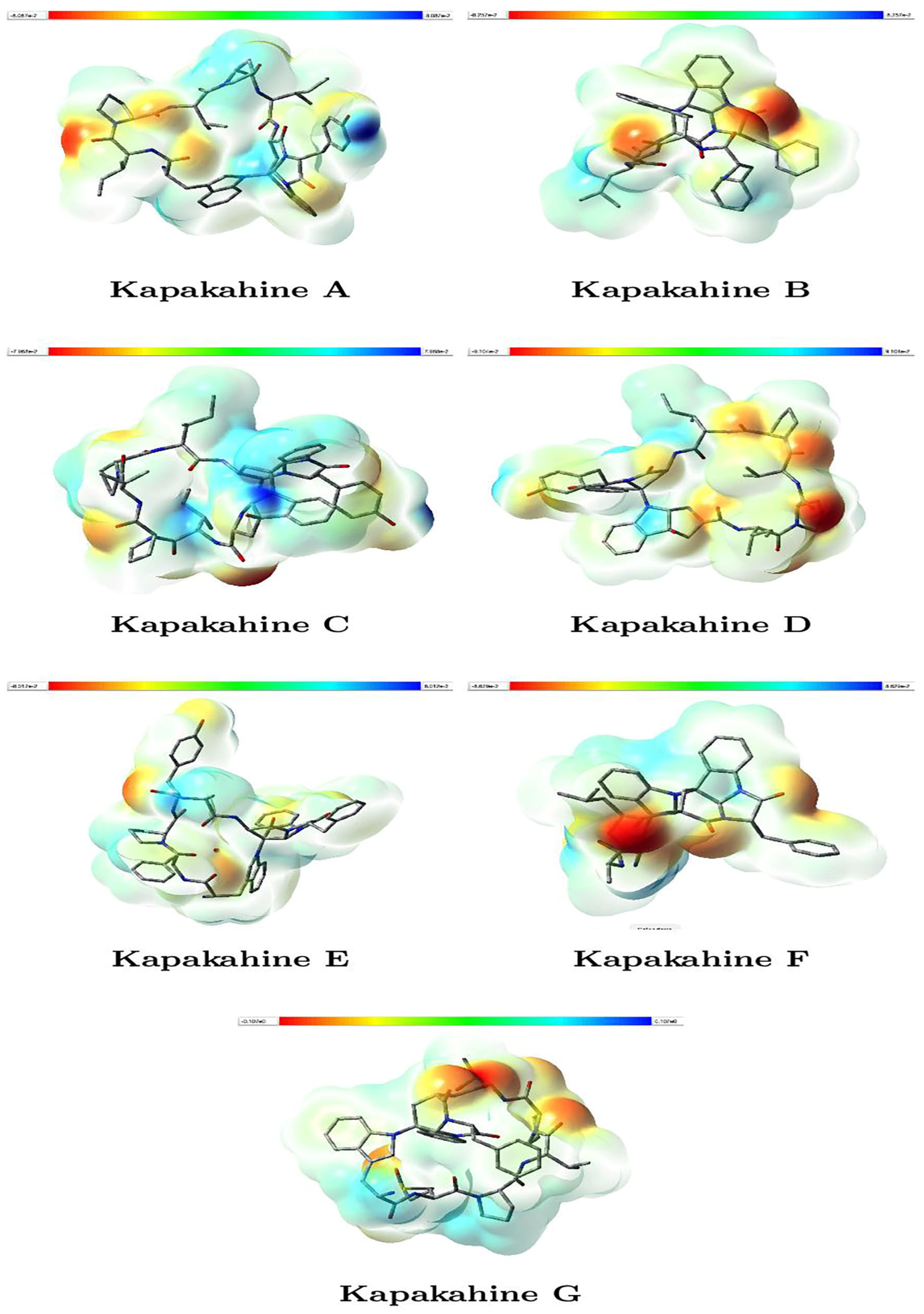
3.2. The Molecular Electrostatic Potential
- Kapakahines display prominent red regions localized on carbonyl oxygens and amide groups, suggesting that these zones are strong nucleophilic centers likely to interact with electrophilic species or metal ions.
- The electrophilic (blue) areas are generally smaller, often surrounding hydrogen atoms or less electron-rich zones, consistent with typical peptide behavior.
- Kapakahine G, with the highest electrophilicity index ( = 1.423 eV) and net electrophilicity ( = 6.258 eV) (Table 3), shows extended blue regions, supporting its pronounced electron-acceptor character and potential interaction with nucleophilic residues in biological systems.
- Kapakahine D, with the lowest electrophilic descriptor (ED = 2.538 eV), presents a more balanced MEP with limited blue zones, suggesting lower reactivity, which matches its milder predicted ADMET profile.
3.3. The Local Hyper-Softness
- In all peptides, LHS > 0 regions (electrophilic centers) are mainly found near amide hydrogen atoms and electron-deficient carbons.
- LHS < 0 zones (nucleophilic centers) overlap with the carbonyl and ether oxygens—corroborating the MEP findings.
- Kapakahine C, which has the highest electronegativity ( = 3.695 eV) and electrophilic descriptor (ED = 7.466 eV), exhibits the most intense and spatially distinct LHS regions. This suggests highly polarized local reactivity, making it a strong candidate for site-selective interactions.
- Kapakahine F, with moderate nucleophilicity N and low , shows more diffuse LHS regions, implying lower spatial reactivity density.
- The intensity and localization of LHS maps also appear to correlate with chemical hardness (). For example, Kapakahine C ( = 5.033 eV) has sharply confined reactive zones, consistent with high chemical rigidity.
3.4. Computational Pharmacokinetic Properties and ADMET
- Absorption: All Kapakahines are substrates and dual inhibitors (I and II) of P-glycoprotein, suggesting they may interact with efflux transporters and influence oral bioavailability and multidrug resistance. This aligns with their moderate to high LogP values (Table 4), indicating sufficient lipophilicity for membrane permeability.
- Distribution:
- −
- BBB permeability values range from −0.626 (F) to −1.106 (G), indicating poor blood–brain barrier penetration, typical of larger peptides.
- −
- CNS permeability values (all < −2) also support their limited access to central nervous system tissues. This correlates with relatively high electronegativity () and electrophilicity () in Table 3, implying a tendency toward hydrophilicity and reduced passive diffusion through lipid membranes.
- Metabolism: All peptides are substrates of CYP3A4, a key metabolic enzyme, while none are substrates of CYP2D6. Notably, Kapakahines A, C, D, and G inhibit CYP3A4, which may pose risks for drug–drug interactions. Their strong nucleophilicity (N) and variable global hardness () suggest potential reactivity with metabolic enzymes.
- Excretion: Total clearance ranges from slightly negative to slightly positive values (F: +0.079), suggesting relatively slow elimination. No Kapakahine is a substrate for OCT2, a renal transporter, implying hepatic over renal clearance. This is consistent with their moderate LogP (Table 4) and relatively large size.
- Toxicity: All peptides are non-AMES toxic and non-inhibitors of hERG I, indicating a favorable genotoxicity and cardiac safety profile. However, all are hERG II inhibitors and predicted to be hepatotoxic, raising concerns for cardiotoxicity and liver injury. These risks may be linked to their net electrophilicity (), especially for Kapakahines G and B, which display the highest values in Table 3, suggesting strong electron-accepting capabilities that could impact interactions with biological macromolecules.
- Kapakahine G: Highest electrophilicity ( = 1.423 eV) and net electrophilicity ( = 6.258 eV); matches its broader ADMET liability (lowest BBB and CNS permeability, high hepatotoxicity and clearance). These values suggest high reactivity with biological targets, enhancing potency but possibly increasing toxicity.
- Kapakahine C: Highest hardness ( = 5.033 eV) and electronegativity ( = 3.695 eV); exhibits lowest total clearance and poor CNS penetration, supporting its chemical stability but reduced excretion. Also, the highest ED value (7.466 eV) may be linked to its specific metabolic behavior.
- Kapakahine D: Lowest net electrophilicity ( = 5.785 eV) and electrophilic descriptor (ED = 2.538 eV); presents lower predicted toxicity risk and moderate metabolic profile. These values could suggest a safer ADMET profile among the set.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| CDFT | Conceptual Density Functional Theory |
| CDFT-CP | Conceptual Density Functional Theory-based Computational Peptidology |
| KID | Koopmans in DFT |
| ADMET | Absorption, Distribution, Metabolism, Excretion and Toxicity |
References
- Agrawal, S.; Adholeya, A.; Deshmukh, S.K. The Pharmacological Potential of Non-ribosomal Peptides from Marine Sponge and Tunicates. Front. Pharmacol. 2016, 7, 333. [Google Scholar] [CrossRef] [PubMed]
- Gogineni, V.; Hamann, M.T. Marine Natural Product Peptides with Therapeutic Potential: Chemistry, Biosynthesis, and Pharmacology. Biochim. Biophys. Acta (BBA)-Gen. Subj. 2018, 1862, 81–196. [Google Scholar] [CrossRef] [PubMed]
- Kamihira, R.; Nakao, Y. Small-Scale Preparation of Fluorescently Labeled Chemical Probes from Marine Cyclic Peptides, Kapakahines A and F. Mar. Drugs 2021, 19, 76. [Google Scholar] [CrossRef]
- Nakao, Y.; Yeung, B.K.S.; Yoshida, W.Y.; Scheuer, P.J.; Kelly-Borges, M. Kapakahine B, a Cyclic Hexapeptide with an α-Carboline Ring System from the Marine Sponge Cribrochalina olemda. J. Am. Chem. Soc. 1995, 117, 8271–8272. [Google Scholar] [CrossRef]
- Nakao, Y.; Kuo, J.; Yoshida, W.Y.; Kelly, M.; Scheuer, P.J. More Kapakahines from the Marine Sponge Cribrochalina olemda. Org. Lett. 2003, 5, 1387–1390. [Google Scholar] [CrossRef]
- Negi, B.; Kumar, D.; Rawat, D.S. Marine Peptides as Anticancer Agents: A Remedy to Mankind by Nature. Curr. Protein Pept. Sci. 2017, 18, 885–904. [Google Scholar] [CrossRef]
- Newhouse, T.; Lewis, C.A.; Baran, P.S. Enantiospecific Total Syntheses of Kapakahines B and F. J. Am. Chem. Soc. 2009, 131, 6360–6361. [Google Scholar] [CrossRef]
- Espejo, V.R.; Rainier, J.D. Total Synthesis of Kapakahine E and F. Org. Lett. 2010, 12, 2154–2157. [Google Scholar] [CrossRef]
- Yeung, B.K.S.; Nakao, Y.; Kinnel, R.B.; Carney, J.R.; Yoshida, W.Y.; Scheuer, P.J.; Kelly-Borges, M. The Kapakahines, Cyclic Peptides from the Marine Sponge Cribrochalina olemda. J. Org. Chem. 1996, 61, 7168–7173. [Google Scholar] [CrossRef]
- Phyo, Y.Z.; Ribeiro, J.; Fernandes, C.; Kijjoa, A.; Pinto, M.M.M. Marine Natural Peptides: Determination of Absolute Configuration Using Liquid Chromatography Methods and Evaluation of Bioactivities. Molecules 2018, 23, 306. [Google Scholar] [CrossRef]
- Varijakzhan, D.; Loh, J.Y.; Yap, W.S.; Yusoff, K.; Seboussi, R.; Lim, S.H.E.; Lai, K.S.; Chong, C.M. Bioactive Compounds from Marine Sponges: Fundamentals and Applications. Mar. Drugs 2021, 19, 246. [Google Scholar] [CrossRef] [PubMed]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; Proft, F.D.; Gázquez, J.L.; Liu, S.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P. Conceptual Density Functional Theory: Status, Prospects, Issues. Theor. Chem. Accounts 2020, 139. [Google Scholar] [CrossRef]
- Geerlings, P. From Density Functional Theory to Conceptual Density Functional Theory and Biosystems. Pharmaceuticals 2022, 15, 1112. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Chattaraj, P.K. Conceptual Density Functional Theory Based Electronic Structure Principles. Chem. Sci. 2021, 12, 6264–6279. [Google Scholar] [CrossRef]
- Chakraborty, A.; Pan, S.; Chattaraj, P.K. Biological Activity and Toxicity: A Conceptual DFT Approach. In Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2012; pp. 143–179. [Google Scholar]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef]
- Flores-Holguín, N.; Frau, J.; Glossman-Mitnik, D. Virtual Screening of Marine Natural Compounds by Means of Chemoinformatics and CDFT-Based Computational Peptidology. Mar. Drugs 2020, 18, 478. [Google Scholar] [CrossRef]
- van de Waterbeemd, H.; Gifford, E. ADMET in silico Modelling: Towards Prediction Paradise? Nat. Rev. Drug Discov. 2003, 2, 192–204. [Google Scholar] [CrossRef]
- Wang, Y.; Xing, J.; Xu, Y.; Zhou, N.; Peng, J.; Xiong, Z.; Liu, X.; Luo, X.; Luo, C.; Chen, K.; et al. In silicoADME/T Modelling for Rational Drug Design. Q. Rev. Biophys. 2015, 48, 488–515. [Google Scholar] [CrossRef]
- Daina, A.; Michielin, O.; Zoete, V. SwissADME: A Free Web Tool to Evaluate Pharmacokinetics, Drug-likeness and Medicinal Chemistry Friendliness of Small Molecules. Sci. Rep. 2017, 7, 42717. [Google Scholar] [CrossRef]
- Tsaioun, K.; Kates, S.A. (Eds.) ADMET for Medicinal Chemists; Wiley-Blackwell: Hoboken, NJ, USA, 2011. [Google Scholar]
- Lewars, E. Computational Chemistry—Introduction to the Theory and Applications of Molecular and Quantum Mechanics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Young, D. Computational Chemistry—A Practical Guide for Applying Techniques to Real-World Problems; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry, 2nd ed.; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Cramer, C.J. Essentials of Computational Chemistry—Theories and Models, 2nd ed.; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Halgren, T.A. Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force Field. II. MMFF94 van der Waals and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem. 1996, 17, 520–552. [Google Scholar] [CrossRef]
- Halgren, T.A. MMFF VI. MMFF94s Option for Energy Minimization Studies. J. Comput. Chem. 1999, 20, 720–729. [Google Scholar] [CrossRef]
- Halgren, T.A.; Nachbar, R.B. Merck Molecular Force Field. IV. Conformational Energies and Geometries for MMFF94. J. Comput. Chem. 1996, 17, 587–615. [Google Scholar] [CrossRef]
- Halgren, T.A. Merck Molecular Force Field. V. Extension of MMFF94 Using Experimental Data, Additional Computational Data, and Empirical Rules. J. Comput. Chem. 1996, 17, 616–641. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Peverati, R.; Truhlar, D.G. Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics. Phys. Chem. Chem. Phys. 2012, 14, 16187. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Martínez-Araya, J.I. Why are the Local Hyper-Softness and the Local Softness more Appropriate Local Reactivity Descriptors than the Dual Descriptor and the Fukui Function, Respectively? J. Math. Chem. 2023, 62, 461–475. [Google Scholar] [CrossRef]
- Gázquez, J.; Cedillo, A.; Vela, A. Electrodonating and Electroaccepting Powers. J. Phys. Chem. A 2007, 111, 1966–1970. [Google Scholar] [CrossRef]
- Chattaraj, P.; Chakraborty, A.; Giri, S. Net Electrophilicity. J. Phys. Chem. A 2009, 113, 10068–10074. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, G.; Tognetti, V.; Joubert, L. Electrophilicity Indices and Halogen Bonds: Some New Alternatives to the Molecular Electrostatic Potential. J. Phys. Chem. A 2020, 124, 2090–2101. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2011, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Lu, T. A Comprehensive Electron Wavefunction Analysis Toolbox for Chemists, Multiwfn. J. Chem. Phys. 2024, 161. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Realization of Conceptual Density Functional Theory and Information-Theoretic Approach in Multiwfn Program. In Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory; John Wiley & Sons: Hoboken, NJ, USA, 2022; Volume 2, pp. 631–647. [Google Scholar] [CrossRef]
- Figueredo, S.; Páez, M.; Torres, F. The Electrophilic Descriptor. Comput. Theor. Chem. 2019, 1157, 34–39. [Google Scholar] [CrossRef]
- Figueredo, S.F.; Quintero, M.A. Electrophilic Descriptor from Third-order Taylor Expansion: The Role of Hyperhardness. Int. J. Quantum Chem. 2024, 124. [Google Scholar] [CrossRef]
- Glossman-Mitnik, D. (Ed.) Density Functional Theory—Recent Advances, New Perspectives and Applications; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Srebrenik, S.; Weinstein, H.; Pauncz, R. Analytical Calculation of Atomic and Molecular Electrostatic Potentials from the Poisson Equation. Chem. Phys. Lett. 1973, 20, 419–423. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. The Fundamental Nature and Role of the Electrostatic Potential in Atoms and Molecules. In Theoretical Chemistry Accounts: Theory, Computation, and Modeling (Theoretica Chimica Acta); Springer: Berlin/Heidelberg, Germany, 2002; Volume 108, pp. 134–142. [Google Scholar] [CrossRef]
- Politzer, P. Atomic and Molecular Energies as Functionals of the Electrostatic Potential. Theor. Chem. Accounts 2004, 111, 395–399. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The Electrostatic Potential: An Overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Electrostatic Potentials at the Nuclei of Atoms and Molecules. Theor. Chem. Accounts 2021, 140, 7. [Google Scholar] [CrossRef]
- Morell, C.; Grand, A.; Toro-Labbé, A. New Dual Descriptor for Chemical Reactivity. J. Phys. Chem. A 2005, 109, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Morell, C.; Grand, A.; Toro-Labbé, A. Theoretical Support for Using the Δf(r) Descriptor. Chem. Phys. Lett. 2006, 425, 342–346. [Google Scholar] [CrossRef]
- Cárdenas, C.; Rabi, N.; Ayers, P.W.; Morell, C.; Jaramillo, P.; Fuentealba, P. Chemical Reactivity Descriptors for Ambiphilic Reagents: Dual Descriptor, Local Hypersoftness, and Electrostatic Potential. J. Phys. Chem. A 2009, 113, 8660–8667. [Google Scholar] [CrossRef]
- Sandoval-Yañez, C.; Mascayano, C.; Martínez-Araya, J.I. A Theoretical Assessment of Antioxidant Capacity of Flavonoids by Means of Local Hyper–Softness. Arab. J. Chem. 2018, 11, 554–563. [Google Scholar] [CrossRef]
- Frau, J.; Hernández-Haro, N.; Glossman-Mitnik, D. Computational Prediction of the pKas of Small Peptides through Conceptual DFT Descriptors. Chem. Phys. Lett. 2017, 671, 138–141. [Google Scholar] [CrossRef]
- Halabi Diaz, A.; Duque-Noreña, M.; Chamorro, E. Unveiling an Electronic LogP Analogue within the Conceptual Density Functional Theory Framework. Chem. Phys. 2024, 584, 112346. [Google Scholar] [CrossRef]

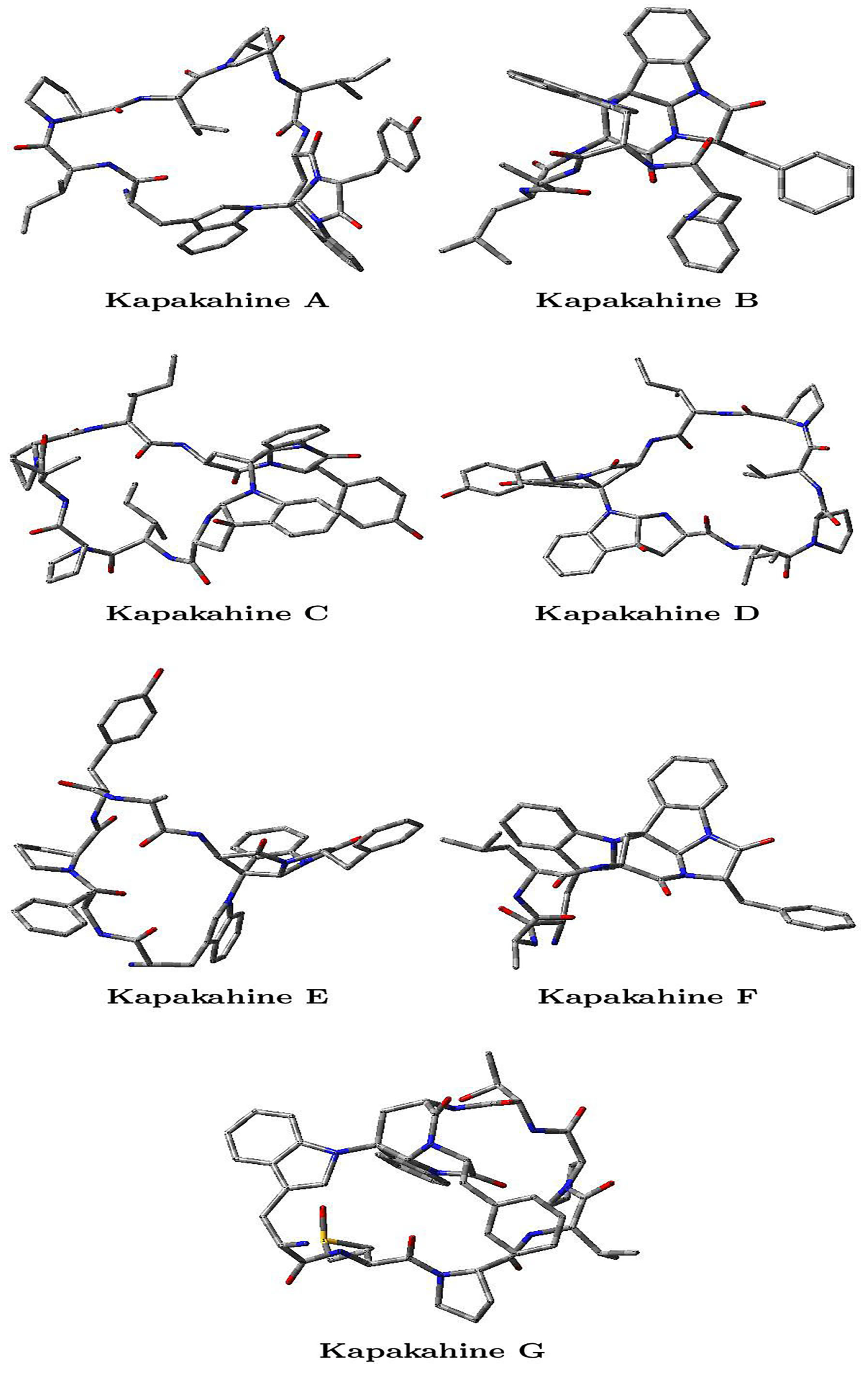

| Molecule | HOMO | LUMO | SOMO | H-L Gap | |||||
|---|---|---|---|---|---|---|---|---|---|
| Kapakahine A | −5.781 | −1.209 | −1.224 | 4.573 | 0.031 | 0.009 | 0.032 | 0.016 | 0.035 |
| Kapakahine B | −5.859 | −1.258 | −1.276 | 4.601 | 0.041 | 0.009 | 0.042 | 0.019 | 0.046 |
| Kapakahine C | −6.212 | −1.179 | −1.189 | 5.033 | 0.002 | 0.005 | 0.005 | 0.011 | 0.012 |
| Kapakahine D | −5.650 | −1.183 | −1.194 | 4.466 | 0.027 | 0.003 | 0.028 | 0.010 | 0.030 |
| Kapakahine E | −5.672 | −1.108 | −1.121 | 4.564 | 0.037 | 0.008 | 0.038 | 0.013 | 0.040 |
| Kapakahine F | −5.772 | −1.107 | −1.127 | 4.666 | 0.035 | 0.011 | 0.037 | 0.021 | 0.042 |
| Kapakahine G | −5.850 | −1.327 | −1.347 | 4.523 | 0.034 | 0.011 | 0.036 | 0.020 | 0.041 |
| Molecule | I1 | I2 | A1 | A2 |
|---|---|---|---|---|
| Kapakahine A | 5.812 | 6.390 | 1.218 | 0.935 |
| Kapakahine B | 5.900 | 6.609 | 1.267 | 0.914 |
| Kapakahine C | 6.214 | 6.424 | 1.183 | 0.608 |
| Kapakahine D | 5.622 | 6.369 | 1.187 | 0.533 |
| Kapakahine E | 5.709 | 6.371 | 1.115 | 0.773 |
| Kapakahine F | 5.807 | 6.452 | 1.118 | 0.875 |
| Kapakahine G | 5.884 | 6.456 | 1.338 | 0.811 |
| Molecule | S | N | ED | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kapakahine A | 3.495 | 4.573 | 1.336 | 0.147 | 0.219 | 3.011 | 4.705 | 1.210 | 5.914 | 1.400 | 3.270 |
| Kapakahine B | 3.558 | 4.601 | 1.376 | 0.178 | 0.217 | 2.934 | 4.818 | 1.260 | 6.079 | 1.437 | 2.872 |
| Kapakahine C | 3.695 | 5.033 | 1.356 | 0.183 | 0.199 | 2.581 | 4.875 | 1.180 | 6.055 | 1.439 | 7.466 |
| Kapakahine D | 3.417 | 4.466 | 1.307 | 0.047 | 0.224 | 3.143 | 4.601 | 1.184 | 5.785 | 1.364 | 2.538 |
| Kapakahine E | 3.390 | 4.564 | 1.259 | 0.160 | 0.219 | 3.121 | 4.498 | 1.108 | 5.605 | 1.346 | 2.871 |
| Kapakahine F | 3.439 | 4.666 | 1.268 | 0.201 | 0.214 | 3.020 | 4.546 | 1.107 | 5.654 | 1.362 | 3.018 |
| Kapakahine G | 3.588 | 4.523 | 1.423 | 0.023 | 0.221 | 2.943 | 4.923 | 1.335 | 6.258 | 1.458 | 3.354 |
| Molecule | pKa | LogP |
|---|---|---|
| Kapakahine A | 12.53 | 2.94 |
| Kapakahine B | 12.50 | 2.59 |
| Kapakahine C | 12.15 | 3.65 |
| Kapakahine D | 12.62 | 2.52 |
| Kapakahine E | 12.53 | 2.25 |
| Kapakahine F | 12.45 | 2.58 |
| Kapakahine G | 12.57 | 2.75 |
| Property | Model Name | Kapakahines | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | ||
| P-glycoprotein Substrate | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Absorption | P-glycoprotein I Inhibitor | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| P-glycoprotein II Inhibitor | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Distribution | BBB Permeability | −1.090 | −0.819 | −1.032 | −1.032 | −0.918 | −0.626 | −1.106 |
| CNS Permeability | −3.644 | −3.403 | −3.940 | −3.940 | −3.606 | −2.599 | −4.315 | |
| CYP2D6 Substrate | No | No | No | No | No | No | No | |
| CYP3A4 Substrate | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| CYP1A2 Inhibitor | No | No | No | No | No | No | No | |
| Metabolism | CYP2C19 Inhibitor | No | No | No | No | No | No | No |
| CYP2C9 Inhibitor | No | No | No | No | No | No | No | |
| CYP2D6 Inhibitor | No | No | No | No | No | No | No | |
| CYP3A4 Inhibitor | Yes | No | Yes | Yes | No | No | Yes | |
| Excretion | Total Clearance | −1.103 | −0.127 | −0.994 | −0.994 | −0.804 | 0.079 | −1.101 |
| Renal OCT2 Substrate | No | No | No | No | No | No | No | |
| AMES Toxicity | No | No | No | No | Yes | No | No | |
| hERG I Inhibitor | No | No | No | No | No | No | No | |
| Toxicity | hERG II Inhibitor | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Hepatotoxicity | Yes | Yes | Yes | Yes | Yes | Yes | Yes | |
| Skin Sensitisation | No | No | No | No | No | No | No | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores-Holguín, N.; Frau, J.; Glossman-Mitnik, D. Exploring the Chemical and Pharmaceutical Potential of Kapakahines A–G Using Conceptual Density Functional Theory-Based Computational Peptidology. Computation 2025, 13, 111. https://doi.org/10.3390/computation13050111
Flores-Holguín N, Frau J, Glossman-Mitnik D. Exploring the Chemical and Pharmaceutical Potential of Kapakahines A–G Using Conceptual Density Functional Theory-Based Computational Peptidology. Computation. 2025; 13(5):111. https://doi.org/10.3390/computation13050111
Chicago/Turabian StyleFlores-Holguín, Norma, Juan Frau, and Daniel Glossman-Mitnik. 2025. "Exploring the Chemical and Pharmaceutical Potential of Kapakahines A–G Using Conceptual Density Functional Theory-Based Computational Peptidology" Computation 13, no. 5: 111. https://doi.org/10.3390/computation13050111
APA StyleFlores-Holguín, N., Frau, J., & Glossman-Mitnik, D. (2025). Exploring the Chemical and Pharmaceutical Potential of Kapakahines A–G Using Conceptual Density Functional Theory-Based Computational Peptidology. Computation, 13(5), 111. https://doi.org/10.3390/computation13050111