A Novel Methodology for Scrutinizing Periodic Solutions of Some Physical Highly Nonlinear Oscillators
Abstract
1. Introduction
- The suggested method is suitable for obtaining an accurate solution for extremely nonlinear oscillators.
- The proposed approach is less complicated and requires less processing and time than the classical perturbation techniques.
- The advantage of the NPA lies in its simplicity compared to other perturbation methods, and there is strong agreement with the numerical solutions.
- The disadvantage of the present technique is that as the amplitude values increase, the solution´s shape is farther away from the numerical solution’s shape
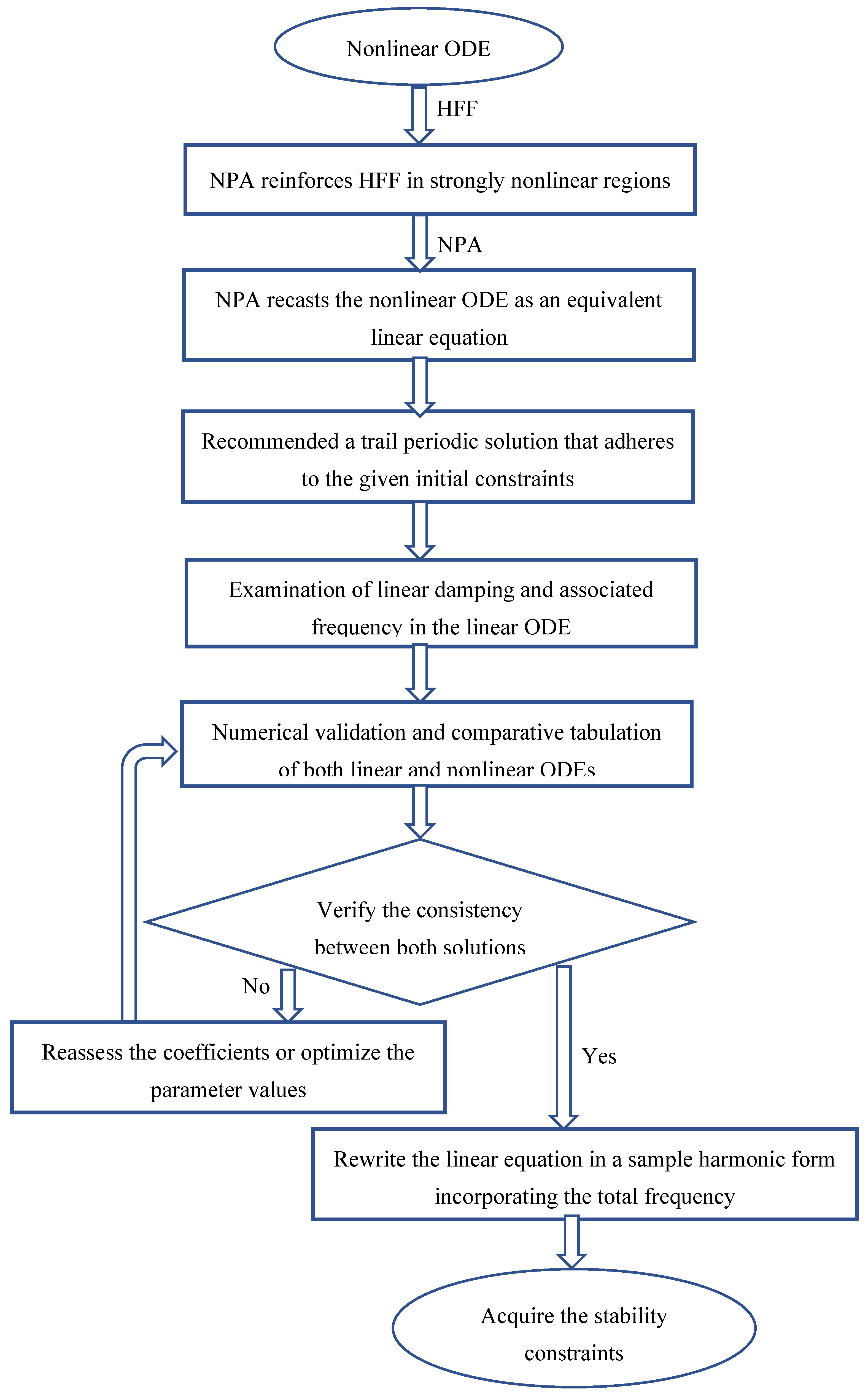
2. Description of the NPA
- Equivalent frequency formula:
- Equivalent damping formula:
- Non-secular part:
3. Applications
3.1. Example 1
3.2. Example 2


3.3. Example 3
3.4. Example 4
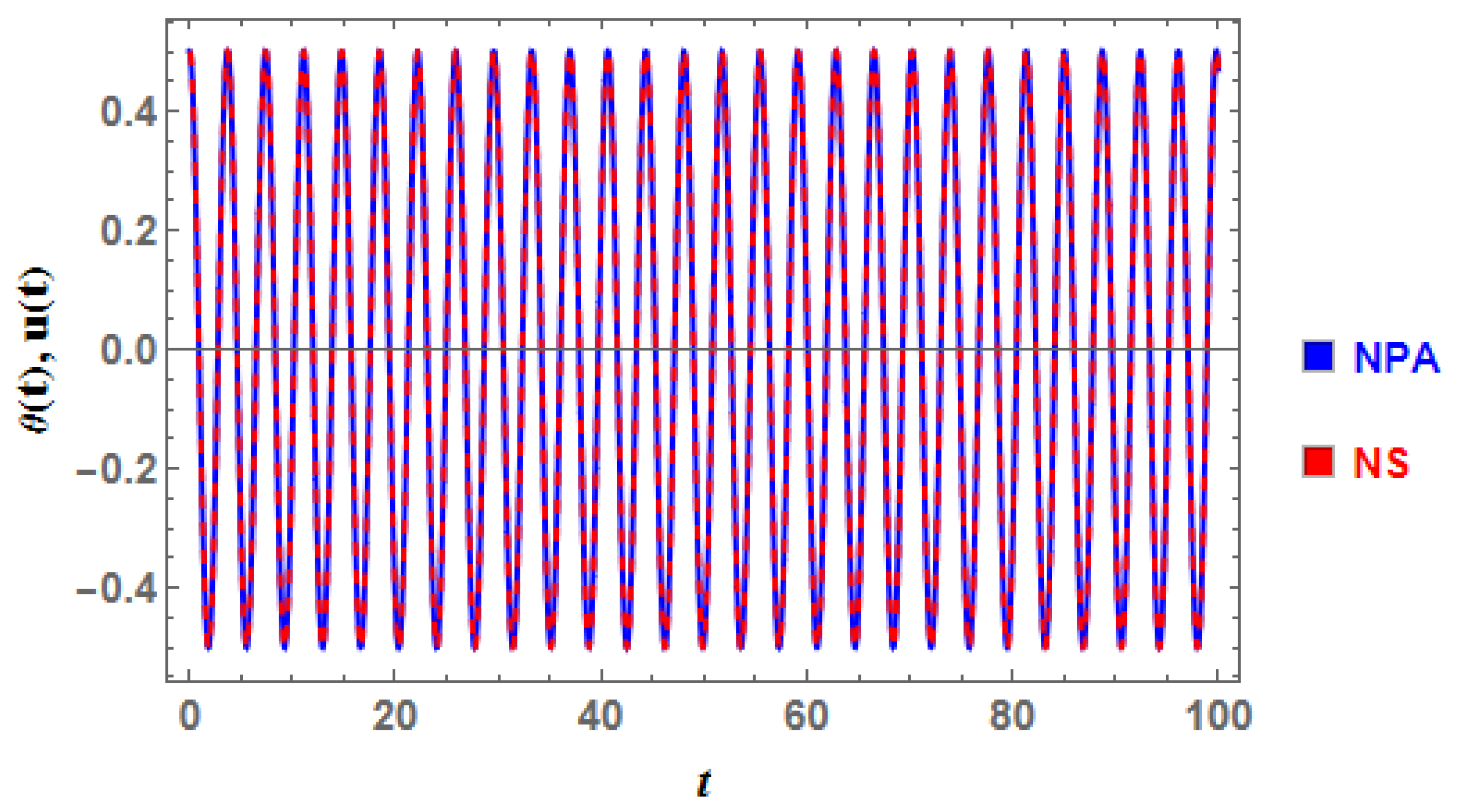


3.5. Example 5
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval Past, J.C. Present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Cao, M.S.; Sha, G.G.; Gao, Y.F.; Ostachowicz, W. Structural damage identification using damping: A compendium of uses and features. Smart Mater. Struct. 2017, 26, 043001. [Google Scholar] [CrossRef]
- Blackwell, C.; Palazotto, A.; George, T.J.; Cross, C.J. The evaluation of the damping characteristics of a hard coating on titanium. Shock. Vib. 2007, 14, 37–51. [Google Scholar] [CrossRef]
- Liang, J.W.; Feeny, B.F. Identifying Coulomb and viscous friction in forced dual-damped oscillators. J. Vib. Acoust. 2004, 126, 118–125. [Google Scholar] [CrossRef]
- Mevada, H.; Patel, D. Experimental determination of structural damping of different materials. Process Eng. 2016, 144, 110–115. [Google Scholar] [CrossRef]
- Zhang, X.; Du, X.; Brownjohn, J. Frequency modulated empirical mode decomposition method for the identification of instantaneous modal parameters of aero elastic systems. J. Wind Eng. Ind. Aerodyn. 2012, 101, 43–52. [Google Scholar] [CrossRef]
- Kulkarni, P.; Bhattacharjee, A.; Nanda, B.K. Study of damping in composite beams. Mater. Today Proc. 2018, 5, 7061–7067. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chintha, H.P. Identification and parameter estimation of cubic nonlinear damping using harmonic probing and Volterra series. Int. J. Non-Linear Mech. 2020, 125, 103518. [Google Scholar] [CrossRef]
- Dou, C.; Fan, J.; Li, C.; Cao, J.; Gao, M. On discontinuous dynamics of a class of friction-influenced oscillators with nonlinear damping under bilateral rigid constraints. Mech. Mach. Theory 2020, 147, 103750. [Google Scholar] [CrossRef]
- Barakat, A.A.; Weig, E.M.; Hagedorn, P. Non-trivial solutions and their stability in a two-degree-of-freedom Mathieu–Duffing system. Nonlinear Dyn. 2023, 111, 22119–22136. [Google Scholar] [CrossRef]
- Öcalan, Ö.; Özkan, U.M. Oscillations of dynamic equations on time scales with advanced arguments. Int. J. Dyn. Syst. Differ. Equ. 2016, 6, 275–284. [Google Scholar] [CrossRef]
- Biçer, E.; Tunç, C. On the asymptotic stability behaviours of solutions of non-linear differential equations with multiple variable advanced arguments. J. Appl. Nonlinear Dyn. 2019, 8, 239–249. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abul-Ez, M.; Zayed, M.; Farea, N.M. Analytical accurate solutions of nonlinear oscillator systems via coupled homotopy-variational approach. Alex. Eng. J. 2022, 61, 5051–5058. [Google Scholar] [CrossRef]
- Kopmaz, O. Free vibrations of a mass grounded by linear and non-linear springs in series. J. Sound Vib. 2006, 289, 689–710. [Google Scholar]
- Manimegalai, K.; Sagar Zephania, C.F.; Bera, P.K.; Bera, P.; Das, S.K.; Sil, T. Study of strongly nonlinear oscillators using the Aboodh transform and the homotopy perturbation method. Eur. Phys. J. Plus 2019, 134, 462. [Google Scholar] [CrossRef]
- Wang, J. The extended Rayleigh-Ritz method for an analysis of nonlinear vibrations. Mech. Adv. Mater. Struct. 2022, 29, 3281–3284. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Wang, J. Forced vibration analysis of multi-degree-of-freedom nonlinear systems with the extended Galerkin method. Mech. Adv. Mater. Struct. 2023, 30, 794–802. [Google Scholar] [CrossRef]
- Abu-As’ad, A.; Asad, J. Power series approach to nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2024, 43, 220–238. [Google Scholar] [CrossRef]
- Shou, D.-H. The homotopy perturbation method for nonlinear oscillators. Comput. Math. Appl. 2009, 58, 2456–2459. [Google Scholar] [CrossRef]
- Hermann, M.; Saravi, M.; Khah, H.E. Analytical study of nonlinear oscillatory systems using the Hamiltonian approach technique. J. Theor. Appl. Phys. 2014, 8, 133. [Google Scholar] [CrossRef]
- Ismail, G.M. An analytical coupled homotopy-variational approach for solving strongly nonlinear differential equation. J. Egypt. Math. Soc. 2017, 25, 434–437. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abu-Zinadah, H. Analytic approximations to non-linear third order jerk equations via modified global error minimization method. J. King Saud Univ.-Sci. 2021, 33, 101219. [Google Scholar] [CrossRef]
- He, J.-H. Comment on He’s frequency formulation for nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul. 2008, 29, 19–22. [Google Scholar] [CrossRef]
- He, J.-H. An approximate amplitude-frequency relationship for a nonlinear oscillator with discontinuity. Nonlinear Sci. Lett. A 2016, 7, 77–85. [Google Scholar]
- He, J.-H. Amplitude-frequency relationship for conservative nonlinear oscillators with odd nonlinearities. Int. J. Appl. Comput. Math. 2017, 3, 1557–1560. [Google Scholar] [CrossRef]
- Ren, Z.-F. He’s frequency-amplitude formulation for nonlinear oscillators. Int. J. Mod. Phys. B 2011, 25, 2379–2382. [Google Scholar] [CrossRef]
- Ren, Z.-F. Theoretical basis of He’s frequency-amplitude formulation for nonlinear oscillators. Nonlinear Sci. Lett. A 2018, 9, 86–90. [Google Scholar]
- Garcıa, A. An amplitude-period formula for a second order nonlinear oscillator. Nonlinear Sci. Lett. A 2017, 8, 340–347. [Google Scholar]
- Antola, R.S. Remarks on an approximate formula for the period of conservative oscillations in nonlinear second order ordinary differential equations. Nonlinear Sci. Lett. A 2017, 8, 348–351. [Google Scholar]
- Younesian, D.; Askari, H.; Saadatnia, Z.; Yazdi, M.K. Frequency analysis of strongly nonlinear generalized Duffing oscillators using He’s frequency-amplitude formulation and He’s energy balance method. Comput. Math. Appl. 2010, 59, 3222–3228. [Google Scholar]
- Ren, Z.-F.; Hu, G.-F. He’s frequency-amplitude formulation with average residuals for nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1050–1059. [Google Scholar] [CrossRef]
- Ismail, G.M.; Moatimid, G.M.; Yamani, M.I. Periodic solutions of strongly nonlinear oscillators using He’s frequency formulation. Eur. J. Pure Appl. Math. 2024, 17, 2154–2171. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S. Dynamical system of a time-delayed ϕ6-Van der Pole oscillator: A non-perturbative approach. Sci. Rep. 2023, 13, 11942. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S.; Ellabban, Y.Y. A novel methodology for a time-delayed controller to prevent nonlinear system oscillations. J. Low Freq. Noise Vib. Act. Control 2024, 43, 525–542. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S.; Galal, A.A. Studying highly nonlinear oscillators using the non-perturbative methodology. Sci. Rep. 2023, 13, 20288. [Google Scholar] [CrossRef] [PubMed]
- Moatimid, G.M.; El-Sayed, A.T.; Salman, H.F. Different controllers for suppressing oscillations of a hybrid oscillator via non-perturbative analysis. Sci. Rep. 2024, 14, 307. [Google Scholar] [CrossRef]
- Alluhydan, K.; Moatimid, G.M.; Amer, T.S. The non-perturbative approach in examining the motion of a simple pendulum associated with a rolling wheel with a time-delay. Eur. J. Pure Appl. Math. 2024, 17, 3185–3208. [Google Scholar] [CrossRef]
- Alluhydan, K.; Moatimid, G.M.; Amer, T.S.; Galal, A. A novel inspection of a time-delayed rolling of a rigid rod. Eur. J. Pure Appl. Math. 2024, 17, 2878–2895. [Google Scholar]
- Alluhydan, K.; Moatimid, G.M.; Amer, T.S.; Galal, A.A. Inspection of a time-delayed excited damping Duffing oscillator. Axioms 2024, 13, 416. [Google Scholar] [CrossRef]
- Ismail, G.M.; Moatimid, G.M.; Alraddadi, I.; Stylianos, V.; Kontomaris, S.V. Scrutinizing highly nonlinear oscillators using He’s frequency formula. Sound Vib. 2025, 59, 2358. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S.; Galal, A.A. Inspection of some extremely nonlinear oscillators using an inventive approach. J. Vib. Eng. Technol. 2024, 12, 1211–1221. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Mohamed, M.A.A.; Elagamy, K.H. Insightful examination of some nonlinear classification linked with Mathieu oscillators. J. Vib. Eng. Technol. 2025, 13, 173. [Google Scholar] [CrossRef]
- Alanazy, A.; Moatimid, G.M.; Amer, T.S.; Mohamed, M.A.A.; Abohamer, M.K. A novel procedure in scrutinizing a cantilever beam with tip mass: Analytic and bifurcation. Axioms 2025, 14, 16. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Mohamed, M.A.A.; Elagamy, K.H. An innovative approach in inspecting a damped Mathieu cubic–quintic Duffing oscillator. J. Vib. Eng. Technol. 2024, 12 (Suppl. S2), S1831–S1848. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Mohamed, M.Y. Nonlinear electro-rheological instability of two moving cylindrical fluids: An innovative approach. Phys. Fluids 2024, 36. [Google Scholar] [CrossRef]
- Alanazy, A.; Moatimid, G.M.; Mohamed, M.A.A. Innovative methodology in scrutinizing nonlinear rolling ship in longitudinal waves. Ocean Eng. 2025, 327, 120924. [Google Scholar] [CrossRef]
- Moatimid, G.M.; El-Bassiouny, A.F.; Mohamed, M.A.A. Novel approach in inspecting nonlinear rolling ship in longitudinal waves. Ocean Eng. 2025, 327, 120975. [Google Scholar] [CrossRef]
- Caughey, T.K. Equivalent linearization techniques. J. Acoust. Soc. Am. 1963, 35, 1706–1711. [Google Scholar] [CrossRef]
- Spanos, P.-T.D.; Iwan, W.D. On the existence and uniqueness of solutions generated by equivalent linearization. Int. J. Non-Linear Mech. 1979, 13, 71–78. [Google Scholar] [CrossRef]
- He, J.-H. Special functions for solving nonlinear differential equations. Int. J. Appl. Comput. Math. 2021, 7, 84. [Google Scholar] [CrossRef]
- Farea, N.M.; Ismail, G.M. Analytical solution for strongly nonlinear vibration of a stringer shell. J. Low Freq. Noise Vib. Act. Control. 2025, 44, 81–87. [Google Scholar] [CrossRef]
- Molla, M.H.U.; Razzak, M.A.; Alam, M.S. Harmonic balance method for solving a large-amplitude oscillation of a conservative system with inertia and static non-linearity. Results Phys. 2016, 6, 238–242. [Google Scholar] [CrossRef]
- Hamdan, M.N.; Shabaneh, H. On the large amplitude free vibrations of restrained uniform beam carring an intermediate lumped mass. J. Sound Vib. 1997, 199, 711–835. [Google Scholar] [CrossRef]
- Sfahani, M.G.; Barari, A.; Ganji, S.S.; Domairry, G.; Rokni, H.B. Dynamic response of a beam carrying a lumped mass along its span. Int. J. Adv. Manuf. Technol. 2013, 64, 1435–1443. [Google Scholar] [CrossRef]
- Cveticanin, L.; Ismail, G.M. Higher-order approximate periodic solution for the oscillator with strong nonlinearity of polynomial type. Eur. Phys. J. Plus 2019, 134, 266. [Google Scholar] [CrossRef]
- Ismail, G.M.; Hosen, M.A.; Mohammadian, M.; El-Moshneb, M.M.; Bayat, M. Nonlinear Vibration of Electrostatically Actuated Microbeam. Mathematics 2022, 10, 4762. [Google Scholar] [CrossRef]
- Bayat, M.; Bayat, M.; Pakar, I. Nonlinear vibration of an electrostatically actuated microbeam. Lat. Am. J. Solids Struct. 2014, 11, 534–544. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, J.; Wan, L. Application of the energy balance method to a nonlinear oscillator arising in the microelectromechanical system (MEMS). Curr. Appl. Phys. 2011, 11, 482–485. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Ghalambaz, M.; Edalatifar, M. Nonlinear oscillation of nanoelectro-mechanical resonators using energy balance method: Considering the size effect and the van der Waals force. Appl. Nanosci. 2016, 6, 309–317. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abul-Ez, M.; Farea, N.M.; Saad, N. Analytical approximations to nonlinear oscillation of nanoelectro-mechanical resonators. Eur. Phys. J. Plus 2019, 134, 47. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S. Analytical approximate solutions of a magnetic spherical pendulum: Stability analysis. J. Vib. Eng. Technol. 2023, 11, 2155–2165. [Google Scholar] [CrossRef]
- Amabili, M. Comparison of shell theories for large-amplitude vibrations of circular cylindrical shells: Lagrangian approach. J. Sound Vib. 2003, 264, 1091–1125. [Google Scholar] [CrossRef]
- Dong, S.-H. A new approach to the relativistic Schrödinger equation with central potential: Ansatz method. Int. J. Theor. Phys. 2001, 40, 559–567. [Google Scholar] [CrossRef]



| Nonlinear ODE | Linear ODE | Absolute Error | |
|---|---|---|---|
| 0 | 0.5 | 0.5 | 0 |
| 5 | |||
| 10 | |||
| 15 | |||
| 20 | |||
| 25 | |||
| 30 | |||
| 35 | |||
| 40 | |||
| 45 | |||
| 50 |
| Nonlinear ODE | Linear ODE | Absolute Error | |
|---|---|---|---|
| 0 | 0.1 | 0.1 | 0 |
| 5 | 0.0284085 | 0.0283927 | |
| 10 | −0.0838879 | −0.0838771 | |
| 15 | −0.0760437 | −0.0760227 | |
| 20 | 0.0407175 | 0.0407073 | |
| 25 | 0.099141 | 0.0991386 | |
| 30 | 0.0156095 | 0.0155889 | |
| 35 | −0.090289 | −0.0902865 | |
| 40 | −0.0668907 | −0.0668586 | |
| 45 | 0.0523244 | 0.0523207 | |
| 50 | 0.0965783 | 0.0965692 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, G.M.; Moatimid, G.M.; Kontomaris, S.V.; Cveticanin, L. A Novel Methodology for Scrutinizing Periodic Solutions of Some Physical Highly Nonlinear Oscillators. Computation 2025, 13, 105. https://doi.org/10.3390/computation13050105
Ismail GM, Moatimid GM, Kontomaris SV, Cveticanin L. A Novel Methodology for Scrutinizing Periodic Solutions of Some Physical Highly Nonlinear Oscillators. Computation. 2025; 13(5):105. https://doi.org/10.3390/computation13050105
Chicago/Turabian StyleIsmail, Gamal M., Galal M. Moatimid, Stylianos V. Kontomaris, and Livija Cveticanin. 2025. "A Novel Methodology for Scrutinizing Periodic Solutions of Some Physical Highly Nonlinear Oscillators" Computation 13, no. 5: 105. https://doi.org/10.3390/computation13050105
APA StyleIsmail, G. M., Moatimid, G. M., Kontomaris, S. V., & Cveticanin, L. (2025). A Novel Methodology for Scrutinizing Periodic Solutions of Some Physical Highly Nonlinear Oscillators. Computation, 13(5), 105. https://doi.org/10.3390/computation13050105






