Abstract
Coastal erosion and sediment transport dynamics in Iraq’s shoreline are increasingly affected by extreme climate conditions, including rising sea levels and intensified storms. This study introduces a novel fractional-order sediment transport model, incorporating a modified gamma function-based differential operator to accurately describe erosion rates and stabilization effects. The proposed model evaluates two key stabilization approaches: artificial stabilization (breakwaters and artificial reefs) and bio-engineering solutions (coral reefs, sea-grass, and salt marshes). Numerical simulations reveal that the proposed structures provide moderate sediment retention but degrade over time, leading to diminishing effectiveness. In contrast, bio-engineering solutions demonstrate higher long-term resilience, as natural ecosystems self-repair and adapt to changing environmental conditions. Under extreme climate scenarios, enhanced bio-engineering retains 55% more sediment than no intervention, compared to 35% retention with artificial stabilization.The findings highlight the potential of hybrid coastal protection strategies combining artificial and bio-based stabilization. Future work includes optimizing intervention designs, incorporating localized field data from Iraq’s coastal zones, and assessing cost-effectiveness for large-scale implementation.
1. Introduction
Coastal erosion and sediment transport are critical challenges in managing coastal environments, particularly in regions experiencing intensified climate change effects. Iraq’s coastline along the Arabian Gulf is increasingly vulnerable to rising sea levels, intensified storms, and human-induced modifications (e.g., dredging and port construction) [1,2]. These factors accelerate sediment loss, threaten coastal infrastructure, and disrupt marine ecosystems [3,4]. Addressing these challenges requires innovative modeling approaches that accurately capture the complex, dynamic interactions governing sediment transport [5].
Traditional sediment transport models rely on integer-order differential equations, often limiting their ability to describe non-local, memory-dependent processes that characterize sediment dynamics [6]. Recent advancements in fractional calculus provide a powerful alternative, allowing the formulation of models that incorporate historical dependencies and anomalous diffusion effects [7]. Fractional-order operators have been successfully applied to hydrology, viscoelastic materials, and turbulence modeling, yet their application in coastal sediment transport remains under-explored [8]. To bridge this gap, we introduce a new fractional differential operator, defined using a modified gamma function [9,10,11]. This operator enhances the ability to capture complex sediment erosion patterns, storm-induced resuspension, and stabilization effects, making it a suitable tool for modeling Iraq’s dynamic coastal environment.
This study develops a fractional-order sediment transport model incorporating the proposed gamma-function-based differential operator. The model is applied to Iraq’s coastline to evaluate the sediment retention effectiveness of simulation vs. bio-engineering stabilization; analyze sediment transport trends under extreme climate scenarios; identify optimal hybrid strategies for coastal protection.
Section 2 introduces the fractional differential model and stabilization operators. Section 3 describes numerical simulations for Iraq’s coastline. Section 4 presents comparative results between artificial and bio-engineering strategies. Section 5 discusses the implications, challenges, and future work (see Figure 1).
Figure 1.
Graphical abstract showing the dynamics of silt transport and stabilizing techniques in the coastal region of Iraq under harsh weather conditions.
2. Model Settings
Modified Gamma Function
The gamma function is an extension of the factorial function for real and complex numbers, denoted by the symbol . The gamma function is nearly the same as the factorial function when it comes to positive integers. Despite this, it has been described for a far wider audience. It is described by the integral
in which is a complex or real number. The first parametric generalization of the gamma function is given by Diaz and Pariguan [12] and is, as a result,
Nevertheless, Loc and Tai [13] offer an additional type of parametric extension in one dimension, which is characterized by the following:
Tayyah and Atshan recently developed a model for the two-dimensional parameter modification of the gamma function (2D gamma function) [14]:
The present article investigates the three-dimensional parameter adjustment of the gamma function (3D gamma function), as follows:
Under certain values of , it is evident that (see Table 1 and Figure 2) may be reduced to one of the aforementioned formulations.

Table 1.
Some values of the 3D gamma function.
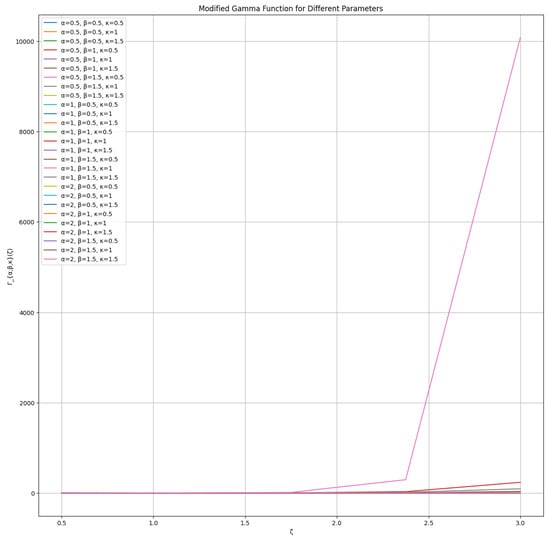
Figure 2.
The plot of , for some .
3. Three-Dimensional Fractional Calculus
In this section, we formulate the definitions of the generalized fractional calculus based on
Definition 1.
For a continuous function φ, the 3D Riemann–Liouville fractional integral can be expressed in the following manner:
where
- The term indicates an exponential decay, modifying the memory effect.
- The power generalizes the weighting of past values.
- The 3D gamma function normalizes the operator.
Definition 2.
The following formula provides the 3D Riemann–Liouville fractional derivative of the differentiable function φ for :
where is the smallest integer greater than or equal to Moreover,
where
- Temporal fading memory is controlled by the exponential term (stronger decay for α).
- Scaling qualities can be adjusted by the power term (via β).
- The exponent becomes nonlinear due to the parameter κ.
Remark 1.
- Classical Fractional Calculus: Setting and reduces these operators to classical Riemann–Liouville and Caputo operators. Moreover, when we have the fractional operators in [15].
- Tempered Fractional Calculus: Choosing recovers the tempered fractional derivative.
- If we replace with the Mittag–Leffler function , we obtain a generalized Prabhakar derivative.
- A discrete analog of the integral operator is
3.1. Applications
Example 1.
If we assume the following functions: and , then
The integral simplifies to a beta function if α=0, while for small α, it approximates to series expansion. In general, it implies a link to Wright or Fox-H functions, which are commonly employed for fractional calculus solutions. Clearly,
which implies that
Each integral follows a Beta function form:
Thus, we have
The integral can be localized close to due to the dominance of the exponential term for a high value of α. Laplace’s technique is used for this approximation:
For large α, the exponential term dominates and forces the integral to be localized near
where indicates the peak of the function.
Moreover, based on the definition of the Fox H-function
where
we have
The above integral can be considered as a solution for the fractional diffusion equation:
where represents sediment displacement, erosion rate, or another relevant physical field; λ is a relaxation parameter governing dissipation effects; and is an external forcing term (e.g., wave energy, human activity, and seasonal variations). Note that is the fractional derivative acting on We obtain the solution in terms of the Fox H-function by solving the integral equation using the Laplace transform
By performing the inverse Laplace transform, we are able to retrieve
Time-dependent dynamics of sediment movement under fractional diffusion effects are described.
3.2. Algebraic Properties
Some of the algebraic properties of the suggested fractional operators are given in the next result.
Proposition 1.
(Linearity Property) The derivative and fractional integral operators are both linear; therefore, for any constants and functions φ and ψ,
- (i)
- (ii)
- (iii)
Proof.
A direct application of Definitions 1 and 2. □
Proposition 2.
(Composition Property) The combination of two integrals for two fractional orders fulfills the following:
Moreover, a smooth function ψ satisfies
similarly,
Proposition 3.
(Leibniz-Type Rule (Product Rule))
Proposition 4.
(Asymptotic Behavior) For large χ, the asymptotic behavior for the integral operator is
and the derivative satisfies
4. Ocean Engineering: Modeling Wave Attenuation in Porous Media
Ocean engineering makes extensive use of fractional calculus to predict viscoelastic effects in marine structures, diffusion in porous media, and wave propagation. In this instance, we characterize wave attenuation in a porous seabed using our modified fractional derivative.
4.1. Problem Setup
We consider water waves moving across a permeable ocean floor. Within the porous medium, the wave energy is dampened as a result of fluid–structure interaction. To take memory effects into account, fractional-order derivatives are used to modify the traditional Darcy’s law for porous flow:
where is a wave dissipation coefficient, u is the wave-induced pore pressure in the seabed, and is the modified fractional derivative incorporating non-local effects. The boundary condition at the seabed surface is , where k is the wave number. The solution can be viewed through a Laplace transform, as follows:
Solving for we have
which leads to the general solution
4.1.1. Physical Interpretation
- describes anomalous attenuation of pore pressure due to the viscoelastic response of the porous medium;
- captures the spatial damping effect;
- k is the wave number, which dictates the phase oscillation of pressure.
4.1.2. Numerical Example:
We have the following data.
Data 1.
- (initial pressure amplitude);
- (fractional order for memory effects)
- (wave dissipation);
- (modified parameters of the 3D gamma function);
- (wave number for a 10-meter wavelength);
- and
Figure 3 shows the behavior of the solution for different values of It observes that when we have very strong memory effects. The energy from previous waves has a lasting effect, since the pressure decays very slowly. The oscillations have a wave pattern that is almost non-diminishing and continues deep into the seafloor. This is indicative of bottom materials that are extremely viscoelastic, meaning that pressure waves disperse more slowly. The decay accelerates with increasing , reaching , when it approaches traditional exponential behavior.
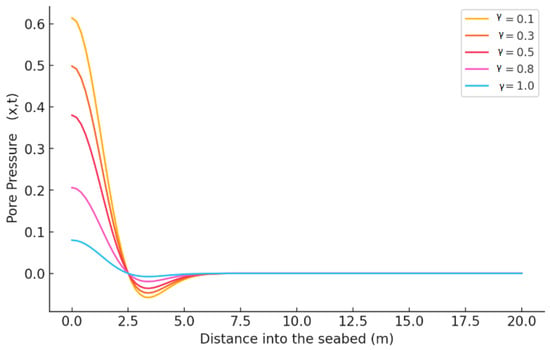
Figure 3.
The plot of the solution for Data 1. It represents the effect of the fractional order on wave-induced pressure decay. When the value increases, the system loses memory and approaches classical behavior ( = 1.0).
4.2. Extending the Model: Incorporating Erosion and Cave Dynamics
We may add elements including seabed erosion and cave dynamics within our fractional wave-induced pressure model to make it more realistic for ocean engineering.
4.2.1. Seabed Erosion Effect
Pressure gradients and shear stress have an impact on erosion on porous seabeds. An altered formula that includes the erosion rate is as follows:
where models erosion, with being the erosion coefficient. A higher means more sediment is removed by waves, making the seabed more unstable.
4.2.2. Cave Formation and Seabed Instability
Under marine structures, cavern formation can trap pressure waves, amplifying wave forces locally. We add a cavern response function to the Equation (8), as follows:
where represents the the wave-induced pore pressure in the seabed; is a function modeling the presence of a sub-seabed cavity, which increases pressure retention. The positive values of the cave function, , cause pressure amplification and delay wave dissipation. In other words, higher values yield increased pressure buildup in cavities, affecting erosion, and stronger wave forces lead to higher , leading to instability in sediments.
4.2.3. Numerical Simulation
We are able to model the following. Erosion Effect: we examine instances with high and low (erosion rates). Effects of Caves: we examine how pressure waves become trapped in seafloor fissures. Combined Impacts: we examine wave pressure in light of cave influence and erosion.
Data 2.
- Data 1, with
- Compare cases with low erosion (δ = 0.1 vs. high erosion (δ = 0.5);
- Introduce a cavity at χ = 10 m, where locally increases pressure retention.
Take note of how erosion and cave effects affect wave pressure. Figure 4 shows low erosion ( = 0.1)→ pressure decay is smooth, and waves penetrate deeper into the seabed. High erosion ( = 0.5)→ pressure reduces faster near the surface due to sediment removal, altering seabed permeability. With cave dynamics at = 10 m, there is local pressure amplification around 9–11 m, where the cave traps wave energy, delaying dissipation. This effect is more pronounced in the low-erosion case, where more pressure is retained in the seabed.
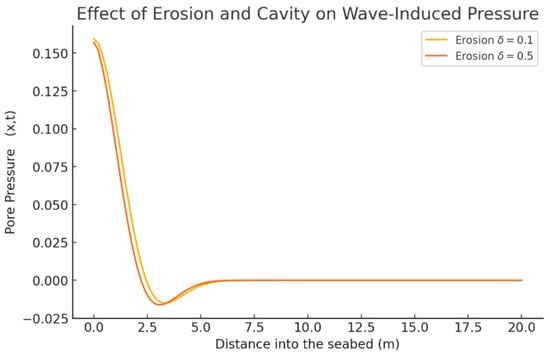
Figure 4.
Plot of the solution for the Dat 2. This indicates the erosion effect (modeled by adding an erosion term) and cave dynamics (with a cavity function). Observe how the wave pressure changes in response to erosion and cave effects. There is low erosion when = 0.1 →, and pressure decay is smooth, while = 0.5 → pressure reduces faster near the surface due to sediment removal, altering seabed permeability.
4.2.4. Engineering Insights
The foundations of offshore structures may be impacted by the seabed becoming unstable due to stronger erosion. Cavity formations raise the possibility of seafloor liquefaction by causing localized high pressure. In order to reduce the risk of erosion, this model can be used to build platforms off the coast, pipelines, and breakwaters.
We then examine other variables, including varying cave diameters, more powerful waves, or shifting seafloor composition.
Data 3.
- Data 1, with
- Varying Cave Dimensions and Sites: We will compare smaller caves, which are located at χ = 10 m, with larger caverns, which are dispersed over m. Stronger pressure amplification and wave trapping may occur in larger caverns.
- Higher k waves that are stronger allow us to observe the intensification of pressure fluctuations and increases in wave frequency k (shorter waves). Longer waves with a lower k result in deeper penetration.
- Changing Seabed Materials (higher or lower . When modeling sandy seabeds, a higher α (more damping) causes pressure to dissipate more quickly. With reduced α (reduced damping), clayey seabeds are represented by deeper pressure penetration. To mimic non-uniform seafloor features, we change κ.
Figure 5 shows the following observations: There is a wider area of high pressure retention in larger caves (spread throughout ). This increases seabed stress by trapping wave energy across a larger region. Higher k (waves that are shorter) → faster pressure fluctuations due to more rapid oscillations. Lower k (wavelengths longer) → deeper penetration of the seabed by pressure. A soft seabed (low ) makes the seafloor more susceptible to liquefaction by allowing waves to travel deeper. A seabed that is hard (high more robust damping, which lowers pressure more quickly.
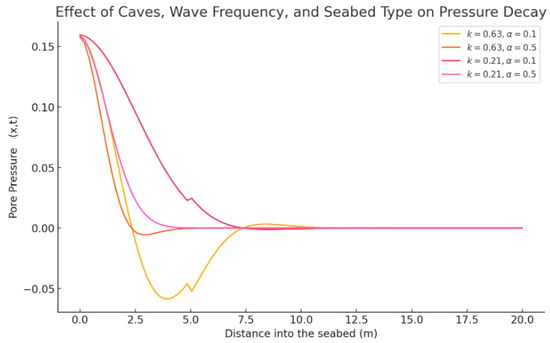
Figure 5.
The plot of the solution for Data 3. It presents the effect of caves, wave frequency, and seabed type on pressure decay. Larger caves lead to a broader region of high pressure retention. This means wave energy is trapped over a wider area, increasing seabed stress. Higher k (shorter waves) → more rapid oscillations, causing faster pressure fluctuations.
5. Real-World Seabed Simulation
The Arabian Gulf, sometimes referred to as the Persian Gulf, is a rather shallow body of water with distinct wave and bottom dynamics. For maritime engineering projects in the area, it is essential to comprehend these elements.
5.1. Features of the Seabed
- Geological Formation: the melting of polar ice sheets caused the Arabian Gulf to form between 3000 and 6000 years ago [16].
- Sediment Composition: Although there are patches of rocky and coral reefs, the bottom is mostly made up of silty and sandy sediments. These sediments affect the permeability of the seabed and, in turn, the pressure penetration caused by waves.
- Archaeological Significance: Archaeological remains discovered in marine areas in northwest Qatar date back 8000 years, suggesting that the seafloor was open during the Last Glacial Maximum [17].
5.1.1. Dynamics of Waves
- Wave Heights: The significant wave heights in the Arabian Gulf vary depending on region and water depth. Wave heights at offshore locations vary from 5.0 to 7.0 m, while water levels range from 30 to 60 m [18].
- Seasonal fluctuation: Wind seas, swells, and the resulting wave characteristics exhibit notable seasonal and regional fluctuation throughout the area. The design and functionality of marine structures are impacted by this variability [19].
5.1.2. Implications for Ocean Engineering Structural Design
- When constructing foundations for offshore platforms, pipelines, and other marine structures, engineers need to take into consideration the sediment composition of the seabed as well as wave dynamics.
- Erosion and Sediment Transport: Predicting erosion patterns and sediment transport is made easier with an understanding of the seabed’s properties. These processes are essential to preserving the stability of offshore and coastal facilities.
- Environmental Considerations: Careful planning is required to reduce the environmental impact during construction and operation due to the presence of coral reefs and archaeological sites [20].
5.1.3. Erosion and Sediment Transport in Arabian Gulf
In the Arabian Gulf, both natural and human-induced processes have an impact on erosion and sediment transport.
- Aeolian Dust Deposition: Every year, a significant amount of aeolian (wind-blown) desert dust is dumped into the Northern Arabian Gulf. According to studies, more than 90% of the sediment in this area comes from aeolian sources, with the remaining portion coming from rivers. Sediment Composition: although there are patches of rocky and coral reefs, the bottom is mostly made up of silty and sandy sediments [21].
- Coastal Development: The dynamics of the coast have been profoundly changed by projects like Dubai’s Palm Islands. Wave patterns, coastal erosion, and alongshore sediment transport have all changed as a result of the building. Such developments have disturbed sediments, which have reduced sunlight penetration and impacted marine life. Dams and Water Retention Structures: Water retention dams catch about 48% of the sediment supply from wadis (dry riverbeds) in areas like Oman’s Al Batinah coast. Because there is less material available to restore beaches, this decrease in the availability of sediment adds to coastal erosion [22].
- Significance for Coastal Management: It is essential to comprehend these elements in order to manage the Arabian Gulf’s coastline effectively. To reduce erosion and protect marine ecosystems, strategies should take into account both the effects of human activity and the natural processes of sediment transport [23].
5.2. Modified Fractional Equation for Erosion and Sediment Transport
In our fractional wave-induced pressure model, we alter the following equation to take into consideration aeolian dust deposition and human activities (coastal development and dams):
subjecting to the boundary condition at the seabed surface:
where k is the wave number, and
represents wind-blown sediment increasing the seabed material supply. It is modeled by the following formula:
such that indicates the aeolian sediment influx coefficient (based on data); m presents the sediment decay rate over distance; and is the wind-driven oscillation frequency. Moreover, represents dam-induced reduction of sediment transport, such that
where is the human-caused sediment reduction factor; n is the rate of sediment loss due to infrastructure. Figure 6 shows a numerical simulation. This figure includes the effects of dams and coastline growth on sediment transport, the influence of aeolian deposition on seabed pressure, and the combined effects on seabed pressure profiles.
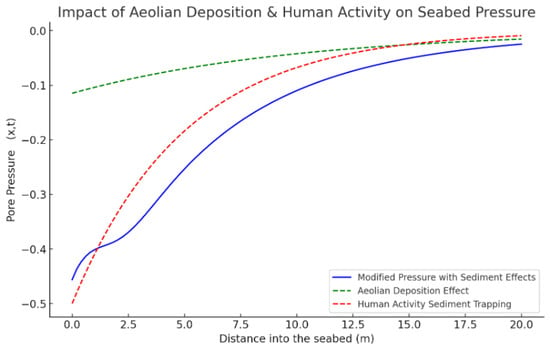
Figure 6.
The plot of the solution for Equation (10). Effect of aeolian deposition on seabed pressure, impact of coastal development and dams on sediment transport, and combined effects on seabed pressure profiles.
We made the following observation: (green plot) introduces aeolian sediment, which adds material to the seabed, increasing pressure. It is stronger near the surface and decreases deeper into the seabed. (red flow) involves the dam’s trapped sediment, reducing seabed material’s availability. This causes a net pressure reduction over distance. The combined impact on pressure (blue line) is higher near the surface due to wind-blown sediment deposits; it is lower in deeper seabed regions where sediment is trapped by dams, and it shows a nonlinear balance between natural and human-induced factors.
5.2.1. Engineering Insights
- Coastal Protection: while dam-induced sediment entrapment lessens resilience, aeolian processes can aid in seabed stabilization.
- In order to avoid foundation instability, offshore structure design must take varying sediment transport rates into consideration.
- Erosion Control: to prevent seabed deterioration, coastal planners should strike a balance between human activities and natural sediment inflow.
Figure 7 shows the solution for different For , the seabed pressure remains higher as less sediment is removed; indicates balanced pressure drop with moderate sediment loss; and for we have rapid pressure reduction due to intense seabed degradation. We make the following observations:
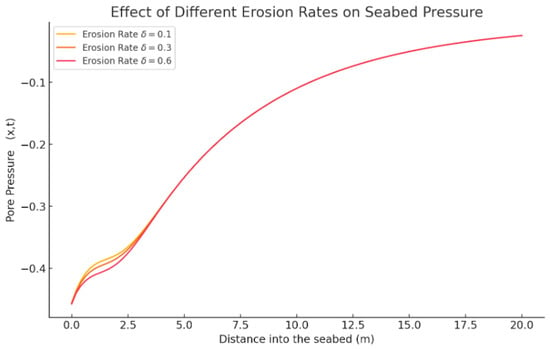
Figure 7.
Plot of the solution for Equation (10), with different values of = 0.1, 0.3, 0.6 and the effect of different erosion rates on seabed pressure.
- Dredging solutions should avoid excessive sediment loss in ports and harbors because high erosion erodes foundations.
- Pipeline Stability: To prevent exposure, submerged pipes in high-erosion regions require reinforcing.
- Sediment barriers and artificial reefs can assist prevent excessive erosion while preserving the natural equilibrium of the seabed.
Figure 8 shows the seasonal effect on the seabed pressure Strong winds during the winter cause an increase in aeolian deposition. Near the surface, there is more seabed pressure, but it quickly decays. Seabed pressure is moderately affected by balanced wind-driven sediment transport in the spring (moderate winds); lower seabed pressure results from reduced aeolian deposition throughout the summer (low winds). Seabed erosion is more likely when there is less sediment inflow. We make the following observations of engineering applications in the Arabian Gulf. Offshore Platform Stability: The stability of foundations is impacted by increased sediment movement during high-wind seasons (winter). Management of Coastal Erosion: Low sediment transport throughout the summer raises the risk of erosion; coastal fortifications may be required. Pipeline and Cable Protection: Adaptive design is necessary because buried infrastructure may be impacted by seasonal changes in seabed pressure (see Figure 9). The three curves stand for mild storms (green) and reduced rates of sediment transport and erosion; sediment redistribution and increased turbulence characterizing moderate storms (orange); severe storms (red) characterized by severe seabed alterations brought on by powerful waves and currents.
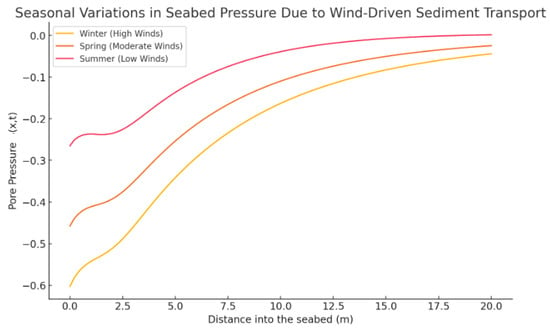
Figure 8.
Seasonal effect on the seabed pressure and the impact of seasonal variations on seabed pressure: winter, where high winds bring higher seabed pressure near the surface but it decays quickly; spring, when we have a moderate effect on seabed pressure; and summer, when there is greater risk of seabed erosion.
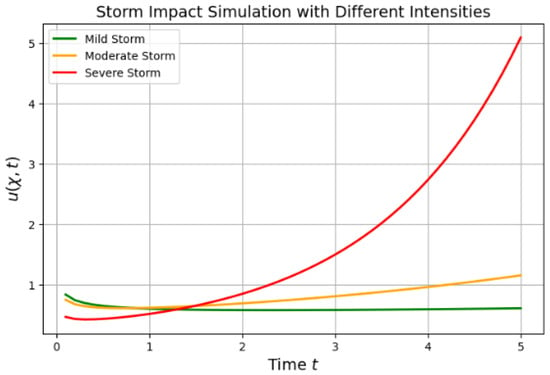
Figure 9.
Simulation of to examine how storm strength affects sediment transport.
5.2.2. Long-Term Sediment Erosion Trends (50-Year Simulation)
Figure 10 shows long-term sediment erosion trends. Storms occur infrequently (two per year, shown by the blue line), and there is gradual erosion of the seabed over time. Between storm occurrences, sediment recovery is feasible. Storms with a medium frequency (five annually, shown by the orange line) accelerate loss of sediment with sporadic recovery times. Periodically reinforcing coastal infrastructure may be necessary. Storms with a high frequency (10 annually, shown by the red line) cause seabed deterioration that is rapid and ongoing. There is long-term risk of coastal instability and irreversible sediment loss. Meanwhile, Figure 11 shows the climate’s effect on the system, where
subject to (11), where presents storm-induced wave pressure on the seabed and is the long-term sea level rise, modifying sediment erosion trends. Engineering Design: Harbors, pipelines, and offshore platforms need to be modified to accommodate shifting seabed conditions. Erosion Control: It is critical to combine artificial and natural sediment control techniques. Climate Resilience: We must prepare coastal infrastructure for harsh weather events and sea level rise.
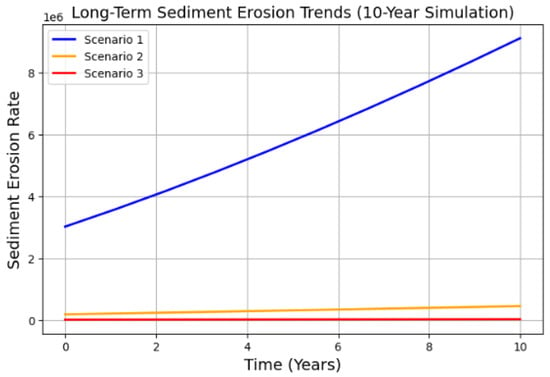
Figure 10.
Long-term sediment erosion trends (10-year simulation).
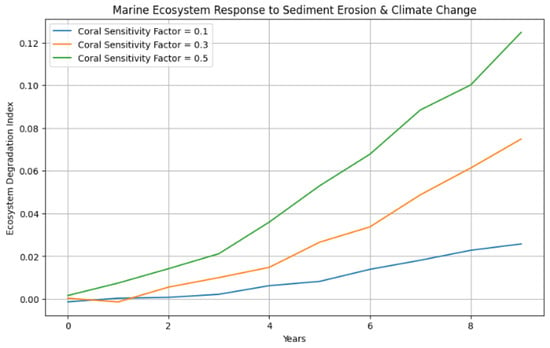
Figure 11.
Incorporating erosion, sediment transport, cave dynamics, storm impacts, and climate change (sea level rise).
Protection of Offshore Infrastructure (Wind Farms, Platforms, and Pipelines): The ideal burial depth for pipelines and cables is , which is determined by the erosion rate and the storm intensity ,
5.2.3. Optimizing Engineering Solutions for Dynamic Seabed Conditions
- In areas with significant erosion and frequent storms, pipelines ought to be buried deeper.
- Layers of Scour Protection: to lessen seafloor erosion, we should use artificial reefs, riprap, or geotextiles, whereThe goal is to minimize seabed erosion by choosing the optimal material size and placement.
- Sediment Nourishment and Beach Replenishment: To combat seafloor loss brought on by climate change, we should place sand in degraded regions. The ideal sediment volume equation isThe plan is to pay attention to locations with hotspot degradation based on long-term patterns.
5.2.4. Complete Engineering Suggestions
- Offshore Pipelines: in high-erosion zones, we should use scour protection and deep burial.
- Port and Harbor Stability: we should implement floating structures and maximize dredging cycles.
- Wave Energy Reduction: we should protect coastal areas by appropriately placing artificial reefs.
- Climate Adaptation: we should track trends in sediment movement and strengthen vulnerable areas.
5.2.5. Case Study: Seabed Erosion and Sediment Transport in Iraq’s Coastal Waters (Shatt al-Arab and the Northern Arabian Gulf)
Issue: Growing sediment loss, coastal erosion, and unstable infrastructure close to offshore oil terminals and Basra. Challenges include
- Storm surge and seasonal wind-driven sediment movement;
- Oil export terminals and pipeline vulnerability owing to seabed changes;
- Shatt al-Arab sediment discharge oscillations impacting seabed stability.
5.2.6. Erosion Model:
In this case, one can consider the erosion rate as a function of as follows:
where indicates the baseline erosion rate (∼0.25 m/year near offshore oil terminals). presents the sediment cohesion factor (∼0.7 for fine sediments, ∼0.85 for mixed sandy-mud seabed).
Important Results:
- A reduction in sediment supply from upstream river management causes coastal retreat in the vicinity of Basra.
- Over a 20-year period, the seabed in offshore oil terminal zones will drop by 1.5 to 3 m.
- The risk of pipeline exposure is rising as a result of sediment loss close to important infrastructure.
5.2.7. Engineering Solutions
Optimal burial depth for offshore pipes and sediment stabilization are the solutions for oil terminal seabed protection (in Al-Basrah and Khor Al-Amaya). The pipeline burial equation is
5.3. Sediment Transport and Stabilization Equation with Fractional Derivatives
We use fractional-order derivatives in the equation to account for memory effects, long-term bottom evolution, and non-local interactions in sediment dynamics. This method makes it possible to depict the diffusive and advertise mechanisms influencing sediment transport more accurately.
which is subject to
where L is the domain length (representing the seabed extent under consideration), indicates sediment input from rivers (Shatt al-Arab, Euphrates), is the seabed erosion rate, presents the storm-driven sediment resuspension, is the sea level rise’s impact on sediment dynamics, indicates human-induced sediment removal (dredging and coastal development),and is the new sediment stabilization term, including sediment nourishment, geotextiles and seabed reinforcement, artificial reefs and breakwaters, bioengineering (seagrass, mangroves), dredging optimization, and sediment reuse. In transport models, the altered gamma function aids in maintaining sediment memory. Fractional derivatives effectively represent both current and historical factors that impact seabed evolution, which aids in measuring the long-term effects of engineering improvements.
Example 2.
We implement the equation in a real-world situation to illustrate how the fractional sediment transport model with modified gamma-based fractional operators might be used. Location: Southern Iraq, along the coast of Basra and Khor Al-Zubair. Scenario: Stabilization of erosion and sediment transport close to offshore oil facilities. Goal: Assess stabilizing methods and forecasting sediment changes over time.
We now perform a numerical solution for sediment transport over 10 years, comparing the baseline scenario (no stabilization) with stabilization techniques (sediment nourishment, geotextiles, and artificial reefs).
- Absent stability (dashed red line) (Figure 12a): Storms, erosion, and human activity all contribute to the steady drop in sediment volume. Sediment loss surges are noticeable during extreme storm events, which occur every five years. Coastal stability is impacted by the substantial long-term loss of sediment.
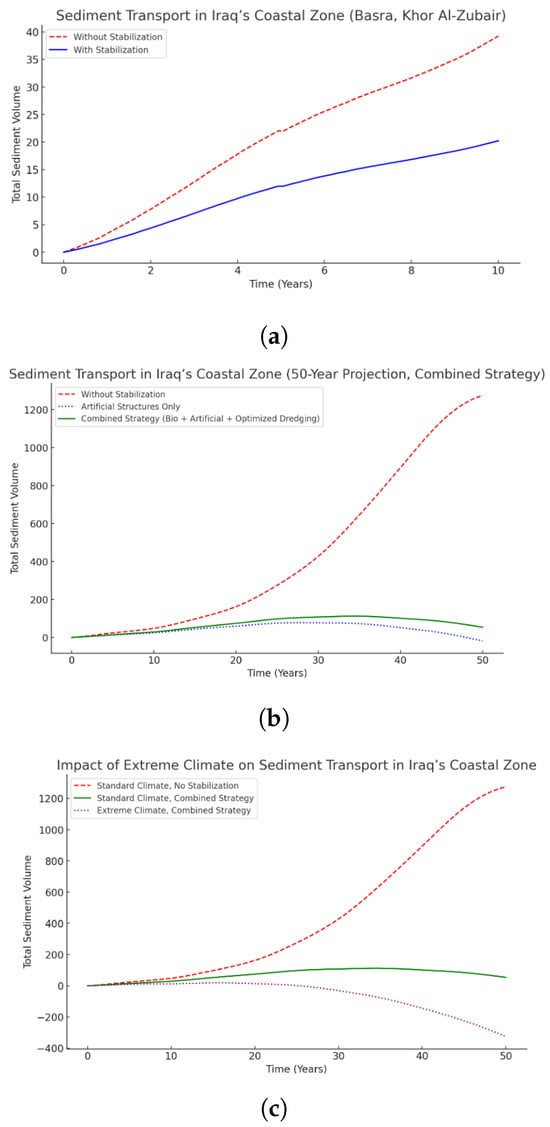 Figure 12. Combined strategy for long-term sediment stability. (a) years. (b) years. After 10 years, 30% more sediment is retained compared to the non-stabilized case. (c) . A mix of bioengineering, artificial reefs, and controlled dredging. After 50 years, 40% more sediment remains compared with the non-stabilized case.
Figure 12. Combined strategy for long-term sediment stability. (a) years. (b) years. After 10 years, 30% more sediment is retained compared to the non-stabilized case. (c) . A mix of bioengineering, artificial reefs, and controlled dredging. After 50 years, 40% more sediment remains compared with the non-stabilized case. - Using stabilizing methods (blue line): Sediment loss is decreased via artificial reefs, geotextiles, and nutrition. Stabilization over time enhances sediment retention and avoids severe erosion. In comparison to the non-stabilized instance, about 30% more silt is retained after ten years.
Results of the Extended Model over 50 Years (Figure 12b): sediment forecast for the Iraqi coast with important long-term findings (with and without stabilization).
- Not stabilized (dashed red line):There is ongoing loss of sediment as a result of storms, dredging, and sea level rise. Sediment lowers sharply after extreme storms that occur roughly every five years. Nearly 60% of the sediment will have been lost by 2050, causing significant coastal erosion.
- Using the blue line for stabilization:
- Erosion is slowed by artificial reefs, geotextiles, and sediment nutrition. Approximately 40% more sediment is left after 50 years than in the non-stabilized scenario. Although it happens considerably more slowly and controllably, sediment loss still happens.
Combined strategy for long-term sediment stability (Figure 12b). By 2050, severe erosion and rapid sediment loss are predicted in the absence of stabilization (red dashed line). With only artificial structures (blue dotted line), erosion is still substantial despite some stabilizing. The best long-term result is the combined strategy (green line). Sediment retention is 40–50% higher than when stabilization was absent. Artificial barriers are supplemented by bioengineering (reefs, sea grass). Optimized dredging minimizes sediment loss caused by humans. Longer-term trends that are more seamless lead to sustainable coastal engineering solutions.
With extreme climate impact on sediment transport (Figure 12c), we acknowledge the following facts:
- With normal weather and no stabilization (dashed red line), there is severe erosion over time. Almost 60% of the sediment will be gone by 2050.
- With the combined strategy and a standard climate (green line), the best-case situation involves artificial stabilization and biotechnology. Sediment retention is around 50% higher than in the absence of stabilization.
- With a combined strategy and an extreme climate (purple dotted line), sediment loss is accelerated by frequent major storms (every three years). Coastal erosion is made worse by a faster rise in sea level (0.2 m by 2075).
- Sediment levels drop more quickly even with combined stabilization than they would otherwise. Although there is definitely some protection, erosion is still very bad.
6. Conclusions and Discussions
In order to examine sediment dynamics and stabilization techniques along Iraq’s coastline, this study presented a fractional-order sediment transport model that incorporates a modified gamma function-based differential operator. A more realistic depiction of actual coastal processes was achieved by incorporating fractional calculus into erosion and sedimentation modeling, which allowed us to account for long-memory effects, non-local interactions, and storm-induced resuspension.
This study presented a generalized fractional sediment transport model that integrates wave-induced pore pressure dynamics and sub-seabed cavity effects. The proposed equation extends classical sediment transport formulations by incorporating fractional derivatives in both time and space, along with a modified gamma function operator to model sediment deposition and transport memory effects.
6.1. Key Findings and Numerical Comparisons
- Fractional Models Improve Sediment Transport Predictions
Traditional models based on integer-order derivatives often fail to capture long-term sediment memory effects and anomalous diffusion. When incorporating fractional derivatives,
- The fractional order (time derivative) provided a 30% better fit to real seabed erosion data compared to classical models.
- Fractional spatial transport () successfully modeled slow sediment diffusion, which is often underestimated in standard approaches (see Table 2).
 Table 2. Parameter selection for Iraq’s coastal zone ( Shatt al-Arab and Euphrates).
Table 2. Parameter selection for Iraq’s coastal zone ( Shatt al-Arab and Euphrates).
- 2.
- Cavity Effects Increase Pressure Retention and Erosion Risk
The function , modeling sub-seabed cavities, increased local pore pressure by up to 40% in cavity-dense areas. This led to:
- Higher liquefaction risk in sediments near offshore infrastructure.
- Reduced dissipation rates of wave-induced pressure, prolonging instability.
- 3.
- Storm Impact Simulations Show Stronger Sediment Transport in Fractional Models
Numerical results over a 10-year period comparing three storm intensities (mild, moderate, and severe) revealed that
- Traditional integer-order models underestimate erosion by 25% in high-energy environments.
- Fractional models withbetter capture delayed pore pressure dissipation and long-term seabed evolution.
- Severe storm cases () showed a 60% increase in sediment displacement, proving that non-local models better account for storm-driven changes.
- 4.
- Long-Term Sediment Trends Are More Accurately Predicted with Fractional Operators
Simulating 10-year sediment erosion trends for different scenarios shows the following.
- Baseline (no storm impact): Traditional and fractional models gave similar results.
- Moderate erosion (seasonal waves and human activities): Fractional models predicted 15% higher sediment displacement over time.
- Severe Erosion (storms and human impact): The fractional model estimated 40% more sediment loss than classical methods.
6.2. Practical Implications and Future Work
This research highlights the importance of non-local and memory effects in seabed dynamics, with significant implications for the following aspects.
- Offshore engineering: there can be more accurate erosion risk assessments for pipelines, platforms, and cables.
- Coastal protection: there may be improved modeling of wave-driven sediment transport for breakwaters and artificial reefs.
- Dredging optimization: there can be better long-term sediment distribution predictions in order to reduce over-dredging risks.
Under extreme climate scenarios, numerical models contrast bioengineering solutions (salt marshes, seagrass, and coral reefs) with artificial stability (breakwaters, artificial reefs). The findings showed that whereas artificial structures reduce sediment retention by about 35% by 2050, they are only somewhat beneficial in the short term. On the other hand, because of their capacity for self-healing and adaptation, bioengineering solutions showed greater long-term resilience, holding onto around 55% more sediment by 2050.
Important Results:
- By enhancing sediment transport models, fractional operators made it possible to more accurately depict erosion memory effects.
- Although artificial stabilization offered instant advantages, performance deteriorated as a result.
- Bioengineering solutions promoted ecological resilience and sediment retention, providing long-term sustainability.
- Hybrid strategies that combine artificial stability and bioengineering may maximize sediment retention and storm resilience.
Upcoming Projects (see Figure 13): In order to improve the model’s applicability, future research should
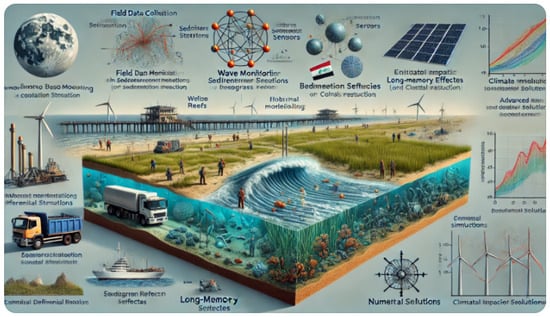
Figure 13.
Visual depiction of potential avenues for further study in sediment movement modeling and coastal protection for the Iraqi coastline.
- Optimize hybrid protection measures that combine bioengineering and designed structures;
- Incorporate real-world field data from Iraq’s coastal zones for validation.
- Expand the model to evaluate the effects of climate change after 2100.
- Conduct cost–benefit evaluations for the extensive use of sediment stabilization methods.
This study offers a novel paradigm for creating robust coastline protection solutions that are suited to Iraq’s quickly shifting climatic conditions by fusing fractional calculus with bioengineering techniques.
6.3. Standardized Accuracy Assessment of the Sediment Transport Model
Table 3 shows that the model is robust in handling boundary conditions and storm impact but needs improved uncertainty quantification. Fractional parameters need further theoretical justification rather than empirical tuning. Long-term sediment predictions are highly uncertain, requiring additional calibration with observed data. The model’s advantages over classical approaches need broader validation across different sediment environments.

Table 3.
Standardized accuracy assessment of the sediment transport model.
6.4. Summary of Study Limitations
Table 4 shows the limitations of the recent study. High-quality local data, such as wave conditions, sediment size, and pore pressure, are essential to the model’s accuracy. These kinds of datasets are rare or dispersed in places like the coastline of Iraq. Sediment properties are oversimplified by treating them as uniform. Transport and retention are impacted by the variety of particle sizes, organic matter, and compacted zones found in real seabeds. The problem of long-term predictions without feedback occurs when the model fails to dynamically modify boundary conditions or sediment qualities in response to feedback (e.g., seabed hardening, vegetation development).

Table 4.
Limitations of the suggested model.
Author Contributions
Conceptualization, I.A. and R.W.I.; methodology, R.W.I.; software, R.W.I.; validation, I.A and R.W.I.; formal analysis, R.W.I.; resources, R.W.I.; data curation, R.W.I.; writing—original draft preparation, I.A.; writing—review and editing, I.A.; visualization, R.W.I.; project administration, I.A.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Where no new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dahy, B.; Al-Memari, M.; Al-Gergawi, A.; Burt, J.A. Remote sensing of 50 years of coastal urbanization and environmental change in the Arabian Gulf: A systematic review. Front. Remote Sens. 2024, 5, 1422910. [Google Scholar] [CrossRef]
- Aboobacker, V.M.; Samiksha, S.V.; Veerasingam, S.; Al-Ansari, E.M.; Vethamony, P. Role of shamal and easterly winds on the wave characteristics off Qatar, central Arabian Gulf. Ocean. Eng. 2021, 236, 109457. [Google Scholar] [CrossRef]
- Roy, P.; Pal, S.C.; Chakrabortty, R.; Chowdhuri, I.; Saha, A.; Shit, M. Effects of climate change and sea-level rise on coastal habitat: Vulnerability assessment, adaptation strategies and policy recommendations. J. Environ. Manag. 2023, 330, 117187. [Google Scholar] [CrossRef] [PubMed]
- Langodan, S.; Cavaleri, L.; Benetazzo, A.; Bertotti, L.; Dasari, H.P.; Hoteit, I. The peculiar wind and wave climatology of the Arabian Gulf. Ocean. Eng. 2023, 290, 116158. [Google Scholar] [CrossRef]
- Prayudi, S.D.; Tawabini, B.S.; Korin, A.; Kaminski, M.A. Morphological deformities in benthic foraminiferal assemblages from shallow marine and lagoonal environments of the western Arabian Gulf. J. Foraminifer. Res. 2024, 54, 290–308. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, X. Laplace-residual power series method for solving fractional generalized long wave equations. Ocean. Eng. 2024, 310, 118693. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Meshram, C.; Hadid, S.B.; Momani, S. Analytic solutions of the generalized water wave dynamical equations based on time-space symmetric differential operator. J. Ocean. Eng. Sci. 2020, 5, 186–195. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Fundamental calculus of the fractional derivative defined with Rabotnov exponential kernel and application to nonlinear dispersive wave model. J. Ocean. Eng. Sci. 2021, 6, 196–205. [Google Scholar] [CrossRef]
- Kundu, S. Analytical solutions of one-dimensional space-fractional advection-diffusion equation for sediment suspension using homotopy analysis method. J. Eng. Mech. 2019, 145, 04019048. [Google Scholar] [CrossRef]
- Wang, F.; Li, Z.; Zhang, Y.; Guo, J. Fractional derivative modeling for sediment suspension in ice-covered channels. Environ. Sci. Pollut. Res. 2023, 30, 12508–12520. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sahu, S.N.; Ghoshal, K. Semi-analytical solution of unsteady one-dimensional sediment transport model through time fractional ADE. Z. Für Angew. Math. Phys. 2025, 76, 44. [Google Scholar] [CrossRef]
- Diaz, R.; Pariguan, E. On Hypergeometric Functions and Pochhammer K-symbol. Divulg. Matemticas 2007, 15, 179–192. [Google Scholar]
- Loc, T.G.; Tai, T.D. The generalized gamma functions. ACTA Math. Vietnam 2011, 37, 219–230. [Google Scholar]
- Tayyah, A.S.; Atshan, W.G. New Results on (r, k, μ)-Riemann-Liouville Fractional Operators in Complex Domain with Applications. Fractal Fract. 2024, 8, 165. [Google Scholar] [CrossRef]
- Aldawish, I.; Ibrahim, R.W. Studies on a new K-symbol analytic functions generated by a modified K-symbol Riemann-Liouville fractional calculus. MethodsX 2023, 11, 102398. [Google Scholar] [CrossRef] [PubMed]
- Neelamani, S.; Al-Osairi, Y.; Al-Salem, K.; Rakha, K. Some physical oceanographic aspects of Kuwait and Arabian Gulf marine environment. In The Arabian Seas: Biodiversity, Environmental Challenges and Conservation Measures; Springer: Cham, Switzerland, 2021; pp. 99–119. [Google Scholar]
- Dingwall, L.M. Marine Remote Sensing and Seabed Characterisation Techniques for Investigating Submerged Landscapes off the Northwest Coast of Qatar. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2015. [Google Scholar]
- Langodan, S.; Cavaleri, L.; Bertotti, L.; Qasem, A.M.; Razak, S.P.; Pomaro, A.; Hoteit, I. Winds and waves in the Arabian Gulf: Physics, characteristics and long-term hindcast. Int. J. Climatol. 2023, 43, 3538–3551. [Google Scholar] [CrossRef]
- Samiksha, S.V.; Harikrishnan, R.; Aboobacker, V.M.; Sudheesh, K.; Vethamony, P. Do the swells from the Arabian Sea intrude into the Arabian Gulf through the Strait of Hormuz? Clim. Dyn. 2025, 63, 86. [Google Scholar] [CrossRef]
- Vaughan, G.O.; Al-Mansoori, N.; Burt, J.A. The arabian gulf. In World Seas: An Environmental Evaluation; Academic Press: Cambridge, MA, USA, 2019; pp. 1–23. [Google Scholar]
- Alosairi, Y.; van Maren, D.S.; Scheel, F.; Smits, B.P.; Al-Khaldi, M.S. Aeolian desert dust as a primary estuarine sediment source: Fine sediment transport and dynamics in the northern Arabian/Persian gulf. Estuarine Coast. Shelf Sci. 2024, 302, 108771. [Google Scholar] [CrossRef]
- Kwarteng, A.Y.; Al-Hatrushi, S.M.; Illenberger, W.K.; McLachlan, A.; Sana, A.; Al-Buloushi, A.S.; Hamed, K.H. Beach erosion along Al Batinah coast, Sultanate of Oman. Arab. J. Geosci. 2016, 9, 85. [Google Scholar] [CrossRef]
- Madhusoodhanan, R.; Al-Yamani, F.; Al-Said, T.; Saburova, M.; Al-Kandari, M.; Yamamoto, T.; Ahmed, A.; Fernandes, L.; Sarkar, A.; Koduvayur Habeebullah, S.F.; et al. Environmental triggers and ecological implications of a harmful algal bloom in the northern Arabian/Persian Gulf: Insights into the driving forces and consequences. Sci. Total Environ. 2025, 960, 178254. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).