Design and Numerical Simulation of a Standing Surface Acoustic Wave-Based Microdevice for Whole Blood Cell Separation
Abstract
1. Introduction
2. SAW-Based Microchips
2.1. Governing Equations
2.2. Modeling
2.2.1. Geometry and Materials
2.2.2. Solver Configuration
3. Results and Discussion
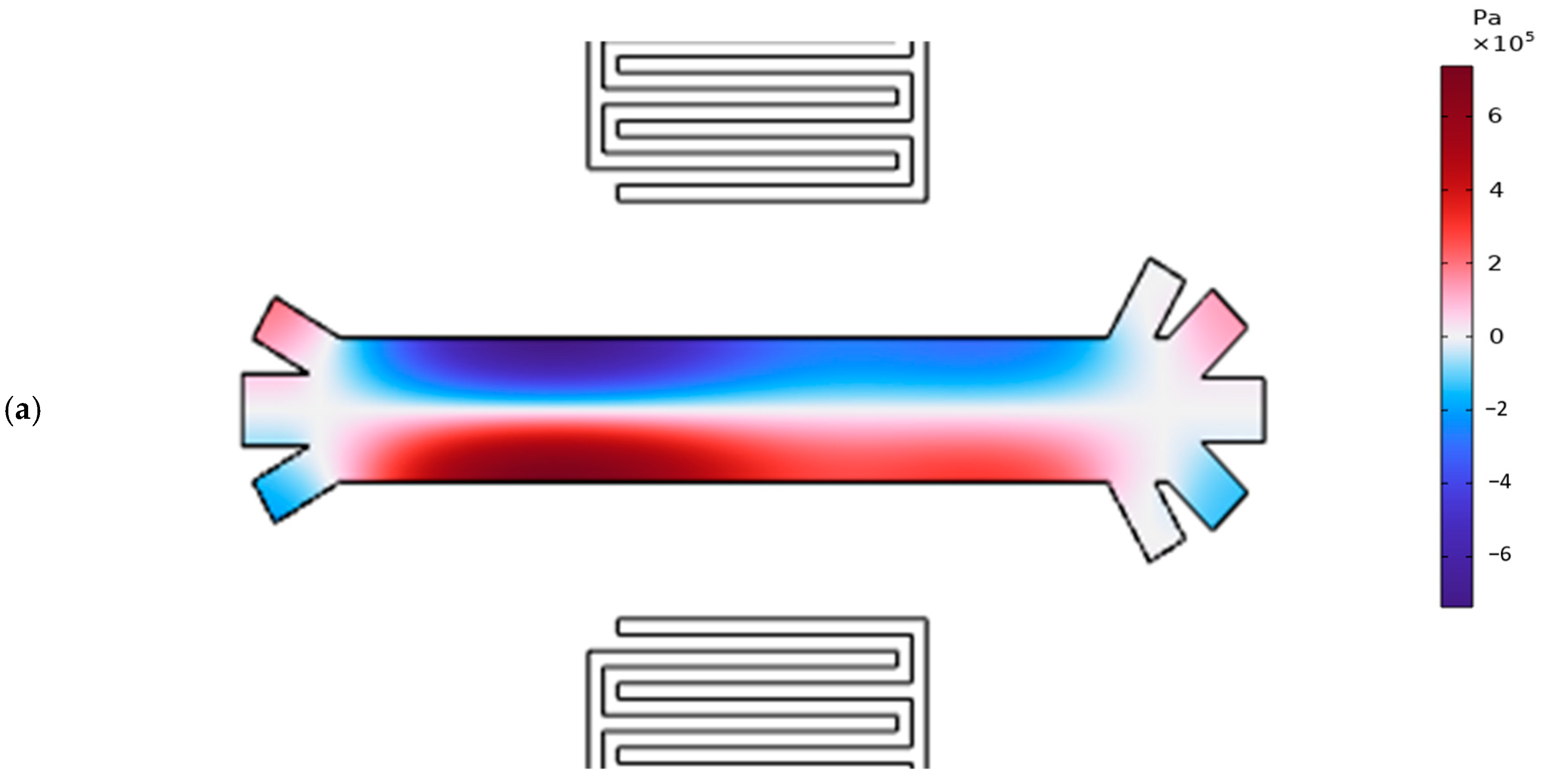
3.1. Model Verification
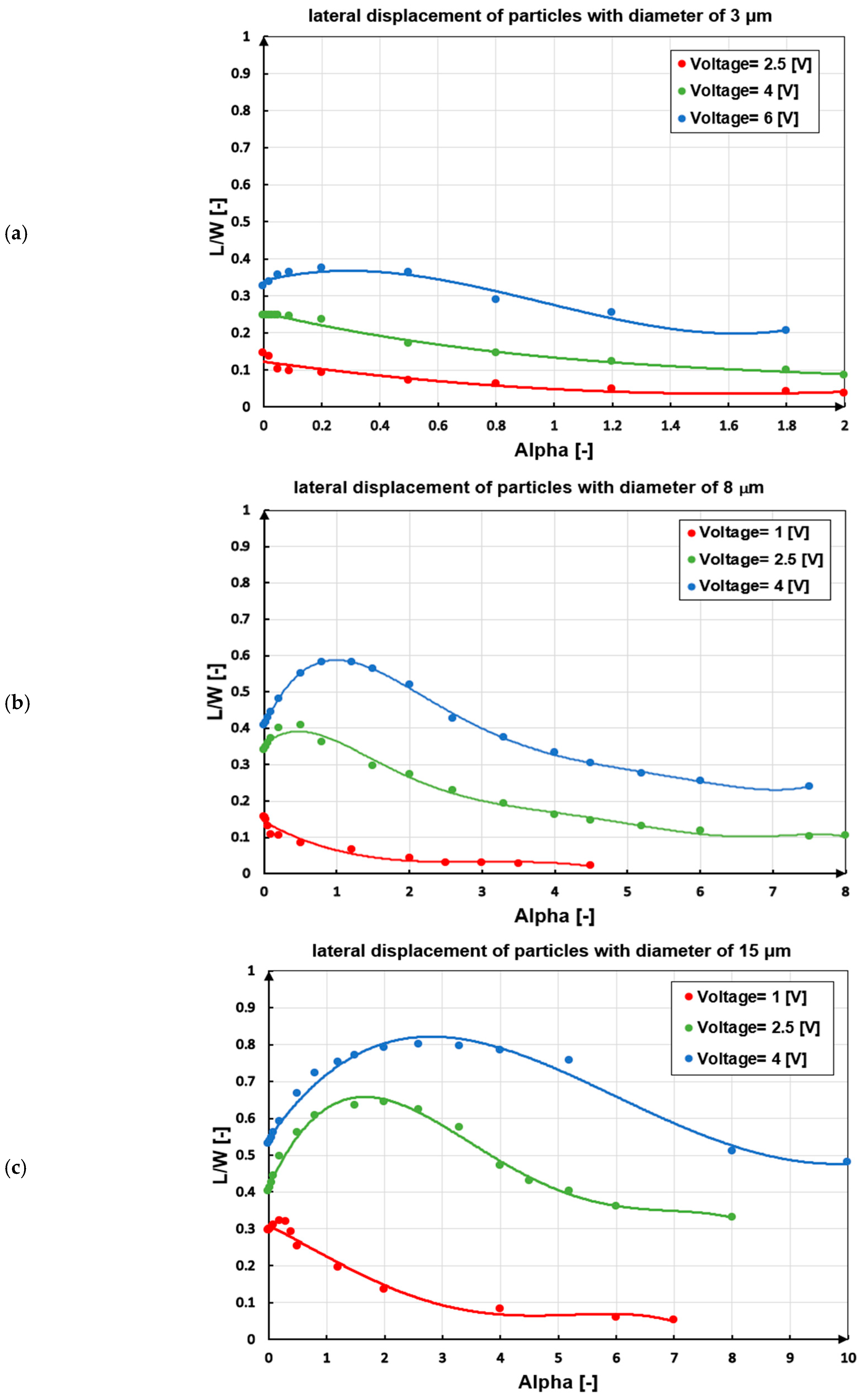
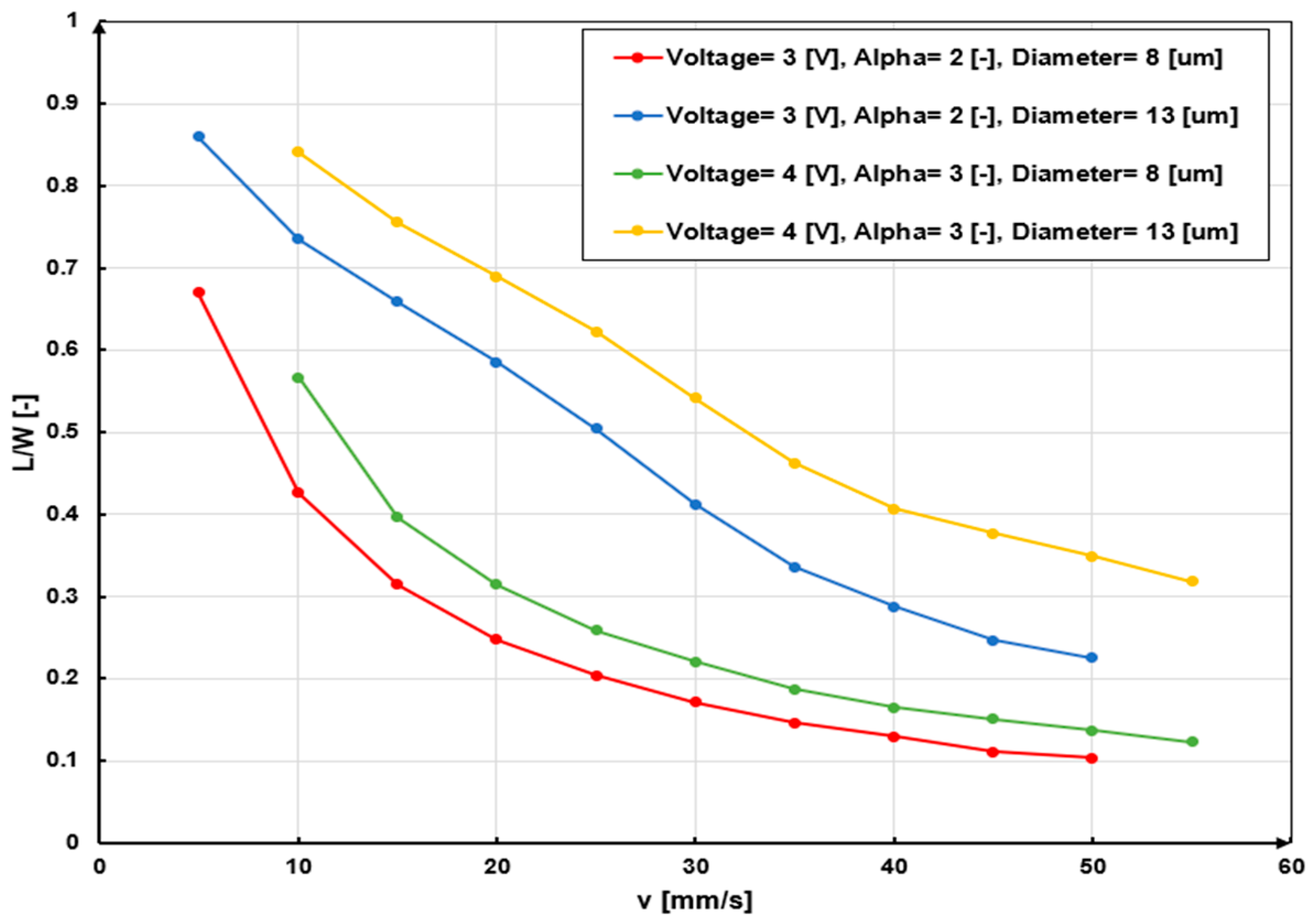
3.2. Parametric Study
3.2.1. Inlet Velocity Ratio ()
3.2.2. Velocity Field
3.2.3. Voltage and Particle Size
3.3. Pressure Acoustic and Particle Trajectory of the Proposed Model
3.4. Guidelines for Designing SSAW-Based Blood Cell Separation Systems
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Letters and Symbols | Description |
| Abbreviation | |
| ARF | Acoustic radiation force |
| BAW | Bulk acoustic wave |
| IDT | Interdigital transducer |
| PAN | Pressure anti-node |
| PLT | Platelet |
| PN | Pressure node |
| RBC | Red blood cell |
| SAW | Surface acoustic wave |
| SSAW | Standing surface acoustic wave |
| TSAW | Traveling surface acoustic wave |
| WBC | White blood cell |
| Latin Letters | |
| Radius of particle, | |
| Speed of sound, | |
| Elasticity matrix of piezoelectric, | |
| Electric displacement vector, | |
| Electric field vector, [] | |
| Frequency, [MHz] | |
| Piezoelectric stress matrix, | |
| Height of the microchannel, | |
| Length of the microchannel, | |
| Lateral displacement of particles, | |
| Mass of particles, [ | |
| Pressure, | |
| Radius of particles, | |
| Time-averaged radiation force potential, [J] | |
| Velocity, | |
| Width of the microchannel, | |
| Half of the width of the microchannel, | |
| Frequency mode in each direction, [-] | |
| Greek Letters | |
| α | Inlet velocity ratio (buffer/blood), [-] |
| ϵ | Strain tensor, [-] |
| ε | Dielectric matrix, [-] |
| κ | Compressibility, [ |
| μ | Viscosity, |
| Bulk viscosity, | |
| Density, [ | |
| σ | Mechanical stress tensor, [ |
| ϕ | Contrast factor, [-] |
| ω | Angular velocity, [] |
References
- Zhou, J.; Mukherjee, P.; Gao, H.; Luan, Q.; Papautsky, I. Label-free microfluidic sorting of microparticles. APL Bioeng. 2019, 3, 041504. [Google Scholar] [CrossRef]
- Zhang, T.; Hong, Z.-Y.; Tang, S.-Y.; Li, W.; Inglis, D.W.; Hosokawa, Y.; Yalikun, Y.; Li, M. Focusing of sub-micrometer particles in microfluidic devices. Lab Chip 2020, 20, 35–53. [Google Scholar] [CrossRef]
- Augustsson, P.; Magnusson, C.; Nordin, M.; Lilja, H.; Laurell, T. Microfluidic, label-free enrichment of prostate cancer cells in blood based on acoustophoresis. Anal. Chem. 2012, 84, 7954–7962. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.-T.; Martin, A.B.; Gandini, A.; Aubry, N.; Massoudi, M.; Antaki, J.F. Design of microfluidic channels for magnetic separation of malaria-infected red blood cells. Microfluid. Nanofluidics 2016, 20, 41. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Cha, B.; Yi, H.G.; Kim, J.; Jeon, J.S.; Park, J. Acoustofluidic separation of bacteria from platelets using tilted-angle standing surface acoustic wave. Sens. Actuators B Chem. 2024, 417, 136161. [Google Scholar] [CrossRef]
- Wu, M.; Ouyang, Y.; Wang, Z.; Zhang, R.; Huang, P.-H.; Chen, C.; Li, H.; Li, P.; Quinn, D.; Dao, M.; et al. Isolation of exosomes from whole blood by integrating acoustics and microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, 10584–10589. [Google Scholar] [CrossRef] [PubMed]
- Karimi, S.; Mojaddam, M.; Majidi, S.; Mehrdel, P.; Farré-Lladós, J.; Casals-Terré, J. Numerical and experimental analysis of a high-throughput blood plasma separator for point-of-care applications. Anal. Bioanal. Chem. 2021, 413, 2867–2878. [Google Scholar] [CrossRef]
- Nepal, S.; Feng, H.; Gale, B.K. Optimization of a microfluidic spiral channel used to separate sperm from blood cells. Biomicrofluidics 2020, 14, 064103. [Google Scholar] [CrossRef]
- Sethu, P.; Sin, A.; Toner, M. Microfluidic diffusive filter for apheresis (leukapheresis). Lab Chip 2006, 6, 83–89. [Google Scholar] [CrossRef]
- Ghoshal, K.; Bhattacharyya, M. Overview of platelet physiology: Its hemostatic and nonhemostatic role in disease pathogenesis. Sci. World J. 2014, 2014, 781857. [Google Scholar] [CrossRef]
- Kuhn, V.; Diederich, L.; Iv, T.C.S.K.; Kramer, C.M.; Lückstädt, W.; Panknin, C.; Suvorava, T.; Isakson, B.E.; Kelm, M.; Cortese-Krott, M.M. Red blood cell function and dysfunction: Redox regulation, nitric oxide metabolism, anemia. Antioxid. Redox Signal. 2017, 26, 718–742. [Google Scholar] [CrossRef]
- Tigner, A.; Ibrahim, S.A.; Murray, I. Histology, White Blood Cell; StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2020. [Google Scholar]
- Cheng, X.; Irimia, D.; Dixon, M.; Sekine, K.; Demirci, U.; Zamir, L.; Tompkins, R.G.; Rodriguez, W.; Toner, M. A microfluidic device for practical label-free CD4+ T cell counting of HIV-infected subjects. Lab Chip 2007, 7, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluid. 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Zhu, P.; Wang, L. Passive and active droplet generation with microfluidics: A review. Lab Chip 2017, 17, 34–75. [Google Scholar] [CrossRef]
- Fadaei, M.; Majidi, S.; Mojaddam, M. Droplet generation in a co-flowing microchannel influenced by magnetic fields applied in parallel and perpendicular to flow directions. J. Magn. Magn. Mater. 2023, 570, 170528. [Google Scholar] [CrossRef]
- Dittrich, P.S.; Manz, A. Lab-on-a-chip: Microfluidics in drug discovery. Nat. Rev. Drug Discov. 2006, 5, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Jahromi, A.K.; Saadatmand, M.; Eghbal, M.; Yeganeh, L. Development of simple and efficient Lab-on-a-Disc platforms for automated chemical cell lysis. Sci. Rep. 2020, 10, 11039. [Google Scholar] [CrossRef]
- Leung, C.M.; de Haan, P.; Ronaldson-Bouchard, K.; Kim, G.-A.; Ko, J.; Rho, S.R.; Chen, S.; Duran, M.S.; Wan, J.M.M.M.; Pingguan-Murphy, S.V.V.; et al. A guide to the organ-on-a-Chinature. Rev. Methods Primers 2022, 2, 33. [Google Scholar] [CrossRef]
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Yiannacou, K.; Sariola, V. Controlled manipulation and active sorting of particles inside microfluidic chips using bulk acoustic waves and machine learning. Langmuir 2021, 37, 4192–4199. [Google Scholar] [CrossRef]
- Wong, S.H.; Ward, M.C.; Wharton, C.W. Micro T-mixer as a rapid mixing micromixer. Sens. Actuators B Chem. 2004, 100, 359–379. [Google Scholar] [CrossRef]
- Fan, R.; Wu, J.; Li, Y.; Zhang, C.; Hui, Z.; Zheng, A. Droplet-based microfluidics for drug delivery applications. Int. J. Pharm. 2024, 663, 124551. [Google Scholar] [CrossRef]
- Bayazidi, S.; Mojaddam, M.; Mohseni, A. Performance optimization of nozzle-diffuser piezoelectric micropump with multiple vibrating membranes by design of experiment (DOE) method. J. Appl. Fluid Mech. 2023, 16, 1356–1370. [Google Scholar]
- Doh, I.; Cho, Y.-H. A continuous cell separation chip using hydrodynamic dielectrophoresis (DEP) process. Sens. Actuators A Phys. 2005, 121, 59–65. [Google Scholar] [CrossRef]
- Çetin, B.; Li, D. Dielectrophoresis in microfluidics technology. Electrophoresis 2011, 32, 2410–2427. [Google Scholar] [CrossRef] [PubMed]
- Pamme, N.; Wilhelm, C. Continuous sorting of magnetic cells via on-chip free-flow magnetophoresis. Lab Chip 2006, 6, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Alnaimat, F.; Dagher, S.; Mathew, B.; Hilal-Alnqbi, A.; Khashan, S. Microfluidics based magnetophoresis: A review. Chem. Rec. 2018, 18, 1596–1612. [Google Scholar] [CrossRef]
- Petersson, F.; Åberg, L.; Swärd-Nilsson, A.-M.; Laurell, T. Free flow acoustophoresis: Microfluidic-based mode of particle and cell separation. Anal. Chem. 2007, 79, 5117–5123. [Google Scholar] [CrossRef]
- Pamme, N. Continuous flow separations in microfluidic devices. Lab Chip 2007, 7, 1644–1659. [Google Scholar] [CrossRef]
- Wu, L.; Guan, G.; Hou, H.W.; Bhagat, A.A.S.; Han, J. Separation of leukocytes from blood using spiral channel with trapezoid cross-section. Anal. Chem. 2012, 84, 9324–9331. [Google Scholar] [CrossRef]
- Sun, J.; Liu, C.; Li, M.; Wang, J.; Xianyu, Y.; Hu, G.; Jiang, X. Size-based hydrodynamic rare tumor cell separation in curved microfluidic channels. Biomicrofluidics 2013, 7, 011802. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, B.; Zand, M.M.; Javidi, R. Numerical simulation of critical particle size in asymmetrical deterministic lateral displacement. J. Chromatogr. A 2021, 1649, 462216. [Google Scholar] [CrossRef] [PubMed]
- McGrath, J.; Jimenez, M.; Bridle, H. Deterministic lateral displacement for particle separation: A review. Lab Chip 2014, 14, 4139–4158. [Google Scholar] [CrossRef] [PubMed]
- Noruzshamsian, O.; Mohseni, A.; Mojaddam, M. Design of a micro-separator for Circulating Tumor Cells (CTCs) from blood flow using hybrid pinched flow fractionation (PFF) and dielectrophoresis methods. J. Solid Fluid Mech. 2020, 10, 281–296. [Google Scholar]
- Tokeshi, M. Applications of Microfluidic Systems in Biology and Medicine; Springer: Singapore, 2019. [Google Scholar]
- Olofsson, K.; Hammarström, B.; Wiklund, M. Acoustic separation of living and dead cells using high density medium. Lab Chip 2020, 20, 1981–1990. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Wang, Y.; Wang, Z.; Duan, X. Microscale acoustic streaming for biomedical and bioanalytical applications. TrAC Trends Anal. Chem. 2023, 160, 116958. [Google Scholar] [CrossRef]
- Rasouli, R.; Villegas, K.M.; Tabrizian, M. Acoustofluidics–changing paradigm in tissue engineering, therapeutics development, and biosensing. Lab Chip 2023, 23, 1300–1338. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J.; Chen, H.; Liu, X. Acoustofluidic precise manipulation: Recent advances in applications for micro/nano bioparticles. Adv. Colloid Interface Sci. 2024, 332, 103276. [Google Scholar] [CrossRef]
- Dykes, J.; Lenshof, A.; Åstrand-Grundström, I.; Laurell, T.; Scheding, S. Efficient removal of platelets from peripheral blood progenitor cell products using a novel micro-chip based acoustophoretic platform. PLoS ONE 2011, 6, e23074. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, M.; Ren, L.; Liu, J.; Whitley, P.H.; Wang, L.; Huang, T.J. High-throughput acoustic separation of platelets from whole blood. Lab Chip 2016, 16, 3466–3472. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Huang, H.; Stratton, Z.; Huang, Y.; Huang, T.J. Continuous particle separation in a microfluidic channel via standing surface acoustic waves (SSAW). Lab Chip 2009, 9, 3354–3359. [Google Scholar] [CrossRef]
- Folch, A. Introduction to bioMEMS; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Wu, M.; Ozcelik, A.; Rufo, J.; Wang, Z.; Fang, R.; Huang, T.J. Acoustofluidic separation of cells and particles. Microsyst. Nanoeng. 2019, 5, 32. [Google Scholar] [CrossRef] [PubMed]
- Taatizadeh, E.; Dalili, A.; Rellstab-Sánchez, P.; Tahmooressi, H.; Ravishankara, A.; Tasnim, N.; Najjaran, H.; Li, I.T.S.; Hoorfar, M. Micron-sized particle separation with standing surface acoustic wave—Experimental and numerical approaches. Ultrason. Sonochemistry 2021, 76, 105651. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Mao, Z.; Peng, Z.; Zhou, L.; Chen, Y.; Huang, P.-H.; Truica, C.I.; Drabick, J.J.; El-Deiry, W.S.; Dao, M.; et al. Acoustic separation of circulating tumor cells. Proc. Natl. Acad. Sci. USA 2015, 112, 4970–4975. [Google Scholar] [CrossRef] [PubMed]
- Şahin, M.A.; Çetin, B.; Özer, M.B. Investigation of effect of design and operating parameters on acoustophoretic particle separation via 3D device-level simulations. Microfluid. Nanofluid. 2020, 24, 8. [Google Scholar] [CrossRef]
- Lei, J.; Cheng, F.; Li, K.; Guo, Z. Numerical simulation of continuous separation of microparticles in two-stage acousto-microfluidic systems. Appl. Math. Model. 2020, 83, 342–356. [Google Scholar] [CrossRef]
- Shamloo, A.; Boodaghi, M. Design and simulation of a microfluidic device for acoustic cell separation. Ultrasonics 2018, 84, 234–243. [Google Scholar] [CrossRef] [PubMed]
- González, I.; Earl, J.; Fernández, L.J.; Sainz, B.; Pinto, A.; Monge, R.; Alcalá, S.; Castillejo, A.; Soto, J.L.; Carrato, A. A label free disposable device for rapid isolation of rare tumor cells from blood by ultrasounds. Micromachines 2018, 9, 129. [Google Scholar] [CrossRef]
- Destgeer, G.; Lee, K.H.; Jung, J.H.; Alazzam, A.; Sung, H.J. Continuous separation of particles in a PDMS microfluidic channel via travelling surface acoustic waves (TSAW). Lab Chip 2013, 13, 4210–4216. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Gupta, S.; Bit, A. Acoustophoresis-based biomedical device applications. In Bioelectronics and Medical Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 123–144. [Google Scholar]
- Ni, Z.; Yin, C.; Xu, G.; Xie, L.; Huang, J.; Liu, S.; Tu, J.; Guo, X.; Zhang, D. Modelling of SAW-PDMS acoustofluidics: Physical fields and particle motions influenced by different descriptions of the PDMS domain. Lab Chip 2019, 19, 2728–2740. [Google Scholar] [CrossRef]
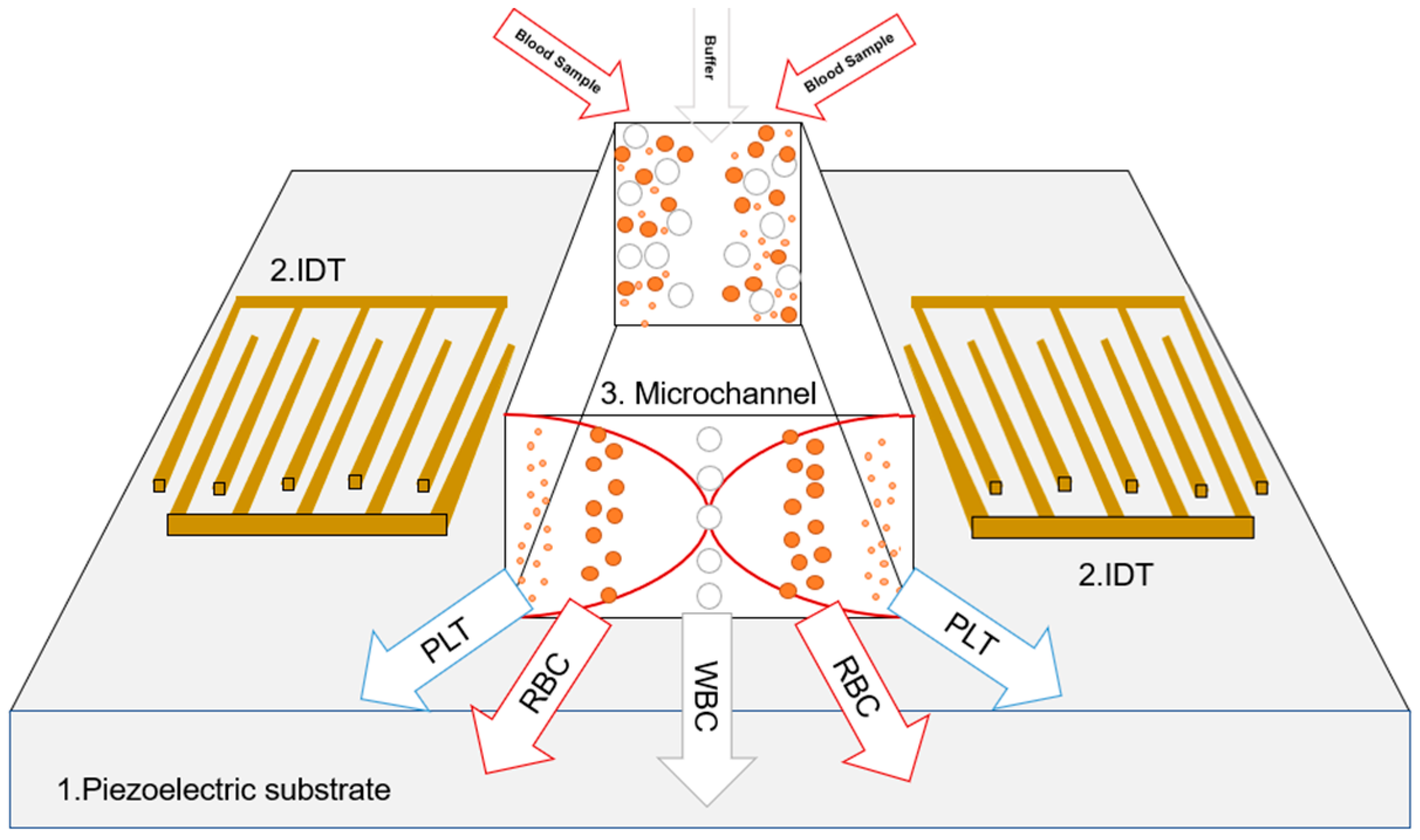






| Specification | Value | Material |
|---|---|---|
| Pitch of IDT | 40 µm | Aluminum |
| Width of IDT | 10 | |
| Number of fingers of IDT | 5 | |
| Length of IDT | 200 µm | |
| Piezoelectric substrate | 1500 µm 750 µm | LiNb |
| Microchannel | 522 µm 90 µm | Water |
| Rotation of side inlets of microchannel | 30 | |
| Rotation of outer outlets of microchannel | 60 | |
| Rotation of middle outlets of microchannel. | 45 |
| Material | Properties | Value |
|---|---|---|
| Water | Density | 998 kg/m 3998 |
| Sound speed | 1481 m/s | |
| Bulk viscosity | 2.47 | |
| Aluminum | Modulus of elasticity | 70 |
| Density | 2700 | |
| Piezoelectric substrate | Density | 4700 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajimoradi, M.; Gevari, M.T.; Pullen, K.R.; Mojaddam, M. Design and Numerical Simulation of a Standing Surface Acoustic Wave-Based Microdevice for Whole Blood Cell Separation. Computation 2025, 13, 42. https://doi.org/10.3390/computation13020042
Hajimoradi M, Gevari MT, Pullen KR, Mojaddam M. Design and Numerical Simulation of a Standing Surface Acoustic Wave-Based Microdevice for Whole Blood Cell Separation. Computation. 2025; 13(2):42. https://doi.org/10.3390/computation13020042
Chicago/Turabian StyleHajimoradi, Maryam, Moein Talebian Gevari, Keith Robert Pullen, and Mohammad Mojaddam. 2025. "Design and Numerical Simulation of a Standing Surface Acoustic Wave-Based Microdevice for Whole Blood Cell Separation" Computation 13, no. 2: 42. https://doi.org/10.3390/computation13020042
APA StyleHajimoradi, M., Gevari, M. T., Pullen, K. R., & Mojaddam, M. (2025). Design and Numerical Simulation of a Standing Surface Acoustic Wave-Based Microdevice for Whole Blood Cell Separation. Computation, 13(2), 42. https://doi.org/10.3390/computation13020042






