Abstract
In this research article, a silicon carbide (SiC) nanocluster has been designed and characterized as an anode electrode for lithium (Li), sodium (Na), potassium (K), beryllium (Be), magnesium (Mg), boron (B), aluminum (Al) and gallium (Ga)-ion batteries through the formation of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters. A vast study on energy-saving by SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC complexes was probed using computational approaches accompanying density state analysis of charge density differences (CDDs), total density of states (TDOS) and molecular electrostatic potential (ESP) for hybrid clusters of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC. The functionalization of Li, Na, K, Be, Mg, B, Al and Ga metal/metalloid elements can raise the negative charge distribution of carbon elements as electron acceptors in SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters. Higher Si/C content can increase battery capacity through SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters for energy storage processes and to improve the rate performance by enhancing electrical conductivity.
1. Introduction
Seeking alternative high-performance anodes for lithium-ion batteries was emphasized in this study. A nanomaterial with a wide bandgap semiconductor with excellent mechanical properties as silicon carbide has been pursued as the anode electrode. A major volume change during the charge–discharge of Si-based nanostructures applied as the anode electrodes for high energy lithium-ion batteries has been thought as the most serious obstacle, inhibiting their commercial usage [1,2,3,4].
Together with the low diffusion barrier, moderate open circuit voltage and excellent electronic conductivity during the sodiation, the researchers proposed that graphitic SiC is a potential material for the Na-ion battery anode. More importantly, they found that the intercalation strength of Na ions into C-based multilayer materials could be enhanced by increasing the number of covalent components in Na–C bonds, which could be realized via doping by atoms (like Li, Be, B, Al, Si or P) with lower electronegativity than that of the C atom [5,6,7,8,9].
Scientists have synthesized SiC through the combustion synthesis path. Structural investigation indicated that the achieved SiC nanowires relate mostly to 3C polytypes with a zincblend structure [10]. Recently, a new micro nanocomposite fibrous aerogel was provided using the synthesis of silicon carbide nanowires in mullite fiber preform through the incorporation of vacuum impregnation and high-temperature pyrolysis [11]. Moreover, nitrogen-doping SiC nanowires were synthesized via three various approaches to increase the conductivity loss of SiC towards improving their electromagnetic wave absorption performance [12].
The novel structure of a SiC monolayer was investigated for sodium and potassium storage using the DFT method. It was revealed that SiC exhibits negative adsorption energy during K/Na adsorption on its surface. Furthermore, the SiC monolayer can efficiently achieve a high content of Na/K loading on both sides of its surface. Additionally, it is demonstrated that the semiconducting SiC monolayer transforms into a metallic state with excellent conductivity upon Na/K adsorption. These findings underscore the potential of the SiC monolayer as a promising candidate in sodium ion batteries and potassium ion batteries [13].
Anode materials of silicon carbide and III-nitride nanosheets are investigated in magnesium ion batteries (MIBs) as possible alternative of lithium- and sodium-ion batteries. The calculated density functional theory reveals higher values of internal energy changes and cell voltages for MIBs with silicon carbide, boron nitride, aluminum nitride and gallium nitride anode materials than the previously reported carbon nanomaterials [14].
While the polarizability of Si is more than that of the C atom, it is assumed that Si-C/Si nanosurface may append to compositions more intensely in hybrid structures compared to the pure-C nanostructures [15,16,17]. The previous investigations of energy-saving devices through H-adsorption have been tailored using DFT calculations with a semiconductor group of Si/Ge/Sn/Pb nano-carbides [18], a Mg-Al nanoalloy [19] and Al/C/Si-doping of a BN nanocomposite [20]. Nanomaterials with notable structures detect undertaking demands in the field of electrocatalysis, fuel cells and energy-saving [21].
The investigations have been performed by outlining the electrochemical reaction mechanisms and challenges associated with Si-based anodes in alkali metal-ion batteries and then various approaches are presented, including the architectural engineering of Si, surface engineering of Si-based materials and the construction of Si-based composites to improve battery performance. Therefore, the anticipated challenges and opportunities in the development of silicon-based anode materials for alkali metal-ion batteries can be discussed [22].
In another study, Dong et al. used titanium silicon carbide (Ti3SiC2, TSC) to prepare a Si-based anode composite (Si/TSC) to improve the performance of LIB. TSC was used as a mechanical strengthening tool and high conductive matrix for the Si-based anode [23]. In this research, several samples were measured for their performance correlated with chemical composition variations to legislate their potency for the first time in Li-, Na-, K-, Be-, Mg-, B-, Al- or Ga-batteries.
2. Theoretical Backgrounds, Materials and Methods
The development of the applied density functional theory (DFT) methodology only became notable after W. Kohn and L. J. Sham released their reputable series of equations which are introduced as Kohn–Sham (KS) equations [24,25]:
By representing the single particle orbitals , all electronic densities physically acceptable for the system of “non-interacting” electrons are written in Equation (3):
Finally, the total energy can be measured by the KS method due to Equation (4):
Therefore, the precise exchange energy functional is described by the Kohn–Sham orbitals in lieu of the density which is cited as the indirect density functional. This research has employed the penetration of the hybrid functional of a three-parameter basis set of B3LYP (Becke, Lee, Yang and Parr) within the conception of DFT upon theoretical computations and basis sets of LANL2DZ for metal atoms and 6–311+G (d,p) for other atoms [26,27]. The popular B3LYP (Becke, three-parameter and Lee–Yang–Parr) and exchange-correlation functional is based on Equation (5) [26,27,28]:
Calculations with spin polarization were performed within density functional theory (DFT) [29]. Figure 1a–h shows Groups 1,2,13 metals-based nanoclusters of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC with the metal capacity number for Li, Na, K (+1), Be, Mg (+2), and B, Al, Ga (+3).
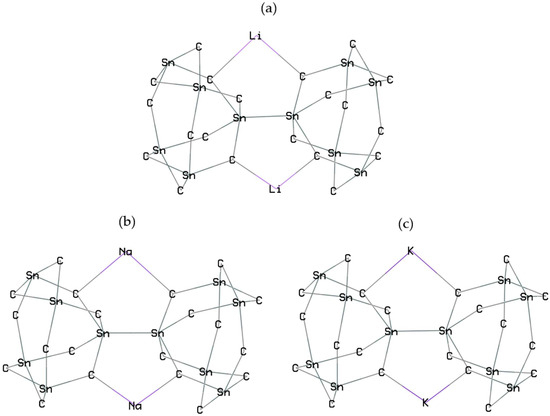
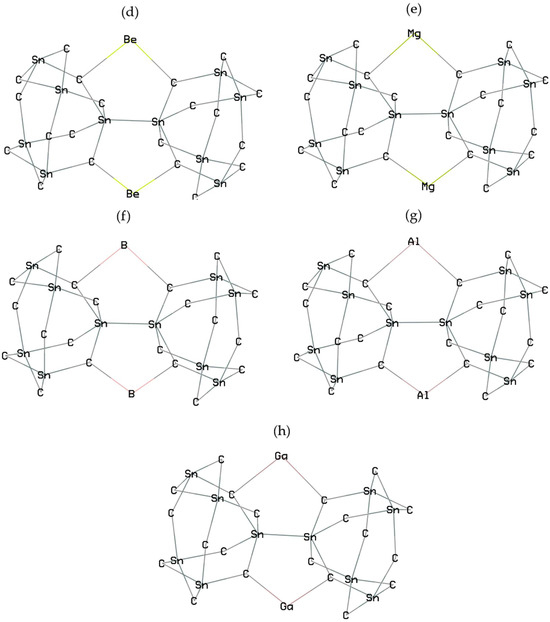
Figure 1.
Doping Li, Na, K, Be, Mg, B, Al or Ga to SiC nanocluster and formation of (a) SiLiC, (b) SiNaC, (c) SiKC, (d) SiBeC, (e) SiMgC, (f) SiBC, (g) SiAlC and (h) SiGaC complexes towards energy storage in novel batteries.
Analysis of the Bader charge parameter [30] has illustrated the energy storage by hybrid clusters of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC complexes with a multiplicity of +1, convergence on the RMS density matrix = 1 × 10−8 and convergence on MAX density matrix = 1 × 10−6 (Figure 1a–h) by Gaussian 16 revision C.01 computational software [31] and the GaussView 6.1 graphical program [32]. An algorithm existed for conducting the decomposition of electronic charge density into atomic contributions. As recommended by Bader, space is divided up into atomic zones where the dividing surfaces are at a minimum in the charge density and the gradient of the charge density is zero along the surface. Instead of indicating the dividing surfaces, the algorithm allocates each point on a regular x, y, z grid to one of the zones [30].
In this investigation, homogenously distributed silicon or carbon elements can be immobilized in the SiC matrix, which prevents their tendency to form agglomeration under battery cycling. The Li/Na/Be/Mg insertion might also result in the cleavage of some C–Li, C–Na, C–Be or C–Mg bonds in the SiC anode material and expansion, providing favorable sites for the subsequent ion insertion in the network (Figure 1a–h).
3. Results and Discussion
3.1. Charge Density Differences Analysis
In Supplementary materials Figure S1 a–h, the charge density differences (CDDs) [33] are shown for SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters with vibration in the district about −12 to +9 Bohr through co-interaction between Groups 1,2,13 metals of Li(31)–Li(32), Na(31)–Na(32), K(31)–K(32), Be(31)–Be(32), Mg(31)–Mg(32), B(31)–B(32), Al(31)–Al(32) and Ga(31)–Ga(32). Moreover, the elements of C(2), C(3), C(7)–C(12), C(14), C(15), C(17), C(18), C(22)–C(27), C(29) and C(30) from SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters displayed a vibration of about −12 to +9 Bohr (Figure S1 a–h).
The charge distribution has been illustrated in Groups 1,2,13 metals captured by the SiC nanostructure towards the formation of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters, respectively (Table S1). The functionalization of Li, Na, K, Be, Mg, B, Al or Ga atoms can augment the negative atomic charge of C(2), C(3), C(7)–C(12), C(14), C(15), C(17), C(18), C(22)–C(27), C(29) and C(30) as electron acceptors in SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC, SiGaC nanoclusters (Figure 2a–h).
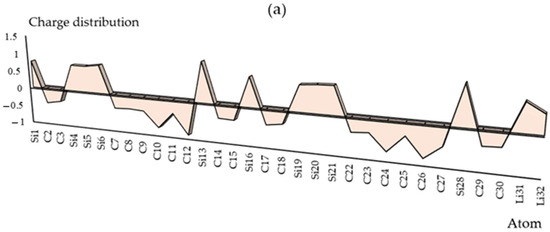
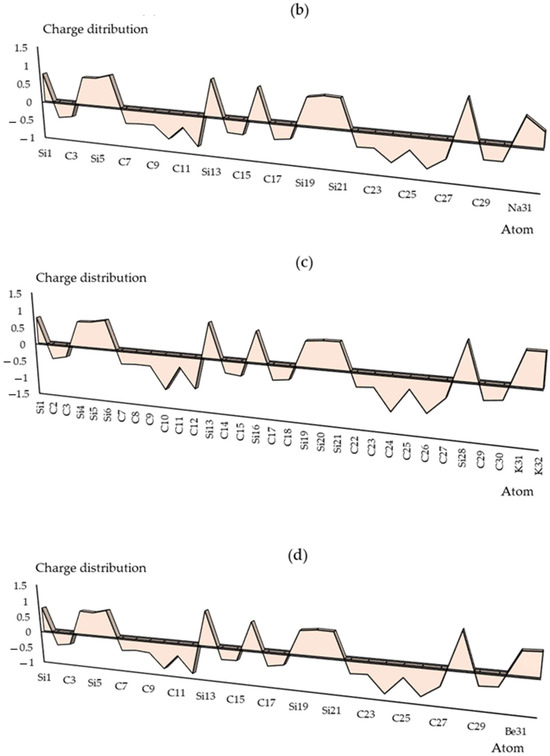
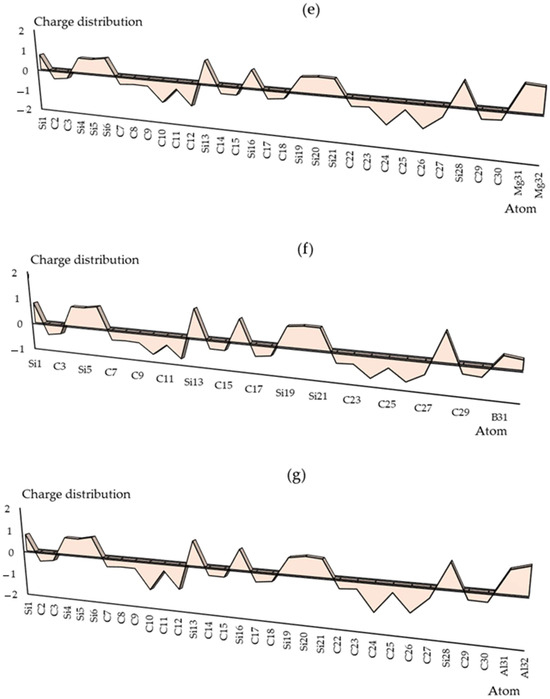
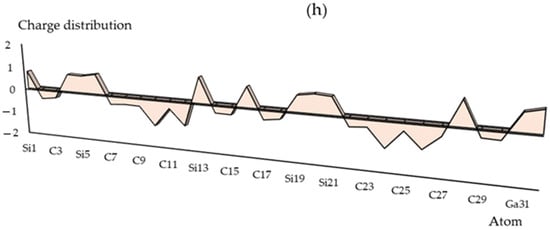
Figure 2.
The changes in charge distribution for (a) SiLiC, (b) SiNaC, (c) SiKC, (d) SiBeC, (e) SiMgC, (f) SiBC, (g) SiAlC and (h) SiGaC nanoclusters.
Electronic metal–carbon interactions play a fundamental role in tuning the electrocatalytic behavior of the metal active phase. The basis of the metal–carbon interaction is the presence of topological and structural defects as well as the heteroatom functional group, silicon, which breaks the perfect symmetry of the graphene layer, providing preferential nucleation and growth sites for metal nanoparticles and single metal site. As can be seen in Figure 2, the electronic states of carbon sites in SiC near the valence band have an electron acceptor character, while the metal ions sites have an electron donor character.
3.2. Total Density of States
In an isolated system (such as a molecule), energy levels are discrete; the concept of “density of state (DOS)” is supposed to be completed with total density of states (TDOS). Therefore, the “original total DOS (TDOS)” of an isolated system can be written as the following [34]:
The normalized Gaussian function is defined as:
“FWHM (full width at half maximum)” is an adjustable parameter in “Multiwfn” [35,36]. While the curve map of “broadened partial DOS (PDOS)” and “overlap DOS (OPDOS)” are valuable for visualizing orbital composition analysis, the “PDOS function of fragment A” is defined as:
where “ is the composition of fragment A in orbital i”. The “OPDOS between fragment A and B” is defined as:
where “ is the composition of total cross term between fragment A and B in orbital i”.
Regarding energy storage by SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters, the TDOSs has been evaluated. This factor can demonstrate the existence of important chemical interactions often on the “convex side” (Figure 3a–h).
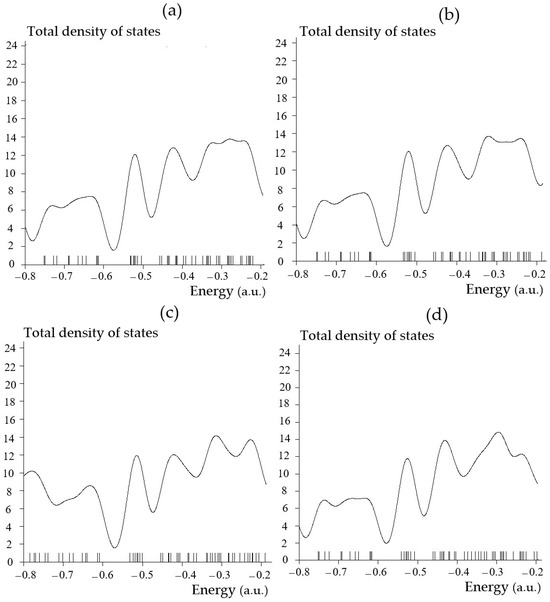
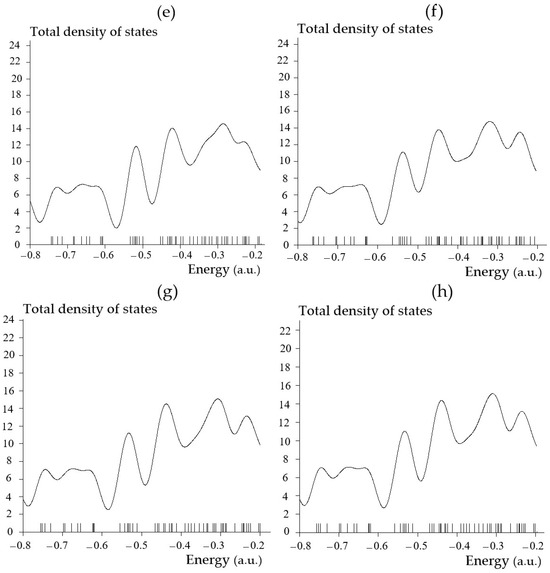
Figure 3.
The graphs of total density of states (TDOSs) graphs versus energy (a.u.) of (a) SiLiC, (b) SiNaC, (c) SiKC, (d) SiBeC, (e) SiMgC, (f) SiBC, (g) SiAlC and (h) SiGaC nanoclusters.
Substitution engineering is an effective modification strategy to enhance the electrochemical performance of electrode materials. In this investigation, the impacts of heteroatom decorating in SiC nanoclusters by substituting the Li atom with heteroatoms (Na, K, Be, Mg, B, Al, and Ga) on the adsorption of main group metals have been systematically investigated using first-principles calculations to evaluate the material performance for application in metal-ion batteries. Therefore, monolayer SiC with heteroatom doping can be applied as a potential anode for metal-ion batteries. This research can clarify the effects of heteroatom decorating and design high-performance electrodes for rechargeable batteries.
3.3. Molecular Electrostatic Potential (ESP)
Molecular electrostatic potential (ESP) has been widely used for the prediction of nucleophilic and electrophilic sites for a long time. It is also valuable in studying hydrogen bonds, halogen bonds, molecular recognitions and the intermolecular interactions of aromatics [37]. This function measures the electrostatic interaction between a unit point charge placed at r and the system of interest. A positive (negative) value implies that the current position is dominated by nuclear (electronic) charges.
ZA is nuclear charge, if pseudopotential is used, then ZA is the number of explicitly expressed electrons. Notice that evaluating ESP is much more time consuming than evaluating other functions. Also note that the ESP in Multiwfn [35,36] is evaluated exactly by nuclear attractive integrals rather than using approximate methods (such as multipole expansion or the numerical Poisson equation); hence, you may find the results generated by Multiwfn [35,36] are somewhat different from those outputted by other quantum chemistry codes. In order to speed up ESP evaluation, Multiwfn [35,36] ignores some integrals that have little contributions. The threshold for ignoring is controlled by “espprecutoff” in settings.ini, enlarging this parameter results in a more accurate ESP value, but also brings more computational cost. The ESP evaluated under default value is accurate enough in general cases.
Trapping of Li, Na, K, Be, Mg, B, Al or Ga atoms by SiC nanostructures (Figure S2a–h) towards the formation of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters (Figure S2a–h).
SiLiC (Figure S2a), SiNaC (Figure S2b), SiKC (Figure S2c), SiBeC (Figure S2d), SiMgC (Figure S2e), SiBC (Figure S2f), SiAlC (Figure S2g) and SiGaC (Figure S2h) have demonstrated electron delocalization through an isosurface map with labeling atoms of C(10), C(12), Si(13), C(24), C(26), Si(28) and X(31)/X(32) (X= Li, Na, K, Be, Mg, B, Al, Ga). In fact, the counter-map of ESP can confirm that SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters may augment the efficiency of energy storage (Figure S2a–h and Table 1).

Table 1.
Cell capacity (C, mAh g−1), dipole moment (D/debye), HOMO(eV), LUMO (eV), energy gap (∆E= ELUMO − EHOMO/eV) and stability energy (Es/kcal/mol) for SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters.
Battery capacity is a measure of a battery’s ability to store a certain amount of charge or energy. It represents the amount of electricity or energy generated due to electrochemical reactions in the battery. It can be defined as battery charge capacity, measured in Ah. The nominal capacity is defined for a new battery used under controlled conditions. Battery state-of-charge is a measure of the amount of charge currently stored in a battery with respect to the fully charged battery. Finally, battery state-of-health is a measure of the overall battery condition [38,39]:
where F, n and M are Faraday constants, the metal capacity numbers for Li, Na, K (+1), Be, Mg (+2), and B, Al, Ga (+3) and the molecular wight, respectively, in the mentioned nanoclusters.
Moreover, the intermolecular orbital overlap integral is important in discussions of intermolecular charge transfer which can calculate HOMO–HOMO and LUMO–LUMO overlap integrals between the Groups 1,2,13 metals and silicon carbide (Table 1). The energy gap ΔE (ELUMO − EHOMO) has shown positive chemical potential mainly related to stability. When the softness is lower than hardness, this means that the compounds are highly stable. The smaller the energy gap ΔE, the greater the reactivity of a molecule. Therefore, replacing Li in SiLiC with another main group metal consisting of Na, K, Be, Mg, B, Al or Ga can enhance the potential utility of SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters in battery energy storage.
In addition, the amount of “Mayer bond order” [40] is generally according to the empirical bond order for the single bond and is nearly 1.0. “Mulliken bond order” [41] with a small accord, alongside empirical bond order, is not appropriate for quantifying bonding strength, for which Mayer bond order always performs better. However, “Mulliken bond order” is a good qualitative indicator for the “positive amount” of bonding and “negative amount” of antibonding which are evacuated and localized, respectively (Table S2).
As is seen in Table S2, the “Laplacian bond order” [42] has a straight cohesion with bond polarity, bond dissociation energy and bond vibrational frequency. The low value of Laplacian bond order might demonstrate that it is insensitive to the calculation degree applied for producing electron density. Generally, the value of “Fuzzy bond order” (Table 2) is near that of the Mayer bond order, especially for low-polar bonds, but much more stable with respect to the change in the basis-set. Computation of “Fuzzy bond order” demands running “Becke’s DFT” numerical integration, owing to which the calculation value is larger than the assessment of the “Mayer bond order” and it can concede more precisely [43]. In the sample of Fuzzy nanoclustering, these intervals are further weighted by the membership degrees. The better the data objects are allocated to nanoclusters, the smaller the error, the greater the density. However, this measurement does not explicitly take the dissociation of different objects into account.

Table 2.
The bond order of Fuzzy from mixed-alpha and beta-density matrix for SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters.
4. Conclusions
Groups of 1,2,13 metals captured by silicon carbide towards the formation of SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC nanoclusters were studied by computational methods through a qualitative screening. The changes in charge density are defined as a notable charge transfer in SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC and SiGaC. Due to the semiconducting nature of SiC, it is usually composited with C for better ionic and electronic conductivities. It is well established that enhancing Li, Na, K, Be, Mg, B, Al or Ga to cell batteries can augment the energy saving properties of cell batteries.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation13110265/s1, Figure S1: CDD graphs for (a) SiLiC, (b) SiNaC, (c) SiKC, (d) SiBeC, (e) SiMgC, (f) SiBC, (g) SiAlC, (h) SiGaC nanoclusters; Figure S2: The shaded (left side) and counter (right side) maps of ESP graphs versus length unit (Bohr) for (a) SiLiC, (b) SiNaC, (c) SiKC, (d) SiBeC, (e) SiMgC, (f) SiBC, (g) SiAlC, (h) SiGaC nanoclusters; Table S1: The atomic charge (Q/coulomb) for SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC, SiGaC nanoclusters; Table S2. The bond order of Mayer, Wiberg, Mulliken and Laplacian from mixed alpha and beta density matrix for SiLiC, SiNaC, SiKC, SiBeC, SiMgC, SiBC, SiAlC, SiGaC nanoclusters.
Author Contributions
Conceptualization, F.M.; Methodology, F.M. and M.M.; Software, F.M. and M.M.; Validation, F.M. and M.M.; Formal Analysis, F.M. and M.M.; Investigation, M.M.; Resources, M.M.; Data Curation, F.M. and M.M.; Writing—Original Draft, F.M.; Writing—Review and Editing, M.M.; Visualization, F.M. and M.M.; Supervision, F.M.; Project Administration, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fan, X.; Deng, D.; Li, Y.; Wu, Q.-H. Recent Progress in SiC Nanostructures as Anode Materials for Lithium-Ion Batteries. Curr. Mater. Sci. 2023, 16, 18–29. [Google Scholar] [CrossRef]
- Zhao, X.; Lehto, V.P. Challenges and prospects of nanosized silicon anodes in lithium-ion batteries. Nanotechnology 2021, 32, 042002. [Google Scholar] [CrossRef]
- Wen, Q.; Qu, F.; Yu, Z.; Graczyk-Zajac, M.; Xiong, X.; Riedel, R. Si-based polymer-derived ceramics for energy conversion and storage. J. Adv. Ceram. 2022, 11, 197–246. [Google Scholar] [CrossRef]
- Ge, M.; Cao, C.; Biesold, G.M.; Sewell, C.D.; Hao, S.-M.; Huang, J.; Zhang, W.; Lai, Y.; Lin, Z. Silicon Anodes: Recent Advances in Silicon-Based Electrodes: From Fundamental Research toward Practical Applications. Adv. Mater. 2021, 33, 2004577. [Google Scholar] [CrossRef] [PubMed]
- Shao, G.; Hanaor, D.A.H.; Wang, J.; Kober, D.; Li, S.; Wang, X.; Shen, X.; Bekheet, M.F.; Gurlo, A. Polymer-Derived SiOC Integrated with a Graphene Aerogel As a Highly Stable Li-Ion Battery Anode. ACS Appl. Mater. Interfaces 2020, 12, 46045. [Google Scholar] [CrossRef] [PubMed]
- Mollaamin, F. Anchoring of 2D layered materials of Ge5Si5O20 for (Li/Na/K)-(Rb/Cs) batteries towards Eco-friendly energy storage. BMC Chem. 2025, 19, 233. [Google Scholar] [CrossRef]
- Wilamowska-Zawlocka, M.; Puczkarski, P.; Grabowska, Z.; Kaspar, J.; Graczyk-Zajac, M.; Riedel, R.; Sorarù, G.D. Silicon oxycarbide ceramics as anodes for lithium ion batteries: Influence of carbon content on lithium storage capacity. RSC Adv. 2016, 6, 104597. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. In Situ Ti-Embedded SiC as Chemiresistive Nanosensor for Safety Monitoring of CO, CO2, NO, NO2: Molecular Modelling by Conceptual Density Functional Theory. Russ. J. Phys. Chem. B 2024, 18, 49–66. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, C.; Xiao, B.; Li, Y.; Cheng, J.; Liu, Z.; Yang, X.; Xu, X.; Cui, H.; Li, Q. Graphitic SiC: A potential anode material for Na-ion battery with extremely high storage capacity. Int. J. Quantum Chem. 2021, 121, e26608. [Google Scholar] [CrossRef]
- Huczko, A.; Dąbrowska, A.; Savchyn, V.; Popov, A.I.; Karbovnyk, I. Silicon carbide nanowires: Synthesis and cathodoluminescence. Phys. Status Solidi (B) 2009, 246, 2806–2808. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Tong, Z.; Zhang, B.; Ji, H. Thermal Radiation Shielding and Mechanical Strengthening of Mullite Fiber/SiC Nanowire Aerogels Using In Situ Synthesized SiC Nanowires. Materials 2022, 15, 3522. [Google Scholar] [CrossRef]
- Shi, R.; Liu, Z.; Liu, W.; Kuang, J. Preparation and Electromagnetic Wave Absorption Properties of N-Doped SiC Nanowires. Materials 2023, 16, 5765. [Google Scholar] [CrossRef]
- Peng, Q.; Rehman, J.; Ullah, M.; Tighezza, A.M.; Hanif, M.B.; Shibl, M.F.; Dai, J. Anchoring of K and Na on the surface of a novel SiC monolayer: First-principles predictions. J. Energy Storage 2024, 104, 114435. [Google Scholar] [CrossRef]
- Khan, A.A.; Ahmad, R.; Ahmad, I. Silicon carbide and III-Nitrides nanosheets: Promising anodes for Mg-ion batteries. Mater. Chem. Phys. 2021, 257, 123785. [Google Scholar] [CrossRef]
- Kamiński, M.; Król, K.; Kwietniewski, N.; Myśliwiec, M.; Sochacki, M.; Stonio, B.; Kisiel, R.; Martychowiec, A.; Racka-Szmidt, K.; Werbowy, A.; et al. The Overview of Silicon Carbide Technology: Status, Challenges, Key Drivers, and Product Roadmap. Materials 2025, 18, 12. [Google Scholar] [CrossRef] [PubMed]
- HaTaha, O.; El Mahdy, A.M.; El Sayed El Shemy, F.; Hassan, M.M. Hydrogen storage in SiC, GeC, and SnC nanocones functionalized with nickel, Density Functional Theory—Study. Int. J. Quantum Chem. 2023, 123, e27023. [Google Scholar] [CrossRef]
- Wei, T.; Zhou, Y.; Sun, C.; Guo, X.; Xu, S.; Chen, D.; Tang, Y. An intermittent lithium deposition model based on CuMn-bimetallic MOF derivatives for composite lithium anode with ultrahigh areal capacity and current densities. Nano Res. 2024, 17, 2763–2769. [Google Scholar] [CrossRef]
- Yadav, A. Monolayered Carbides of Main Group Elements (Si, Ge, Sn and Pb) for NO2 Gas Sensing: Insights from First-Principle Studies. Silicon 2022, 14, 12683–12692. [Google Scholar] [CrossRef]
- Liu, W.; Li, S.; Pan, H.; Zhang, Y.; Pan, Z.; Wang, S.; Ren, Y.; Qin, G. Development of Novel Mg-Al-Mn-Based Alloys with High-Strength and Ductility via Co-Addition of Ce and Ca. Metals 2025, 15, 361. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Electric and Magnetic Evaluation of Aluminum–Magnesium Nanoalloy Decorated with Germanium Through Heterocyclic Carbenes Adsorption: A Density Functional Theory Study. Russ. J. Phys. Chem. B 2023, 17, 658–672. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Adsorption ability of Ga5N10 nanomaterial for removing metal ions contamination from drinking water by DFT. Int. J. Quantum Chem. 2024, 124, e27348. [Google Scholar] [CrossRef]
- Tareq, F.K.; Rudra, S. Enhancing the performance of silicon-based anode materials for alkali metal (Li, Na, K) ion battery: A review on advanced strategies. Mater. Today Commun. 2024, 39, 108653. [Google Scholar] [CrossRef]
- Dong, Z.; Gu, H.; Du, W.; Feng, Z.; Zhang, C.; Jiang, Y.; Zhu, T.; Chen, G.; Chen, J.; Liu, Y. Si/Ti3SiC2 composite anode with enhanced elastic modulus and high electronic conductivity for lithium-ion batteries. J. Power Sources 2019, 431, 55–62. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Glenna, D.M.; Jana, A.; Perez, C.M.; Qian, J. Real-space Kohn–Sham density functional theory for complex energy applications. Chem. Commun. 2025, 61, 10273–10286. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Feng, H.; Cheng, Z.; Lu, Z.; He, Q. Advances in DFT-Based Computational Tribology: A Review. Lubricants 2025, 13, 483. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dennington, R.; Keith, T.A.; Millam, J.M. (Eds.) GaussView, Version 6.06.16; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Xu, Z.; Qin, C.; Yu, Y.; Jiang, G.; Zhao, L. First-principles study of adsorption, dissociation, and diffusion of hydrogen on α-U (110) surface. AIP Adv. 2024, 14, 055114. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Graphene-based resistant sensor decorated with Mn, Co, Cu for nitric oxide detection: Langmuir adsorption & DFT method. Sens. Rev. 2023, 43, 266–279. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Lu, T. A comprehensive electron wavefunction analysis toolbox for chemists, Multiwfn. J. Chem. Phys. 2024, 161, 082503. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Wu, S.; Ren, M. Industrial Basic Capacity Research: Theory and Measurement. Systems 2024, 12, 502. [Google Scholar] [CrossRef]
- Bašić, H.; Bobanac, V.; Pandžić, H. Determination of Lithium-Ion Battery Capacity for Practical Applications. Batteries 2023, 9, 459. [Google Scholar] [CrossRef]
- Mayer, I. Improved definition of bond orders for correlated wave functions. Chem. Phys. Lett. 2012, 544, 83–86. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Doping of Graphene Nanostructure with Iron, Nickel and Zinc as Selective Detector for the Toxic Gas Removal: A Density Functional Theory Study. C 2023, 9, 20. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Bond Order Analysis Based on the Laplacian of Electron Density in Fuzzy Overlap Space. J. Phys. Chem. A 2013, 117, 3100–3108. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Pedrycz, W.; Yang, S.-H.; Boutat, D. Consensus of T-S Fuzzy Fractional-Order, Singular Perturbation, Multi-Agent Systems. Fractal Fract. 2024, 8, 523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).