Computation in Algebraic Hyperstructures
Abstract
1. Introduction
2. Overview of Hypercompositional Structures
3. A General Definition for the Relation
3.1. The Fundamental Relation on Hypergroupoids
- We say that ρ is regular on the right if for all ,Similarly, the regularity on the left can be defined. An equivalence relation that is both regular on the right and regular on the left is called regular.
- We say that ρ is strongly regular on the right if for all ,Similarly, the strong regularity on the left can be defined. An equivalence relation that is both strongly regular on the right and on the left is called strongly regular.
- for all .
3.2. The Heart of a Hypergroup and of an -Group
4. Computing the Set of Finite Hyperproducts and the Relation in a Hypergroupoid
- Manually, filling the subset into a matrix for each pair ;
- Automatically, using a defining function that specifies the hyperoperation for all such pairs.
| Listing 1. Example of input data. |
 |
| Listing 2. The b_hypercomposition on H = {a,b,c}. |
 |
| Listing 3. MatLab code for new_from_function. |
 |
| Algorithm 1 Computation of the set of all finite hyperproducts. |
Input: finite set H and Cayley table M defining a hyperoperation Output: of all finite hyperproducts
|
| Algorithm 2 Computation of the relation. |
Input: finite set H and Cayley table M defining a hyperoperation Output:
|
4.1. An Increasing Chain of Subsets of H to Compute
- (the set of singletons);
- For , .
- for all .
- The sequence must eventually stabilize; that is, there exists such that for all . We will call m the stabilization index.
- Let m be the stabilization index. Then m is the minimum value such that .
- It follows immediately by Definition 4.
- By Item 1, we have that extends to for all . But for all , and since H is finite, so is . Therefore, the sequence must eventually stabilize to some finite number .
- It is enough to prove that if is such that , then for all , and hence . We use induction in j. The base case follows from the hypothesis. Assuming , we prove . Since we also have . It follows that
| ∘ | z1 | z2 | z3 | z4 |
| z1 | {z1} | {z2} | {z3,z4} | {z4} |
| z2 | {z2} | {z1,z2} | {z3,z4} | {z3,z4} |
| z3 | {z3} | {z3,z4} | {z1,z2} | {z1,z2} |
| z4 | {z3,z4} | {z3,z4} | {z1,z2} | {z1,z2} |
4.2. Algorithm Computing and
| Algorithm 3 Warshall algorithm for transitive closure. |
Input: A finite set H, a relation on H Output: The transitive closure
|
5. Computation of the Heart in Hypergroups and -Groups
- Step 1:
- Find the -equivalence classes of H.
- Step 2:
- Find at least one partial identity . (Note that not all hypergroups have identities, but every hypergroup has partial identities.)
- Step 3:
- Determine the heart by finding the -equivalence class of e.
- Step 1:
- Find the quotient set .
- Step 2:
- Implement the hyperoperation as in Equation (1), which will turn it into the fundamental group.
- Step 3:
- Find the identity and obtain the elements in its class.
5.1. Computation of the Heart of a Hypergroup
| Algorithm 4 Computation of partial identities in H. |
Input: A finite set H, the Cayley table M defining a hyperoperation Output: The set of partial identities in H
|
| Algorithm 5 Computation of the class of an element with respect to an equivalence . |
Input: A finite set H, an element x in H, an equivalence Output: The -class of x
|
| Algorithm 6 Compute the heart of a hypergroup. |
Input: A finite set H, the Cayley table M Output: The heart
|
5.2. Computation of the Heart of an -Group
| Algorithm 7 Compute the quotient set of H modulo an equivalence . |
Input: A finite set H, an equivalence relation Output: The quotient set
|
| Algorithm 8 Computation of the fundamental group. |
Input: A finite set H, a Cayley table M defining a hyperoperation Output: The fundamental group
|
| Algorithm 9 Computation of identities in H. |
Input: A finite set H, a Cayley table M defining the hyperoperation Output: The set of identities in H
|
6. Experimental Analysis of the Stabilization Index
- The mean stabilization index m remains small and increases only slightly with , staying close to 3 even for .
- The ratio decreases, supporting the hypothesis that m grows most sublinearly with the cardinality of H.
- Standard deviations decrease slightly as cardinality increases, indicating that larger random hypergroupoids tend to have even more consistent stabilization indices.
- The minimum and maximum values show that, although the mean is stable, some variation still exists among random instances.
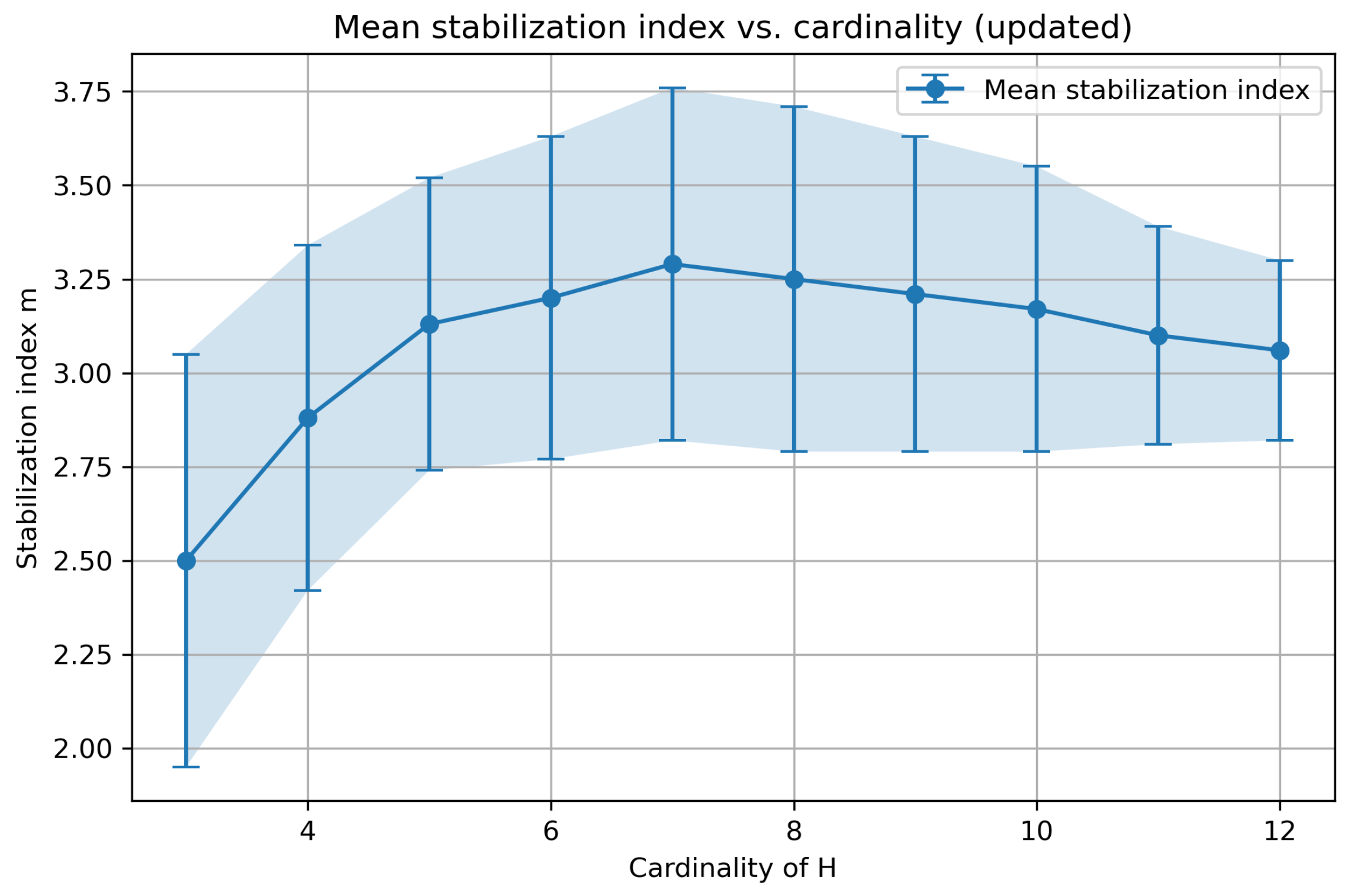
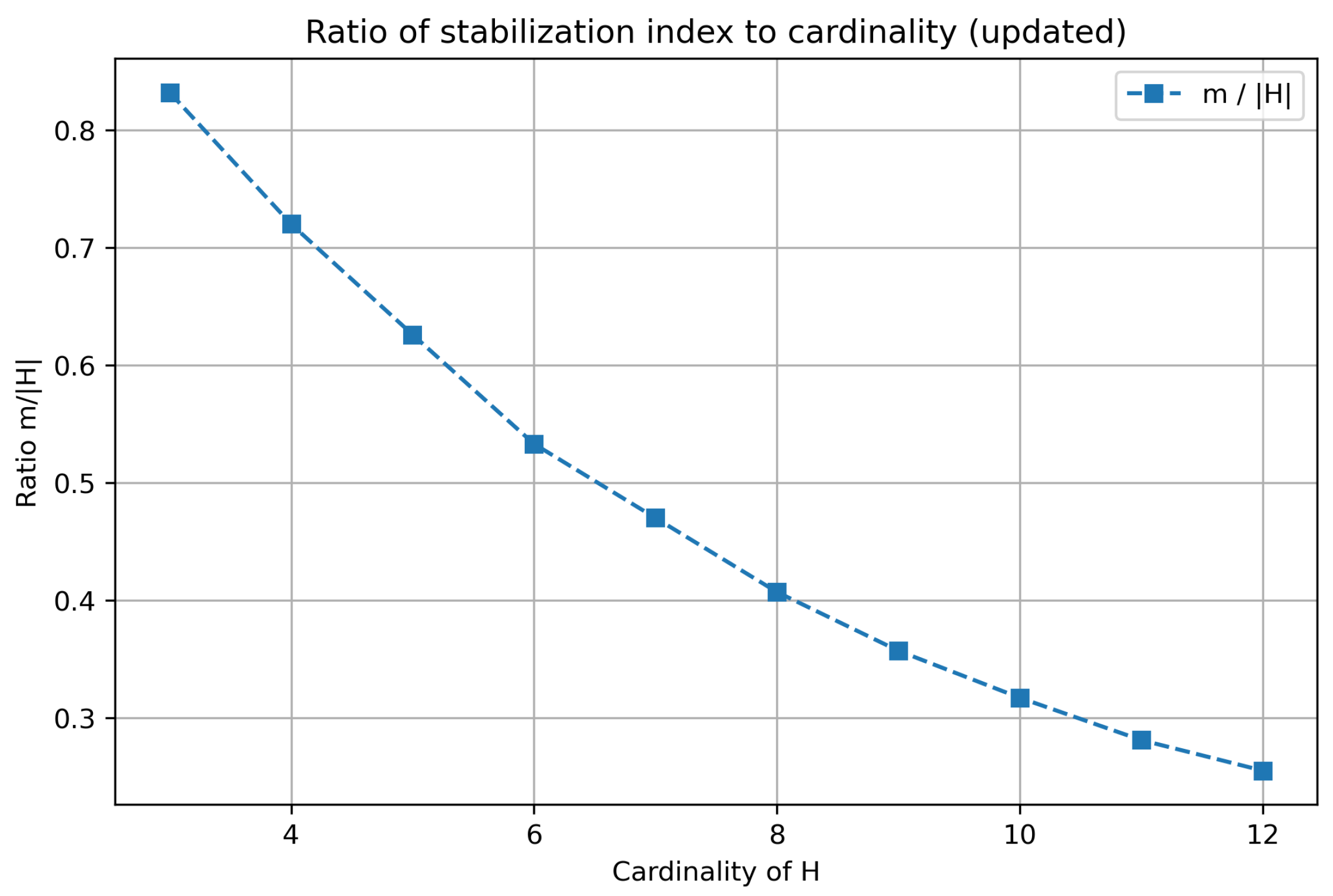

| Mean m | Std. Dev. | Min | Max | Ratio | |
|---|---|---|---|---|---|
| 3 | 2.50 | 0.55 | 2 | 4 | 0.832 |
| 4 | 2.88 | 0.46 | 2 | 4 | 0.720 |
| 5 | 3.13 | 0.39 | 2 | 6 | 0.626 |
| 6 | 3.20 | 0.43 | 3 | 6 | 0.533 |
| 7 | 3.29 | 0.47 | 3 | 5 | 0.470 |
| 8 | 3.25 | 0.46 | 3 | 5 | 0.407 |
| 9 | 3.21 | 0.42 | 3 | 5 | 0.357 |
| 10 | 3.17 | 0.38 | 3 | 5 | 0.317 |
| 11 | 3.10 | 0.29 | 3 | 4 | 0.281 |
| 12 | 3.06 | 0.24 | 3 | 4 | 0.255 |
7. A Matlab R2018B Session
| Listing 4. A hypercompositional structure of order 7. |
 |
| Listing 5. Verification of hypergroup axioms for H7. |
 |
| Listing 6. Partial identities analysis. |
 |
| Listing 7. Computation of the heart of H7. |
 |
| Listing 8. Computation of the heart of a Hv-group. |
 |
| Listing 9. Computation of the heart of a Hv-group. |
 |
8. Computational Performance of Heart Computation in Hypergroups
| Algorithm 10 Computation of the heart of an -group(). |
Input: A finite set H, a Cayley table M defining the hyperoperation Output: The heart
|
8.1. Execution Time Analysis in MatLab R2018b
| Listing 10. Execution times for the computation of the heart of H7 in MATLAB. |
 |
8.2. Execution Time Analysis in Rust version 1.91.0
8.3. Complexity Analysis
9. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marty, F. Sur une généralisation de la notion de groupe. In Proceedings of the 8 ème Congrès des Mathématiciens, Scandinaves, Stockholm, Sweden, 14–18 August 1934; pp. 45–49. [Google Scholar]
- Krasner, M.; Kuntzmann, J. Remarques sur les hypergroupes. C. R. Acad. Sci. 1947, 224, 525–527. [Google Scholar] [CrossRef]
- Krasner, M. Sur la Primitivité des Corps B-Adiques; Mathematica: Cluj, Romania, 1937; Volume 13, pp. 72–191. [Google Scholar]
- Wall, H.S. Hypergroups. Amer. J. Math. 1937, 59, 77–98. [Google Scholar] [CrossRef]
- Dresher, M.; Ore, O. Theory of Multigroups. Amer. J. Math. 1938, 60, 705–733. [Google Scholar] [CrossRef]
- Feng, Y.; Leoreanu-Fotea, V. Algorithm for Determining the Strong Fuzzy Grade of a Hypergroup. Algorithms 2025, 18, 540. [Google Scholar] [CrossRef]
- Pourhaghani, A.; Anvariyeh, S.M.; Davvaz, B. Algorithms for Finding Specific Elements in Algebraic Hyperstructures with One Hyperoperation. Math. Int. Res. 2025, 10, 49–70. [Google Scholar]
- Pourhaghani, A.; Anvariyeh, S.M.; Davvaz, B. An algorithm to calculate the members of the relation β in hypergroupoids. J. Algebr. Hyperstruct. Log. Algebr. 2024, 5, 137–152. [Google Scholar] [CrossRef]
- Corsini, P. Prolegomena of Hypergroup Theory; Aviani: Udine, Italy, 1993. [Google Scholar]
- Corsini, P.; Leoreanu, V. Applications of Hyperstructure Theory; Advances in Mathematics; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2003. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Hyperring Theory and Applications; International Academic Press: Palm Harbor, FL, USA, 2008. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Krasner Hyperring Theory; World Scientific: Singapore, 2024. [Google Scholar]
- Davvaz, B. Semihypergroups Theory; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Davvaz, B.; Vougiouklis, T. A Walk Through Weak Hyperstructures; World Scientific Publishing Company: Singapore, 2018. [Google Scholar] [CrossRef]
- Davvaz, B.; Leoreanu-Fotea, V. Hypergroup Theory; World Scientific Book: Singapore, 2022; ISBN 978–9811249389. [Google Scholar]
- Massouros, G.G. On the hypergroup theory. In Fuzzy Systems & AI-Reports and Letters; Romanian Academy: Bucharest, Romania, 1995; Volume 4. [Google Scholar]
- Massouros, C.; Massouros, G. An Overview of the Foundations of the Hypergroup Theory. Mathematics 2021, 9, 1014. [Google Scholar] [CrossRef]
- Massouros, G. Hypercompositional Structures in the Theory of the Languages and Automata. Sci. Ann. Cuza Univ. 1994, 3, 65–74. [Google Scholar]
- Massouros, G.; Massouros, C. Hypercompositional Algebra, Computer Science and Geometry. Mathematics 2020, 8, 1338. [Google Scholar] [CrossRef]
- Leoreanu-Fotea, V.; Hoskova-Mayerova, S. Join Spaces and Lattices. Axioms 2024, 13, 705. [Google Scholar] [CrossRef]
- Koskas, M. Groupoides, Demi-hypergroupes et hypergroupes. J. Math. Pures Appl. 1970, 49, 155–192. [Google Scholar]
- Sureau, Y. Hypergroupes opérant transitivement sur un ensemble. In Annales Scientifiques de l’Université de Clermont; Mathématiques; UER de Sciences Exactes et Naturelles de l’Université de Clermont: Clermont-Ferrand, France, 1979; Volume 68, pp. 83–96. [Google Scholar]
- Freni, D. A note on the core of a hypergroup and on the transitive closure β★ of β. Riv. Mat. Pura Appl. 1991, 8, 153–156. [Google Scholar]
- Leoreanu, V. On the heart of join spaces and of regular hypergroups. Riv. Mat. Pura Appl. 1996, 17, 133–142. [Google Scholar]
- Leoreanu, V. The heart of some important classes of hypergroups. Pure Math. Appl. 1998, 9, 351–360. [Google Scholar]
- Leoreanu, V. The class of hypergroups in which the heart is the set of identities. Mathematics 1999, 54, 49–54. [Google Scholar]
- Hošková-Mayerová, Š.; Antampoufis, N. A Brief Survey on the Two Different Approaches of Fundamental Equivalence Relations on Hyperstructures. Ratio Math. 2017, 33, 47–60. [Google Scholar]
- Vougiouklis, T. Fundamental relations in hyperstructures. Bull. Greek Math. Soc. 1999, 42, 113–118. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press: Palm Harbor, FL, USA, 1994. [Google Scholar]
- Tahan, M.A.; Davvaz, B. Hv module of functions over Hv ring of arithmetics and its fundamental modules. An. St. Univ. Ovidius Constanţa 2024, 32, 5–18. [Google Scholar]
- Zare, A.; Davvaz, B. On topological quotient hyperrings and α*-relation. An. St. Univ. Ovidius Constanța 2025, 33, 179–193. [Google Scholar]
- Dramalidis, A. Geometical Hv-Structures. Structure Elements of Hyperstructures. In Proceedings of the 13-AHA Conference-Algebraic Hyperstructures and Their Applications, Samothrace, Greece, 1–9 September 2002; Lygeros, N., Vougiouklis, T., Eds.; Spanidis Press: Alexandoupolis, Greece, 2005; pp. 41–52. [Google Scholar]
- Talotti, E. Heart_Hypergroups, GitHub Repository. 2025. Available online: https://github.com/enh11/heart_hypergroups (accessed on 30 September 2025).
- Talotti, E. Hypercompositional_Structures, GitHub Repository. 2025. Available online: https://github.com/enh11/hypercompositional_structures (accessed on 15 October 2025).
- Rosen, K. Discrete Mathematics and Its Applications, 8th ed.; McGraw Hill: New York, NY, USA, 2018. [Google Scholar]
| Method | Time (s) |
|---|---|
| Shortcut (Algorithm 6) | 0.138 |
| Naive -group method | 0.539 |
| Method | Time |
|---|---|
| Shortcut (Algorithm 6) | 142.956 s |
| Naive -group method | 7.55193 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Talotti, E.; Leoreanu-Fotea, V. Computation in Algebraic Hyperstructures. Computation 2025, 13, 261. https://doi.org/10.3390/computation13110261
Feng Y, Talotti E, Leoreanu-Fotea V. Computation in Algebraic Hyperstructures. Computation. 2025; 13(11):261. https://doi.org/10.3390/computation13110261
Chicago/Turabian StyleFeng, Yuming, Enrico Talotti, and Violeta Leoreanu-Fotea. 2025. "Computation in Algebraic Hyperstructures" Computation 13, no. 11: 261. https://doi.org/10.3390/computation13110261
APA StyleFeng, Y., Talotti, E., & Leoreanu-Fotea, V. (2025). Computation in Algebraic Hyperstructures. Computation, 13(11), 261. https://doi.org/10.3390/computation13110261







