Abstract
Accurate geoid determination is essential for height system unification and for converting Global Navigation Satellite System (GNSS) ellipsoidal heights to orthometric heights. This study demonstrates a national-scale workflow that integrates digitized Soviet-era gravimetric maps at 1:200,000 scale with modern satellite and ancillary datasets to compute a high-resolution gravimetric geoid for Kazakhstan. Legacy gravity maps were systematically digitized, harmonized, and quality-controlled, then integrated with a global geopotential model (XGM2019e_2159) for long-wavelength information and a digital elevation model (FABDEM) for terrain corrections. Geoid computation employed the Least-Squares Modification of Stokes’ Formula, with spectral testing used to select optimal parameters; external control and validation relied on an extensive set of GNSS observations and geometric levelling benchmarks from the national network. The resulting geoid surface captures the country’s full topographic range, from the Caspian Depression to the Tien Shan and Altai. After regression-based removal of residual tilts linked to distortions in the Baltic 1977 height system, we achieved a root-mean-square error of 0.066 m. The integrated use of 1:200,000 gravity maps and modern satellite-derived models yields accuracy improvements over widely used global solutions, establishing a consistent vertical reference for Kazakhstan and supporting datum modernization, GNSS-based heighting, infrastructure development, and environmental monitoring. These results show that digitized Soviet-era gravity maps, when fused with modern satellite datasets, can provide robust, high-accuracy geoid solutions.
1. Introduction
The precise determination of the geoid, which is defined as the equipotential surface that closely approximates the mean sea level, represents a fundamental challenge in geodetic science. It is of prime importance for various scientific, engineering, and geophysical applications. Geoid modelling involves the integration of global geopotential models with terrestrial gravity anomalies and local topographic data to achieve high accuracy [1]. Traditionally, gravimetric geoid determination has relied on extensive ground-based gravity surveys, which can be resource-intensive and geographically sparse in certain regions [2]. Consequently, the integration of Global Navigation Satellite System (GNSS) and levelling data has emerged as a crucial approach, offering a direct means to evaluate and refine geoid models by providing geometric geoid undulations at specific points [3].
A high-accuracy geoid model offers a cost-effective alternative, enabling direct conversion of ellipsoidal heights obtained from GNSS derived ellipsoidal heights into orthometric heights, without the need for extensive levelling campaigns [4]. Such an approach is essential for supporting a wide range of geoscientific and engineering applications, including large-scale infrastructure projects, cadastral surveying, environmental monitoring, and national mapping programmes [5,6]. Despite significant advancements in satellite gravimetry and computational techniques, achieving greater geoid accuracy remains a persistent challenge, particularly in regions with complex topographical and gravimetric characteristics. Expensive field surveys in remote and rugged terrain, along with a lack of GNSS stations, often result in inadequate data density for robust geoid determination [7,8]. Moreover, temporal variations in the Earth’s gravity field, caused by mass redistribution processes such as ice sheet melting or hydrological changes, further necessitate the requirement for continuous monitoring and periodic updates of geoid models to maintain their precision over time [9,10,11].
Regional geoid models are particularly critical for practical applications within specific geographical areas, where local geodynamic processes and geological structures significantly influence the gravity field [12,13]. They offer enhanced resolution and accuracy compared to global models, addressing the limitations imposed by sparse data in challenging terrains like mountainous regions [14,15,16]. Global geopotential models (GGMs) like EGM2008 [17], EIGEN-6C4 [18], and XGM2019e [19] provide adequate accuracy for many regional and global-scale applications, they cannot fully capture the short-wavelength gravity field features associated with geographies having complex terrain. Consequently, their direct use for high-precision engineering and surveying in the region can lead to systematic biases and reduced accuracy, particularly in mountainous areas [20]. Developing a dedicated local geoid model mitigates these shortcomings by incorporating detailed local gravity observations, refined topographic modelling, and advanced computation methods tailored to the country’s geophysical characteristics.
In addition to the geodetic benefits, establishing a local geoid model carries strategic significance. It ensures independence from foreign datasets, supports national sovereignty in spatial data management, and underpins all engineering and infrastructure projects with a unified and precise vertical reference system [21]. For large-scale projects such as the construction of transportation corridors, hydrotechnical structures, and energy infrastructure high-accuracy orthometric heights derived from a local geoid model improve design reliability and reduce construction risks [22].
Modern geoid modelling techniques, such as the least-squares modification of Stokes’ formula (LSMS/LSMSA), provide the tools needed to achieve the required accuracy under complex terrain conditions. The LSMS approach, in particular, offers flexibility to incorporate heterogeneous gravity datasets, apply topographic/terrain corrections, and perform stochastic modelling of residual gravity signals, making it well suited for mountainous and seismically active regions [23,24,25].
Kazakhstan is a country characterized by its vast and diverse topography, encompassing flat plains, deserts, and the high mountains of the Tian Shan range, which presents unique challenges for precise geoid determination. Furthermore, the country’s limited coverage of uniformly distributed gravimetric data, coupled with the sparse availability of GNSS/levelling benchmarks, exacerbates the complexity of establishing a high-precision vertical datum [26]. The complex terrain and substantial variations in elevation necessitate a robust regional geoid model that can accurately reflect the intricate gravity field behaviour across the region. Although global models provide a starting point, their accuracy remains insufficient for engineering and surveying in such a geodynamically complex region. Despite the importance of a unified vertical datum, Kazakhstan currently lacks a dedicated, validated national geoid model. This deficiency hinders various geodetic and practical applications, making the development of such a model a pressing necessity for the country’s infrastructural development and scientific advancement [27].
To address this gap, the present study develops the first high-accuracy gravimetric geoid model for Kazakhstan, termed QazGM2025. The model is computed using the Least-Squares Modification of Stokes’ formula (LSMSA/KTH method), which allows the optimal integration of heterogeneous datasets. Specifically, we combined digitized Soviet-era gravimetric maps, recently acquired absolute gravity measurements, GNSS/levelling benchmarks from the national geodetic network, and high-resolution topographic data (FABDEM). The model is evaluated against independent GNSS/levelling data and benchmarked against leading global models (EGM2008, EIGEN-6C4, and XGM2019e). This study not only delivers a precise reference surface with ~6 cm accuracy but also establishes the foundation for Kazakhstan’s modern vertical datum, enabling robust support for surveying, engineering, and geoscientific applications.
2. Study Area
The focus area is the Republic of Kazakhstan (Figure 1), which, despite encompassing vast expanses of lowland terrain, is characterized by highly diverse topography ranging from extensive steppe and desert plains to some of the highest mountain ranges in Central Asia. The western and northern parts of the country are dominated by the Caspian Depression and the West Siberian Plain, while the central Kazakh Uplands feature hilly and plateau landscapes of complex geological structure. The southeastern and southern margins of Kazakhstan include the towering mountain systems of the Tien Shan and Zhetysu Alatau, with elevations exceeding 7000 m, presenting significant challenges for precise geoid modelling due to steep relief gradients and active tectonics [28].
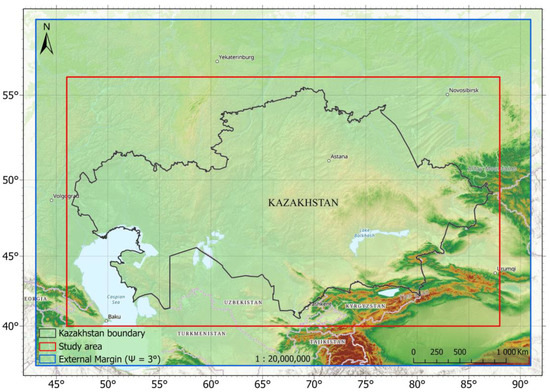
Figure 1.
The layout of the study area (highlighted in red rectangle). The outer rectangle surrounds the study area at a spherical distance of Ψ = 3°.
The territory of Kazakhstan extends approximately from 40° N to 56° N in latitude and from 46° E to 88° E in longitude. However, to minimize edge effects during geoid modelling for the main focus area, the computation region was extended beyond the national boundaries, covering the approximate range from 38° N to 58° N in latitude and from 44° E to 90° E in longitude. This expanded area ensures that boundary effects are properly accounted for, allowing for a more accurate representation of the geoid across Kazakhstan’s complex and varied terrain [29].
3. Methodology
The geoid modelling methodology adopted in this study integrates multi-source gravimetric data and advanced computational techniques to achieve high precision, particularly in areas with complex topography. Figure 2 illustrates the structured workflow for geoid determination and evaluation using a hybrid approach that combines global gravity models with regional terrestrial data. We used the Least -Squares Modification of Stokes’ formula to optimally integrate diverse datasets, ensuring a robust and accurate geoid determination. The process begins with the digitization of historical gravimetric maps, including datum transformation from Pulkovo to WGS84, application of systematic corrections, validation against terrestrial gravity observations, and integration with global datasets. The systematic corrections comprised the transition from the normal Helmert formula to GRS80, the exclusion of the Honkasalo correction and of the Potsdam system correction, and other corrections, as detailed in the study [30]. GNSS/levelling data at first- to third-order levelling benchmarks are employed for input data evaluation, optimization of Stokes’ kernel modification parameters, and final model validation. Normal heights of control points are converted to orthometric heights. The optimal GGM and digital terrain model are selected based on statistical consistency with GNSS/levelling data.
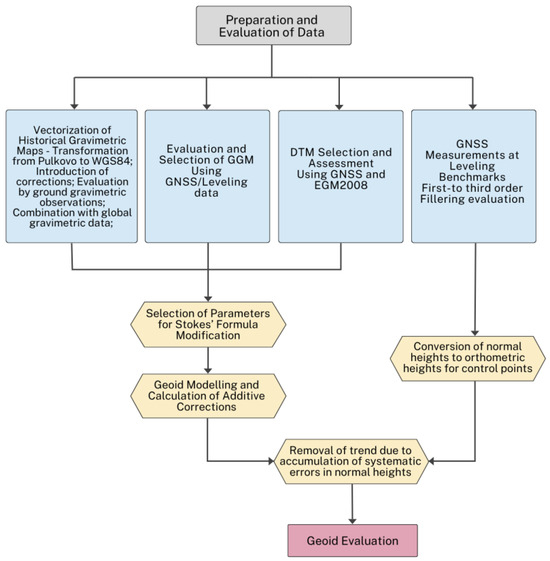
Figure 2.
General concept of geoid model development and evaluation.
The geoid is computed with additive corrections—topographic, atmospheric, ellipsoidal, and downward continuation. The final stage comprises rigorous accuracy assessment using independent GNSS/levelling benchmarks and trend removal of systematic effects.
3.1. Data Collection and Database Compilation
3.1.1. Gravity Data
The regional gravity database compiled for QazGM2025 incorporates a heterogeneous collection of historical gravimetric data for Kazakhstan and neighbouring countries, as well as contemporary terrestrial observations from the Modern Gravimetric Framework of Kazakhstan, where absolute gravity observations were conducted in 2023–2024 by the National Centre for Geodesy and Spatial Information [31].
In this study, the core dataset consists of digitized Soviet-era gravimetric maps at a scale of 1:200,000, providing dense coverage for approximately 90% of Kazakhstan (Figure 3). The remaining 10%—primarily the Kazakhstan sector of the Caspian Sea and selected transboundary areas—was completed using gravity materials extracted from archival technical reports [32,33,34]. The maps were originally compiled from ground-based gravity surveys conducted primarily with SN-3, GAK, and GR-2K gravimeters, which were widely used during that period for regional-scale geodetic campaigns. For standardization, the gravity observations were reduced to Bouguer anomalies using intermediate crustal densities of 2.30 g/cm3 or 2.67 g/cm3, accompanied by records of free-air anomalies, terrain corrections, and observation heights [35]. This systematic framework provided a consistent baseline for the construction of Kazakhstan’s first digital gravity database.
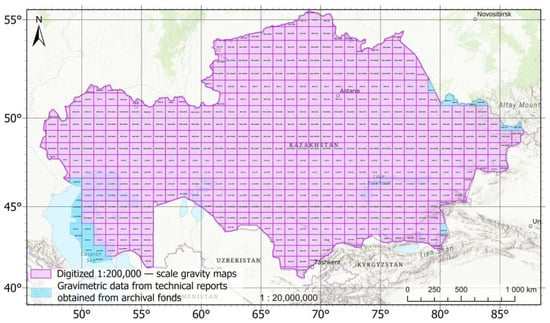
Figure 3.
Gravimetric data coverage of Kazakhstan based on digitized 1:200,000 maps and archival technical reports.
A total of 591 gravimetric map sheets at a 1:200,000 scale and archival technical reports were digitized to ensure full coverage of the study area. The maps were prepared in Bouguer reductions using an intermediate layer density of 2.67 g/cm3 with terrain correction, and included observation heights where available. In regions where Bouguer reduction maps with 2.67 g/cm3 density and terrain correction, or corresponding elevation maps, were not available, maps computed with a lower density of 2.30 g/cm3 were digitized instead. The digitization followed a multi-stage workflow designed to ensure positional and numerical accuracy: the original sheets were scanned at 600 dpi, georeferenced to the Pulkovo 1942/Gauss–Krüger coordinate system, and vectorized to extract gravity anomaly values, observation heights, and terrain corrections. A preliminary anomaly surface was generated using Ordinary Kriging interpolation (250 m grid) to identify and correct discrepancies. The resulting dataset was then transformed into WGS 84 coordinates using the standard transformation parameters (EPSG: 15865) [30].
Although the digitized terrestrial gravity data provide dense coverage across almost the entire territory Kazakhstan, some areas in the mountainous and border regions remain undersampled. To ensure complete spatial coverage required by the modified Stokes’ formula, which necessitates gravity information within a 3° spherical cap around the study area, additional data were incorporated from the global model WGM2012 (5′ × 5′ resolution). This model was used to compensate for the lack of terrestrial measurements in the outer boundary zone and adjacent territories where national data are unavailable (Figure 4). As a result, the final gravity database consists of 651,862 terrestrial measurement points (0.24 points/km2, ~13.8 per 5′ grid cell), complemented by 103,854 global points from WGM2012, yielding a total of 755,716 data points. This integration ensured both dense coverage and improved homogeneity across the entire study area, forming the basis for subsequent geoid computation.
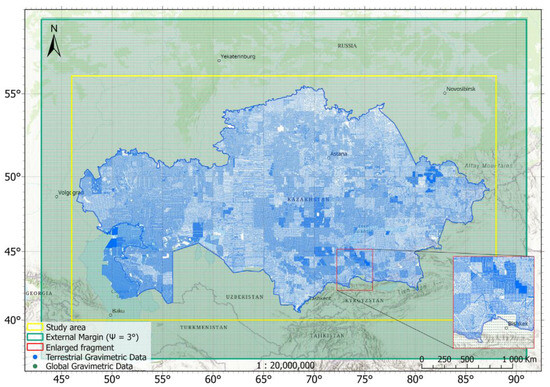
Figure 4.
The distribution of terrestrial gravity data and incorporated global anomalies from the WGM2012 model, with an enlarged fragment showing data density and the boundary of integration.
To assess the reliability of the digitized historical dataset, we compared it with recent absolute gravity measurements obtained from the Modern Gravimetric Framework of Kazakhstan. This network includes 76 absolute stations and 142 nearby relative stations (within ~50 km), observed using a Micro-g LaCoste A10 absolute gravimeter (Micro-g LaCoste, Inc., Lafayette, CO, USA) and Scintrex CG-6 Autograv relative gravimeters (Scintrex Limited, Concord, ON, Canada). The expanded uncertainty of these measurements was below 10 μGal at all 218 stations. Statistical comparison revealed a mean difference of only 0.66 mGal between the reconstructed values from the Soviet-era maps and the modern absolute observations, confirming the overall consistency of the historical dataset for use in regional geoid modelling.
3.1.2. GNSS/Levelling Points
A dataset of 3653 GNSS/levelling points, evenly distributed across Kazakhstan (Figure 5), was selected as the primary reference for the validation of all datasets used in this study. These control points were established under the National Spatial Data Infrastructure (NSDI) project, which led to the creation of the official national reference frame QazTRF-23, replacing the outdated SK-42 system with an ITRF-consistent framework [31].
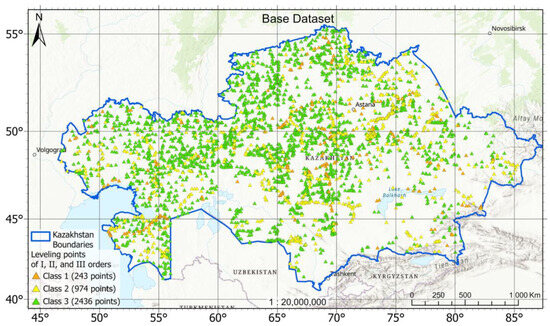
Figure 5.
Distribution of GNSS/levelling control points in Kazakhstan (3653 Points).
From approximately 45,600 GNSS stations surveyed nationwide, over 10,000 were associated with geometric levelling benchmarks. However, because the majority of these belonged to the 4th accuracy class, unsuitable for high-precision applications, they were excluded. After filtering, only benchmarks along first- and second-order levelling lines, supplemented by a subset of reliable third-order stations, were retained. This selection resulted in 3653 points, comprising 243 first-order, 974 second-order, and 2436 third-order stations.
The geodetic framework follows the “general-to-specific” principle, transferring high-accuracy coordinates from 11 Fundamental Astronomical and Geodetic Network (FAGN) stations to the Astronomical and Geodetic Network (AGN), Geodetic Densification Network (GDN), and the State Levelling Network (SLN). At FAGN stations, continuous 24 h GNSS sessions with dual-frequency receivers were processed using Bernese GNSS Software (version 5.2), incorporating precise satellite ephemerides, Earth orientation parameters, tidal models, and IGS reference stations. The adjustment achieved absolute accuracies of 0.10–0.15 m, with relative accuracies better than 0.02 m horizontally and 0.03 m vertically. Validation against AUSPOS online GNSS processing services confirmed differences within 0.015 m horizontally and 0.03 m vertically.
By establishing this unified and high-accuracy coordinate framework, Kazakhstan’s geodetic network provides a robust basis for geoid model evaluation. Importantly, the GNSS/levelling benchmarks were also used to validate the DEM and to assess the performance of global geopotential models, ensuring consistency in the validation framework across all datasets employed in this study.
3.1.3. Digital Elevation Model
For the topographic component of the geoid modelling, the FABDEM dataset was used. FABDEM is a global digital elevation model derived from the Copernicus GLO-30 DEM [36,37,38], corrected to represent the bare-earth surface by removing vegetation and building artefacts [39]. It provides a spatial resolution of 1 arc-second (~30 m), enabling accurate representation of terrain variations across Kazakhstan, including the steep gradients of the Tien Shan and Zhetysu Alatau ranges [40].
The quality of FABDEM over the study area was assessed using GNSS-derived elevations from control points and EGM2008 geoid height. The comparison showed a mean bias of 0.397 m, a standard deviation of 1.365 m, and an RMSE of 1.422 m. These results confirm that FABDEM provides sufficient vertical accuracy for use in computations of the geoid model.
3.1.4. Global Geopotential Models
To establish the optimal long-wavelength gravity field for geoid modelling in Kazakhstan, we evaluated several recent high-resolution global geopotential models (GGMs) collected by the International Centre for Global Earth Models [41]. These included XGM2019e_2159, an enhanced combination model incorporating GRACE, GOCE, and terrestrial gravity data up to degree/order 2190 [19]; SGG-UGM-2, derived from GOCE satellite gravity gradients combined with surface gravity [42]; GECO, a hybrid model integrating satellite-only solutions with EGM2008 long-wavelength information [20] EIGEN-6C4, which combines GRACE and GOCE data with extensive surface gravity observations up to degree/order 2190 [18]; and the widely used EGM2008, which incorporates both satellite and terrestrial data to the same spectral resolution [17].
These models were tested against GNSS/levelling benchmarks distributed across the study area to identify the model that shows the highest consistency with local observations and could therefore serve as the reference for subsequent geoid computations. For each benchmark, height anomalies derived from GNSS/levelling were compared with the corresponding model-predicted values.
3.2. Geoid Model Development and Validation
3.2.1. Least—Squares Modification of Stokes’ (LSMSA) Approach
The gravimetric geoid is commonly determined using Stokes’ formula, which relates gravity anomalies on the Earth’s surface to geoid undulations [43]. However, direct application of Stokes’ integral requires globally complete and error-free data, a condition that is rarely met in practice. In addition, truncating the integral to regional domains introduces errors due to unmodelled long-wavelength signals [2,6,44].
To overcome these limitations, the Least-Squares Modification of Stokes’ Formula (LSMSA or KTH method) was developed [45]. This approach modifies the classical Stokes kernel by introducing least-squares optimal coefficients that minimize the expected error in the estimated geoid height [43,46,47,48,49]. The method achieves this by optimally balancing contributions from three main sources: the long-wavelength gravity field provided by a Global Geopotential Model (GGM), the medium- and short-wavelength gravity anomalies derived from terrestrial and airborne observations, and the residual terrain effects obtained from high-resolution digital elevation models (DEMs).
In this framework, the geoid undulation at a given location is expressed as
where is a fundamental term representing the primary approximation of the geoid height, obtained from Stokes’ formula using gravity anomalies referenced to a mean spherical surface before applying specific correction terms. accounts for topographic correction, corrects for the difference between gravity anomalies observed at the Earth’s surface and those referenced to the geoid level, mitigating distortions in mountainous regions. and are parameters accounting for atmospheric and ellipsoidal corrections.
The key principle of LSMSA is the modification of Stokes’ kernel to minimize the propagation of data errors into the computed geoid heights [50]. This is achieved by estimating optimal modification parameters from the empirical covariance functions of residual gravity anomalies, fitted to analytical models. The modification degree, spectral weighting factors, and combination coefficients are then determined to balance the spectral content of terrestrial anomalies and the long-wavelength information from the GGM.
Once the modification parameters are established, the gravimetric geoid is computed directly by applying the least squares optimized Stokes’ integral to the prepared set of terrestrial gravity anomalies. The formulation inherently allows for the rigorous incorporation of additive corrections, which compensate for effects not modelled in the main integral [51,52].
These features make LSMSA particularly well-suited for Kazakhstan’s geodynamically complex terrain, where data coverage is irregular and large elevation variations necessitate careful treatment of residual terrain effects. All stages of geoid computation described herein were implemented within the LSMSSOFT software environment [53]. This sophisticated approach ensures that the resulting geoid model is not only accurate but also robust against inherent data limitations and topographic complexities [54,55].
3.2.2. Parameter Testing Approach
A critical aspect of the LSMSA method is the selection of spectral and stochastic parameters that govern the balance between contributions from the global geopotential model and terrestrial gravity anomalies. Two parameters are particularly important: the maximum spherical harmonic degree/order (L, M) used to truncate the Stokes’ integral, and the a priori error variance of the terrestrial gravity anomalies (C(0)).
The truncation degree controls the spectral resolution of the residual gravity field included in the modified Stokes’ integral. Lower degrees emphasize long-wavelength signals but risk omitting shorter-wavelength information, while higher degrees capture finer detail but may amplify observational noise. To identify a suitable compromise, we tested a range of truncation degrees from 180 to 760, in line with previous studies of regional geoid modelling [3,47,56].
The parameter C(0) represents the stochastic characterization of gravity anomaly errors, influencing the relative weight assigned to terrestrial gravity data in the least-squares solution [57,58]. To account for different assumptions of observational uncertainty, values of 1, 3, and 9 mGal2 were considered, consistent with the accuracy level of the digitized Soviet-era gravimetric dataset and its validation against modern absolute gravity measurements.
For each combination of parameters, the LSMSSOFT software was used to compute preliminary geoid solutions. Their performance was subsequently evaluated against GNSS/levelling benchmarks, and the optimal configuration was selected based on statistical measures of residual differences.
3.2.3. Validation of Geoid Model
This rigorous validation process is crucial for verifying the accuracy and reliability of the QazGM2025 model for practical geodetic applications within Kazakhstan, especially given the historical nature of some input data [59]. To assess the accuracy of the computed geoid model, comparisons were made against the GNSS/levelling benchmarks described in Section 3.1.2. Since the official vertical reference system of Kazakhstan is realized in terms of normal heights, the comparison required a consistent transformation. Following [60], the geoid heights were derived from GNSS/levelling anomalies using:
where is the Bouguer anomaly, is the normal gravity at the standard latitude (), and H is the topographic height at the computation point.
The accuracy assessment of the derived geoid model was carried out using the classical approach, by comparing the modelled geoid heights with their observed counterparts, obtained as the difference between ellipsoidal and orthometric heights at benchmarks of the national levelling network of Kazakhstan. As control points, benchmarks from first- and second-order precise levelling, as well as lower-accuracy third-order points, were employed, totaling 3653 stations. Residuals were calculated as:
The scatter of the points selected in this way revealed that the variations in the differences ΔN exhibit a pronounced shift and a slope from northwest to southeast, indicating the accumulation of systematic errors in the data. To approximate this constant trend, we employed a linear model dependent on latitude and longitude coordinates. The model coefficients were determined using linear regression, which, for a spherical surface, takes the form:
where φ and λ—latitude and longitude, a, b, c and d—model coefficients [61,62].
The coefficients of this model were estimated using the least-squares method, providing an empirical correction surface that links the gravimetric geoid to the official height reference system.
4. Results
4.1. Evaluation of Global Geopotential Models
To identify the most suitable long-wavelength gravity field for geoid modelling in Kazakhstan, five recent high-resolution global geopotential models (GGMs) were evaluated against the GNSS/levelling benchmarks described in Section 3.1.2. The models tested included XGM2019e_2159, EIGEN-6C4, GECO, SGG-UGM-2, and EGM2008. For each benchmark, the observed geometric height anomaly derived from GNSS/levelling was compared with the corresponding model-predicted value, and the differences were analyzed statistically. The resulting parameters are presented in Table 1.

Table 1.
Statistics of differences between GGM points and ground points with gravity data.
The comparative analysis demonstrates that XGM2019e_2159 and EIGEN-6C4 yield the lowest RMSE values (0.140 m), with identical standard deviations and mean biases. GECO and SGG-UGM-2 perform only marginally worse (RMSE = 0.146 m and 0.143 m, respectively), while EGM2008 shows the largest dispersion (RMSE = 0.148 m). Although EIGEN-6C4 exhibits a slightly narrower residual range than XGM2019e, the differences are not statistically significant.
Considering its broader spectral content, inclusion of the most recent GRACE and GOCE satellite data, and assimilation of dense terrestrial gravity information, XGM2019e_2159 was selected as the long-wavelength reference model for subsequent LSMSA computations in this study. This selection aligns with practices in other regions where XGM2019e has demonstrated robust performance, even in areas with limited terrestrial data availability [19]. Therefore, the choice of XGM2019e_2159 is expected to provide a highly accurate and consistent long-wavelength gravity field for the QazGM2025 model.
4.2. LSMSA Parameter Optimization
The selection of optimal parameters for the Least-Squares Modification of Stokes’ Formula with Additive Corrections is critical for achieving a precise gravimetric geoid model [43]. The LSMSA method requires the specification of two key parameters: the maximum spherical harmonic degree/order (L, M) used to truncate the Stokes’ integral and the error variance of terrestrial gravity anomalies, denoted as C(0). To evaluate their influence on the computed geoid, a series of test solutions were generated by systematically varying these parameters. Truncation degrees from 180 to 760 were tested in combination with gravity anomaly error variances of 1, 3, and 9 mGal2. The performance of each configuration was assessed against GNSS/levelling benchmarks using the statistical measures of mean difference, standard deviation, and RMSE.
The results (Table 2) indicate that geoid accuracy is sensitive to the choice of truncation degree. At very low truncation (L = 180), the omission of short-wavelength components results in larger discrepancies, while at higher degrees (L ≥ 500) the amplification of noise leads to increased scatter. A balanced performance was obtained for L = M = 300, which consistently produced the lowest RMSE values across the tested error variances.

Table 2.
Statistics for fitting a combination of spherical harmonic coefficients with error variance of ground gravity data.
Similarly, the assumed error variance of terrestrial gravity anomalies (C(0)) influenced the weighting of input data in the least-squares solution. The best performance was achieved for C(0) = 1 mGal2, which reflects the reliability of the digitized Soviet-era gravimetric dataset after validation with modern absolute measurements. Larger values of C(0) (3–9 mGal2) reduced the influence of terrestrial gravity and degraded the fit to GNSS/levelling benchmarks.
Based on the evaluations described above, the final configuration for computing the QazGM2025 model was defined as follows: The terrestrial gravity anomalies, digitized from historical maps and supplemented by WGM2012 data in under sampled regions, were combined with the long-wavelength spherical harmonic coefficients from XGM2019e. Topographic information was provided by the FABDEM DEM, while the LSMSA was implemented with a modification degree of L = M = 300, an assumed terrestrial gravity data error variance of C(0) = 1 mGal2, and an integration cap radius of Ψ = 1°. This configuration was used to generate the final gravimetric geoid surface for Kazakhstan.
4.3. Computed Geoid Surface
Using the optimized LSMSA configuration, the QazGM2025 gravimetric geoid model was computed for the territory of Kazakhstan. The resulting surface reflects the combined influence of the long-wavelength field from XGM2019e, the medium- and short-wavelength signal from terrestrial gravity anomalies, and the residual terrain effects derived from the FABDEM digital elevation model.
The applied corrections (Figure 6)—topographic, analytical downward continuation, ellipsoidal, and atmospheric—improved the initial geoid estimates by accounting for terrain mass effects, gravity field continuation, reference surface geometry, and atmospheric mass distribution. The largest adjustments were due to topographic effects (up to −3.86 m), while ellipsoidal and atmospheric terms contributed at the millimetre level. The resulting geoid model computed using the LSMS method (Figure 7) captures the major gravity field patterns across Kazakhstan, with heights ranging from −67.75 m in the southeast to 20.70 m in the northwest, clearly reflecting the influence of complex topography and crustal density variations. The lowest values occur in the western Caspian Depression, where negative geoid undulations are characteristic of thick sedimentary basins and low crustal density. The highest values are observed in the Tien Shan and Altai mountain ranges, where steep relief and crustal thickening dominate the gravity field. Intermediate values are found across the central steppes and plateaus, producing a smooth transition between extremes.
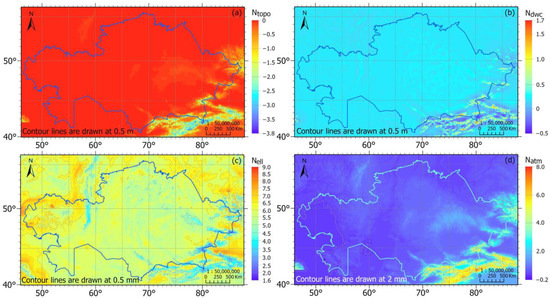
Figure 6.
Corrections to approximate geoid heights using (a) topographic correction, m. (b) correction for analytical downward continuation, m. (c) ellipsoidal correction, mm. (d) atmospheric correction, mm.
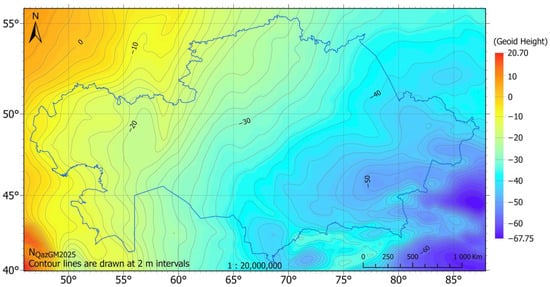
Figure 7.
Geoid height by the method of Least squares Modification of Stokes formula with additional corrections NLSMSA, m.
Furthermore, the computed geoid surface of Kazakhstan has been presented at a resolution of 5′ × 5′, highlighting the major spatial patterns (Figure 7). The model captures the expected correlation between geoid undulations and large-scale tectonic and topographic structures, providing a realistic representation of the regional gravity field. The final geoid surface serves as the foundation for subsequent accuracy assessment and validation against GNSS/levelling benchmarks.
4.4. Validation of the Developed Geoid Model
The computed QazGM2025 model was validated against 3653 GNSS/levelling benchmarks distributed across Kazakhstan. The comparison of observed and modelled geoid heights revealed systematic differences, with a pronounced northwest–southeast tilt in the residuals. This large-scale distortion is consistent with cumulative errors in normal heights introduced by the realization of the Baltic 1977 vertical reference system. To account for this effect, the residuals were modelled using a linear regression function of latitude and longitude. The estimated coefficients were:
Application of the regression correction significantly improved the agreement between QazGM2025 and GNSS/levelling observations. The RMSE decreased from 0.185 m to 0.066 m, while the mean bias was effectively eliminated (Table 3).

Table 3.
Descriptive statistics and RMSE for geoid height differences.
Spatial trends of the residuals are illustrated in Figure 8 (with respect to longitude (a) and latitude (b)), and their geographical distribution in Figure 9. The distribution of corrected residuals is presented in Figure 10. The histograms in Figure 11 illustrate that, after correction, the residuals closely follow a normal distribution centred near zero, confirming the absence of systematic bias.
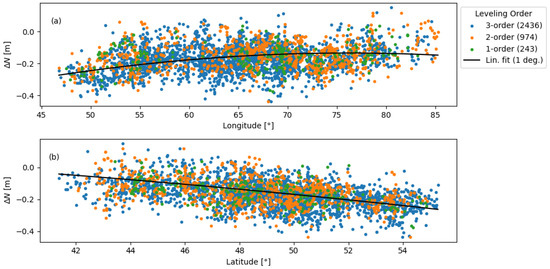
Figure 8.
Spatial trends of residuals at levelling benchmarks: (a) versus longitude; (b) versus latitude. The solid line shows the least-squares trend; colours denote terrain classes (1–3; counts in parentheses). Units: in metres.
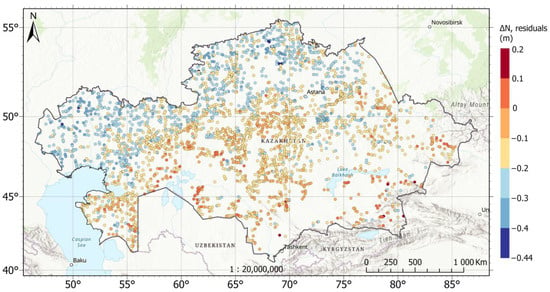
Figure 9.
A map of the spatial distribution of residuals at levelling benchmarks.
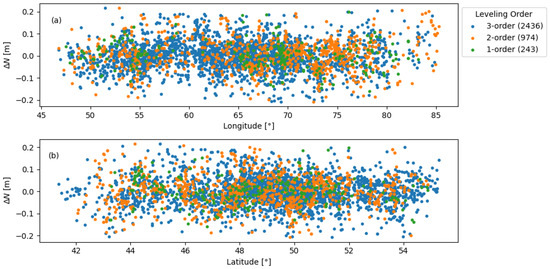
Figure 10.
Residuals after removing offset and tilt (a) versus longitude; (b) versus latitude.
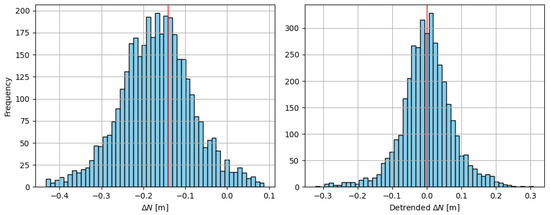
Figure 11.
Histograms of ΔN differences before and after applying the correction.
Importantly, the analysis showed no clear accuracy advantage for first-order benchmarks compared to second- and third-order sites. The dispersion of residuals within each order was similar, indicating that the QazGM2025 model achieves a consistent level of accuracy across the heterogeneous national levelling network. This robust validation process, leveraging a comprehensive dataset of GNSS/levelling benchmarks, underscores the high precision and reliability of the QazGM2025 model in representing the regional geoid for Kazakhstan.
4.5. Comparison with Existing Global Geopotential Models
To evaluate the performance of QazGM2025 relative to existing global solutions, its accuracy was compared with that of five widely used GGMs: XGM2019e, EIGEN-6C4, GECO, SGG-UGM-2, and EGM2008. The validation was performed using the same set of GNSS/levelling benchmarks, ensuring consistency across datasets.
The comparison (Table 1 and Table 3) demonstrates that while the best-performing GGMs (XGM2019e and EIGEN-6C4) achieve RMSE values of approximately 0.14 m, the corrected QazGM2025 model reduces this error to 0.066 m, representing an improvement of more than 50%. The reduction in bias and the near-normal distribution of residuals further confirm the superiority of the regional model over global solutions.
These results confirm that incorporating dense terrestrial gravity anomalies, refined DEM-based terrain corrections, and optimal LSMSA parameterization significantly enhances the accuracy of geoid determination in Kazakhstan compared to global models alone.
5. Discussion
The QazGM2025 model demonstrates a high-accuracy fit to ground truth, with GNSS/levelling comparisons yielding a root-mean-square error of 0.066 m after applying a regression correction. This post-correction performance indicates that most systematic differences (e.g., bias and tilt between the gravimetric geoid and the levelling datum) have been removed, leaving only small random residuals.
The LSMSA approach itself is a proven technique in modern geoid modelling—it facilitates the optimal combination of terrestrial gravity measurements with a geopotential model to mitigate truncation [54,63]. The success of QazGM2025 (reflected in its ~0.07 m agreement with GNSS/levelling) attests to the effectiveness of this method and the improved data inputs. After removing datum biases, the remaining geoid discrepancies are on the order of a few centimetres, which is a strong validation of the model’s internal consistency. Minor residuals can be attributed to localized gravity field complexities (e.g., rugged topography, geologic density variations) and the uneven distribution of input data, but overall, the results confirm that the model achieves the expected precision for a regional gravimetric geoid.
The performance and methodology of QazGM2025 can be benchmarked against global and regional geoid models from other countries with comparable geographical challenges. While global geopotential models such as EGM2008 and EIGEN-6C4 provide advancements in geodetic applications, their accuracy can vary significantly depending on data availability for specific regions, with Central Asia exhibiting errors up to 35 cm [8]. The previous Kazakh geoid model (KazGM2015) showed GNSS/levelling discrepancies ranging from −0.295 m to +0.327 m (std. dev. ≈ 0.17 m) [64]. Similarly, Turkey’s recent gravimetric geoid (Turkey-ITUGRG2021) was computed with a very similar approach (LSMSA with remove-restore using XGM2019 gravity model), and the model achieved an accuracy of about 10.1 cm before any fitting, and ~8.6 cm after a 7-parameter corrector surface was applied [65]. The IRG2018 model of Iran, incorporating a remove-restore technique, though using least-squares collocation and a hybrid solution attained roughly 20 cm RMS agreement with GNSS/levelling after incorporating over 1200 levelling points [66]. The current QazGM2025 model’s enhanced performance underscores the criticality of integrating local gravimetric data with improved global models for regional geoid refinement, surpassing the capabilities of purely global solutions [67].
A reliable high-resolution geoid model such as QazGM2025 provides immediate and concrete benefits to a wide range of stakeholders in Kazakhstan. Geodetic surveyors and civil engineers are among the primary beneficiaries: with this model, they can directly obtain orthometric heights (physical elevations) from GNSS readings, streamlining surveying workflows for infrastructure projects. Urban planning and cadastral authorities benefit by easily tying development projects to the official height system, while hydrologists and disaster managers can integrate LiDAR, river gauge, and coastal data within a unified datum for accurate flood mapping and reservoir management. The model also supports environmental monitoring and geoscience, enabling consistent tracking of Caspian Sea level fluctuations, glacier retreat, snowpack dynamics, and land subsidence. In effect, QazGM2025 ensures that accurate, consistent height information is readily available to a broad range of stakeholders, strengthening infrastructure, resource management, and environmental resilience.
Despite these advances, several limitations remain. The geoid’s absolute accuracy is constrained by data quality, particularly the absence of absolute gravity control points and sparse coverage in mountainous and border regions, where errors may exceed the national RMSE. Future campaigns, such as airborne gravimetry and new GNSS benchmarks, are needed to densify observations. The model is also static, while long-term processes (tectonic uplift, hydrological mass change, post-glacial rebound) can cause centimetre-level geoid variations over decades. Periodic updates, potentially incorporating GRACE/GRACE-FO time-variable gravity data, will be essential to maintain precision. Finally, global integration is required: QazGM2025 should be tied to the International Height Reference Frame (IHRF) to ensure cross-border consistency. Methodologically, refinements to LSMSA assumptions and tests with alternative approaches (e.g., least-squares collocation, multi-resolution models) could further improve local performance.
In conclusion, while QazGM2025 is a significant leap forward, and provides a solid foundation in regional geoid building for Kazakhstan. However, ongoing efforts in data collection, methodological refinement, and global integration will be essential to further enhance the geoid model. Such future work will ensure that Kazakhstan’s vertical reference frame remains accurate, robust, and interoperable, supporting the country’s needs well into the future.
6. Conclusions
This study presents the first dedicated solution to the problem of geoid determination for Kazakhstan, addressing long-standing challenges in regional gravity field modelling and vertical datum unification. A comprehensive geodetic information base was established, combining digitized Soviet-era gravimetric maps, modern absolute gravity control, and GNSS/levelling benchmarks. The validation of the digitized gravity dataset confirmed its suitability for regional geoid modelling, while a comparative evaluation of global geopotential models identified XGM2019e_2159 as the optimal long-wavelength reference field. For the topographic component, the FABDEM DEM was verified as sufficiently accurate for geoid computation.
The geoid was computed using the Least-Squares Modification of Stokes’ formula (LSMSA) with optimized parameters (L = M = 300; C(0) = 1 mGal2), integrating terrestrial gravity anomalies, global model coefficients, and DEM-based corrections. Validation against 3653 GNSS/levelling benchmarks demonstrated that systematic distortions in the national height system could be corrected through regression adjustment, reducing the RMSE from 0.102 m to 0.066 m. The resulting QazGM2025 geoid model outperforms global models, achieves stable centimetre-level accuracy across diverse terrain, and provides a reliable and consistent vertical reference surface.
These results establish QazGM2025 as a robust foundation for modernizing Kazakhstan’s vertical datum, enabling GNSS-based height determination, unification of the national height system, and future alignment with the International Height Reference Frame (IHRF). Ongoing improvements in data coverage, absolute gravity control, and dynamic model updates will further enhance its accuracy and ensure its utility for surveying, infrastructure development, and environmental monitoring.
Author Contributions
Conceptualization, D.S. and A.U.; methodology, D.S. and A.U.; software, D.S., A.U. and M.K.; validation, D.S., A.U. and R.S.; formal analysis, A.U. and D.S.; investigation, D.S. and A.U.; resources, A.U., S.N. and R.S.; data curation, M.K. and N.Z.; writing—original draft preparation, D.S. and A.U.; writing—review and editing, D.S. and A.U.; visualization, M.K. and N.Z.; supervision, D.S. and A.U.; project administration, S.N. and A.U.; funding acquisition, S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant numbers: BR21882366, AP19175328).
Data Availability Statement
Data are contained within this article.
Acknowledgments
The authors thank Anel Islyamova (RSE National Centre of Geodesy and Spatial Information, Astana 010000, Kazakhstan) for kindly providing the QazTRF-23 network materials used for validation. We are grateful to all the authors of the articles that were discussed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abbak, R.A.; Erol, B.; Ustun, A. Comparison of the KTH and Remove–Compute–Restore Techniques to Geoid Modelling in a Mountainous Area. Comput. Geosci. 2012, 48, 31–40. [Google Scholar] [CrossRef]
- Ellmann, A.; Märdla, S.; Oja, T. The 5 Mm Geoid Model for Estonia Computed by the Least Squares Modified Stokes’s Formula. Surv. Rev. 2020, 52, 352–372. [Google Scholar] [CrossRef]
- Tarrío Mosquera, J.A.; Caverlotti Silva, M.; Isla, F.; Prado, C. Assessment of Hybrid Geoids in Chile and Spain, Combining GGM and GNSS/Leveling Observations. Geod. Geodyn. 2021, 12, 65–92. [Google Scholar] [CrossRef]
- Xu, W.; Chen, G.; Yang, D.; Ding, K.; Dong, R.; Ma, X.; Han, S.; Zhang, S.; Zhang, Y. Enhancing Regional Quasi-Geoid Refinement Precision: An Analytical Approach Employing ADS80 Tri-Linear Array Stereoscopic Imagery and GNSS Gravity-Potential Leveling. Remote Sens. 2024, 16, 2984. [Google Scholar] [CrossRef]
- Shen, W.; Han, J. Global Geoid Modeling and Evaluation. In Geodetic Sciences-Observations, Modeling and Applications; IntechOpen: London, UK, 2013; ISBN 953-51-1144-2. [Google Scholar][Green Version]
- Odera, P.A.; Fukuda, Y. Recovery of Orthometric Heights from Ellipsoidal Heights Using Offsets Method over Japan. Earth Planets Space 2015, 67, 134. [Google Scholar] [CrossRef]
- Elshewy, M.A.; Trung Thanh, P.; Elsheshtawy, A.M.; Refaat, M.; Freeshah, M. A Novel Approach for Optimizing Regional Geoid Modeling over Rugged Terrains Based on Global Geopotential Models and Artificial Intelligence Algorithms. Egypt. J. Remote Sens. Space Sci. 2024, 27, 656–668. [Google Scholar] [CrossRef]
- Fazilova, D.; Magdiev, H.; Halimov, B. High-Precision Satellite Leveling and Investigation of the Local Geoid Model in the Territory of Kashkadarya Region. EPRA Int. J. Econ. Growth Environ. Issues 2020, 8, 31–35. [Google Scholar] [CrossRef]
- Ferrara, G.; Parente, C. Adaptation of the Global Geoid Model EGM2008 on Campania Region (Italy) Based on Geodetic Network Points. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 46, 145–150. [Google Scholar] [CrossRef]
- Siegismund, F.; Köhl, A.; Rummel, R.; Stammer, D. Temporal Variations of the Marine Geoid. J. Geophys. Res. Ocean. 2020, 125, e2020JC016433. [Google Scholar] [CrossRef]
- Timmen, L.; Gerlach, C.; Rehm, T.; Völksen, C.; Voigt, C. Geodetic-Gravimetric Monitoring of Mountain Uplift and Hydrological Variations at Zugspitze and Wank Mountains (Bavarian Alps, Germany). Remote Sens. 2021, 13, 918. [Google Scholar] [CrossRef]
- Łyszkowicz, A. Quasigeoid for the Area of Poland Computed by Least Squares Collocation. Tech. Sci. 2010, 13, 147–164. [Google Scholar] [CrossRef]
- Ghazal, N.K.; Saray, N.S.L. A Comparison of Orthometric Heights Calculated from (GPS/Leveling) and (EGM08) Methods Based–GIS. J. Phys. Conf. Ser. 2021, 1879, 032072. [Google Scholar] [CrossRef]
- Jiang, L.; Andersen, O.B.; Nielsen, K.; Zhang, G.; Bauer-Gottwein, P. Influence of Local Geoid Variation on Water Surface Elevation Estimates Derived from Multi-Mission Altimetry for Lake Namco. Remote Sens. Environ. 2019, 221, 65–79. [Google Scholar] [CrossRef]
- Dilalos, S.; Alexopoulos, J.D. Regional Gravity Model of Greece Based on Satellite, Marine and Terrestrial Data. Pure Appl. Geophys. 2023, 180, 2807–2826. [Google Scholar] [CrossRef]
- Jiang, T.; Dang, Y.; Zhang, C. Gravimetric Geoid Modeling from the Combination of Satellite Gravity Model, Terrestrial and Airborne Gravity Data: A Case Study in the Mountainous Area, Colorado. Earth Planets Space 2020, 72, 189. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, 2011JB008916. [Google Scholar] [CrossRef]
- Foerste, C.; Bruinsma, S.; Flechtner, F.; Abrykosov, O.; Dahle, C.; Marty, J.; Lemoine, J.; Biancale, R.; Barthelmes, F.; Neumayer, K.; et al. EIGEN-6C3—The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 1949 of GFZ Potsdam and GRGS Toulouse; American Geophysical Union: Washington, DC, USA, 2011; Volume 2011, p. G51A-0860. [Google Scholar]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The Combined Global Gravity Field Model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Gilardoni, M.; Reguzzoni, M.; Sampietro, D. GECO: A Global Gravity Model by Locally Combining GOCE Data and EGM2008. Stud. Geophys. Geod. 2016, 60, 228–247. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Carrion, D.; De Gaetani, C.I.; Albertella, A.; Rossi, L.; Sona, G.; Batsukh, K.; Toro Herrera, J.F.; Elger, K.; Barzaghi, R.; et al. Open Access to Regional Geoid Models: The International Service for the Geoid. Earth Syst. Sci. Data 2021, 13, 1653–1666. [Google Scholar] [CrossRef]
- Deakin, R.E. The Geoid What’s It Got to Do with Me? Aust. Surv. 1996, 41, 294–305. [Google Scholar] [CrossRef]
- Ellmann, A. The Geoid for the Baltic Countries Determined by the Least Squares Modification of Stokes’ Formula; Universitetsservice US AB: Stockholm, Sweden, 2004. [Google Scholar]
- Nergizci, M.; Abbak, R.A.; Arisoy, M.O. The Effect of Crustal Density Heterogeneity on Determining Gravimetric Geoid: Example in Central Anatolia, Türkiye. J. Asian Earth Sci. 2024, 264, 106037. [Google Scholar] [CrossRef]
- Eshagh, M. Least-squares Modification of Stokes’ Formula with EGM08. Geod. Ir Kartogr. 2009, 35, 111–117. [Google Scholar] [CrossRef]
- Sjöberg, L.E. Geoid Model Validation and Topographic Bias. J. Geod. Sci. 2022, 12, 38–41. [Google Scholar] [CrossRef]
- Lee, J.; Kwon, J.H. Review the Status of Korean Geoid Model Development since 2000s and Future Improvement Plan. Terr. Atmos. Ocean. Sci. 2022, 33, 12. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Y.; Li, Z.; Fang, G.; Xiang, Y.; Li, Y.; Ji, H. Recent Changes in Water Discharge in Snow and Glacier Melt-Dominated Rivers in the Tienshan Mountains, Central Asia. Remote Sens. 2020, 12, 2704. [Google Scholar] [CrossRef]
- Kraemer, R.; Prishchepov, A.V.; Müller, D.; Kuemmerle, T.; Radeloff, V.C.; Dara, A.; Terekhov, A.; Frühauf, M. Long-Term Agricultural Land-Cover Change and Potential for Cropland Expansion in the Former Virgin Lands Area of Kazakhstan. Environ. Res. Lett. 2015, 10, 054012. [Google Scholar] [CrossRef]
- Shoganbekova, D.; Urazaliyev, A.; Sermiagin, R.; Nurakynov, S.; Kozhakhmetov, M.; Zhaksygul, N.; Islyamova, A. Evaluation of a Soviet-Era Gravimetric Survey Using Absolute Gravity Measurements and Global Gravity Models: Toward the First National Geoid of Kazakhstan. Geosciences 2025, 15, 404. [Google Scholar] [CrossRef]
- Information System “State Geodetic Support”. Available online: https://ggo.gov.kz/ (accessed on 30 August 2025).
- Kovrizhnykh, P.N. Report on the Results of the Project: “Gravity–Magnetic Surveys in the Kazakhstan Sector of the Caspian Sea (KSCS), Conducted in 2010–2011.” Republican Budget Program 040: “Regional Geological Mapping, Prospecting–Evaluation and Exploration Works”; National Geological Service of the Republic of Kazakhstan (Archive): Astana, Kazakhstan, 2011. [Google Scholar]
- Kovrizhnykh, P.N. Technical Report on 1:100,000-Scale Gravimetric Surveys of the Kurmangazy Structure Conducted in 2006; National Geological Service of the Republic of Kazakhstan (Archive): Astana, Kazakhstan, 2008. [Google Scholar]
- Seleznev, A.M. Report on the Results of Gravimetric Surveys for 1966 over Map Sheets M-44-XII, XVIII; M-44-57-B,G; 68-G; 69-V; 81-A,B, Carried Out by the Bukhtarma Party of the AGE; National Geological Service of the Republic of Kazakhstan (Archive): Astana, Kazakhstan, 1966. [Google Scholar]
- Sermiagin, R.A.; Kemerbayev, N.T.; Kassymkanova, K.-K.M.; Kalen, E.; Mussina, G.A.; Shkiyeva, M.K.; Samarkhanov, K.B.; Batalova, A.T.; Rakhimzhanov, A.N.; Zhumakanov, A.B.; et al. A historical overview of gravimetric surveys in Kazakhstan. Geod. Cartogr. 2024, 1012, 53–64. [Google Scholar] [CrossRef]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m Global Map of Elevation with Forests and Buildings Removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Yan, B.; Yue, L.; Wang, L. Global DEMs Vary from One to Another: An Evaluation of Newly Released Copernicus, NASA and AW3D30 DEM on Selected Terrains of China Using ICESat-2 Altimetry Data. Int. J. Digit. Earth 2022, 15, 1149–1168. [Google Scholar] [CrossRef]
- Shoganbekova, D. Assessment of Digital Elevation Models Accuracy for Local Geoid Modeling. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2024, 5, 151–156. [Google Scholar] [CrossRef]
- Osama, N.; Shao, Z.; Freeshah, M. The FABDEM Outperforms the Global DEMs in Representing Bare Terrain Heights. Photogramm. Eng. Remote Sens. 2023, 89, 613–624. [Google Scholar] [CrossRef]
- Marsh, C.B.; Harder, P.; Pomeroy, J.W. Validation of FABDEM, a Global Bare-Earth Elevation Model, against UAV-Lidar Derived Elevation in a Complex Forested Mountain Catchment. Environ. Res. Commun. 2023, 5, 031009. [Google Scholar] [CrossRef]
- Ince, E.S.; Barthelmes, F.; Reißland, S.; Elger, K.; Förste, C.; Flechtner, F.; Schuh, H. ICGEM—15 Years of Successful Collection and Distribution of Global Gravitational Models, Associated Services, and Future Plans. Earth Syst. Sci. 2019, 11, 647–674. [Google Scholar] [CrossRef]
- Liang, W.; Li, J.; Xu, X.; Zhang, S.; Zhao, Y. A High-Resolution Earth’s Gravity Field Model SGG-UGM-2 from GOCE, GRACE, Satellite Altimetry, and EGM2008. Engineering 2020, 6, 860–878. [Google Scholar] [CrossRef]
- Kiamehr, R.; Sjöberg, L.E. An Optimum Way to Determine a Precise Gravimetric Geoid Model Based on the Least-Squares Modification of Stokes’ Formula—A Case Study of Sweden. Acta Geod. Geophys. Hung. 2010, 45, 148–164. [Google Scholar] [CrossRef]
- Oduyebo, O.F.; Ono, M.N.; Okiemute, E.S. Practical Local Geoid Modelling of Benin City, Nigeria from Gravimetric Observations Using the Modified Stokes Integral. Int. J. Adv. Eng. Manag. Sci. (IJAEMS) 2019, 5, 608–617. [Google Scholar] [CrossRef]
- Sjöberg, L.E. A General Model for Modifying Stokes’ Formula and Its Least-Squares Solution. J. Geod. 2003, 77, 459–464. [Google Scholar] [CrossRef]
- Ågren, J.; Sjöberg, L.E.; Kiamehr, R. The New Gravimetric Quasigeoid Model KTH08 over Sweden; Walter de Gruyter GmbH: Berlin, Germany, 2009. [Google Scholar]
- Sjöberg, L.E. Unbiased Least-Squares Modification of Stokes’ Formula. J. Geod. 2020, 94, 92. [Google Scholar] [CrossRef]
- Yildiz, H.; Forsberg, R.; Ågren, J.; Tscherning, C.; Sjöberg, L. Comparison of Remove-Compute-Restore and Least Squares Modification of Stokes’ Formula Techniques to Quasi-Geoid Determination over the Auvergne Test Area. J. Geod. Sci. 2012, 2, 53–64. [Google Scholar] [CrossRef]
- Pa’suya, M.F.; Din, A.H.M.; Yusoff, M.Y.M.; Abbak, R.A.; Hamden, M.H. Refinement of Gravimetric Geoid Model by Incorporating Terrestrial, Marine, and Airborne Gravity Using KTH Method. Arab. J. Geosci. 2021, 14, 2003. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. Gravity Inversion and Integration; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 3-319-50298-0. [Google Scholar]
- Kuczynska-Siehien, J. Geoid Determination for the Area of Poland by the Least Squares Modification of Stokes’ Formula. Acta Geodyn. Geomater. 2015, 13, 19–26. [Google Scholar] [CrossRef]
- Märdla, S.; Ellmann, A.; Ågren, J.; Sjöberg, L.E. Regional Geoid Computation by Least Squares Modified Hotine’s Formula with Additive Corrections. J. Geod. 2018, 92, 253–270. [Google Scholar] [CrossRef]
- Abbak, R.A.; Ustun, A. A Software Package for Computing a Regional Gravimetric Geoid Model by the KTH Method. Earth Sci. Inform. 2015, 8, 255–265. [Google Scholar] [CrossRef]
- Abdalla, A.; Mogren, S. Implementation of a Rigorous Least-Squares Modification of Stokes’ Formula to Compute a Gravimetric Geoid Model over Saudi Arabia (SAGEO13). Can. J. Earth Sci. 2015, 52, 823–832. [Google Scholar] [CrossRef]
- Janák, J.; Vańiček, P.; Foroughi, I.; Kingdon, R.; Sheng, M.B.; Santos, M.C. Computation of Precise Geoid Model of Auvergne Using Current UNB Stokes-Helmert’s Approach. Contrib. Geophys. Geod. 2017, 47, 201–229. [Google Scholar] [CrossRef]
- Kamto, P.G.; Adiang, C.M.; Nguiya, S.; Kamguia, J.; Yap, L. Refinement of Bouguer Anomalies Derived from the EGM2008 Model, Impact on Gravimetric Signatures in Mountainous Region: Case of Cameroon Volcanic Line, Central Africa. Earth Planet. Phys. 2020, 4, 639–650. [Google Scholar] [CrossRef]
- Nyoka, C.J.; Din, A.H.M.; Pa’suya, M.F.; Omar, A.H. A Combined Regional Geopotential Model Using Optimized Global Gravity Field Solutions. IOP Conf. Ser. Earth Environ. Sci. 2022, 1051, 012001. [Google Scholar] [CrossRef]
- Trojanowicz, M. Estimation of Optimal Quantitative Parameters of Selected Input Data Used in Local Quasigeoid Modelling by the GGI Method. J. Spat. Sci. 2015, 60, 167–178. [Google Scholar] [CrossRef]
- Foroughi, I.; Vaníček, P.; Novák, P.; Kingdon, R.W.; Sheng, M.; Santos, M.C. Optimal Combination of Satellite and Terrestrial Gravity Data for Regional Geoid Determination Using Stokes-Helmert’s Method, the Auvergne Test Case; Springer: Berlin/Heidelberg, Germany, 2017; pp. 37–43. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Herbert Wichmann Verlag: Karlsruhe, Germany, 1980. [Google Scholar]
- Pa’suya, M.F.; Md Din, A.H.; Abbak, R.A.; Hamden, M.H.; Yazid, N.M.; Aziz, M.A.C.; Samad, M.A.A. Hybrid Geoid Model over Peninsular Malaysia (PMHG2020) Using Two Approaches. Stud. Geophys. Geod. 2022, 66, 98–123. [Google Scholar] [CrossRef]
- Krdžalić, D.; Abbak, R.A. A Precise Geoid Model of Bosnia and Herzegovina by the KTH Method and Its Validation. Surv. Rev. 2023, 55, 513–523. [Google Scholar] [CrossRef]
- Liu, Q.; Schmidt, M.; Sánchez, L. Combination of Different Observation Types through a Multi-Resolution Representation of the Regional Gravity Field Using the Pyramid Algorithm and Parameter Estimation. J. Geod. 2022, 96, 80. [Google Scholar] [CrossRef]
- Shoganbekova, D.; Fan, H.; Pentayev, T. Gravimetric Geoid Model over Kazakhstan. In Proceedings of the 15th International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management (SGEM), Albena, Bulgaria, 18–24 June 2015; pp. 283–290. [Google Scholar] [CrossRef]
- Hirt, C.; Yang, M.; Kuhn, M.; Bucha, B.; Kurzmann, A.; Pail, R. SRTM2gravity: An Ultrahigh Resolution Global Model of Gravimetric Terrain Corrections. Geophys. Res. Lett. 2019, 46, 4618–4627. [Google Scholar] [CrossRef]
- Ramouz, S. IRG2018: A Regional Geoid Model in Iran Using Least Squares Collocation. Stud. Geophys. Geod. 2019, 63, 191–214. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, H.; Wang, B.; Chen, S.; Li, H. Performance Comparison of Geoid Refinement between XGM2016 and EGM2008 Based on the KTH and RCR Methods: Jilin Province, China. Remote Sens. 2020, 12, 324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).