Linear Heat Diffusion Inverse Problem Solution with Spatio-Temporal Constraints for 3D Finite Element Models

Abstract

High-voltage ceramic insulators are routinely exposed to short-duration overvoltages such as lightning impulses, switching surges, and partial discharges. These events occur on microsecond to millisecond timescales and can produce highly localized thermal spikes that are difficult to measure directly but may compromise long-term material integrity. This paper addresses the estimation of the internal temperature distribution immediately after a lightning impulse by solving a three-dimensional inverse heat conduction problem (IHCP). The forward problem is modeled by the transient heat diffusion equation with constant thermal diffusivity, discretized using the finite element method (FEM). Surface temperature measurements are assumed available from a 12 kV ceramic post insulator and are used to reconstruct the unknown initial condition. To address the ill-posedness of the IHCP, a spatio-temporal regularization framework is introduced and compared against spatial-only regularization. Numerical experiments investigate the effect of measurement time ($T=60$ s, 600 s, and 1800 s), mesh resolution (element sizes of 20 mm, 15 mm, and 10 mm), and measurement noise ($\sigma =1$ K and 5 K). The results show that spatio-temporal regularization significantly improves reconstruction accuracy and robustness to noise, particularly when early-time measurements are available. Moreover, it is observed that mesh refinement enhances accuracy but yields diminishing returns when measurements are delayed. These findings demonstrate the potential of spatio-temporal IHCP methods as a diagnostic tool for the condition monitoring of ceramic insulators subjected to transient electrical stresses.

1. Introduction

High-voltage ceramic insulators are critical components in electrical power systems, ensuring reliable insulation and mechanical support in distribution and subtransmission networks [1]. During operation, these insulators are routinely subjected to transient electrical stresses such as lightning impulses, switching surges, and partial discharge activity. Although these events occur on microsecond to millisecond timescales, they can produce highly localized thermal effects that may initiate degradation mechanisms such as microcracking, erosion, or aging of the ceramic material. Accurate knowledge of the internal temperature distribution immediately after such transient events is therefore essential for assessing the condition of insulators and predicting their long-term performance [2].

Direct measurement of internal temperatures within ceramic insulators is not feasible in practice due to the opaque material structure and the very fast dynamics of the thermal response based on linear or nonlinear dynamical models [3]. Instead, temperature data are typically available only at the external surface, measured by sensors or infrared thermography at relatively low sampling rates while using models that can be represented by neural networks [4]. This situation naturally leads to the formulation of an IHCP, in which internal temperature fields or initial conditions are reconstructed from limited and noisy surface data and where the structure of the system can be represented by FEM [5]. However, IHCPs are well known to be ill-posed—small perturbations in the measurements may cause large instabilities in the solution [6]—and additional regularization is required to obtain meaningful reconstructions [7].

Several methods have been proposed in the literature to stabilize IHCPs, including Tikhonov regularization [8], Bayesian inference [9], and Kalman filtering [10]. Most existing work focuses on homogeneous or simple geometries [11], and applications are largely confined to metals, polymers, or biomedical tissues. By contrast, little attention has been given to ceramic insulators in high-voltage applications, where thermal diffusivity is low and heat transfer is strongly influenced by transient boundary conditions [12]. Moreover, the specific challenge of reconstructing an unknown initial condition after a short-duration electrical event has not been adequately addressed.

In this work, we investigate the use of spatio-temporal regularization within a finite element framework to reconstruct the initial temperature distribution of a 12 kV ceramic post insulator subjected to a lightning impulse. The forward problem is modeled by the three-dimensional heat diffusion equation with constant thermal diffusivity and convective boundary conditions. Surface measurements are simulated at different times ($T=60$ s, 600 s, and 1800 s), with varying levels of noise and mesh resolutions. The performance of the proposed spatio-temporal approach is compared against a baseline spatial-only regularization strategy, and reconstruction errors are systematically analyzed. The main contributions of this paper are as follows:

• Formulation of the IHCP for ceramic insulators subjected to lightning impulses, with emphasis on reconstructing the unknown initial conditions.
• Introduction of a spatio-temporal regularization framework that enhances stability and accuracy compared to spatial-only methods.
• Comprehensive numerical experiments analyzing the influence of measurement timing, mesh resolution, and measurement noise on reconstruction performance.
• Demonstration of the applicability of the proposed method to the realistic 3D complex geometries and operating conditions of high-voltage ceramic insulators.

This paper is organized as follows: in Section 2, the theoretical framework that includes the dynamic forward and inverse solution with spatio-temporal constraints is presented. In Section 3, the numerical results considering a 12 kV ceramic insulator are presented. Finally, in Section 4, the conclusions and future works are addressed.

2. Theoretical Framework

2.1. Three-Dimensional Heat Diffusion Equation in Ceramic Insulators

High-voltage ceramic insulators in distribution and subtransmission networks are exposed to ultraviolet radiation and thermal radiations. In addition, electrical stresses are caused by the quasi electrostatic field that exists due to the high voltage transmission line; occasionally, this stress can increase momentarily on the insulators during switching or lightning impulses, which are transient overvoltages and localized discharges that occur on timescales of microseconds to milliseconds [13]. These events, although brief, can produce localized heating patterns that are not easily captured by steady-state thermal analysis and may have significant implications for material integrity [14]. The main categories of such events include: switching surges, partial discharge (PD) bursts, and lightning impulses [15]. In this study, we will focus on lightning impulses as they are difficult to measure directly. Lightning strikes or nearby discharges can induce very fast overvoltage transients with rise times in the range of 0.5–5 $\mathsf{\mu }$s and total durations of 40–100 $\mathsf{\mu }$s. In ceramic insulators, the rapid voltage change causes intense but short-lived dielectric stresses. Although the total energy is relatively low compared to long-term load heating, the high current density in localized conduction or flashover paths can produce instantaneous temperature rises at defect sites, pollution layers, or near metal fittings. These thermal spikes are highly non-uniform and can act as seeds for crack initiation or glazing degradation.

These short-duration events are challenging to measure directly within the insulator body, but they produce spatially non-uniform transient thermal fields whose surface manifestations can be detected with fast-response infrared sensors. By applying the IHCP formulation, one can estimate the initial internal temperature distribution immediately after the event using only time-resolved surface temperature data. Such a capability is valuable for the condition monitoring of high-voltage ceramic insulators, enabling predictive maintenance before catastrophic failure.

The transient temperature field $u(\mathbf{x},t)$ in the ceramic insulator is governed by the three-dimensional heat diffusion equation, with a constant thermal diffusivity $\alpha$ [7]:

$${\displaystyle \frac{\partial u}{\partial t}}=\alpha {\nabla }^{2}u,\mathbf{x}\in \mathsf{\Omega },t>0.$$

(1)

It is worth noting that (1) considers constant thermal diffusivity $\alpha$, which may oversimplify real insulator behavior; however, the proposed approach can be extended to $\alpha$ with nonlinear or spatial-dependent behavior, as we proposed in [16,17]. These considerations can be useful for non-uniform defects, pollution layers, or heterogeneous materials.

Two types of boundary conditions are considered: convection boundaries for top and lateral surfaces ${\mathsf{\Gamma }}_c$, given by

$$-k{\displaystyle \frac{\partial u}{\partial n}}=h\left(u-u_{\infty }\right),\mathbf{x}\in {\mathsf{\Gamma }}_c,t>0,$$

(2)

where k is the thermal conductivity, h is the convection heat transfer coefficient, $u_{\infty }$ is the ambient temperature, and ${\displaystyle \frac{\partial u}{\partial n}}$ is the outward normal derivative, and adiabatic boundaries for the base ${\mathsf{\Gamma }}_q$, given by

$${\displaystyle \frac{\partial u}{\partial n}}=0,\mathbf{x}\in {\mathsf{\Gamma }}_q,t>0.$$

(3)

The initial temperature distribution given by

$$u(\mathbf{x},0)=u_0\left(\mathbf{x}\right),\mathbf{x}\in \mathsf{\Omega },$$

(4)

and where $u_0\left(\mathbf{x}\right)$ is unknown and will be reconstructed by solving the inverse heat conduction problem. To this end, the system is discretized in space and time. The space discretization is performed by a Finite Element Method (FEM) by considering the weak form of (1) whit $u\in V$ as follows [18]:

$${\int }_{\mathsf{\Omega }}{\displaystyle \frac{\partial u}{\partial t}}vd\mathsf{\Omega }+D{\int }_{\mathsf{\Omega }}\nabla u·\nabla vd\mathsf{\Omega }=0,\forall v\in V.$$

(5)

This solution can be approximated by

$$u(x,y,z,t)\approx \sum _j{u}_j\left(t\right){\varphi }_j(x,y,z),$$

using linear basis functions over tetrahedral elements. The resulting system can be rewritten in a general form:

$$M{\displaystyle \frac{d\mathbf{u}}{dt}}+\alpha K\mathbf{u}=0,$$

with

$$M_{ij}={\int }_{\mathsf{\Omega }}{\varphi }_i{\varphi }_{j}d\mathsf{\Omega },K_{ij}={\int }_{\mathsf{\Omega }}\nabla {\varphi }_i·\nabla {\varphi }_{j}d\mathsf{\Omega }.$$

and M being the global mass matrix and K being the stiffness matrix.

The time discretization is obtained by using implicit Euler time integration:

$$(M+\mathsf{\Delta }t\alpha K){\mathbf{u}}^{n+1}=M{\mathbf{u}}^n,A={(M+\mathsf{\Delta }t\alpha K)}^{-1}M.$$

the state equation being given by

$$\begin{array}{c}\hfill u^{n+1}=A{u}^n\end{array}$$

(6)

and the measurement equation being given by

$$\begin{array}{c}\hfill y^n=C{u}^n\end{array}$$

(7)

where $y\in {\mathbb{R}}^{p\times 1}$ is the measurement vector corresponding to the surface elements.

The global mass M and stiffness K matrices are assembled by adding local contributions from each tetrahedron. This formulation enables the solution of diffusion problems in complex 3D geometries or unstructured meshes.

2.2. Inverse Problem with Spatio-Temporal Regularization

The goal of the inverse problem is to estimate the initial state ${\mathbf{u}}^0$ from a final observation ${\mathbf{u}}^T$ [7]. Due to the ill-posedness of the problem, spatial and temporal regularization terms are introduced to stabilize the solution. This approach enhances reconstruction by enforcing spatial and temporal smoothness [19].

The cost functional for the inverse problem with both spatial and temporal regularization is defined as

$$J\left({\mathbf{u}}^0\right)={\parallel C{A}^{N_t}{\mathbf{u}}^0-C{\mathbf{u}}^T\parallel }_2^2+\lambda {\parallel L{\mathbf{u}}^0\parallel }_2^2+\gamma {\parallel \mathcal{D}{\mathbf{u}}^0\parallel }_2^2,$$

where

• $A^{N_t}$ is the time-evolution operator applied over $N_t$ time steps,
• L is the spatial regularization operator (e.g., a central difference matrix),
• $\lambda$ is the spatial regularization parameter,
• $\mathcal{D}$ is the temporal regularization operator,
• $\gamma$ is the temporal regularization parameter.

The analytical solution that minimizes the cost functional is obtained by solving the following linear system using Krylov subspace methods such as GMRES (Generalized Minimal Residual Method):

$$\left(A^{N_t^{\top }}{C}^{\top }C{A}^{N_t}+\lambda L^{\top }L+\gamma {\mathcal{D}}^{\top }\mathcal{D}\right){\mathbf{u}}^0=A^{N_t^{\top }}{C}^{\top }{\mathbf{u}}^T.$$

The temporal regularization operator $\mathcal{D}$ is defined as

$$\mathcal{D}=\left[\begin{array}{c}I\\ A\\ A^2\\ ⋮\\ A^{N_t-2}\end{array}\right](A-I)=\left[\begin{array}{c}A-I\\ A^2-A\\ ⋮\\ A^{N_t-1}-A^{N_t-2}\end{array}\right],$$

and reflects the recursive nature of the time evolution governed by

$${\mathbf{u}}_n=A^n{\mathbf{u}}_0,\mathrm{for}n=0,1,\dots ,N_t-1.$$

Hence, the vector $\mathcal{D}{\mathbf{u}}^0$ is constructed as

$$\mathcal{D}{\mathbf{u}}^0=\left[\begin{array}{c}A-I\\ A^2-A\\ ⋮\\ A^{N_t-1}-A^{N_t-2}\end{array}\right]{\mathbf{u}}^0=\left[\begin{array}{c}A{\mathbf{u}}^0-{\mathbf{u}}^0\\ A^2{\mathbf{u}}^0-A{\mathbf{u}}^0\\ ⋮\\ A^{N_t-1}{\mathbf{u}}^0-A^{N_t-2}{\mathbf{u}}^0\end{array}\right]=\left[\begin{array}{c}{\mathbf{u}}^1-{\mathbf{u}}^0\\ {\mathbf{u}}^2-{\mathbf{u}}^1\\ ⋮\\ {\mathbf{u}}^{N_t-1}-{\mathbf{u}}^{N_t-2}\end{array}\right].$$

Thus, $\mathcal{D}{\mathbf{u}}^0$ represents the vector of first-order temporal differences between consecutive time steps. It is worth noting that, in order to accelerate the convergence of the algorithm, a preconditioner M is included in the solution. The preconditioner M is computed at each iteration by considering

$$\begin{array}{c}\hfill M\approx \mathrm{diag}\left\{A^{N_t}\right\},\end{array}$$

(8)

The inverse problem with only spatial regularization ($\gamma =0$) is formulated as

$$J\left({\mathbf{u}}^0\right)={\parallel C{A}^{N_t}{\mathbf{u}}^0-C{\mathbf{u}}^T\parallel }_2^2+\lambda {\parallel L{\mathbf{u}}^0\parallel }_2^2,$$

and its minimizer satisfies the linear system

$$\left(A^{N_t\top }{C}^{\top }C{A}^{N_t}+\lambda L^{\top }L\right){\mathbf{u}}^0=A^{N_t\top }{C}^{\top }{\mathbf{u}}^T.$$

(9)

This system is also solved using Krylov subspace methods such as GMRES.

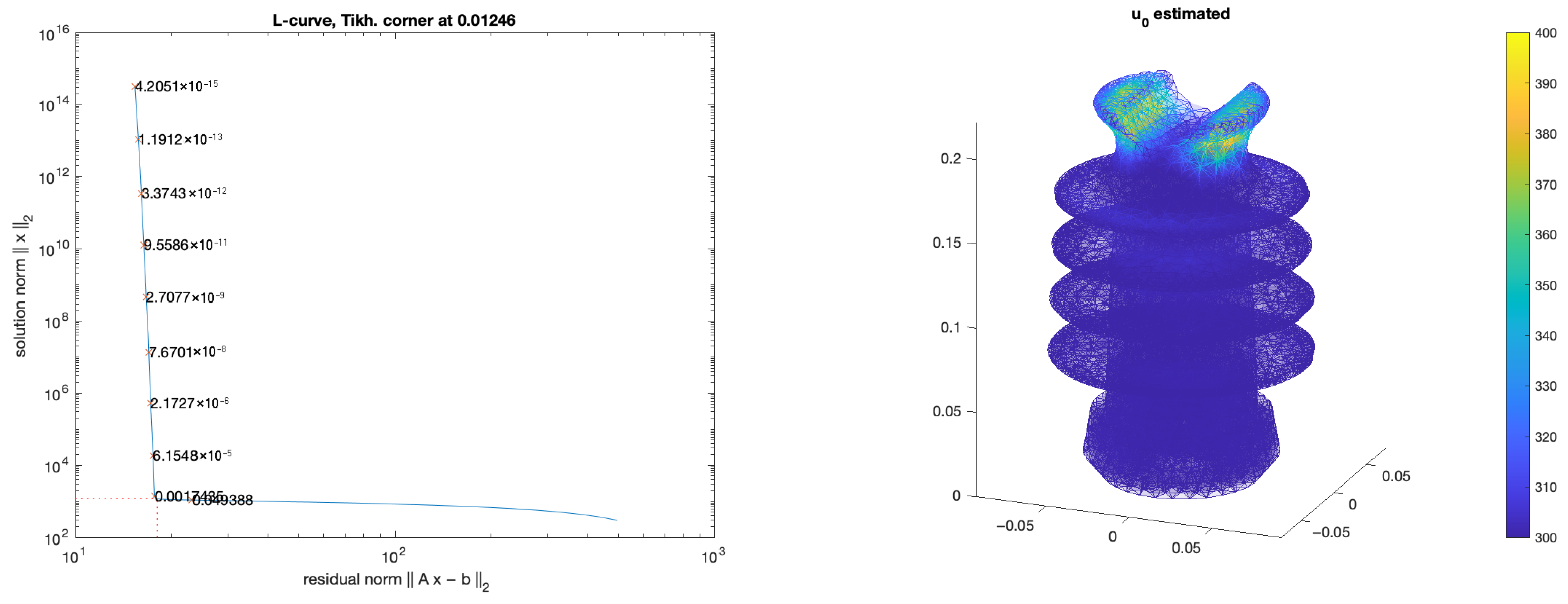
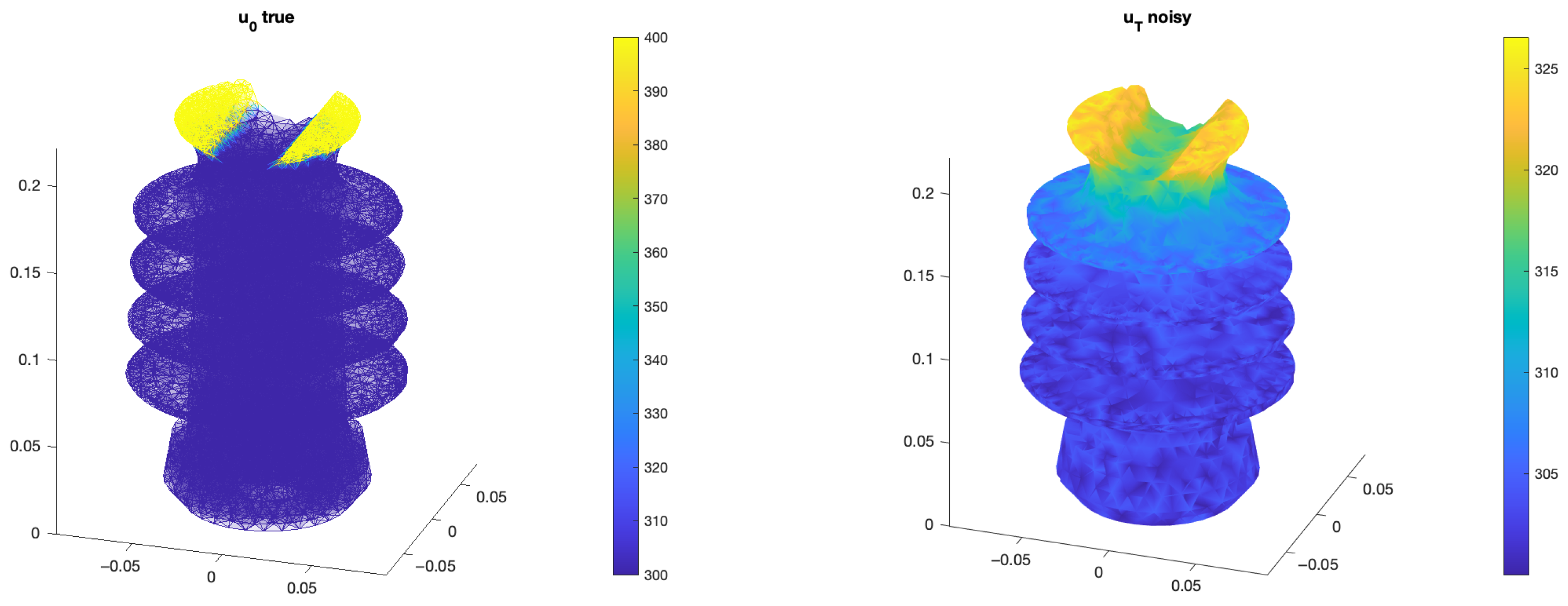
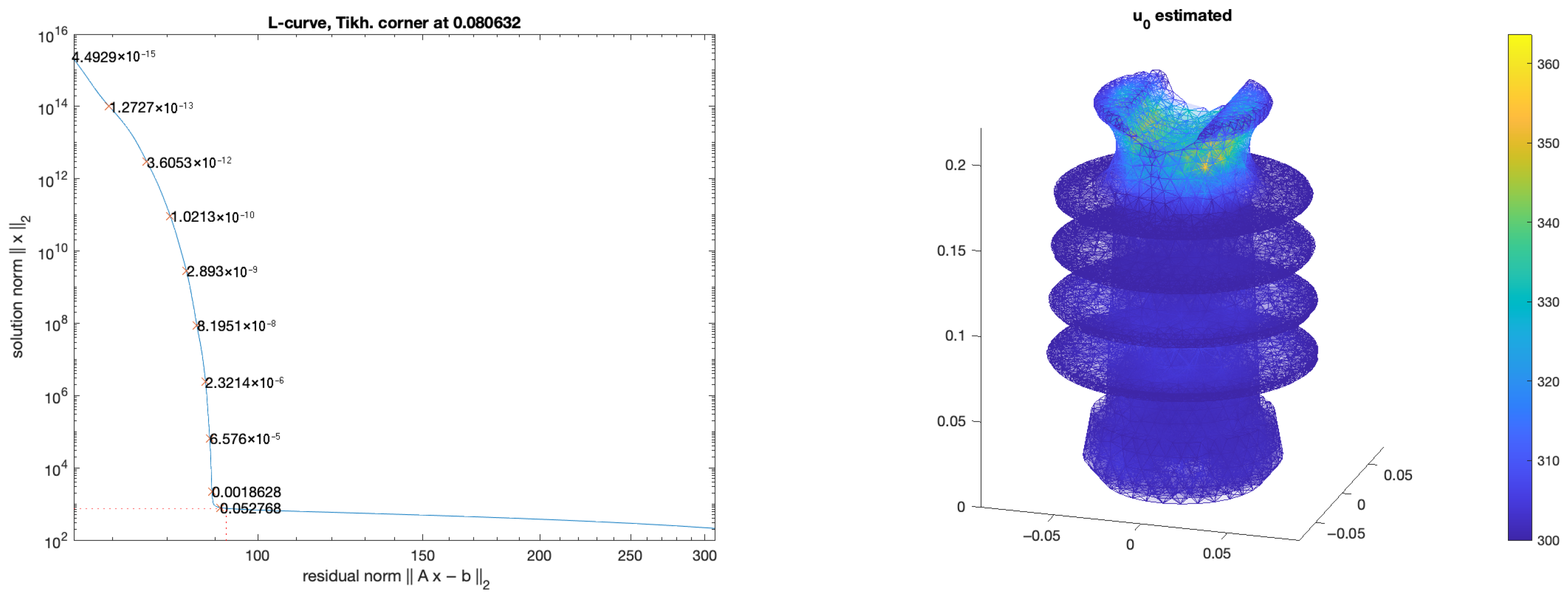
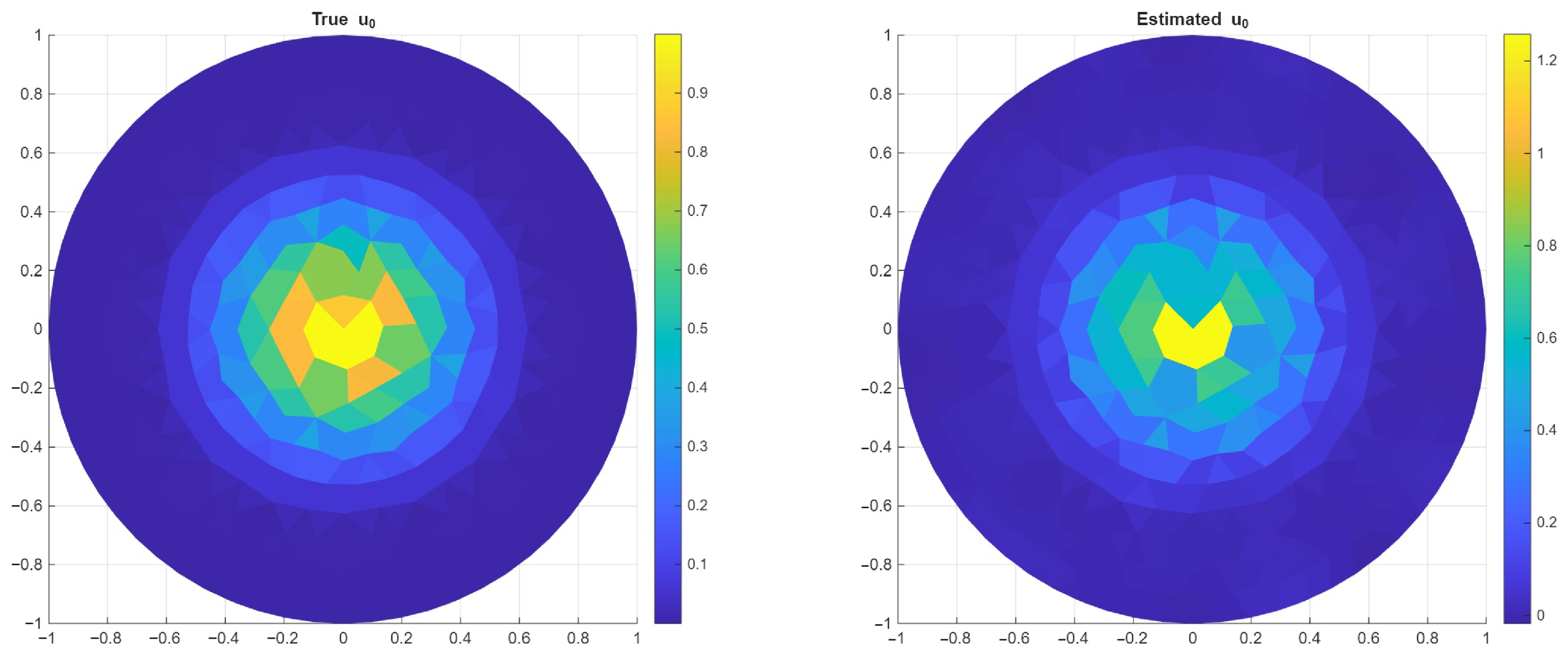
3. Numerical Results

The study considers a 12 kV ceramic insulator of height $H=0.22\mathrm{m}$ subjected to a short-duration electrical stress in the form of a lightning impulse. The lightning impulse is modeled as an instantaneous temperature rise of $\mathsf{\Delta }T=100\mathrm{K}$ applied uniformly over the top surface of the insulator at $t=0$. The 3D model of the insulator is available at [20]. The 3D model is shown in Figure 1.

The forward heat diffusion problem is solved in three dimensions using the FEM. The computational domain is discretized with tetrahedral elements of three different characteristic sizes—$h_e=20\mathrm{mm}$, $15\mathrm{mm}$, and $10\mathrm{mm}$—to evaluate the effect of spatial resolution on reconstruction accuracy. Figure 2 shows the meshes for each of the selected element sizes. The meshes are obtained by using the function generateMesh from Matlab 2025b.

The thermal diffusivity of the porcelain material (porcelain, alumina, zirconia, steatite, etc.) is in the range of $\alpha =5\times {10}^{-7}{\mathrm{m}}^2/\mathrm{s}$ to $\alpha =2\times {10}^{-6}{\mathrm{m}}^2/\mathrm{s}$ [21]. In this work, the thermal diffusivity is assumed constant, with a value $\alpha =6.4\times {10}^{-7}{\mathrm{m}}^2/\mathrm{s}$, and the ambient temperature $u_{\infty }$ is assumed to be 300 K.

Temperature measurements are acquired from the top surface using a sampling rate of one sample every 6 s for a total of 300 measurements.

For the inverse problem, three different T measurements assumptions are analyzed:

$$T=60\mathrm{s},T=600\mathrm{s},T=1800\mathrm{s}.$$

In each case, the unknown initial temperature distribution $u_0\left(\mathbf{x}\right)$ is reconstructed from the measurement set.

The inverse heat conduction problem is solved using the proposed spatio-temporal constrained regularization method. For comparison, reconstructions are also performed with a spatially constrained approach only. The quality of the reconstruction is evaluated in terms of the relative reconstruction error:

$$E_{\mathrm{rel}}={\displaystyle \frac{\parallel u_{\mathrm{rec}}-u_{\mathrm{true}}{\parallel }_2}{\parallel u_{\mathrm{true}}{\parallel }_2}}.$$

The effect of both the regularization approach and the mesh resolution on reconstruction accuracy is reported.

The spatial regularization parameter $\lambda$ is computed for each case by using the L-curve method described in [22]. For the spatio-temporal regularization, the spatial regularization parameter $\lambda$ and the temporal regularization parameter $\gamma$ are computed for each case by using a generalization of the L-surface method named the L-hypersurface method described in [23], where the stability of parameter selection and computational time is discussed.

In

Table 1. Finite element experiments.

Element Size	20 mm	15 mm	10 mm
Number of finite elements	2334	3584	5323
Surface elements for measurements	1864	2849	3930

are shown the number of finite elements and the surface elements used for measurements for each element size. In

Table 2. Relative error with $u_T$ at $T=60$.

Element Size		20 mm	15 mm	10 mm
Spatial
$\sigma =1\mathrm{K}$	$\lambda$	0.0105	0.0107	0.0095
	$E_{rel}$	0.4915	0.4825	0.4806
$\sigma =5\mathrm{K}$	$\lambda$	0.0598	0.0584	0.0487
	$E_{rel}$	0.5861	0.5545	0.5262
Spatio-temporal
$\sigma =1\mathrm{K}$	$\lambda$	0.0105	0.0107	0.0095
	$\gamma$	0.0169	0.0162	0.0162
	$E_{rel}$	0.4216	0.4168	0.4106
$\sigma =5\mathrm{K}$	$\lambda$	0.0598	0.0584	0.0487
	$\gamma$	0.0797	0.0635	0.0095
	$E_{rel}$	0.5709	0.5392	0.5041

is shown the performance of the proposed spatio-temporal approach and its comparison with the spatial solution in terms of the relative error by considering a noise level of $\sigma =1$ K and $\sigma =5$ K, for the three element sizes described in Table 1. These results are obtained by considering that the noisy measurement is obtained at time $T=60$ s, with a sampling rate of 6 s.

The results shown in Table 2 are summarized in Figure 3, where it can be seen that mesh refinement improves accuracy but spatio-temporal regularization provides an additional and more consistent improvement across all noise levels and mesh sizes. This suggests that the proposed spatio-temporal framework is not only robust to measurement noise but also computationally efficient, since it allows reducing errors without relying solely on mesh refinement.

In addition, the results in Figure 3 show that the proposed spatio-temporal regularization consistently achieves lower relative errors than the spatial-only approach for both noise levels and across all mesh resolutions. Physically, this improvement arises from the additional temporal smoothness constraint introduced by the parameter $\gamma$, which stabilizes the inversion by coupling information between consecutive time steps. In contrast, the purely spatial regularization relies only on instantaneous spatial gradients, making it more sensitive to measurement noise and temporal sparsity. By enforcing temporal coherence, the spatio-temporal formulation effectively suppresses oscillations and compensates for the information loss due to low sampling rate (6 s), leading to more accurate reconstructions even under higher noise conditions ($\sigma =5$ K). The observed trend across mesh refinements further indicates that the spatio-temporal scheme maintains its stability and accuracy without requiring excessively fine discretizations, thus providing a more reliable and physically consistent estimate of the temperature field evolution.

Table 3. Computational time for the inverse problem.

Element Size	20 mm	15 mm	10 mm
Spatial	$3.2752$ s	$34.0432$ s	$58.0998$ s
Spatio-temporal	$54.7850$ s	$163.6687$ s	$742.8743$ s

shows the computational time of the dynamic inverse problem experiments by considering a measurement of $T=60$ s and a noise with $\sigma =1$ K. It is worth noting that this time does not include the required time for hyperparameter selection.

Table 3 summarizes the computational time required to solve the dynamic inverse problem for a single measurement taken at $T=60$ s with a noise level of $\sigma =1$ K. It is important to note that these times exclude the hyperparameter selection process (e.g., L-curve or L-surface search). As expected, the computational time increases significantly with mesh refinement due to the larger number of degrees of freedom in the finite element model. The increase is approximately one order of magnitude when refining the mesh from 20 mm to 10 mm. Furthermore, incorporating the spatio-temporal regularization considerably increases the overall computational burden, since it involves the solution of additional adjoint equations and the evaluation of temporal gradients across all time steps. However, the spatio-temporal formulation provides a substantially better reconstruction accuracy compared to the spatial-only case, especially for early measurement times, as previously shown in Table 2. This indicates that, although the spatio-temporal regularization incurs a higher computational cost (roughly between 15 and 20 times the spatial-only case for the coarsest mesh), it yields a more stable and accurate inverse reconstruction without the need for excessive mesh refinement. Therefore, for practical applications where computational resources are limited, a coarse mesh with spatio-temporal constraints offers the best compromise between accuracy and efficiency.

In addition, the computational results in Table 3 indicate that the full finite element inversion, particularly when including spatio-temporal regularization, incurs significant computational costs. Even for the coarsest mesh (20 mm), the inversion requires nearly one minute per estimation, excluding hyperparameter tuning. Consequently, direct application of the high-fidelity FEM–adjoint formulation in field scenarios is impractical for real-time monitoring, where updates would be required at sub-second to few-second intervals. Therefore, the proposed methodology must be adapted through reduced-order modeling or surrogate-based inference to achieve real-time feasibility while preserving estimation accuracy.

The same test is performed by considering that the $u_T$ measurement is at time $T=600$ s and $T=1800$. The results are shown in

Table 4. Relative error for the spatial regularization.

		$\mathit{T}=600$ s			$\mathit{T}=1800$ s
Element Size		20 mm	15 mm	10 mm	20 mm	15 mm	10 mm
$\sigma =1\mathrm{K}$	$\lambda$	0.0182	0.0152	0.0125	0.0356	0.0353	0.0242
	$E_{rel}$	0.8572	0.8319	0.7955	0.9369	0.9393	0.9170
$\sigma =5\mathrm{K}$	$\lambda$	0.0894	0.0814	0.0522	0.0968	0.1012	0.0806
	$E_{rel}$	0.8800	0.8641	0.8212	0.9510	0.9502	0.9309

and

Table 5. Relative error for the spatio-temporal regularization.

		$\mathit{T}=600$ s			$\mathit{T}=1800$ s
Element Size		20 mm	15 mm	10 mm	20 mm	15 mm	10 mm
$\sigma =1\mathrm{K}$	$\lambda$	0.0208	0.0170	0.0147	0.0348	0.0338	0.0135
	$\gamma$	0.0072	0.0060	0.044	0.0041	0.0033	0.0035
	$E_{rel}$	0.8432	0.8134	0.7355	0.9329	0.9338	0.9039
$\sigma =5\mathrm{K}$	$\lambda$	0.0894	0.0814	0.0522	0.0968	0.1022	0.0806
	$\gamma$	0.0371	0.0235	0.024	0.0181	0.0158	0.0119
	$E_{rel}$	0.8764	0.8606	0.8076	0.9501	0.9487	0.9297

, respectively. In these cases, the sampling time used for the forward problem is 6 s, but for the inverse problem the sampling time is modified for each case for a total of 10 samples.

In Table 4 and Table 5, it can be noted that, similarly to Table 2, the reconstruction error increases as T increases (i.e., the later the first measurement, the more diffusion has destroyed information about the localized initial spike). In addition, the proposed spatio-temporal regularization yields a lower reconstruction error than spatial-only regularization, especially when early-time measurements are available. Moreover, finer meshes provide improved reconstruction at the cost of larger computational time. However, if measurements are too late, mesh refinement yields diminishing returns because information is already lost. On another hand, it can be noted that measurement noise degrades all reconstructions. However, the spatio-temporal regularization gives better robustness to noise in comparison with the spatial regularization.

Overall, the results in Table 4 and Table 5 confirm the effectiveness of the proposed spatio-temporal regularization in mitigating noise and compensating for information loss over longer diffusion times. As the measurement time T increases, the diffusive process smooths the temperature gradients and reduces the sensitivity of the inverse problem, leading to higher reconstruction errors. The temporal coupling enforced by the parameter $\gamma$ stabilizes the inversion by incorporating the temporal evolution of the state, effectively filtering high-frequency noise and recovering smoother, physically consistent temperature fields. This is particularly beneficial when the data are sparse in time or strongly affected by noise, as temporal regularization constrains the solution trajectory rather than individual snapshots. Consequently, the spatio-temporal approach achieves better accuracy and robustness than the spatial-only case, even for coarse meshes and late-time measurements, highlighting its potential for stable thermal field estimation under realistic conditions.

An example of the initial $u_0$ for a 10 mm element size and an example of the $u_T$ noisy surface measurements with $\sigma =1\mathrm{K}$ at $T=600$ are shown in Figure 4.

The corresponding L-curve for the spatial regularization parameter, as well as the estimated initial condition from the $T=600$ measurement $u_0$ estimated, are shown in Figure 5.

The visual results in Figure 4 and Figure 5 provide additional insight into the performance of the proposed approach. The L-curve clearly exhibits a well-defined corner, confirming the suitability of the regularization parameter selected for the spatial case. The reconstructed initial condition, $u_0$ estimated, closely reproduces the main spatial features of the true $u_0$, demonstrating that the inverse formulation effectively compensates for the diffusive smoothing and measurement noise. Despite the information loss inherent in the thermal process at $T=600$ s, the regularization strategy constrains the solution to a physically meaningful subspace, avoiding overfitting to noise. It is worth mentioning that this qualitative agreement reinforces the quantitative trends observed in Table 2, Table 3, Table 4 and Table 5, highlighting the robustness and stability of the proposed spatio-temporal regularization framework.

Another example is analyzed by considering $u_T$ noisy surface measurements with $\sigma =5\mathrm{K}$ at $T=1800$ s, as shown in Figure 6.

The corresponding L-curve and the initial estimated condition from the measurement at $T=1800$ are shown in Figure 7.

The results shown in Figure 6 and Figure 7 illustrate the challenges of reconstructing the initial temperature field from late-time, highly noisy measurements. At $T=1800$ s, the diffusion process has significantly attenuated spatial gradients, resulting in a much smoother $u_T$ distribution. Despite this, the L-curve remains a useful diagnostic for identifying an optimal regularization level, ensuring a balance between data fidelity and stability. The reconstructed $u_0$ exhibits a physically consistent spatial pattern, although fine-scale features are unavoidably smoothed out due to both temporal diffusion and noise contamination. These results confirm that while the inverse solution deteriorates for delayed measurements and higher noise, the spatial and spatio-temporal regularization still mitigate overfitting and preserve the main thermal structure, consistent with the quantitative results in Table 4 and Table 5.

Example on a 2D Circle

Additionally, a two-dimensional test case was performed to further validate the proposed inverse formulation using a circular geometry discretized with the finite element method (FEM). The circular domain was defined with a radius of $R=1$ m, and the total simulation time was set to $T=0.1$ s. The temporal domain was divided into $N_t=50$ uniform steps, resulting in a sampling interval of $\mathsf{\Delta }t=2\times {10}^{-3}$ s. A constant diffusion coefficient of $\alpha =0.1{\mathrm{m}}^2/\mathrm{s}$ was assumed to represent a homogeneous isotropic material. A noise of $\sigma =0.01$ was considered. The true initial temperature distribution was defined as

$$u_0^{\mathrm{true}}(x,y)=exp\left(-{\displaystyle \frac{x^2+y^2}{0.1}}\right),$$

representing a smooth Gaussian profile centered at the origin that mimics a localized heat source diffusing over time. This 2D configuration provides a simplified yet representative setup to evaluate the performance and stability of the proposed inverse reconstruction method. Two experiments were conducted to evaluate the computational performance and reconstruction accuracy of the proposed inverse spatial formulation using different mesh resolutions. To this end, the spatial discretization employed two finite element sizes of $h=0.05$ m and $h=0.1$ m.

In the first experiment, a mesh with element size $h=0.1$ was employed, consisting of 381 triangular elements. The total elapsed time for the L-curve method used to determine the optimal regularization parameter was $0.1384$ s, while the inverse spatial reconstruction required $0.0357$ s. The resulting residual error was $E_{\mathrm{res}}=0.0336$. Figure 8 shows the triangulation and the noisy measurement.

Figure 9 shows the triangulation and the noisy measurement.

In the second experiment, the mesh was refined to an element size of $h=0.05$, corresponding to 1515 elements. The elapsed time for the L-curve computation increased to $0.3228$ s, and the inverse spatial reconstruction required $1.8310$ s. Despite the higher computational cost due to mesh refinement, the residual error slightly decreased to $E_{\mathrm{res}}=0.0321$, indicating an improvement in reconstruction accuracy. Figure 10 shows the triangulation and the noisy measurement.

Figure 11 shows the triangulation and the noisy measurement.

These experiments show that the proposed approach can be easily extended to any system described by FEM.

4. Conclusions

This work has presented a methodology for estimating the internal temperature distribution of high-voltage ceramic insulators subjected to lightning impulses based on solving the inverse heat conduction problem with spatio-temporal regularization. The main conclusions are as follows:

• The reconstruction of the unknown initial condition is strongly dependent on the availability of early measurements. When the first measurement is delayed (e.g., $T=1800$ s), the information loss due to thermal diffusion leads to a significant increase in reconstruction error.
• The proposed spatio-temporal regularization consistently outperforms spatial-only regularization. By enforcing both spatial and temporal smoothness, it achieves lower relative errors and better robustness against measurement noise.
• Mesh refinement improves the accuracy of reconstructions; however, its effect diminishes when measurements are taken at later times. This indicates that regularization strategies are more effective than simply refining the mesh for compensating information loss.
• Measurement noise degrades the reconstruction quality in all cases, but the spatio-temporal method exhibits improved stability compared to the spatial approach.
• The framework developed here provides a promising tool for the non-intrusive thermal characterization of ceramic insulators during transient electrical stresses, enabling condition monitoring and predictive maintenance in distribution and subtransmission networks, with potential applications to in the predictive maintenance of electrical insulators.

Future work will focus on extending the methodology to account for heterogeneous material properties by using a nonlinear thermal diffusivity term, experimental validation using infrared thermography, and real-time implementation for field monitoring. In addition, the proposed methodology can be extended to estimate the initial temperature conditions to any system that can be measured only superficially using thermo-graphic cameras, and where the structure of the element has a complex 3D geometry that can be modeled using FEM.