An Analysis of the Computational Complexity and Efficiency of Various Algorithms for Solving a Nonlinear Model of Radon Volumetric Activity with a Fractional Derivative of a Variable Order
Abstract
1. Introduction
1.1. Object of Research
1.2. Theoretical and Practical Significance of the Research
1.3. Subject of Research
1.4. Article Structure
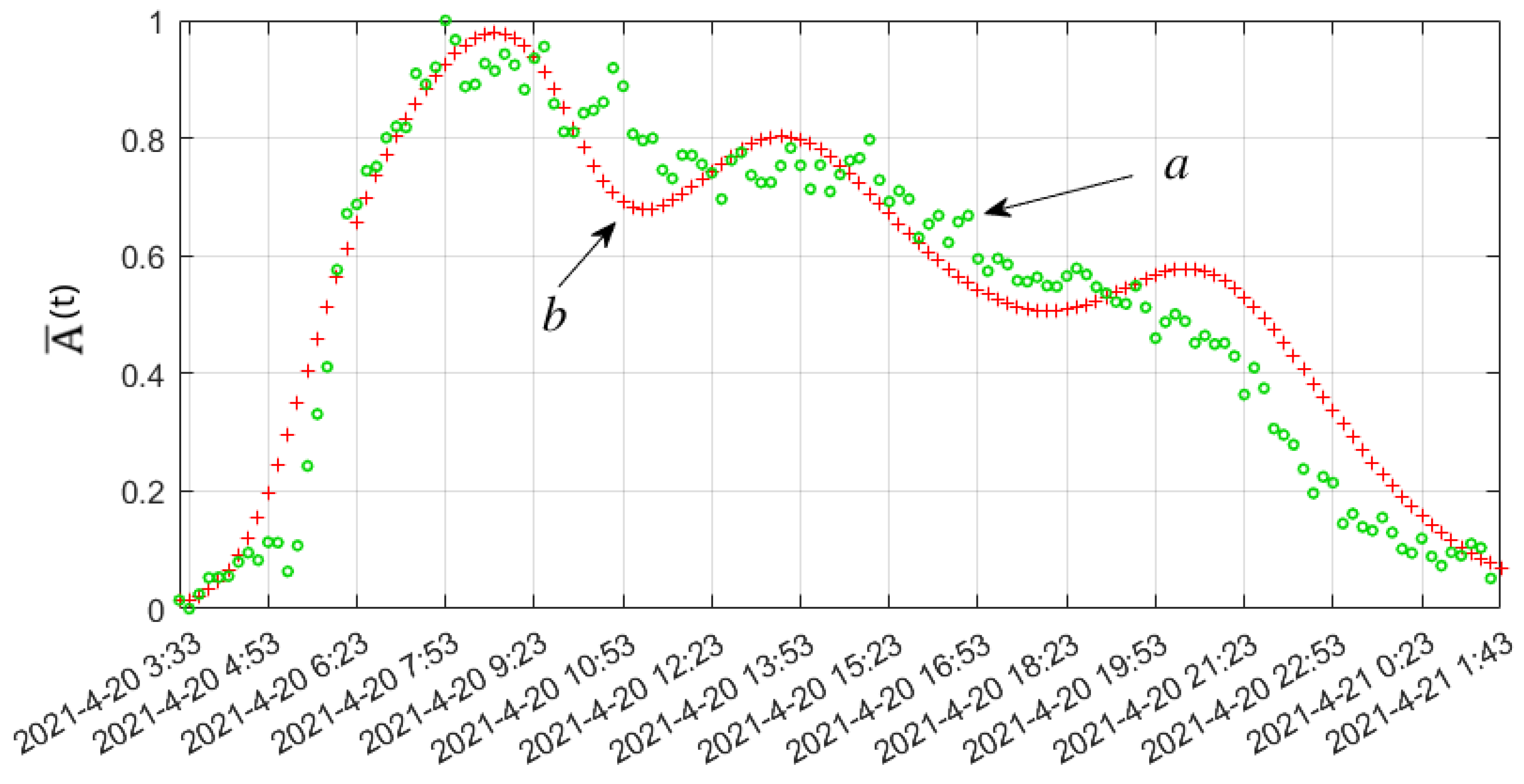
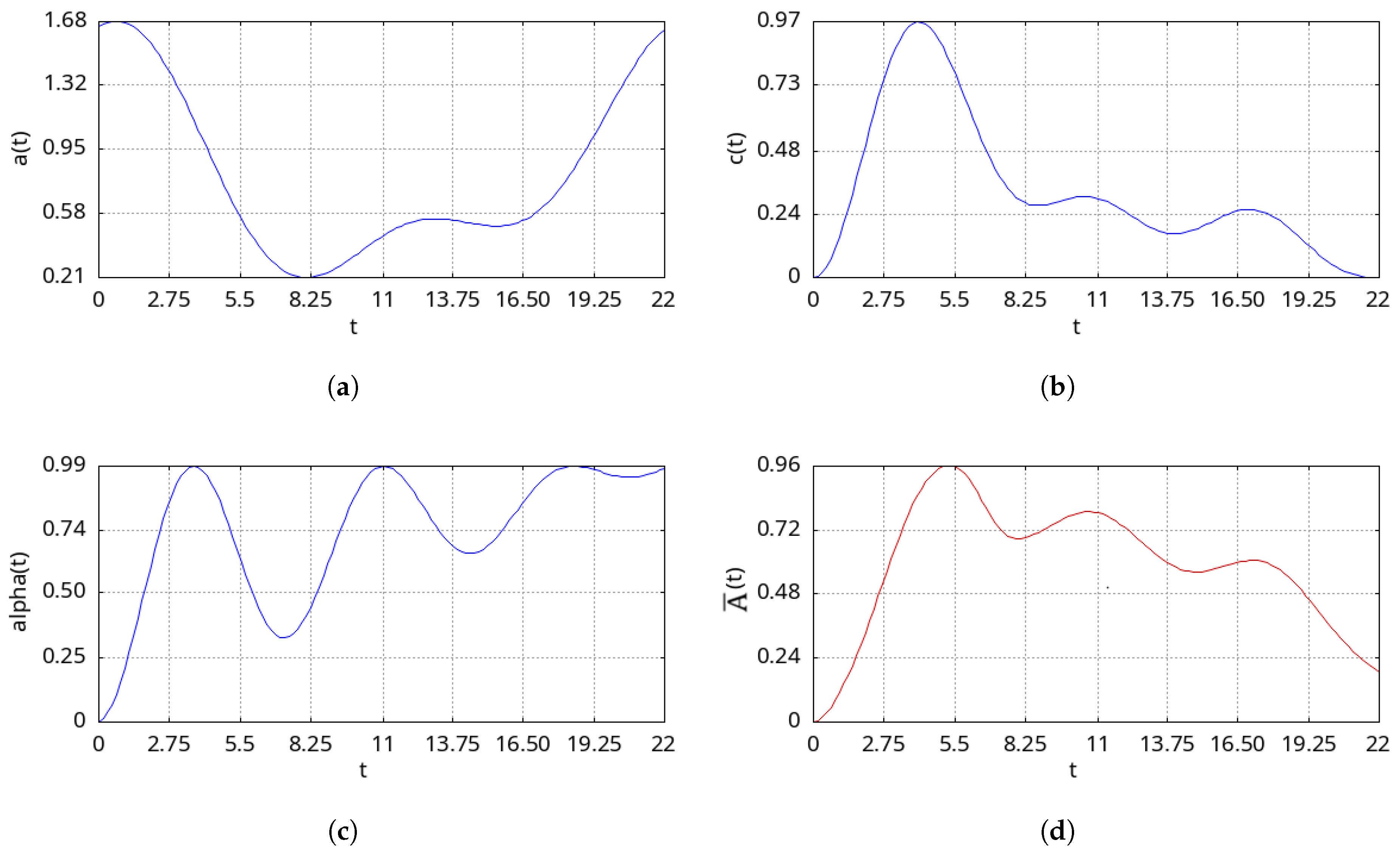
2. Test Example
- —RVA in dimensionless form;
- —RVA, —maximum RVA value observed in the data; —RVA at the initial moment in time;
- —time of the process under consideration; and —initial and final moments in time;
- —a function, like the member it stands for, related to the output from the chamber into the surrounding atmosphere at a pressure difference between the internal (chamber) and atmospheric pressures, for example, when passing in the vicinity of a cyclone observation point;
- —the air exchange rate;
- —a function describing the diffusion mechanism of transport into the chamber [37];
- —a model member describing the delay associated with time non-locality in the process of transport through the geological environment.
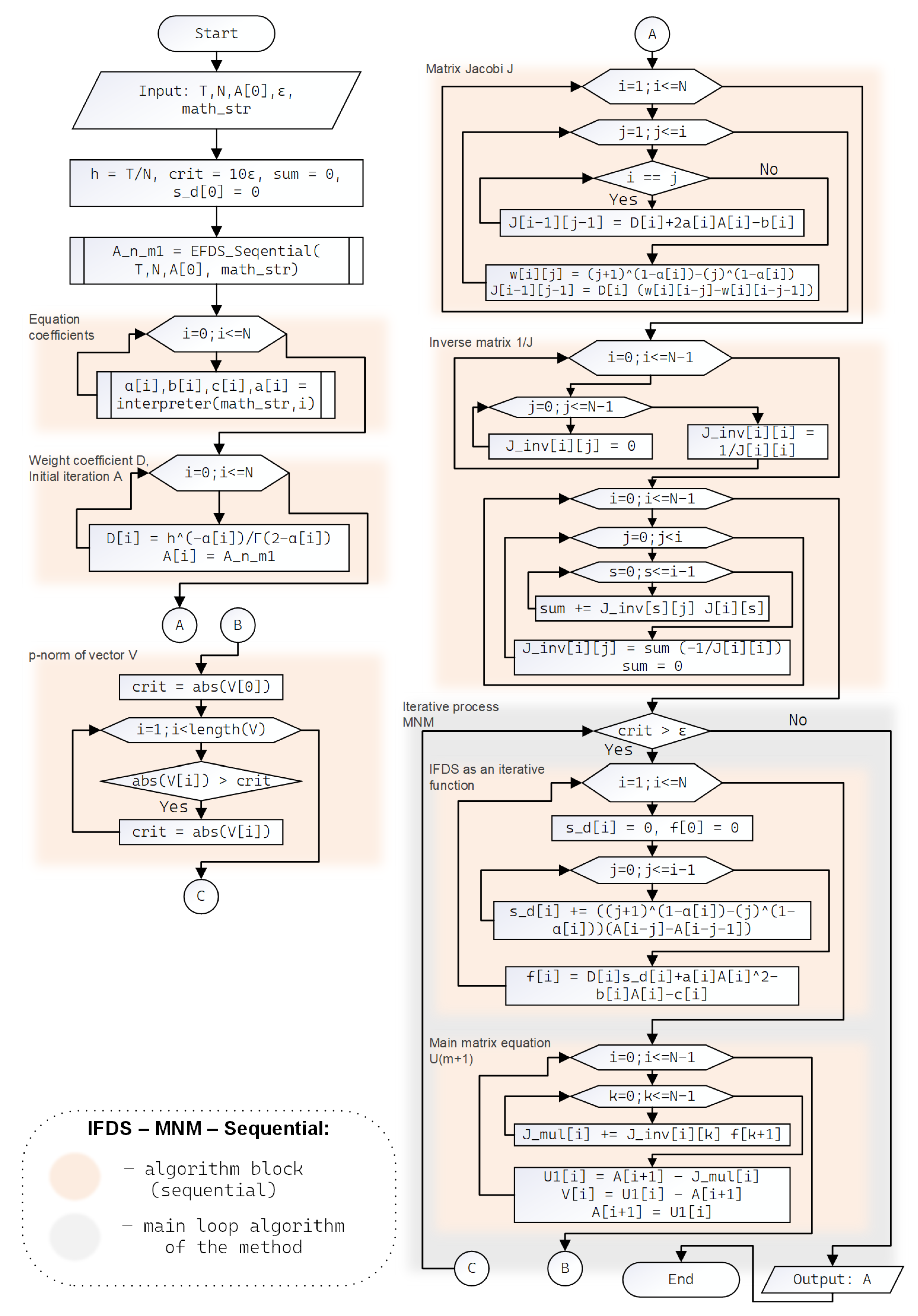
3. Sequential Algorithms for Numerical Solutions
4. Average Execution Time Using Different Algorithms
- —the execution time of a test example of size N spent by sequential (EFDS, IFDS-MNM) algorithms;
- —the execution time of a test example of size N spent by parallel (EFDS-omp, IFDS-MNM-omp) algorithms based on the OpenMP API [44], on a machine with CPU threads;
- —RAM usage when executing a test example of size N using sequential (EFDS, IFDS-MNM) algorithms;
- —RAM usage when executing a test example of size N using parallel (EFDS-omp, IFDS-MNM-omp) algorithms;
- —RAM usage when executing a test example of size N using hybrid parallel (EFDS-hybrid, IFDS-MNM-hybrid) algorithms on a machine with CPU threads and a fixed number g;
- —similarly, the use of node GPU memory when executing a test example of size N using hybrid parallel (EFDS-hybrid, IFDS-MNM-hybrid) algorithms.
5. Complexity Estimates for Sequential Algorithms
- For the sequential EFDS algorithm, the asymptotically exact estimate of time complexity is of the order of ;
- For the sequential IFDS-MNM algorithm, the asymptotically exact estimate of time complexity is of the order of .
- For the sequential EFDS algorithm, the asymptotically exact estimate of memory complexity is of the order of ;
- For the sequential IFDS-MNM algorithm, the asymptotically exact estimate of memory complexity is of the order of .

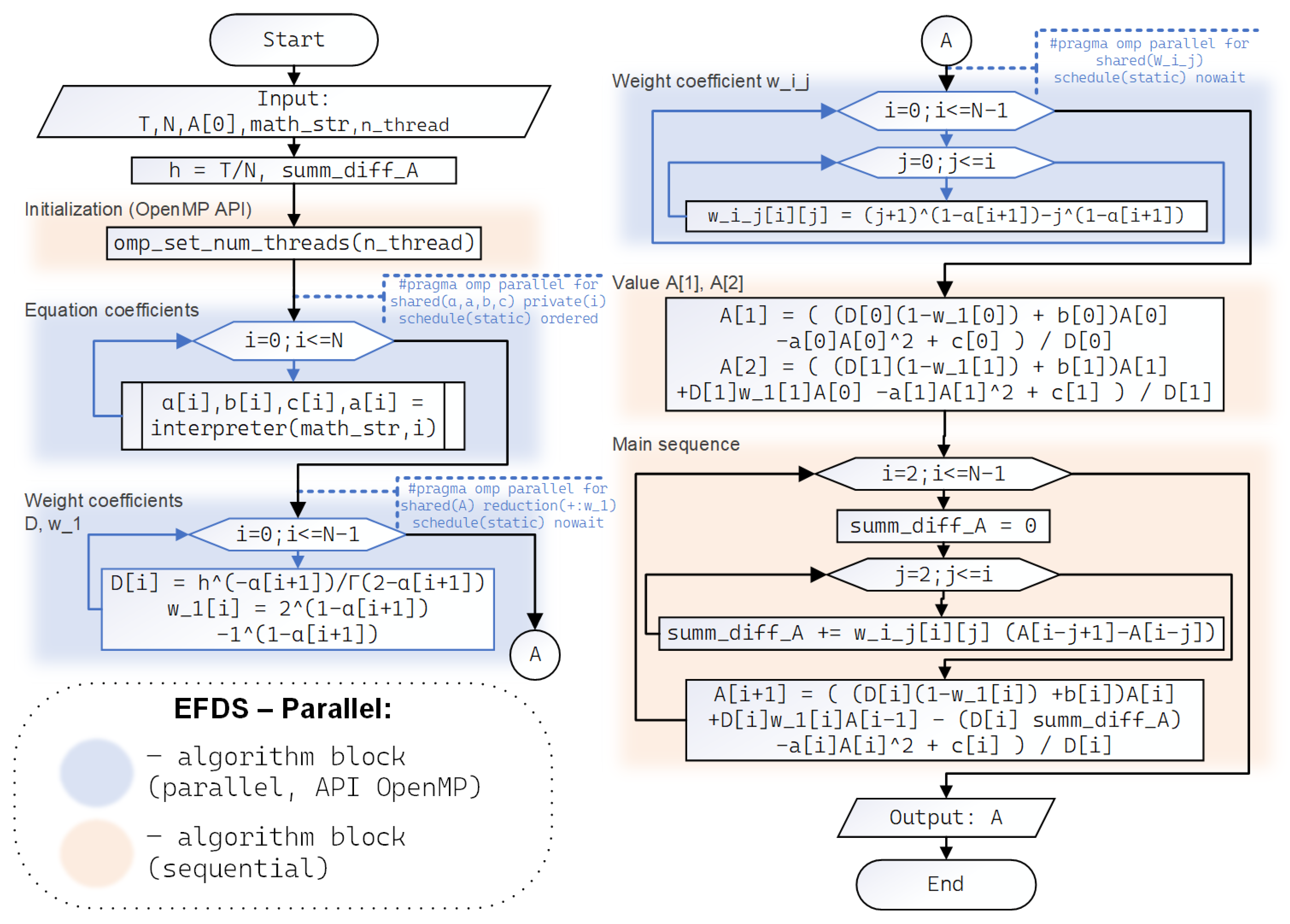
6. Parallel Algorithms EFDS and IFDS-MNM
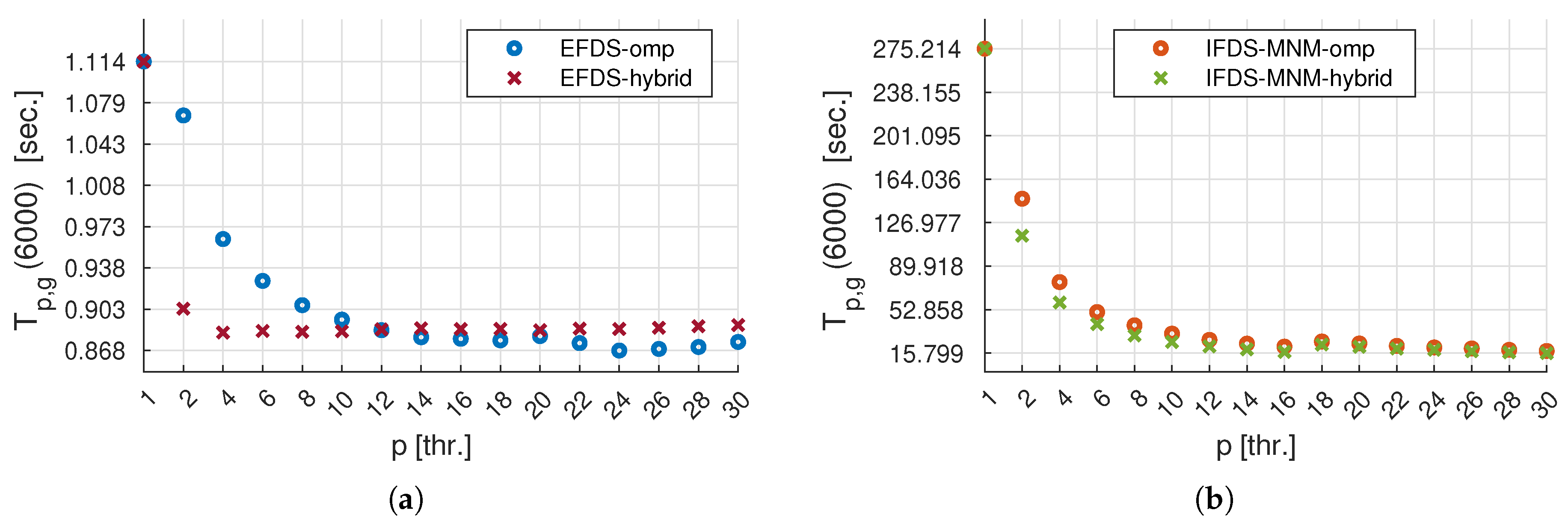
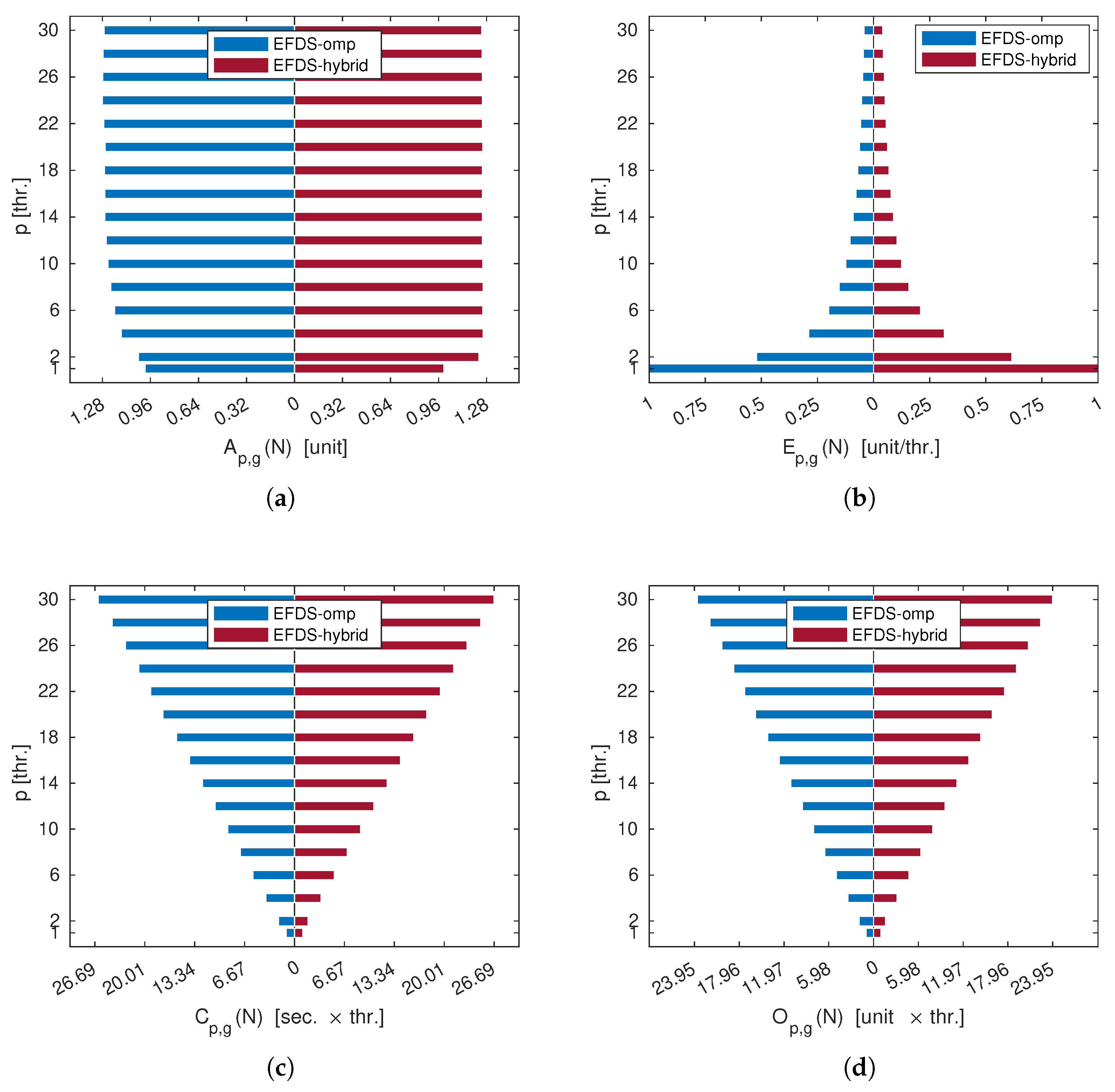
7. Analysis of Efficiency and Optimal CPU Usage for Parallel Algorithms
- is the acceleration in [unit] that the parallel version of the algorithm provides in comparison with the sequential one and is calculated as follows:where is the theoretical case, provided that there are no delays in parallelization for the task before it is sent to different CPU threads for calculation.
- is the efficiency, in [units/thr.], of using a given number of p CPU threads and is determined via the following ratio:where, for , we get that .
- is the cost in [sec. × thr.], which is determined by the product of a given number of p CPU threads and T execution time of the parallel algorithm. The cost is determined by the following ratio:
- is the cost-optimal indicator in [units. × thr.], is characterized by a cost proportional to the complexity of the most efficient sequential algorithm [49] and is calculated as follows:
8. Complexity Estimates for Parallel Algorithms
- For the parallel EFDS-omp and EFDS-hybrid algorithms, the asymptotically exact estimate of time complexity is of the order of ;
- For the parallel IFDS-MNM-omp and IFDS-MNM-hybrid algorithms, the asymptotically exact estimate of time complexity is close to the order of .

- For the parallel EFDS-omp and EFDS-hybrid algorithms, the asymptotically exact estimate of memory complexity is of the order of ;
- For the parallel IFDS-MNM-omp and IFDS-MNM-hybrid algorithms, the asymptotically exact estimate of memory complexity is close to the order of .
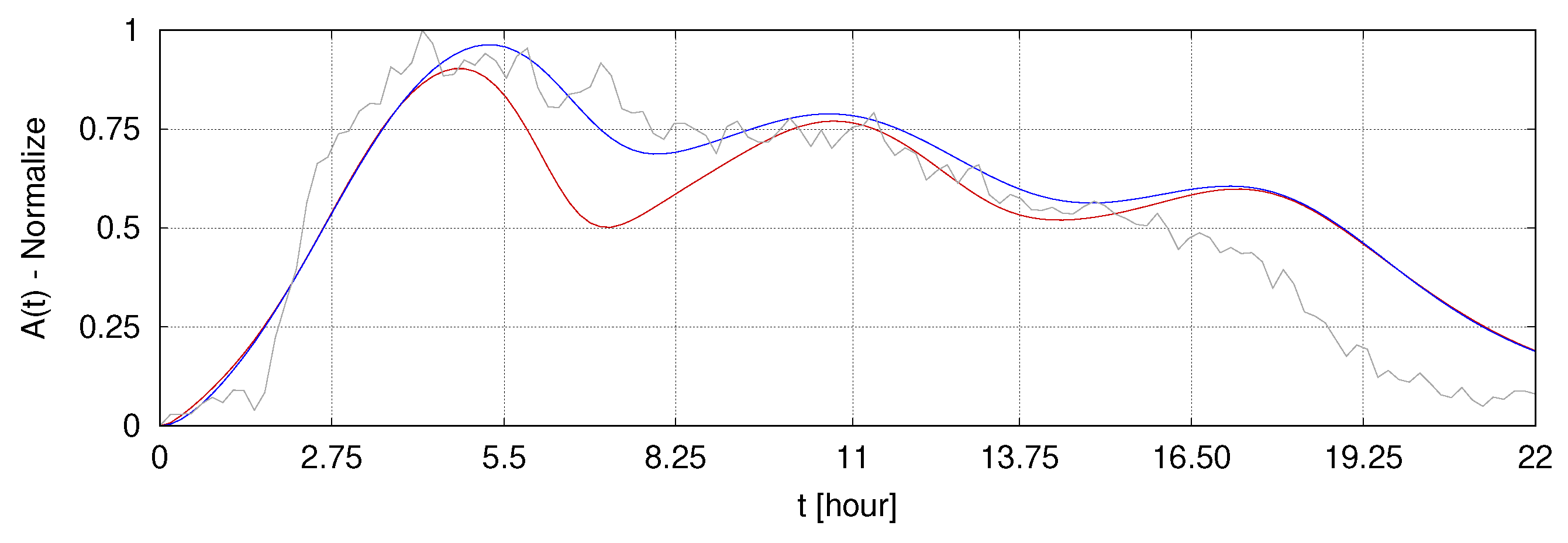
9. Application of the Discussed Algorithms in Solving Inverse Problems of RVA Dynamics
10. Conclusions
- The EFDS sequential algorithm has asymptotically exact complexity estimates in both T (time) and RAM (memory) of the order of ;
- The IFDS-MNM sequential algorithm has asymptotically exact complexity estimates in both T (time) and RAM (memory) of the order of ;
- The analysis efficiency and optimal CPU utilization showed that, for all the parallel algorithms considered, increasing the number of CPU threads beyond 16 does not provide a significant performance gain;
- It has been shown that the parallel algorithms EFDS-omp and -hybrid do not provide a significant increase in calculation speed (approximately ) compared to EFDS;
- At the same time, the parallel algorithms IFDS-MNM-omp and IFDS-MNM-hybrid provide a significant increase in computation speed by factors of 13 and 17, respectively, with RAM usage increasing by no more than 2.5 and 5 times, respectively, compared to the sequential IFDS-MNM;
- The parallel algorithms EFDS-omp and EFDS-hybrid have an asymptotically exact time complexity estimate of order , but according to the RAM model, the estimate is of order ;
- The parallel algorithms IFDS-MNM-omp and IFDS-MNM-hybrid have asymptotically exact complexity estimates in terms of T and RAM of order ;
- It can also be seen that, when solving a test example with a uniformly increasing input data size of N and an optimal number of CPU threads of 16, using -hybrid algorithms provides a significant advantage over -omp algorithms only when solving problems with 15,000, but with the total memory consumption of computing nodes, it is 4 times more. This is due to the fact that operations on vectors and matrices are carried out mainly on the GPU, which offers an advantage over the CPU when working with tensors of large dimensions;
- The application of the present parallel algorithms can accelerate calculations when solving inverse problems and when selecting an algorithm suitable for the problem.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RVA | Radon Volumetric Actuvity |
| CPU | Central Processing Unit |
| GPU | Graphic Processing Unit |
| EFDS | Explicit Finite-Difference Scheme |
| IFDS | Implicit Finite-Difference Scheme |
| MNM | Modified Newton’s Nethod |
| OpenMP | Open Multi-Processing |
| CUDA | Compute Unified Device Architecture |
| API | Application Programming Interface |
| PRAM | Parallel Random Access Machine |
| RAM | Random Access Memory |
References
- Yasuoka, Y.; Shinogi, M. Anomaly in atmospheric radon concentration: A possible precursor of the 1995 Kobe Japan, earthquake. Health Phys. 1997, 72, 759–761. [Google Scholar] [CrossRef]
- Barberio, M.D.; Gori, F.; Barbieri, M.; Billi, A.; Devoti, R.; Doglioni, C.; Petitta, M.; Riguzzi, F.; Rusi, S. Diurnal and Semidiurnal Cyclicity of Radon (222Rn) in Groundwater, Giardino Spring, Central Apennines, Italy. Water 2018, 10, 1276. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Cantzos, D.; Alam, A.; Dimopoulos, S.; Petraki, E. Electromagnetic and Radon Earthquake Precursors. Geosciences 2024, 14, 271. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Panagiotaras, D.; Cantzos, D.; Yannakopoulos, P.; Nomicos, C.; Stonham, J. Radon-222: A Potential Short-Term Earthquake Precursor. Earth Sci. Clim. Change 2015, 6, 1000282. [Google Scholar] [CrossRef]
- Firstov, P.P.; Makarov, E.O. Dynamics of Subsoil Radon in Kamchatka and Strong Earthquakes; Vitus Bering Kamchatka State University: Petropavlovsk-Kamchatsky, Russia, 2018; p. 148. (In Russian) [Google Scholar]
- Dubinchuk, V.T. Radon as a precursor of earthquakes. In Proceedings of the Isotopic Geochemical Precursors of Earthquakes and Volcanic Eruption, Vienna, Austria, 9–12 September 1991; IAEA: Vienna, Austria, 1993; pp. 9–22. [Google Scholar]
- Huang, P.; Lv, W.; Huang, R.; Luo, Q.; Yang, Y. Earthquake precursors: A review of key factors influencing radon concentration. J. Environ. Radioact. 2024, 271, 107310. [Google Scholar] [CrossRef]
- Kristiansson, K.; Malmqvist, L. Evidence for nondiffusive transport of 86Rn in the ground and a new physical model for the transport. Geophysics 1982, 47, 1444–1452. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Times Books: New York, NY, USA, 1982; p. 468. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Anomalous Diffusion. In An Introduction to Anomalous Diffusion and Relaxation; Springer: Berlin/Heidelberg, Germany, 2023; pp. 189–236. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Makarov, E.O.; Parovik, R.I. Hereditary Mathematical Model of the Dynamics of Radon Accumulation in the Accumulation Chamber. Mathematics 2023, 11, 850. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Makarov, E.O.; Parovik, R.I. Research of Stress-Strain State of Geo-Environment by Emanation Methods on the Example of alpha(t)-Model of Radon Transport. Bull. KRASEC Phys. Math. Sci. 2023, 44, 86–104. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers. Vol. I. Background and Theory; Springer: Berlin/Heidelberg, Germany, 2013; p. 373. [Google Scholar] [CrossRef]
- Parovik, R.I.; Shevtsov, B.M. Radon transfer processes in fractional structure medium. Math. Model. Comput. Simul. 2010, 2, 180–185. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier Science: Boston, MA, USA, 2006; p. 540. [Google Scholar]
- Cai, M.; Li, C. Theory and Numerical Approximations of Fractional Integrals and Derivatives; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2020; p. 317. [Google Scholar] [CrossRef]
- Nakhushev, A.M. Fractional Calculus and Its Application; Fizmatlit: Moscow, Russia, 2003; p. 272. (In Russian) [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011; p. 218. [Google Scholar]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M.; Fabrizio, M. On the notion of fractional derivative and applications to the hysteresis phenomena. Meccanica 2017, 52, 3043–3052. [Google Scholar] [CrossRef]
- Novozhenova, O.G. Life And Science of Alexey Gerasimov, One of the Pioneers of Fractional Calculus in Soviet Union. FCAA 2017, 20, 790–809. [Google Scholar] [CrossRef]
- Shao, J. Mathematical Statistics, 2nd ed.; Springer: New York, NY, USA, 2003; p. 592. [Google Scholar]
- Tarantola, A. Inverse Problem Theory: Methods for Data Fitting and Model Parameter Estimation; Elsevier Science Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 1987; p. 613. [Google Scholar]
- Tverdyi, D.A. Restoration of the order of fractional derivative in the problem of mathematical modelling of radon accumulation in the excess volume of the storage chamber based on the data of Petropavlovsk-Kamchatsky geodynamic polygon. NEWS Kabard.-Balkar. Sci. Cent. RAS 2023, 116, 83–94. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Parovik, R.I.; Makarov, E.O. Estimation of radon flux density changes in temporal vicinity of the Shipunskoe earthquake with MW = 7.0, 17 August 2024 with the use of the hereditary mathematical model. Geosciences 2025, 15, 30. [Google Scholar] [CrossRef]
- Mueller, J.L.; Siltanen, S. Linear and Nonlinear Inverse Problems with Practical Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2012; p. 351. [Google Scholar] [CrossRef]
- Dennis, J.E., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1996; p. 394. [Google Scholar]
- Kabanikhin, S.I.; Iskakov, K.T. Optimization Methods for Solving Coefficient Inverse Problems; NGU: Novosibirsk, Russia, 2001; p. 315. (In Russian) [Google Scholar]
- Tverdyi, D.A.; Parovik, R.I. The optimization problem for determining the functional dependence of the variable order of the fractional derivative of the Gerasimov-Caputo type. Bull. KRASEC Phys. Math. Sci. 2024, 47, 35–57. (In Russian) [Google Scholar] [CrossRef]
- Tverdyi, D.A. Refinement of Variable Order Fractional Derivative of Gerasimov-Caputo Type by Multidimensional Levenberg-Marquardt Optimization Method. In Computing Technologies and Applied Mathematics; Gibadullin, A., Gordin, S., Eds.; CTAM 2024, Springer Proceedings in Mathematics & Statistics; Springer: Berlin/Heidelberg, Germany, 2025; Volume 500, pp. 159–173. [Google Scholar] [CrossRef]
- More, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis. Lecture Notes in Mathematics; Watson, G.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; Volume 630, pp. 105–116. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Parovik, R.I. Hybrid GPU–CPU Efficient Implementation of a Parallel Numerical Algorithm for Solving the Cauchy Problem for a Nonlinear Differential Riccati Equation of Fractional Variable Order. Mathematics 2023, 11, 3358. [Google Scholar] [CrossRef]
- Tverdyi, D.A.; Parovik, R.I. Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation. Fractal Fract. 2022, 6, 23. [Google Scholar] [CrossRef]
- Bogaenko, V.A.; Bulavatskiy, V.M.; Kryvonos, I.G. On Mathematical modeling of Fractional-Differential Dynamics of Flushing Process for Saline Soils with Parallel Algorithms Usage. J. Autom. Inf. Sci. 2016, 48, 1–12. [Google Scholar] [CrossRef]
- Bohaienko, V.O. A fast finite-difference algorithm for solving space-fractional filtration equation with a generalised Caputo derivative. Comput. Appl. Math. 2019, 38, 105. [Google Scholar] [CrossRef]
- Bohaienko, V.O. Parallel finite-difference algorithms for three-dimensional space-fractional diffusion equation with phi–Caputo derivatives. Comput. Appl. Math. 2020, 39, 163. [Google Scholar] [CrossRef]
- Vasilyev, A.V.; Zhukovsky, M.V. Determination of mechanisms and parameters which affect radon entry into a room. J. Environ. Radioact. 2013, 124, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Kurnosov, M.G. Introduction to Data Structures and Algorithms: A Textbook; Avtograf: Novosibirsk, Russia, 2015; p. 178. (In Russian) [Google Scholar]
- Storer, J.A. An Introduction to Data Structures and Algorithms; Birkhäuser: Boston, MA, USA, 2012; p. 599. [Google Scholar]
- Borzunov, S.V.; Kurgalin, S.D.; Flegel, A.V. Workshop on Parallel Programming: A Study Guide; BVH: Saint Petersburg, Russia, 2017; p. 236. (In Russian) [Google Scholar]
- Brent, R.P. The parallel evaluation of general arithmetic expressions. J. Assoc. Comput. Mach. 1974, 21, 201–206. [Google Scholar] [CrossRef]
- Corman, T.H.; Leiserson, C.E.; Rivet, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, UK, 2009; p. 1292. [Google Scholar]
- Supinski, B.; Klemm, M. OpenMP Application Programming Interface Specification Version 5.2; Independently Published: North Charleston, SA, USA, 2021; p. 669. [Google Scholar]
- Sanders, J.; Kandrot, E. CUDA by Example: An Introduction to General-Purpose GPU Programming; Addison-Wesley Professional: London, UK, 2010; p. 311. [Google Scholar]
- Cheng, J.; Grossman, M.; McKercher, T. Professional Cuda C Programming, 1st ed.; Wrox Pr Inc.: New York, NY, USA, 2014; p. 497. [Google Scholar]
- King, K.N. C Programming: A Modern Approach, 2nd ed.; W.W. Norton & Company: New York, NY, USA, 2008; p. 832. [Google Scholar]
- Kenneth, R. Pointers on C, 1st ed.; Pearson: London, UK, 1997; p. 640. [Google Scholar]
- Gergel, V.P.; Strongin, R.G. High Performance Computing for Multi-Core Multiprocessor Systems. Study Guide; Moscow State University Publishing: Moscow, Russia, 2010; p. 544. (In Russian) [Google Scholar]







| N | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 | 2400 | 2600 | 2800 | 3000 |
| EFDS | 0.026 | 0.055 | 0.084 | 0.113 | 0.144 | 0.170 | 0.203 | 0.236 | 0.272 | 0.302 | 0.337 | 0.370 | 0.406 | 0.442 | 0.483 |
| IFDS-MNM | 0.074 | 0.212 | 0.448 | 0.823 | 1.374 | 2.044 | 3.028 | 4.418 | 5.882 | 7.843 | 9.994 | 13.10 | 16.61 | 20.97 | 25.75 |
| N | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 | 2400 | 2600 | 2800 | 3000 |
| EFDS | 0.006 | 0.012 | 0.018 | 0.024 | 0.030 | 0.036 | 0.042 | 0.048 | 0.054 | 0.061 | 0.067 | 0.073 | 0.079 | 0.085 | 0.091 |
| IFDS-MNM | 0.243 | 0.944 | 2.103 | 3.720 | 5.794 | 8.326 | 11.31 | 14.76 | 18.66 | 23.03 | 27.85 | 33.13 | 38.86 | 45.06 | 51.71 |
| p | EFDS -omp | EFDS -hybrid | IFDS-MNM -omp | IFDS-MNM -hybrid |
|---|---|---|---|---|
| 2 | 1.068 | 0.903 | 147.388 | 115.829 |
| 4 | 0.963 | 0.883 | 76.355 | 58.927 |
| 6 | 0.927 | 0.884 | 50.780 | 40.516 |
| 8 | 0.906 | 0.884 | 39.479 | 30.801 |
| 10 | 0.894 | 0.884 | 32.373 | 25.315 |
| 12 | 0.885 | 0.886 | 27.071 | 21.527 |
| 14 | 0.879 | 0.887 | 23.887 | 18.934 |
| 16 | 0.878 | 0.886 | 21.325 | 16.810 |
| 18 | 0.876 | 0.886 | 25.700 | 23.091 |
| 20 | 0.880 | 0.885 | 23.977 | 21.175 |
| 22 | 0.874 | 0.886 | 21.963 | 19.667 |
| 24 | 0.868 | 0.886 | 20.629 | 18.510 |
| 26 | 0.869 | 0.887 | 19.747 | 17.398 |
| 28 | 0.871 | 0.888 | 18.538 | 16.427 |
| 30 | 0.875 | 0.889 | 17.638 | 15.799 |
EFDS -omp | EFDS -hybrid | EFDS -hybrid | IFDS-MNM -omp | IFDS-MNM -hybrid | IFDS-MNM -hybrid | |
|---|---|---|---|---|---|---|
| RAM– alg. | 0.183 | 0 | 206.428 | 0 | ||
| RAM | 68.847 | 137.512 | 137.466 | 275.115 | 549.797 | 549.728 |
| N | EFDS -omp | EFDS -hybrid | IFDS-MNM -omp | IFDS-MNM -hybrid |
|---|---|---|---|---|
| 1000 | 0.138 | 0.140 | 0.377 | 0.337 |
| 2000 | 0.282 | 0.274 | 1.095 | 0.985 |
| 3000 | 0.420 | 0.414 | 2.735 | 2.388 |
| 4000 | 0.568 | 0.558 | 5.513 | 4.965 |
| 5000 | 0.721 | 0.728 | 11.455 | 10.288 |
| 6000 | 0.878 | 0.892 | 20.918 | 16.829 |
| 7000 | 1.042 | 1.050 | 33.812 | 28.511 |
| 8000 | 1.222 | 1.224 | 52.337 | 42.891 |
| 9000 | 1.392 | 1.394 | 74.270 | 63.681 |
| 10,000 | 1.559 | 1.569 | 103.685 | 85.078 |
| 11,000 | 1.743 | 1.752 | 143.353 | 126.858 |
| 12,000 | 1.939 | 1.944 | 193.125 | 159.268 |
| 13,000 | 2.124 | 2.145 | 264.476 | 225.509 |
| 14,000 | 2.327 | 2.320 | 365.500 | 275.562 |
| 15,000 | 2.507 | 2.516 | 465.145 | 391.044 |
| N | EFDS -omp | EFDS -hybrid | EFDS -hybrid | IFDS-MNM -omp | IFDS-MNM -hybrid | IFDS-MNM -hybrid |
|---|---|---|---|---|---|---|
| 1000 | 1.938 | 3.845 | 3.838 | 7.706 | 15.339 | 15.327 |
| 2000 | 7.690 | 15.320 | 15.305 | 30.670 | 61.195 | 61.172 |
| 3000 | 17.258 | 34.424 | 34.401 | 68.893 | 137.569 | 137.535 |
| 4000 | 30.640 | 61.157 | 61.127 | 122.375 | 244.461 | 244.415 |
| 5000 | 47.836 | 95.520 | 95.482 | 191.116 | 381.870 | 381.813 |
| 6000 | 68.848 | 137.512 | 137.466 | 275.116 | 549.797 | 549.728 |
| 7000 | 93.674 | 187.134 | 187.080 | 374.374 | 748.241 | 748.161 |
| 8000 | 122.314 | 244.385 | 244.324 | 488.892 | 977.203 | 977.112 |
| 9000 | 154.770 | 309.265 | 309.196 | 618.668 | 1236.683 | 1236.580 |
| 10,000 | 191.040 | 381.775 | 381.699 | 763.702 | 1526.680 | 1526.566 |
| 11,000 | 231.125 | 461.914 | 461.830 | 923.996 | 1847.195 | 1847.069 |
| 12,000 | 275.024 | 549.683 | 549.591 | 1099.548 | 2198.227 | 2198.090 |
| 13,000 | 322.739 | 645.081 | 644.981 | 1290.359 | 2579.777 | 2579.628 |
| 14,000 | 374.268 | 748.108 | 748.001 | 1496.429 | 2991.844 | 2991.684 |
| 15,000 | 429.611 | 858.765 | 858.650 | 1717.758 | 3434.429 | 3434.258 |
| Sequential, | -omp, | -hybrid, | |
|---|---|---|---|
| EFDS | 0.058 | 0.1 | 0.242 |
| IFDS-MNM | 1.515 | 0.662 | 0.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tverdyi, D. An Analysis of the Computational Complexity and Efficiency of Various Algorithms for Solving a Nonlinear Model of Radon Volumetric Activity with a Fractional Derivative of a Variable Order. Computation 2025, 13, 252. https://doi.org/10.3390/computation13110252
Tverdyi D. An Analysis of the Computational Complexity and Efficiency of Various Algorithms for Solving a Nonlinear Model of Radon Volumetric Activity with a Fractional Derivative of a Variable Order. Computation. 2025; 13(11):252. https://doi.org/10.3390/computation13110252
Chicago/Turabian StyleTverdyi, Dmitrii. 2025. "An Analysis of the Computational Complexity and Efficiency of Various Algorithms for Solving a Nonlinear Model of Radon Volumetric Activity with a Fractional Derivative of a Variable Order" Computation 13, no. 11: 252. https://doi.org/10.3390/computation13110252
APA StyleTverdyi, D. (2025). An Analysis of the Computational Complexity and Efficiency of Various Algorithms for Solving a Nonlinear Model of Radon Volumetric Activity with a Fractional Derivative of a Variable Order. Computation, 13(11), 252. https://doi.org/10.3390/computation13110252






