A Finite-Time Extended State Observer with Prediction Error Compensation for PMSM Control

Abstract

This paper proposes a finite-time extended state observer (FTESO) integrated with model predictive control (MPC) for high-performance control of permanent magnet synchronous motors (PMSMs). A disturbance-aware predictive model is constructed by incorporating lumped disturbances into the PMSM current equations, addressing load fluctuations and parameter uncertainties. The FTESO, designed with nonlinear gains and Lyapunov stability, ensures rapid disturbance estimation and is embedded into a feedforward-compensated MPC with a composite cost function considering current error and voltage increment. Simulations show that under sudden load disturbances, FTESO-MPC achieves faster recovery and a smaller steady-state error than LESO-MPC; when inductance triples, FTESO-MPC maintains smooth convergence, whereas LESO-MPC exhibits oscillations with d-axis current peaks near 200 A. Under resistance or flux variations, FTESO-MPC sustains stable regulation with less ripple, confirming its superior tracking accuracy and robustness compared with LESO-MPC.

1. Introduction

In recent years, the rapid growth of global transportation demand has significantly increased the deployment of electric drive systems. Among various applications, electric vehicles (EVs), electric buses, and urban rail transit are typical examples. In these systems, electric drives play a crucial role in ensuring reliable and efficient operation [1,2]. At the heart of these applications lies the electric drive system, which directly determines the dynamic performance and operational reliability of the equipment. Particularly, permanent magnet synchronous motors (PMSMs) have gained widespread application due to their high power density, excellent responsiveness, and suitability for advanced control. However, in real-world operating conditions, PMSM-driven systems are frequently subjected to load disturbances, parameter uncertainties, and unmodeled dynamics [3]. These challenges necessitate the development of advanced control strategies that can achieve strong disturbance rejection and maintain stable speed performance under practical operating conditions.

Traditional speed control strategies, such as proportional–integral (PI) control and feedforward decoupling methods [4,5,6,7,8], have demonstrated satisfactory performance in light-load or steady-state conditions. However, these methods typically assume that external disturbances and model uncertainties are negligible, which becomes invalid under dynamic operating conditions. In scenarios with significant parameter variations or abrupt load changes, such controllers often fail to adjust the control law in a timely manner, resulting in increased output deviations and degraded regulation performance. To address this issue, control strategies with built-in disturbance estimation and compensation mechanisms have attracted increasing research attention. The Extended State Observer (ESO) [9,10,11,12,13] has emerged as a widely used technique in nonlinear control systems, owing to its ability to dynamically estimate generalized disturbances—including external perturbations, modeling errors, and unmodeled dynamics—by augmenting the system state. By incorporating these estimated disturbances into the control loop, ESO-based methods can effectively mitigate the impact of uncertainties, allowing the controller to operate as if under ideal model conditions. This significantly enhances the robustness and adaptability of the control system under complex and uncertain environments.

Despite the theoretical clarity and implementation simplicity of conventional ESO structures, which are mostly based on linear state-space models and finite-difference estimations, their performance deteriorates in the presence of high-speed disturbances or rapid state transitions. In applications such as coal unloading crawlers, where load impacts are abrupt and disturbances occur frequently, the inherent estimation delay of linear ESOs often becomes a limiting factor [14,15,16]. To address this limitation, recent studies have introduced various structural improvements, among which the Finite-Time Convergent Extended State Observer (FTESO) [17,18,19,20,21,22] has gained significant attention. FTESO incorporates nonlinear feedback gains and sliding-mode terms into the observer design, enabling the estimated disturbance to converge to its true value within a finite time. This structure offers substantial improvements in estimation speed and tracking accuracy compared to conventional ESOs, especially in scenarios with rapidly changing system states or high-frequency disturbances. As demonstrated in [22], FTESO-based control systems exhibit significantly reduced current and speed recovery times, lower overshoot, and minimized steady-state errors under dynamic disturbance conditions. These advantages make FTESO particularly suitable for enhancing the robustness and dynamic performance of electric drive systems.

Although Model Predictive Control (MPC) has demonstrated excellent capabilities in dynamic optimization and multi-objective control, its performance remains highly dependent on the accuracy of the internal model. Under non-ideal modeling conditions, such as parameter uncertainties or external disturbances, MPC may generate prediction deviations that lead to suboptimal control actions. To address this limitation, an effective solution is to incorporate disturbance estimates provided by an ESO into the MPC framework, forming a disturbance-observation–based predictive compensation structure [23,24,25]. This integrated ESO-MPC architecture enhances the model adaptation capability of MPC by dynamically correcting prediction errors induced by unmodeled dynamics. In practical applications, such a scheme improves the controller’s ability to respond rapidly to and recover stably from sudden load disturbances. Recent studies have explored several variants of this approach, including ESO-MPC, Finite-Time ESO-MPC (FTESO-MPC), and disturbance-compensated rolling optimization schemes, with promising results in motor drives, power converters, and other dynamic systems [26,27,28]. In these frameworks, the ESO is typically used to estimate current disturbances, voltage shifts, or internal state fluctuations, and feed these estimates into the MPC optimization process. This enables the cost function to be adaptively corrected in real time, thereby improving decision-making accuracy. Moreover, due to the real-time estimation capability of the ESO, its outputs can be directly utilized as feedback to update the internal prediction model, enhancing the robustness and adaptability of the control system under complex operating conditions.

While the integration of FTESO and MPC successfully combines the multi-variable optimization capability of predictive control with the disturbance estimation and adaptation strengths of finite-time observers, its effectiveness still relies on certain assumptions regarding model accuracy and parameter availability. In practice, the design, tuning, and real-time implementation of the observer–controller structure can introduce additional complexity and computational burden, which may limit its applicability in highly dynamic and resource-constrained systems [29,30,31]. This challenge becomes more pronounced in scenarios such as coal unloading equipment, where strong nonlinearities, multiple concurrent disturbances, and significant system uncertainties are present. Under such conditions, the system model may deviate considerably from reality, and the behavior of external disturbances may be difficult to model explicitly. Consequently, FTESO-MPC–based control strategies may exhibit limited robustness and adaptability, especially when faced with rapidly changing or unknown operating conditions. Motivated by these limitations, further enhancement of disturbance-resilient control design is required to ensure reliable operation in complex industrial systems.

In this context, the proposed control strategy can be interpreted as an integrated-architecture (IA)-based control scheme, in which the finite-time extended state observer (FTESO) and the model predictive controller (MPC) are designed within a unified framework rather than as separated modules. This integrated architecture allows the observer and controller to interact in real time: the FTESO rapidly estimates lumped disturbances and feeds them directly into the MPC optimization process, while the MPC updates its cost function and prediction model based on these estimations. Such mutual coupling forms a closed-loop coordination between disturbance observation and predictive compensation, significantly improving dynamic adaptability and robustness. By combining the fast finite-time convergence of the observer with the optimal decision-making of predictive control, the IA-based FTESO–MPC scheme achieves superior disturbance rejection, faster transient response, and smoother control action compared with conventional cascaded approaches. This integration highlights the key innovation of the present work and provides a more systematic foundation for robust and adaptive PMSM control.

To address the challenges of strong external disturbances and parameter uncertainties commonly encountered in electric drive systems, this paper develops a disturbance-aware current prediction model for PMSMs, which incorporates a lumped disturbance term to represent unmodeled dynamics and external perturbations. An FTESO is designed based on nonlinear feedback gain, enabling rapid and accurate estimation of current disturbances within a finite convergence time. The estimated disturbance is then embedded into the MPC framework, forming a disturbance-compensated composite controller. A multi-objective cost function is constructed, which simultaneously considers current tracking error and voltage increment regulation, thereby enabling real-time feedforward compensation of system disturbances and smooth voltage response adjustment. The proposed IA-based FTESO–MPC scheme significantly improves robustness and dynamic performance under complex conditions, providing an effective solution for robust and stable PMSM operation.

The main contributions of this study can be summarized as follows:

(1)

A finite-time extended state observer (FTESO) is developed to achieve rapid and accurate estimation of lumped disturbances in PMSM drives, ensuring convergence within a finite time under strong nonlinear and time-varying conditions.

(2)

A novel affine-interval-based nonlinear gain function is introduced into the observer design, which guarantees global smoothness and eliminates the chattering phenomenon commonly observed in conventional sliding-mode ESOs.

(3)

A disturbance-aware current prediction model is constructed, incorporating parameter perturbations and unmodeled dynamics as lumped disturbances to enhance model fidelity under practical uncertainties.

(4)

A multi-objective cost function is formulated to simultaneously minimize current tracking error and voltage increment, improving both dynamic response and energy efficiency.

(5)

An integrated-architecture (IA)-based FTESO–MPC control framework is established, allowing real-time interaction between disturbance estimation and predictive optimization, thereby improving robustness, convergence speed, and steady-state accuracy compared with conventional ESO–MPC or deadbeat control approaches.

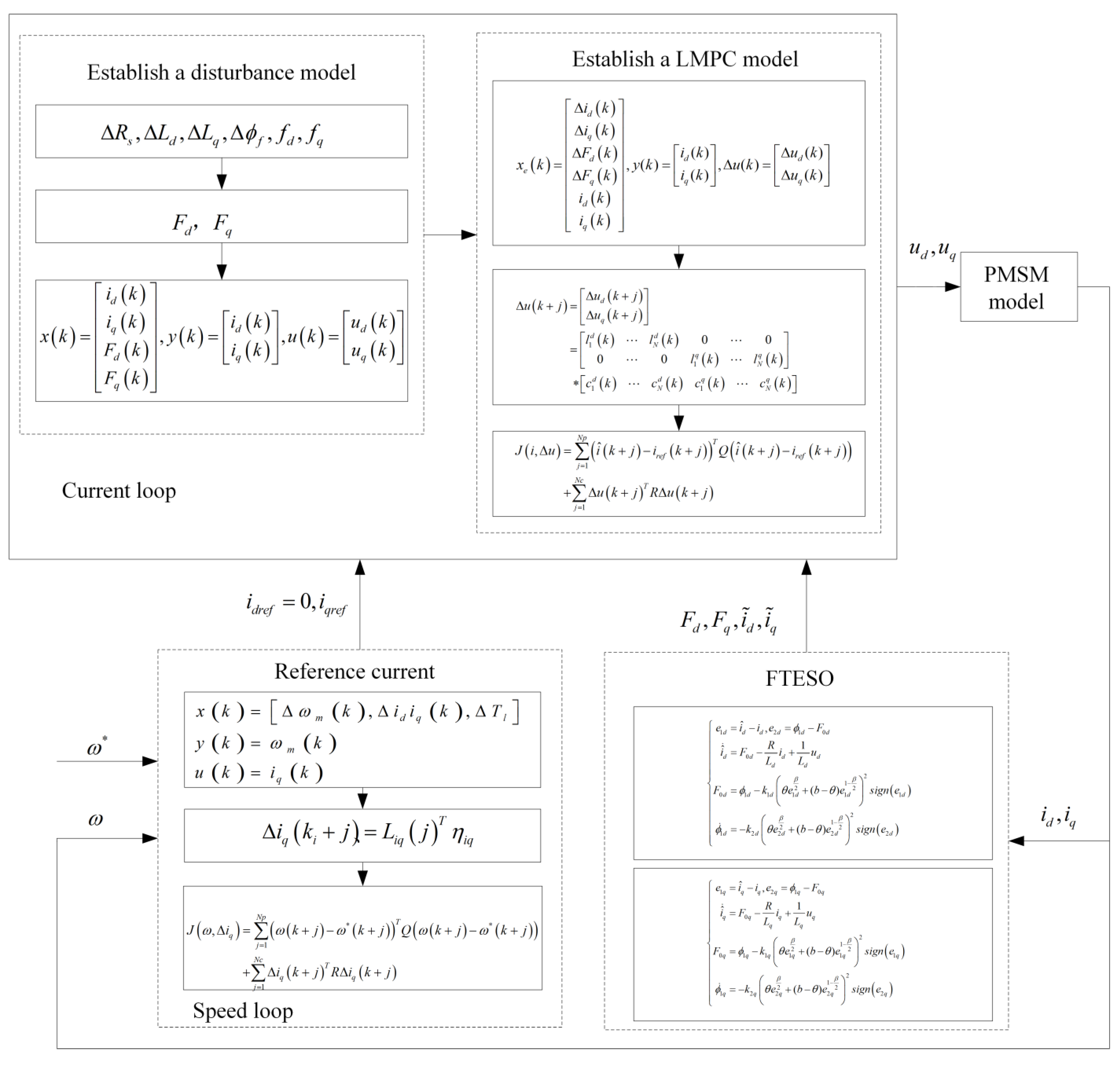
2. Disturbance-Aware Modeling of PMSM for Control Design

Accurately modeling the behavior of PMSMs under complex and dynamic load conditions is crucial for developing advanced control strategies that ensure robust performance and effective disturbance rejection. Conventional PMSM current models are often based on idealized assumptions and fail to capture parameter variations, mechanical disturbances, and environmental influences—factors that significantly affect control accuracy in practical applications. In real-world industrial and transportation scenarios, PMSMs frequently operate under harsh and variable conditions. Motor parameters such as inductance and resistance may change due to temperature fluctuations, magnetic saturation, and manufacturing deviations. At the same time, load disturbances can be introduced by uneven mass distribution, mechanical shocks, friction changes, or transmission backlash. These effects lead to strong nonlinearities and uncertainties in the system, greatly increasing control complexity and posing challenges for achieving stable and reliable motor operation. To better capture these real-world uncertainties and to provide a reliable foundation for sustainable and disturbance-resilient control design, this study incorporates aggregated disturbance terms $f_d$ and $f_q$ into the standard PMSM current model [32]:

$$\begin{array}{l}{L}_d{\displaystyle \frac{d{i}_d}{dt}}=-R{i}_d+P{L}_q{\omega }_m{i}_q+u_d+f_d\\ L_q{\displaystyle \frac{d{i}_q}{dt}}=-R{i}_q-P{L}_d{\omega }_m{i}_d-P{\omega }_m{\varphi }_f+u_q+f_q\end{array}$$

(1)

where these terms represent the unmodeled dynamics and disturbance effects along the d-axis and q-axis, respectively. The modified model offers a more realistic and energy-aware representation of PMSM dynamics, enabling the design of predictive controllers tailored to the demands of efficient electric drive systems in modern transportation applications.

Assuming further that the incremental variations of the stator resistance, d-axis inductance, q-axis inductance, and permanent magnet flux linkage are denoted by $\Delta R_s$, $\Delta L_d$, $\Delta L_q$, and $\Delta {\varphi }_f$, respectively, the current model in Equation (1) can be reformulated to incorporate parameter perturbations as follows:

$$\begin{array}{c}\left(L_d+\Delta L_d\right){\displaystyle \frac{d{i}_d}{dt}}=-\left(R+\Delta R\right)i_d+P\left(L_q+\Delta L_q\right){\omega }_m{i}_q+u_d\\ \left(L_q+\Delta L_q\right){\displaystyle \frac{d{i}_q}{dt}}=-\left(R+\Delta R\right)i_q-P\left(L_d+\Delta L_d\right){\omega }_m{i}_d-P{\omega }_m\left({\varphi }_f+\Delta {\varphi }_f\right)+u_q\end{array}$$

(2)

Building upon Equation (2), the model can be further reformulated to explicitly incorporate both motor parameter variations and external disturbance effects, yielding the following extended representation:

$$\begin{array}{c}{\displaystyle \frac{d{i}_d}{dt}}=-{\displaystyle \frac{R}{L_d}}{i}_d+F_d+{\displaystyle \frac{u_d}{L_d}}\\ {\displaystyle \frac{d{i}_q}{dt}}=-{\displaystyle \frac{R}{L_q}}{i}_q+F_q+{\displaystyle \frac{u_q}{L_q}}\end{array}$$

(3)

where $F_d$ and $F_q$ represent the lumped disturbances that result from the combined effects of motor parameter variations and external perturbations. It should be noted that in practical PMSM drive systems, inverter nonlinearities such as dead-time, switching delay, and voltage saturation inevitably introduce additional voltage distortion. These effects can be equivalently regarded as lumped disturbances acting on the stator voltage model. Therefore, their influence is implicitly included in the total disturbance term of the system dynamics.

$$\begin{array}{c}{F}_d=-{\displaystyle \frac{\Delta L_d}{L_d}}{\displaystyle \frac{d{i}_d}{dt}}-{\displaystyle \frac{\Delta R}{L_d}}{i}_d+{\displaystyle \frac{P\left(L_q+\Delta L_q\right)}{L_d}}{\omega }_m{i}_q+{\displaystyle \frac{f_d}{L_d}}\\ F_q=-{\displaystyle \frac{\Delta L_q}{L_q}}{\displaystyle \frac{d{i}_q}{dt}}-{\displaystyle \frac{\Delta R}{L_q}}{i}_q-{\displaystyle \frac{P\left(L_d+\Delta L_d\right)}{L_q}}{\omega }_m{i}_d-{\displaystyle \frac{P{\omega }_m\left({\varphi }_f+\Delta {\varphi }_f\right)}{L_q}}+{\displaystyle \frac{f_q}{L_q}}\end{array}$$

(4)

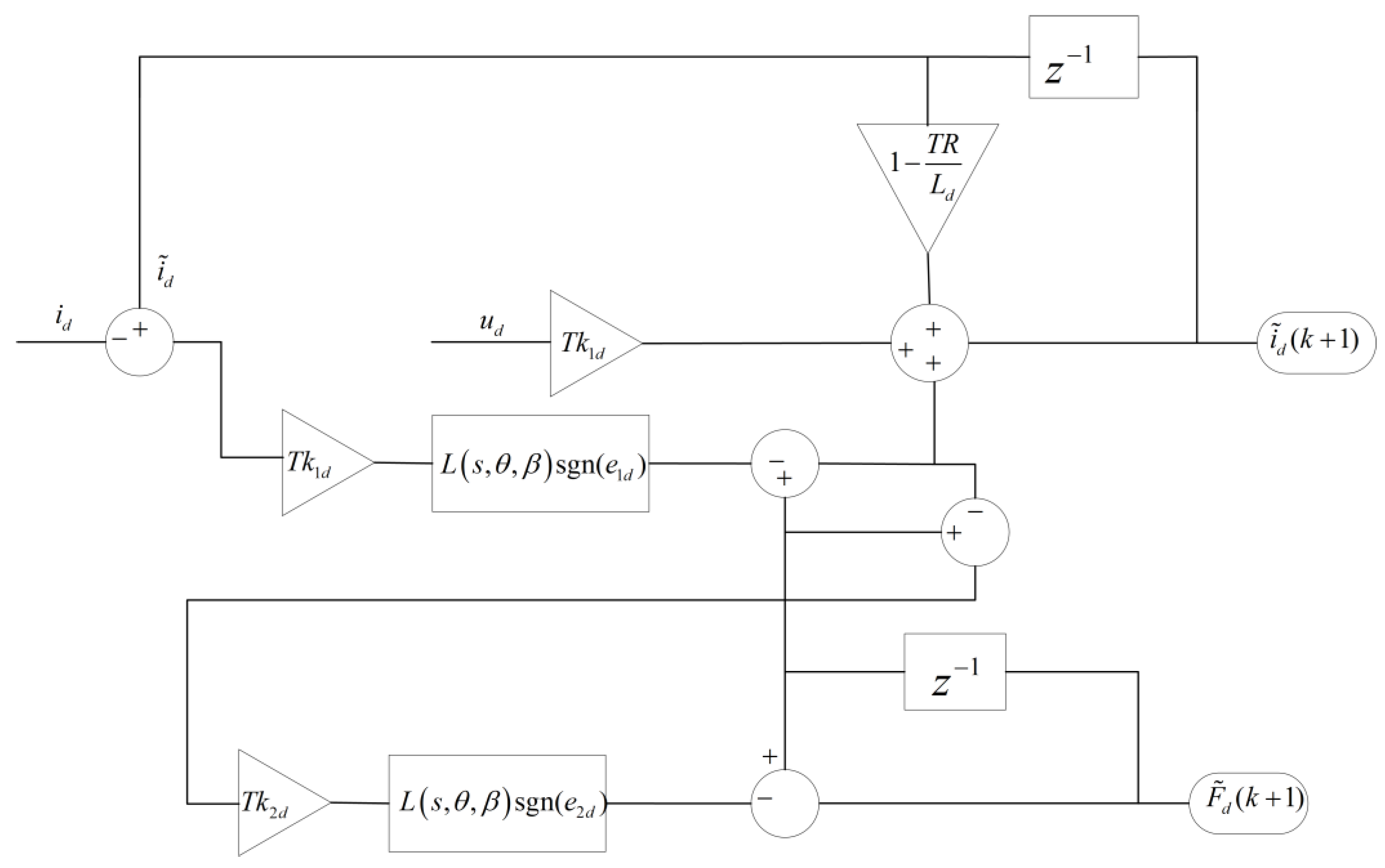
By setting the sampling period as $T_s$, Equation (4) can be discretized as follows:

$$\begin{array}{c}{i}_d\left(k+1\right)=-{\displaystyle \frac{T_{s}R}{L_d}}{i}_d\left(k\right)+T_s{F}_d\left(k\right)+{\displaystyle \frac{T_s}{L_d}}{u}_d\left(k\right)\\ i_q\left(k+1\right)=-{\displaystyle \frac{T_{s}R}{L_q}}{i}_q\left(k\right)+T_s{F}_q\left(k\right)+{\displaystyle \frac{T_s}{L_q}}{u}_q\left(k\right)\end{array}$$

(5)

Based on Equation (5), a disturbance prediction model for the PMSM is constructed by treating the d-axis current $i_d$, q-axis current $i_q$, and the lumped disturbances $F_d$ and $F_q$ as system state variables. It is assumed that the disturbance terms $F_d$ and $F_q$ remain constant over the prediction horizon $N_p$. Accordingly, an extended state-space model is formulated to capture both system dynamics and disturbance evolution:

$$\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}$$

(6)

where

$$x\left(k\right)=\left[\begin{array}{c}{i}_d\left(k\right)\\ i_q\left(k\right)\\ F_d\left(k\right)\\ F_q\left(k\right)\end{array}\right],y\left(k\right)=\left[\begin{array}{c}{i}_d\left(k\right)\\ i_q\left(k\right)\end{array}\right],u\left(k\right)=\left[\begin{array}{c}{u}_d\left(k\right)\\ u_q\left(k\right)\end{array}\right]$$

(7)

$$A=\left[\begin{array}{cccc}-{\displaystyle \frac{T_{s}R}{L_d}}& 0& 0& 0\\ 0& -{\displaystyle \frac{T_{s}R}{L_q}}& 0& 0\\ 0& 0& T_s& 0\\ 0& 0& 0& T_s\end{array}\right],B=\left[\begin{array}{c}{\displaystyle \frac{T_s}{L_d}}\\ {\displaystyle \frac{T_s}{L_q}}\end{array}\right],C=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right]$$

(8)

Let $\Delta i_d\left(k\right)$ and $\Delta i_q\left(k\right)$ denote the incremental errors of the d-axis and q-axis currents, and $\Delta F_d\left(k\right)$ and $\Delta F_q\left(k\right)$ represent the incremental disturbance estimation errors. Based on Equation (6), the incremental prediction model of the stator currents can be derived as follows:

$$\begin{array}{c}{x}_e\left(k+1\right)=A_e{x}_e\left(k\right)+B_e\Delta u\left(k\right)\\ y\left(k\right)=C_e{x}_e\left(k\right)\end{array}$$

(9)

where

$$\begin{array}{c}{x}_e\left(k\right)=\left[\begin{array}{c}\Delta i_d\left(k\right)\\ \Delta i_q\left(k\right)\\ \Delta F_d\left(k\right)\\ \Delta F_q\left(k\right)\\ i_d\left(k\right)\\ i_q\left(k\right)\end{array}\right],y(k)=\left[\begin{array}{c}{i}_d(k)\\ i_q(k)\end{array}\right],\Delta u(k)=\left[\begin{array}{c}\Delta u_d(k)\\ \Delta u_q(k)\end{array}\right]\\ A_e=\left[\begin{array}{cccccc}-{\displaystyle \frac{T_{s}R}{L_d}}& 0& 0& 0& 0& 0\\ 0& -{\displaystyle \frac{T_{s}R}{L_q}}& 0& 0& 0& 0\\ 0& 0& T_s& 0& 0& 0\\ 0& 0& 0& T_s& 0& 0\\ -{\displaystyle \frac{T_{s}R}{L_d}}& 0& 0& 0& 0& 0\\ 0& -{\displaystyle \frac{T_{s}R}{L_q}}& 0& 0& 0& 0\end{array}\right],B_e=\left[\begin{array}{cc}{\displaystyle \frac{T_s}{L_d}}& 0\\ 0& {\displaystyle \frac{T_s}{L_q}}\\ 0& 0\\ 0& 0\\ {\displaystyle \frac{T_s}{L_d}}& 0\\ 0& {\displaystyle \frac{T_s}{L_q}}\end{array}\right],\\ C_e=\left[\begin{array}{cccccc}0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]\end{array}$$

(10)

3. Feedforward-Based Compound Control Design

3.1. Finite-Time Convergent Extended State Observer

To enhance the disturbance rejection capability of the PMSM control system under complex and time-varying conditions, and to improve the accuracy of model predictive control, this study develops an FTESO. The observer is designed to estimate, in real time, the d-axis and q-axis currents of the PMSM along with the corresponding lumped disturbances. These estimated disturbances are incorporated as extended state variables into the predictive control framework, enabling proactive and efficient compensation. By enhancing disturbance suppression and dynamic adaptability, the proposed method contributes to more robust and stable motor drive performance under complex operating conditions.

Design of an FTESO for d-axis current:

$$\left\{\begin{array}{l}{e}_{1d}={\widehat{i}}_d-i_d,e_{2d}={\varphi }_{1d}-F_{0d}\\ {\dot{\widehat{i}}}_d=F_{0d}-{\displaystyle \frac{R}{L_d}}{i}_d+{\displaystyle \frac{1}{L_d}}{u}_d\\ F_{0d}={\varphi }_{1d}-k_{1d}{\left(\theta e_{1d}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )e_{1d}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{1d}\right)\\ {\dot{\varphi }}_{1d}=-k_{2d}{\left(\theta e_{2d}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )e_{2d}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{2d}\right)\end{array}\right.$$

(11)

Design of an FTESO for q-axis current:

$$\left\{\begin{array}{l}{e}_{1q}={\widehat{i}}_q-i_q,e_{2q}={\varphi }_{1q}-F_{0q}\\ {\dot{\widehat{i}}}_q=F_{0q}-{\displaystyle \frac{R}{L_q}}{i}_q+{\displaystyle \frac{1}{L_q}}{u}_q\\ F_{0q}={\varphi }_{1q}-k_{1q}{\left(\theta e_{1q}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )e_{1q}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{1q}\right)\\ {\dot{\varphi }}_{1q}=-k_{2q}{\left(\theta e_{2q}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )e_{2q}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{2q}\right)\end{array}\right.$$

(12)

where ${\widehat{i}}_d$ and ${\widehat{i}}_q$ represent the estimated values of the d-axis and q-axis currents, respectively, while $F_{od}$ and $F_{0q}$ denote the estimated disturbance components along the d-axis and q-axis. The parameters $k_{1d}$, $k_{2d}$, $k_{1q}$ and $k_{2q}$ are adjustable gains within the FTESO design. Regardless of the initial magnitude of current or disturbance estimation errors, the observer ensures that all deviations converge to their reference values or predefined bounds within a finite time. These bounds can be arbitrarily small, demonstrating the high precision and fast convergence characteristics of the proposed finite-time extended observer. Some details are in Figure 1.

3.2. Stability Analysis

Theorem 1.

The nonlinear dynamics can be expressed as:

$$\dot{s}\left(t\right)=-L\left(s,\theta ,\beta \right)=-{\left(\theta s{(t)}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )s{(t)}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^2,s\left(0\right)=s_0$$

(13)

where, given that $\theta >0$, $b-\theta >0$, and $0<\beta <1$, the nonlinear function exhibits finite-time convergence. For any initial value $s_0$, the time required for the function to converge to the origin and to $\rho$ can be respectively expressed as:

$$\begin{array}{c}{t}_0={\displaystyle \frac{1}{1-\beta }}\left({\displaystyle \frac{1}{\theta (b-\theta )}}-{\displaystyle \frac{1}{{\theta }^2{s}_0^{1-\beta }+\theta (b-\theta )}}\right)\\ t_{\rho }={\displaystyle \frac{1}{1-\beta }}\left({\displaystyle \frac{1}{\theta {\rho }^{1-\beta }+(b-\theta )}}-{\displaystyle \frac{1}{{\theta }^2{s}_0^{1-\beta }+\theta (b-\theta )}}\right)\end{array}$$

(14)

The upper bound of the convergence time is given by:

$$T_{\max }={\displaystyle \frac{1}{\theta \left(b-\theta \right)\left(1-\beta \right)}}$$

(15)

In contrast to the conventional finite-time extended state observers that employ the discontinuous fal(·) function [9], the proposed FTESO introduces a redesigned nonlinear gain term inspired by the definition of affine intervals in convex affine subspace theory. This nonlinear mapping ensures global differentiability, thereby eliminating the non-smooth transition near the origin that commonly causes chattering and numerical instability in traditional designs. By reformulating the nonlinear feedback law into an affine-type continuous structure, the observer achieves smooth finite-time convergence [33,34,35] and enhanced robustness against system uncertainties and external disturbances. Moreover, the continuous nature of the affine-interval-based function improves the numerical stability of the discrete-time implementation, reducing sensitivity to sampling noise and quantization errors. The redesigned nonlinearity preserves the fast finite-time convergence characteristics while ensuring global smoothness, which facilitates both digital realization and theoretical analysis. As a result, the proposed FTESO provides a balanced structure that combines the advantages of finite-time convergence, robustness, and computational smoothness, making it more suitable for high-performance PMSM drive control.

Proof of Theorem 1.

Let the Lyapunov candidate function be defined as $V(s)={\displaystyle \frac{s^2}{2}}\ge 0$. Taking the time derivative of $V$, we obtain:

$$\begin{array}{ll}\dot{V}& =s\dot{s}\\ & =-s{\left(\theta s^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )s^{1-{\displaystyle \frac{\beta }{2}}}\right)}^2\\ & =-V^{{\displaystyle \frac{1+\beta }{2}}}{\left(\theta +(b-\theta )V^{{\displaystyle \frac{1-\beta }{2}}}\right)}^2\end{array}$$

(16)

Since $\theta >0,b-\theta >0$, it follows that $(b-\theta )V^{{\displaystyle \frac{1-\beta }{2}}}>0$. Therefore, the time derivative of the Lyapunov function satisfies $\dot{V}\le -{\theta }^2{V}^{{\displaystyle \frac{1+\beta }{2}}}$. Given that $0<\beta <1$, we have $1<1+\beta <2$, which implies $0<{\displaystyle \frac{1+\beta }{2}}<1$. This confirms that the nonlinear function converges to the equilibrium point in finite time.

When $V\ne 0$, then:

$${\displaystyle \frac{1}{V^{\frac{1+\beta }{2}}}}{\displaystyle \frac{dV}{dt}}={\left(\theta +(b-\theta )V^{{\displaystyle \frac{1-\beta }{2}}}\right)}^2$$

(17)

Let $m=V^{{\displaystyle \frac{1-\beta }{2}}}$, then:

$$\begin{array}{c}{\displaystyle {\int }_{m\left(0\right)}^{m\left(t\right)}\frac{dm}{{\left(\theta +(b-\theta )m\right)}^2}}={\displaystyle {\int }_0^t\left(\beta -1\right)}dt\\ s^{1-\beta }\left(t\right)=m\left(t\right)={\displaystyle \frac{1}{{\theta }^2\left(\beta -1\right)t+\frac{{\theta }^2}{\theta \left(b-\theta \right)+{\theta }^{2}m\left(0\right)}}}-{\displaystyle \frac{\theta \left(b-\theta \right)}{{\theta }^2}}\end{array}$$

(18)

Case 1:

For any initial condition $s_0$, the settling time of $s$ to reach the origin can be derived from Equation (18) as follows:

$$t={\displaystyle \frac{1}{1-\beta }}\left({\displaystyle \frac{1}{\theta \left(b-\theta \right)}}-{\displaystyle \frac{1}{{\theta }^2{s}_0^{1-\beta }+\theta \left(b-\theta \right)}}\right)$$

(19)

Case 2:

For any initial state $s_0$, the convergence time of $s$ to a predefined threshold $\rho$ can be determined based on Equation (18) as follows:

$$t_{\rho }={\displaystyle \frac{1}{\theta \left(1-\beta \right)}}\left({\displaystyle \frac{1}{\theta {\rho }^{1-\beta }+\left(b-\theta \right)}}-{\displaystyle \frac{1}{{\theta }^2{s}_0^{1-\beta }+\left(b-\theta \right)}}\right)$$

(20)

where the convergence rate increases as the value of $\beta$ decreases.

Case 3:

Based on the above two scenarios, the convergence time is a strictly increasing function of the initial value $s_0$. Therefore, the convergence time $T_{\max }$ is bounded:

$$T_{\max }={\displaystyle \frac{1}{\theta \left(b-\theta \right)\left(1-\beta \right)}}$$

(21)

From Equations (3) and (11), the following expression can be derived:

$$\begin{array}{ll}{\dot{e}}_{1d}& ={\dot{\widehat{i}}}_d-{\dot{i}}_d\\ & =F_{0d}-F_d\\ & ={\varphi }_{1d}-F_d-k_{1d}{\left(\theta e_{2d}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta )e_{2d}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{2d}\right)\end{array}$$

(22)

$$\begin{array}{ll}{e}_{2d}& ={\varphi }_{1d}-F_{0d}\\ & ={\varphi }_{1d}-\left({\dot{\widehat{i}}}_d-{\displaystyle \frac{R}{L_d}}{i}_d+{\displaystyle \frac{1}{L_d}}{u}_d\right)\\ & ={\varphi }_{1d}-\left({\dot{e}}_{1d}+F_d\right)\end{array}$$

(23)

Let $e_{3d}={\varphi }_{1d}-F_d$, then:

$$\begin{array}{ll}{\dot{e}}_{3d}& ={\dot{\varphi }}_{1d}-{\dot{F}}_d\\ & =-k_{2d}{\left(\theta {\left(e_{3d}-{\dot{e}}_{1d}\right)}^{{\displaystyle \frac{\beta }{2}}}+\left(b-\theta \right){\left(e_{3d}-{\dot{e}}_{1d}\right)}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{3d}-{\dot{e}}_{1d}\right)-{\dot{F}}_d\end{array}$$

(24)

It follows from the preceding analysis that both $e_{1d}$ and $e_{3d}$ achieve finite-time convergence. Upon system stabilization, the condition ${\dot{e}}_{1d}=0$ is satisfied, and Equation (24) is thereby evaluated as:

$$\begin{array}{ll}{\dot{e}}_{3d}& ={\dot{\varphi }}_{1d}-{\dot{F}}_d\\ & =-k_{2d}{\left(\theta {(e_{3d})}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta ){(e_{3d})}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^{2}sign\left(e_{3d}\right)-{\dot{F}}_d\end{array}$$

(25)

It can thus be concluded that:

$${\left(\theta {(e_{3d})}^{{\displaystyle \frac{\beta }{2}}}+(b-\theta ){(e_{3d})}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^2\le \xi$$

(26)

For $\theta {\left(e_{3d}\right)}^{{\displaystyle \frac{\beta }{2}}}>\left(b-\theta \right){\left(e_{3d}\right)}^{1-{\displaystyle \frac{\beta }{2}}}$, then:

$${\left(2\left(b-\theta \right){\left(e_{3d}\right)}^{1-{\displaystyle \frac{\beta }{2}}}\right)}^2\le \xi ,|e_{3d}|\le {\left({\displaystyle \frac{\xi }{4{\left(b-\theta \right)}^2}}\right)}^{{\displaystyle \frac{1}{2-\beta }}}$$

(27)

For $\theta {\left(e_{3d}\right)}^{{\displaystyle \frac{\beta }{2}}}<\left(b-\theta \right){\left(e_{3d}\right)}^{1-{\displaystyle \frac{\beta }{2}}}$, then:

$${\left(2\theta {(e_{3d})}^{{\displaystyle \frac{\beta }{2}}}\right)}^2\le \xi ,|e_{3d}|\le {\left({\displaystyle \frac{\xi }{4{\theta }^2}}\right)}^{{\displaystyle \frac{1}{\beta }}}$$

(28)

According to Equations (27) and (28), by appropriately tuning the parameters $\theta$ and $b$, the estimated values produced by the observer can accurately approximate the true system states, with the estimation error reduced to an arbitrarily small level. This capability enables precise state feedback, supporting disturbance suppression and dynamic adaptability of PMSMs under dynamic operating conditions. □

3.3. Composite Controller Design

Assuming a sampling period of $T_s$, the extended state observer models defined in Equations (11) and (12) are discretized using the zero-order hold method.

A discrete-time finite-time convergent extended state observer is developed for the d-axis current channel:

$$\left\{\begin{array}{l}{e}_{1d}\left(k\right)={\widehat{i}}_d\left(k\right)-i_d\left(k\right),e_{2d}\left(k\right)={\varphi }_{1d}\left(k\right)-F_{0d}\left(k\right)\\ {\widehat{i}}_d\left(k+1\right)={\widehat{i}}_d\left(k\right)+T{F}_{0d}\left(k\right)-{\displaystyle \frac{TR}{L_d}}{i}_d\left(k\right)+{\displaystyle \frac{T}{L_d}}{u}_d\left(k\right)\\ F_{0d}\left(k\right)={\varphi }_{1d}\left(k\right)-T{k}_{1d}{\left(\theta e_{1d}^{{\displaystyle \frac{\beta }{2}}}\left(k\right)+\left(b-\theta \right)e_{1d}^{1-{\displaystyle \frac{\beta }{2}}}\left(k\right)\right)}^{2}sign\left(e_{1d}\left(k\right)\right)\\ {\varphi }_{1d}\left(k+1\right)={\varphi }_{1d}\left(k\right)-T{k}_{2d}{\left(\theta e_{2d}^{{\displaystyle \frac{\beta }{2}}}\left(k\right)+\left(b-\theta \right)e_{2d}^{1-{\displaystyle \frac{\beta }{2}}}\left(k\right)\right)}^{2}sign\left(e_{2d}\left(k\right)\right)\end{array}\right.$$

(29)

A discrete-time finite-time convergent extended state observer is developed for the q-axis current channel:

$$\left\{\begin{array}{l}{e}_{1q}\left(k\right)={\widehat{i}}_q\left(k\right)-i_q\left(k\right),e_{2q}\left(k\right)={\varphi }_{1q}\left(k\right)-F_{0q}\left(k\right)\\ {\widehat{i}}_q\left(k+1\right)={\widehat{i}}_q\left(k\right)+T{F}_{0q}\left(k\right)-{\displaystyle \frac{TR}{L_q}}{i}_q\left(k\right)+{\displaystyle \frac{T}{L_q}}{u}_q\left(k\right)\\ F_{0q}\left(k\right)={\varphi }_{1q}\left(k\right)-T{k}_{1q}{\left(\theta e_{1q}^{{\displaystyle \frac{\beta }{2}}}\left(k\right)+\left(b-\theta \right)e_{1q}^{1-{\displaystyle \frac{\beta }{2}}}(k)\right)}^{2}sign\left(e_{1q}\left(k\right)\right)\\ {\varphi }_{1q}\left(k+1\right)={\varphi }_{1q}\left(k\right)-T{k}_{2q}{\left(\theta e_{2q}^{{\displaystyle \frac{\beta }{2}}}\left(k\right)+\left(b-\theta \right)e_{2q}^{1-{\displaystyle \frac{\beta }{2}}}\left(k\right)\right)}^{2}sign\left(e_{2q}\left(k\right)\right)\end{array}\right.$$

(30)

To ensure precise tracking of the reference current trajectory while mitigating voltage oscillations caused by power device switching, a multi-objective cost function is constructed based on current tracking error and voltage increment minimization. This formulation not only enhances dynamic current response and reduces transient overshoot, but also minimizes copper losses and thermal stress, thereby improving the overall disturbance suppression and dynamic adaptability of the PMSM drive system in electric drive system applications.

$$\begin{array}{ll}J\left(i,\Delta u\right)& ={\displaystyle \sum _{j=1}^{Np}{\left(\widehat{i}\left(k+j\right)-i_{ref}\left(k+j\right)\right)}^T}Q\left(\widehat{i}\left(k+j\right)-i_{ref}\left(k+j\right)\right)\\ & +{\displaystyle \sum _{j=1}^{Nc}\Delta u{\left(k+j\right)}^T}R\Delta u\left(k+j\right)\end{array}$$

(31)

At the current sampling instant $k$, the prediction horizon is defined as $N_p$, and the control horizon as $N_c$. The time index $k+j$ denotes the $j$-th prediction step starting from moment $k$. The predicted current vector at $k+j$ is given by $\widehat{i}\left(k+j\right)=\left[\begin{array}{c}{\widehat{i}}_d\left(k+j\right)\\ {\widehat{i}}_q\left(k+j\right)\end{array}\right]$ representing the estimated d-axis and q-axis currents of the PMSMs. The reference current vector is denoted as $i_{ref}\left(k+j\right)=\left[\begin{array}{c}{i}_{dref}\left(k+j\right)\\ i_{qref}\left(k+j\right)\end{array}\right]$, which corresponds to the desired d-axis and q-axis currents at time $k+j$. The control increment of voltage input is defined as $\Delta u\left(k+j\right)=\left[\begin{array}{c}\Delta u_d\left(k+j\right)\\ \Delta u_q\left(k+j\right)\end{array}\right]$, where $\Delta u_d$ and $\Delta u_q$ represent the incremental voltage inputs for the d- and q-axes, respectively. To balance current tracking precision and input effort, $Q$ is introduced as the weighting matrix for current tracking errors, and $R$ is the weighting matrix for voltage increments. This formulation lays the foundation for optimizing the control input in a predictive framework that improves dynamic response and ensures stable current regulation—critical for reliable high-performance electric drive systems.

According to the predictive control strategy adopted in the relevant literature [36], the incremental control inputs for the d-axis and q-axis voltages are parameterized using Laguerre functions:

$$\begin{array}{ll}\Delta u\left(k+j\right)& =\left[\begin{array}{c}\Delta u_d\left(k+j\right)\\ \Delta u_q\left(k+j\right)\end{array}\right]\\ & =\left[\begin{array}{cccccc}{l}_1^d\left(k\right)& \dots & l_N^d\left(k\right)& 0& \dots & 0\\ 0& \dots & 0& l_1^q\left(k\right)& \dots & l_N^q\left(k\right)\end{array}\right]\\ & \ast \left[\begin{array}{cccccc}{c}_1^d\left(k\right)& \dots & c_N^d\left(k\right)& c_1^q\left(k\right)& \dots & c_N^q\left(k\right)\end{array}\right]\end{array}$$

(32)

where this approach expresses the control input sequence as a weighted combination of orthonormal Laguerre basis functions, enabling a compact representation with significantly fewer decision variables. Specifically, the voltage increments $\Delta u_d\left(k+j\right)$ and $\Delta u_q\left(k+j\right)$ over the prediction horizon are mapped to a set of Laguerre coefficients, which serve as the new optimization variables. By leveraging the orthogonality and recursive structure of Laguerre functions, the method achieves a notable reduction in computational complexity, thereby enhancing the real-time applicability of the predictive controller. Furthermore, this coefficient-based formulation enables smoother control transitions and more stable voltage regulation, which helps maintain consistent system performance and prolong component lifespan.

The composite control law based on the finite-time convergent observer and disturbance compensation can be derived by substituting Equations (1), (11), (12), and (32) into Equation (31).

$$\begin{array}{ll}u\left(k+1\right)& =u\left(k\right)+\Delta u\left(k+1\right)\\ & =u\left(k\right)-L^T{\Omega }^{-1}\psi \left(x_e\left(k\right)-{\widehat{x}}_e\left(k\right)\right)\end{array}$$

(33)

Let $\Delta u\left(k+1\right)=\left[\begin{array}{l}\Delta u_d\left(k+j\right)\\ \Delta u_q\left(k+j\right)\end{array}\right]$ represent the incremental voltages along the d-axis and q-axis at prediction step $k+j$. The matrix $\Omega$ denotes the weight assigned to the current tracking error, while $R$ represents the weight assigned to the control voltage increment.

Therefore, the structure of the predictive control scheme incorporating the designed FTESO is illustrated in Figure 2.

4. Result Analysis

To validate the disturbance rejection capability of the proposed FTESO-based predictive controller, this section presents both simulation and experimental evaluations. A comparative analysis is conducted against the LESO-based predictive controller reported in the literature. Emphasis is placed on assessing not only the tracking accuracy and dynamic performance but also the control system’s contribution to enhanced disturbance suppression and dynamic adaptability under complex load conditions, which aligns with the overarching goal of advancing robust control strategies for high-performance electric drive systems.

To assess the dynamic response characteristics of the control system under realistic operating conditions, simulation experiments were conducted considering both time-varying load disturbances and parametric uncertainties in the PMSM. Two control strategies—FTESO-based predictive control and conventional LESO-based predictive control—were evaluated and compared. The simulation settings, including motor parameters, observer configurations, and disturbance profiles, are detailed in

Table 1. Speed Loop LMPC Controller Parameters.

Parameter	Description	Value
$N_p$	Prediction horizon	1
$a$	Laguerre factor	0.5
$N$	Number of Laguerre terms	4
$q_{\omega }$	Speed error weighting factor	1,000,000
$r$	Control input increment weighting factor	0.1

,

Table 2. Current Loop LMPC Controller Parameters.

Parameter	Description	Value
$N_p$	Prediction horizon	1
$N_c$	Control horizon	1
$a_1$	Laguerre factor for d-axis current	0.5
$a_2$	Laguerre factor for q-axis current	0.5
$N_1$	Number of Laguerre terms for d-axis current	4
$N_2$	Number of Laguerre terms for q-axis current	4
$q_{i_d}$	Weighting factor for d-axis current tracking error	100,000
$q_{i_q}$	Weighting factor for q-axis current tracking error	100,000
$r$	Weighting factor for input increment	0.01

and

Table 3. FTESO-MPC and LESO-MPC Parameters.

FTESO	$k_{1d}$	$k_{2d}$	$k_{1q}$	$k_{2q}$	$\theta$	$\beta$	$b$
	5000	0.01	0.01	0.01	0.1	0.9	1
Linear ESO	$k_{1d}$	$k_{2d}$	$k_{1q}$	$k_{2q}$
	5000	0.01	0.01	0.01

. These scenarios are designed to reflect typical working conditions in electric vehicle applications, where external load variation and parameter drift pose challenges to stable and reliable motor operation. By observing current regulation, control smoothness, and torque response under these variations, the effectiveness of the proposed controller in enhancing robustness and maintaining high-performance operation is quantitatively analyzed.

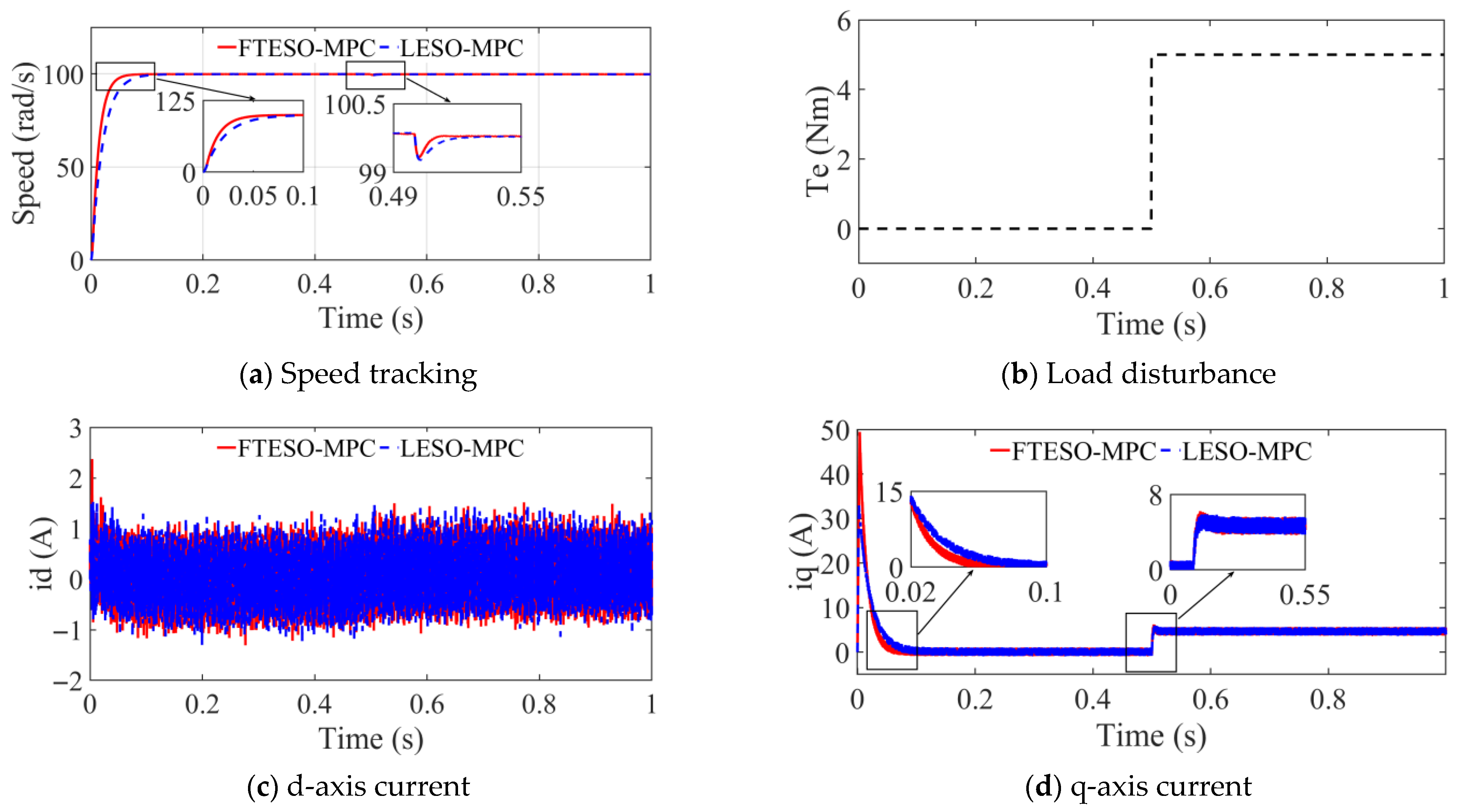
Under the condition of load increase, the dynamic response curves of different control strategies are illustrated in Figure 3. This figure presents the simulated speed response of the proposed FTESO-MPC and the benchmark LESO-MPC controllers when the PMSM is subjected to a sudden external load disturbance. Specifically, Figure 3b depicts the load profile: the PMSM is initially set to track a reference speed of 100 rad/s and starts from no-load conditions. At a specific time instant, an external torque load of 5 N·m is suddenly applied. As shown in Figure 3a, both FTESO-MPC and LESO-MPC demonstrate satisfactory speed tracking performance during the no-load start-up and acceleration phase. However, the FTESO-MPC exhibits superior dynamic performance. In the initial acceleration phase (0~0.1 s), FTESO-MPC responds significantly faster than LESO-MPC, quickly converging to the reference speed with a smaller steady-state error. This indicates that FTESO-MPC possesses enhanced dynamic response characteristics and regulation precision. When the external load is abruptly increased, the LESO-MPC controller shows a larger speed dip and a longer recovery time. In contrast, the FTESO-MPC maintains better disturbance rejection, with less speed fluctuation and faster recovery to steady-state. These results verify that FTESO-MPC achieves more effective compensation against load perturbations, offering improved robustness and faster transient recovery. Such advantages are particularly beneficial for electric drive systems, where precise and rapid adaptation to variable load conditions contributes directly to improved stability and enhanced control reliability.

Corresponding to this is the analysis shown in Figure 3d. During the motor start-up phase, the d-axis current experiences an initial surge followed by a rapid decrease toward its steady-state value. The FTESO-MPC controller exhibits a faster current decay rate and reaches the steady state within a shorter time frame compared to the LESO-MPC, which takes noticeably longer to stabilize. When the external load suddenly increases to 5 N·m, a sharp transient occurs in the d-axis current. FTESO-MPC promptly adjusts the current to a new steady-state value, while LESO-MPC responds with slower current convergence and more pronounced oscillations. This demonstrates the superior transient performance of FTESO-MPC in quickly compensating for current disturbances, ensuring system stability, and minimizing overshoot. In particular, FTESO-MPC leads to smaller current deviation and reduced settling time, whereas LESO-MPC shows larger current fluctuations and a slower recovery. These observations further confirm that FTESO-MPC provides faster dynamic adaptation to abrupt load changes, maintaining system stability and reducing the risk of excessive current stress, which is critical for ensuring system reliability and energy efficiency. Figure 4 presents the dynamic response of both controllers under a load-decreasing scenario. The trends remain consistent with those in Figure 3, further validating the disturbance rejection capability of FTESO-MPC across various operating conditions. This robustness under load transients is essential for electric drive systems, where high-frequency load variations frequently occur under real-world operating conditions.

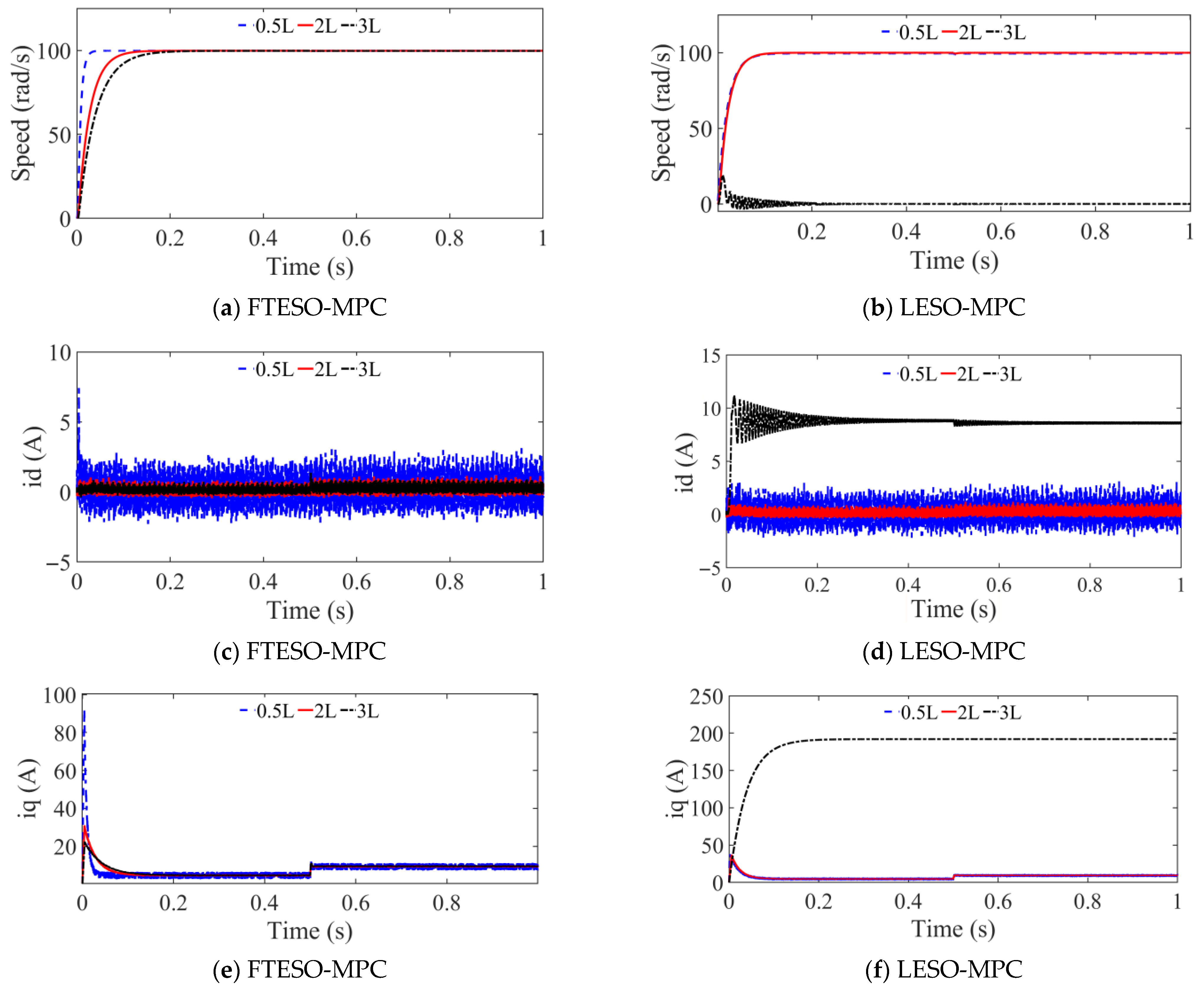
Figure 5 illustrates the dynamic response curves of different control strategies under varying inductance conditions. Specifically, the figure compares the performance of FTESO-MPC and LESO-MPC when system inductance is subject to step changes, with all other load conditions consistent with those in Figure 3b. The purpose of this simulation is to evaluate how well each controller adapts to inductance variations, which are common in practical electric drive systems due to temperature fluctuations, magnetic saturation, or structural uncertainties. As observed in Figure 5a, the FTESO-MPC maintains robust dynamic performance across all inductance scenarios. When the inductance is reduced to 0.5 times its nominal value, the system exhibits fast rise time and minimal overshoot, indicating strong regulation capabilities. With a doubled inductance (2×), the system still achieves smooth convergence toward the target speed without noticeable overshoot, demonstrating good control stability. Even under a more challenging condition of triple inductance (3×), the FTESO-MPC maintains a stable response, with only a moderate increase in settling time and no observable oscillation. These results underscore the controller’s robustness and adaptability to parameter uncertainties, which are crucial in energy-efficient electric drive systems operating under dynamic environments. In contrast, Figure 5b shows that while LESO-MPC performs adequately under small inductance variations (0.5× and 2×), its control performance degrades significantly when inductance increases to 3×. The system exhibits pronounced oscillations during the initial phase and takes considerably longer to stabilize, reflecting poor disturbance rejection and limited adaptability to parameter shifts. This sensitivity to inductance variation highlights the limitations of LESO-MPC in handling system uncertainty, which may compromise both stability and energy efficiency in practical applications. Overall, the comparison confirms that FTESO-MPC offers superior robustness and dynamic adaptability, making it a more suitable solution for high-performance electric drive systems, where varying electrical parameters and external disturbances are prevalent.

This observation is further supported by the current response curves in Figure 5e,f, which reveal significant differences between FTESO-MPC and LESO-MPC under varying inductance conditions, particularly in terms of the d-axis current behavior. The two control strategies exhibit noticeably different response characteristics as the inductance multiplier changes. In the initial transient phase of the d-axis current response, FTESO-MPC demonstrates superior dynamic performance by more effectively suppressing abrupt current surges and enabling faster convergence to the steady-state value. In contrast, LESO-MPC shows a considerable current overshoot under the 3× inductance condition, with peak current values approaching 200 A—significantly higher than in other scenarios. This excessive overshoot indicates that LESO-MPC struggles to mitigate current shocks when faced with drastic inductance variations, leading to pronounced current fluctuations that compromise system stability. During the steady-state phase, FTESO-MPC maintains relatively stable d-axis current levels across all inductance cases, with minimal ripple, highlighting its robust disturbance rejection capability. On the other hand, LESO-MPC continues to exhibit substantial current oscillations under the 3× inductance condition. The steady-state error under such a condition is also noticeably larger for LESO-MPC, reflecting its limited adaptability to substantial parameter uncertainties. Overall, these results further validate the effectiveness of FTESO-MPC in ensuring reliable current regulation under changing inductance environments. Such robustness is particularly crucial in electric drive systems, where maintaining stable current control not only ensures operational safety and efficiency but also prevents excessive current fluctuations that can compromise reliability.

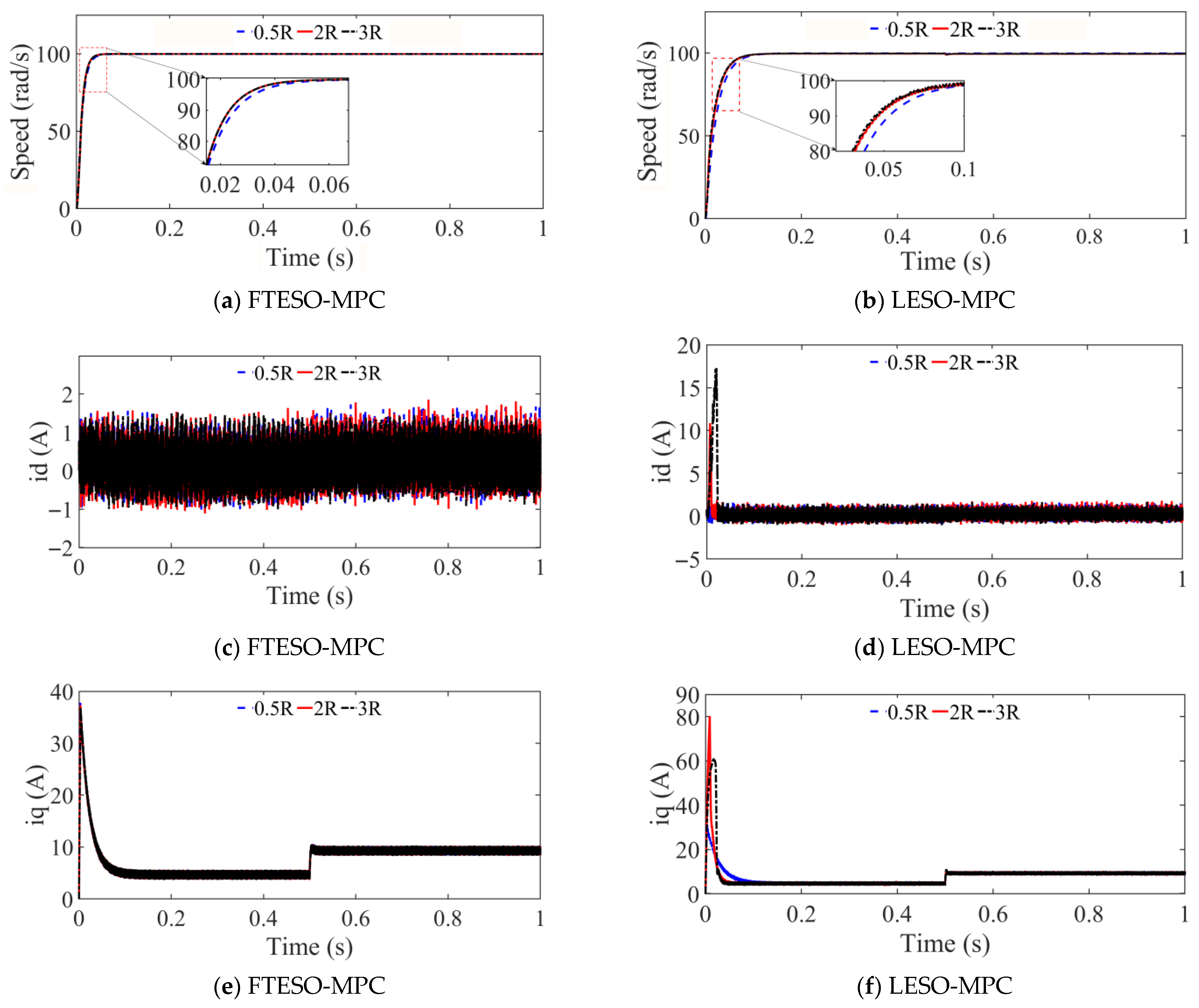
Figure 6 illustrates the simulation results comparing the dynamic responses of FTESO-MPC and LESO-MPC controllers under varying stator resistance conditions. The purpose of this comparison is to assess each controller’s ability to maintain stable system performance in the presence of parameter uncertainty, a critical concern for energy-efficient electric drive systems operating in sustainable transportation environments. The external load conditions are consistent with those specified in Figure 3b. As shown in Figure 6a, during the startup phase (0~0.2 s), both FTESO-MPC and LESO-MPC controllers successfully accelerate the motor from standstill to the reference speed of 100 rad/s. Under nominal resistance, the two controllers exhibit similar transient performance. However, as the resistance increases to 2× and 3× the nominal value, noticeable differences emerge. The FTESO-MPC maintains smooth and responsive tracking behavior with minimal overshoot or oscillation. In contrast, the LESO-MPC shows a slower dynamic adjustment, especially under 3× resistance, indicating reduced adaptability. The superior robustness of FTESO-MPC stems from its use of a finite-time convergent observer, which enables rapid and accurate disturbance estimation. This enhances the control system’s resilience under varying resistive conditions, a feature especially valuable for electric vehicles where operating conditions and thermal environments frequently change. Further validation is presented in Figure 6e,f, which show the corresponding d-axis current responses. The FTESO-MPC demonstrates superior dynamic current regulation, quickly adapting to resistance changes with smaller transient deviations and faster convergence to steady-state values. Conversely, the LESO-MPC exhibits greater current ripple and significant overshoot, particularly under 0.5× and 3× resistance conditions. These findings confirm that FTESO-MPC not only enhances transient current control but also ensures greater system reliability and thermal stability, aligning with the broader goal of improving robust performance in electric drive systems.

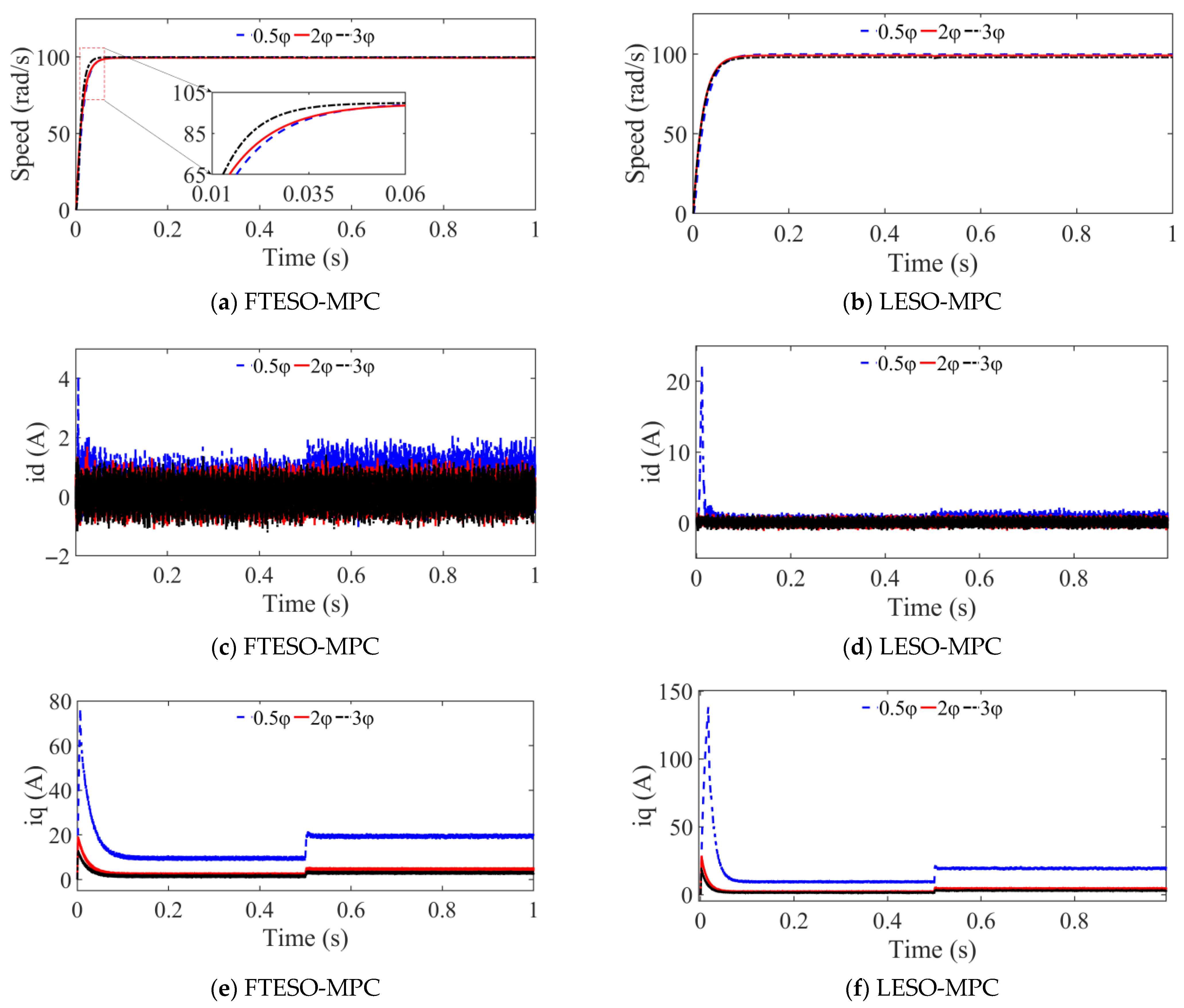
Figure 7 illustrates the dynamic response curves of FTESO-MPC and LESO-MPC under varying flux linkage conditions. This set of simulations aims to evaluate the adaptability of both control strategies to flux linkage deviations, which are common in real-world electric vehicle operations due to temperature effects, magnetic saturation, or aging of motor materials. The load conditions used in this analysis follow the settings depicted in Figure 3b. As shown in Figure 7a, when the flux linkage decreases to 0.5 times its nominal value, both controllers exhibit fast transient response with minimal overshoot. However, under increased flux linkage conditions (2× and 3×), differences between the two controllers become more evident. While both controllers ensure system convergence to the target speed, LESO-MPC shows slower dynamic response. In contrast, FTESO-MPC demonstrates shorter rise times and a more efficient convergence process, indicating superior responsiveness and enhanced adaptability to system variations. Corresponding observations from Figure 7e,f reveal significant distinctions in q-axis current behavior. FTESO-MPC maintains smoother current responses across all flux linkage variations, even under extreme deviations. On the other hand, LESO-MPC suffers from larger current fluctuations, particularly at the onset of flux disturbances. When flux linkage is reduced (0.5×), LESO-MPC exhibits considerable q-axis current overshoot, reflecting its limited capability to cope with rapid magnetic weakening. Conversely, FTESO-MPC quickly stabilizes the current and achieves better damping, contributing to reduced energy losses and improved thermal reliability. Moreover, in high-flux scenarios (2× and 3×), FTESO-MPC continues to deliver consistent and stable q-axis current control, minimizing ripple and ensuring optimal current utilization. LESO-MPC, however, shows persistent instability in current regulation, which can negatively impact overall system reliability. These results confirm that FTESO-MPC not only enhances disturbance rejection but also supports the development of resilient PMSM drive systems—critical for ensuring stable and robust operation in practical applications.

Table 4. Performance comparison between FTESO-MPC and LESO-MPC under representative scenarios.

Scenario	Metric/Observation	LESO-MPC	FTESO-MPC
Sudden load disturbance	Recovery time	Longer, larger speed drop	Faster recovery, smaller speed drop
	Steady-state error	Noticeable residual error	Very small, almost eliminated
Inductance ↑ 3×	Current response	Pronounced oscillations; d-axis peak ≈ 200 A	Smooth convergence; no oscillation
Resistance ↑ 3×	Current regulation	Slower response, large ripple	Stable response, reduced ripple
Flux linkage variations (0.5×–3×)	Transient stability	Overshoot and instability	Smooth convergence, stable tracking
Overall robustness	Under parameter uncertainties & disturbances	Limited robustness	Strong robustness and adaptability

↑ indicates an increase in the parameter.

summarizes the comparative performance of the proposed FTESO-MPC and the conventional LESO-MPC under representative disturbance scenarios. As can be seen, FTESO-MPC achieves faster recovery and smaller steady-state error under sudden load disturbances, maintains smooth current convergence without oscillation when the inductance increases threefold, and exhibits stable regulation with reduced ripple under resistance and flux linkage variations. In contrast, LESO-MPC suffers from slower recovery, larger current peaks, and instability in these cases. This table highlights the overall advantages of FTESO-MPC in terms of disturbance rejection, transient stability, and robustness under parameter uncertainties.

5. Conclusions

This paper addresses the robust control of PMSMs in nonlinear disturbance environments, focusing on a composite control strategy that integrates disturbance observation and predictive compensation. To cope with typical challenges—such as sudden load fluctuations, parameter variations, and external disturbances—a current prediction model incorporating lumped disturbance terms was established based on the conventional PMSM framework. This model captures the coupled influence of electromagnetic perturbations, parameter uncertainties, and flux linkage variations, thereby providing a more realistic representation of motor dynamics under practical operating conditions.

To overcome the estimation delays and slow convergence typically observed in conventional LESOs, an FTESO with a nonlinear gain structure was proposed. By employing exponential-type feedback and Lyapunov-based stability design, the observer guarantees global finite-time convergence, enabling rapid and accurate estimation of current disturbances. These estimations are then directly integrated into the MPC for real-time compensation and control input updates, significantly enhancing the system’s disturbance rejection capability and control precision. Furthermore, a composite cost function was designed by incorporating both current tracking error and voltage increment, enabling dynamic optimization of the control input based on the disturbance observations. To meet the requirements for real-time digital controller implementation, the FTESO was discretized and embedded into a fully integrated feedforward-compensated FTESO-MPC control framework suitable for engineering applications.

Finally, the effectiveness of the proposed strategy was validated through comprehensive simulation studies under a range of representative disturbance scenarios, including abrupt load changes and severe variations in resistance, inductance, and flux linkage. Comparative results with the LESO-MPC approach demonstrate that the FTESO-MPC controller consistently achieves superior speed tracking accuracy, faster disturbance convergence, and improved transient performance. Notably, under significant parameter uncertainties, the controller is able to promptly estimate and compensate for disturbances, thereby ensuring robust and adaptive control of PMSMs—laying a solid foundation for practical engineering applications. Despite these contributions, this study still has some limitations. First, the proposed FTESO-MPC framework has only been validated through simulations, and experimental verification on real hardware platforms (e.g., DSPs or FPGAs) remains to be carried out. Second, the design and tuning of observer gains and cost-function weights involve empirical choices, which may limit generalization across different PMSM drive systems. Third, the additional computational cost introduced by the integrated FTESO-MPC structure may pose challenges for implementation in real-time embedded environments. Future work will address these limitations by developing systematic co-tuning approaches, performing hardware-in-the-loop tests, and extending the method to sensorless and multi-motor applications.