Advanced Dynamic Responses of Thick FGM Spherical Shells Analyzed Using TSDT Under Thermal Vibration
Abstract
1. Introduction
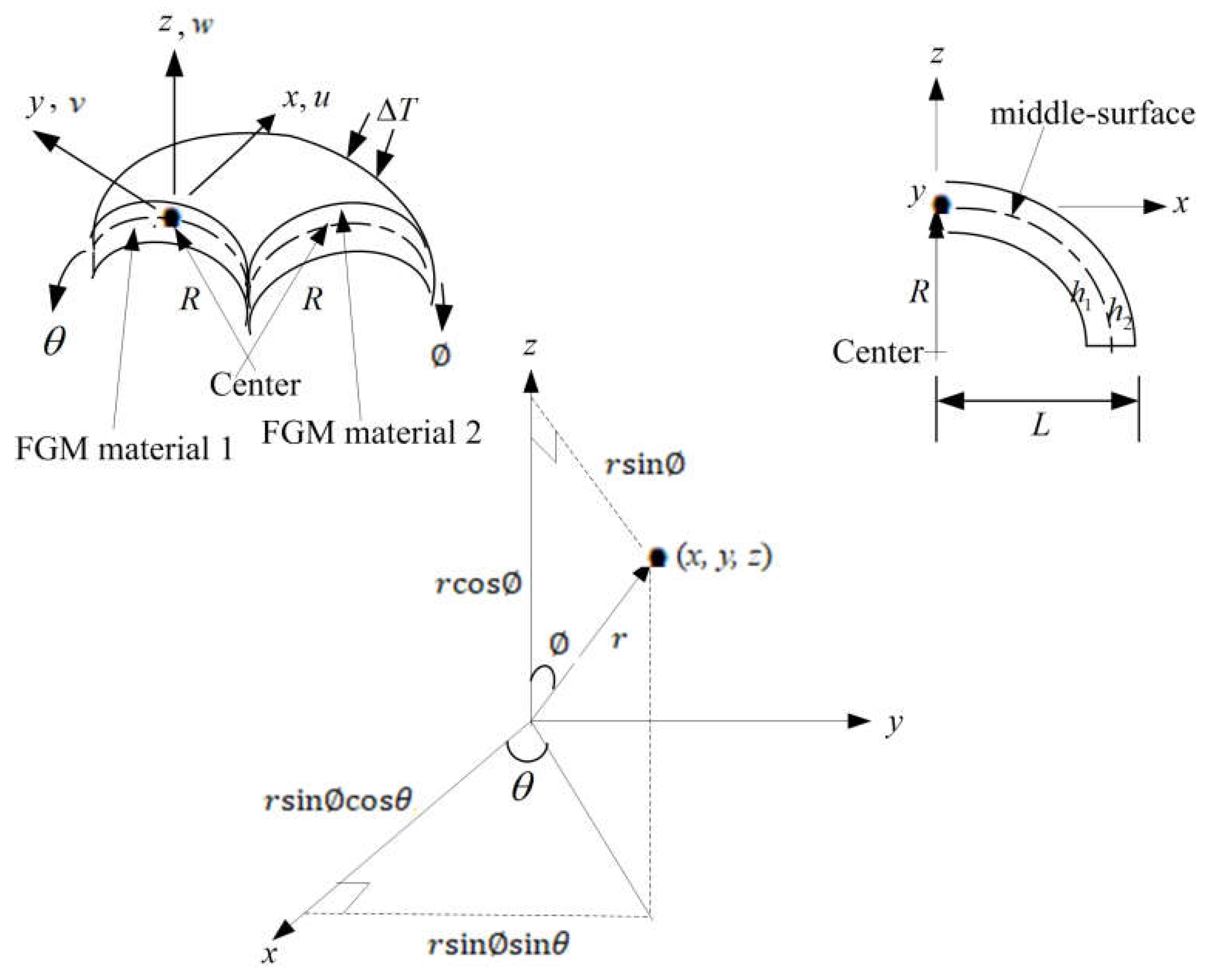
2. Materials and Methods
2.1. TSDT Displacements
2.2. Thermal Load Under ∆T
3. Theory and Calculation
3.1. Dynamic GDQ Discrete Equations of Motion
3.2. GDQ Implementation
4. Results
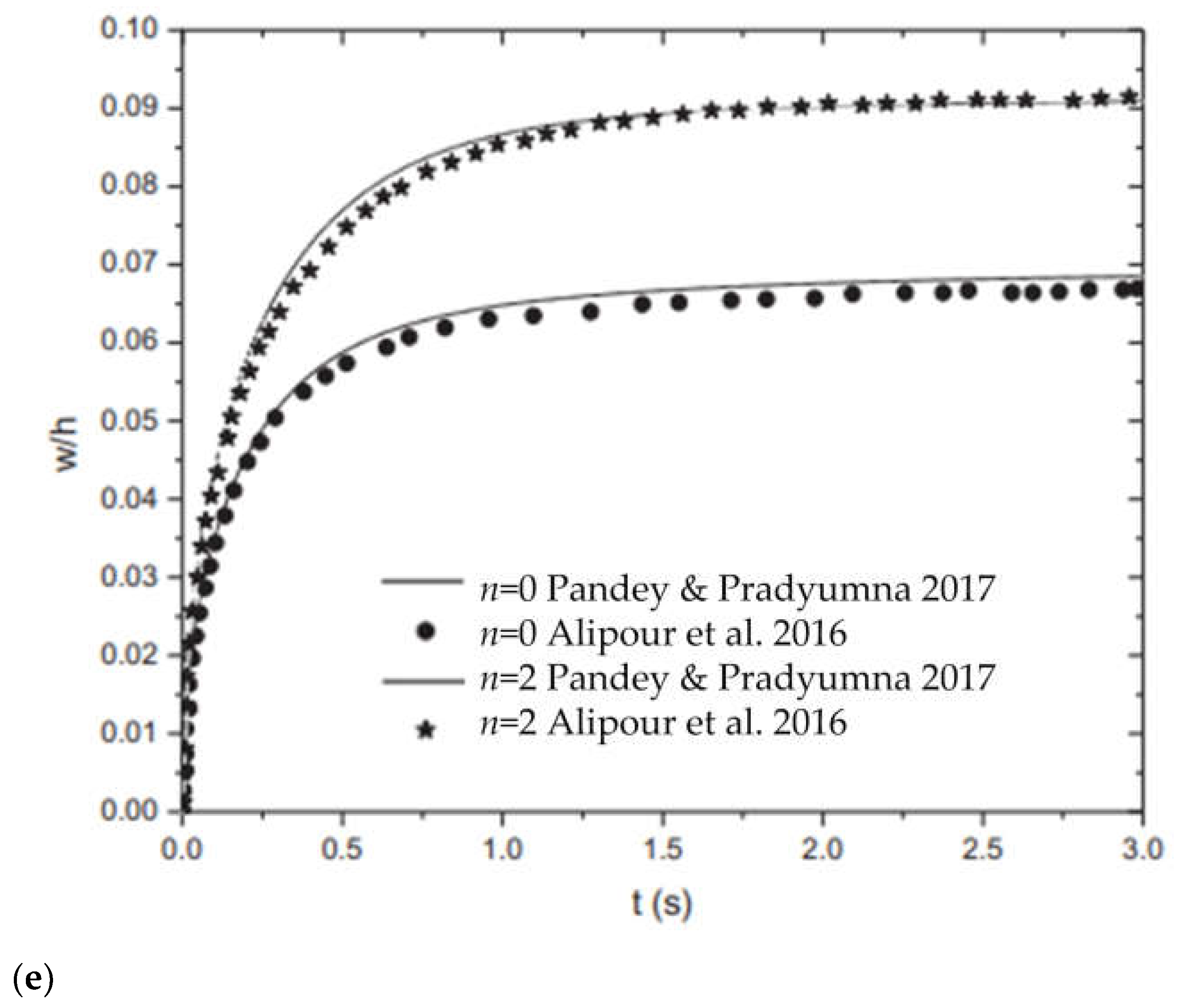
4.1. Dynamic Convergence
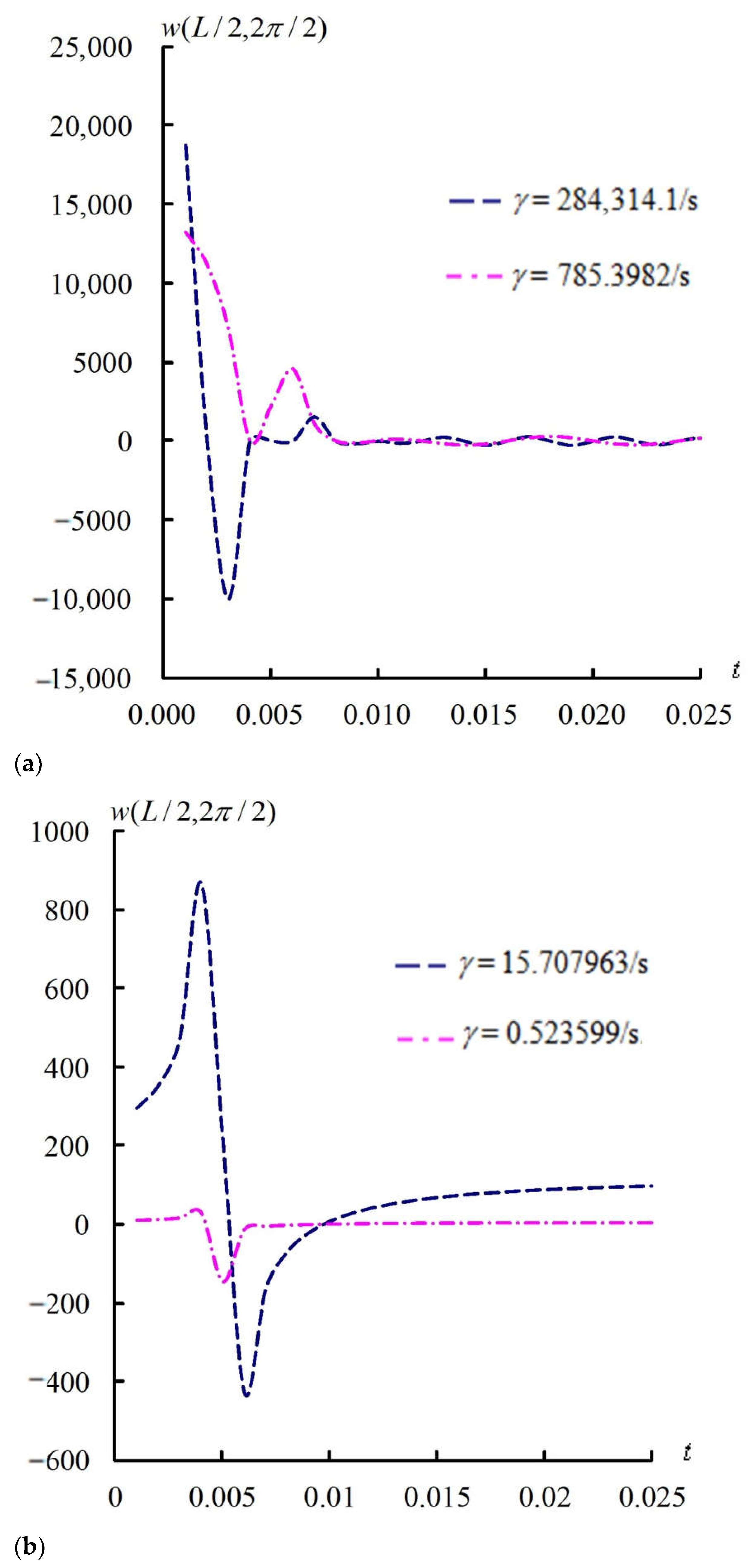
4.2. Time Responses of and
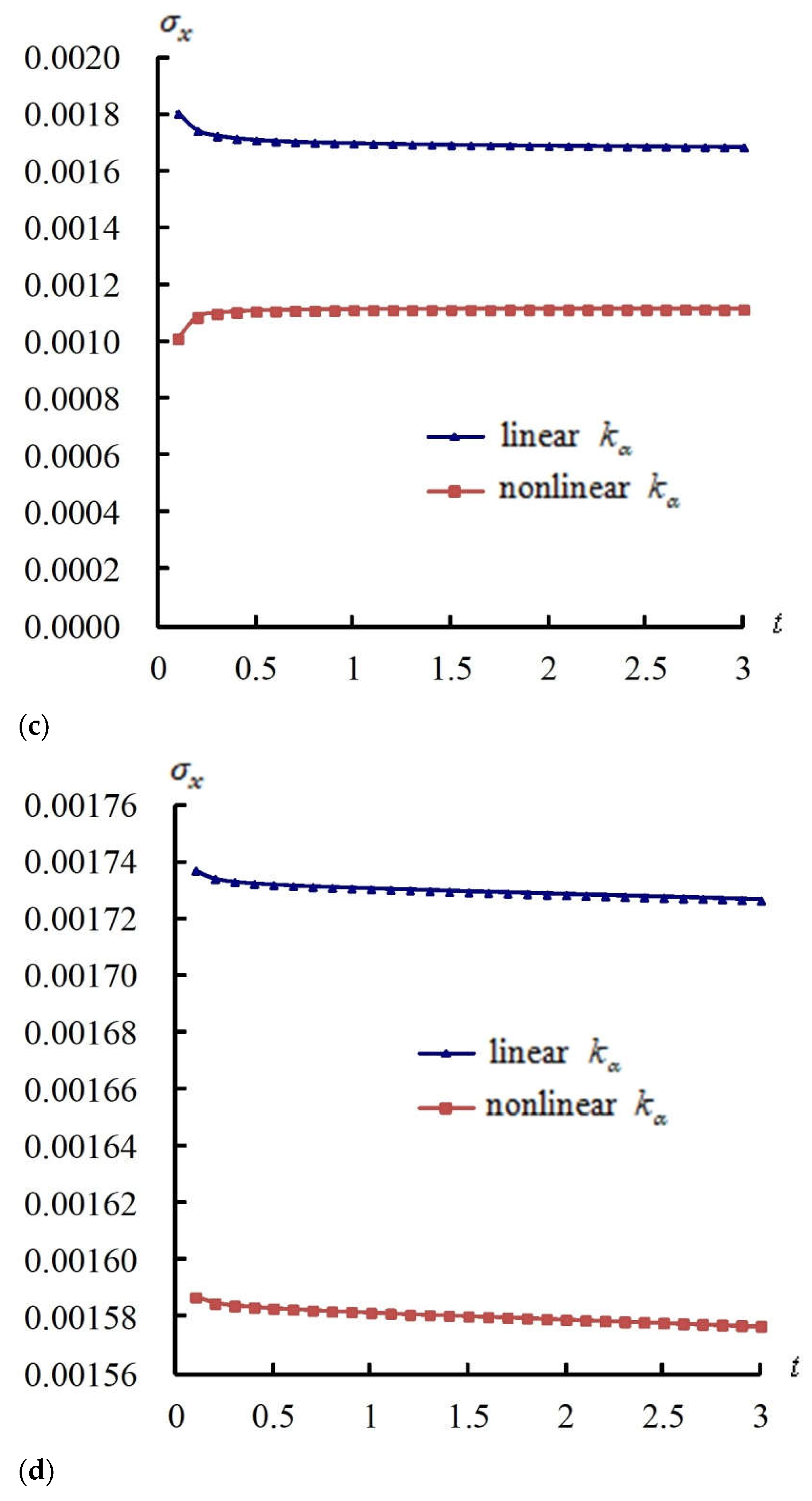
4.3. Responses of and vs. T and
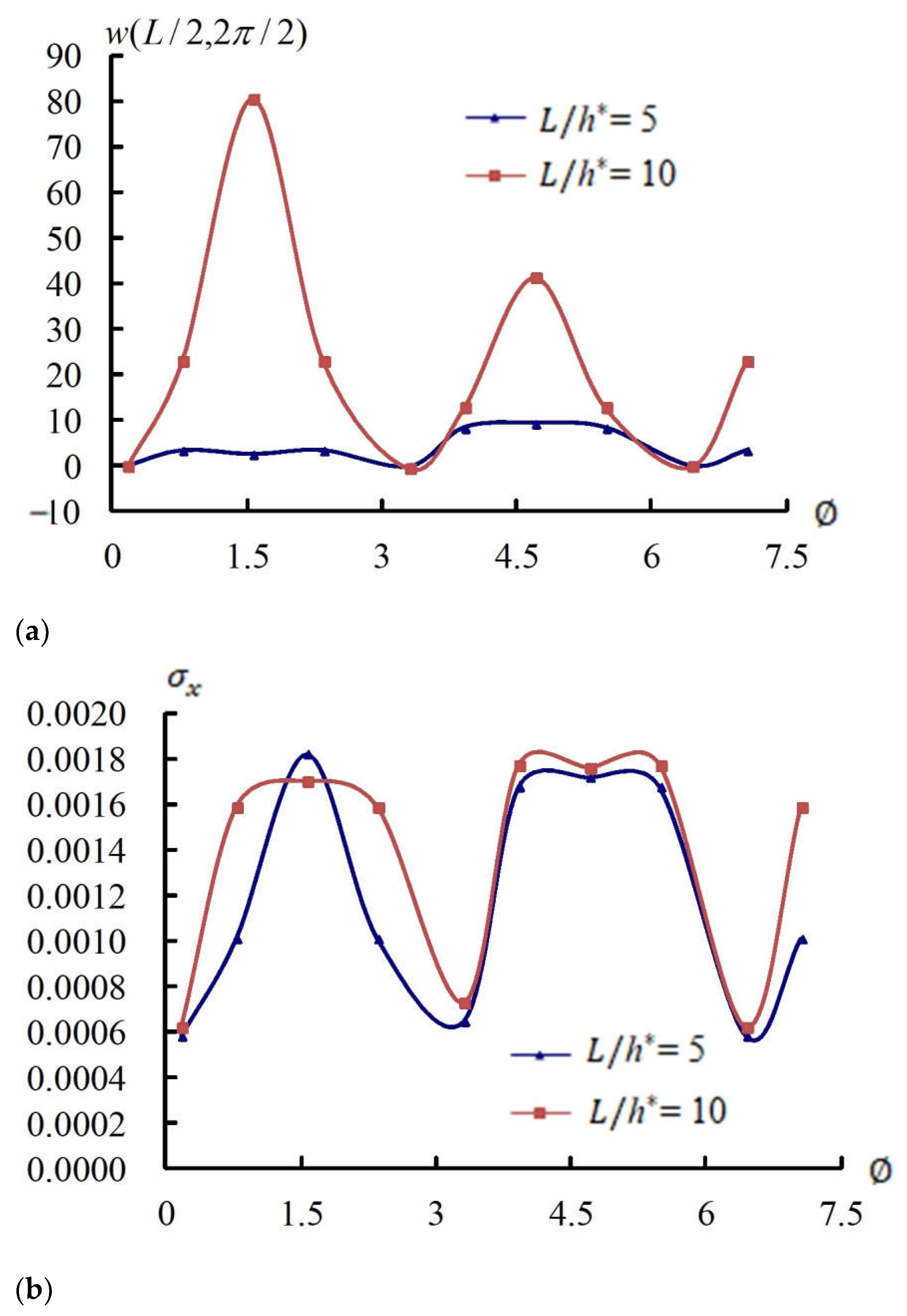
4.4. Responses of and vs.
4.5. Transient Responses of
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tang, H.; Dai, H.L. Nonlinear vibration analysis of CFRP spherical shell panel under hygrothermal effects. Compos. Struct. 2021, 274, 114343. [Google Scholar] [CrossRef]
- Stampouloglou, I.H.; Theotokoglou, E.E.; Karaoulanis, D.E. The radially nonhomogeneous isotropic spherical shell under a radially varying temperature field. Appl. Math. Model. 2021, 94, 350–368. [Google Scholar] [CrossRef]
- Papargiri, A.; Kalantonis, V.S.; Kaziki, D.; Vafeas, P.; Fragoyiannis, G. Revisiting an analytical solution for the three-shell spherical human head model in electroencephalography. Partial Differ. Equ. Appl. Math. 2021, 4, 100178. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Ning, J. Deformation and failure of thin spherical shells under dynamic impact loading: Experiment and analytical model. Thin-Walled Struct. 2021, 161, 107403. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, D. Vibration analysis of functionally graded stiffened shallow shells under thermo-mechanical loading. Mater. Today Proc. 2021, 44, 4590–4595. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Malekzadeh, P.; Gholipour, F. Thermoelastic analysis of FG-GPLRC spherical shells under thermo-mechanical loadings based on Lord-Shulman theory. Compos. Part B 2019, 164, 400–424. [Google Scholar] [CrossRef]
- Ranjbar, J.; Alibeigloo, A. Response of functionally graded spherical shell to thermo-mechanical shock. Aerosp. Sci. Technol. 2016, 51, 61–69. [Google Scholar] [CrossRef]
- Bacer, L.; Zamolo, R.; Miotti, D.; Nobile, E. Adaptive RBF-FD meshless solution of 3D fluid flow and heat transfer problems. Eng. Anal. Bound. Elem. 2025, 179, 106367. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, Z.; Shi, Z.; Xie, H.; Sun, Y.; Gu, Z.; Xiao, J.; Xu, J. Static analysis of temperature-dependent FGM spherical shells under thermo-mechanical loads. Buildings 2025, 15, 2709. [Google Scholar] [CrossRef]
- Wiegold, T.; Kurzeja, P.; Klinge, S.; Mosler, J. Non-linear thermo-mechanical modeling of hollow sphere shells using isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2025, 446, 118227. [Google Scholar] [CrossRef]
- Mamandi, A. Yielding onset in FGM thick-walled spherical shells under thermo-mechanical loading. J. Reinf. Plast. Compos. 2024. [Google Scholar] [CrossRef]
- Zannon, M.; Abu-Rqayiq, A.; Al-bdour, A. Free vibration analysis of thick FGM spherical shells based on a third-order shear deformation theory. Eur. J. Pure Appl. Math. 2020, 13, 766–778. [Google Scholar] [CrossRef]
- Dai, Y.; Hong, X.; Liu, J.F.; Zhang, L. The nonlinear dynamic response of functionally graded material flat spherical shells. Adv. Mater. Res. 2012, 479–481, 1399–1402. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Malikan, M.; Eremeyev, V.A.; Akgöz, B.; Civalek, Ö. On the generalized model of shell structures with functional cross-sections. Compos. Struct. 2021, 272, 114192. [Google Scholar] [CrossRef]
- Khoa, N.M.; Tung, H.V. Nonlinear thermo-mechanical stability of shear deformable FGM sandwich shallow spherical shells with tangential edge constraints. Vietnam J. Mech. 2017, 39, 351–364. [Google Scholar] [CrossRef] [PubMed]
- Nejad, M.Z.; Hoseini, Z.; Niknejad, A.; Ghannad, M. Steady-state creep deformations and stresses in FGM rotating thick cylindrical pressure vessels. J. Mech. 2015, 31, 1–6. [Google Scholar] [CrossRef]
- Nematollahi, M.A.; Dini, A.; Hosseini, M. Thermo-magnetic analysis of thick-walled spherical pressure vessels made of functionally graded materials. Appl. Math. Mech. 2019, 40, 751–766. [Google Scholar] [CrossRef]
- Hajlaoui, A.; Triki, E.; Frikha, A.; Wali, M.; Dammak, F. Nonlinear dynamics analysis of FGM shell structures with a higher order shear strain enhanced solid-shell element. Lat. Am. J. Solids Struct. 2017, 14, 72–91. [Google Scholar] [CrossRef]
- Narendra, K.; Pradhan, S.C. Vibration control of Fgm thick shells using higher order shear deformation theory. J. Aerosp. Sci. Technol. 2023, 61, 451–474. [Google Scholar] [CrossRef]
- Meftah, A.; Dehbi, A.; Yahiaoui, M. Effect of porosity distribution rate for the analysis of free vibrations of imperfect functionally graded plates. Stud. Eng. Exact Sci. 2025, 6, e13175. [Google Scholar] [CrossRef]
- Hong, C.C. Thermal vibration of thick FGM spherical shells by using TSDT. Int. J. Mech. Mater. Des. 2021, 17, 367–380. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced dynamic thermal vibration of laminated FGM plates with simply homogeneous equation by using TSDT and nonlinear varied shear coefficient. Appl. Sci. 2022, 12, 11776. [Google Scholar] [CrossRef]
- Pandey, S.; Pradyumna, S. A finite element formulation for thermally induced vibrations of functionally graded material sandwich plates and shell panels. Compos. Struct. 2017, 160, 877–886. [Google Scholar] [CrossRef]
- Alipour, S.M.; Kiani, Y.; Eslami, M.R. Rapid heating of FGM rectangular plates. Acta Mech. 2016, 227, 421–436. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Haghi, P. Wave propagation analysis of size-dependent rotating inhomogeneous nanobeams based on nonlocal elasticity theory. J. Vib. Control 2017, 24, 17. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Size-dependent thermally affected wave propagation analysis in nonlocal strain gradient functionally graded nanoplates via a quasi-3D plate theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 232, 162–173. [Google Scholar] [CrossRef]
- Asrari, R.; Ebrahimi, F.; Kheirikhah, M.M. On scale–dependent stability analysis of functionally graded magneto-electro-thermo-elastic cylindrical nanoshells. Struct. Eng. Mech. 2020, 75, 659–674. [Google Scholar]
- Arefi, M.; Kiani, M.; Civalek, O. 3-D magneto-electro-thermal analysis of layered nanoplate including porous core nanoplate and piezomagnetic face-sheets. Appl. Phy. A 2020, 126, 76. [Google Scholar] [CrossRef]
- Guo, H.; Zhuang, X.; Rabczuk, T. A deep collocation method for the bending analysis of Kirchhoff plate. Mater. Contin. 2019, 59, 433–456. [Google Scholar] [CrossRef]
- Zhuang, X.; Guo, H.; Alajlan, N.; Zhu, H.; Rabczuk, T. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur. J. Mech.-A/Solids 2021, 87, 104225. [Google Scholar] [CrossRef]
- Zhen, W.; Cheung, Y.K.; Lo, S.; Wanji, C. On the thermal expansion effects in the transverse direction of laminated composite plates by means of a global–local higher-order model. Int. J. Mech. Sci. 2010, 52, 970–981. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced dynamic thermal vibration of thick functionally graded material plates with nonlinear varied shear and third-order shear deformation theory. Symmetry 2025, 17, 851. [Google Scholar] [CrossRef]


| (1/mm2) | GDQ Grids | ||||
|---|---|---|---|---|---|
| = 0.5 | = 1 | = 2 | |||
| 0.925925 | 10 | 7 × 7 | –0.105900 | –0.134211 | 0.183353 |
| 9 × 9 | –0.105718 | –0.133953 | 0.183347 | ||
| 11 × 11 | –0.105725 | –0.133966 | 0.183396 | ||
| 13 × 13 | –0.105720 | –0.133975 | 0.183327 | ||
| 5 | 7 × 7 | 0.143114 | –0.021353 | 0.032313 | |
| 9 × 9 | 0.140667 | –0.021401 | 0.032365 | ||
| 11 × 11 | 0.140681 | –0.021401 | 0.032373 | ||
| 13 × 13 | 0.140711 | –0.021400 | 0.032354 | ||
| 0 | 10 | 7 × 7 | 0.010220 | –0.000465 | 0.011511 |
| 9 × 9 | 0.010220 | –0.000465 | 0.011509 | ||
| 11 × 11 | 0.010220 | –0.000465 | 0.011509 | ||
| 13 × 13 | 0.010220 | –0.000465 | 0.011509 | ||
| 5 | 7 × 7 | 0.001389 | 0.009798 | 0.002504 | |
| 9 × 9 | 0.001389 | 0.009800 | 0.002504 | ||
| 11 × 11 | 0.001389 | 0.009800 | 0.002504 | ||
| 13 × 13 | 0.001389 | 0.009800 | 0.002504 | ||
| Constituent Material | ||||||
|---|---|---|---|---|---|---|
| SUS304 | (Pa) | 201.04 × 109 | 0 | 3.079 × 10−4 | −6.534 × 10−7 | 0 |
| 0.3262 | 0 | −2.002 × 10−4 | 3.797 × 10−7 | 0 | ||
| (Kg/m3) | 8166 | 0 | 0 | 0 | 0 | |
| (K−1) | 12.33 × 10−6 | 0 | 8.086 × 10−4 | 0 | 0 | |
| (W/(mK)) | 15.379 | 0 | 0 | 0 | 0 | |
| (J/(KgK)) | 496.56 | 0 | −1.151 × 10−3 | 1.636 × 10−6 | −5.863 × 10−10 | |
| Si3N4 | (Pa) | 348.43 × 109 | 0 | −3.70 × 10−4 | 2.16 × 10−7 | −8.946 × 10−11 |
| 0.24 | 0 | 0 | 0 | 0 | ||
| (Kg/m3) | 2370 | 0 | 0 | 0 | 0 | |
| (K−1) | 5.8723 × 10−6 | 0 | 9.095 × 10−4 | 0 | 0 | |
| (W/(mK)) | 13.723 | 0 | 0 | 0 | 0 | |
| (J/(KgK)) | 555.11 | 0 | 1.016 × 10−3 | 2.92 × 10−7 | −1.67 × 10−10 |
(1/mm2) | (1/s) | ||||||
|---|---|---|---|---|---|---|---|
| T = 1 K | T = 100 K | T = 300 K | T = 600 K | T = 1000 K | |||
| 5 | 0.5 | 0.9259250 | 0.017753 0.030261 | 0.019616 0.042820 | 0.002242 0.017373 | 0.002483 0.018059 | 0.003476 0.019515 |
| 1 | 0.9259250 | 0.018323 0.017553 | 0.015267 0.017667 | 0.001043 0.032885 | 0.001225 0.018680 | 0.034586 0.020544 | |
| 2 | 0.9259250 | 0.001478 0.018310 | 0.005019 0.035069 | 0.007050 0.018562 | 0.006940 0.019306 | 0.022372 0.021639 | |
| 10 | 0.9259250 | 0.002686 0.019477 | 0.002724 0.041641 | 0.002792 0.019424 | 0.002914 0.020212 | 0.003098 0.023438 | |
| 8 | 0.5 | 0.9259250 | 0.027982 0.068177 | 0.002177 0.028099 | 0.001361 0.048065 | 0.001483 0.029955 | 0.056226 0.031924 |
| 1 | 0.9259250 | 0.002221 0.028821 | 0.001572 0.029106 | 0.000686 0.029721 | 0.000802 0.030896 | 0.033925 0.064964 | |
| 2 | 0.9259250 | 0.000954 0.030012 | 0.005579 0.030189 | 0.007748 0.030672 | 0.007564 0.074640 | 0.002882 0.035115 | |
| 10 | 0.9259250 | 0.001917 0.031958 | 0.001944 0.031918 | 0.001991 0.032147 | 0.002079 0.033439 | 0.002210 0.038010 | |
| 10 | 0.5 | 0.9259250 | 0.002178 0.071210 | 0.001683 0.033721 | 0.001090 0.034853 | 0.001186 0.036169 | 0.046005 0.061677 |
| 1 | 0.9259250 | 0.001709 0.034198 | 0.001251 0.034778 | 0.000556 0.035819 | 0.000649 0.037175 | 0.040729 0.038822 | |
| 2 | 0.9259250 | 0.000770 0.035435 | 0.005767 0.035926 | 0.007701 0.036853 | 0.007537 0.038253 | 0.002178 0.040465 | |
| 10 | 0.9259250 | 0.001585 0.037492 | 0.001608 0.037801 | 0.001647 0.038502 | 0.001720 0.076383 | 0.001828 0.043298 | |
| Location | Constraints |
|---|---|
| i = 1 | |
| i = N | |
| j = 1 | |
| j = M |
| Parameter Values | Physical Rationale |
|---|---|
| T = 1 K, 100 K, 300 K, 600 K, 1000 K | environmental temperature |
| = 0.1, 0.2, 0.5, 1, 2, 5, 10 | power-law index of FGM |
| = 5, 10 | length-to-thickness ratio |
| = 1.2 mm | thickness |
| = 0/mm2, 0.925925/mm2 | coefficient term for TSDT displacement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.-C. Advanced Dynamic Responses of Thick FGM Spherical Shells Analyzed Using TSDT Under Thermal Vibration. Computation 2025, 13, 245. https://doi.org/10.3390/computation13100245
Hong C-C. Advanced Dynamic Responses of Thick FGM Spherical Shells Analyzed Using TSDT Under Thermal Vibration. Computation. 2025; 13(10):245. https://doi.org/10.3390/computation13100245
Chicago/Turabian StyleHong, Chih-Chiang. 2025. "Advanced Dynamic Responses of Thick FGM Spherical Shells Analyzed Using TSDT Under Thermal Vibration" Computation 13, no. 10: 245. https://doi.org/10.3390/computation13100245
APA StyleHong, C.-C. (2025). Advanced Dynamic Responses of Thick FGM Spherical Shells Analyzed Using TSDT Under Thermal Vibration. Computation, 13(10), 245. https://doi.org/10.3390/computation13100245







