Mechanical Evaluation of Topologically Optimized Shin Pads with Advanced Composite Materials: Assessment of the Impact Properties Utilizing Finite Element Analysis

Abstract

In this paper, the evaluation of the mechanical performance of novel, designed topologically optimized shin pads with advanced materials will be conducted with the aid of Finite Element Analysis (FEA) to assess the endurance of the final structure on impact phenomena extracted from actual real-life data acquired from contact sports. The main focus of the developed prototype is to have high-enough energy absorption capabilities and vibration isolation properties, crucial for the development of trustworthy protective equipment. The insertion of advanced materials with controlled weight fractions and lattice geometries aims to strategically improve those properties and provide tailored characteristics similar to the actual human skeleton. The final design is expected to be used as standalone protective equipment for athletes or as a protective shield for the development of human lower limb prosthetics. In this context, computational investigation of the dynamic mechanical response was conducted by replicating a real-life phenomenon of the impact during a contact sport in a median condition of a stud kick impact and an extreme case scenario to assess the dynamic response under shock-absorption conditions and the final design’s structural integrity by taking into consideration the injury prevention capabilities. The results demonstrate that the proposed lattice geometries positively influence the injury prevention capabilities by converting a severe injury to light one, especially in the gyroid structure where the prototype presented a unified pattern of stress distribution and a higher reduction in the transmitted force. The incorporation of the PA-12 matrix reinforced with the reused ground tire rubber results in a structure with high enough overall strength and crucial modifications on the absorption and damping capabilities vital for the integrity under dynamic conditions.

1. Introduction

Injury prevention in the sports industry is a very important aspect of research with emotional, health, and financial contributions to the sports organizations and the players. The football industry is rapidly evolving with a revenue growth rate of approximately 8–10% on a yearly basis and total produced revenue of around 40 billion euros, especially in the most prestigious European Football Leagues Associations. The total number of professional, amateur, and youth league football players is constantly on the rise, and the need for assessing and minimizing the injury risks is evident not only in the big market teams but also in the lower divisions where funding is limited [1,2]. Based on the fast-paced philosophy of modern football, the majority of those injuries (70–80% of the total injuries) refer to the lower limb region and are mainly contact injuries, varying from bruises and contusions to more serious injuries that can be caused by ligament tears and bone and tendon fractures. Roughly 60% of the aforementioned leg injuries involve below-knee injuries, mainly in the ankle region and the tibia/fibula bones [3,4,5]. Fractures in the fibula and tibia are mainly evident in football, and along with them, the danger of permanent damage to the bones, tendons, or neighboring ligaments may occur based on the severity of the injury. The injury severity is mainly split into four basic categories depending on the recovery time and complexity. In an effort to minimize contact injuries and enhance safety, the insertion of shin guards as protective equipment was included in the game of football and in other contact sports, and this equipment stands as a mandatory part of the overall athletic gear, according to the recent regulations [6,7,8,9]. In

Table 1. Different types of injuries on the tibia/fibula area and the severity of them based on the estimated recovery span on days [3,4,5,6].

Injury Severity (Recovery Time)	Injury Type	Possible Incident That Causes the Injury
Slight (1–3 days)	Irritations–Microtrauma	Repetitive number of tackles
	Shin Splints	Overuse or overstressed (Design Related)
Mild (4–7 days)	Bone Bruise/Contusion	Severe Impact
Moderate (8–28 days)	Vascular Injury/Hematoma	Severe Impact
	Bone Bruise/Contusion	Severe Impact
	Tibial Compartment Syndrome	Heavy shock blow to the tibia/fibula region
Severe (over 28 days)	Tibial Compartment Syndrome	Heavy shock blow to the tibia/fibula region
	Bone Fracture	Happens in heavy shock blow, especially if it is a stud kick

, a brief overview of the possible leg injuries in football is presented, along with their severity based on the estimated recovery timeline.

Conventionally developed injection-molded shin guards tended to minimize light to moderate contact injuries, but the bulky, heavy design did not provide enough shock absorption to mitigate the active stresses and lower the risk of more severe injuries such as bone fractures. This inability could lead to higher stress distribution and allocation to other articulations, such as the knee or the ankle, and lead to long-term permanent damage due to cumulative fatigue. As is visible from Table 1, the existing designs do not resolve the injury issue at a satisfying rate and are also responsible for the development of some minor injuries related to the wearable that could be minimized with an improved, optimized design. 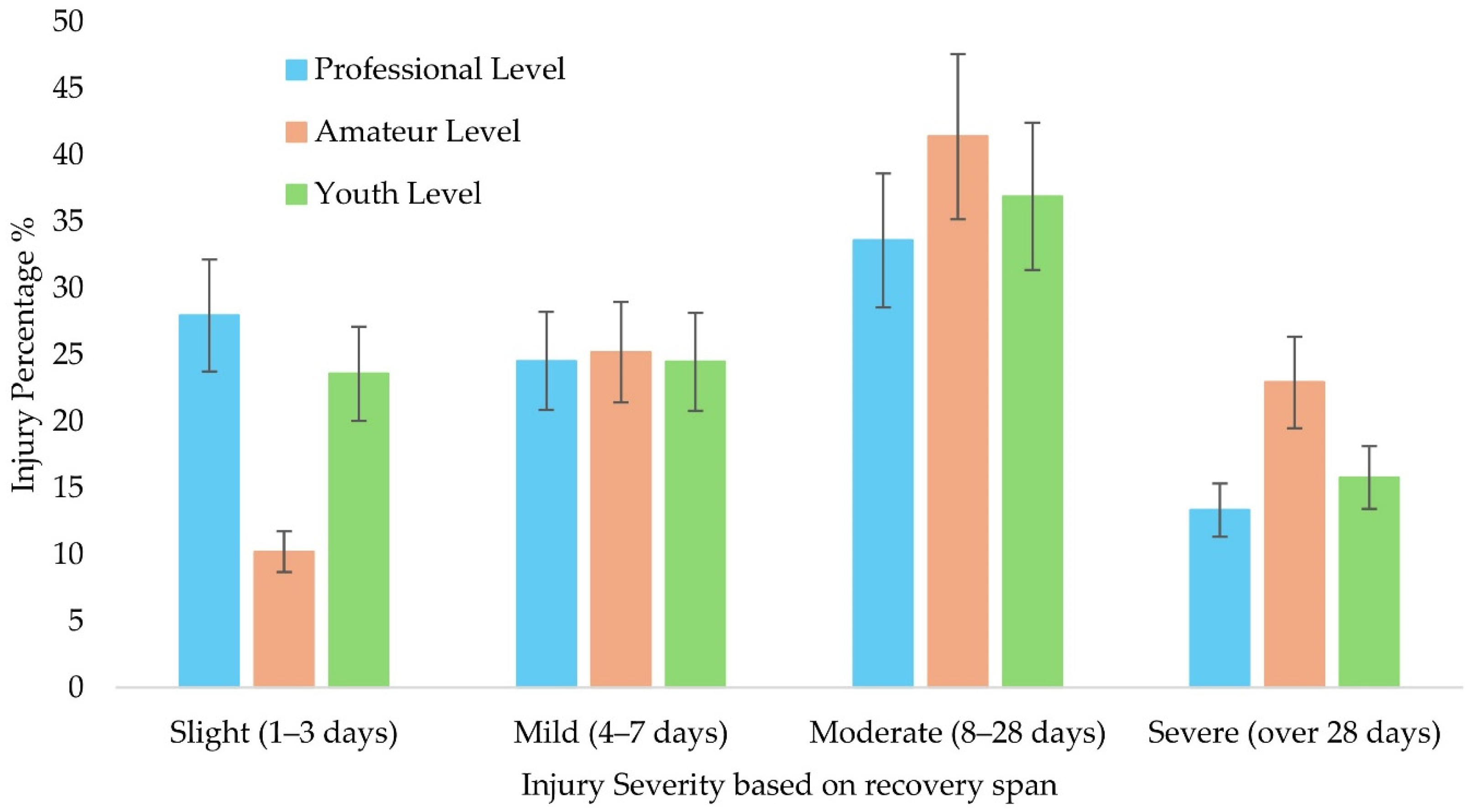In Figure 1, an overview of the different injuries’ severity allocation is presented based on the estimated recovery time according to recent metrics for the calendar year of 2023.

As is visible from Figure 1, especially in amateur-level athletes, where the emphasis on the recovery process after the activities is not the proposed one and the conditioning of the athletes is worse compared to the professional athletes, the injury risk and severity are elevated. A slight elevation in the more severe injuries is also observed in the youth-level leagues. The reevaluation and optimization of the conventionally designed shin guards could lead to a decreased number of serious injuries with results on the physical and social life of the athletes while simultaneously allowing the better development of their skill level, especially for youth players where the projected growth and potential is still higher and based mainly on the availability factor (fit for football activities) and the frequent efficient training [10,11,12,13].

In this context, many optimization strategies based on design, material selection, and manufacturing processes have been studied with the aim of providing tailored mechanical properties, shape, size, and weight for each unique athlete. Additive manufactured shin guards have been studied at the prototype level, utilizing different composite materials, with the reinforcement being mainly in fiber form (carbon, glass). The results indicated the final structure presented slightly more suitable mechanical properties regarding the overall stiffness and the impact capabilities and overall improved strength-to-weight ratio [14,15,16,17]. Besides the non-eco-friendly conventional fibers, alternatives such as the reused tire rubbers could enhance the damping and the energy absorption capabilities, leading to structures that ensure maximum comfort and reduce the cases of mild injuries due to poor manufacturing while simultaneously helping address the more severe ones with effective stress distribution, as it was shown in the previous literature [18,19,20,21].

It was also observed that in all cases, the initial bulk solid design was inadequate for constant use, and therefore strategic material removal processes (density-based removal or truss-based removal) for the development of repetitive geometric patterns were analyzed, with the ultimate goal of achieving a lightweight structure with maximized performance metrics compatible and tailored for the demands of the high-strength shock impacts. This process is widely known as topology optimization, with many applications in industrial processes and products in the automotive and aerospace industries. Lattice geometries have proved to enhance the structure’s elasticity and result in more unified stress distribution and energy absorption efficiency, especially in the case of the Triply Periodic Minimal Surface (TPMS) structures. Combined with high-precision manufacturing techniques that allow the rapid transformation of a design to a prototype, could help enhance the compatibility of this structure to the human leg, allowing maximum comfort due to light bumps and high crashworthiness in the more extreme cases of hits, such as the stud kicks incidents in competitive games [22,23,24].

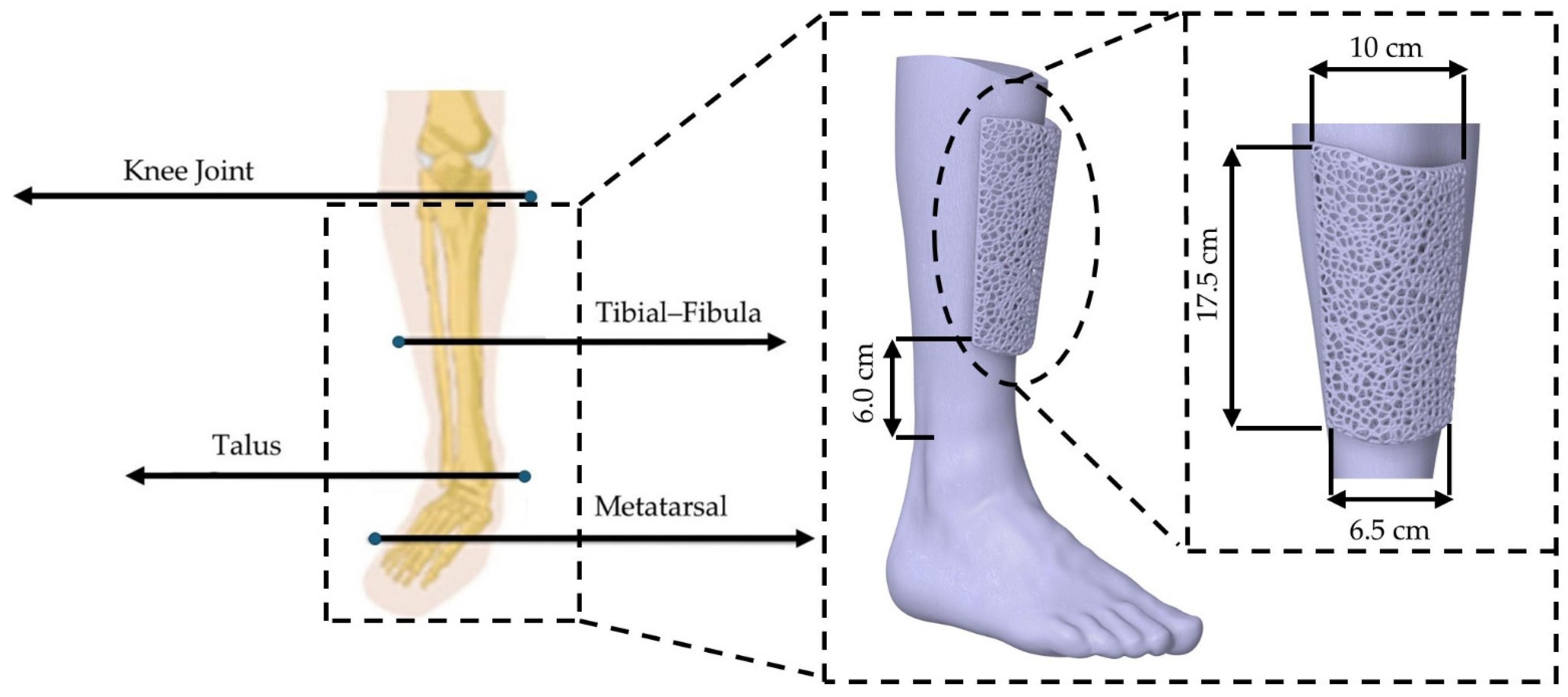
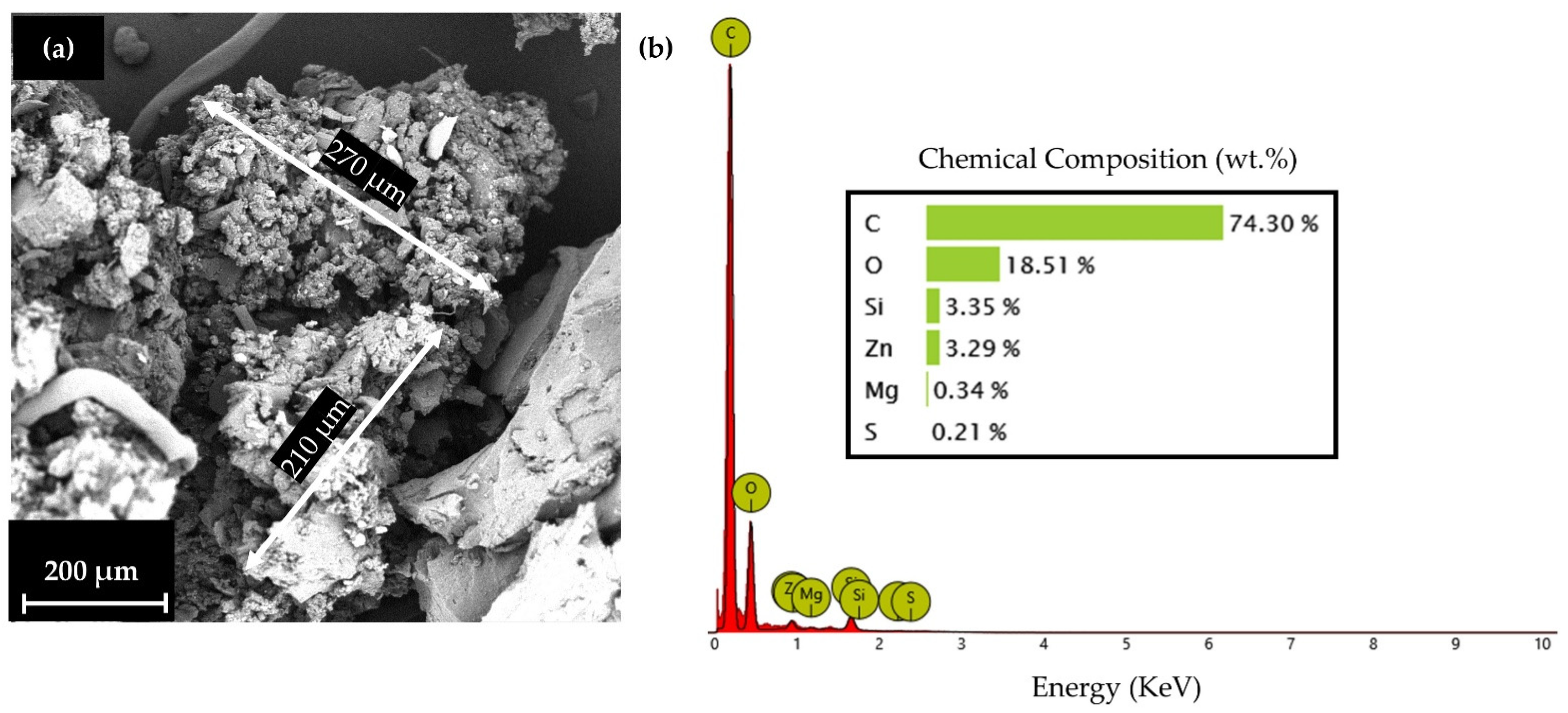
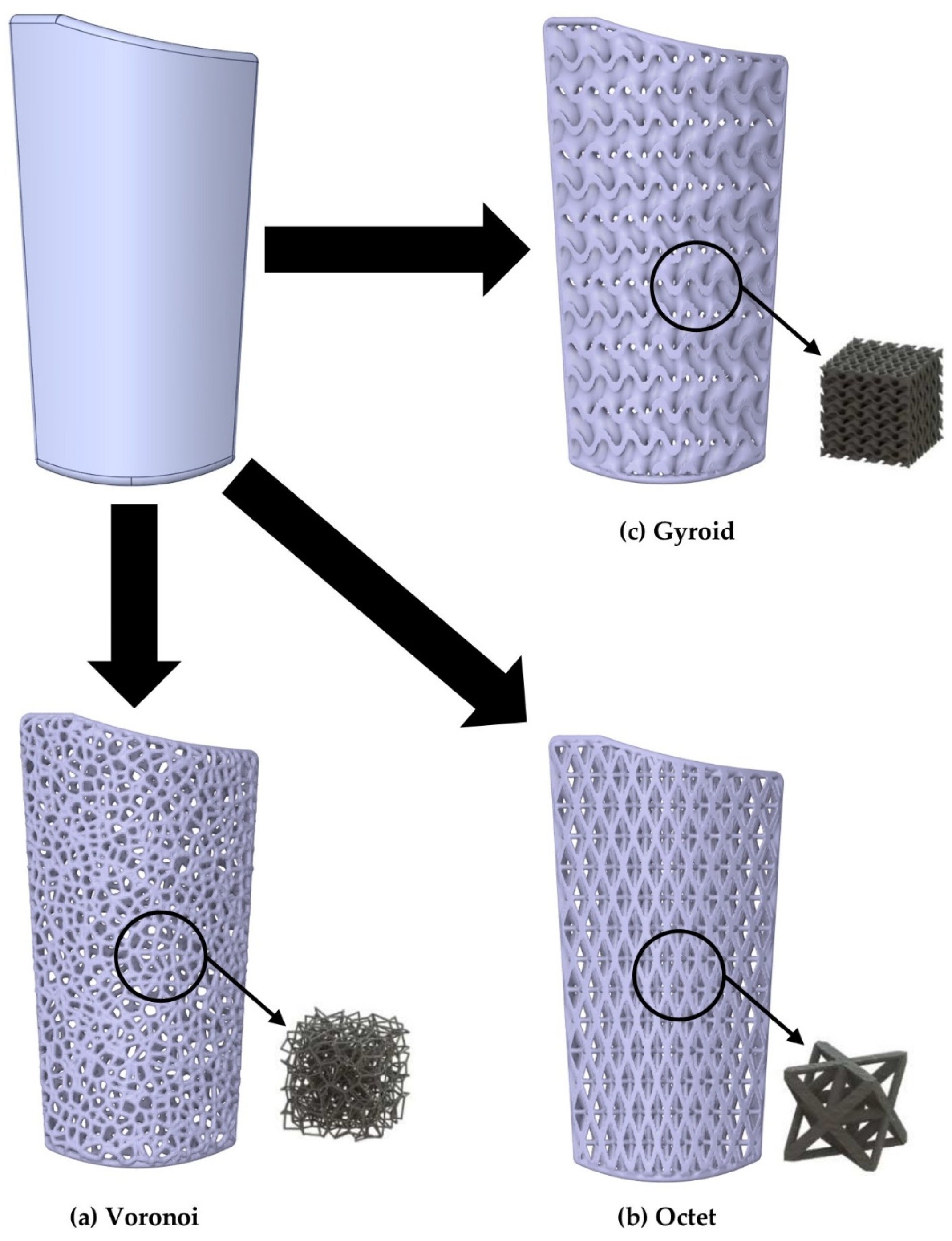
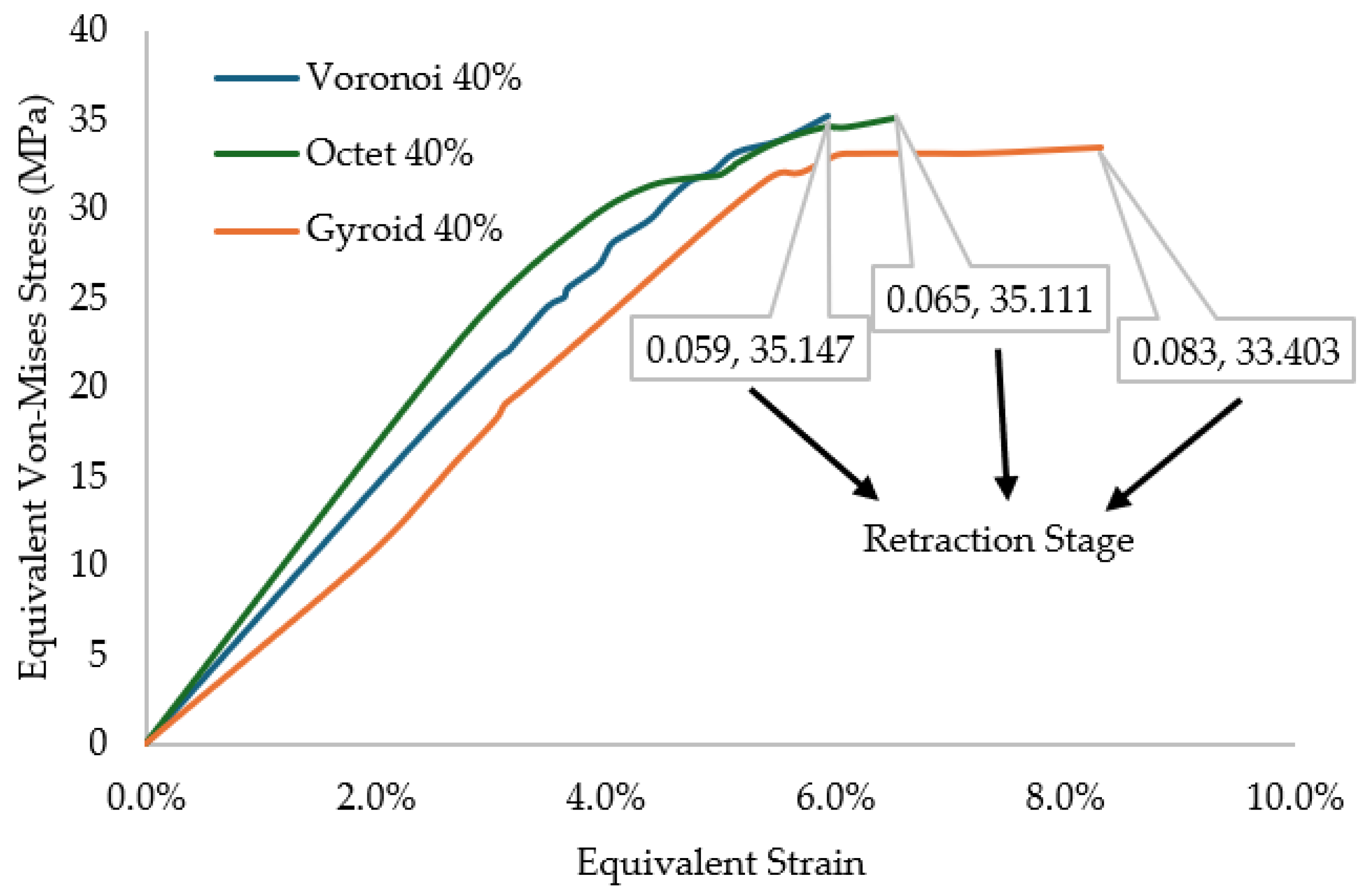
In this paper, a computational investigation of topologically optimized shin guards is conducted to assess the optimal lattice geometry with a focus on efficient impact absorption and damping capabilities, ensuring maximum comfort and minimization of severe tibia-fibula injuries due to hard kicks on the regions during sports activities. In this context, an initial draft bulk design was designed aligned with the shape of an average male athlete’s leg, and with the aid of 3D scanning, three different lattice geometries, (2.5D Voronoi, Strut Octet, and TPMS gyroid) were utilized for the customized prototypes on the same relative density (40%), which was confirmed in previous cases as the solution for optimal energy absorption combined with adequate enough overall strength. For the material selection, a PA-12-based composite was selected with ground tire rubber (GTR) insertion of 10 wt.%. The GTR insertion was proved in a different study that improved crucial elasticity properties, and the matrix material presented similar mechanical properties to other thermoplastics that were already studied in the literature [14,15,19,21,22,24]. The three aforementioned prototypes underwent impact testing with the aid of Finite Element Analysis (FEA) to assess the dynamic mechanical response in real-life based scenarios in the extreme case of a stud kick to the shin area, which was described as the condition where the maximum forces were generated. An assessment of the overall stresses and the distribution of those was conducted, providing valuable insights regarding the structures’ elasticity, force tolerance, energy dissipation, and shock absorption properties. The results indicated that the gyroid structure shin guard presented the most unified stress distributions and ensured the maximum comfort and safety and was proposed as the go-to solution in this use case. The novelty in this paper lies in the proper material selection that can promote environmental sustainability, the utilization of complex lattice geometries for the provision of tailored dynamic properties, and the real-life simulation of the stud’s kick impact testing, providing results that can be used directly for possible upcycling with rapid manufacturing technologies such as 3D printing. An indicative flowchart of this current study is presented in Figure 2.

2. Materials and Methods

2.1. Design Conceptualization

To study the effect of the different lattice geometries, an initial draft solid prototype was developed. To accurately replicate the angles on the tibial region and design a draft with an exact fit, a 3D scan of an amateur football player’s leg was conducted with the aid of an Artec Eva™ 3D scanner (Artec 3D, Luxembourg, Luxembourg), and the raw data were converted to a compatible 3D CAD design file (3D Slicer, Version 5.6.2.). The Artec Eva™ has an accuracy of 0.1 mm for small to medium-sized objects. To achieve the maximum precision and the accurate illustration of the leg’s morphology, the high-definition data acquisition mode was utilized, capturing 18 million points per second at a scanning speed of 16 frames per second. The metrics were then compared to benchmarks regarding the dimensions and the morphology of the average shin regions in male athletes in order to assess the size of the proposed shin guards based on the existing market. In this case, a medium-sized shin guard was selected and designed with the aid of Solidworks ™ Version PDM 2023 (Dassault Systemes SE, Vélizy-Villacoublay, France) as a preliminary design. Players in the wide attacking positions have to face the maximum number of challenges. The average winger in today’s game has a median height of 1.71–1.75 m, and his weight varies between 65 and 70 kg. The shin guard’s height was measured at 16.5 cm, and the maximum length was 10 cm, narrowed down to 6.5 cm in the calf region below. According to the analytics, the optimal way to wear shin guards is inside the sock and at a placement around 5–7 cm above the ankle in the interface between the talus area and the tibial-fibula area [25,26,27]. In Figure 3, the expected fit of the proposed shin guard models on the tibial region is illustrated; as a reference point, the model with the Voronoi lattice geometries is presented. The metrics of the human leg were taken from an amateur football player and are presented in

Table A1. Athlete’s main metrics.

Position	Left Winger (LW)
Height (cm)	173
Weight (kg)	67
Knee-Ground Height (cm)	52
Ankle Height (cm)	10
Shin Height (cm)	29
Calve Perimeter (cm)	37
Below Calve Perimeter (cm)	22

in Appendix A.

2.2. Materials

To develop an appropriate material model, an experimental analysis of the filler effect was conducted in a previous study. The selected reinforcement is an acquired waste ground tire rubber (RETIRE ABEE, Drama, Greece), which presented positive effects as a filler material regarding the energy absorption and the damping capabilities. Since the rubber’s effect is not studied in this case study, the weight fraction of 10 wt.% was selected as it was proven as optimal in previous cases where energy dissipation capabilities were demanded. The process consisted of shredding, removing inadequate additives, such as steel wires, and milling the remaining rubber into appropriate shape and size particles for further exploitation with advanced manufacturing technologies. In Figure 4, a preliminary analysis of the filler was conducted with the aid of the Phenom ProX (Thermo Fisher Scientific, Waltham, MA, USA) scanning electron microscope (SEM).

2.3. Topological Optimization

The insertion of the proposed lattice geometries was performed with the aid of nTopology™ Version 5.9.2 (nTopology Inc., New York, NY, USA). A 2.5D lattice geometry (Voronoi), a strut-based (octet) structure, and a triply periodic mimical surface (TPMS) (gyroid) structure were selected in this use case. Generally, in the development of architected materials, the ideal relative densities vary based on the different types of lattice structures. Densities above 60% tend to present minimal changes in the properties of the final structure compared to a 100% solid one, while relative densities below 20% tend to present foam-like behavior [24,28]. The optimization process’s objective function was to minimize the transmitted force and achieve the maximum energy absorption (EA) per unit cell. The optimization constraints were the material’s failure limits and the design constraints according to the European standard for protective equipment regarding performance and safety [29]. A generic algorithm (GA) with the following objective functions was developed as follows:

$$\max \mathrm{f}(\mathrm{r}.\mathrm{d}.)={\mathrm{E}\mathrm{A}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}(\mathrm{r}.\mathrm{d}.)$$

(1)

$$\min \mathrm{f}(\mathrm{r}.\mathrm{d}.)={\mathrm{F}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{e}\mathrm{d}}(\mathrm{r}.\mathrm{d}.)$$

(2)

where r.d. is applied relative density of each lattice geometry and the following constraints:

$$\mathsf{\sigma }(\mathrm{r}.\mathrm{d}.)<{\mathsf{\sigma }}_{\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}},\mathrm{V}(\mathrm{r}.\mathrm{d}.)<{\mathrm{V}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$$

where σ(r.d.) is the projected unit cells developed stress and V(r.d.) the projected volume of the optimized design. Based on the GA, an average of 40–45% relative density was selected for all cases in order to efficiently observe the effects of each type of architected material with conformal design in order not to modify the angularity of the bulk prototype, which was designed based on the curvature of the shin region. In

Table 2. Final metrics of the proposed prototypes.

Prototype	Bulk Mass/Final Mass (g)	Relative Density (%)	Unit Cell Length (mm)	Strut/Wall Thickness (mm)
Voronoi Shin Guard	111/50	41	20	2.20
Octet Shin Guard	111/55	44	20	2.90
Gyroid Shin Guard	111/56	45	5	2.35

, the main critical metrics regarding the wall thickness and the length of the unit cell for each structure are presented, and in Figure 5, an illustration of the overall final prototypes is provided.

2.4. Finite Element Analysis

The final optimized design was evaluated with the aid of ANSYS™ Version 2024 R2 (ANSYS, Inc., Canonsburg, PA, USA) in loads reflecting those of a stud kick in a football match, which was proved to be the ultimate integrity test regarding this specific use case. The optimized prototypes were inserted and attached to the scanned leg, and with the aid of the explicit dynamics model, the impact process of the kick was accurately simulated. Regarding the material model, an equivalent unit cell was produced, and the material properties were calculated with the aid of the Material Designer tool in ANSYS ™ Version 2024 R2, and a Representative Volume Element (RVE) of the proposed composite (PA-12/GTR 10 wt.%) was constructed. The proposed material presented similar properties in all 3 axes (x, y, and z), and therefore, the isotropic elasticity model was utilized in this case. The developed models were inserted into an explicit dynamics model that accurately simulated the process of the kick in the shin guard area. For the material model, experimental identification of the mechanical response and the properties of the microstructure was already conducted [24,28].

2.5. Evaluation of the Boundary Conditions and the Prototype’s Performance

For the development of the impact study, an explicit dynamics model was developed with the aid of ANSYS™ Version 2024 R2 (ANSYS, Inc., Canonsburg, PA, USA). Regarding the boundary conditions, the leg was considered the fixed area since, during the impact, the leg is, in most cases, on the ground. Also, this situation is the one where the leg and the shin guard have to tolerate the whole impact energy compared to cases where the foot is off the ground. To recreate the kicking motion, an impactor with studs was created. The average metallic stud diameter is around 3 mm, and the average impactor’s speed is around 3 m/s in the case of a football kick, according to the European standard for protective equipment (EN 13601:2009) [29]. The translated contact speed was calculated with the aid of the following equation:

$${\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{t}}={\displaystyle \frac{{\mathrm{m}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}·{\mathrm{V}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}+{\mathrm{m}}_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{n}}·{\mathrm{V}}_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{n}}}{{\mathrm{m}}_{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}+{\mathrm{m}}_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{n}}}}\mathrm{m}/\mathrm{s}$$

(3)

In this equation, the leg’s velocity (V_shin) is considered 0 since the leg in this case is considered stable on the ground. The impactor’s velocity (V_impactor) and the effective mass (m_impactor) have been considered to be the whole leg area since the impactor is on the move in a motion replicating a tackle towards the ball that ended by hitting the shin instead. The overall energy that was transmitted to the leg and not absorbed by the pad is translated into the equivalent forces on the tibial area with the aid of the following equation:

$${\mathrm{F}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}}={\displaystyle \frac{{\mathrm{E}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}}}{{\mathrm{d}}_{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\text{-}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{e}}}}={\displaystyle \frac{{\mathrm{E}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{l}}-{\mathrm{E}}_{\mathrm{p}\mathrm{a}\mathrm{d}}}{{\mathrm{d}}_{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\text{-}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{u}\mathrm{e}}}}\mathrm{N}$$

(4)

where E_internal is the overall energy generated by the system during the impact process and E_pad is the energy that was absorbed by the shin guard. For the soft-tissue deformation, according to the literature, this value ranges between 3.5 and 6 mm, and it presents minimal variation regardless of the impact’s intensity; therefore, a median value of 4 mm was taken into consideration for this use case. Accurate modeling of the soft tissue would result in excessive computational cost due to the high number of required elements. Therefore, some key bone and tissue properties were incorporated to develop the simplified leg model for the shin-guard fit, as illustrated previously in Figure 3. In general, the average bone consists of the solid outer part and the inner bone marrow, but for the development of the material model, an average unified bone was selected, in accordance with relevant studies regarding the mechanical response of the tibial and fibula bones [30,31,32]. In

Table 3. Shin regions components crucial properties [30,31,32].

Component	Young’s Modulus (MPa)	Yield Strength (MPa)	Fracture Stress (MPa)
Tibial Bone	1393 ± 123	95 ± 8	155 ± 12
Fibula Bone	1287 ± 116	69 ± 6	127 ± 11
Soft Skin Tissue	0.2 ± 0.04	-	7.6 ± 0.8

, some key metrics regarding the leg properties and the soft tissue properties that were utilized for the material model are presented.

The transmitted force is compared to the tibia’s tolerance to compare the possible injuries after the impact and evaluate the performance of the guard based on the provided safety for the user. According to the literature, the maximum tolerated force of the tibial bone is around 3000 N [33,34,35,36]. In

Table 4. Injury aggravation based on calculated transmitted forces [6,10,11,32].

Transmitted Force (N)	Injury Severity	Possible Injury
0–400	Slight	Mild Pain
401–1000	Mild	Contusion
1001–3000	Moderate	Tissue Damage
3001+	Severe	Fracture

, a benchmark of the possible injuries after the impact is presented based on the equivalent transmitted forces on the shin region.

3. Results

3.1. Material Model and Mesh Generation Process

To identify the material model, a study on the microstructure with the aid of the material designer was conducted. For the precise description of the rubber particles’ distribution, the short fibers model was utilized after taking into consideration the SEM analysis of Figure 4 with a particle range deviation of 200–300 μm and a weight fraction of 10 wt.%. In

Table 5. Main mechanical properties of the PA-12/GTR 10 wt.% representative volume element unit cell.

Property Direction	Young’s Modulus (E), MPa	Shear Modulus (G), MPa	Poisson’s Ratio	Yield Strength (σ), MPa
X-axis	1224.1	440.62	0.389	29.9
Y-axis	1218.0	440.69	0.381	30.3
Z-axis	1224.9	442.78	0.383	30.2

, the results of the material model development are presented regarding the Young’s modulus, the shear modulus, and the Poisson ratio to assess the final material behavior of the proposed composite. Based on the provided info regarding the material properties, the matrix and reinforcements morphology, and the distribution of the reinforcement inside the unit cell, the material designer automatically generated those estimated properties in all three dimensions (x, y, and z). The z-axis was considered to be the anterior–posterior direction (impact direction), the x-axis is the longitudinal direction of the shin, and the y-axis was considered to be the lateral direction across the leg. The comparison of those properties in all three dimensions could provide feedback regarding the degree of homogeneity and the isotropic or anisotropic nature of the final composite.

The results from Table 5 indicate that the composites’ behavior approaches isotropic standards with minimal deviations due to anisotropies (less than 10%). Therefore, the isotropic elasticity model was utilized in this use case. For the extraction of mesh-independent results, an evaluation of the equivalent von Mises stresses compared to the total number of elements was conducted in order to achieve the optimal mesh to eliminate stress singularities. An indicative example of the mesh convergence process for the Voronoi Shin Guards is presented in Figure 6.

From Figure 6, it is hinted that the convergence region is around the mark of 130,000 to 200,000 total elements. The deviation of the developed von Mises stress value was below 5%, and a plateau is observed in this region. Therefore, a median value of 150,000 was selected in this case. A similar procedure was followed in all cases. Regarding the mesh concentration, the main Region of Interest (ROI) was selected to be the triple point between the impactor, the shin guard, and the outer skin of the leg in the shin region. To ensure that in all cases the worst-case scenario is taken into consideration, the whole leg was set as fixed to the ground, replicating a challenge on the standing leg, therefore ensuring that all generated forces would be present in the ROI. Finer mesh was selected on the shin guard since complex lattice geometries were applied, and the contact area between the guard and the leg was used to determine the developed forces in the structure and the human leg. The mesh for the impactor was rougher in order to replicate the geometry of the football shoe studs, which are designed to make micro-punctures to the pitch’s surface and provide stability during the player’s movement, especially in rainy conditions. In Figure 7, an illustration of the different ROIs is presented, and the mesh size for each region for the reference prototype of the Voronoi shin guard.

3.2. Finite Element Analysis Dynamic Results

3.2.1. Evaluation of the Structural Integrity According to the European Standards

For the evaluation of the structural integrity of the proposed shin guards, the boundary conditions regarding the impact velocity at the contact point and the duration of the stud kick were assessed with the aid of the European standard for protective equipment (EN 13601:2009) [29]. The impact velocity for the shin guard testing was set at 3 m/s, and the impact duration was set at 2 milliseconds (0.002 s). Those values present a moderate ferocity impact, describing the average conditions of a stud kick [33]. In Figure 8, the developed von Mises stresses are presented based on the equivalent elastic strain for all structures along with the equivalent finite element analysis contours.

The results of Figure 8 indicate that in all cases, a similar response is observed with mild deviations regarding mainly the elastic strain. This result was expected since similar relative density and the same basic composite were applied in all cases. The observed deviations occurred based on the different behavior of each architected material. The elastic strain at the retraction point is higher in the case of the gyroid shin guard, which was expected since TPMS structures tend to present greater elasticity due to their mild bending-dominated behavior. On the contrary, the strut octet structure presents a brittle-like and stretching-dominated behavior. This is also translated in Figure 8 by the higher overall stress at the retraction point; this value indicates that, in terms of absolute strength, the octet shin guard presents the better response. Regarding the Voronoi structure, it seems that the structure presents less overall strength and approaches a mild stretching-dominated behavior similar to the strut-type octet shin guard. Since Voronoi is a stochastic structure without a regular pattern, the behavior of the prototype could vary based on the unit cell properties (length, thickness) and the impact angle or region [28,37,38,39]. In Figure 9, the stress contours at the retraction point are presented for all three prototypes.

The contours of Figure 9 confirm the indication of a brittle-like behavior in the octet structure. This is visible from the localized stress concentrations on the impact region only. The octet structures seem to present better absolute strength, but the narrow stress distribution indicates less energy-absorbing capabilities, which could result in negative effects in terms of force mitigation and result in chronic discomfort. This inadequate absorption could lead to issues in other articulations, resulting in possible knee chondromalacia or other generic knee injuries after long-term use. In the cases of the Voronoi and the gyroid designed shin guards, a wider stress distribution is observed, meaning more unified absorption and less shock discomfort to the user due to the equivalent force reaction. In the case of the gyroid structure, the distribution is approaching a specific pattern, while in the case of the Voronoi structure, the contours tend to be more randomized. This difference is present mainly because of the different geometry type, since Voronoi does not present a specific pattern. The fact that important stress concentrations are presented at the edges of the guard indicates that the applied forces are approaching the structure’s maximum strength. In

Table 6. Overall force and work production on the system.

Shin Guard Type	Internal Energy (mJ)	Energy Absorbed (mJ)	Force Reaction (N)
Voronoi	477.68	6.13	206.23
Octet	519.56	9.69	260.81
Gyroid	600.72	67.61	217.38

, the overall forces generated during the impact and the internal energy of the system are presented.

The metrics of Table 6 confirm the minimal absorption of the Octet Shin Guard due to the structures’ stretching-dominated behavior. The energy dissipation of the Voronoi and the Octet Shin Guards is proportional to the overall energy that was generated during the impact. The gyroid shin guard seems to present higher absorption efficiency. The overall reaction force presents the generative force of the kick. Compared to the metrics of Table 4 regarding the possible injury severity, the overall forces generated could result in mild pain or bruising. This was expected since the majority of the tackles do not result in moderate or severe injuries where the player is unable to continue. Overall, all structures present suitable integrity for long-term use regarding the overall stress tolerance, something that is also indicated by the linear behavior on the stress–strain curve in Figure 8, which hints at elastic deformation.

3.2.2. Evaluation of Energy Dispersion on the Extreme Case Scenario

Besides the structural integrity of the shin guard in moderate cases, another crucial value to describe the efficacy of the prototype is the ability to reduce the number of forces transmitted to the leg by a fair amount to prevent serious injuries. Commercial shin guards present a fair force transmission reduction rate between 68 and 77% in leg breaking forces (2500–4000 N), resulting in protection from severe injuries and a reduction in those by 15–20% [2,10,12,33]. To assess the force reduction capabilities of the shin guard, an extreme case of a leg-breaking kick was conceptualized. According to sports analytics, high-intensity kicks in combat sports can reach impact velocities in the range of 7–9 m/s, with the high end mainly present in martial arts sports. For the case of the football shin guards’ efficiency, an average leg velocity of 7 m/s was utilized. To calculate the impact velocity on the shin region, Equation (3) was utilized. For the impactor’s mass, all body areas that contribute to the human motion are taken into consideration. The average lower body mass from the hip and below is equivalent to 15% of the overall body mass. Therefore, the mass of the leg region from the hip to the foot is considered as 7.5% of the total impactor’s mass. To calculate the mass on the recipient area, the overall shin region plus the shin guard’s mass were considered, and since the foot is fixed on the ground, the recipient’s velocity was set to 0 m/s. In

Table 7. Main metrics to conceptualize the extreme case scenario.

Shin Guard Type	Impactors Mass (kg)	Recipient Mass (kg)	Offenders’ Velocity (m/s)	Impact Velocity on the Shin Region (m/s)
Voronoi	5.1	1.250	7	5.63
Octet		1.255		5.61
Gyroid		1.256		5.60

, the main metrics are presented and the final impact velocity is based on Equation (3) for each specific use case scenario. The overall body mass was considered 67 kg for an average-height winger or full-back since most sliding tackle challenges tend to happen in these positions, as it was previously discussed in Section 2.1.

Since the results of Table 7 indicate that the deviation of the impact velocity for each case is minimal (less than 1%), an average impact velocity of 5.6 m/s was used in all cases for an impact duration time of 0.02 s, similar to the European Standard for protective equipment testing [29]. The results of the stress contours for the extreme case scenario are presented in Figure 10.

The results of Figure 10 indicate that in all cases, the ferocity of the impact results in permanent deformation of the structure, which is visible by the plateau in all three curves in the elastic strain of 3.5–4.5% based on each case. As expected, the gyroid structure seems to present higher plastic deformation and slightly less stress tolerance due to its bending-dominated nature. The Voronoi structure seems to present minimal plastic deformation, and the octet structure presents a moderate plastic region. The overall stress tolerance is higher in the octet and the Voronoi structure. In Figure 11, the stress contours at the retraction point are presented for all three prototypes.

From the contours of Figure 11, it is visible that the stresses in this case have been distributed to wider shin guard areas, indicating a plastic deformation in all cases. The octet structure still presents higher localized stresses in the impact region, while in the other two cases, a more uniform stress distribution is observed. In the gyroid structure, the widespread distribution seems to follow a specific pattern, while in the Voronoi structure, the stress concentrations are widespread in random areas of the shin guard and especially on the edges of the prototype, hinting that the failure point is closer than in the other two cases. A representation of the generated internal energy and forces is briefly presented in

Table 8. Overall force and work production on the system in the extreme case scenario.

Shin Guard Type	Internal Energy (mJ)	Energy Absorbed (mJ)	Force Reaction (N)
Voronoi	3458.4	1359.1	3219.2
Octet	3662.3	1715.4	3132.8
Gyroid	3275.3	2189.9	3408.3

.

From the metrics of Table 8, it is visible that all structures have inserted a plastic deformation range, visible by the increased absorption rate in all three cases. The developed forces in all cases are above 2500–3000 N, meaning that the impact would result in a leg break in all cases. The absorption rate is again better in the gyroid structure, which is confirmed by the absolute number and the extended plastic region of Figure 10.

3.3. Performance Evaluation Overview and Comparison to the Commercial Shin Guards

To assess the overall performance of the three proposed prototypes, a calculation of injury prevention was conducted. The difference between the absorbed energy and the overall internal energy of the system from Table 8 is the energy that the shin region handled during the impact. This difference was converted to the equivalent transmitted force with the aid of Equation (4). For soft tissue deformation, a median value of 4 mm was utilized in all cases, as it was described in Section 2.5. The final transmitted forces were also compared to the overall generated forces to assess the efficiency and compare it to the commercial shin guards. The overall performance evaluation regarding injury prevention and the force reduction efficiency is presented in

Table 9. Performance overview of the proposed prototypes in leg-breaking forces.

Shin Guard Type	Unabsorbed Energy (mJ)	Transmitted Force (N)	Force Transmission Reduction (%)
Voronoi	2099.3	524.8	83.6
Octet	1946.9	486.7	84.4
Gyroid	1085.4	271.4	91.9

.

From Table 9, it is visible that all the structures present adequate force transmission reduction to the leg compared to commercial shin guards. It is also worth mentioning that the application of each prototype could lower the injury severity from a possible fracture to a less severe injury (compared with the metrics of Table 4), with significantly less recovery time and long-term effect on the athlete’s health. With a direct comparison of the final transmitted forces with Table 1, in the cases of the Voronoi and octet structure, it indicates that a potential fracture with a possible recovery time of multiple months and maybe permanent long-term effects on the health of the athlete could be converted to a mild injury such as a bone bruise or contusion with no permanent effects and an estimated recovery time of 1–2 weeks, and in the case of the gyroid structure this potential fracture could be converted to a microtrauma with an estimated recovery of several days or just some discomfort that is not ruling out the athlete from football activities completely. The influence of the lattice geometries on elasticity and absorption properties was known and also aligned with results from previous research studies. Especially for TPMS-based structures, the natural curvature in their shape leads to smooth stress reduction and fewer stress concentrations [17,28,37]. The results indicate that the application of architected materials in the case of protective sports equipment can improve the product’s efficiency and the user’s safety.

4. Conclusions

In this paper, an investigation of the dynamic behavior of topologically optimized shin guards through a computational impact response assessment was conducted. From the investigation process, the stress tolerance, the energy absorption efficiency, and the transmitted force reduction (in absolute numbers and their rate) were extracted to assess the effect of the different lattice geometries on the structural integrity of the developed prototypes, the injury prevention capabilities, and the overall efficacy regarding safety and comfort. The relative density of the prototypes was kept at 40% to ensure the influence of each different type of architected material on the overall response of the developed prototype, and for the base material, a composite of PA-12 with 10 wt.% of reused GTR was utilized. The GTR efficacy on the absorption properties was already assessed in previous research. The final prototypes presented better force reduction efficacy compared to commercial shin guards, 80–90% compared to 70–80% of the already existing ones, according to the literature around shin guard efficacy [2,33,40], and aided in the reduction in potential leg-breaking transmitted forces to forces that could result in a mild injury or some discomfort with minimal or no recovery time demand. All prototypes presented adequate stress tolerance when tested according to the European standard for football shin guards (EN 13601:2009). Overall, the results of this computational study indicate that there is potential room for further upcycling. In later stages, the development of an actual prototype to test in a lab-scale environment with the aid of impact testing (e.g., drop impact) or fatigue analysis to assess the long-term durability is an adequate intermediate step before the development of an actual pair designed for youth-level players to assess it in milder physical conditions before the final developed models for professional or amateur adult athletes. Also, possible fracture analysis on conditions beyond the failure point could provide valuable information for different use cases or for analyzing the long-term efficacy and expected life cycle of the proposed designs.