Abstract
Customised orthotic insoles play a critical role in addressing foot pathologies and improving comfort and biomechanical alignment for patients with specific needs. The use of 3D printing technology for the manufacturing of orthotic insoles has received considerable attention in recent years due to its potential for customisation, rapid prototyping, and cost-effectiveness. This paper presents the implementation of an algorithm purposely developed to generate an Additive Manufacturing File (AMF) containing the geometry of a patient-specific insole and the stiffness distribution based on pressure analysis from a baropodometric board. The generated file is used to 3D print via Fused Deposition Modelling an insole with a variable infill percentage depending on the pressure distribution on the patient’s foot. Three inputs are used as source data for the AMF file coding: (i) the 3D model that defines the geometry of the insole designed by the orthopaedist; (ii) the pressure map of the patient’s feet obtained with a baropodometric board; and (iii) the stiffness of the material that will be used to fabricate the insole. The proposed approach allows the fabrication of a patient-specific insole, capable of restoring the correct pressure distribution on the foot by varying the infill percentage. Two types of insoles were successfully fabricated using the implemented algorithm: the first was 3D printed, adding a top layer to be ready-to-use; the second was 3D printed without a top surface to be further customised with different coatings. The method described in this paper is robust for the fabrication of customised insoles and aims at overcoming the limitations of the traditional approach based on milling machining (e.g., time, costs, and path planning) since it can be easily integrated into any orthopaedic workshop.
1. Introduction
The orthopaedic insole is a medical device designed to modify the articular relationships of the foot by acting on the sole to achieve a morpho-structural balance of the limb, both in static and dynamic conditions [1,2]. The basic structure of the insole is composed of: (a) a base that compensates for discrepancies or over-pronation in the heel, that is typically produced using a very rigid and lightweight material; (b) a shock-absorbing structure, to absorb the shock caused by walking that can be transmitted to the upper part of the body; and (c) a cover material in contact with the skin that must be biocompatible and prevent the proliferation of fungi and bacteria. There are three types of insoles: corrective, pain-relieving, and biomechanical [3]. The first is used to correct childhood diseases, as during this period, the musculoskeletal system can be easily deformed by external stresses [4]. The second type has the aim to reduce, limit, and when possible, eliminate the pain caused by a pre-existing condition in elderly patients. The third type, starting from a biomechanical analysis of the patient’s gait, aims at restoring and normalising the foot–ground contact while maintaining proper foot pronation–supination and weight transfer. This high level of customisation in orthotic design finds wide application in the treatment of diabetic feet.
The orthopaedist uses a baropodometric board [5] or insole with a planar pressure sensor [6] to analyse the footprint and the foot pressure distribution of the patient [7] and this information is used to design the insole in specific Computer Aided Design (CAD) software [7]. Successively, the orthopaedist chooses the stiffness of the insole and the material that best adapts to the treatment of the patient’s condition and the insole is then ready to be produced by milling machines.
Nowadays, insoles are fabricated by three-axis milling machines [8] from a block of Ethylene–Vinyl Acetate (EVA). EVA can be produced at various densities, and different layers can be stacked one on top of the other to obtain the desired stiffness of the insole. The orthopaedist and the patient choose the type of coating to apply on the top of the insole. This coating, if present, can be leather or antistatic fabric with silver fibres. The first is robust and thin while maintaining its biocompatibility; however, its use results in an increase in production costs and lead times. The second aims at making the material antibacterial, thus preventing the proliferation of bacteria and fungi on the fabric’s surface, while also significantly reducing unpleasant smells.
The traditional production method has limitations [9]. Firstly, an increase in the complexity of the insole geometry results in an increase in complexity in the milling machine structure (e.g., >three axes needed), with higher costs and a longer design time. Moreover, after the milling process, the insole must be post-processed using cutting and smoothing tools. Secondly, subtractive techniques have a lot of manufacturing waste that cannot be used to produce a new object. Additionally, the insole has different stiffness in different zones depending on pathologies, and to achieve this, the orthopaedist has to combine multiple materials together.
A promising approach is offered by additive manufacturing (AM) technologies, also known as 3-dimensional (3D) printing, which fabricates an object by overlapping material in a layer-by-layer fashion. In this paper, we focused our attention on Fused Deposition Modelling (FDM), which offers multiple advantages in insole production. In the AM pipeline, the preparation of the 3D printing file is known as “slicing”. The slicing software takes one or more files (e.g., .obj, .stl, .3MF, .AMF) as the input, which potentially includes additional coded information in metadata, such as the infill pattern and density, as well as specifications on the material required to print the object [10]. At the end of processing, the slicer generates a specific file (e.g., in G-code format) containing the machine commands to fabricate the object with the 3D printer. Considering the insole shape, there would be no waste of material subtractive manufacturing is used. Moreover, thanks to FDM technology, the mechanical behaviour of 3D-printed objects can be modified by acting on the infill pattern and density [11,12], and there is no need for post-processing.
Indeed, 3D printing can be an alternative to the traditional manufacturing of insoles [13,14,15,16]. Srivastava et al. [17] developed a strategy to obtain the insole from 3D laser foot scanner data to model the inner structure of the insole to restore normal pressure distribution. Jafarzadeh et al. [12] used a Computed Tomography (CT) scan to create a model of the bones, ligaments, and soft tissue of a diabetic patient’s foot and, through finite elements analysis, they obtained the foot planar pressure. Subsequently, the pressure was used to calculate the correct shape of the insole and the stiffness capable of minimising foot pressure. Another approach is provided by Zuñiga et al. [18] who developed a different strategy to correct the distribution of loads on the feet of diabetic patients. They used a 3D scanner to acquire the foot geometry and used this 3D model to design an insole using Gensole [19], a web browser software for designing an insole from a 3D model of a foot. In Gensole, an insole is designed using the following workflow: Firstly, a simple model of the insole is created using a sketch, and then the sketch is extruded and modified to represent a generic standard insole. In the next step, a 3D scan of the patient’s foot and their data (such as their weight and height) are loaded and the 3D model of the foot is located by the user on the top of the insole. Depending on the part of the foot that is brought into contact with the insole, the shape of the latter is modified by the program. Finally, the software estimates the pressure distribution, divides it into groups, and the user assigns a density to each of these groups; a 3D model is calculated by the software and all the information is coded into an Additive Manufacturing File (AMF). Using Gensole, the authors created an insole that exploits the variable infill density distribution to recover the right pressure and reduce pain in patients.
Ma et al. [9] developed an insole with an adjustable gradient elastic modulus. They created an ellipsoidal structural unit; the elastic modulus can vary according to four parameters that define the geometry of a single structural element. Using different parameters for each element, a porous structure with an adjustable gradient can be designed. Interestingly, Jin et al. [20] developed a heel support for patients with lower-extremity diseases, such as Achilles tendinitis and leg length difference. This type of hybrid “partial” insole can improve biomechanical performance in planar pressure distribution and stability movement. Davia-Aracil et al. [8] developed a CAD methodology for the design and manufacturing of insoles through 3D printing. In their software, the proposed graphic interface guides the user to the design of an inner structure inside the model. This structure is used to modulate the mechanical behaviour of the insole. With this technique, the model can be hollow at a specific point or can be filled with different materials, ensuring a different density to modify cushioning properties and pressure.
In this paper, we propose a new approach for modulating the mechanical properties of a 3D printable insole, starting from a 3D model created by an orthopaedic specialist and using the pressure distribution acquired through a baropodometric board. We use these data to define the specific areas to modify the infill density [21,22] inside the insole, thus controlling stiffness [23] and re-establishing the correct foot pressure distribution. Model data are then automatically encoded in an AMF file through a purposely developed script to easily perform the 3D printing procedure with a generic 3D printing machine.
2. Materials and Methods
2.1. Data Acquisition
The initial information required for our methodology was the pressure distribution from a baropodometric analysis and a 3D model insole designed by an orthopaedist.
In this study, the planar distribution was acquired using a commercial baropodometric board. The pressure data thus obtained were not dependent on the weight of the patient and could directly be used as the input to the algorithm described in the following sections. The board software does not allow the exporting of data and foot pressure distribution, which can only be visually evaluated (a screenshot acquired from the software is visible in Figure 1). The correlation between the colour in the graph (Figure 1 section a) and the real measured pressure can be reversely computed. A screenshot of the pressure distribution (Figure 1 section a) and the colourmap (Figure 1 section b) were saved as separate images. These two images and the maximum and mean pressure (Figure 1 section c) were used as the input in a specifically developed Matlab® script to evaluate the pressure data (Section 2.3, available as Supplementary Materials).
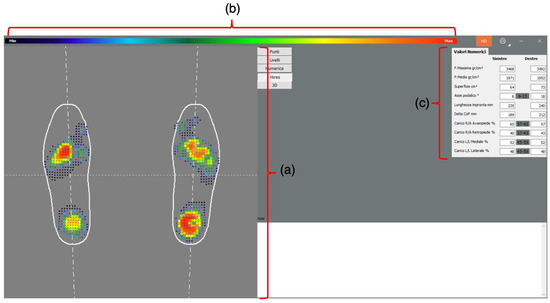
Figure 1.
A screenshot acquired from the Sensor Medica software; this image is used to evaluate the planar pressure distribution from the patient’s feet: (a) pressure distribution, (b) a colourmap used to represent the data in the graph and to estimate the relation between the graph colour and the pressure magnitude, and (c) numerical data used for the estimation.
The insole geometry was provided by an orthopaedist according to patient pathology in the Stereolithography (STL) file format. The STL file contains the definition of a closed surface that defines the volume to be 3D printed. However, usually, the insole is modelled inside software optimised for Computer Numerical Control (CNC) milling, for which the top surface definition is enough to produce an object, and thus, the insole model only contains the definition of the upper portion. Being an open surface, this model is not printable and, as a consequence, a Matlab® script was developed to make the STL file printable (Section 2.3, live script available upon reasonable request).
2.2. Mechanical Characterisation and FEM Analysis
In order to modulate the local stiffness of the insole based on the pressure in a specific area through the infill density, the mechanical properties of the material were characterised. Thermoplastic polyurethane (TPU) “Varioshore TPU” provided by colorFabb was selected to print the insole using the Satres Helios Ortho 3D printer. This material contains foaming agents activated by temperature, and the stiffness of the material can be controlled with the extrusion temperature; consequently, the higher the temperature, the softer the material will be, in a range between 200 °C and 250 °C.
The mechanical characterisation of samples printed at different temperatures was performed using a Zwick-Roell ProLine Z001 tensile testing machine equipped with a 100 N load cell, following the International Organization for Standardization. (2019). Plastics — Determination of flexural properties (ISO Standard No. 178:2019). https://www.iso.org/standard/70513.html (accessed on 30 July 2024). Three different specimens (dimensions , and ) were 3D printed, varying the extrusion temperature to 250 °C (Figure 2(a1)), 225 °C (Figure 2(a2)), and 200 °C (Figure 2(a3)), respectively, and were successively characterised through a three-point bending mechanical test with a strain rate of 1 (Figure 2b).

Figure 2.
(a) Three samples 3D printed via FDM using Varioshore TPU at different temperatures (1–250 °C, 2–225 °C, and 3–200 °C). Scale bar = 5 mm. (b) Test setup during a three-point bending mechanical test.
The equivalent elastic modulus of a 3D-printed structure was evaluated. A cubic pattern was selected (Figure 3a), composed of a cube inclined by 33 degrees with respect to the X axis and 45 degrees with respect to the Z axis of the Cartesian plane with its origin in the centre of the cube. This infill pattern was chosen to minimise the anisotropy introduced by the 3D printing process and to ensure a more uniform mechanical response of the structure, given the same infill density. Twelve specimens were printed with different percentages of infill (90%, 80% (Figure 3(b1)), 70%, 60%, 50%, 40%, 35% (Figure 3(b3)), 30%, 25%, 20%, 15%, and 10%) to test their printability. To obtain the relationship between the elastic modulus and the infill percentage, we used the finite element method (FEM). Three-dimensional models representing the infill distribution at the different infill percentages were obtained using Autodesk® Fusion 360 CAD software (Figure 3(b2,b4)); then, the Abaqus software v2022 was used to simulate a force of 1 N on the top surface and to calculate the resulting deformation (Figure 3c) for each of the 3D models previously designed.

Figure 3.
(a) An example of a cubic infill pattern; on the right side is the slicer preview of the infill pattern and on the left side is the result of the print, (b1) 3D printed specimens with an 80% infill density percentage, (b2) a CAD model representing the inner structure of the specimen at 80% infill density, (b3) 3D printed specimens with a 35% infill density percentage, and (b4) a CAD model representing the inner structure of the specimen at 35% infill density. Scale bar = 10 mm. (c) The schematic of the FEM analysis implementation on a specimen with 35% infill density: a 1 N force is applied on the top surface (blue arrow).
2.3. Data Processing
A Matlab® script was purposely developed to process the data and obtain the AMF file starting from the pressure distribution data. The input files needed were as follows:
- The images containing the pressure distribution and the colourmap to estimate the pressure values (Figure 1a).
- The STL file containing the 3D model of the insole to be printed.
- The relationship between the elastic modulus and the infill pattern density previously computed.
Subsequently, the script will return an AMF file as the output. The file will contain a description of the geometry to which unique metadata will be associated, describing portions of the insole that require a different infill density. The metadata will also include instructions regarding the infill pattern geometry to be used and the unit of measurement to use when representing the model. These data can be then processed by any slicing software.
The Matlab® script was divided into the following sub-sections:
- Loading and repairing of the STL file: the vertices and the normal vectors of the triangles that define the surface are loaded (Figure 4a). The STL files obtained from the orthopaedic CAD software (FreeStepTM 2.0 by Sensor Medica, version 2.00.010) usually only have the upper surface of the insole defined and also have discrepancies on the boundaries (Figure 4a, detail view). These defects are repaired using Laplacian smoothing with surface preservation. Subsequently, the points representing the insole surface are stored, obtaining a point cloud that defines the upper portion of the insole. Successively, a 3D volume is obtained, creating a closed surface. Accordingly, the points are projected on the X-Y plane, duplicating the point cloud and setting the Z coordinates to zero. The resulting volume is obtained by triangulation using a combination of Matlab® functions. Firstly, “alphaShape()” defines a virtual surface that completely encloses the point cloud and which can be tightened or loosened, fitting around the points using the parameter “alpha”. The best alpha value is chosen using the command “criticalAlpha” to obtain the smallest value that produces a shape with a single region. To finalise the definition of the geometry, the ‘alphaTriangulation()’ command is used to describe the volume through triangles and vertices, and the result of this operation is processed with the ‘triangulation()’ function to create the final object. The subsequent operations involve refining the obtained object with the ‘freeBoundary’ function to eliminate the ‘free edges’ of the mesh (the edges or outer boundaries of the mesh that are not shared with other elements) and with an additional Laplacian smoothing operation applied to the entire surface to remove any artefacts introduced by previous operations (Figure 4b).
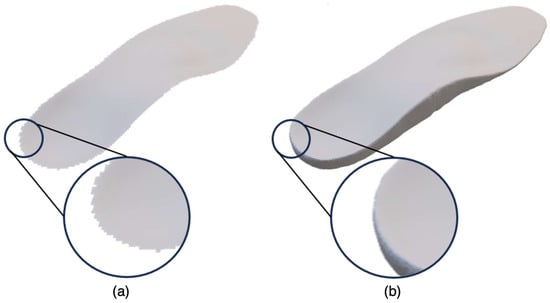 Figure 4. (a) Raw model: rendering of the STL file created by the orthopaedist that only defines the upper surface of the insole. This type of model cannot be printed since it does not describe a volume but only an open surface. (b) The repaired model after extrusion Laplacian smoothing and 3D volume reconstruction.
Figure 4. (a) Raw model: rendering of the STL file created by the orthopaedist that only defines the upper surface of the insole. This type of model cannot be printed since it does not describe a volume but only an open surface. (b) The repaired model after extrusion Laplacian smoothing and 3D volume reconstruction. - Loading of the image containing the pressure distribution: the pixels of the image (Figure 1a) are stored in three matrices according to Red Green Blue (RGB) encoding. Accordingly, data are divided into two groups, for the left and the right foot, respectively (Figure 5a). The following procedure is reported for the left foot and is then repeated for the right one. A roto-translation matrix that permits the registration of the pressure distribution to the 3D model of the insole is computed; to this end, a 2D-2D registration using singular value decomposition (SVD) is used. To perform this technique, input files must be prepared as follows: Firstly, a matrix with the same dimensions as the one containing the image data, in terms of rows and columns, is generated (Figure 5a). In the new matrix, called the ‘edge mask’, all the elements are null except for the values that encode the colour white in the original image. As an example, in the mask, the value 1 will be present only when, in the same position in the R, G, and B matrices, the value 255 is present (Figure 5b). Secondly, the non-null elements inside the ‘edge mask’ are converted into 3D points, using the position of the non-null element in terms of row and column as coordinates; for example, the element in the second row and fourth column becomes a point with coordinates x = 2 and y = 4. The final preparatory operation consists of assigning to the points that describe the insole geometry a Z coordinate equal to 0 (Figure 5c). At this point, SVD is performed to register the pressure distribution on the insole model: “A” is the matrix containing the coordinates of the point cloud describing the STL file and “B” is the matrix containing the coordinates of the point cloud obtained from pressure distribution. The coordinates of the points are coded in X, Y, and Z coordinates, where X is in the first column, Y in the second column, and Z in the last column. In both matrices, the elements of the third column are equal to zero. The initial step involves estimating the centre of gravity (), as a row vector (Equation (1)) of a point cloud “A” and subtracting it from each point within the matrix “A”, resulting in a new matrix referred to as “” (Equation (2)). “N” is the number of points belonging to “A”, “” is the i-th element of point cloud “A” and “u” is a unitary vector (N 1) used to subtract the to each “”.
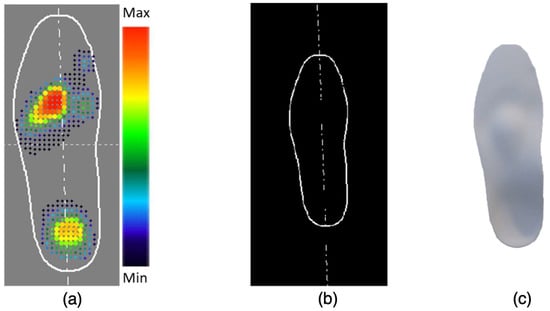 Figure 5. (a) The pressure distribution acquired from the barometric board. (b) Extraction of the white pixels from the previous image: this image is used to register the image to the STL file. (c) Rendering of the STL file to be registered.
Figure 5. (a) The pressure distribution acquired from the barometric board. (b) Extraction of the white pixels from the previous image: this image is used to register the image to the STL file. (c) Rendering of the STL file to be registered.
Subsequently, SVD is applied to the product of “” and “” yielding three matrices: “U”, “S”, and “V”. The matrix “U” is used for registration, satisfying three conditions for a roto-translation matrix. Specifically, “U” must be an identity matrix, its inverse must be equal to its transpose, and its determinant must always be one. The first two requirements are inherently met through SVD (Equation (3)).
However, the determinant of “U” may be either 1 or −1. To resolve this ambiguity, a preliminary determinant calculation is conducted. If the result is less than zero, the element in the third row and third column of the “U” matrix is negated, resulting in a matrix denoted as “UA”, ensuring a determinant equal to one. The same process is applied to matrix “B”, yielding “UB”. The rotation matrix “R”, aligning “B” to “A”, is obtained by multiplying the transposed “UB” by “UA” (Equation (4)).
- 3.
- Estimation of the pressure distribution magnitude: the image containing the colourmap (Figure 1b) is used together with the image loaded during the first step (Figure 6a). From the colourmap, a single pixel is obtained for each colour, and the two images are then loaded and stored in different matrices following the RGB coding. The three matrices thus obtained represent the colour in the pressure distribution while the colourmap is represented by three vectors. The pressure magnitude is estimated by comparing the colours in the colourmap vectors with the image representing the pressure. A new matrix is thus created and where a match is found, the index representing the correspondent colour into the colormap is written. Due to the low quality of the Figure 1 acquisition (127 × 309 pixels), there was not a complete match between the colours; therefore, the comparison was performed with a 10% tolerance (Figure 6b). At this point to obtain the values of pressure from the previous matrix, the “interp1()” function is used, and the obtained values are compared with the mean and the maximum pressure obtained from Figure 6a.
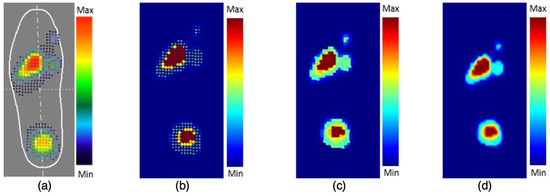 Figure 6. (a) The pressure distribution acquired from the baropodometric board software with the associated colourmap. (b) The result of the local pressure estimation from the first image. (c) The result of the densification process actuated by the algorithm described in step four. (d) The application of Gaussian filtering on the densified data.
Figure 6. (a) The pressure distribution acquired from the baropodometric board software with the associated colourmap. (b) The result of the local pressure estimation from the first image. (c) The result of the densification process actuated by the algorithm described in step four. (d) The application of Gaussian filtering on the densified data. - 4.
- Data refinement: previously obtained data are processed. Firstly, data are densified to define specific areas in the 3D model of the insole. An algorithm was developed that uses the data from the previous step as pixels in an image. The algorithm starts initialising a new empty matrix with the same dimension as the matrix containing data to be thickened; subsequently, the matrix containing data is scanned from the left to the right and from the top to the bottom. Every value greater than zero is compared with the eight adjacent “pixels” using the median operator, and the result is written in the newly created matrix in the same position as the central data. This operation is repeated for all the elements excluding the first and final row and column. The result of this operation is Figure 6c. This operation was repeated twice to obtain a uniform distribution of data. The last step of the refinement is filtering, performed to remove the artefacts resulting from interpolation. A Gaussian filter with a standard deviation equal to 2 was used to achieve the result shown in Figure 6d.
- 5.
- Data classification to create the masks: data are divided into five groups using the histogram of information refined in the previous step. A histogram with five classes with the same width is used to classify each pressure data point according to its class.
- 6.
- Conversion of the refined data pressure into 3D points: a method similar to that described in step 2 is used. During this conversion, all the points are associated with a specific class and a pressure value. Subsequently, the point cloud is registered on the 3D model using the roto-translation matrix previously obtained. At this point, five areas are defined in the 3D model using the point cloud that contains the pressure distribution and the classification, but there is no uniqueness between the points generated from pressure data and the points describing the geometry within the STL file. The points of the geometry are thus classified by taking the i-th point from the point cloud that describes the pressure distribution, finding the nearest point of geometry and assigning it the same value as the class contained in the point cloud. The comparison is repeated for all the points belonging to the previously cited point cloud. Accordingly, to create an AMF file a mesh must be created for each zone where a specific infill density is needed. Therefore, a triangulation method is used as in the first step, and it is applied to each point of the STL file with the same classification. As an example, all the points with a class number equal to 1 are selected and triangulated obtaining a new STL file that describes only the points exposed to the pressure defined into the first class. This is repeated for all the classes. At this point, there is an STL file that describes all the insole geometry and other five STL files that describe specific areas based on the applied pressure.
- 7.
- Stiffness assignment to the areas of the STL file: Equation (5) is used to determine the elastic modulus of each area.
- 8.
- Coding of the AMF file and related metadata: the functions “fopen” and “fprintf” are used to write the AMF file line by line. In the first row of the file, the file name and the unit of measurement are defined; successively, the mesh definition starts, writing all the points inside the list of unique vertices. Additionally, the entire insole geometry is described using triangles whose vertices are the points listed within the list of unique vertices. Metadata that define the cubic infill pattern and the infill density computed in the previews part are also written. This operation is repeated for all five different infill percentages defined in the previous steps; the output is an AMF file containing the 3D model of the insole and the specific infill based on the applied pressure in that area.
2.4. Slicing and 3D Printing
A slicer able to read an AMF file type is needed. Prusa Slicer was used since it can process the AMF format efficiently, reading the geometry, the type and percentage infill, and the pattern that is coded inside the file. Additionally, after the file is loaded, the percentage values displayed in a panel on the right side of the program window can be checked. Ultimately, Prusa Slicer has proven to be a winning choice due to its excellent compatibility with AMF files and its ability to make modifications to the file even at a later stage before starting the print.
The printing parameters were set to obtain the best compromise between speed and quality, and a nozzle with a 1 mm diameter was used to decrease the printing time. Two different profiles were created in order to produce the insole. The first was designed to be used immediately after printing, without any post-processing. The second profile was designed to produce an insole without the upper surface, giving the orthopaedic technician more freedom in deciding the type of coating for covering the top portion. In both cases, the same printing parameters were used, as reported in Table 1. The use of a single layer for both the bottom and top surface was primarily influenced by two factors: (i) the introduction of the minimum number of solid layers within the insole, thereby allowing for optimal modulation of the volume provided by the insole; (ii) the nozzle size used (i.e., 1 mm diameter), which allows for a greater contact area between layers with the same extruded pattern. This is due to the extruded line having a width 2.5 times greater.

Table 1.
Printing parameters for the fabrication of two different insoles (with and without top surface).
3. Results
3.1. Mechanical Characterisation and FEM Analysis
Mechanical characterisation was performed on the fifteen 3D-printed samples. The raw data from the universal testing machine were evaluated according to International Organization for Standardization. (2019). Plastics—Determination of flexural properties (ISO Standard No. 178:2019). https://www.iso.org/standard/70513.html (accessed on 30 July 2024) and linear regression was performed for each of the five specimens printed with the same temperatures (200 °C, 225 °C, and 250 °C). The results are summarised in Figure 7a.
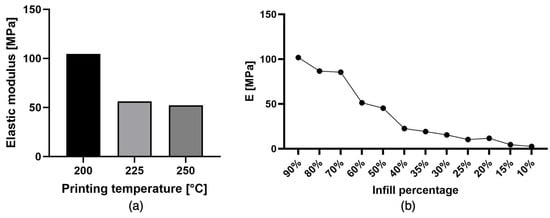
Figure 7.
(a) The average elastic moduli obtained from the mechanical characterisation of the three types of samples printed at 200 °C, 225 °C, and 250 °C. The standard deviation is 4.94 × 10−5, 4.08 × 10−5, and 1.70 × 10−5, respectively. (b) The elastic modulus trend vs. the infill density. Data are from the FEM analysis.
This characterisation provides the elastic modulus value of the material to be used for the FEM analysis. Successively, in order to obtain the widest range of elastic moduli that can be modulated by the infill density, the extrusion temperature was set at 200 °C for all subsequent tests.
The FEM analysis aims at determining how the apparent elastic modulus changes with different infill percentages. Twelve simulations were carried out, one for each infill percentage (90%, 80%, 70%, 60%, 50%, 40%, 35%, 30%, 25%, 20%, 15%, and 10%). A load of 1 N was applied to the top face of the model (Figure 3c) under quasi-static loading conditions, with a fixed boundary condition imposed on the bottom part. The resulting vertical deformation was measured, and the apparent elastic modulus was calculated for each specimen. The variation in stiffness as a function of the infill density is summarised in Figure 7b.
3.2. Data Processing
The roto-translation matrix computed during the second step of the data processing allowed for the registration of the geometry contained in the STL file to the pressure distribution. This result is achieved using the boundary of the pressure distribution image (Figure 5b) and the registration of the image is shown in Figure 8a; the insole and the boundary of pressure distribution are represented in blue and orange, respectively.
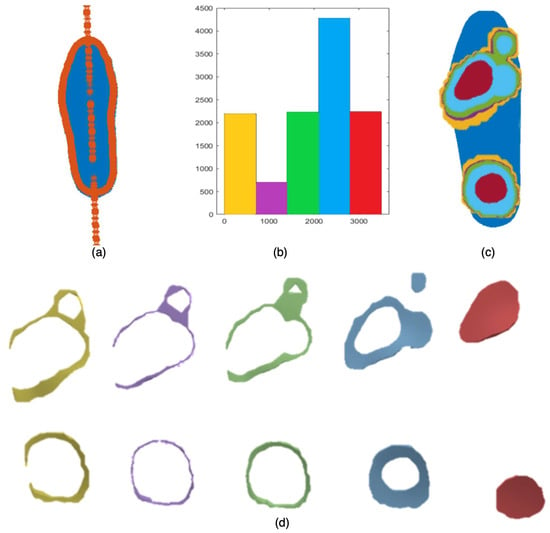
Figure 8.
(a) The result of the registration: in blue are the points from the STL file and in orange are the points from the image showing the white edge. (b) The histogram of estimated pressure from Figure 6: data are divided into five classes. (c) The classification of the points in the STL file based on the pressure group estimated in the previous step. (d) The 3D model obtained from step 6 of data processing. These five 3D models represent the location in the insole where the infill pattern will be modified based on pressure distribution.
The classification of the magnitude pressure distribution is performed by the histogram (step 5 of the data processing). The histogram divides the data into five groups (Figure 8b) and for each pressure datum, a number based on the class of membership is assigned. Following the registration and classification of the pressure data, they are used to define different zones on the insole geometry (Figure 8c). The highlighted parts of the geometry are triangulated using the methods described in steps 1 and 6 of the data processing. According to that, five STL files are created, one for each class obtained from the histogram. Finally, there are six STL files, one that represents the whole geometry and the other five that represent the different infill in each zone (Figure 8d). The AMF can be created using the five STL files that are used to define the stiffness within the insole. The infill density is calculated using Equation (5) and the percentage of infill is encoded in the metadata within the AMF file.
3.3. Slicing and 3D Printing
The slicing of the AMF file is performed by Prusa Slicer v2.8.0; the software recognises efficiently all the areas and their infill density, as shown in Figure 9a. Within this CAM preview, particular emphasis is placed on showcasing the infill pattern (depicted in red) embedded within the insole and, in particular, the different infill densities can be seen in the heel area and in the metatarsal areas; an additional visual enhancement is provided by a green layer at the bottom for enhanced clarity.

Figure 9.
(a) The CAM preview from Prusa Slicer: for visualisation purposes, a green layer is added to the bottom of the insole and the infill pattern is shown in red. (b) The insole used to refine the printing parameters: this model has all the same critical features as the heel support and the metatarsal zone. (c) The second type of insole designed to be fabricated and used immediately after printing without post-processing. (d) The third type of insole, with the inner structure exposed, that can be covered with a thin film. Scale bar = 40 mm.
Three types of insoles were printed: one for the testing and refining of the print parameters and the other two with infill density distribution controlled by the pressure distribution.
The insole shown in Figure 9b was used to determine the optimal printing parameters for rapid material extrusion. The purpose of this test insole was not to be manufactured based on pressure distribution but rather to verify that, with the parameters listed in Table 1, all critical features, such as the heel support and the metatarsal zone, were accurately produced. This section of the insole incorporates all key features, demonstrating that the additive manufacturing approach can successfully fabricate these complex elements.
Moreover, the first version of the insole was designed to be used immediately after 3D printing without post-processing (Figure 9c). The third version of the insole (Figure 9d) did not have the upper layer exposing the infill pattern and was specifically designed to be covered with a different type of material. Therefore, the insole was successfully 3D printed and maintained its shape during torsion and bending. Future developments will include testing the insoles on patients.
4. Discussion
Analysing the advantages of the algorithm proposed in the presented work, a key aspect concerns data acquisition. The patient data required for the algorithm, in fact, are acquired during a simple examination using relatively cheap equipment (e.g., a baropodometric board, priced at EUR 2000 to EUR 4000). The advantage of using this tool relies on the ability to provide all the information that the algorithm requires in a single procedure. For this reason, no other methods of acquiring the patient’s information are necessary, unlike in [12], where a CT scan was used to reconstruct bones, ligaments and tissues, or as reported in [17] where a model of the patient’s foot was obtained using a 3D scanner. The reason why only the pressure distribution is needed in our algorithm is that the orthopaedist’s experience is enough to create the best shape of the insole, ensuring the patient’s well-being. Considering alternative methods to obtain the pressure distribution of the feet, using the gait analysis reported by [7], the baropodometric board is the method that takes the least amount of time to perform the measurement and is the least invasive approach for the patient. Moreover, the proposed algorithm is fully decoupled from the material study and execution process. As it is implemented, the algorithm does not require a direct connection with the software used to estimate the apparent elastic modulus, allowing for flexibility in calculating this value. In fact, the proposed approach can also be applied to other structural problems, provided the mechanical conditions are similar to those encountered in an insole.
Another advantage of the implemented method is that FEM analysis is only used to characterise the material and not to design the insole, as reported by [12]. The FEM analysis, in fact, is here used to obtain deeper knowledge of the mechanical behaviour of the material, allowing faster computation by the software when the insole material distribution has to be computed.
Considering the additive manufacturing step for the production of orthopaedic insoles, the proposed approach based on modifying the mechanical response of specific areas of the insole varying the infill density brings numerous advantages. As an example, the use of various infill percentages allows the production of customised insoles independently from the machine and the material used, since all commercial and in-house developed 3D printers are capable of producing objects with different types of infill. On the other hand, when using customised or embossed shapes as done in [8,9], it could be difficult to guarantee the printability of the object, which strongly depends on the material and the printer used.
Considering the possible types of insoles (i.e., corrective [4], analgesic [3], and biomechanical [8]), only the last two are supported by the algorithm. This is due to three key aspects of the algorithm: (i) the required stiffness can be calculated automatically; (ii) the range of stiffness must have a maximum of 100 MPa (this value can be changed by exploring other materials); and (iii) the distribution of different stiffnesses can be automatically calculated from the pressure values. Taking into account the corrective insole, instead, this should make a permanent deformation of the foot and to achieve this, highly rigid materials (i.e., Polyvinyl chloride (PVC) and Polypropylene (PP) [24]) have to be placed in specific points of the insole by the orthopaedist. For this reason, this type of insole is not supported because these components should be manually placed inside the model, and they have to be stiff enough to modify the foot but not too rigid to cause an injury [25].
Another category of insoles that are not supported is those designed for people who have a partial amputation of the foot. This particular type of insole should have a different approach caused by the different pressure distribution due to the amputation and the material should be softer in contact with the stump to be comfortable while it also should be rigid enough to remain in place where in contact with the shoe; moreover, due to the high customisation of these prostheses, this makes it difficult to automate the fabrication process.
Another advantage of the presented algorithm is that it requires minimal training of the user since it is semi-independent and the changes and information about the infill distribution inside the insole can be displayed step by step during the execution of the program. In addition, the algorithm has been designed to be better integrated into the production chain, replacing complex milling machine preparation with a simple workflow provided by additive manufacturing.
Future Developments
In the future, we aim to address several key aspects to further enhance the proposed algorithm and its application in the production of customised insoles. A primary objective will be the integration of direct access to data from the baropodometric platform, which will significantly improve the accuracy of plantar pressure mapping. This improvement will allow for more accurate pressure distribution, leading to an even more precise customisation of the insole’s stiffness profile. In parallel, it would be highly beneficial to develop the capability to design the insole shape directly within the software, thereby avoiding the loss of quality that can occur during model import procedures.
Another area of future research will focus on expanding the range of materials used in insole production. This approach will not only enable better adaptation to the different pathologies and needs of patients but also open new possibilities for customising the mechanical properties of the insoles, ensuring greater versatility in meeting clinical demands. Moreover, as we expand the range of available materials, we also plan to further develop the software and the automatic positioning of rigid components within the insole, enhancing the algorithm and leveraging advanced 3D printing technologies, such as those based on robotic arms.
Finally, it is crucial to consider potential developments towards the creation of sensorised insoles. Recent advancements in dynamic microelectronics, inspired by biological principles and capable of modifying their shape in response to external chemical and electrical stimuli [26], using technologies like micro-origami tessellation, could revolutionise this field. These technologies could enable the creation of sensorised insoles through 3D Origami Sensing, combining gait analysis with electromyography (EMG) for the continuous monitoring of gait patterns and the ability to make dynamic adjustments to the insole model [27]. These future developments not only improve the current approach but also open new research avenues that could have a significant impact on the production and clinical application of customised orthopaedic insoles.
5. Conclusions
In summary, a protocol was developed that is capable of semi-independently generating an insole with stiffness controlled by the pressure distribution recorded by a baropodometric board. The stiffness information is embedded in an AMF file that can be read by a slicer. Within the slicer, we can examine the insole infill distribution data and make modifications if necessary.
Two versions of the insole were obtained: The first was designed for fast production and immediate use, requiring no post-processing. The second was designed to be covered with various materials, according to the patient’s needs: These coatings can be used to increase comfort inside the footwear or eliminate unpleasant smells.
Both insoles were printed without the perimeter wall because if this feature is present, it can introduce a solid structure inside the insole that can cause cuts, abrasions, and irritation to the feet.
We were able to produce insoles in a short time, reducing the printing time from five hours to two and a half hours. The extended time of printing is due to the elasticity of the filament used. However, we reduced the printing time using a larger nozzle; another strategy to decrease the printing time is to use a higher layer thickness since this type of application does not require a high resolution. The use of the method shown in this article to produce 3D printed insoles can lead to more and better customisation of orthopaedic insoles, while simultaneously maintaining production times comparable to traditional procedures (CNC milling machines), ensuring a low cost and reducing material waste. The capability to control infill density and consequently the stiffness in any specific area of the insole provides a significant advantage to orthopaedists treating the patient’s pathology.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation12090184/s1. File S1: Matlab code for AMF file coding starting from the pressure distribution obtained with a baropodometric board.
Author Contributions
Conceptualisation, F.D. and J.G.; methodology, F.S and G.M.F.; software, F.S.; validation, F.S., F.D. and C.D.M.; formal analysis, C.D.M.; investigation, F.S.; resources, F.D. and J.G.; data curation, F.S.; writing—original draft preparation, F.S. and G.M.F.; writing—review and editing, C.D.M.; supervision, F.D. and J.G.; project administration, F.D.; funding acquisition, F.D. and C.D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out with the support of the Dieng srl company, which provided the instrumentation for the experimental validation, and was also partially supported by the European Union by the Next Generation EU project ECS00000017 Tuscany Health Ecosystem (THE, PNRR, Spoke 4: Nanotechnologies for diagnosis and therapy). Moreover, the authors acknowledge the support of the Crosslab Additive Manufacturing of the Department of Information Engineering of the University of Pisa.
Data Availability Statement
Data available on request.
Conflicts of Interest
Authors Fabio Diana and Jacopo Gai were employed by the company Diengcorp srl. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare no conflicts of interest.
References
- Ma, C.Z.H.; Wong, D.W.C.; Wan, A.H.P.; Lee, W.C.C. Effects of Orthopedic Insoles on Static Balance of Older Adults Wearing Thick Socks. Prosthet. Orthot. Int. 2018, 42, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Kolling, S.; Neubert, M.; Subke, J.; Griesemann, J. Material Modeling of Orthopedic Insoles. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009. [Google Scholar]
- Chhikara, K.; Gupta, S.; Chanda, A. Development of a Novel Foot Orthosis for Plantar Pain Reduction. Mater. Today Proc. 2022, 62, 3532–3537. [Google Scholar] [CrossRef]
- Aydoğan, Ö.; Yazici, N.H.; Tarakci, D.; Atilgan, E. Effect of Custom Design Insole Applications with 3D Modelling on Baropodometric Parameters in Individuals with Pes Planus. Int. J. Disabil. Sports Health Sci. 2023, 6, 399–407. [Google Scholar] [CrossRef]
- Baumfeld, D.; Baumfeld, T.; Da Rocha, R.L.; Macedo, B.; Raduan, F.; Zambelli, R.; Alves Silva, T.A.; Nery, C. Reliability of Baropodometry on the Evaluation of Plantar Load Distribution: A Transversal Study. Biomed. Res. Int. 2017, 2017, 5925137. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Díaz, C.R.; Marques, C.; Pontes, M.J.; Frizera, A. 3D-Printed POF Insole: Development and Applications of a Low-Cost, Highly Customizable Device for Plantar Pressure and Ground Reaction Forces Monitoring. Opt. Laser Technol. 2019, 116, 256–264. [Google Scholar] [CrossRef]
- Klöpfer-Krämer, I.; Brand, A.; Wackerle, H.; Müßig, J.; Kröger, I.; Augat, P. Gait Analysis—Available Platforms for Outcome Assessment. Injury 2020, 51, S90–S96. [Google Scholar] [CrossRef]
- Davia-Aracil, M.; Hinojo-Pérez, J.J.; Jimeno-Morenilla, A.; Mora-Mora, H. 3D Printing of Functional Anatomical Insoles. Comput. Ind. 2018, 95, 38–53. [Google Scholar] [CrossRef]
- Ma, Z.; Lin, J.; Xu, X.; Ma, Z.; Tang, L.; Sun, C.; Li, D.; Liu, C.; Zhong, Y.; Wang, L. Design and 3D Printing of Adjustable Modulus Porous Structures for Customized Diabetic Foot Insoles. Int. J. Lightweight Mater. Manuf. 2019, 2, 57–63. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer International Publishing: Cham, Switzerland, 2021; Volume 17, ISBN 978-3-030-56126-0. [Google Scholar]
- Beloshenko, V.; Beygelzimer, Y.; Chishko, V.; Savchenko, B.; Sova, N.; Verbylo, D.; Voznyak, A.; Vozniak, I. Mechanical Properties of Flexible Tpu-Based 3d Printed Lattice Structures: Role of Lattice Cut Direction and Architecture. Polymers 2021, 13, 2986. [Google Scholar] [CrossRef]
- Jafarzadeh, E.; Soheilifard, R.; Ehsani-Seresht, A. Design Optimization Procedure for an Orthopedic Insole Having a Continuously Variable Stiffness/Shape to Reduce the Plantar Pressure in the Foot of a Diabetic Patient. Med. Eng. Phys. 2021, 98, 44–49. [Google Scholar] [CrossRef]
- Xu, R.; Wang, Z.; Ren, Z.; Ma, T.; Jia, Z.; Fang, S.; Jin, H. Comparative Study of the Effects of Customized 3D Printed Insole and Prefabricated Insole on Plantar Pressure and Comfort in Patients with Symptomatic Flatfoot. Med. Sci. Monit. 2019, 25, 3510–3519. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.W.; Hu, C.J.; Yang, W.W.; Chou, L.W.; Wei, S.H.; Chen, C.S.; Sun, P.C. Biomechanical Evaluation and Strength Test of 3D-Printed Foot Orthoses. Appl. Bionics Biomech. 2019, 2019, 4989534. [Google Scholar] [CrossRef] [PubMed]
- Dombroski, C.E.; Balsdon, M.E.R.; Froats, A. The Use of a Low Cost 3D Scanning and Printing Tool in the Manufacture of Custom-Made Foot Orthoses: A Preliminary Study. BMC Res. Notes 2014, 7, 443. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-K.; Joo, J.-Y. Effects of Custom-Made 3D Printed Insoles for Flat-Foot People on Gait Parameters: A Preliminary Study. In Proceedings of the 35th Conference of the International Society of Biomechanics in Sports, Cologne, Germany, 14–18 June 2017. [Google Scholar]
- Srivastava, V.; Gaur, H. Revolutionary Development in Orthopedic Insole by Additive Manufacturing. J. Crit. Rev. 2020, 7, 1943–1947. [Google Scholar]
- Zuñiga, J.; Moscoso, M.; Padilla-Huamantinco, P.G.; Lazo-Porras, M.; Tenorio-Mucha, J.; Padilla-Huamantinco, W.; Tincopa, J.P. Development of 3D-Printed Orthopedic Insoles for Patients with Diabetes and Evaluation with Electronic Pressure Sensors. Designs 2022, 6, 95. [Google Scholar] [CrossRef]
- Gensole. Available online: http://gensole.com/ (accessed on 30 July 2024).
- Jin, H.; Xu, R.; Wang, S.; Wang, J. Use of 3D-Printed Heel Support Insoles Based on Arch Lift Improves Foot Pressure Distribution in Healthy People. Med. Sci. Monit. 2019, 25, 7175–7181. [Google Scholar] [CrossRef]
- Rodríguez-Parada, L.; De La Rosa, S.; Mayuet, P.F. Influence of 3D-Printed TPU Properties for the Design of Elastic Products. Polymers 2021, 13, 2519. [Google Scholar] [CrossRef]
- Mogan, Y.; Periyasamy, R. Thermoplastic Elastomer Infill Pattern Impact on Mechanical Properties 3D Printed Customized Orthotic Insole. ARPN J. Eng. Appl. Sci. 2016, 11, 6519–6524. [Google Scholar]
- Nace, S.E.; Tiernan, J.; Holland, D.; Ni Annaidh, A. A Comparative Analysis of the Compression Characteristics of a Thermoplastic Polyurethane 3D Printed in Four Infill Patterns for Comfort Applications. Rapid Prototyp. J. 2021, 27, 24–36. [Google Scholar] [CrossRef]
- Yick, K.L.; Tse, C.Y. Textiles and Other Materials for Orthopaedic Footwear Insoles. In Handbook of Footwear Design and Manufacture; Elsevier Inc.: Amsterdam, The Netherlands, 2013; pp. 341–371. ISBN 9780857098795. [Google Scholar]
- Nouman, M.; Dissaneewate, T.; Chong, D.Y.R.; Chatpun, S. Effects of Custom-Made Insole Materials on Frictional Stress and Contact Pressure in Diabetic Foot with Neuropathy: Results from a Finite Element Analysis. Appl. Sci. 2021, 11, 3412. [Google Scholar] [CrossRef]
- Merces, L.; Ferro, L.M.M.; Thomas, A.; Karnaushenko, D.D.; Luo, Y.; Egunov, A.I.; Zhang, W.; Bandari, V.K.; Lee, Y.; McCaskill, J.S.; et al. Bio-Inspired Dynamically Morphing Microelectronics toward High-Density Energy Applications and Intelligent Biomedical Implants. Adv. Mater. 2024, 36, 2313327. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.H.; Vanloo, J.; Kim, W.S. 3D Origami Sensing Robots for Cooperative Healthcare Monitoring. Adv. Mater. Technol. 2021, 6, 2000938. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).