Abstract
This paper studies the kinematics and dynamics of a poly-articulated robot. The robot can be used in hardly accessible places and special environments. The poly-articulated robot includes two main parts: a flexible unit and an actuation unit. The flexible unit consists of three modules specially designed for serving in a complex 3D workspace. Each module has flexible vertebrae and rigid disks. The poly-articulated robot simulation is achieved with the MSC Adams 2012 and ANSYS R14.5 software. Thus, we aim to determine whether the variation laws depend on the time of the kinematic parameters for each part in a specific motion, considering each part has to act as a rigid body or a deformable body. Using the finite element method, the stress and deformations for normal and critical positions are calculated for the poly-articulated robot. To validate the simulation models designed in this research, an experimental analysis of the proposed poly-articulated robot is developed. The command and control unit was equipped with motion sensors that allow to identify the position of each flexible unit module.
1. Introduction
Nowadays, poly-articulated robots are widely used in domains like industrial, medical, military and aerospace, due to their specific design for accomplishing tasks in a complex workspace.
Their conceptual design is inspired from elephant trunks, snakes and even octopus tentacles like the ones from [1,2,3,4,5,6]. These are characterized by a large number of DOFs due to their highly articulated structure. Thus, by considering the previously mentioned fundamental domains, these robots are well suited for exploration operations in highly constrained environments.
The large DOF is determined by the use of a number of serially connected links and actuated joints, like [7,8], when designing such robots.
An important design task, specific to the ones used in the medical domain, is to have a miniaturized structure size for use in endoscopy [9] or cholecystectomy [10]. Thus, this design task will trigger new problems to be solved, like stiffness, increased dexterity and precise control guidance [11].
Despite the imposed tasks, these robots need to go through several design stages that involve complex kinematic and dynamic analyses of the poly-articulated structure. On the other hand, the command and control unit should have a specific design architecture in order to work perfectly with a poly-articulated structure like the ones from [12,13].
By considering design concepts similar to the ones from [14,15,16,17], a major and common design objective imposed for the poly-articulated robot structure can be remarked. This design objective is to obtain an S-shaped spatial trajectory developed by the poly-articulated structure in a Cartesian coordinate system.
Another argument of this design task is to have a parametrized S-shaped spatial trajectory. This will involve complex dynamic analyses, like the ones performed in [18,19,20]. Also, this can be accomplished by designing a continuum robot concept characterized by combining rigid bodies with flexible ones like [21,22,23].
By having in sight the ones presented in [20,21,22], our research aim is to design a robot with a poly-articulated structure that can develop a parametrized S-shaped spatial trajectory by using a combination of rigid bodies with flexible ones.
Thus, our contribution to this research field is to develop, design and test a proto-type able to accomplish the desired aims. Another research peculiarity is to achieve the proposed aims by using modern design techniques and software, such as MSC Adams and ANSYS. Thus, the research core is based on the Craig–Bampton method, presented in [23], for elaborating the mathematical models used in kinematic and dynamic analyses. Other original contribution is the architecture, though similar poly-articulated robots can be found, like the ones from [24,25,26].
In order to achieve the mentioned objectives, this research is organized as follows. Starting from our own original contribution, we drew up a robot design principle characterized by nine DOFs, which combines rigid bodies with flexible ones. Based on this principle, two different flexible units—a cylindrical and a tronconic one—will be de-signed and experimentally tested. This is presented in the second part of the research, along with the working principle.
The novelty brought about through this research emphasizes an elaborated prototype characterized by constructive simplicity of the flexible unit, the design of a flexible unit in a modular form that can be combined anytime (by lowering or increasing the DoF), and a new shape of the flexible unit, namely a tronconic shape of this, which will contribute to the improvement and control of a variable stiffness. By having in sight the processed virtual models, there will be mentioned several parameters for virtual simulations setup, and these are valuable for other future research.
As previously mentioned, the research core focuses on a dynamic analysis of the proposed poly-articulated unit, and the approach consists of elaborating a mathematical model based on the Craig–Bampton method from [23], presented in the third part of this research. This mathematical model represents the background for virtual simulations of the poly-articulated robot and numerical processing in dynamic conditions with the aid of the MSC Adams and ANSYS software.
To validate the elaborated poly-articulated concept, several virtual simulations in different environments have been performed. One will be accomplished in MSC Adams, where the poly-articulated unit was imported and the combination between flexible and rigid bodies was properly defined. This is presented in the fourth part of the research, where significant results were obtained by considering imposed constraints similar to reality.
Another interface was created in the ANSYS environment, and several virtual simulations in dynamic conditions will be performed to study the contact between the unit components of the poly-articulated robot. This case will be presented in the fifth part of the research, where more attention will be given to the contact definition during virtual simulations in order to achieve a good behavior of the entire robotic system and to validate the proposed concept.
Based on the significant results that will have been obtained, the last part of the re-search will present the prototype, and a range of experimental tests will prove the efficacy of the dynamic analyses performed with the aid of the Craig–Bampton method, combined with modern techniques.
2. Virtual Prototyping of the Poly-Articulated Robot
A poly-articulated robotic system was designed that has two major units: a flexible unit and an actuation unit.
The flexible unit structure has three modules, and each module contains three flexible vertebrae and rigid disks. These modules are connected through a flexible central element. Thus, the entire flexible unit has nine flexible vertebrae that are actuated through nine electric motors. These electric motors represent the actuation unit, and the translational motion is assured using screw and nut joint transmissions.
Two types of flexible units—a cylindrical and a tronconic one—were designed. The latter, i.e., the tronconic form, has a major advantage, which consists of an easy and accurate control of the stiffness of the flexible unit across all three modules. The tronconic concept of the flexible unit assures a variable stiffness across its own length, and this will ensure enhanced flexibility onto the distal module, according to Figure 1.
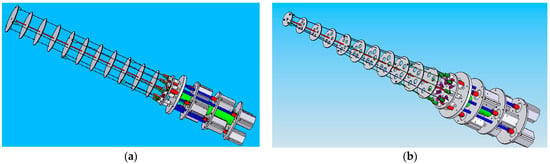
Figure 1.
Flexible unit types proposed through this research: (a) flexible unit with a cylindrical architecture, and (b) flexible unit with a tronconic form.
The cylindrical form of the flexible unit implies technological facilities, so that the manufacturing processes are much easier than in the case of the tronconic form, and it was also seen that this can be done with low costs.
The robot workspace was defined by the mobility limits of the flexible unit, and this was designed in a modular form in order to have a simplified control for the robot configuration and its evaluated workspace. The deformed shape of the flexible unit seems to be a snake-like form, and thus, the term “snake-like robot” can be assigned to the entire designed system.
The robot’s mechanical structure is designed so that the axial displacements can be adjusted, and this ensures the robot’s kinematic precision. In particular, the flexible unit was designed for two types: one with a cylindrical structure and the other with a conic structure. The robot’s mechanical parts were built at the laboratories of the Faculty of Mechanics, and the command and control unit was designed at the Faculty of Automation, Computers and Electronics of the University of Craiova [21].
Thus, the poly-articulated robot was designed according to the 3D model presented in Figure 2. Figure 3 shows an exploded view with a proper identification of the components of the poly-articulated robotic system 3D model.
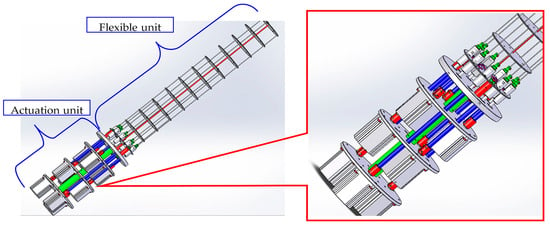
Figure 2.
Virtual model of the poly-articulated robot in a parametrized form.
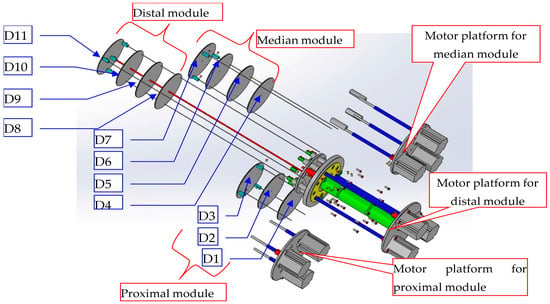
Figure 3.
A virtual model of the poly-articulated robot—expanded view.
The working principle of the robot depends on the motor actuation control, which, in this case, is represented by the nine stepper motors. The robot architecture consists of three modules (proximal, median and distal), and each module is actuated by three stepper motors in order to develop combined motions in a 3D working space. The stepper motors are directly connected to power screw transmissions, which will pull or release the actuation cables. Thus, the power screw transmissions will transform the rotational motion of the stepper motor shaft in a translational motion imposed on the nut component connected to an actuation cable. Thus, the motion is based on screwing and unscrewing the power transmissions, which will determine the shortening or prolonging of the continuum robot motion. In this way, the tentacle curvature will be changed with the variation of the actuation cables.
Figure 3 shows the backbone of the tentacle—the central component marked in red, which represents an elastic rod manufactured from steel, which sustains the whole structure and permits the bending sequence. Thus, the working principle depends on which cable is shortened or extended, and the tentacle bends in different planes. Each cable will contribute to making a motion with different angles, depending on the initial coordinate frame attached to the manipulator segment, for example, allowing a 3D motion. Thus, Figure 1 shows both flexible unit models, and it can be seen that they use the same number of components, the only difference being given by the shape of the disks. This was designed in a parametrized form, considering the definition of the precise contour conditions. The obtained model respects the kinematic conditions and was also designed in two variants, compatible with MSC Adams 2012 and ANSYS R 14.5 software. These are shown in Figure 4 and Figure 5.
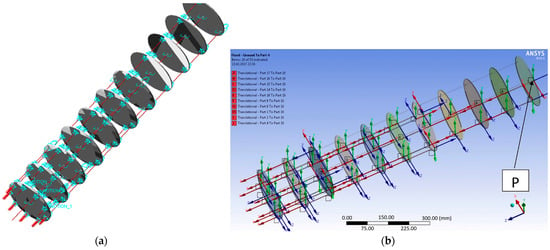
Figure 4.
Poly-articulated cylindrical robot kinematic models using (a) MSC Adams and (b) ANSYS software.
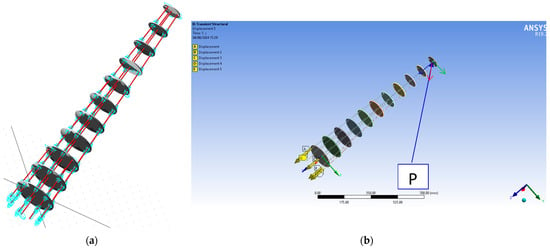
Figure 5.
Poly-articulated tronconic robot kinematic models using (a) MSC Adams and (b) ANSYS software.
3. Mathematical Models
In the case of the MSC Adams software robot analysis, the mathematical model is based on the Craig–Bampton method. The principle of the method is presented in [23] and assumes the following theoretical considerations: by transforming a rigid body into a flexible one, a procedure is characterized by taking into account only the small linear strain of the proposed body, depending on a local reference coordinate system; the proposed rigid body will be meshed into finite elements. In this way, a finite number of DOFs will be identified.
Nodal displacements can be expressed like a linear combination between a small number of proper vectors, named modal forms and assigned to a Ǿ parameter. For a deformable body “i”, these are represented by
where u—nodal displacements; M—number of mode shapes; qj—modal coordinates.
Equation (1) also represents the connection between a wide set of physical coordinates and a small set of modal coordinates, namely qj.
The Craig–Bampton method allows optimizing the obtained modal base by considering two DOF sets, i.e., contour degrees of freedom uB, which are used for load applications or for connecting a flexible body to a rigid one; internal degrees of freedom uI, i.e., the internal degrees of freedom of the flexible element, which can be condensed using super-element techniques.
For the kinematic analysis of a flexible body (element), two reference coordinate systems will be considered as follows: T′i (xi,yi,zi)—the reference coordinate system attached to a flexible body; T0 (X,Y,Z)—the global reference coordinate system.
Some interest nodes can be identified by meshing up the flexible body into finite elements. Markers with proper local reference coordinate systems can be placed on the identified interest nodes.
Thus, a “Pi” marker can be assigned on a flexible body, and its position can be defined in a global coordinate reference system as follows:
where —the position vector of the T′i local coordinate system origin, depending on the T0 global reference system; —position vector of the Pi—marker (undeformed position), depending on the T′i local coordinate system; —the position vector of the P′i—marker, depending on the TPi—reference system, which is centered in the Pi—marker.
A scheme of the coordinate system position placed on a simplified model is shown in Figure 6. The coordinate transformation matrices will be identified by taking into account Equation (2), and the following results will be obtained:
where represents the origin position of the T′i local reference system, depending on the TO global reference system.
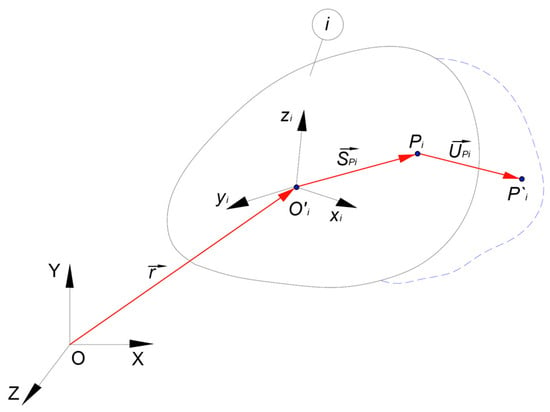
Figure 6.
Coordinate systems location on a flexible body for the Craig–Bampton method.
Thus, the generalized coordinate system vector of the flexible body in an undeformed situation is
where xi, yi, zi—the coordinates of the original mobile reference system, namely T′i(xi, yi, zi)—fixed, with a deformable body—i; ψi, θi and φi—Euler angles describing the space orientation of the i—body; A0i—matrix of the coordinate transformation created from the director cosines of the T′i, local reference system, depending on the T0 global reference system; —deformation vector expressed in the T′i local reference system.
The deformation displacement vector can be expressed as a modal superposition in a matrix form as
where —is a part of the modal matrix that corresponds to Pi—marker translational DOF. This matrix has a 3xM dimension, where M represents the modal forms number; qi—modal generalized coordinates vector.
Using the previous equations, the generalized coordinate vector can be defined for a flexible body as follows:
Equation (7) shows the qi modal coordinates (i = 1… M), which characterize the generalized coordinates of the flexible element.
The angular deformation of a flexible element can be obtained by using a modal superposition:
where is a part of the modal matrix that corresponds to rotational degrees of freedom for the Pi—node. It has a 3 × M dimension, where M is the mode number.
The solid-deformable motion is analyzed for a Ki marker that performs rotations with small angles, depending on its local reference system.
Each marker is defined through a proper coordinate system. In the case of the Ki—marker orientation, depending on the T0 global reference system, a coordinate transformation matrix was given, namely A0Ki, where
where A0i is the transformation matrix obtained by crossing from the local reference system to the i body, namely T′i, to the global reference system T0; AiPi is the transformation matrix that results from changing the orientation due to Pi—node deformation; APiKi is the constant transformation matrix that was defined when the marker was placed on the flexible body. The presented elements represent input data for the used procedure for transforming a rigid body into a deformable one, with the aid of MSC Adams software.
A0Ki = A0i·AiPi·APiKi
4. Dynamic Modeling with MSC Adams
The flexible unit was analyzed with MSC Adams 2012 software. Thus, it was created as a flexible interface for importing the flexible unit CAD geometry in 2D and 3D in MSC Adams. There was defined the material properties for the proper components (steel for vertebrae and aluminum for the disks), and also, there will be allocated local reference systems for each component of the flexible unit. There were defined kinematic joints together with the attached reference systems. These consist of 21 kinematic elements, namely 10 flexible elements and 11 rigid elements represented by the disks, according to Figure 2. The links between these kinematic elements were provided by 75 kinematic joints, namely 21 fixed joints and 54 translational joints with a single DOF. This unit was actuated through 6 joint motors. Figure 7 shows the motor joint definition. The motion is represented by the vectors MOTION_1, MOTION_2 and MOTION_3 (Figure 7). The displacement Uy, in Figure 7 represent the motion along the central axis shown in Figure 3. The motion sequence is at follows: IF (time—1: 0, 0, —2 × time)—motion_1—proximal module; IF (time—1:0, 0, —1.5 × time)—motion_2—median module; IF (time—2:—2 × time, 0, 0) —motion_3—distal module.
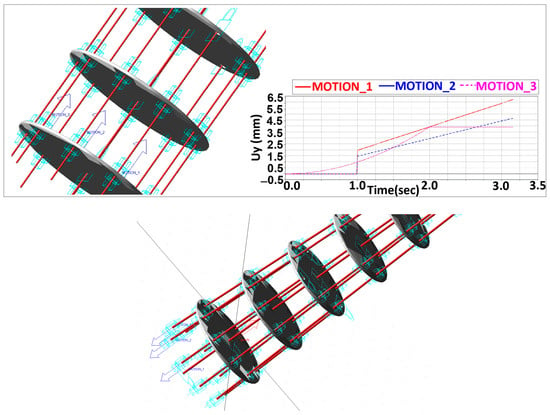
Figure 7.
Motor joint displacement setup on a 3-s time interval for both analyzed flexible units.
For this, a robot motion analysis in a kinematic or dynamic mode will be possible by considering the flexible unit as a mechanism with deformable elements. Considering the elaborated Craig and Bampton mathematical models [9,20], ADAMS 2012 software will allow performing a modal dynamic analysis of any flexible mechanical system by superimposing the rigid-solid motion onto a deformable-solid one.
There were transformed nine actuation vertebrae from rigid bodies to flexible bodies as follows: each body was meshed in finite elements (Element type: solid, Element shape: tetrahedral, Element order: quadratic and Edge shape: mixed); there were defined the connection conditions with other elements through a procedure that consists of nodes identification master–slave type.
The flexible elements—generically referred to as elastic vertebrae—were meshed into tetrahedral finite elements. The modal dynamic analysis was performed for 77 mode shapes.
After this, there were determined the natural frequencies and vibration proper modes, and in this way, there were created the proper conditions for applying the modal super-position method (Craig–Bampton) to achieve the mechanism dynamic analysis.
For solving the differential equations system, there were used the WSTIFF integration module, with SI2 formulations and an integrating step set at 0.01.
The contact from the translational joints was a set of solid rigid-solid deformable type.
During the virtual simulations, kinematic parameter motion laws were identified in the case of the node placed on the extremity of the central vertebrae, depending on the reference coordinate system placed on the mass center of the first disk, which was considered fixed in space for the actuation unit.
Figure 8 shows a few flexible unit-deformed shapes in a 3D workspace, which resulted during motor joint actuation in different actuation modes.
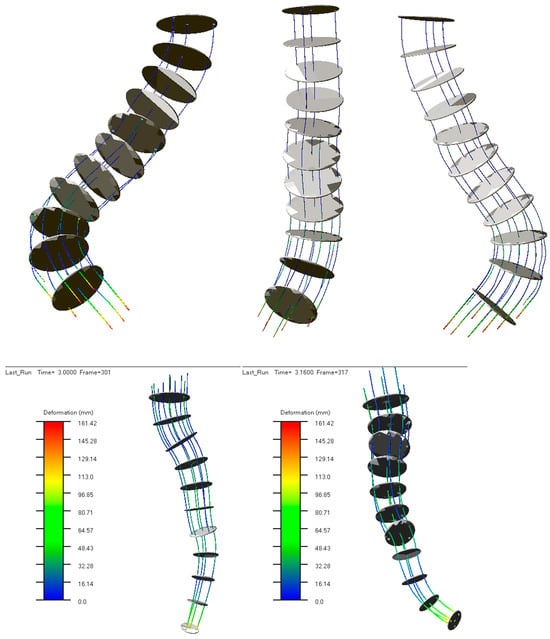
Figure 8.
Deformed shapes of the flexible unit for both analyzed forms processed under the MSC Adams environment.
The obtained results are represented by displacement components of the end disk (D11) for distal module no.2 and the end disk (D7) for median module no.1, according to Figure 2. Some nodes located at the mass center of the proposed disks were considered for measurement during the deformable-solid virtual simulation.
Figure 9 represents the nodal translational deformation for node no. 14405 placed in the mass center of the final disk D11 across the distal module. It can be seen that the maximum displacement values are recorded in a transversal plane defined by the x and y axes of the local reference system.
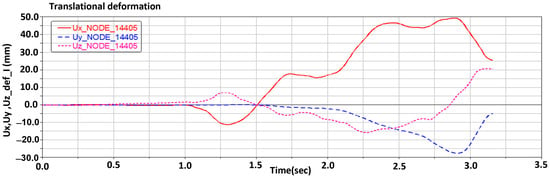
Figure 9.
Translational deformation components for the distal module corresponding to the node from disk D11 vs. time.
Figure 10 represents the nodal translational deformation for node no. 14401 placed in the mass center of the final disk D7 across the median module. Also, in this case, it can be noticed that the maximum displacement values are recorded in a transversal plane of the flexible unit, but these values are smaller than the ones reported in Figure 7. This is caused by the median module stiffness, which is higher than the one for the distal module.
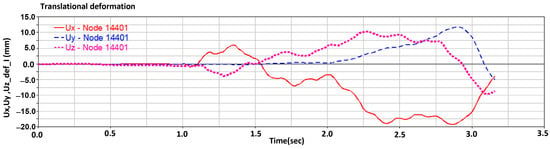
Figure 10.
Translational deformation components for the distal module corresponding to the node from disk D7 vs. time.
5. Dynamic Modeling with ANSYS
In this case, the robotic system from Figure 2 was considered, and, for this, a dynamic analysis was performed with the ANSYS R14.5 package [8]. Firstly, the geometric model was imported, and the second step was to mesh this into finite elements, as it can be seen in Figure 9. The third step was to define the contact between disks and vertebrae, and the contour conditions were established at its end.
The kinematic links were considered to be flexible, and increased attention has been devoted to the network of finite elements in the contact areas where these were resized, according to Figure 11. Thus, this research frame presents, as a detailed example, the case of the flexible unit characterized by a cylindrical form. In the other case, i.e., the tronconic form of the flexible unit, a similar approach was implemented, with similar results.
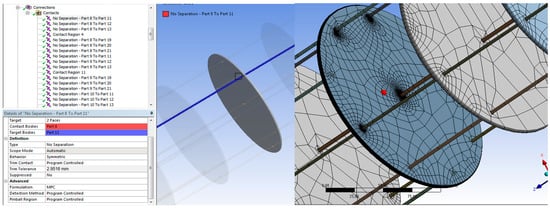
Figure 11.
Contact definition between elastic vertebrae and flexible unit disks.
Regarding the initial setup of the analysis, there were defined the contact modeling parameters, the solver type and the time for sequence setup of the proper virtual processing. Thus, for the solver type and time setup, we define the following parameters: Number of steps: 3; Initial time step: 0.1 s; Minimum time step: 0.001; Maximum time step: 0.002; Solver type: Direct; Numerical dumping: 0.1. In case of the contact modeling, there were defined contact parameters in case of the specific joints modeling, respectively, the nine actuating vertebrae and disks as follows: Type contact: No separation; Behavior: Symmetric; Formulation: MPC; Detection Method: Nodal-Normal to Target. The contact between the disks and the central flexible element was done as follows: Type: Bounded; Behavior: Symmetric; Formulation: Pure Penalty; Detection Method: Nodal-Normal to Target. According to Figure 2, the disk D1 was fixed in space.
In the fourth step, the motor parameters were defined, as it can be remarked in Figure 12.
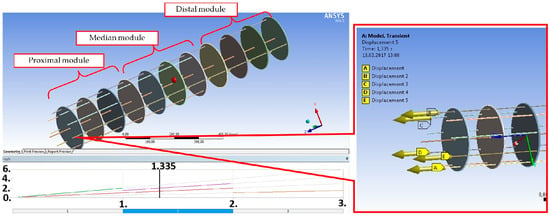
Figure 12.
Definition of the flexible unit motor elements in case of the cylindrical form.
A simulation setup for the actuation mode during the time sequence was performed for all flexible unit modules according to Figure 12, with proper motions: median module, uz1 = t (t ≤ 2); distal (final) module uz2 = 2t (t ≤ 1); proximal (base) module uz3 = 0.5t (1 ≤ t ≤ 2); distal (final) module uz4 = 1.5t (1 ≤ t ≤ 2); distal (final) module uz5 = 0.5t (2 ≤ t ≤ 3).
After processing all the input data, increased attention was given to the motion of the components of the robotic system, according to two reference systems, i.e., a global coordinate system and a local one placed at the center of the base disk. Thus, the variation laws in the motion of kinematic parameters were identified, depending on the time for the chosen markers, namely the ones placed at the centers of reference disks for proximal, medial and distal modules. The motion developed by these markers was analyzed after three components of the proper coordinate system.
The reference disks are the ones actuated directly by the motor vertebrae (final disks from each module). Thus, several results were obtained, which are shown in the diagrams from Figure 13, Figure 14 and Figure 15, and these represent the displacement components on the X and Z axes for the marker placed on the local coordinate system attached to the final disk of the proximal module.
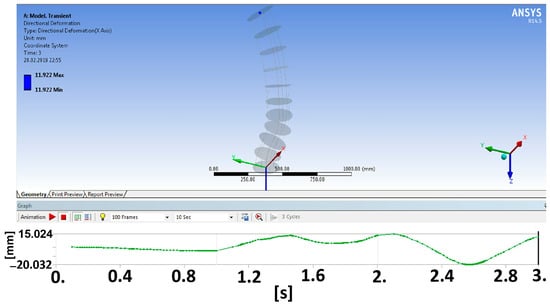
Figure 13.
The displacement component variation on the X-axis for the final disk from the distal module in a local coordinate system vs. time.
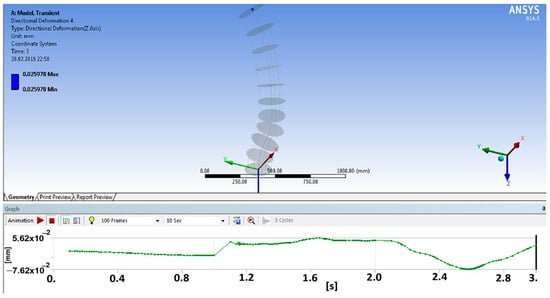
Figure 14.
The displacement component variation on the Z-axis for the final disk from the distal module in a local coordinate system vs. time.
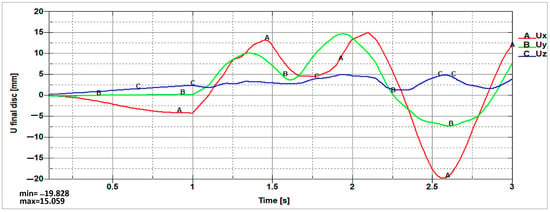
Figure 15.
The elastic displacement variation of the final disk marker from the proximal module vs. time.
Each module is successively actuated or simultaneously with the other two, according to the desired configuration of the robotic system described in the proposed workspace.
The axes that define the analyzed flexible unit transversal plane are X and Y. Thus, Figure 13 shows a deformed shape of the analyzed flexible unit, depending on the time corresponding to the X-axis component for the final disk D11 mass center of the distal module. This variation was calculated according to a local reference system placed on the D7 base disk. It was recorded until a value of 15.059 mm was reached. Similarly, we calculated the displacement for the Z-axis variation, depending on the time for the mass center final disk D11 of the distal module. This is shown in Figure 14, and a maximum value of 0.056298 mm was obtained.
Figure 15 shows a total displacement ranging from a minimum value of −19.828 mm to a maximum of 15.059 mm. Thus, a total displacement amplitude of approximately 35 mm was obtained.
Figure 16 outlines the deformed shape of the flexible unit and the displacement variation on the Y-axis.
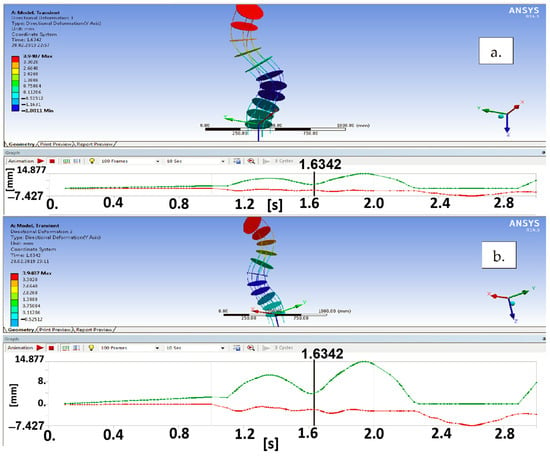
Figure 16.
The variation of the deformed shape of the flexible unit across the Y-axis of the local coordinate system across time ((a)—isometric view; (b)—rotated view in the X–Y plane).
Based on this result, it can be seen that the transversal displacements are compatible with the deformed shape of the flexible unit. Also, the deformed shape can be evaluated by considering the elastic vertebrae from the flexible unit structure, namely Figure 17, where the resulting displacement variation is shown for two vertebrae, namely a motor one and a driven vertebra.
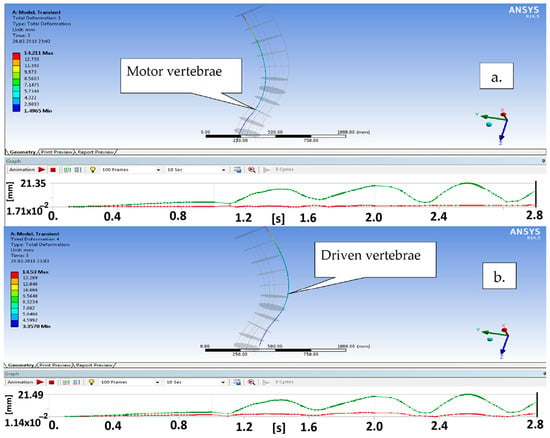
Figure 17.
The resulting displacement variation for vertebrae in a global coordinate system vs. time ((a)—motor vertebrae; (b)—driven vertebrae).
Finally, in Figure 17 it was analyzed the displacement variations for distal module vertebrae.
Also, the deformations, displacements and von Mises stress were obtained in the case of each vertebra for two distinctive cases: when this was a motor element and when this was a driven element.
Thus, in Figure 18, we can see the resulting displacements for median module vertebrae over a time interval of 3 s. After numerical processing, values of 4.3 mm were obtained for the motor vertebra and 4.1 mm for the driven vertebra.
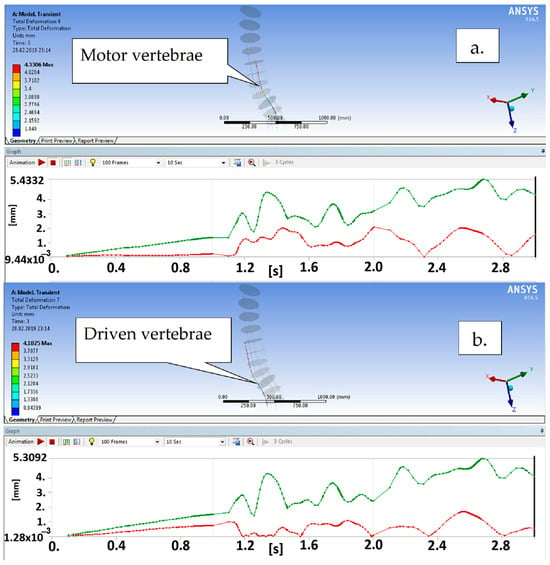
Figure 18.
The resulting displacement variation for the vertebrae of the median module in the global coordinate system vs. time ((a)—motor vertebrae; (b)—driven vertebrae).
The oscillation amplitude is correlated with the stiffness of all the modules of the flexible unit and also with the setup of the actuation commands.
Based on Figure 19, the resulting displacements of vertebrae from the proximal module actuation are characterized by maximum displacement curves that are almost identical and reach values around 2.288 mm. Also, different displacement values were obtained for all the modules during numerical processing. This occurs due to the stiffness that will be increased by passing from the distal module to the median and then to the proximal module, which has a higher stiffness than the other two.
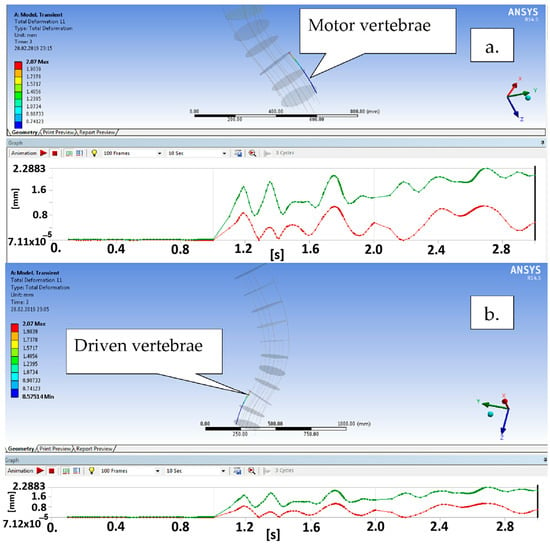
Figure 19.
The resulting displacement variation for the vertebrae of the proximal module in the global coordinate system vs. time ((a)—motor vertebrae; (b)—driven vertebrae).
Other results, like the resulting elastic displacements for the entire flexible unit on different temporal time moments, are reported in Figure 20. Thus, in Figure 20, we can remark on the deformed shape that is compatible with the recorded variations in the case of the resulting elastic displacements. Also, the total elastic deformation has a maximum value of 21.83 mm, and its shape variation is compatible with the deformed flexible shape.
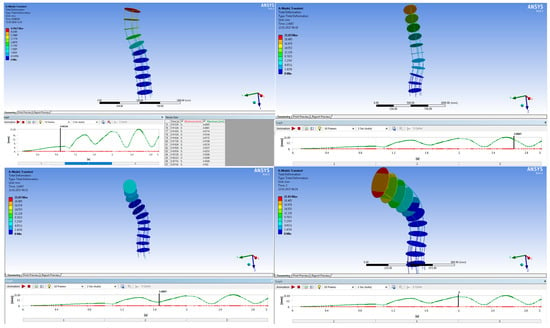
Figure 20.
Snapshots of the acquired distribution of elastic displacement for various temporal moments vs. time.
The major results obtained through this analysis are represented by the von Mises stress and deformations of the flexible unit in the case of the interest markers allocated on the final disk of each module. These are reported in Figure 21, Figure 22 and Figure 23.
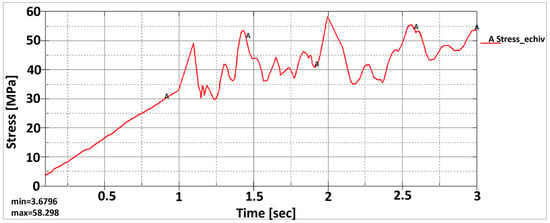
Figure 21.
Equivalent von Mises stress distribution vs. time.
Figure 22.
Actuation modes represented in steps vs. time for the whole flexible unit.
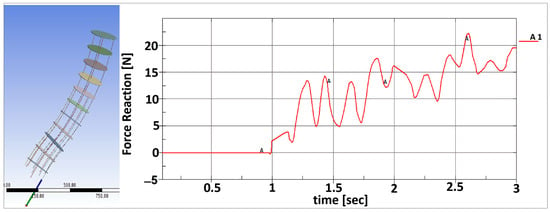
Figure 23.
The reaction force distribution for the motor vertebra of the distal module depends on the time interval of 2 s (1 to 3 s).
For the results of von Mises stress, the maximum value was 58.298 MPa, and the stress distribution was also influenced by the actuation setup and stiffness for all modules of the flexible unit structure. Thus, Figure 22 shows a smooth linear evolution. For the first step interval according to Figure 21, at a range of 32 MPa, the equivalent von Mises stress evolution will have an unbalanced behavior between 32 MPa and 58.298 MPa. Another particular aspect is that the equivalent von Mises stress starts from a minimum value of 3.67 MPa. This value results from an initial stiffness of the poly-articulated unit, even when it is not actuated.
Other results, like the reaction forces from several flexible unit components, are reported in diagrams from Figure 24, Figure 25, Figure 26 and Figure 27. By having in sight these results, along the 1–3 s time interval, the force of the drive vertebra used for final disk actuation from the distal module, namely D11, reaches a value of 25 N, as shown in Figure 23.
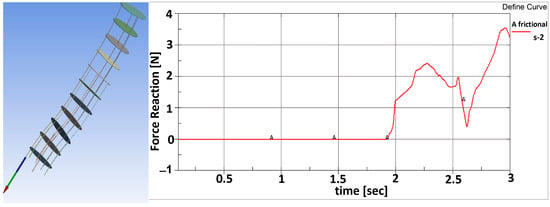
Figure 24.
The reaction force distribution for a driven vertebra of the distal module depends on the time interval of 1 s.
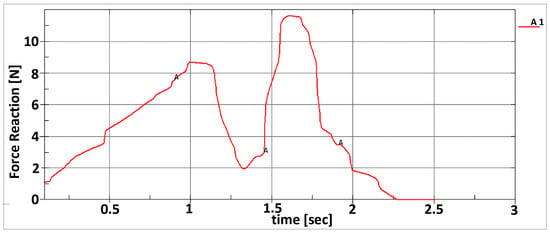
Figure 25.
The reaction force distribution for the motor vertebra of the median module depends on the time interval of 2 s.
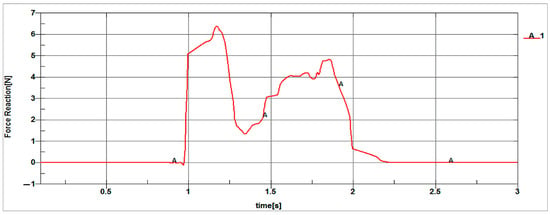
Figure 26.
The reaction force distribution for a driven vertebra of the median module depends on the time interval of 1 s.
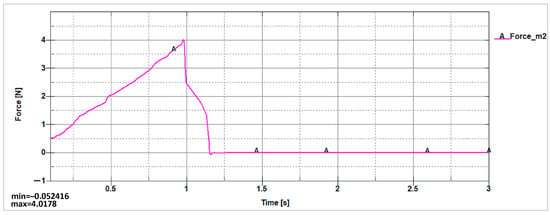
Figure 27.
The reaction force distribution for a driven vertebra of the proximal module depends on a time interval of 1 s.
In Figure 24, the obtained reaction force for driven vertebra during the actuation of the distal module has a variation ranging from 0 to 3.5 N. This happens along a 2–3 s time interval.
For the actuation of the distal module, the drive vertebra actuation force records an almost linear time variation, as can be seen in Figure 25. This was produced in a period of 0 to 2 s and reached a maximum value of 11.8 N.
The reaction force from the median module-driven vertebra became active during the period of 1 to 2 s and reached values ranging from 0 to 6.5 N, according to Figure 26.
Figure 27 shows a reaction force on the first time interval ranging from 0 to 2 s. This reaches a maximum value of 4 N at the end of the actuation period. This also has a smooth linear evolution and starts from 0.5 N, when the entire poly-articulated unit will be actuated.
The distribution of the contact parameter results was analyzed for an intermediary disk and the central vertebrae. The obtained results were represented by frictional stress, penetration factor and contact pressure for a time interval of 3 s. These results are shown in Figure 28, Figure 29 and Figure 30.
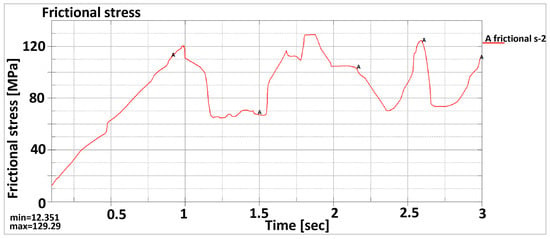
Figure 28.
The frictional stress distribution depends on time.
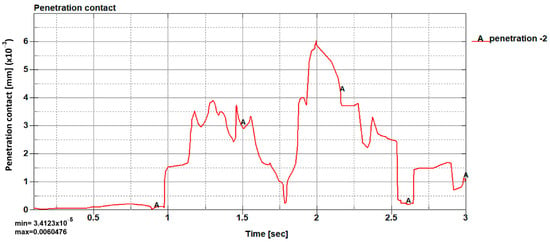
Figure 29.
The penetration contact variation for the mechanical system contact definition vs. time.

Figure 30.
The poly-articulated robotic system prototype equipped with the two flexible unit forms: (a) cylindrical form and (b) tronconic form.
Figure 29 shows that the penetration factor between contact surfaces and the targeted surfaces is very small and can be neglected. According to Figure 29, this reaches a maximum value of 0.0060476 mm. During actuation, the frictional stress reaches a value of almost 130 MPa, and it has an unbalanced behavior due to the friction between elements and straight contact, as can be seen in Figure 28. During simulations, a symmetric pressure distribution can be noticed when a module is actuated, and another is released. The oscillations, which occur during virtual simulations that can be remarked on the variation curves from Figure 25, Figure 26, Figure 27, Figure 28 and Figure 29, are caused mainly by contact definition parameters setup, contact type, integration step and method, correlated to the time interval for monitoring the system motion.
6. Prototype of the Poly-Articulated Robotic System
The experimental prototype was created according to the design parameters imposed by the 3D virtual model, but this was also validated through the virtual simulation outputs. This has two main units, namely one for the robotic system actuation and the other represented by the flexible unit. The translation motion was transformed and transmitted from the rotational motors through nine nut–screw mechanical transmissions to the considered module from the flexible unit. The actuation unit also has mechanical devices, which are used for axial displacement compensation. The designed prototypes for both flexible unit forms, i.e., the cylindrical and the tronconic one, are shown in Figure 30. The actuation unit, which is common to both solutions, is shown in Figure 31 and Figure 32.

Figure 31.
The poly-articulated robotic actuation unit.

Figure 32.
Guiding systems for the nut–screw mechanical transmissions.
7. Experimental Motion Analysis
Both prototypes were experimentally evaluated through several tests in dynamic conditions. The purpose of this analysis is to validate the experimental prototype and also to analyze the command and control protocols. In order to achieve the proposed aims, CONTEMPLAS video motion equipment was used [27]. The principle of this analysis is shown in Figure 33. Thus, the experimental test results of the evaluated robotic system are presented for one solution, namely the one with a tronconic form.
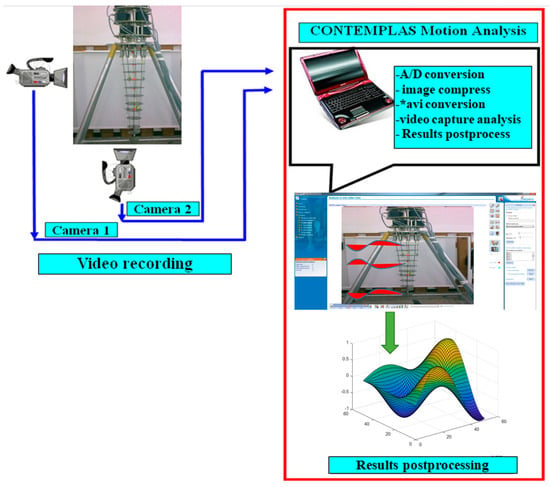
Figure 33.
CONTEMPLAS motion analysis workflow.
This equipment has two cameras that can record video sequences up to 350 frames/second. The video recording was done by keeping the same conditions imposed through virtual simulations, namely period and working actuation modes for all modules. The first step of the proposed experimental analysis was to perform a setup for the equipment and also for the poly-articulated robotic system in order to evaluate its workspace. This is shown in Figure 34. The video cameras were placed at an angle of 90 degrees between them and a distance of 2.5 m from the analyzed prototype, as can be seen in Figure 34.

Figure 34.
Experimental analysis setup for the analyzed robotic system.
Twelve reflexive markers were attached to the poly-articulated robotic system to evaluate the workspace, which was characterized by the developed experimental trajectories. The equipment hardware and Templo Plus V2010 software can identify the marker position in each sequence of the recorded video sequence. In this case, the task for the analyzed markers attached to the central vertebrae was trajectory variations, according to Figure 35. Some snapshots during trajectory evaluation can be observed in Figure 36.

Figure 35.
Marker attachment on the poly-articulated robotic system.

Figure 36.
Some snapshots during the experimental tests for trajectory evaluation.
By having in sight the obtained experimental analysis tests, a comparative study was done based on the obtained results through virtual simulations and the ones from experimental tests. This analysis was done with LS-Dyna R7.1 software in order to establish the accuracy of the performed motion. Thus, the most important results are represented through the total deformation of the entire poly-articulated robotic system. This comparative study will be focused on monitoring the central marker position situated on the end disk from the distal module. These results are shown in Figure 37, Figure 38 and Figure 39, where the behavior of the deformation components represents the proof of validation of the poly-articulated robotic system prototype.
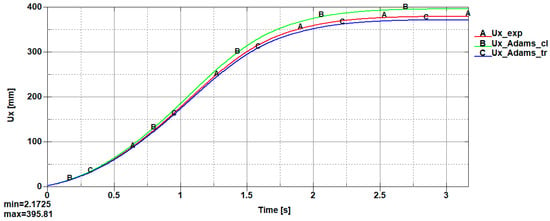
Figure 37.
Total displacement on the X-axis of the poly-articulated robotic system vs time: A—Experimental tronconic model; B—Adams virtual model with a cylindrical flexible unit; C—Adams virtual model with a tronconic form of the flexible unit.
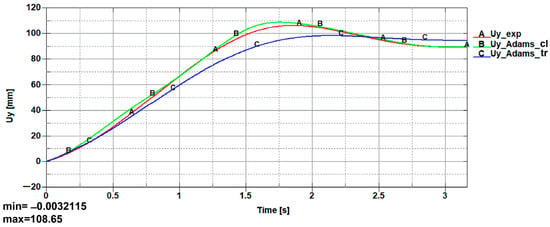
Figure 38.
Total displacement on the Y-axis of the poly-articulated robotic system vs time: A—Experimental tronconic model; B—Adams virtual model with a cylindrical flexible unit; C—Adams virtual model with a tronconic form of the flexible unit.
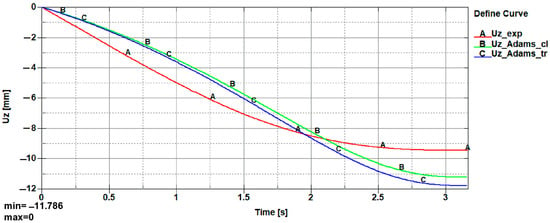
Figure 39.
Total displacement on the Z-axis of the poly-articulated robotic system vs time: A—Experimental tronconic model; B—Adams virtual model with a cylindrical flexible unit; C—Adams virtual model with a tronconic form of the flexible unit.
Thus, Figure 37 shows a diagram of the X-direction total displacement for the obtained prototype, respectively, virtual simulations carried out with MSC Adams software. From this, it can be remarked that all models have the same trajectory, ranging from 0 to a maximum value of 398.22 mm obtained for the poly-articulated robot virtual model with a cylindrical form of the flexible unit. In the case of the experimental prototype, this reaches a value of 382.31 mm and is much closer to the third one, respectively, to the one characterized by a flexible unit with a tronconic form. The third one reaches a value of 380.77 mm. Thus, the accuracy is around 4.188%.
By having in sight the plot reported in Figure 38, it can be observed that all paths of the analyzed models have an appropriate trajectory in the case of the Y-axis total displacement, and a maximum value of 109.63 mm was recorded, which corresponds to the poly-articulated robot virtual model characterized by a flexible unit with a cylindrical form. In the case of the prototype analyzed during experimental tests, the maximum recorded value was 106.32 mm. In the third case, namely the virtual model characterized by the tronconic form, this reaches a maximum value of 99.64 mm. In this case, an accuracy of 6.064% was established.
A similar comparative analysis was done in the case of total displacement on the Z-axis, as it was reported in the diagram from Figure 39. In this case, all paths have appropriate trajectories, but different values were recorded for the analyzed models. By having in sight the poly-articulated virtual model simulated with MSC Adams, with a tronconic form of the flexible unit, a minimum value of –11.774 mm can be observed, but a minimum value of –9.678 mm was recorded for the experimental analysis of the poly-articulated robot prototype. In the latter case, namely the robotic system virtual model with a cylindrical form of the flexible unit, a minimum value of –11.33 millimeters was recorded, which results in an accuracy of 8.783%.
8. Conclusions
A prototype of a poly-articulated robotic system was validated in this research. This robot can be used in several fundamental domains like the automotive industry, medicine, military defense and even architecture. The virtual prototyping of the robotic system was developed with MSC Adams. An interface was defined for importing the proposed CAD model with all mechanism components considered as subassemblies and also considering the imposed contour conditions. An equivalent kinematic model of the proposed mechanical system was built by having in sight the kinematic joints and some local reference systems located in the mass centers of the flexible unit links, respectively, in the joint centers. The motor joints were defined according to motion laws set for all actuators on a time interval of 3 s. A procedure was identified for transforming the solid bodies into deformable ones by meshing them in tetrahedral finite elements. This was done by taking into account the connection type between elements and the definition of the node setup in the master and slave mode.
An elastic dynamic analysis was performed, which implies crossing two stages: a modal analysis for evaluating the natural frequencies and the mode shapes for the flexible kinematic elements and a dynamic analysis of the flexible unit based on the Craig–Bampton method in order to establish the kinematic parameter variation, depending on time.
The prototype validation core focuses on the motion of central vertebrae as a rigid body but also as a deformable body. The motion analysis was performed on specific nodes/markers, depending on the global reference system and on other local reference systems.
The rigid body motion is defined through a generalized coordinate system set that represents the mobile reference system origin identification according to the global reference system and its orientation through Euler angles. The deformable body motion was defined through a modal coordinate set based on the Craig–Bampton method.
The elastic deformation variations were determined depending on the time for angular and linear displacements for the end node placed in the central vertebrae. It is important to remark that the diagram results represented through numerical values and curve trajectories from virtual simulations are similar to the ones obtained in the experimental analysis for the designed robotic system prototype.
The virtual prototyping created with Ansys has a complex nature, using the dynamic characterization of the contact models created between deformable elements and disks. The performed dynamic analysis has a nonlinear behavior.
For the contact definition, the following conditions were taken into account: the translational motion between actuation vertebrae and disks, the finite element network at the level of contact areas, penetration phenomena between the contact surfaces and targeted ones and differential equations between the contact type and integration method. The processed model evaluated with Ansys software is completely different from the one analyzed with MSC Adams, because all the elements are in contact, and these are considered deformable ones.
Variation laws of the kinematic parameters were identified through this analysis, depending on time and stress, deformations, strain and the resulting actuation forces from the drive elements. The flexible unit deformed shapes were obtained through numerical simulations. These shapes define the robotic system workspace and are influenced by the time setup for the command and control procedure. The deformation behavior of the central vertebrae was kept in sight through time variation diagrams.
The major contribution brought about by this research is represented by the contact model development with dumping control possibilities; the penetration depth between different surface types such as contact and target; the normal stiffness factor for tests and the choice of suitable ones from ANSYS-allowed formulations (Pure penalty, MPC, Augmented Lagrange and Normal Lagrange). Thus, the obtained flexible unit geometrical model was analyzed and parametrized with the aid of the DesignModeller module from ANSYS R14.5 software, with a view to envisaging future research like optimization processes of the components in a dynamic mode.
The virtual models of the flexible unit achieved in MSC Adams 2012 and ANSYS R14.5 software are parametrized, with optimization possibilities under kinematic- and dynamic-specific conditions.
The robotic system architecture, which includes the actuation system, i.e., the command and control unit, represents the fundamental base of a robotic system conceptual design for a future miniaturized robotic system especially designed for minimally invasive surgery procedures like [17].
Author Contributions
Conceptualization, N.D. and S.D.; methodology, S.D. and N.D.; software, I.G.; validation, C.C., S.D. and N.D.; formal analysis, I.G.; investigation, C.C.; resources, S.D.; data curation, S.D. and I.G.; writing—original draft preparation, C.C.; writing—review and editing, C.C. and N.D.; visualization, N.D.; supervision, C.C. and N.D.; project administration, N.D.; funding acquisition, N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data generated in the current research is pre-sented in the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bajo, A.; Simaan, N. Hybrid Motion/Force Control of Multibackbone Robots. Int. J. Robot. Res. 2015, 35, 1–13. [Google Scholar] [CrossRef]
- Hannan, M.; Walker, I. The ‘Elephant Trunk’ Manipulator, Design and Implementation. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Como, Italy, 8–12 July 2001; pp. 14–19. [Google Scholar]
- Hirose, S. Biologically Inspired Robots: Snake-like Locomotors and Manipulators; Applied Mechanics Reviews; Oxford University Press: Oxford, UK, 1995; Volume 48, p. 27. [Google Scholar]
- Kim, Y.; Cheng, S.; Kim, S.; Iagnemma, K. Design of a Tubular Snake-Like Manipulator with Stiffening Capability by Layer Jamming. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Roppenecker, D.B.; Schuster, L.; Coy, J.A.; Traeger, M.F.; Entsfellner, K.; Lueth, T.C. Modular Body of the Multi Arm Snake-Like Robot. In Proceedings of the International Conference on Robotics and Biomimetics, Bali, Indonesia, 5–10 December 2014. [Google Scholar]
- Gu, X.; Ren, H. A Survey of Transoral Robotic Mechanisms: Distal Dexterity, Variable Stiffness, and Triangulation. Cyborg Bionic Syst. 2023, 4, 0007. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Ma, Z.; Yan, S.; Zhou, Y. Cucker–Smale Flocking Behavior for Multiagent Networks With Coopetition Interactions and Communication Delays. IEEE Trans. Syst. Man Cybern. Syst. 2024, 1–10. [Google Scholar] [CrossRef]
- Shi, L.; Ma, Z.; Yan, S.; Ao, T. Flocking Dynamics for Cooperation-Antagonism Multi-Agent Networks Subject to Limited Communication Resources. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1396–1405. [Google Scholar] [CrossRef]
- Kim, S.-H.; Choi, H.-S.; Keum, B.; Chun, H.-J. Robotics in Gastrointestinal Endoscopy. Appl. Sci. 2021, 11, 11351. [Google Scholar] [CrossRef]
- Clark, A.B.; Mathivannan, V.; Rojas, N. A Continuum Manipulator for Open-Source Surgical Robotics Research and Shared Development. IEEE Trans. Med. Robot. Bionics 2021, 3, 277–280. [Google Scholar] [CrossRef]
- Ivanescu, M.; Cojocaru, D.; Bizdoaca, N.; Florescu, M.; Popescu, N.; Popescu, D.; Dumitru, S. Boundary Control by Boundary Observer for Hyper-redundant Robots. Int. J. Comput. Commun. Control 2010, 5, 755–767. [Google Scholar] [CrossRef]
- Xu, S.; He, B.; Zhou, Y.; Wang, Z.; Zhang, C. A Hybrid Position/Force Control Method for a Continuum Robot With Robotic and Environmental Compliance. IEEE Access 2019, 7, 100467–100479. [Google Scholar] [CrossRef]
- Wooten, M.B.; Walker, I.D. Environmental Interaction With Continuum Robots Exploiting Impact. IEEE Robot. Autom. Lett. 2022, 7, 10136–10143. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Galloway, K.; Godage, I.; Simaan, N.; Barth, E. Modal-Based Kinematics and Contact Detection of Soft Robots. Soft Robot. 2020, 8, 298–309. [Google Scholar] [CrossRef]
- Liu, H.; Farvardin, A.; Pedram, S.A.; Iordachita, I.; Taylor, R.H.; Armand, M. Large Deflection Shape Sensing of a Continuum Manipulator for Minimally-Invasive Surgery. In Proceedings of the IEEE International Conference on Robotics and Automation ICRA, Seattle, WA, USA, 26–30 May 2015; pp. 201–206. [Google Scholar]
- Desai, J.P.; Sheng, J.; Cheng, S.S.; Wang, X.; Deaton, N.J.; Rahman, N. Towards Patient-Specific 3D-Printed Robotic Systems for Surgical Interventions. IEEE Trans. Med. Robot. Bionics 2019, 1, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Dumitru, N.; Ciurezu-Gherghe, L.; Copilusi, C.; Geonea, I.; Dumitru, S. Theoretical and experimental study methods for a robotic system with deformable elements used in minimally invasive surgery. Mech. Mach. Theory 2022, 167, 104459. [Google Scholar] [CrossRef]
- Zhang, Z.; Dequidt, J.; Back, J.; Liu, H.; Duriez, C. Motion control of cable-driven continuum catheter robot through contacts. IEEE Robot. Autom. Lett. 2019, 4, 1852–1859. [Google Scholar] [CrossRef]
- Oliver-Butler, K.; Till, J.; Rucker, D.C. Continuum robot stiffness under external loads and prescribed tendon displacements. IEEE Trans. Robot. 2019, 35, 403–419. [Google Scholar] [CrossRef]
- Goldman, R.E.; Bajo, A.; Simaan, N. Compliant Motion Control for Multisegment Continuum Robots with Actuation Force Sensing. IEEE Trans. Robot. 2014, 30, 890–902. [Google Scholar] [CrossRef]
- Dumitru, S.; Cojocaru, D.; Marghitu, D. Computer Aided Design of a Hyper-redundant Manipulator. Adv. Electr. Comput. Eng. 2013, 13, 51–56. [Google Scholar] [CrossRef]
- Grazioso, S.; Di Gironimo, G.; Siciliano, B. A geometrically exact model for soft continuum robots: The finite element deformation space formulation. Soft Robot. 2019, 6, 790–811. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, C.C. Coupling of Substructures for Dynamics Analyes. AIAA J. 1998, 6, 1313–1319. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, K.; Qian, K.; Hao, J.; Zhang, Z.; Shi, C. An Operating Stiffness Controller for the Medical Continuum Robot Based on Impedance Control. Cyborg Bionic Syst. 2024, 8, 0110. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Zhang, S.; Li, F.; Fu, R.; Li, H.; Zou, S.; Ma, N.; Qu, S.; Li, J. A Versatile Continuum Gripping Robot with a Concealable Gripper. Cyborg Bionic Syst. 2023, 4, 0003. [Google Scholar] [CrossRef]
- Chirikjian, G.S.; Burdick, J.W. A Modal Approach to Hyper-Redundant Manipulator Kinematics. IEEE Trans. Robot. Autom. 1994, 10, 343–353. [Google Scholar] [CrossRef]
- CONTEMPLAS User Manual. Available online: www.contemplas.com (accessed on 23 July 2018).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).