1. Introduction
The waverider is a distinct configuration of a hypersonic vehicle engineered to maintain the shock wave generated by the vehicle attached to its leading edge, offering numerous advantages [
1]: (a) this shock wave effectively separates the flow fields on the upper and lower surfaces of the vehicle, thus preventing high-pressure flow from spilling from the lower to the upper surface at the leading edge; (b) it ensures a uniform flow on the lower surface, which is optimal for scramjet engine intake; (c) the design of the waverider is derived through reverse engineering from a known flow field around a conical shape. This design approach will be elaborated on in later sections of this work.
The concept of the waverider was first put forward by Nonweiler in 1963 [
2]. At that time, the available technology was not advanced enough to produce a hypersonic air-breathing vehicle. Sandlin and Pessin offered an in-depth explanation of the design methodology for waveriders [
1]. A broad analysis of the significant design challenges associated with hypersonic flight vehicles is discussed in the work of Sziroczak and Smith [
3], where two types of vehicles, hypersonic transports and space launchers, are examined. Although these are distinct from waveriders, they share many design and construction challenges. Zhang et al. employed the three-dimensional Class–Shape Function Transformation (CST) method to determine the geometric shapes of Hypersonic Gliding Vehicles (HGVs) [
4]. Inviscid modeling methods, relying on modified Newton theory and the Prandtl–Meyer equation, were used to assess the aerodynamics of these vehicles. The use of the NSGA-II multi-objective optimization algorithm helped achieve designs with high lift–drag ratios and substantial volumetric efficiency. In his Ph.D. thesis, K. Kontogiannis considered the parameterization and manipulation of waverider forebody geometries, proposing a new three-dimensional leading-edge waverider design method, shifting from inverse to direct design methodologies [
5]. Additionally, Son et al. described an optimization framework for the inverse design of hypersonic waveriders [
6].
Since its introduction, the waverider has been a focal point of research. After conceptualizing the design, the next phase involves its analytical assessment. Various methods such as engineering correlations, flight tests, wind tunnel tests, and numerical simulations are employed not only for analysis but also for validating concepts and accumulating knowledge. While effective in the subsonic domain, these methods have shown limitations in reliability and implementation at hypersonic speeds. Ongoing research aims to refine these methods to master the hypersonic domain.
During the early quest for hypersonic flight, NASA designed, constructed, and tested a hypersonic vehicle [
7]. The vehicle demonstrated that it was capable of achieving speeds up to Mach 8. However, a closer look at wind tunnel data revealed an interesting phenomenon. It was observed that the vehicle’s aerodynamic performance parameter lift–drag ratio (L/D) decreased as Mach number increased. Kuchemann documented a decreasing trend in maximum L/D with increasing Mach numbers through extensive empirical research [
8], highlighting a significant challenge in traditional aerodynamic design and methodology in the hypersonic regime. Moreover, Bowcutt introduced a multidisciplinary approach to optimize waverider configurations, achieving relatively higher L/D ratios at higher Mach numbers [
9], a finding later corroborated by other researchers [
10,
11]. Nonweiler originally developed the waverider design technique in the 1950s to create a hypersonic wing for re-entry purposes [
12]. Despite early challenges due to the inherent sharpness of the waverider’s leading edge, which led to significant aerothermodynamic loads, and the limited volumetric efficiencies of initial thin configurations [
7] that did not account for viscous effects, advancements in numerical methods and computational resources in the 1980s enabled Bowcutt to optimize waveriders by predicting the viscous effects on their performance [
9]. This has spurred continued interest and research into waverider designs, although practical application in producing operational hypersonic vehicles remains a challenge.
Since Nonweiler [
2] introduced the waverider design concept, leveraging wedge flow dynamics to create the first waverider in aerospace science, numerous design studies have aimed to refine and optimize his initial concept. The majority of these studies model the flow as two-dimensional and inviscid, either planar or axisymmetric [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22]. A smaller subset has considered three-dimensional inviscid flow, both without and with chemical reactions, as in references [
23,
24,
25,
26,
27,
28] and [
29,
30], respectively. Only a limited number of investigations have addressed three-dimensional viscous flow, incorporating turbulence [
31]. This study focuses on analyzing the full three-dimensional viscous flow field around the designed waverider.
2. Waverider Design Methodology
Waveriders are crafted using an inverse design methodology, a process that leverages the characteristics of a hypersonic flow environment. This approach utilizes the streamlines of the inviscid flow field post-shock as the basis for designing the compression stream surface, typically the lower surface of the waverider geometries. The end result is a streamlined geometry optimized for hypersonic flows. The geometry of the lower surface, defined by a set of adjacent streamlines, ensures the leading edge remains attached to the shock wave. Below is an outline of the algorithm used to generate waverider geometries:
Determining and designing the initial flow field in the direction of the flow.
Solving for the flow field using computational fluid dynamics methods, such as the Taylor–Maccoll equation [
32], or the Euler, or Navier–Stokes equations.
Mapping out the streamlines.
Applying osculating cone theory along the spanwise direction.
Refining and finalizing the model design.
To specify the initial flow conditions from which the waverider is derived, a cone with a predetermined angle
is first designed. Then, the inlet boundary conditions like Mach number, pressure, and temperature are set, and the resultant flow field is computed. After calculating the flow field, the streamlines can be computed by numerically solving the following set of ordinary differential equations (ODEs):
Using the Runge–Kutta method, the above set of equations can be integrated in time to obtain each streamline coordinate.
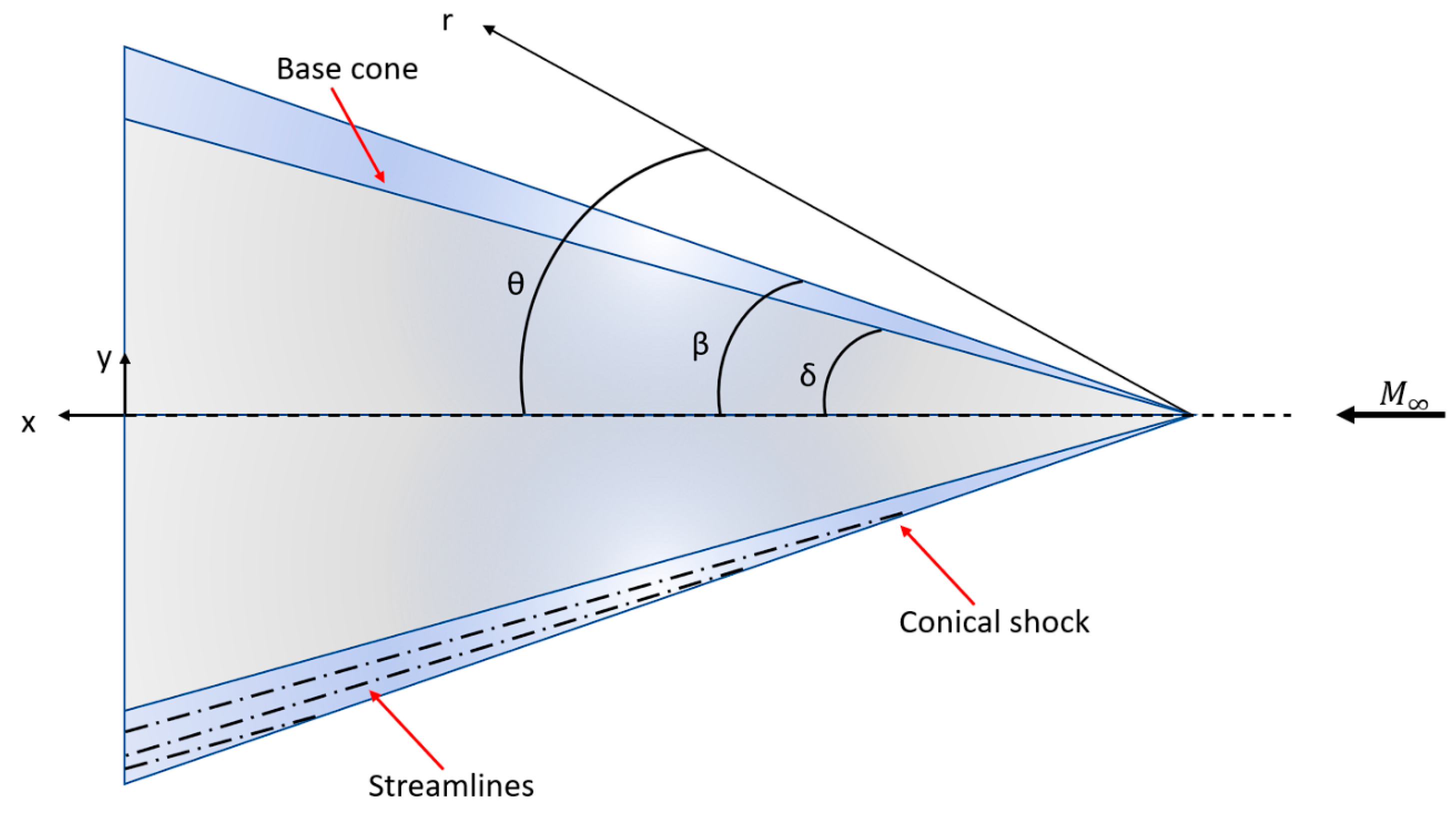
A schematic overview of the streamlines traced from a conical shock is depicted in
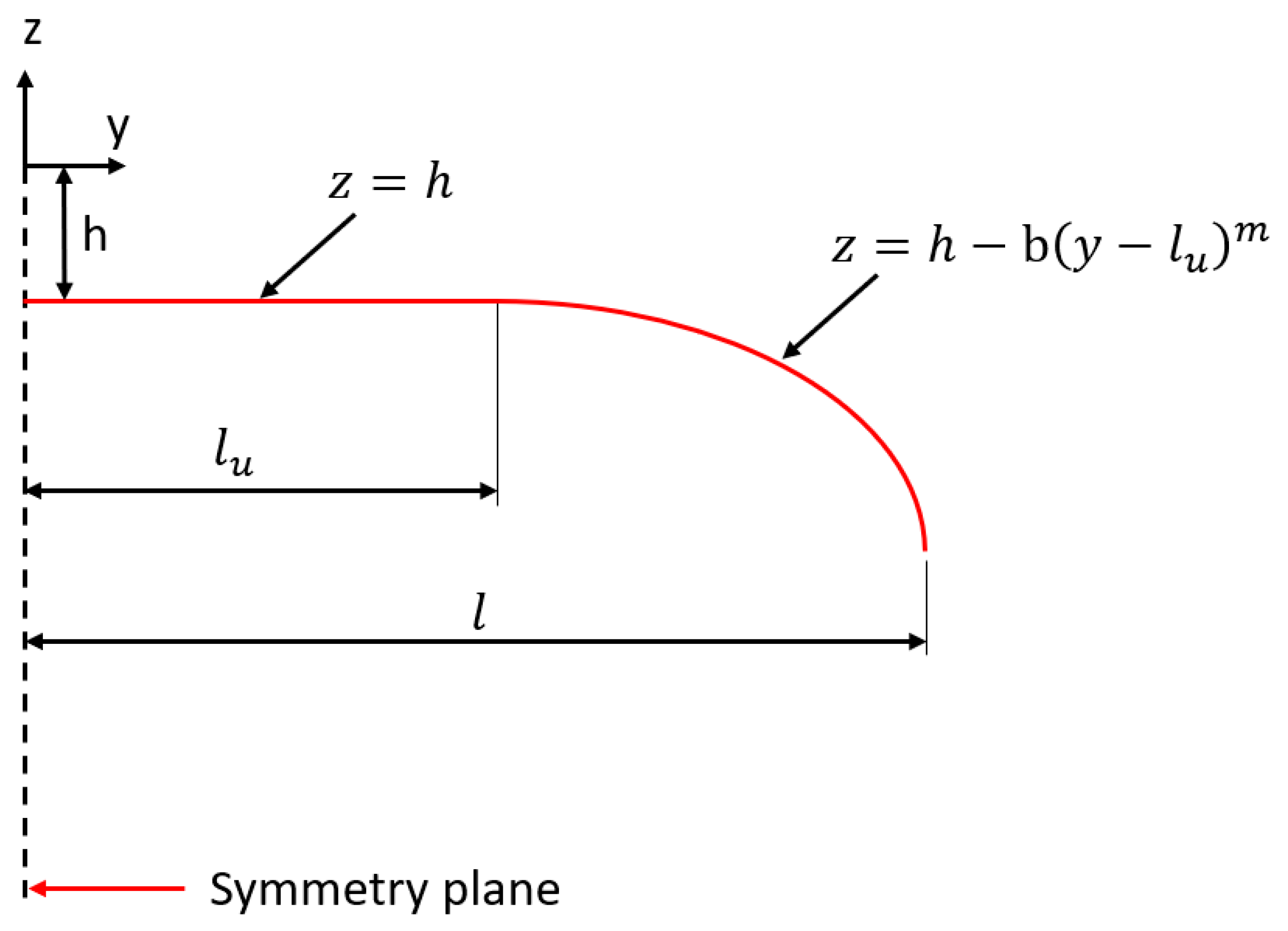
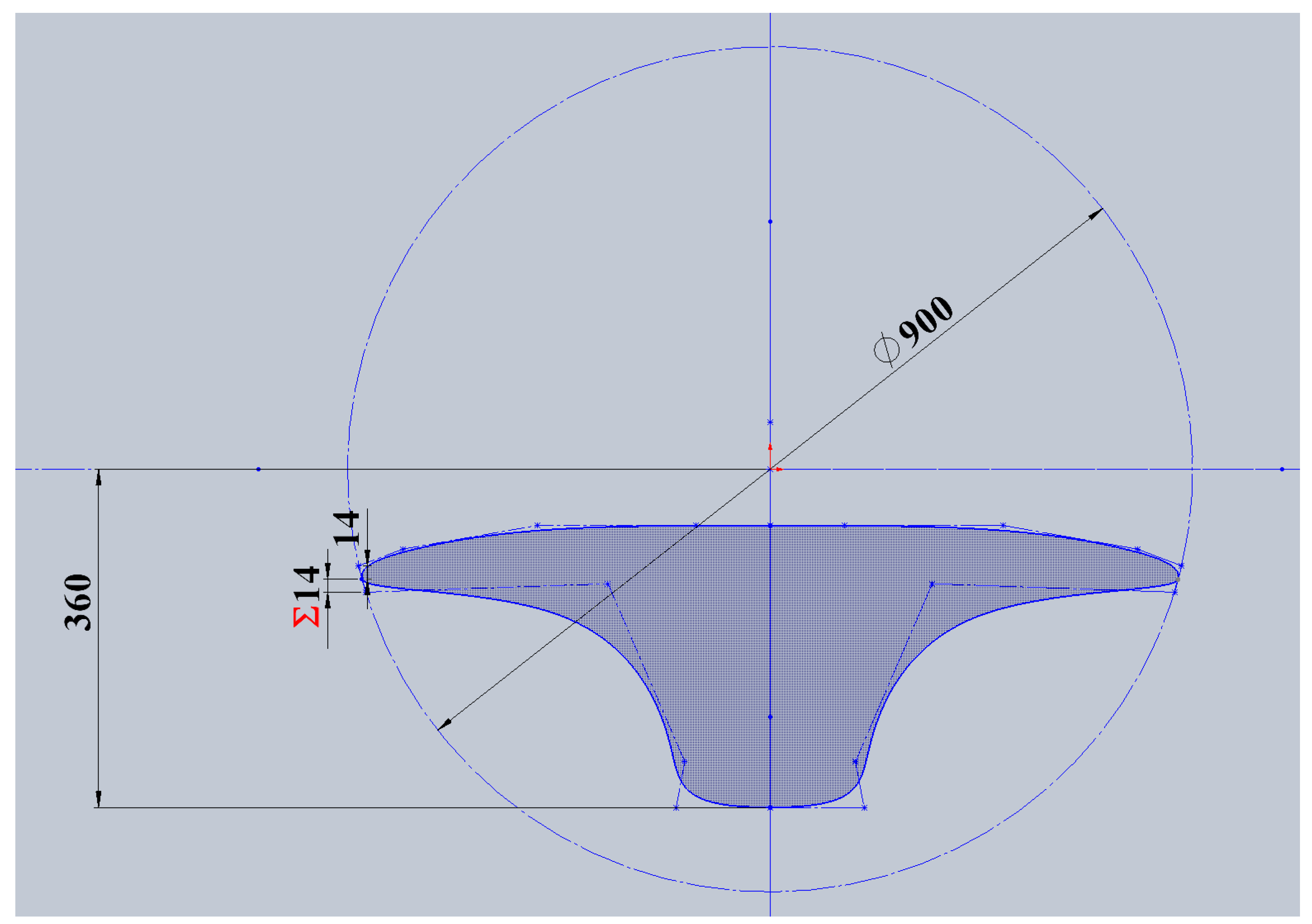
Figure 1. To establish a waverider geometry using the cone-derived method, one must first define a base curve. This curve is then projected onto the shock, aligned parallel to the freestream, to form the leading edge. Subsequently, the streamlines are traced backward from the leading-edge positions on the shock to the base plane, creating the waverider’s compression (lower) surface. Beyond the analytical Equation (1), an alternative, simpler method can be employed to trace the streamlines by following tangential paths to the base cone surface, thus facilitating the generation of the compression surface geometry. The base curve equation, essential for designing the waverider, is illustrated around the symmetry plane in
Figure 2. The total width of the waverider is denoted by
, with
representing the flat section of the curve. The curved section of the curve is determined by the equation depicted in
Figure 2. The value of
is calculable from
,
, and
, values that are defined following the resolution of the initial conical flow field.
For a practical waverider design, addressing the sharpness of the leading edge is crucial. Thus, a pragmatic design strategy incorporates blunting techniques to manage this characteristic. Blunting the leading edge and the junctions where two stream surfaces converge mitigates heating effects and results in a geometry more feasible for manufacturing. However, blunting does deviate from the ideal waverider design, allowing some pressure leakage from the lower to the upper surface, which in turn increases drag and diminishes the aerodynamic efficiency of the waverider. Studies [
33,
34] have demonstrated that while blunting reduces the heat flux experienced by the vehicle, it adversely impacts the lift–drag ratio (L/D). Despite this, a blunted waverider design can still offer superior aerodynamic performance compared to other design alternatives. The extent and nature of the blunting are crucial and require a balance between reducing thermal stresses and optimizing aerodynamic efficiency. With various possible configurations for a waverider, there are numerous approaches to designing a blunt leading edge.
There are two primary methods for blunting the leading edge of a waverider: one involves removing material from the edge, while the other entails adding material to it [
35]. Tincher and Burnett have proposed that the addition of material to the leading edge incurs a lower aerodynamic penalty compared to material removal [
35]. This approach is favored because it allows for maintaining more of the original aerodynamic profile, potentially minimizing the negative impacts on performance that are associated with leading edge modifications.
4. Application to a Specific Waverider Design
In the development of a waverider designed for Mach 7, the initial step involved crafting a 7-degree cone, 2 m in length with a 1 cm blunt leading edge, as depicted in
Figure 3. The three-dimensional flow field around this cone was then resolved using the Direct Simulation Monte Carlo (DSMC) method. The simulation conditions were derived from the US standard atmosphere model, representing the flow characteristics at an altitude of 90 km. The specific flow conditions and the parameters used in the DSMC simulation are detailed in
Table 1 and
Table 2, respectively. In the present simulations, the gas comprises 79% N
2 and 21% O
2; rotational and vibrational relaxation numbers are treated as constants. The rotational relaxation number was set to Z
rot = 5 for both N
2 and O
2, whereas a vibrational relaxation number Z
vib = 52,600 for N
2 and Z
vib = 17,900 for O
2 have been used. Elastic collisions are performed using the Variable Soft Sphere (VSS) model [
39] while inelastic collisions are performed using the Borgnakke–Larsen model [
40]. For the selection of collision partners, we utilized the near-collision partner algorithm. This algorithm selects collision partners within a sphere whose radius is the distance a particle travels in one timestep. This approach enables the use of a grid cell size larger than one mean free path while maintaining collision accuracy [
41] although our cell size is close to 1/3 of the mean free path. Due to the low temperatures occurring in these flight conditions, chemical reactions are not enabled; thus, the flow is assumed to be in thermal equilibrium. All the simulations were conducted in the ARCHER2 UK supercomputing facility.
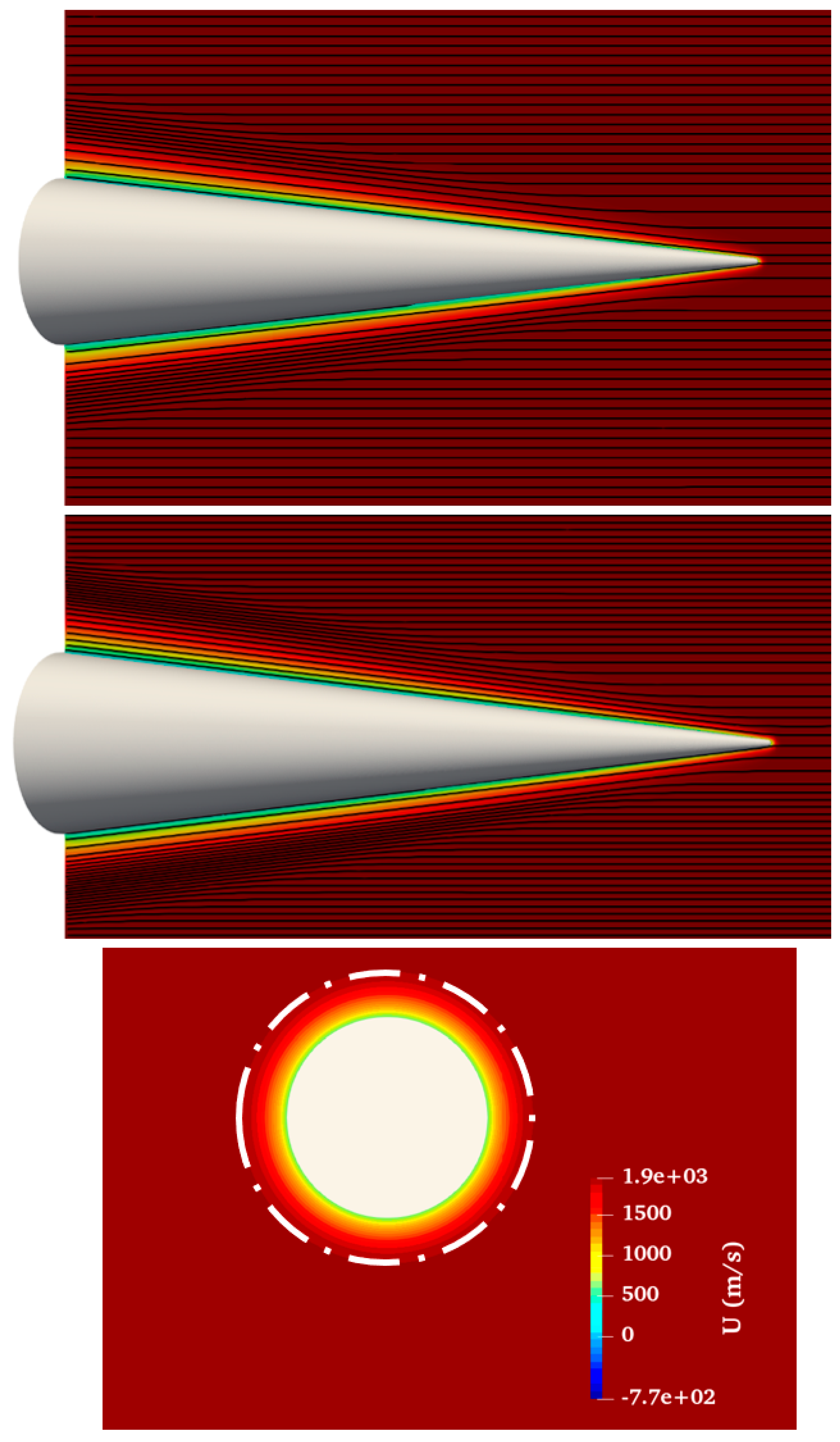
As it was previously mentioned, all the simulations were carried out using the open-source parallel DSMC code SPARTA (Stochastic Parallel Rarefied-gas Time-accurate Analyzer), which was developed at Sandia National Laboratories [
38]. After computing the three-dimensional flow field around the 7-degree cone, the flow streamlines were extracted at specific parallel planes to delineate the shockwave boundaries.
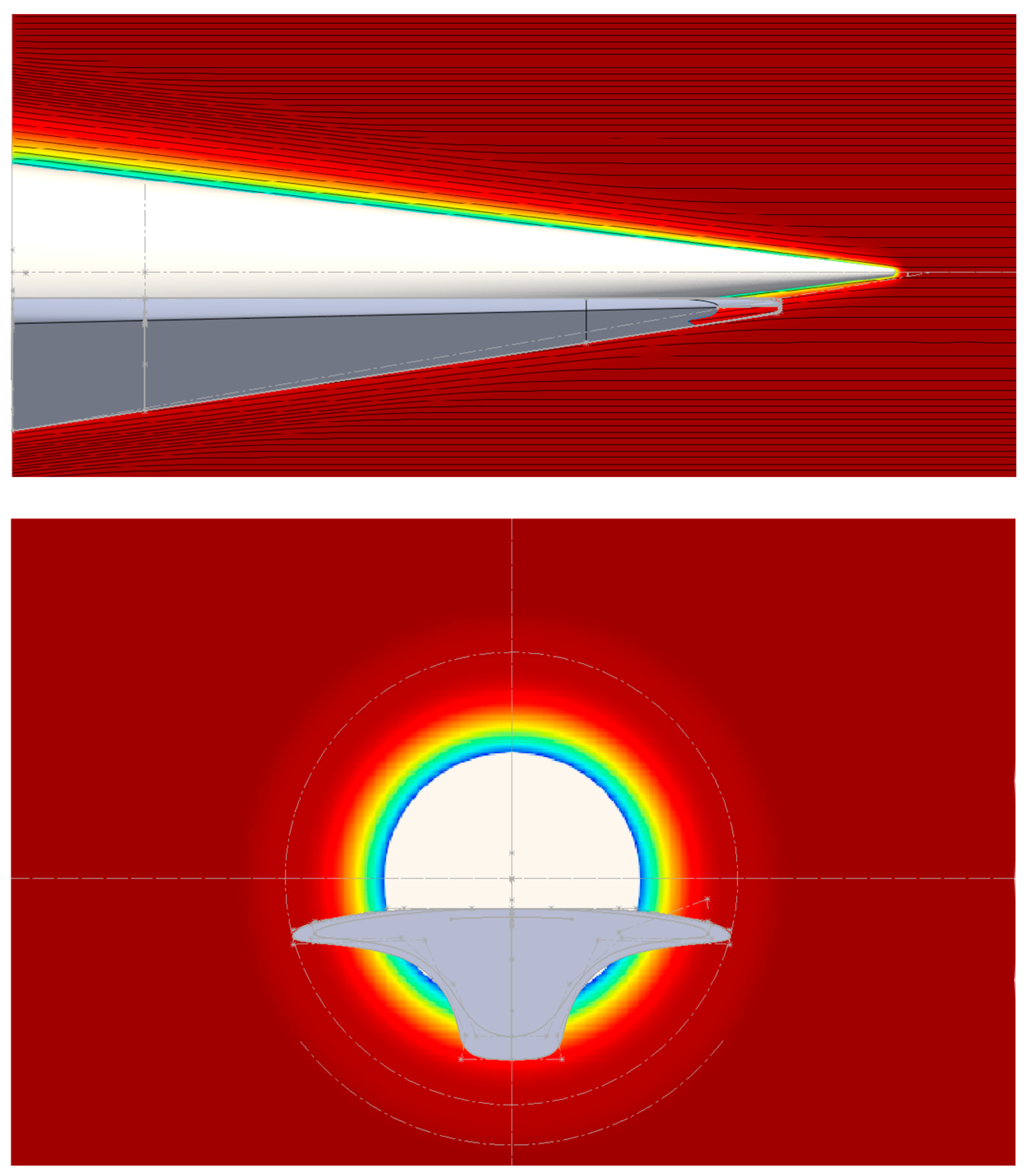
Figure 4 offers a visualization of these calculated flow field streamlines. The shock boundaries are discernible by the bending of the flow streamlines in both the side and top planes, and by a change in the color of the streamwise velocity flow field at the rear plane behind the cone.
After obtaining the flow planes from the DSMC simulation, these are imported into a Computer-Aided Design (CAD) software (SolidWorks 2021) to precisely define the geometry of the waverider. The design process begins at the rear of the vehicle, crafting curves that are tangent to the observed circular shock shape, with the first characteristic cross-section displayed in
Figure 5 (bottom) and
Figure 6. As seen in
Table 1, due to the low Reynolds number the flow falls within the laminar regime.
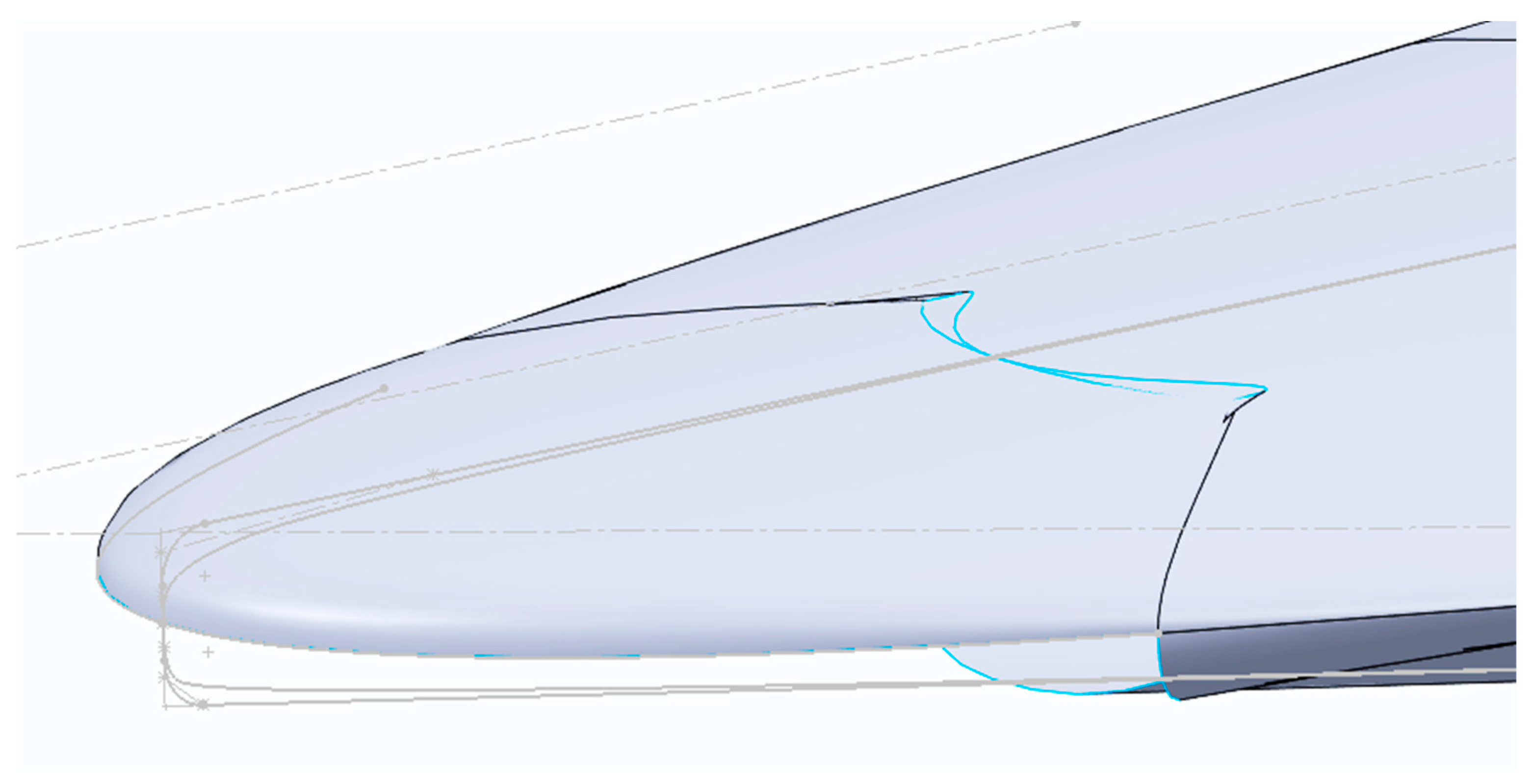
To ensure the design remains practical for real-world applications, the leading edges of the waverider are fashioned to be blunt rather than sharp. To accurately control the bluntness of the leading edges, a four-point Bezier curve is utilized to sculpt the leading-edge profile. This method provides the flexibility to finely adjust the curvature and thus tailor the aerodynamic and thermal properties of the edge. Similarly, additional sections along the waverider’s longitudinal axis are designed at intervals of every 30 cm. Both the upper and lower surfaces of the waverider are defined by the shockwave boundaries generated from the initially prescribed 7-degree cone geometry. This approach ensures that the final waverider design is optimized within the constraints set by the initial flow conditions and the aerodynamic needs of hypersonic travel.
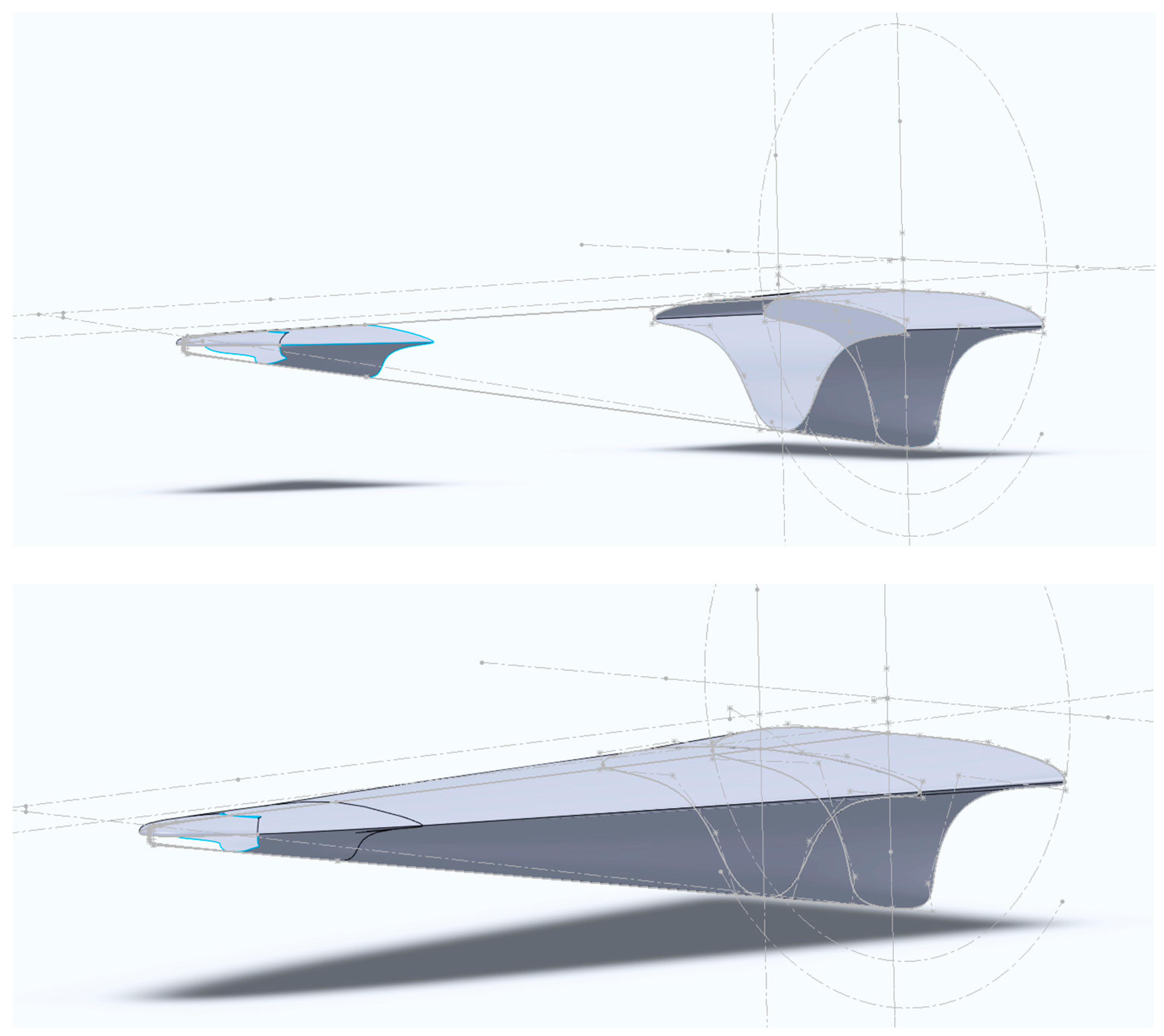
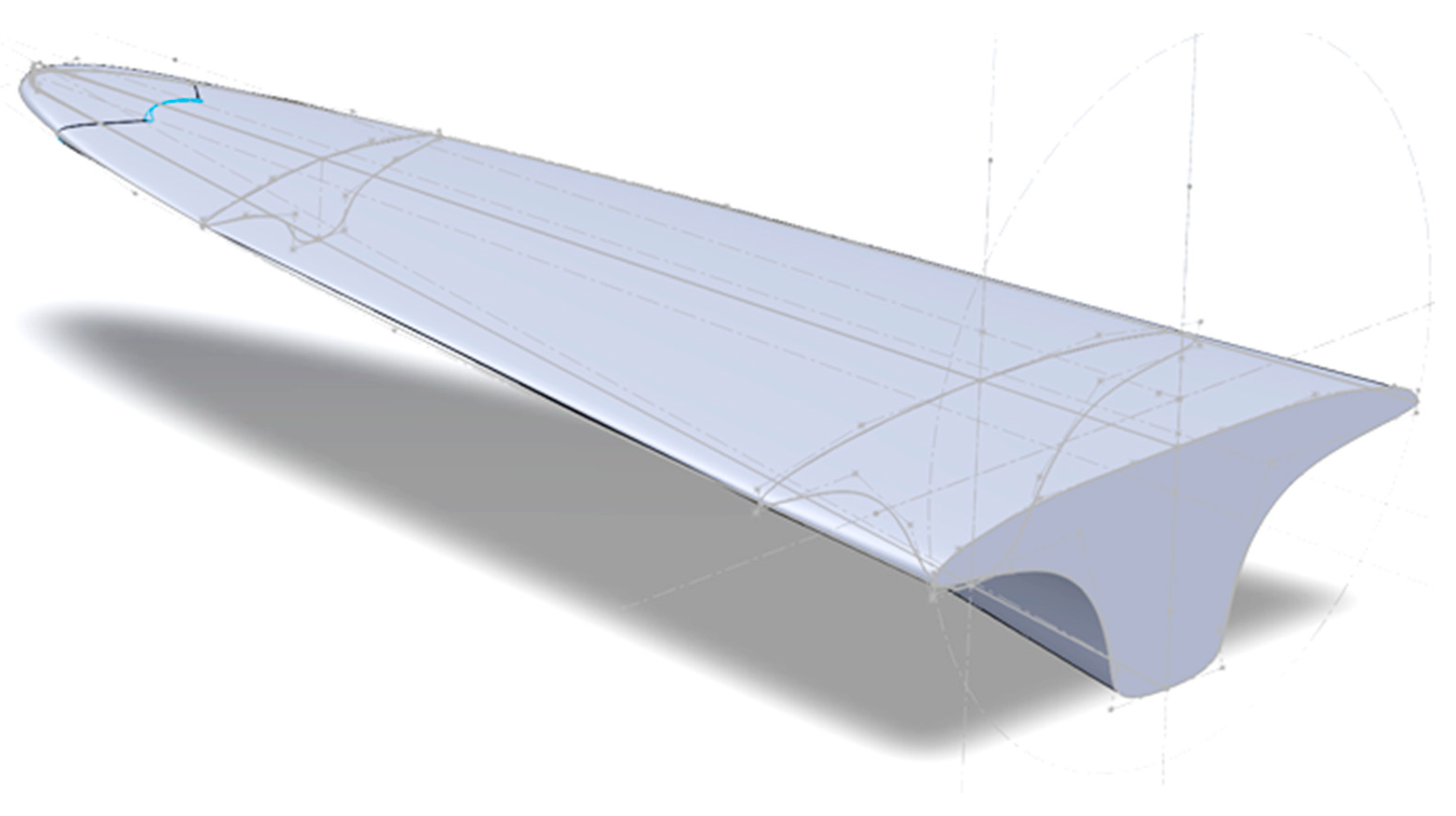
Figure 7 provides a visual representation of the various sections of the waverider geometry, although not all the sections are displayed to maintain clarity. Upon completing the design of all the sections, a loft operation with tangency constraints is employed to generate the surfaces of the waverider. To simplify the design process and leverage the symmetry of the flow field, only half of the final geometry is initially designed. This half is then mirrored around the symmetry plane to produce the complete vehicle structure.
The methodology of the osculating cones, as described earlier, serves as a robust computational framework for designing hypersonic waveriders. Hypersonic aerodynamics involves dealing with extreme temperatures, high pressures, and intricate shock wave interactions, making the design process inherently complex. By breaking down the methodology into discrete steps, this approach allows for a detailed focus on both the theoretical and practical aspects, guiding the creation of these advanced hypersonic vehicles. This structured design process ensures that each aspect of the vehicle’s performance and structural integrity is considered, leading to the development of effective and efficient hypersonic waveriders.
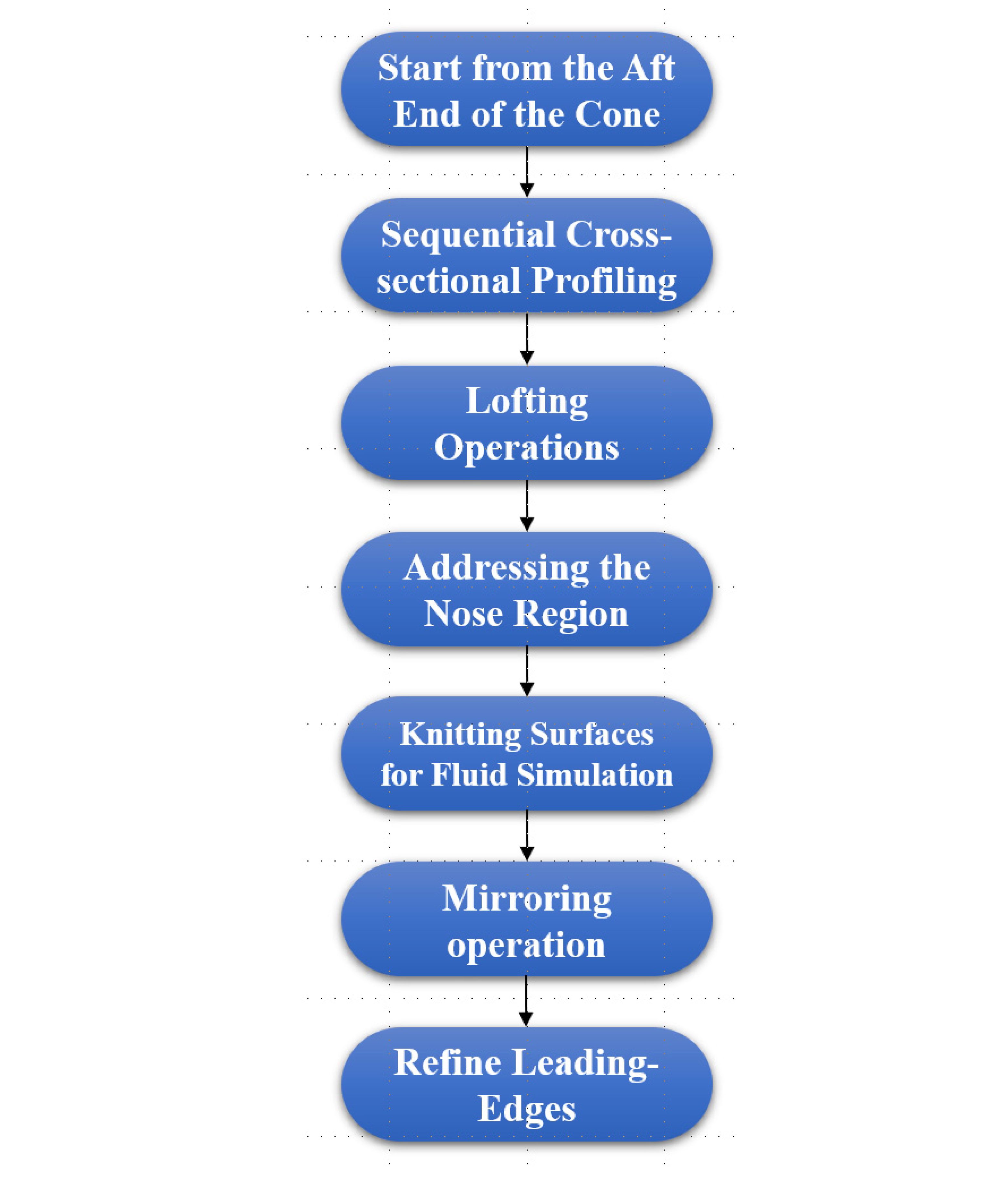
The design process for a hypersonic waverider involves a meticulous and structured approach, crucial for achieving aerodynamic efficiency and structural integrity under extreme conditions. Here is a detailed breakdown of each step in the design procedure:
- Step 1:
Initiating at the Aft End of the Cone
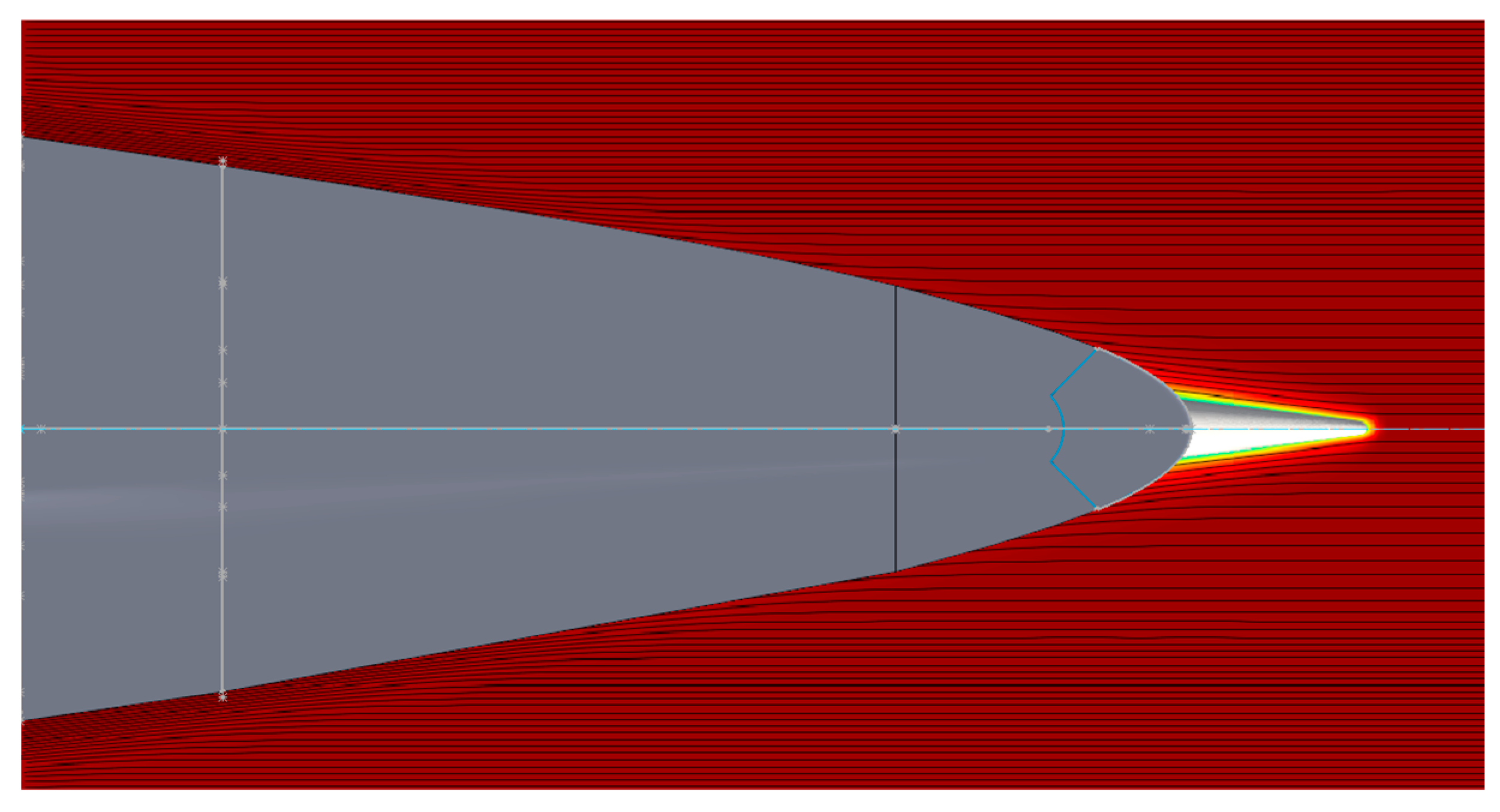
The design process begins at the trailing end of a cone, which is pivotal for setting the initial conditions of the flow field. Here, the shock wave boundaries are meticulously defined, shown as dashed white lines in
Figure 4 (bottom). This foundational step is critical as it establishes the first profile of the waverider. The design ensures that both the leading edge and the lower surface of this profile are tangentially aligned with the shock wave boundaries, minimizing drag and enhancing aerodynamic efficiency.
- Step 2:
Sequential Cross-section Profiling
Moving forward, the cross-sectional planes are taken at intervals of about 30 to 40 cm along the cone’s length. Each plane provides a template for shaping a segment of the vehicle’s body, tailored to the specific aerodynamic conditions of that segment. This step is akin to sculpting the individual slices of the vehicle, each optimized for its particular flow dynamics.
- Step 3:
Lofting Operation
The individual profiles generated in Step 2 are then interconnected through a lofting operation. This technique merges the profiles to form the continuous outer skin of the waverider, as seen in
Figure 7. The operation uses interpolation methods to ensure a smooth contour transition between sections. However, the profiles narrow as they approach the cone’s apex, which presents challenges in maintaining the structural and aerodynamic continuity.
- Step 4:
Addressing the Nose Region
In the nose region, where profiles become exceedingly slender, traditional lofting techniques are less effective. To address this, boundary surfaces that conform to the curvature of the original cone are introduced. As depicted in
Figure 8, these surfaces form the nose section’s outer skin, integrating seamlessly with the lofted sections to maintain aerodynamic integrity.
- Step 5:
Knitting Surfaces for Fluid Simulation
Following the design of the nose and main body sections, a knitting operation is employed to merge all the surface segments into a unified, watertight structure. This integration is crucial for the accuracy of subsequent fluid dynamics simulations, ensuring no gaps or inconsistencies exist that could compromise the model’s stability or precision. The completion of this step results in a complete vehicle geometry, illustrated in
Figure 9.
- Step 6:
Mirroring Operation
To enhance design efficiency and reduce computational demands, only half of the vehicle is modeled initially. The other half is created through a mirroring operation along a symmetry plane. This strategy not only simplifies the construction process but also facilitates faster iterations and refinements during the design phase, effectively halving the computational resources required.
- Step 7:
Refined Leading-Edge Design
This step in the waverider design methodology underscores the importance of optimizing the leading edges, which play a critical role in the vehicle’s overall performance and survivability in hypersonic conditions. Unlike the typical hypersonic designs that feature sharp leading edges to minimize drag and maximize speed, this approach recognizes the trade-offs such sharp edges bring, including high stress concentrations and reduced thermal resilience. These factors can lead to structural failures when subjected to the intense heat and pressure of hypersonic flight.
To address these challenges, the design incorporates three-point Bezier curves to blunt the leading edges. This technique allows for precise control over the curvature and tangency of the edges, making it possible to tailor them specifically to the demands of high-speed aerodynamics and thermal stress management. The Bezier curves not only help in smoothing the transition of the flow over the vehicle but also enhance the thermal robustness by distributing the stresses and heat more evenly across the surface. The use of Bezier curves in this context provides a balance between aerodynamic efficiency and structural integrity, ensuring the leading edges are not only effective in minimizing aerodynamic drag but are also capable of withstanding the harsh conditions of hypersonic flight. This nuanced approach results in a leading-edge design that is both geometrically optimized and thermodynamically durable, setting a new standard for hypersonic vehicle design. Through these steps, the waverider design is developed with precision, addressing both the high demands of hypersonic travel and the practical aspects of vehicle manufacture and simulation.
The osculating cones methodology is a sophisticated framework that draws from the fields of aerodynamics, computational fluid dynamics (CFD), and applied mathematics. This approach forms a holistic and in-depth pathway for designing hypersonic waveriders, effectively addressing the complex challenges associated with hypersonic flows and structural dynamics. The integration of these multi-disciplinary domains ensures that the resulting waverider design achieves not only aerodynamic efficiency but also exhibits enhanced thermal and structural robustness.
In the first phase of this computational exploration, the creation of an accurate computational mesh is crucial. This mesh is instrumental in precisely capturing the intricate geometric details of the waverider, particularly in the areas of high sensitivity, such as the leading edges. The precision in modeling these edges is paramount because even slight inaccuracies can lead to significant aerodynamic repercussions. This meticulousness in the mesh design is essential for replicating the intended geometrical features and ensuring that the simulations reflect the true aerodynamic behavior of the waverider. The computational surface mesh used in the Direct Simulation Monte Carlo (DSMC) method is specifically tailored to accommodate the unique characteristics of the waverider’s design, as illustrated in
Figure 10. This mesh allows for the detailed and accurate simulation of the flow dynamics around the waverider, capturing the essential interactions between the vehicle’s surface and the hypersonic flow. The DSMC method, known for its ability to model rarefied gas dynamics effectively, is particularly well-suited for analyzing the aerodynamic properties of vehicles operating at the upper edges of the atmosphere, where conventional CFD methods might struggle. For the simulation of the final waverider design, we used the SPARTA DSMC code, consistent with the simulation of the initial shock-generating cone. This consistency was maintained because the flight conditions did not change. As shown in
Figure 11 (bottom) the Knudsen number falls within the upper end of the slip regime or within the transition regime.
5. Simulation Results
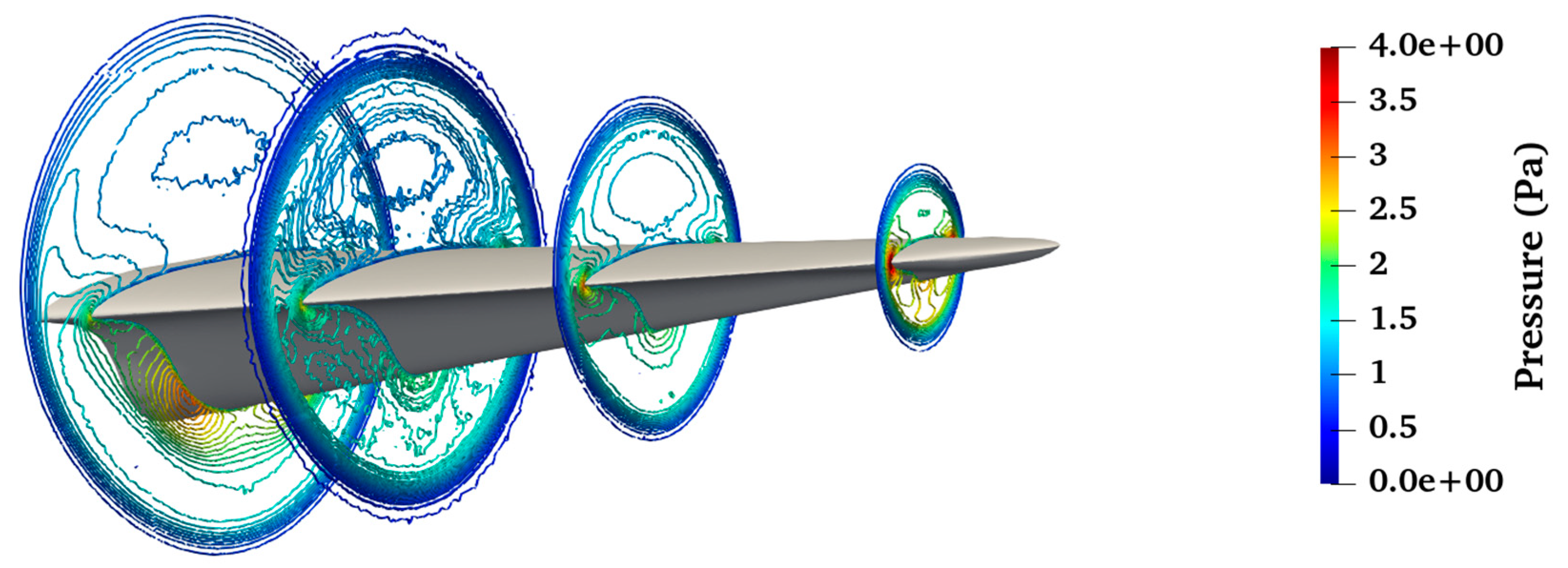
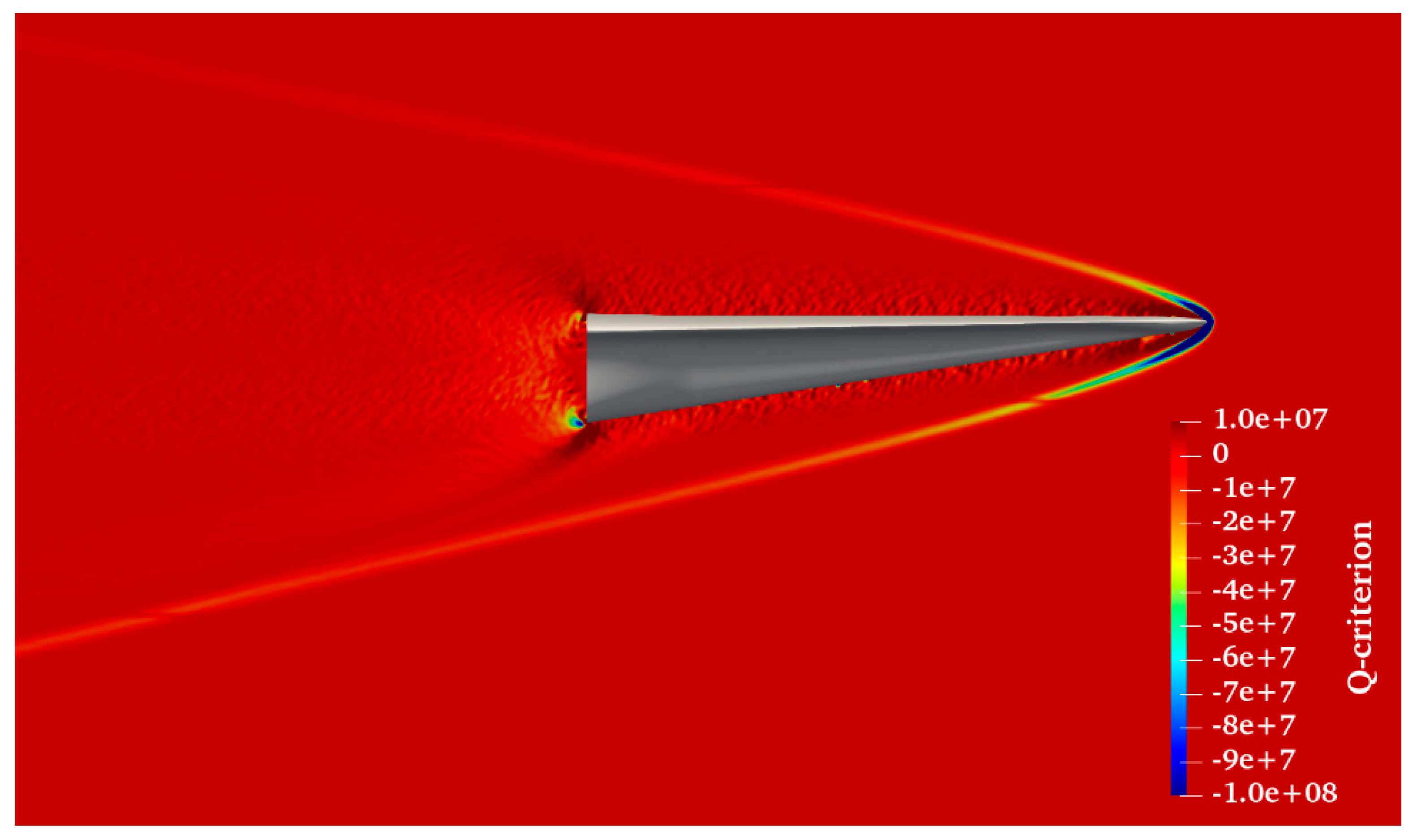
Due to the extensive computational demands associated with simulating hypersonic flows, several strategies are implemented to optimize the use of computational resources. One effective technique is the simulation of only half of the waverider’s geometry, with the resulting flow field then being symmetrically mirrored across a predefined plane. This approach significantly reduces the computational load without sacrificing the accuracy of the results. A key objective of these simulations is to confirm the correct positioning of the shock wave relative to the vehicle’s leading edges. This verification is conducted by analyzing the pressure contours and Q-criterion plots, which are displayed in
Figure 11 and
Figure 12, respectively.
The Q-criterion, calculated using Equation (2), involves
the antisymmetric component of the velocity gradient representing vorticity, and
, the symmetric component representing the rate of strain.
According to the established criteria, positive Q-criterion values signify regions within the flow field where vorticity predominates, suggesting the areas of rotational flow. Conversely, negative values indicate the dominance of strain rate or viscous stresses [
42,
43]. This criterion is a critical diagnostic tool for analyzing the flow characteristics around the waverider. For instance, in
Figure 13, the negative Q-criterion values observed below the leading edge signal the presence of a shock in that area. The associated pressure contour plots, illustrated in
Figure 11, reveal a distinct pressure buildup around the leading edges of the waverider, confirming the effective attachment of the shock wave to the vehicle’s geometry.
Moreover,
Figure 11 graphically depicts the pressure distribution on the surface of the waverider. As anticipated, increased pressure levels are prominent around the leading edges and nose section, validating the presence of an attached shock wave. This integration of various computational diagnostics—from mesh optimization to detailed pressure and Q-criterion analyses—offers a thorough assessment of the waverider’s aerodynamic performance. These results underscore the computational rigor and physical validity of the waverider design, particularly regarding the attachment of shock waves to the leading edges.
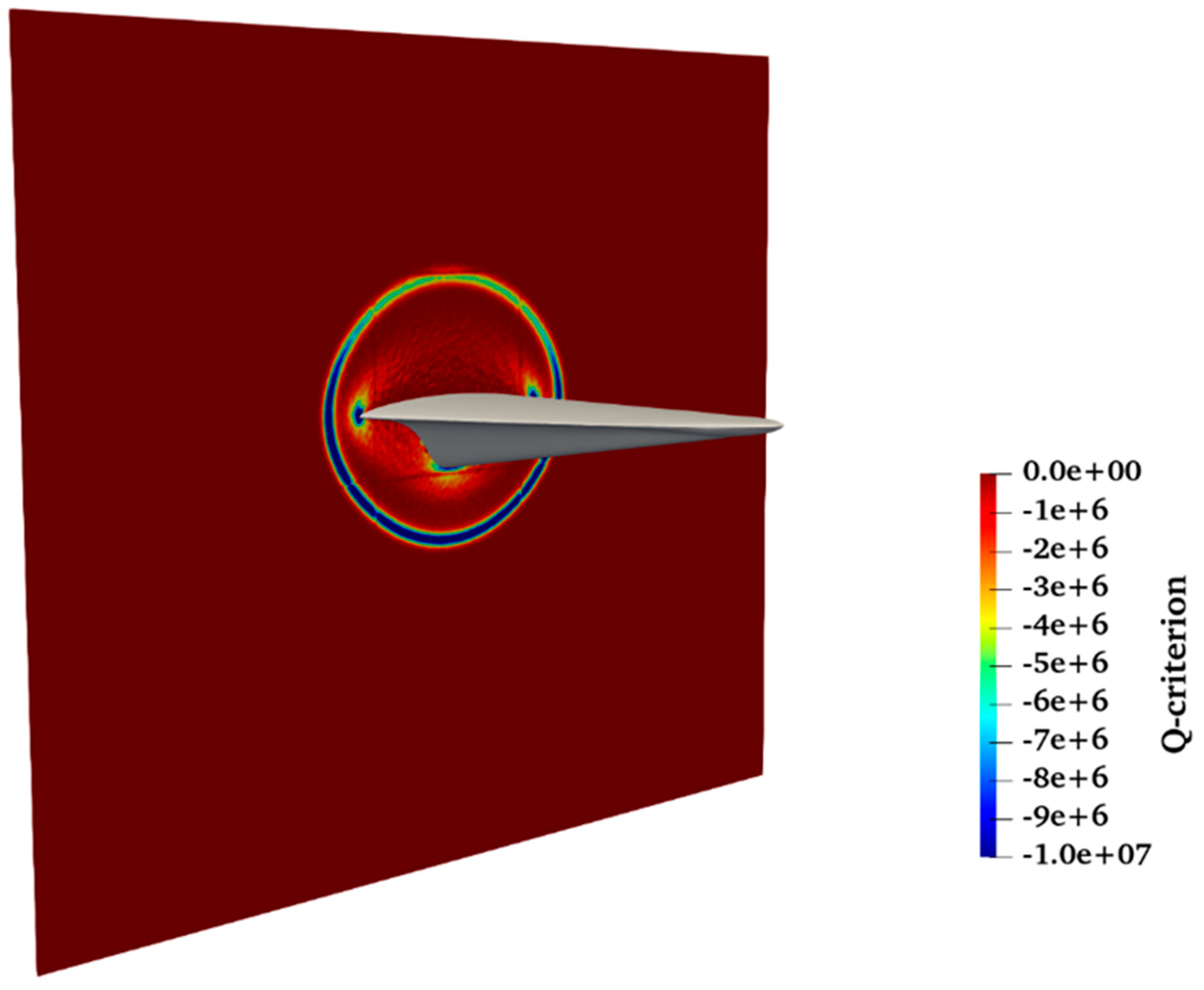
Figure 13 depicts the Q-criterion contours on the plane of symmetry, while
Figure 14 shows the corresponding contours on a vertical plane at the rear of the vehicle, where the concentrated blue regions at the wing tips and under the fuselage indicate attached shocks, further demonstrating the aerodynamic efficacy of the design.
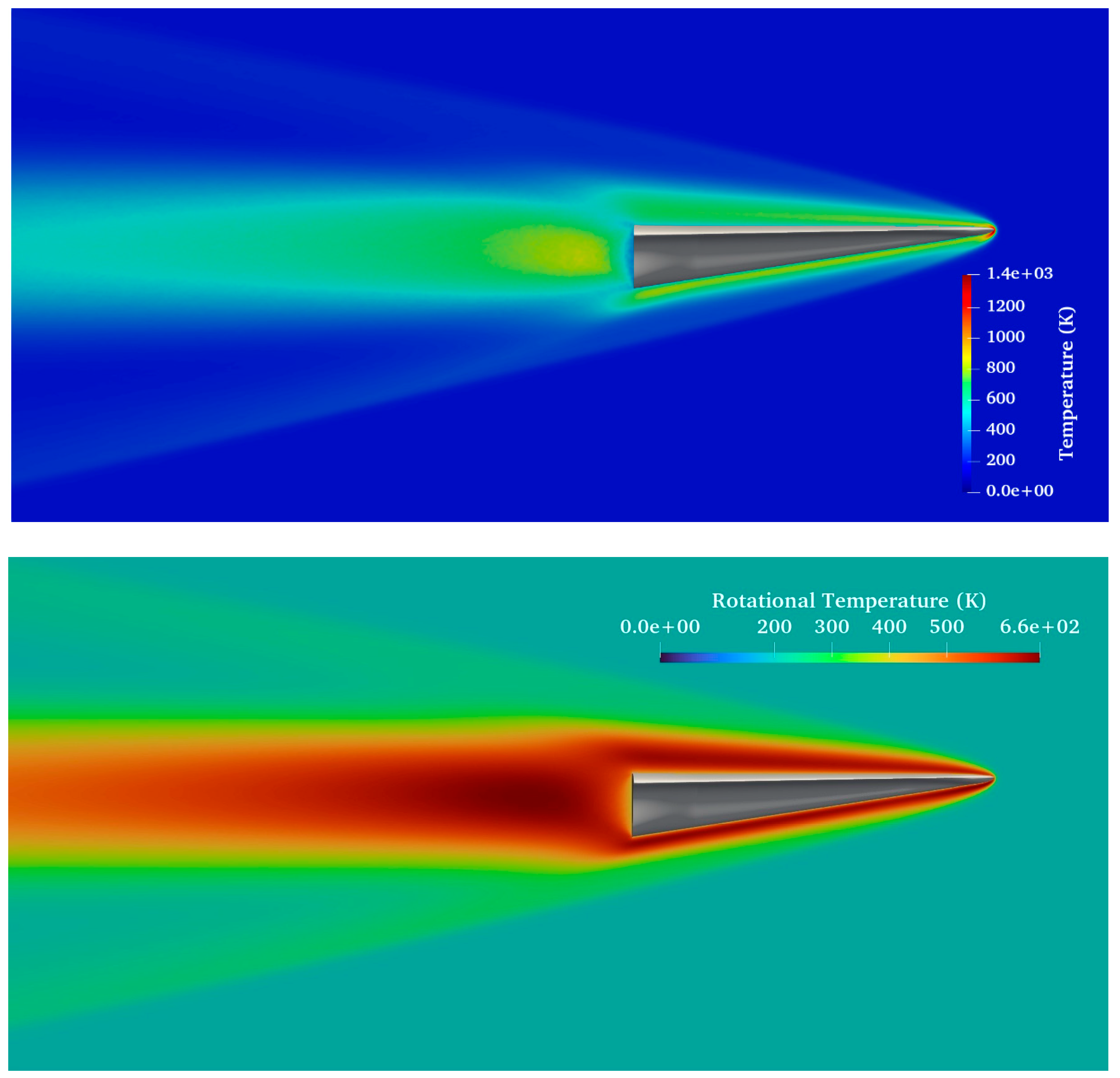
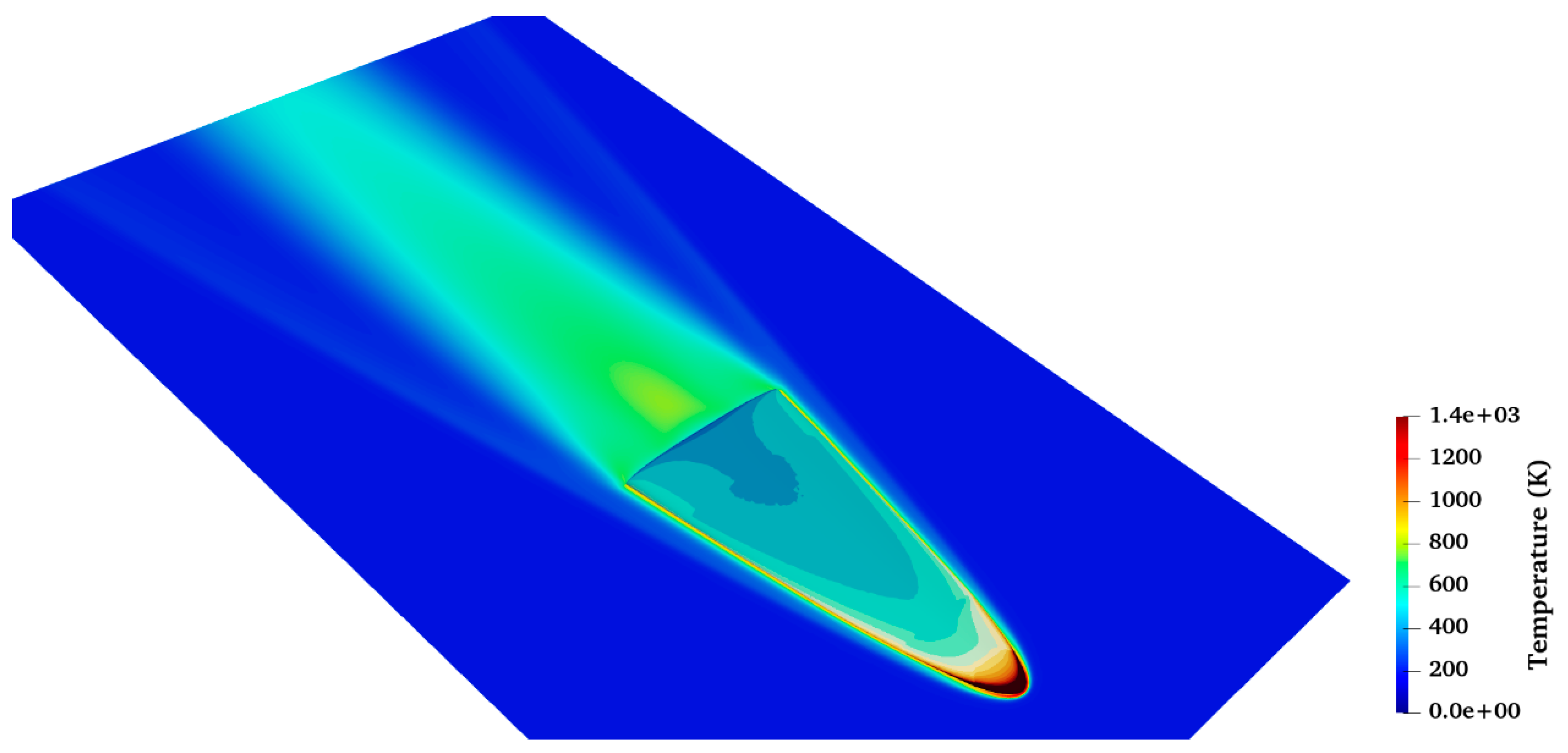
Figure 15 and
Figure 16 present the streamwise velocity contours and the temperature field around the vehicle. These figures are crucial for understanding how the vehicle interacts with the flow at high speeds. In particular, the simulations reveal important thermal dynamics and fluid flow characteristics. For the specific flow conditions applied in this study, the temperature field around the vehicle shows significant thermal variations. A peak temperature of 1400 Kelvin is observed just in front of the nose section of the waverider, indicating areas where aerodynamic heating is most intense due to the rapid flow deceleration. This information is vital for assessing the thermal resistance and structural integrity of the waverider under operational conditions.
In
Figure 17,
Figure 18,
Figure 19 and
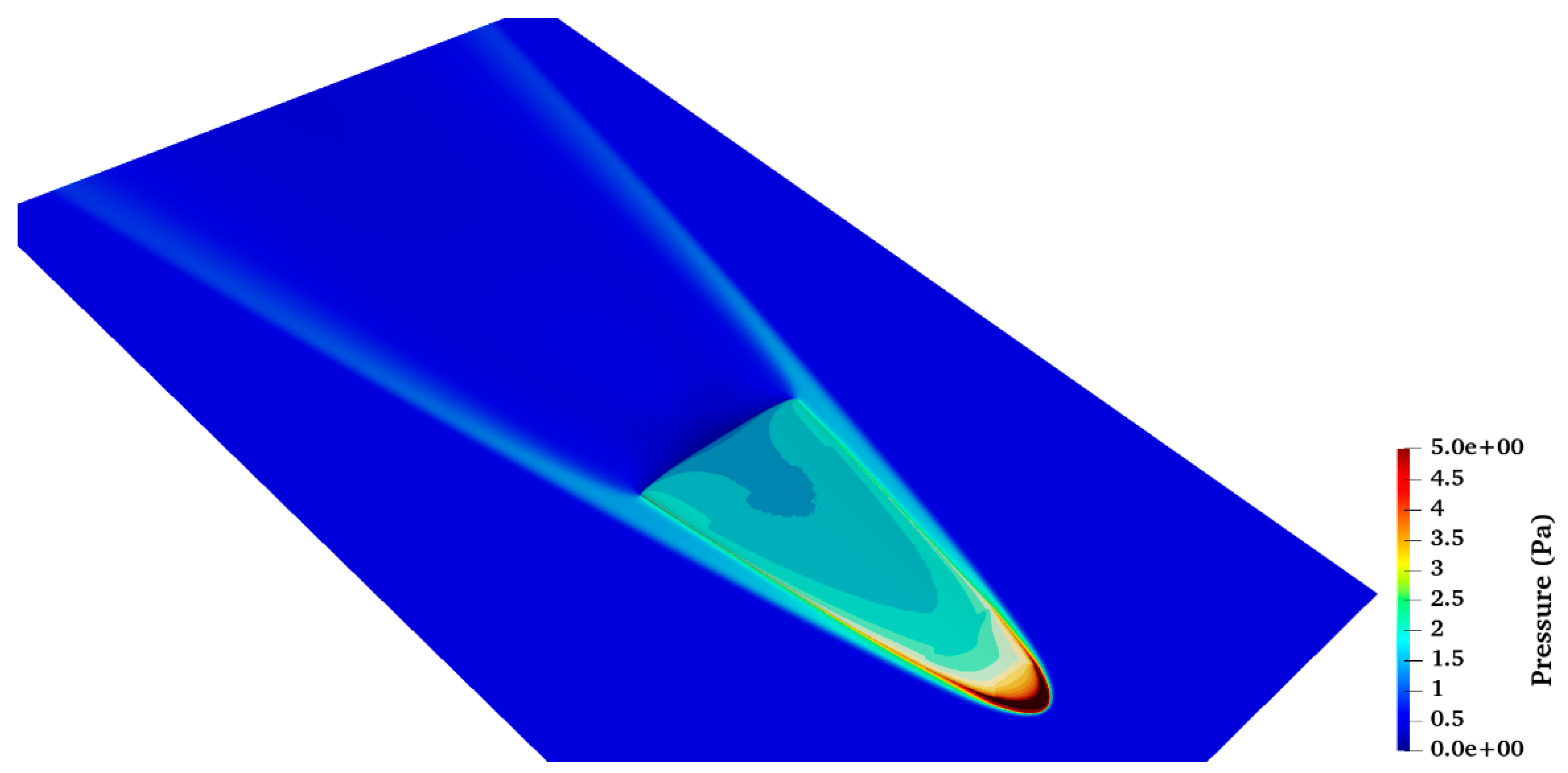
Figure 20, various flow properties are illustrated on a plane parallel to the waverider, with the surface of the vehicle distinctly highlighted by the variations in the surface pressure. Specifically,
Figure 17 displays the pressure contours on this plane, providing a clear visualization of how the pressure varies in response to the shape and aerodynamics of the vehicle. Notably, considering that the free-stream pressure is established at 0.55 Pa, there is a significant pressure increase observed around the nose of the waverider, rising to an order of magnitude higher than the ambient conditions. Additionally, the pressure around the leading edges of the waverider is approximately four times higher than that of the free-stream pressure. This detailed mapping of pressure distribution is critical for evaluating the aerodynamic performance and structural stresses experienced by the waverider during operation.
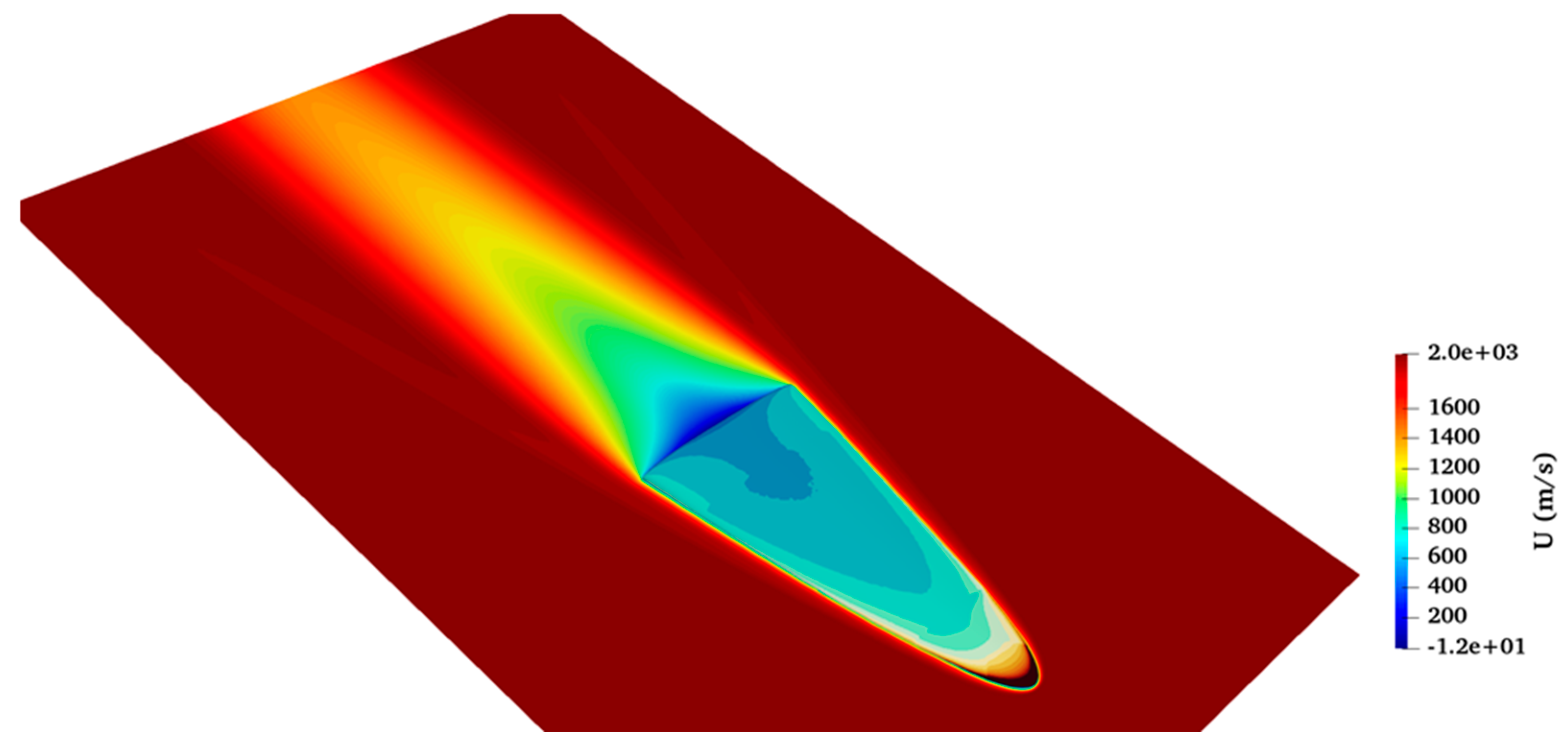
Figure 18 contains the velocity contours on the same plane. In this figure, the attachment of the shock to the leading edge and the nose of the vehicle can be clearly observed. As can be observed in
Figure 19, the temperature around the leading edges is 800 K, which is about four times higher than the free-stream temperature of 196 K (with a peak of around 1400 K at the nose of the vehicle).
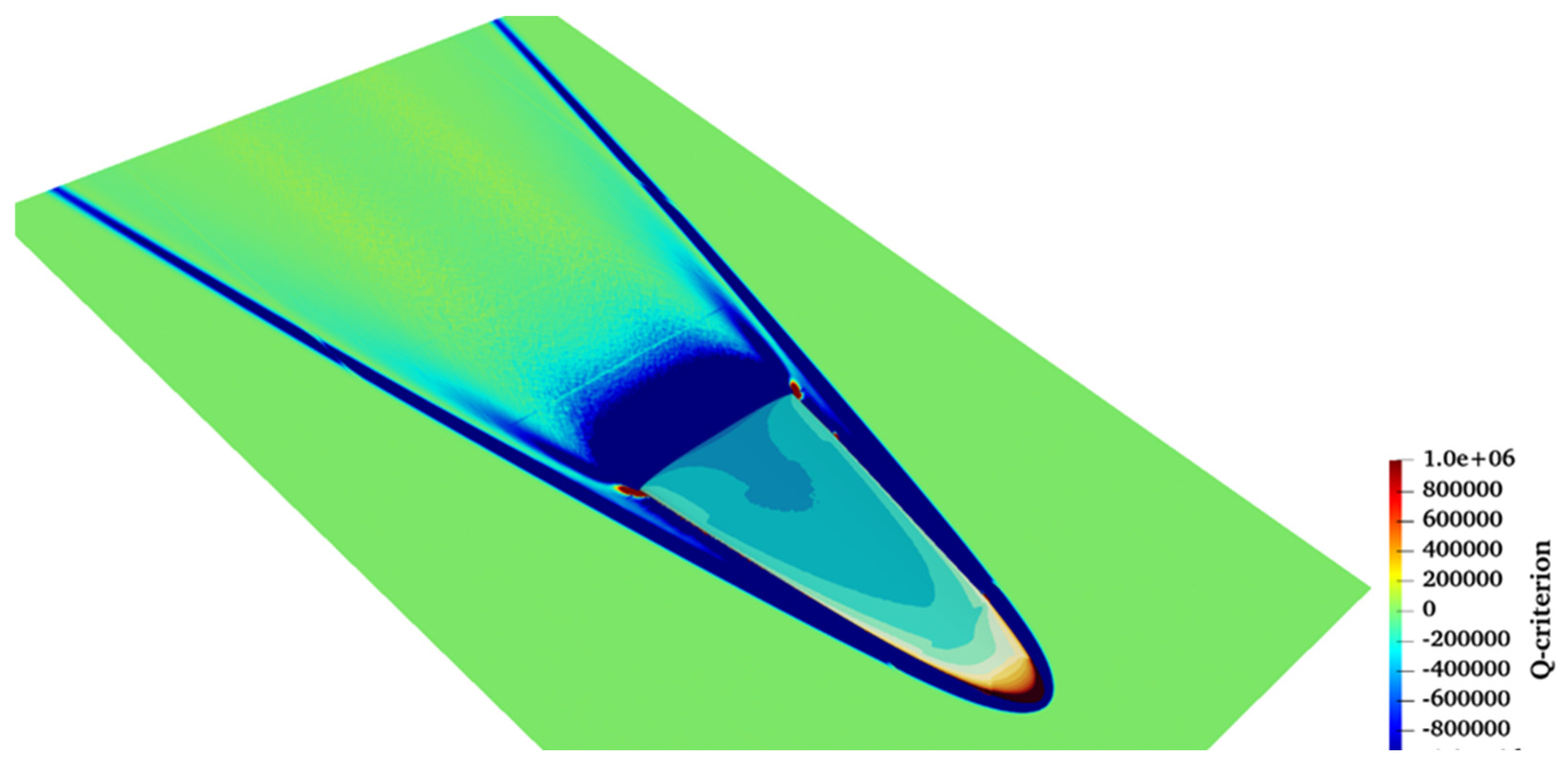
In
Figure 20, the Q-criterion is meticulously illustrated on the same plane parallel to the waverider, effectively capturing the entire field of the attached shock wave. This visualization underscores the precise areas where the shock remains attached to the surface of the waverider, a critical aspect of its aerodynamic design. Additionally, the positive values of the Q-criterion in this figure indicate the formation of two distinct vortices, located symmetrically, one on each side, at the tip of the vehicle’s rear section. These vortices are pivotal in understanding the flow dynamics at the rear of the waverider, particularly how they influence the overall stability and control of the vehicle at high speeds. For a more detailed observation of these vortices,
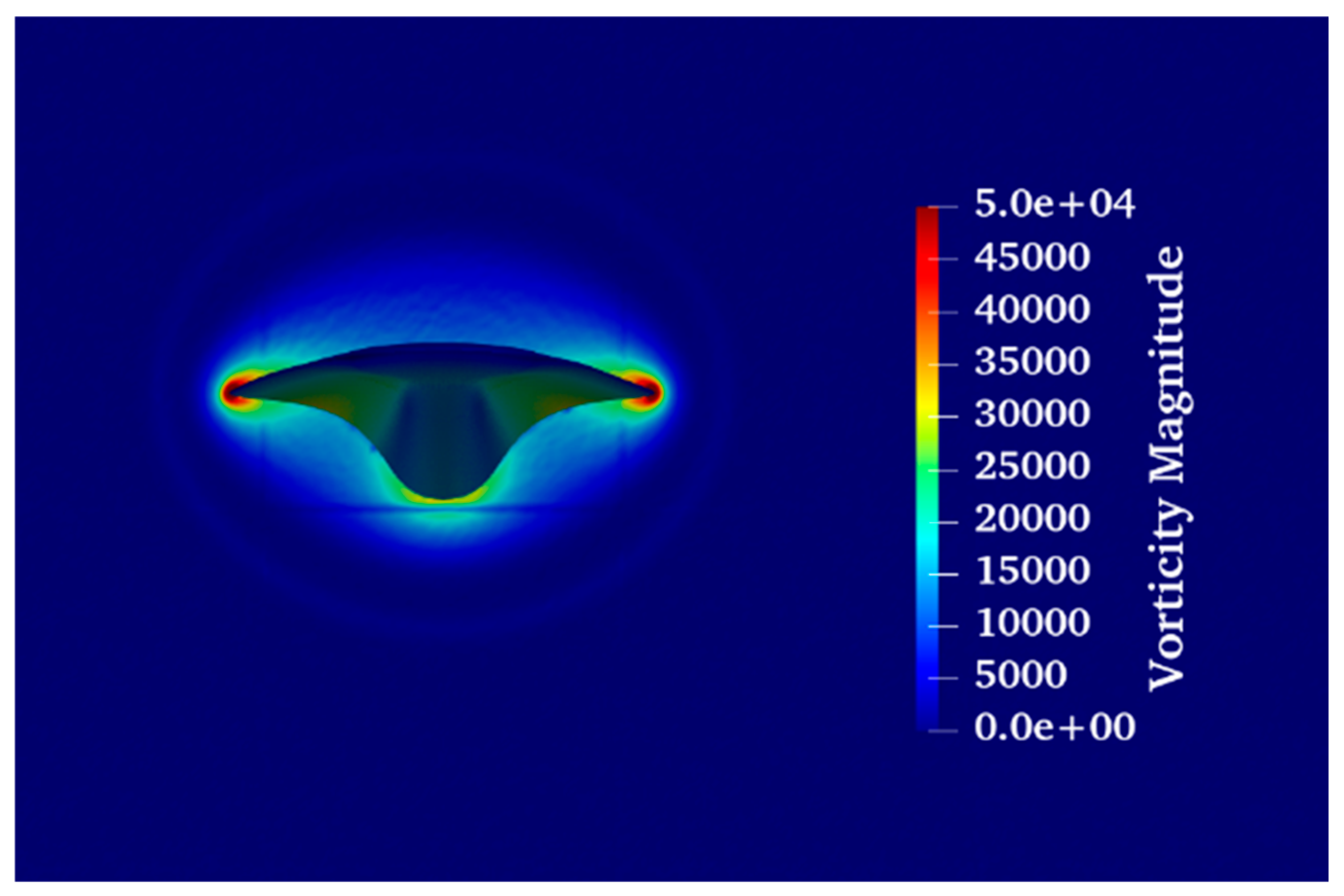
Figure 21 provides an enhanced view where the vorticity at the rear of the waverider is plotted. In this figure, the two vortices are distinctly highlighted in red, offering a stark contrast against the rest of the flow field. This color differentiation not only emphasizes the location and intensity of the vortices but also aids in analyzing their structure and interaction with the surrounding flow. The depiction of these vortices in such vivid detail is crucial for engineers and designers to evaluate the aerodynamic interactions at play and to refine the waverider’s design for optimized performance.
Given the intricate design of the waverider, it was deemed necessary to employ the three-dimensional iso-surfaces of the Q-criterion to fully capture the complex spatial characteristics of the shocks and the structured vortices surrounding the vehicle.
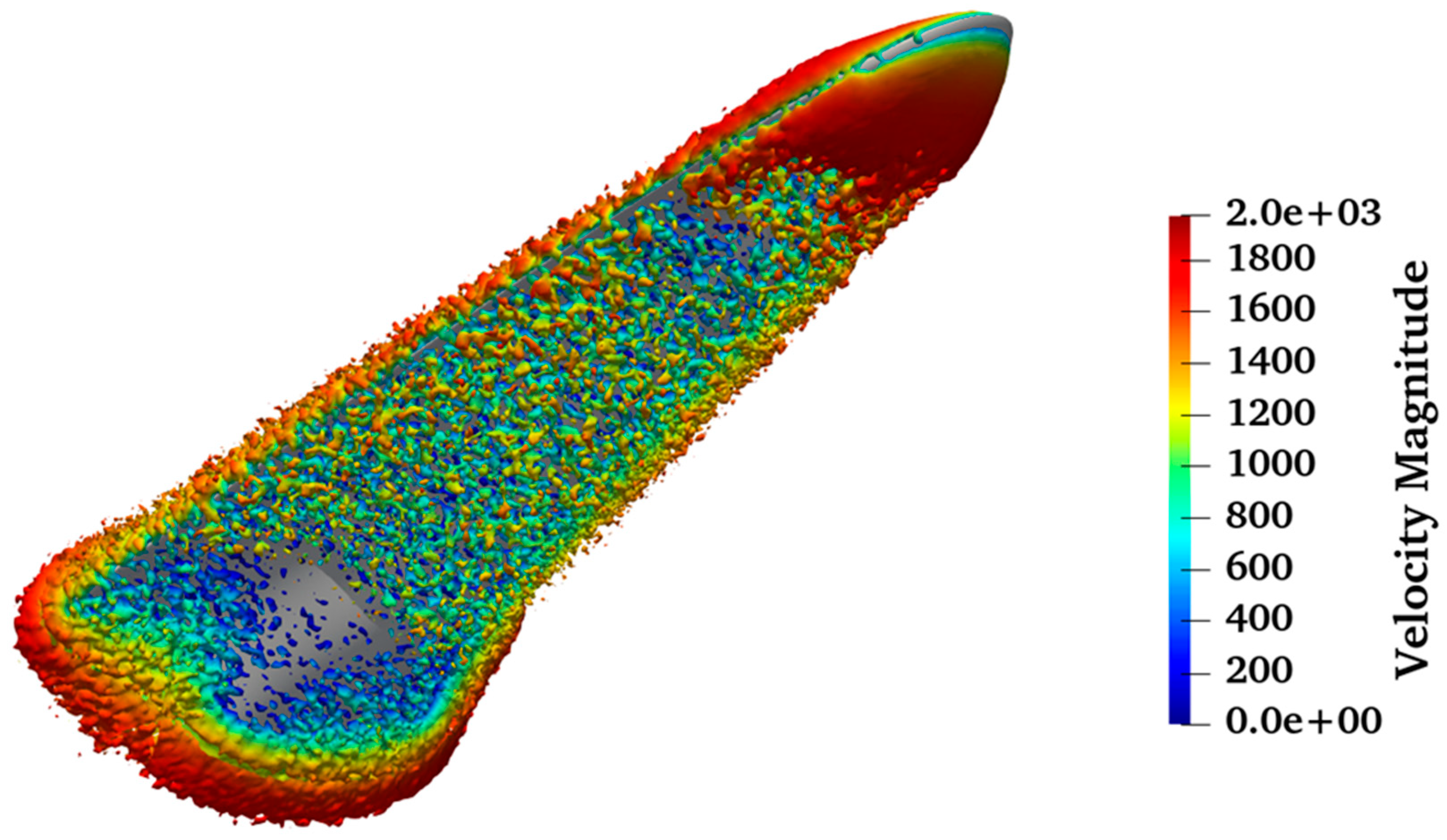
Figure 22 illustrates these three-dimensional Q-criterion contours enveloping the vehicle, with the contours colored by vorticity magnitude to emphasize the variations in the rotational flow behavior. The transparent grey iso-surfaces distinctly outline the external shape of the shock waves, providing a comprehensive view of their three-dimensional form. Notably, parts of the shock wave close to the compression surface are also visible in the same figure, offering a detailed look at how the shock interacts with the vehicle’s structure.
In
Figure 23, these contours are similarly plotted but are instead colored by velocity magnitude to highlight the differences in flow speed. As depicted in this figure, approximately 30 cm downstream from the nose of the vehicle—where the compression surface becomes steeper—the vortices detach from the main flow and continue downstream towards the higher pressure regions at the back of the vehicle. This separation is critical for understanding the aerodynamic behavior of the waverider. Additionally, as the angle of the compression surface increases towards the vehicle’s rear, a noticeable pressure rise occurs, and the flow velocity significantly reduces, slowing down by about 1000 m/s within just a few centimeters. These detailed visualizations and analyses of flow dynamics are essential for assessing the performance implications of the vehicle’s design under operational conditions.
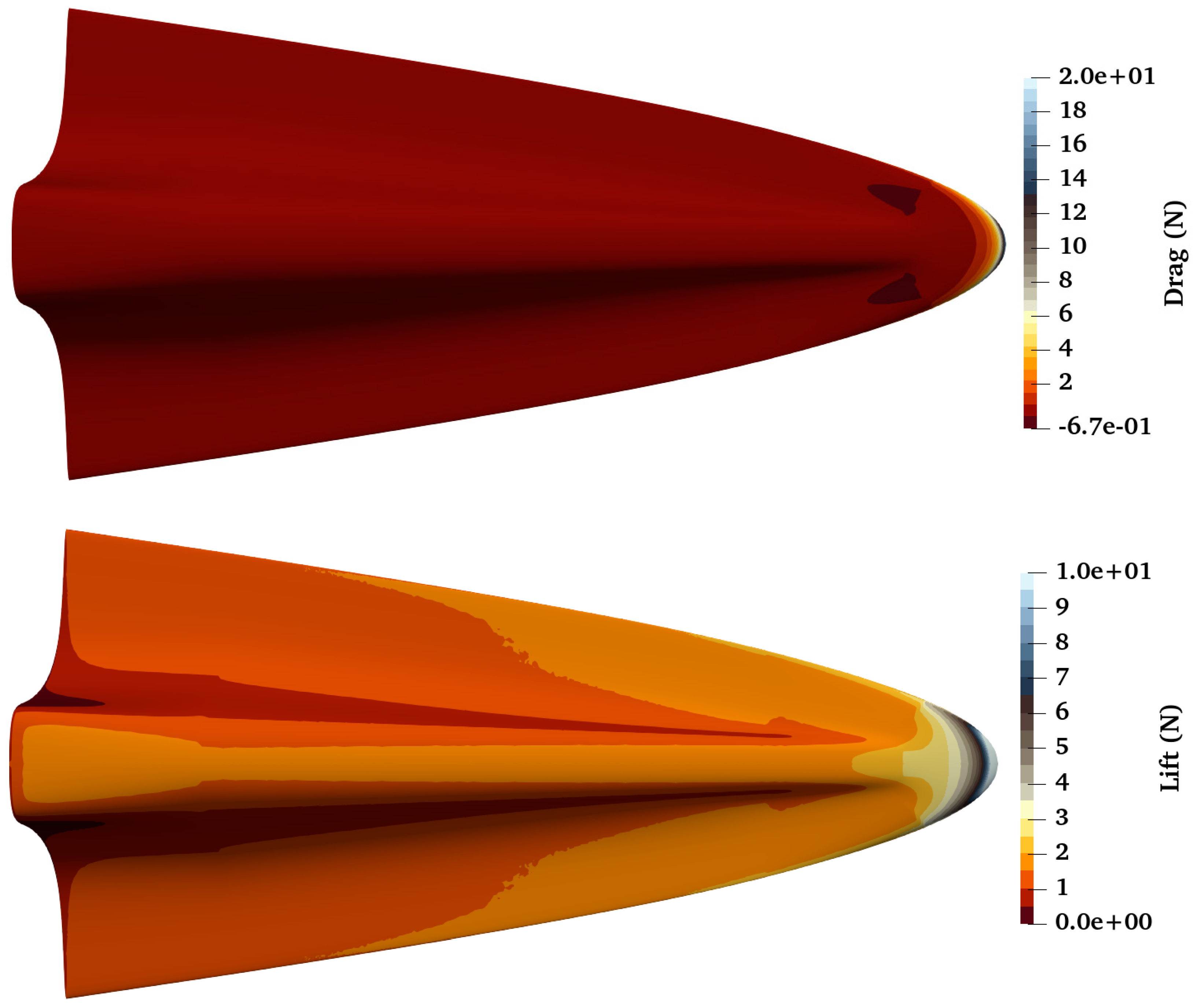
To determine the aerodynamic forces acting on the waverider, the shear stresses and pressure components across its three-dimensional surface were meticulously calculated. These calculations facilitate the precise measurement of lift and drag forces per unit surface area, with the results displayed in
Figure 24. The analysis of this figure reveals that the maximum drag primarily occurs at the tip of the nose, while a significant amount of lift is generated in the area just below the nose. By integrating the forces measured across all the surface cells, the total lift and drag for the waverider were computed, yielding a lift–drag ratio (L/D) of 2.18. According to existing studies, this L/D ratio is typical for a waverider operating at a 0-degree angle of attack [
44], indicating that a value above 2.0 is indicative of effective aerodynamic performance under the chosen design conditions.
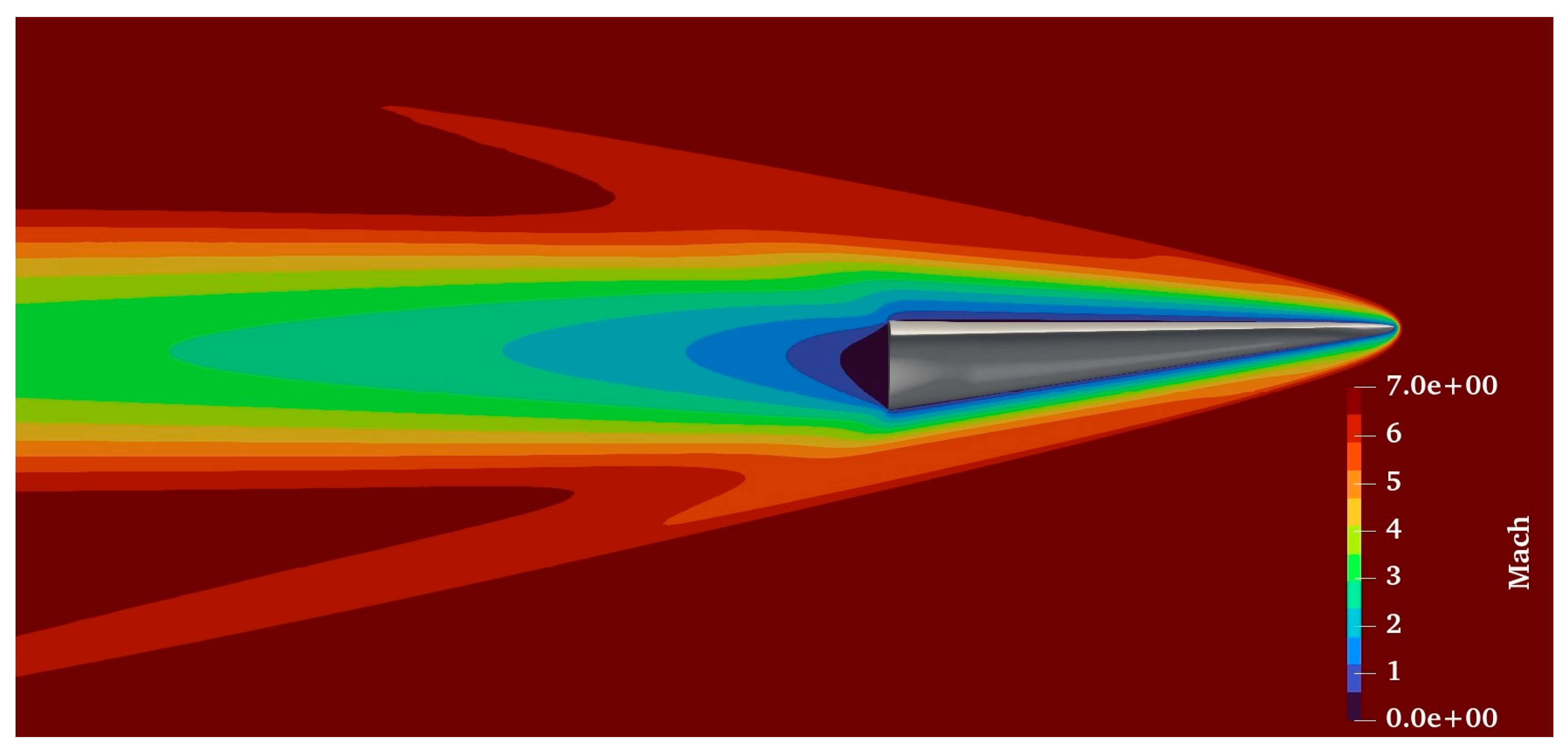
The Knudsen number contours, based on the waverider length, are depicted in
Figure 11 (bottom), while the Mach number contours at the plane of symmetry are depicted in
Figure 25. As demonstrated the Knudsen number around the vehicle is within the transitional regime, which justifies the use of the DSMC method.
For this study, only a single angle of attack was investigated; however, the authors in [
44] suggest that a slight increase in the angle of attack could potentially enhance the L/D ratio by two to three times, thereby significantly improving performance. It is also noteworthy that waveriders are commonly analyzed at altitudes between 25 km and 40 km in the open literature, unlike the 90 km altitude considered in this study. The elevated altitude impacts the generation of lift due to different fluid dynamics, necessitating a larger compression surface than what is typically seen in waveriders operating at lower altitudes. This adaptation is a critical design modification that enhances the vehicle’s performance in the rarified atmospheric conditions encountered at high altitudes.
6. Conclusions
In the comprehensive design and analysis of a Mach 7 waverider, intricate computational methodologies were employed to accurately simulate the vehicle’s aerodynamic properties. After applying the osculating cone methodology, for the definition of the waverider’s geometry, a precise computational mesh was constructed to capture the complex surface geometry, particularly around the waverider’s critical leading edges. An advanced simulation technique, the Direct Simulation Monte Carlo (DSMC) method, was used to resolve the three-dimensional flow field around the vehicle. This simulation not only detailed the pressure and thermal conditions surrounding the waverider but also highlighted the structural interactions of the shock waves, validated through the visualizations of streamwise velocity and temperature fields.
Further refinement of the simulation model involved creating the three-dimensional iso-surfaces of the Q-criterion to intricately map out the shock and vortex structures around the waverider. This allowed for an in-depth examination of the flow dynamics, particularly the attachment of shock waves and the formation of vortices at the critical sections of the vehicle. Such detailed analyses were essential for confirming the aerodynamic efficiency of the design. Additionally, the use of layered meshing techniques facilitated the accurate capture of boundary layer phenomena, crucial for assessing the vehicle’s performance under the extreme conditions of hypersonic flight.
The culmination of these extensive simulations was the calculation of lift and drag forces, where the lift–drag ratio was determined to be 2.18, indicative of efficient aerodynamic performance for a waverider at a zero-degree angle of attack. These findings are significant, as they not only demonstrate the waverider’s capability under the stipulated design conditions but also suggest potential improvements for future designs. For instance, adjustments in the angle of attack could further optimize the vehicle’s performance. This study’s insights into high-altitude aerodynamics, where different fluid dynamics necessitate modifications such as larger compression surfaces, pave the way for the enhanced designs of future hypersonic vehicles operating in near-space environments.