Abstract
This study explores a technique for enhancing the punching strength of reinforced concrete (RC) flat slabs, namely carbon fiber reinforced polymer (CFRP). Four large-scale RC flat slabs were fabricated, to assess the efficacy of this strengthening method. One slab served as a reference and the three other specimens were strengthened with CFRP, as a method of external strengthening. These slabs, featuring identical overall dimensions and flexural steel reinforcement, underwent testing until failure, under the influence of concentrated patch loads. A concrete plastic damage constitutive model (CDP) was developed and employed to examine the strength of two-way RC slabs. Additionally, to enhance the strength of existing RC slabs, carbon fiber reinforced polymer (CFRP) strips are affixed to the tension surface of the sections. The research begins with the calibration of a numerical model, based on data from laboratory tests. The objective of this study is to constrain the plastic behavior of two-way RC slabs reinforced with CFRP, with a focus on establishing an optimal elasto-plastic analysis, aimed at controlling concrete damage plasticity using CFRP, and employing a plastic limit load multiplier. Subsequently, a series of numerical simulations, incorporating different variables, are conducted to investigate shear behavior. The numerical results indicate that an increase in the strengthening ratio has a significant impact on shear strength. Finite element simulations are carried out using Abaqus CAE®/2018.
1. Introduction
Recently, the use of lightweight carbon fiber reinforced composite materials that are nonmetallic has increased for the purpose of repairing and reinforcing concrete structures. “Strengthening a structural member” is a process undertaken when the existing member’s strength is deemed inadequate. Such deficiencies can manifest due to construction errors, such as excessive downward pressure on the steel bars into the cross section during the building process, alterations in the intended capacity, or reductions in capacity caused by human error or environmental factors [1]. Civil engineering has witnessed the economical and effective implementation of CFRPs for the development and rehabilitation of deteriorating structures. Numerous variables affect the application of CFRPs for the reinforcement of RC members, including fiber type, fiber distribution, fiber orientation, and bond schemes [2].
Many researchers investigated CFRP reinforcement methods including laminates, bars, or sheets. There are numerous benefits of CFRP composites over conventional materials. The construction industry is progressively adopting these benefits for infrastructure applications—durability, transportability in any length, exceptionally high strength, lightweight, requiring less mechanical fastening, requiring less expensive maintenance, requiring shorter construction periods, minimizing interruptions, having a long service life, and facilitating rapid installation [3,4]. Limam et al. [5], in 2003, provided an experimental investigation and a limit analysis modeled on RC slabs reinforced with CFRP laminate. The findings from the experimental study indicated that externally applying the CFRP plates effectively enhanced the strength of RC slabs. Mosallam and Mosalam [6], in 2003, examined the ultimate response of reinforced and unreinforced concrete slabs that had been retrofitted and repaired with CFRP laminates, through an experimental and analytical investigation. The carbon fiber/epoxy and E-glass/epoxy composite systems significantly strengthened the repaired areas. Additionally, retrofitting slabs with CFRP systems improved structural integrity. Limam et al. [7], in 2005, used 2D finite element analysis to quantify the elastic response of simply supported two-way reinforced concrete slabs with CFRP laminates, concentrating on orthotropic composite plates with a central load. Hosseini [8], in 2016, conducted an experimental program and used computational techniques to evaluate the load-deflection properties of reinforced concrete slabs, highlighting the effects of CFRP percentage, tensile longitudinal bar percentage, and CFRP elasticity modulus. The findings showed that prestressing CFRP laminates with NSM can improve RC slab fracture resistance, serviceability, yield capacity, and ultimate loads. Yılmaz et al. [9], in 2018, utilized a combination of experimental and numerical methods to examine the impact behavior of two-way RC slabs reinforced with CFRP strips. The findings indicated that reinforcing RC slabs with CFRP strips increased their rigidity and toughness and the maximal acceleration values measured from test specimens correspondingly rose. Akhundzada et al. [10], in 2019, used unidirectional CFRP laminates to test the efficiency of various strengthening techniques for internal slab-column connections and examined how laminate thickness and anchoring affect strengthening. The findings revealed that strengthening decreased maximum deflection by 50%, increased ultimate load by 25%, increased cracking load, and significantly reduced radial crack length. Mercimek et al. [11], in 2022, examined RC flat slab efficacy-enhancing methods. The strengthening methods were CFRPs, shear stud, and textile-reinforced mortar (TRM). This study used Abaqus CAE® to simulate the experiment and compare the results to the actual results. The results showed that TRM was the best out of the three strengthening methods used to improve RC slab performance under punching loads. Türer et al. [12], in 2023, devised a CFRP strip reinforcing technique to mitigate punching strength loss from two square holes close to the column in two-way RC flat slabs. The specimen’s initial stiffness, load–displacement characteristics, energy dissipation capabilities, maximum load-bearing capacities, and CFRP-enhanced failure patterns were studied at varied opening sizes and positions. For numerical analysis, Abaqus CAE® was used to model the specimens.
On the other hand, a lot of researchers used the other types of CFRPs (sheet or bar) in strengthening the two-way reinforced concrete slabs. Enochsson et al. [13], in 2007, examined the structural response of two-way RC slabs reinforced with CFRP sheets, with sawn-up holes, under uniform loads. Both numerical and experimental methods are used to evaluate CFRPs’ ability to absorb excess sectional forces. The results show that externally bonded CFRP sheets may support slabs with openings better than steel-reinforced slabs. Esfahani et al. [14], in 2009, investigated methods for using CFRP sheets to increase the flat slabs’ resistance against punching shear. The test results underwent comparison with the formulas outlined in both the BS 8110 and ACI 318 Codes. The findings from this investigation align well with outcomes reported by fellow researchers, demonstrating that the addition of CFRP sheets to the slabs’ tension side effectively enhances the slabs’ punching.
Meisami et al. [15], in 2013, evaluated the potential of FRP rods to enhance shear strength, using an analysis of the punched shear performance of concrete slabs reinforced with epoxy resin and CFRP rods. The experimental findings showed that the selected reinforcement method improved the slabs’ maximum load-bearing capacity and ability to withstand deformation, while also preventing possible brittle failures from vertical point loads. Elsanadedy et al. [16], in 2015, aimed to illustrate the efficacy of utilizing externally bonded CFRP composites for improving the flexural capacity of RC one-way slabs. The study encompassed both experimental testing and computational analysis, utilizing FE analysis. A comparison was conducted between the experimental and numerical findings, resulting in a satisfactory level of agreement. Behzard, Sharbatdar, and Kheyroddin [17], in 2015, showcased the efficacy of a novel technology that combines CFRP materials to enhance the flexural strength of existing RC two-way slabs with a thin layer of concrete covering. The test results have shown the feasibility and effectiveness of this technology in enhancing the flexural behavior of reinforced concrete two-way slabs. A 3D nonlinear numerical model was created using the FE approach, to accurately forecast the flexural behavior of the tested slabs. Mahmoud et al. [18], in 2021, studied the performance of high-strength RC slabs reinforced with CFRP sheets, to enhance their bending strength. The findings from the test were compared together to draw conclusions regarding the extent of CFRP enhancement; the load-carrying capability of the specimens improved after reinforcement using high-strength materials—thin concrete slabs.
The concrete damage plasticity (CDP) model is widely used in structural engineering to assess the behavior of concrete structures under various loads. The CDP model, a continuum-based model, takes into consideration the intricate behavior of concrete, such as cracking, crushing, and plastic deformation. This non-linear model is essential for designing and analyzing buildings that experience significant pressures, as it accurately represents the behavior of concrete after it reaches its peak strength. The CDP model was successfully applied in several situations, including earthquake engineering, blast-resistant building design, and reinforced concrete construction. This discovery might have important implications for the design and construction of reinforced concrete structures, especially in areas prone to earthquakes where ductility is a critical factor [19]. Various combinations of damage and plasticity were explored by Carol et al. [20] in 2001, Ibrahim et al. [21] in 2023, and Rad et al. [22] in 2023. Gatuingt and Pijaudier-Cabot [23], in 2002, and Kratzig and Polling [24], in 2004, utilized isotropic damage in their research, elucidating various combinations of plasticity types. Lubliner et al. [25], in 1989; Imran and Pantaopoulou [26], in 2001; and Ananiev and Ozbolt [27], in 2004, explored theories that describe plasticity in nominal stress space.
This study aims to investigate the impact of varying strengthening ratios on the ultimate load, cracking load, crack width, and deflection. The recent studies did not investigate the behavior of RC two-way slabs with these specific ratios of CFRP. Furthermore, this study demonstrated the need to implement CFRP reinforcement to mitigate the damage to concrete and steel structures using Abaqus CAE®. This research shed light on the performance of CFRP in RC two-way slabs and how its strength might be improved. Engineers and researchers can utilize the findings as a reference for determining the appropriate proportion of reinforcement ratios to employ, to attain certain structural objectives. As well as the fact that this study possesses various distinctive elements that distinguish it as a novel study, it begins by investigating two-way RC slabs experimentally, as well as carrying out an ideal elasto-plastic analysis that focuses on managing concrete damage plasticity using CFRPs and applying a plastic limit load multiplier, with the intention of controlling the plastic deformation of two-way reinforced concrete slabs that have been strengthened with CFRPs. To further our comprehension of how various strengthening ratios affect the behavior of two-way RC slabs, these percentages were derived by testing three specimens; then, their tension and compression behaviors were investigated and compared to the control slab, which did not contain CFRPs. Finally, experimental testing and numerical analysis were utilized in this study for a more thorough evaluation and validation of the findings, which increases the study’s credibility and practicality. It was of the utmost importance to validate numerical models that were derived from the results of laboratory tests, with a particular emphasis on confirming the strengthening ratio. A sequence of simulations that are based on the limitations have been set. As a means of accurately representing the caused damage in the concrete, the numerical model was calibrated by making use of the CDP model. There was an evaluation of the effect of load multipliers on concrete deterioration, using both elastic and plastic analysis. All these parameters were considered and their effects were studied.
Following this introduction, Section 2 provides a comprehensive explanation of the concrete constitutive model. Then, the experimental work that includes the details of the model and the materials’ properties are present in Section 3. The test set-up and discussion of the experimental data are presented in Section 4. Additionally, Section 5 presents specific information on the numerical model, including the specifics, calibration procedure, and discussion of the numerical findings. Finally, the most significant findings and conclusions are presented in Section 6.
2. Theoretical Background
2.1. Concrete Constitutive Model
Concrete’s nonlinear reaction to stress, compression, and bending is modeled using the CDP model. The concepts of continuum damage mechanics state that loading damages and degrades material. The model considers compressive and tensile damage. Micro-cracking in the material causes strength loss in tensile damage and stiffness, according to the model. The model describes compressive damage as crushing, which reduces strength and stiffness. The model also accounts for plasticity, which causes the material to deform permanently once the stress is removed. With isotropic hardening, the model properly depicts the material’s plastic reaction. The modulus of elasticity, which describes compressive and tensile concrete behavior inside the calibrated model, must be obtained experimentally to implement the CDP model. Monographs and the relevant literature provide detailed information on the procedure. This article briefly describes the concrete constitutive model and then elaborates on essential points. Elastic and plastic components may be examined in the strain tensor value (ij) using Prandtl–Reuss theory and elasto-plastic deformations, as explained below [19,28].
The equation for scalar damage elasticity provides us with understanding regarding the interplay between strains and stresses within a material.
Hence, serves as an abbreviation indicating a reduction in elastic stiffness.
where represents the initial stiffness in elasticity of the material before any damage occurs, while “d” serves as a single degradation parameter ranging from a state of 0, indicating no damage, to a state of 1, representing complete damage. Following the hypothesis of scalar damage, a single degradation variable, denoted as d, is employed to characterize the reduction in stiffness in all directions. The effective internal stress is described utilizing fundamental concepts from continuum damage mechanics, as outlined below:
The relation of scalar reduction correlates with the internal stress, , to the internal stress’s effectiveness, :
When d equals 0, the effective internal stress, , coincides with the stress within the structure, . As damage occurs, the zone characterized by the effective internal stress, which opposes external loads, gains greater significance than the internal stress itself. Expressing the diminished elastic tensor and the integration of nominal stress, as defined in Equation (4), into a modified version of Equation (2) results in the following equation:
The interaction between internal stress and strain constitutes the damage plasticity constitutive model.
The cyclical performance of concrete under uniaxial stress, characterized by the formation and sealing of micro-cracks, was explored to understand the intricate degradation mechanism. Damage models for concrete traditionally considered compressive crushing and tensile cracking, with and representing compression and tension damage ranging from a state of 0, indicating no damage, to a state of 1, representing complete damage, and and denoting internal stress that is efficacious under tension and compression, respectively. Figure 1 [19] illustrates the anticipated impact of plastic deformation on the concrete’s reactions to uniaxial tension and compression.
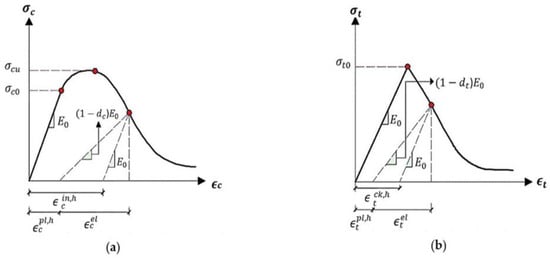
Figure 1.
Response of concrete under the uniaxial loading conditions: (a) in compression, (b) in tension.
The manifestation of concrete’s response to compression and tension stress in its uniaxial compressive and tensile behavior, as elucidated using the CDP model, is depicted by the follow equations:
Here, signifies the modulus of elasticity of the pristine material, while and denote the corresponding plastic deformations in compression and tension. This enables the derivation of the effective uniaxial compressive stress, , and tensile stress, .
The tensile strain, , is equivalent to ; the compressive strain, , is equivalent to . Consequently, and represent the equivalent elastic strains under compression and tension. Through the utilization of the expressions = and = for tensile strain and compressive strain, respectively, during tension and compression, the elastic strains are represented by and , respectively.
Ultimately, the model that has been calibrated employs the CDP constitutive model to depict the concrete’s behavior under both compression and tension. This depiction aligns with the properties of concrete in compression and tension, as illustrated in Figure 1. Subsequently, the validation of these properties was conducted using Abaqus CAE® and, after running Abaqus CAE®, the parameters for the CDP model were acquired, preparing the model for testing with various concrete mixes.
2.2. Utilizing the Static Principles of Plastic Limit Analysis
Incorporating the static framework of plastic limit analysis into the method of optimization enables the consideration of concrete slabs’ plastic behavior under different loading conditions, ensuring that the designs that have been optimized meet the state of the plastic limit requirements. An in-depth study of the original development of the static limit analysis principle is essential to understand the fundamental notion of the newly created technique. Contemplating an elasto-plastic body subjected to a steadily increasing force, , to comprehend the formula for proportional loading, also known as one-parameter loading [29,30], the following is obtained:
Here, denotes the constant initial applied force externally and is a scalar factor for load amplification that steadily rises. As is further elevated, the zones of plastic deformation of the body gradually expand, reaching a well-defined intensity, . At this point, unconstrained plastic deformation occurs, allowing for constant expansion in displacements and plastic deformations to be accomplished through external forces throughout the loading phase. Under a sustained external stress, an elasto-plastic body reaches its plastic limit state, wherein the entire body or specific sections undergo unrestricted deformation into a plastic form. The ultimate load at plastic deformation, , equals times the load at the elastic limit, . Equilibrium equations play a crucial role during the plastic limit phase, as forces and stresses can persist in static equilibrium. For instance, we demonstrate by contrasting the stress, , in a body experiencing quasi-static equilibrium at the plastic limit load = to the stress, , within arbitrary static permissibility force and stress = , meeting the yield condition.
where the symbol k represents the plastic characteristics of the material. The concept of imaginary velocities can be extended to the force and stress fields by considering a body capable of deformation with volume V and surface of loading and also by incorporating kinematically permissible strain rate and velocities .
These two equations are subtracted to give the following:
Each surface point needs to be normalized to ensure compliance with both the convexity of the yield surface and the normality criterion, resulting in all points falling within the normal distribution.
hence, Equation (16) yields:
In this depiction, the integral symbolizes that external forces perform work on the actual body’s velocities. The plastic limit condition avoids the occurrence of negative work, the condition must remain positive. The enhanced aspect of uniqueness and convexity in the procedure is demonstrated by the outlined steps. The incorporation of this element into topology design does not escalate the mathematical complexity of the method.
3. Experimental Work
An experimental program was undertaken to investigate the performance of two-way RC slabs strengthened with CFRP laminates. The investigation entails the construction of four two-way slab specimens supported at each end and subjected to concentrated load. All slab specimens had identical dimensions, 1200 mm × 1200 mm × 130 mm, as illustrated in Figure 2a. The specimens were categorized as GA, GB, or GC, with slab G0 serving as the control slab specimen. Furthermore, experimental measurements were conducted in the laboratory to assess concrete properties. The test specimens were produced using concrete that had a compressive strength of 30 MPa, as measured by its typical cylindrical strength. For the purpose of evaluating the compressive strength of concrete, a total of three cylinders measuring a diameter of 150 mm and a height of 300 mm and three cubes measuring side length of 150 mm were employed. These specimens were subjected to a 28-day curing period, after which their qualities in both tension and compression were examined, resulting in average concrete values. Table 1 displays the compressive strength results of concrete for both cylinders and cubes. The experimental measurements conducted in the laboratory encompassed evaluations of both concrete compressive behavior and tensile behavior, as illustrated in Figure 3.
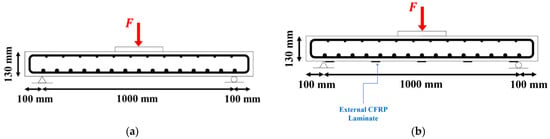
Figure 2.
Typical slab specimen. (a) Control slab without strengthening, (b) slabs strengthened with CFRPs.

Table 1.
Compressive strength of concrete.
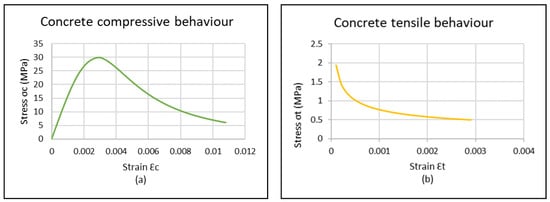
Figure 3.
Concrete’s experimental characteristics in (a) compression and (b) tension.
In all specimens, the primary tensile reinforcement is composed of fifteen steel bars, each with 10 mm diameter, positioned with 61 mm spacing center-to-center and the compression reinforcement consisted of twelve steel bars, each with 6 mm diameter, positioned with 85 mm spacing center-to-center. The characteristics of the reinforcements are detailed in Table 2.

Table 2.
Properties of materials (reinforcement bars).
The parametric study was designed in relation to NSM CFRP laminates strengthening. This procedure involves affixing CFRP laminate strips to the underside of the slab using an adhesive substance known as epoxy resin. The mechanical properties of CFRP and epoxy are displayed in Table 3. The designation of this group is as follows:

Table 3.
Properties of materials (CFRP and epoxy).
- Slab GA was reinforced with five strips of CFRP laminates in both directions with 1.2 mm thickness and 15 mm width, as shown in Figure 2b.
- Slab GB was reinforced with five strips of CFRP laminates in both directions with 1.2 mm thickness and 30 mm width.
- Slab GC was reinforced with five strips of CFRP laminates in both directions with 1.2 mm thickness and 45 mm width.
4. Test Procedure and the Response of Concrete Slabs
The structural performance of the two-way RC slab was monitored at each loading stage, using instrumentation. Data on various parameters including central deflection, fracture widths, initial crack load, and eventual failure load were collected during each loading increment. The testing continued until failure was observed; the maximum burden was recorded. Using a load cell with a capacity of 700 kN, deflection measurements were taken at the center of the bottom tension face of the slab specimens. A dial gauge graduated to 0.01 mm increments was employed for the load measurements.
The specimens undergoing examination were meticulously positioned within the specialized frame apparatus, disregarding their own weight. In the initial phases of the experiment, a load of 5 kN was progressively applied. At zero loading, initial dial gauge readings were obtained. As the applied force progressively escalated by 5 kN at each phase, cracks form on the concrete slabs’ surfaces, documented using a pencil. Concurrently, the initial cracking load was recorded at each load increment, fracture breadth was assessed utilizing steel fillers, and deflection data were gathered via the dial gauge. Following the completion of this procedure, loading continued with the subsequent load step, in accordance with the same protocol. The burden continued to increase until it reached its maximum value, at which juncture it was documented.
Table 4 presents the load of cracking (Pcr), ultimate load (Pu), width of cracks (Wcr) at the ultimate load, and the central deflections (Δv) at the ultimate load. The control slab is designed to undergo flexural failure. For comparative analysis, the following was performed:

Table 4.
The experimental findings from the slab testing.
The control slab specimens underwent testing without any strengthening technique. Its design aimed for flexural failure. The load was systematically increased and the slab’s behavior was closely monitored. During the initial phase of testing, the slab exhibited elastic behavior until the emergence of the first crack. The first crack became evident in the constant moment region at a load of 120 kN. With continued loading, flexural cracks commenced in the specimens, extending towards the edges, and widening rapidly. At a load of 241 kN, slab G0 experienced flexural failure, marked by a sudden increase in deflection, while the load remained constant.
External CFRP laminates strengthening—in this procedure, CFRP laminate strips were affixed to the underside of the slab using epoxy resin as the adhesive material. The initiation of the initial crack occurred at a load of 190.6 kN for GA, 208.5 kN for GB, and 237.28 kN for GC. At loads of 455 kN, 498 kN, and 564 kN, GA, GB, and GC slabs experienced failure through a punching mode, respectively. Comparing to the control slab G0, there were increases in ultimate loads by 88.7%, 107%, and 134% for slabs GA, GB, and GC, emphasizing the notable influence of augmenting the reinforcement ratio within CFRP laminates. While the load remained constant, there was a rapid increase in deflection. For comparative analysis, the control slab was compared to these three specimens; Figure 4 illustrates the load deflection behavior for the control slab alongside the GA, GB, and GC, experimentally. Observably, it is apparent that, by increasing the applied load, there is a proportional rise in damage intensity, signifying that the additional load induces supplementary initial stresses in both concrete and steel components. This emphasizes the importance of complementary strain energy in representing plastic damage. Ultimately, the adept management of this factor alleviates instances of plastic damage and failure. Table 4 reveals that using CFRP laminate in strengthening the concrete slabs enhanced the ultimate load, in contrast to the control slab. Furthermore, slab GC demonstrated the maximum ultimate load and the smallest crack width. The data also indicate that slabs strengthened with CFRP laminates experienced punching failure, while slab GA failed due to debonding. These results underscore the effective capacity of CFRP in enhancing the ultimate load bearing capability of slabs, concurrently reducing the central deflection and the crack width under equivalent loads.
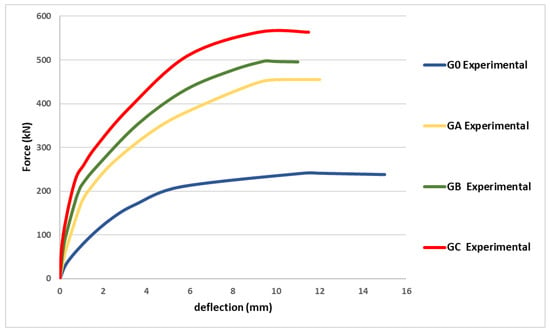
Figure 4.
Experimentally load deflection relationships for all models.
5. Numerical Modeling
FE analysis was employed to replicate the nonlinear response exhibited by two-way RC slabs strengthened with CFRP laminates, as depicted in Figure 5. The damage plasticity model was adopted in this study, to represent concrete inside the Abaqus CAE®. The modeling process involved four simply supported two-way RC slabs, derived from the experimental outcomes of one specimen-tested slab as a control slab, without using CFRP, as well as three strengthened concrete slabs with CFRP in different ratios. The concrete slab was modeled using the 8-node solid (C3D8R) element; as for the reinforcement bars, they were depicted as 2-node linear beam elements (T3D2). An embedded region was employed to simulate the bond between concrete and reinforcements. Additionally, the bond between concrete and CFRP was modeled as a surface-to-surface contact, as specified in the Abaqus CAE® manual. Steel-bearing plates (250 mm × 250 mm × 25 mm) were strategically placed to prevent local failure caused by crushing, utilizing the (C3D8R) 8-node solid element for modeling. Boundary conditions were selected to include a pin support at the first end for rotation and a roller support at the other end for rotation and horizontal movement. Additionally, at the center of the slab a concentrated vertical load was applied to simulate the experimental conditions. To ensure accuracy, a fine mesh was applied, resulting in a total element count for the slabs approximately equal to 21,600 elements. The impact of varying mesh sizes on both numerical precision and computational efficiency was analyzed, revealing that a mesh size of 20 yielded the highest level of accuracy.
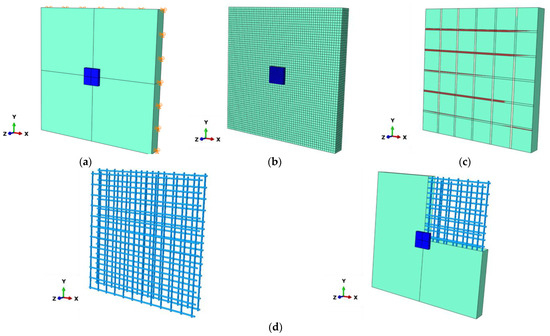
Figure 5.
Details of the numerical model: (a) supporting and loading conditions, (b) details of the mesh, (c) strengthening details, and (d) details of reinforcement.
For model validation, the slab was compared to a recent study with similar properties and analysis approaches. The validation process involved 3D finite element models, using Abaqus CAE® and the CDP model. Experimental results from four simply supported two-way slabs were used for validation. Concrete material properties were determined through standard cube tests for compressive behavior and split-cylinder tests for tensile behavior, revealing an average compressive strength of f c` = 30 MPa.
Both compressive crushing and tensile cracking are acknowledged as forms of failure mechanisms within the dataset, pertaining to concrete damage plasticity, derived from the tests of the mechanical properties on specimens. The integration of these traits within Abaqus CAE® facilitates the determination of CDP parameters, ensuring an accurate representation of concrete’s desired damage behavior. Following sensitivity analyses, the CDP plasticity parameters are determined using the information provided in Table 5. However, it is important to note that these CDP parameters stay consistent throughout the following optimization iterations. In Figure 5, the numerical model is illustrated.

Table 5.
Inserted CDP data for concrete.
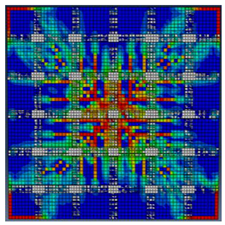
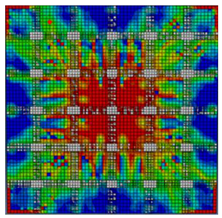
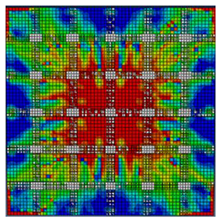
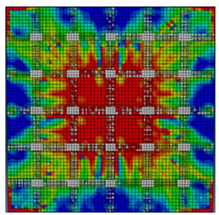
Figure 6 highlights the congruence in tension damage patterns showcasing a significant reduction in red damaged areas in the flexural portion of the slabs, with the use of CFRP; the Abaqus CAE® calibrated numerical models exhibited strong agreement with experimental findings, affirming the model’s efficacy in predicting the performance of two-way RC slabs reinforced with CFRPs. The comparable results produced by both experimental and numerical methods are demonstrated in Figure 7.
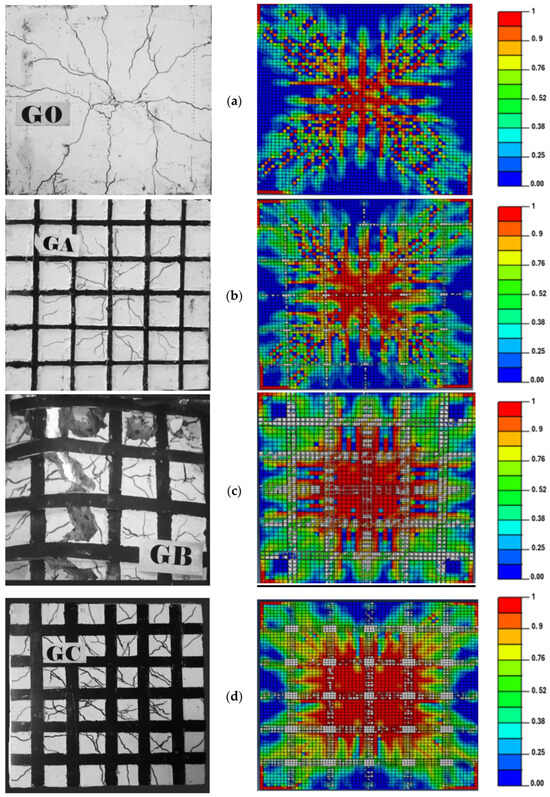
Figure 6.
Comparison of damage patterns experimentally and numerically. (a) Control slab without CFRP, (b) slab GA, (c) slab GB, and (d) slab GC.
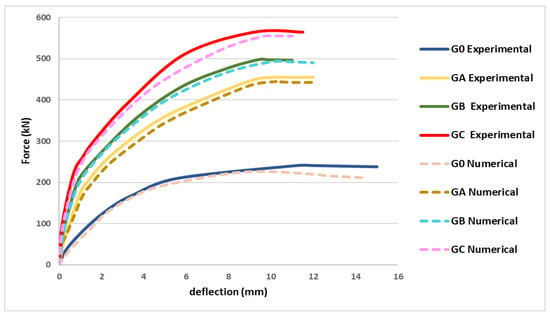
Figure 7.
Experimental and numerical load deflection relationships for all four models.
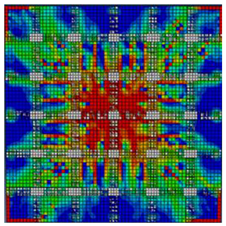
Furthermore, Table 6 illustrates alternative findings, presenting the percentages of tension concrete damage (%) observed in each case at different loads in specimen GC. The percentages are graphically depicted in Table 6, with red denoting areas of high damage intensity and blue indicating undamaged regions. Damage intensity rises with increasing load, suggesting that additional stress is introduced into the concrete, steel, and CFRP materials. This highlights the importance of incorporating complementary strain energy to accurately depict plastic damage. Overall, the effective control of this role mitigates plastic damage and failure occurrences.

Table 6.
Comparison of damage patterns for slab GC.
6. Results and Conclusions
This research investigated the elasto-plastic numerical modeling of reinforced concrete slabs strengthened with CFRP laminates. In order to accomplish this objective, the numerical model was validated by utilizing experimental data and the concrete damage plasticity (CDP) constitutive model in Abaqus CAE®, which was employed to depict the behavior of the concrete. Consequently, it is feasible to draw the subsequent conclusions regarding this endeavor.
- The performance of the reinforced slabs was distinctly influenced by the strengthening ratios. It was observed that an elevation in the strengthening ratio consistently led to a higher ultimate strength.
- The enhancement of reinforcement ratios across all the three specimens led to a rise in initial cracking, alongside a simultaneous decrease in deflection.
- Strengthening through CFRP laminate exhibited superior ultimate strength, cracking load, and minimized crack width, when compared to the control slab.
- The damage pattern presented in the data reflects the percentages of concrete damage due to tension. It can be deduced that, as the applied load rises, the severity of damage also increases. This suggests that the additional load imparts additional initial stresses to both the steel and concrete components. The function of complementary strain energy is emphasized by reflecting the plastic damage and, by controlling it, the plastic damage and failure may also be managed.
- The outcomes underscored the commendable efficacy of CFRPs in enhancing the ultimate load capacity of slabs, while simultaneously decreasing crack width and central deflection under equivalent loads.
- Alternatively, based on the numerical findings, varying quantities of CFRP strips have been observed to influence the behavior of the slabs. A comparison between experimental and numerical data reveals that the presence of CFRPs results in an increase in the slabs’ ultimate load capacity, serving as additional support to withstand shear stress and confine the concrete section, thereby inducing a more brittle and abrupt failure mode.
- In general, a reduction in the number of CFRP strips tends to exacerbate the extent of red area propagation, suggesting potential damage to either the steel or concrete. Conversely, employing more CFRP strips tends to mitigate the expansion of these red areas, akin to the effect observed with lower reinforcement ratios. In such cases, structures endure elevated stresses under lighter loads, when lower strengthening ratios are applied, resulting in failure at correspondingly lower loads.
- Linear behavior was observed in all specimens up to the first cracking load, with the load deflection curve at mid-span potentially approximated by a bilinear or trilinear curve.
Author Contributions
Methodology, M.M.R.; writing—original draft preparation, Z.S.S.; conceptualization, Z.S.S.; formal analysis, Z.S.S.; resources, M.M.R.; writing—review and editing, M.M.R.; software, Z.S.S. and M.M.R.; visualization, Z.S.S.; investigation, Z.S.S.; validation, Z.S.S. and M.M.R.; supervision, M.M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon corroborated request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Binici, B. Punching Shear Strengthening of Reinforced Concrete Slabs Using Fiber Reinforced Polymers. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2003. [Google Scholar]
- Bisby, L.A.; Fitzwilliam, J. An introduction to FRP composites for construction. ISIS Educ. Modul. Manit. Can. 2006. [Google Scholar]
- Khan, A.R.; Baluch, M.H.; Al-Gadhib, A.H. Repair and Strengthening of Reinforced Concrete Structures Using CFRP Plates. In Proceedings of the International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 7–12 June 2004. [Google Scholar]
- Ombres, L.; Mazzuca, P. Residual Flexural Behavior of PBO FRCM-Strengthened Reinforced Concrete Beams after Exposure to Elevated Temperatures. J. Compos. Constr. 2024, 28, 4023063. [Google Scholar] [CrossRef]
- Limam, O.; Foret, G.; Ehrlacher, A. RC two-way slabs strengthened with CFRP strips: Experimental study and a limit analysis approach. Compos. Struct. 2003, 60, 467–471. [Google Scholar] [CrossRef]
- Mosallam, A.S.; Mosalam, K.M. Strengthening of two-way concrete slabs with FRP composite laminates. Constr. Build. Mater. 2003, 17, 43–54. [Google Scholar] [CrossRef]
- Limam, O.; Nguyen, V.T.; Foret, G. Numerical and experimental analysis of two-way slabs strengthened with CFRP strips. Eng. Struct. 2005, 27, 841–845. [Google Scholar] [CrossRef]
- Hosseini, M.M.; Dias, S.; Barros, J. Flexural strengthening of reinforced low strength concrete slabs using prestressed NSM CFRP laminates. Compos. Part B Eng. 2015, 90, 14–29. [Google Scholar] [CrossRef]
- Yılmaz T, Kıraç N, Anil Ö, Erdem RT, Sezer C. Low-velocity impact behaviour of two way RC slab strengthening with CFRP strips. Constr. Build. Mater. 2018, 186, 1046–1063. [Google Scholar] [CrossRef]
- Akhundzada, H.; Donchev, T.; Petkova, D. Strengthening of slab-column connection against punching shear failure with CFRP laminates. Compos. Struct. 2019, 208, 656–664. [Google Scholar] [CrossRef]
- Mercimek, Ö.; Ghoroubi, R.; Erbaş, Y.; Anil, Ö. Comparison of strengthening methods to improve punching behavior of two-way RC flat slabs. Structures 2022, 46, 1495–1516. [Google Scholar] [CrossRef]
- Türer, A.; Mercimek, Ö.; Anıl, Ö.; Erbaş, Y. Experimental and numerical investigation of punching behavior of two-way RC slab with different opening locations and sizes strengthened with CFRP strip. Structures 2023, 49, 918–942. [Google Scholar] [CrossRef]
- Enochsson, O.; Lundqvist, J.; Täljsten, B.; Rusinowski, P.; Olofsson, T. CFRP strengthened openings in two-way concrete slabs—Experimental and numerical study. Constr. Build. Mater. 2007, 21, 810–826. [Google Scholar] [CrossRef]
- Esfahani, M.R.; Kianoush, M.R.; Moradi, A.R. Punching shear strength of interior slab–column connections strengthened with carbon fiber reinforced polymer sheets. Eng. Struct. 2009, 31, 1535–1542. [Google Scholar] [CrossRef]
- Meisami, M.H.; Mostofinejad, D.; Nakamura, H. Punching shear strengthening of two-way flat slabs using CFRP rods. Compos. Struct. 2013, 99, 112–122. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Alsayed, S.H.; Al-salloum, Y.A. Experimental and FE study on RC one-way slabs upgraded with FRP composites. KSCE J. Civ. Eng. 2015, 19, 1024–1040. [Google Scholar] [CrossRef]
- Behzard, P.; Sharbatdar, M.K.; Kheyroddin, A. Strengthening of existing RC two-way slabs using new combined FRP fabric/rod technique. J. Rehabil. Civ. Eng. 2015, 3, 30–44. [Google Scholar]
- Mahmoud, H.S.; Hawileh, R.A.; Abdalla, J.A. Strengthening of high strength reinforced concrete thin slabs with CFRP laminates. Compos. Struct. 2021, 75, 114412. [Google Scholar] [CrossRef]
- Rad, M.M.; Ibrahim, S.K.; Lógó, J. Limit design of reinforced concrete haunched beams by the control of the residual plastic de-formation. Structures 2022, 39, 987–996. [Google Scholar] [CrossRef]
- Carol, I.; Rizzi, E.; Willam, K. On the formulation of anisotropic elastic degradation. I. Theory based on a pseudo-logarithmic damage tensor rate. Int. J. Solids Struct. 2001, 38, 491–518. [Google Scholar] [CrossRef]
- Khaleel Ibrahim, S.; Movahedi Rad, M. Limited Optimal Plastic Behavior of RC Beams Strengthened by Carbon Fiber Polymers Using Reliability-Based Design. Polymers 2023, 15, 569. [Google Scholar] [CrossRef] [PubMed]
- Rad, M.M.; Papp, F.; Ibrahim, S.K.; Szép, J.; Gosztola, D.; Harrach, D. Elasto-plastic analysis and optimal design of composite integral abutment bridge extended with limited residual plastic deformation. Sci. Rep. 2023, 13, 5461. [Google Scholar] [CrossRef] [PubMed]
- Gatuingt, F.; Pijaudier-Cabot, G. Coupled damage and plasticity modelling in transient dynamic analysis of concrete. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 1–24. [Google Scholar] [CrossRef]
- Krätzig, W.B.; Pölling, R. An elasto-plastic damage model for reinforced concrete with minimum number of material parameters. Comput. Struct. 2004, 82, 1201–1215. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Imran, I.; Pantazopoulou, S.J. Plasticity model for concrete under triaxial compression. J. Eng. Mech. 2001, 127, 281–290. [Google Scholar] [CrossRef]
- Ananiev, S.; Ozbolt, J. Plastic–damage model for concrete in principal directions. In Fracture Mechanics of Concrete Structures; Li, V., Leung, C.K.Y., William, K.J., Billington, S.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 271–278. [Google Scholar]
- Szép, J.; Habashneh, M.; Lógó, J.; Rad Movahedi, M. Reliability assessment of reinforced concrete beams under elevated temperatures: A probabilistic approach using finite element and physical models. Sustainability 2023, 15, 6077. [Google Scholar] [CrossRef]
- Habashneh, M.; Movahedi Rad, M. Plastic-Limit Probabilistic Structural Topology Optimization of Steel Beams. Appl. Math. Model. 2024, 128, 347–369. [Google Scholar] [CrossRef]
- Habashneh, M.; Cucuzza, R.; Domaneschi, M.; Movahedi Rad, M. Advanced Elasto-Plastic Topology Optimization of Steel Beams under Elevated Temperatures. Adv. Eng. Softw. 2024, 190, 103596. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).