The Study of Molecules and Processes in Solution: An Overview of Questions, Approaches and Applications
Abstract
1. Introduction
2. Models for the Computational Study of Solvent Effects
2.1. Implicit Solvation Models
2.2. Explicit Solvation Models
2.3. Quantum Mechanical/Classical and Quantum Mechanical/Continuum Hybrid Approaches
3. Applications Relevant to Industry-Related Issues
3.1. The Search for Green Solvents
3.2. Predicting Solubility
3.3. Solvents for Extraction Processes
3.4. Deep Eutectic Solvents
3.5. Ionic Liquids
3.5.1. Nature and Properties of Ionic Liquids
3.5.2. Representative Models and Applications of Ionic Liquids
3.5.3. How Ionic Liquids Dissolve Cellulose
3.6. Nanoparticles in Liquid Media
3.6.1. Nanoparticles and Their Properties
3.6.2. Carbon Nanotubes
3.6.3. Silica Nanoparticles
3.6.4. Multiscale Modelling Options
3.7. Representative Examples of Other Types of Investigation Topics
3.7.1. Organometallic Catalysis
3.7.2. The Medium in Lithium-Ion Batteries
3.7.3. The Behaviour of Liquid Mixtures
3.7.4. Solvents Influencing Chemical Reactions
3.7.5. Ions in Solution
3.7.6. Studies in Solution to Understand the Properties of Natural Materials
4. Computational Studies Concerning the Solvent Role in the Interactions and Activities of Biologically Active Molecules and Biomolecules
4.1. The Complexity of Biomolecules and Biochemical Processes
4.2. Solvents and the Structure of Proteins
4.2.1. Water Molecules in and around Proteins’ Structures
4.2.2. Water Molecules and Proteins’ Folding
4.2.3. Proteins in Non-Aqueous Solvent
4.3. Solvents and the Structure of DNA
4.4. Solvent Roles in Protein–Protein Interactions
4.5. Solvent Roles in Protein–DNA Interactions
4.6. Solvent Roles in the Ligand–Protein Interactions
4.6.1. Interactions of Proteins with Small Molecules
4.6.2. Enzymes: Proteins That Are Catalysts
4.7. Solvent Roles in the Interactions between DNA and Other Molecules
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- From a quote at the end of a Gaussian-16 output.
- Reichardt, C. Solvents and solvent effects: An introduction. Org. Process Res. Dev. 2007, 11, 105–113. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mammino, L.; Kabanda, M.M. Considering the Medium when Studying Biologically Active Molecules: Motivation, Options and Challenges. In Frontiers in Computational Chemistry; Ul-Haq, Z., Madura, J.D., Eds.; Bentham Science Publishers: Sharjah, United Arab Emirates, 2014; pp. 197–256. [Google Scholar]
- Anastas, P.T.; Williamson, T.C. Green Chemistry: Designing Chemistry for the Environment; American Chemical Society: Washington, DC, USA, 1996. [Google Scholar]
- Anastas, P.T.; Warner, J.C. Green Chemistry: Theory and Practice; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Tundo, P.; Anastas, P.T. Green Chemistry, Challenging Perspectives; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Anastas, P.T.; Kirchhoff, M.M. Origins, current status, and future challenges of green chemistry. Acc. Chem. Res. 2002, 35, 686–694. [Google Scholar] [CrossRef]
- Welton, T. Solvents and sustainable chemistry. Proc. R. Soc. A 2015, 471, 20150502. [Google Scholar] [CrossRef] [PubMed]
- Constable, D.J.C.; Jimenez-Gonzalez, C.; Henderson, R.K. Perspective on solvent use in the pharmaceutical industry. Org. Process Res. Dev. 2007, 11, 133–137. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Linke, P. Multiobjective molecular design for integrated process-solvent systems synthesis. AIChE J. 2006, 52, 1057–1070. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Linke, P. Efficient integration of optimal solvent and process design using molecular clustering. Chem. Eng. Sci. 2006, 61, 6316–6336. [Google Scholar] [CrossRef]
- Bardow, A.; Steur, K.; Gross, J. Continuous-Molecular Targeting for Integrated Solvent and Process Design. Ind. Eng. Chem. Res. 2010, 49, 2834–2840. [Google Scholar] [CrossRef]
- Zhou, T.; Zhou, Y.; Sundmacher, K. A hybrid stochastic-deterministic optimization approach for integrated solvent and process design. Chem. Eng. Sci. 2017, 159, 207–216. [Google Scholar] [CrossRef]
- Keßler, T.; Kunde, C.; Linke, S.; Sundmacher, K.; Kienle, A. Integrated computer-aided molecular and process design: Green solvents for the hydroformylation of long-chain olefines. Chem. Eng. Sci. 2022, 249, 117243. [Google Scholar] [CrossRef]
- Winterton, N. The green solvent: A critical perspective. Clean Technol. Environ. Policy 2021, 23, 2499–2522. [Google Scholar] [CrossRef]
- Breslow, R. The Principles of and Reasons for Using Water as a Solvent for Green Chemistry, Part 5. Reactions in Water. In Handbook of Green Chemistry; Wiley: Hoboken, NJ, USA, 2010; pp. 1–29. [Google Scholar] [CrossRef]
- Simon, M.-O.; Li, C.-J. Green chemistry oriented organic synthesis in water. Chem. Soc. Rev. 2012, 41, 1415–1427. [Google Scholar] [CrossRef] [PubMed]
- Majhi, K.C.; Karfa, P.; Kumar, S.; Madhuri, R. Water as the Green Solvent in Organic Synthesis. Mater. Res. Found. 2019, 54, 182–201. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, G.; Jiang, L.; Cai, Y.; Gao, Y.; Yang, W.; He, X.; Zeng, Q.; Xing, G.; Jia, Y.; et al. Water, a Green Solvent for Fabrication of High-Quality CsPbBr3 Films for Efficient Solar Cells. ACS Appl. Mater. Interfaces 2020, 12, 5925–5931. [Google Scholar] [CrossRef] [PubMed]
- Beckman, E.J. Supercritical and near-critical CO2 in green chemical synthesis and processing. J. Supercrit. Fluids 2004, 28, 121–191. [Google Scholar] [CrossRef]
- Nalawade, S.P.; Picchioni, F.; Janssen, L.P.B.M. Supercritical carbon dioxide as a green solvent for processing polymer melts: Processing aspects and applications. Prog. Polym. Sci. 2006, 31, 19–43. [Google Scholar] [CrossRef]
- Sánchez-Vicente, Y.; Cabañas, A.; Renuncio, J.A.R.; Pando, C. Supercritical CO2 as a green solvent for eucalyptus and citrus essential oils processing: Role of thermal effects upon mixing. RSC Adv. 2013, 3, 6065–6075. [Google Scholar] [CrossRef]
- Vandeponseele, A.; Draye, M.; Piot, C.; Chatel, G. Subcritical water and supercritical carbon dioxide: Efficient and selective eco-compatible solvents for coffee and coffee by-products valorization. Green Chem. 2020, 22, 8544–8571. [Google Scholar] [CrossRef]
- Soren, S.; Sahoo, T.; Panda, J.; Senapati, D.K.; Sahu, J.R.; Rath, C.K.; Sahu, R. Carbon Dioxide-Based Green Solvents. In Carbon Dioxide Utilization to Sustainable Energy and Fuels; Inamuddin, Boddula, R., Ahamed, M.I., Khan, A., Eds.; Advances in Science, Technology & Innovation; Springer: Cham, Switzerland, 2022; pp. 323–333. [Google Scholar]
- Petigny, L.; Özel, M.Z.; Périno, S.; Wajsman, J.; Chemat, F. Water as Green Solvent for Extraction of Natural Products. In Green Extraction of Natural Products: Theory and Practice; Chemat, F., Strube, J., Eds.; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar] [CrossRef]
- Castro-Puyana, M.; Marina, M.L.; Plaza, M. Water as green extraction solvent: Principles and reasons for its use. Curr. Opin. Green Sustain. Chem. 2017, 5, 31–36. [Google Scholar] [CrossRef]
- Hartonen, K.; Riekkola, M.-L. Water as the First Choice Green Solvent. In The Application of Green Solvents in Separation Processes; Elsevier: Amsterdam, The Netherlands, 2017; pp. 19–55. [Google Scholar] [CrossRef]
- Skyner, R.E.; McDonagh, J.L.; Groom, C.R.; van Mourik, T.V.; Mitchell, J.B.O. A review of methods for the calculation of solution free energies and the modelling of systems in solution. Phys. Chem. Chem. Phys. 2015, 17, 6174–6191. [Google Scholar] [CrossRef]
- Mennucci, B. Multiscale strategies for describing environment effects: From solvents to biomatrices. In Green Chemistry and Computational Chemistry—Shared Lessons in Sustainability; Mammino, L., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 263–280. [Google Scholar]
- Tomasi, J.; Persico, M. Molecular interactions in solution: An overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Ahuir, J.L.; Silla, E.; Tuñón, I. GEPOL: An improved description of molecular surfaces. III. A new algorithm for the computation of a solvent-excluding surface. J. Comput. Chem. 1994, 5, 1127–1138. [Google Scholar] [CrossRef]
- Pascual-Ahuir, J.L.; Silla, E.; Tomasi, J.; Bonaccorsi, R. Electrostatic interaction of a solute with a continuum. Improved description of the cavity and of the surface cavity bound charge distribution. J. Comput. Chem. 1987, 8, 778–787. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Miertus, S.; Tomasi, J. Approximate evaluations of the electrostatic free-energy and internal energy changes in solution processes. Chem. Phys. 1982, 65, 239–245. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef] [PubMed]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. Implicit solvation models: Equilibria, structure, spectra, and dynamics. Chem. Rev. 1999, 99, 2161–2200. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: Theoretical bases, computational implementation, and numerical applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Soteras, I.; Curutchet, C.; Bidon-Chanal, A.; Orozco, M.; Luque, F.J. Extension of the MST model to the IEF formalism: HF and B3LYP parametrizations. J. Mol. Struct. THEOCHEM 2005, 727, 29–40. [Google Scholar] [CrossRef]
- Mennucci, B. Continuum solvation models: What else can we learn from them? J. Phys. Chem. Lett. 2010, 1, 1666–1674. [Google Scholar] [CrossRef]
- Lipparini, F.; Mennucci, B. Perspective: Polarizable continuum models for quantum-mechanical descriptions. J. Chem. Phys. 2016, 144, 160901–160909. [Google Scholar] [CrossRef] [PubMed]
- Amovilli, C.; Barone, V.; Cammi, R.; Cancès, E.; Cossi, M.; Mennucci, C.; Pomelli, C.S.; Tomasi, J. Recent advances in the description of solvent effects with the polarisable continuum model. Adv. Quantum Chem. 1999, 32, 227–259. [Google Scholar]
- Barone, V.; Cossi, M.; Tomasi, J. A new definition of cavities for the computation of solvation free energies by the polarizable continuum model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Pomelli, C.S.; Tomasi, J.; Cossi, M.; Barone, V. Effective generation of molecular cavities in the polarizable continuum model by the DefPol procedure. J. Comp. Chem. 1999, 20, 1693–1701. [Google Scholar] [CrossRef]
- Tomasi, J. Cavity and reaction field: “robust” concepts. Perspective on “Electric moments of molecules in liquids”—Onsager, L. (1936) J. Am. Chem. Soc. 58: 1486. Theor. Chem. Acc. 2000, 103, 196–199. [Google Scholar] [CrossRef]
- Takano, Y.; Houk, K.N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2005, 1, 70–77. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. The COSMO and COSMO-RS solvation models. WIREs Comput. Mol. Sci. 2011, 1, 699–709. [Google Scholar] [CrossRef]
- Touaibia, M.; Fabiano-Tixier, A.-S.; Chemat, F. Chloropinane and Chloromenthene as Novel Solvents for Solubilisation of Natural Substances. Molbank 2021, 2021, M1205. [Google Scholar] [CrossRef]
- Zhou, T.; McBride, K.; Linke, S.; Song, Z.; Sundmacher, K. Computer-Aided Solvent Selection and Design for Efficient Chemical Processes. Curr. Opin. Chem. Eng. 2020, 27, 35–44. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Mammino, L.; Kabanda, M.M. Adducts of acylphloroglucinols with explicit water molecules: Similarities and differences across a sufficiently representative number of structures. Int. J. Quantum Chem. 2010, 110, 2378–2390. [Google Scholar] [CrossRef]
- Mammino, L. Adducts of arzanol with explicit water molecules: An ab initio and DFT study. In Concepts, Methods and Applications of Quantum Systems in Chemistry and Physics; Wang, Y.A., Thachuk, M., Krems, R., Maruani, J., Eds.; Springer: Cham, Switzerland, 2018; Volume 31, pp. 281–304. [Google Scholar]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Shiga, M.; Masia, M. Boundary based on exchange symmetry theory for multilevel simulations. I. Basic theory. J. Chem. Phys. 2013, 139, 044120. [Google Scholar] [CrossRef]
- Takahashi, H.; Kambe, H.; Morita, A. A simple and effective solution to the constrained QM/MM simulations. J. Chem. Phys. 2018, 148, 134119. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Waller, M.P. Adaptive quantum mechanics/molecular mechanics methods. WIRES Comput. Mol. Sci. 2016, 6, 369–385. [Google Scholar] [CrossRef]
- Duster, A.W.; Wang, C.H.; Garza, C.M.; Miller, D.E.; Lin, H. Adaptive quantum/molecular mechanics: What have we learned, where are we, and where do we go from here? WIRES Comput. Mol. Sci. 2017, 7, e1310. [Google Scholar] [CrossRef]
- de Jesus, S.S.; Maciel Filho, R. Are ionic liquids eco-friendly? Renew. Sustain. Energy Rev. 2022, 157, 112039. [Google Scholar] [CrossRef]
- Crinnion, W.J. The CDC fourth national report on human exposure to environmental chemicals: What it tells us about our toxic burden and how it assists environmental medicine physicians. Altern. Med. Rev. 2010, 15, 101–109. [Google Scholar] [PubMed]
- Quesne, M.G.; Silveri, F.; de Leeuw, N.H.; Catlow, C.R.A. Advances in Sustainable Catalysis: A Computational Perspective. Front. Chem. 2019, 7, 182. [Google Scholar] [CrossRef] [PubMed]
- Bubalo, M.C.; Vidović, S.; Redovniković, I.R.; Jokić, S. Green solvents for green technologies. J. Chem. Technol. Biotechnol. 2015, 90, 1631–1639. [Google Scholar] [CrossRef]
- Gu, Y.; Jérôme, F. Bio-based solvents: An emerging generation of fluids for the design of eco-efficient processes in catalysis and organic chemistry. Chem. Soc. Rev. 2013, 42, 9550–9570. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Mondal, A.; Balasubramanian, S. Recent advances in modeling green solvents. Curr. Opin. Green Sustain. Chem. 2017, 5, 37–43. [Google Scholar] [CrossRef]
- Hansen, C.M. The universality of the solubility parameter. Ind. Eng. Chem. Prod. Res. Dev. 1969, 8, 2–11. [Google Scholar] [CrossRef]
- Faasen, D.P.; Jarray, A.; Zandvliet, H.J.W.; Kooij, E.S.; Kwiecinski, W. Hansen solubility parameters obtained via molecular dynamics simulations as a route to predict siloxane surfactant adsorption. J. Colloid Interface Sci. 2020, 575, 326–336. [Google Scholar] [CrossRef]
- Crowley, J.D.; Teague, G.S., Jr.; Lowe, J.W., Jr. A three-dimensional approach to solubility. J. Paint Technol. 1966, 38, 269–280. [Google Scholar]
- Durand, M.; Molinier, V.; Kunz, W.; Aubry, J.M. Classification of organic solvents revisited by using the COSMO-RS approach. Chem. Eur. J. 2011, 17, 5155–5164. [Google Scholar] [CrossRef]
- Garcia-Chavez, L.Y.; Hermans, A.J.; Schuur, B.; de Haan, A.B. COSMO-RS assisted solvent screening for liquid-liquid extraction of mono ethylene glycol from aqueous streams. Sep. Purif. Technol. 2012, 97, 2–10. [Google Scholar] [CrossRef]
- Moity, L.; Durand, M.; Benazzouz, A.; Pierlot, C.; Molinier, V.; Aubry, J.-M. Panorama of sustainable solvents using the COSMO-RS approach. Green Chem. 2012, 14, 1132–1145. [Google Scholar] [CrossRef]
- Benazzouz, A.; Moity, L.; Pierlot, C.; Molinier, V.; Aubry, J.-M. Hansen approach versus COSMO-RS for predicting the solubility of an organic UV filter in cosmetic solvents. Colloids Surf. A Physicochem. Eng. Asp. 2014, 458, 101–109. [Google Scholar] [CrossRef]
- Filly, A.; Fabiano-Tixier, A.S.; Fernandez, X.; Chemat, F. Alternative Solvents for Extraction of Food Aromas; Experimental and COSMO-RS Study. LWT Food Sci. Technol. 2015, 61, 33–40. [Google Scholar] [CrossRef]
- Kundi, V.; Ho, J. Predicting Octanol–Water Partition Coefficients: Are Quantum Mechanical Implicit Solvent Models Better than Empirical Fragment-Based Methods? J. Phys. Chem. B 2019, 123, 6810–6822. [Google Scholar] [CrossRef] [PubMed]
- Del Pilar Sánchez-Camargo, A.; Pleite, N.; Herrero, M.; Cifuentes, A.; Ibáñez, E.; Gilbert-López, B. New Approaches for the Selective Extraction of Bioactive Compounds Employing Biobased Solvents and Pressurized Green Processes. J. Supercrit. Fluids 2017, 128, 112–120. [Google Scholar] [CrossRef]
- Li, Z.; Smith, K.H.; Stevens, G.W. The use of environmentally sustainable bio-derived solvents in solvent extraction applications—A review. Chin. J. Chem. Eng. 2016, 24, 215–220. [Google Scholar] [CrossRef]
- Li, Y.; Fabiano-Tixier, A.S.; Ginies, C.; Chemat, F. Direct green extraction of volatile aroma compounds using vegetable oils as solvents: Theoretical and experimental solubility study. LWT Food Sci. Technol. 2014, 59, 724–731. [Google Scholar] [CrossRef]
- Bundeesomchok, K.; Filly, A.; Rakotomanomana, N.; Panichayupakaranant, P.; Chemat, F. Extraction of α-Mangostin from Garcinia mangostana L. Using Alternative Solvents: Computational Predictive and Experimental Studies. LWT Food Sci. Technol. 2016, 65, 297–303. [Google Scholar] [CrossRef]
- Filly, A.; Fabiano-Tixier, A.-S.; Lemasson, Y.; Roy, C.; Fernandez, X.; Chemat, F. Extraction of aroma compounds in blackcurrant buds by alternative solvents: Theoretical and experimental solubility study. Comptes Rendus Chim. 2014, 17, 1268–1275. [Google Scholar] [CrossRef]
- Moongkarndi, P.; Kosem, N.; Kaslungka, S.; Luanratana, O.; Pongpan, N.; Neungton, N. Antiproliferation, antioxidation and induction of apoptosis by Garcinia mangostana (mangosteen) on SKBR3 human breast cancer cell line. J. Ethnopharmacol. 2004, 90, 161–166. [Google Scholar] [CrossRef]
- Nganlasom, J.; Suttitum, T.; Jirakulsomchok, D.; Puapairoj, A. Effects of Centella asiatica Linn. leaves and Garcinia mangostana Linn. hull on the healing of dermal wounds in diabetic rats. Srinagarind Med. J. 2008, 23, 402–407. [Google Scholar]
- Nualkaew, N.; Morita, H.; Shimokawa, Y.; Kinjo, K.; Kushiro, T.; De-Eknamkul, W.; Ebizuka, Y.; Abe, I. Benzophenone synthase from Garcinia mangostana L. pericarps. Phytochemistry 2012, 77, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Sakagami, Y.; Iinuma, M.; Piyasena, K.; Dharmaratne, H. Antibacterial activity of α-mangostin against vancomycin-resistant enterococci (VRE) and synergism with antibiotics. Phytomedicine 2005, 12, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Pothitirat, W.; Chomnawang, M.T.; Gritsanapan, W. Anti-acne inducing bacteria activity and α-mangostin content of Garcinia mangostana fruit rind extracts from different provenience. Songklanakarin J. Sci. Technol. 2009, 31, 41–47. [Google Scholar]
- Pothitirat, W.; Chomnawang, M.T.; Gritsanapan, W. Anti-acne-inducing bacterial activity of mangosteen fruit rind extracts. Med. Princ. Pract. 2010, 19, 281–286. [Google Scholar] [CrossRef]
- Nutrizio, M.; Gajdoš Kljusurić, J.; Marijanović, Z.; Dubrović, I.; Viskić, M.; Mikolaj, E.; Režek Jambrak, A. The potential of high voltage discharges for green solvent extraction of bioactive compounds and aromas from rosemary (Rosmarinus officinalis L.)—Computational simulation and experimental methods. Molecules 2020, 25, 3711. [Google Scholar] [CrossRef]
- Cascant, M.M.; Breil, C.; Garrigues, S.; de la Guardia, M.; Fabiano-Tixier, A.S.; Chemat, F. A green analytical chemistry approach for lipid extraction: Computation methods in the selection of green solvents as alternative to hexane. Anal. Bioanal. Chem. 2017, 409, 3527–3539. [Google Scholar] [CrossRef] [PubMed]
- Yara-Varon, E.; Fabiano-Tixier, A.S.; Balcells, M.; Canela-Garayoa, R.; Bily, A.; Chemat, F. Is it possible to substitute hexane with green solvents for extraction of carotenoids? A theoretical versus experimental solubility study. RSC Adv. 2016, 6, 27750–27759. [Google Scholar] [CrossRef]
- Ozturk, B.; Winterburn, J.; Gonzalez-Miquel, M. Orange peel waste valorisation through limonene extraction using bio-based solvents. Biochem. Eng. J. 2019, 151, 107298. [Google Scholar] [CrossRef]
- Linke, S.; McBride, K.; Sundmacher, K. Systematic green solvent selection for the hydroformylation of long-chain alkenes. ACS Sustain. Chem. Eng. 2020, 8, 10795–10811. [Google Scholar] [CrossRef]
- Neves, B.J.; Braga, R.C.; Melo-Filho, C.C.; Moreira-Filho, J.T.; Muratov, E.N.; Horta Andrade, C. QSAR-Based Virtual Screening: Advances and Applications in Drug Discovery. Front. Pharmacol. 2018, 9, 1275. [Google Scholar] [CrossRef]
- Benfenati, E.; Manganaro, A.; Gini, G. VEGA-QSAR: AI inside a platform for predictive toxicology. In CEUR Workshop Proceedings, Proceedings of the Workshop on Popularize Artificial Intelligence 2013 (PAI 2013), Turin, Italy, 5 December 2013; CEUR Foundation: Bologna, Italy, 2013. [Google Scholar]
- Abbott, A.P.; Capper, G.; Davies, D.L.; Rasheed, R.K.; Tambyrajah, V. Novel solvent properties of choline chloride/urea mixtures. Chem. Commun. 2003, 39, 70–71. [Google Scholar] [CrossRef] [PubMed]
- Francisco, M.; van den Bruinhorst, A.; Kroon, M.C. Low-transition-temperature mixtures (LTTMs): A new generation of designer solvents. Angew. Chem. Int. Ed. 2013, 52, 3074–3085. [Google Scholar] [CrossRef] [PubMed]
- Souza, O.A.; Rinaldo, D.; Porto, C.M.; Sambrano, J.R.; Morgon, N.H.; de Souza, A.R. Computer simulation applied to structural analysis and experimental applications of natural deep eutectic solvents. In Green Chemistry and Computational Chemistry—Shared Lessons in Sustainability; Mammino, L., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 281–298. [Google Scholar]
- Espino, M.; Fernández, M.d.l.A.; Gomez, F.J.V.; Silva, M.F. Natural designer solvents for greening analytical chemistry. TrAC Trends Anal. Chem. 2016, 76, 126–136. [Google Scholar] [CrossRef]
- Dai, Y.; van Spronsen, J.; Witkamp, G.-J.; Verpoorte, R.; Choi, Y.H. Natural deep eutectic solvents as new potential media for green technology. Anal. Chim. Acta 2013, 766, 61–68. [Google Scholar] [CrossRef]
- El Kantar, S.; Rajha, H.N.; Boussetta, N.; Vorobiev, E.; Maroun, R.G.; Louka, N. Green Extraction of Polyphenols from Grapefruit Peels Using High Voltage Electrical Discharges, Deep Eutectic Solvents and Aqueous Glycerol. Food Chem. 2019, 295, 165–171. [Google Scholar] [CrossRef]
- Abbott, A.P.; Boothby, D.; Capper, G.; Davies, D.L.; Rasheed, R.K. Deep Eutectic Solvents formed between choline chloride and carboxylic acids: Versatile alternatives to ionic liquids. J. Am. Chem. Soc. 2004, 126, 9142–9147. [Google Scholar] [CrossRef]
- Zhu, R.; Cao, S.; Tian, J.; Luo, M.; You, J.; Chen, Z. Computational design of deep eutectic solvent functionalized ZIF-8/biochar with high selectivity for mephedrone: Experimental validation and microscopic mechanism. J. Clean. Prod. 2023, 399, 136687. [Google Scholar] [CrossRef]
- Shah, F.U.; An, R.; Muhammad, N. Editorial: Properties and applications of ionic liquids in energy and environmental science. Front. Chem. 2020, 8, 627213. [Google Scholar] [CrossRef]
- Nasirpour, N.; Mohammadpourfard, M.; Heris, S.Z. Ionic liquids: Promising compounds for sustainable chemical processes and applications. Chem. Eng. Res. Des. 2020, 160, 264–300. [Google Scholar] [CrossRef]
- Das, R.N.; Roy, K. Advances in QSPR/QSTR models of ionic liquids for the design of greener solvents of the future. Mol. Divers. 2013, 17, 151–196. [Google Scholar] [CrossRef]
- Olivier-Bourbigou, H.; Magna, L.; Morvan, D. Ionic liquids and catalysis: Recent progress from knowledge to applications. Appl. Catal. A 2010, 373, 1–56. [Google Scholar] [CrossRef]
- Bruzzone, S.; Chiappe, C.; Focardi, S.E.; Pretti, C.; Renzi, M. Theoretical descriptor for the correlation of aquatic toxicity of ionic liquids by quantitative structure–toxicity relationships. Chem. Eng. J. 2011, 175, 17–23. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree–Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Anastas, P.T.; Bartlett, L.B.; Kirchhoff, M.M.; Williamson, T.C. The role of catalysis in the design, development, and implementation of green chemistry. Catal. Today 2000, 55, 11–22. [Google Scholar] [CrossRef]
- Anastas, P.T.; Kirchhoff, M.M.; Williamson, T.C. Catalysis as a foundational pillar of green chemistry. Appl. Catal. Gen. 2001, 221, 3–13. [Google Scholar] [CrossRef]
- Ha, S.H.; Lan, M.N.; Lee, S.H.; Hwang, S.M.; Koo, Y.M. Lipase-catalyzed biodiesel production from soybean oil in ionic liquids. Enzyme Microb. Technol. 2007, 41, 480–483. [Google Scholar] [CrossRef]
- Kim, H.S.; Ha, S.H.; Sethaphong, L.; Koo, Y.-M.; Yingling, Y.G. The relationship between enhanced enzyme activity and structural dynamics in ionic liquids: A combined computational and experimental study. Phys. Chem. Chem. Phys. 2014, 16, 2944–2953. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Kuanar, M.; Stoyanova-Slavova, I.B.; Slavov, S.H.; Dobchev, D.A.; Karelson, M.; Acree, W.E., Jr. Quantitative structure–property relationship studies on Ostwald solubility and partition coefficients of organic solutes in ionic liquids. J. Chem. Eng. Data 2008, 53, 1085–1092. [Google Scholar] [CrossRef]
- Cao, B.; Dua, J.; Dua, D.; Suna, H.; Zhua, X.; Fu, H. Cellobiose as a model system to reveal cellulose dissolution mechanism in acetate-based ionic liquids: Density functional theory study substantiated by NMR spectra. Carbohydr. Polym. 2016, 149, 348–356. [Google Scholar] [CrossRef] [PubMed]
- Youngs, T.G.; Holbrey, J.D.; Deetlefs, M.; Nieuwenhuyzen, M.; Costa Gomes, M.F.; Hardacre, C. A molecular dynamics study of glucose solvation in the ionic liquid 1,3-dimethylimidazolium chloride. ChemPhysChem 2006, 7, 2279–2281. [Google Scholar] [CrossRef] [PubMed]
- Youngs, T.G.A.; Hardacre, C.; Holbrey, J.D. Glucose solvation by the ionic liquid 1,3-dimethylimidazolium chloride: A simulation study. J. Phys. Chem. B 2007, 111, 13765–13774. [Google Scholar] [CrossRef]
- Derecskei, B.; Derecskei-Kovacs, A. Molecular dynamic studies of the compatibility of some cellulose derivatives with selected ionic liquids. Mol. Simul. 2006, 32, 109–115. [Google Scholar] [CrossRef]
- Rabideau, B.D.; Agarwal, A.; Ismail, A.E. The role of the cation in the solvation of cellulose by imidazolium-based ionic liquids. J. Phys. Chem. B 2014, 118, 1621–1629. [Google Scholar] [CrossRef]
- Payal, R.S.; Bejagam, K.K.; Mondal, A.; Balasubramanian, S. Dissolution of cellulose in room temperature ionic liquids: Anion dependence. J. Phys. Chem. B 2015, 119, 1654–1659. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Li, Y.; Wang, J.; Liu, X.; Zhang, S. Towards a molecular understanding of cellulose dissolution in ionic liquids: Anion/cation effect, synergistic mechanism and physicochemical aspects. Chem. Sci. 2018, 9, 4027–4043. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, X.; Zhang, S.; Yao, Y.; Yao, X.; Xu, J.; Lu, X. Dissolving process of a cellulose bunch in ionic liquids: A molecular dynamics study. Phys. Chem. Chem. Phys. 2015, 17, 17894–17905. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Wang, J.; Zhang, S. Insight into the cosolvent effect of cellulose dissolution in imidazolium-based ionic liquid systems. J. Phys. Chem. B 2013, 117, 9042–9049. [Google Scholar] [CrossRef] [PubMed]
- Huo, F.; Liu, Z.; Wang, W. Cosolvent or antisolvent? A molecular view of the interface between ionic liquids and cellulose upon addition of another molecular solvent. J. Phys. Chem. B 2013, 117, 11780–11792. [Google Scholar] [CrossRef] [PubMed]
- Velioglu, S.; Yao, X.; Devemy, J.; Ahunbay, M.G.; Tantekin-Ersolmaz, S.B.; Dequidt, A.; Costa Gomes, M.F.; Padua, A.A. Solvation of a cellulose microfibril in imidazolium acetate ionic liquids: Effect of a cosolvent. J. Phys. Chem. B 2014, 118, 14860–14869. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Balamurugan, K.; Shi, J.; Subramanian, V.; Simmons, B.A.; Singh, S. Theoretical insights into the role of water in the dissolution of cellulose using IL/water mixed solvent systems. J. Phys. Chem. B 2015, 119, 14339–14349. [Google Scholar] [CrossRef] [PubMed]
- Rabideau, B.D.; Ismail, A.E. Mechanisms of hydrogen bond formation between ionic liquids and cellulose and the influence of water content. Phys. Chem. Chem. Phys. 2015, 17, 5767–5775. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, R. Recent progress and perspectives on the toxicity of carbon nanotubes at organism, organ, cell, and biomacromolecule levels. Environ. Int. 2012, 40, 244–256. [Google Scholar] [CrossRef] [PubMed]
- Joudeh, N.; Linke, D. Nanoparticle classification, physicochemical properties, characterization, and applications: A comprehensive review for biologists. J. Nanobiotechnol. 2022, 20, 262. [Google Scholar] [CrossRef]
- Hoet, P.H.M.; Brüske-Hohlfeld, I.; Salata, O.V. Nanoparticles known and unknown risks. J. Nanobiotechnol. 2004, 2, 12. [Google Scholar] [CrossRef]
- Jeevanandam, J.; Barhoum, A.; Chan, Y.S.; Dufresne, A.; Danquah, M.K. Review on nanoparticles and nanostructured materials: History, sources, toxicity and regulations. Beilstein J. Nanotechnol. 2018, 9, 1050–1074. [Google Scholar] [CrossRef] [PubMed]
- Turan, N.B.; Erkan, H.S.; Engin, G.O.; Bilgili, M.S. Nanoparticles in the aquatic environment: Usage, properties, transformation and toxicity—A review. Process Saf. Environ. Prot. 2019, 130, 238–249. [Google Scholar] [CrossRef]
- Barnard, A.S. How can ab initio simulations address risks in nanotech? Nat. Nanotechnol. 2009, 4, 332–335. [Google Scholar] [CrossRef] [PubMed]
- Gajewicz, A.; Rasulev, B.; Dinadayalane, T.C.; Urbaszek, P.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Advancing risk assessment of engineered nanomaterials: Application of computational approaches. Adv. Drug Deliv. Rev. 2012, 64, 1663–1693. [Google Scholar] [CrossRef]
- Cook, E.; Labiento, G.; Chauhan, B.P.S. Fundamental Methods for the Phase Transfer of Nanoparticles. Molecules 2021, 26, 6170. [Google Scholar] [CrossRef]
- Xu, N.; Liu, Z.; Lv, Y.; Liu, S.; Yang, S.; Zhang, W. Improved Coarse-Grained Model for Nanoparticles Based on the Martini Force Field and Its Application in Molecular Dynamics Simulation on Gel Ink. Langmuir 2022, 38, 14172–14184. [Google Scholar] [CrossRef]
- Wagener, P.; Jakobi, J.; Rehbock, C.; Chakravadhanula, V.S.K.; Thede, C.; Wiedwald, U.; Bartsch, M.; Kienle, L.; Barcikowski, S. Solvent-surface interactions control the phase structure in laser-generated iron-gold core-shell nanoparticles. Sci. Rep. 2016, 6, 23352. [Google Scholar] [CrossRef]
- Leekumjorn, S.; Gullapalli, S.; Wong, M.S. Understanding the Solvent Polarity Effects on Surfactant-Capped Nanoparticles. J. Phys. Chem. B 2012, 116, 13063–13070. [Google Scholar] [CrossRef] [PubMed]
- Filippov, A.V.; Starov, V. Interaction of Nanoparticles in Electrolyte Solutions. J. Phys. Chem. B 2023, 127, 6562–6572. [Google Scholar] [CrossRef]
- Chintha, D.; Veesam, S.K.; Boattini, E.; Filion, L.; Punnathanam, S.N. Modeling of effective interactions between ligand coated nanoparticles through symmetry functions. J. Chem. Phys. 2021, 155, 244901. [Google Scholar] [CrossRef]
- Hafiz, M.; Hassanein, A.; Talhami, M.; AL-Ejji, M.; Hassan, M.K.; Hawari, A.H. Magnetic nanoparticles draw solution for forward osmosis: Current status and future challenges in wastewater treatment. J. Environ. Chem. Eng. 2022, 10, 108955. [Google Scholar] [CrossRef]
- Wörle-Knirsch, J.M.; Krug, H.F. Cause I’m CNT, not dynamite. Nano Today 2006, 1, 48. [Google Scholar] [CrossRef]
- Lacerda, L.; Bianco, A.; Prato, M.; Kostarelos, K. Carbon nanotubes as nanomedicines: From toxicology to pharmacology. Adv. Drug Deliv. Rev. 2006, 58, 1460–1470. [Google Scholar] [CrossRef] [PubMed]
- Sasidharan, A.; Panchakarla, L.S.; Chandran, P.; Menon, D.; Nair, S.; Rao, C.N.R.; Koyakutty, M. Differential nano-bio interactions and toxicity effects of pristine versus functionalized graphene. Nanoscale 2011, 3, 2461–2464. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, Y.; Kobayashi, N.; Shinohara, N.; Myojo, T.; Tanaka, I.; Nakanishi, J. Hazard assessments of manufactured nanomaterials. J. Occup. Health 2010, 52, 325–334. [Google Scholar] [CrossRef]
- Schinwald, A.; Murphy, F.A.; Jones, A.; MacNee, W.; Donaldson, K. Graphene-based nanoplatelets: A new risk to the respiratory system as a consequence of their unusual aerodynamic properties. ACS Nano 2012, 6, 736–746. [Google Scholar] [CrossRef] [PubMed]
- Mananghaya, M.; Rodulfo, E.; Santos, G.N.; Villagracia, A.R. Theoretical investigation on the solubilization in water of functionalized single-wall carbon nanotubes. J. Nanotechnol. 2012, 2012, 780815. [Google Scholar] [CrossRef]
- Gao, H.; Kong, Y.; Cui, D.; Ozkan, C.S. Spontaneous insertion of DNA oligonucleotides into carbon nanotubes. Nano Lett. 2003, 3, 471–473. [Google Scholar] [CrossRef]
- Monajjemi, M.; Mollaamin, F. Molecular modeling study of drug–DNA combined to single walled carbon nanotube. J. Clust. Sci. 2012, 23, 259–272. [Google Scholar] [CrossRef]
- Onsager, L. Electric Moments of Molecules in Liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Obata, S.; Honda, K. Dynamic behavior of carbon nanotube and bio-/artificial surfactants complexes in an aqueous environment. J. Phys. Chem. C 2011, 115, 19659–19667. [Google Scholar] [CrossRef]
- Nivetha, G.F.; Vetrivelan, V.; Muthu, S.; Prasath, M. Adsorption behavior, different green solvent effect and surface enhanced Raman spectra (SERS) investigation on inhibition of SARS-CoV-2 by antineoplastic drug Carmofur with silver/gold/platinum loaded silica nanocomposites: A combined computational analysis and molecular modelling approach. Results Chem. 2023, 6, 101096. [Google Scholar]
- Stals, P.J.M.; Cheng, C.-Y.; van Beek, L.; Wauters, A.C.; Palmans, A.R.A.; Han, S.; Meijer, E.W. Surface water retardation around single-chain polymeric nanoparticles: Critical for catalytic function? Chem. Sci. 2016, 7, 2011–2015. [Google Scholar] [CrossRef] [PubMed]
- Odegard, G.M. Computational Multiscale Modeling—Nanoscale to Macroscale. In Comprehensive Composite Materials II; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, pp. 28–51. [Google Scholar]
- Lavino, A.D.; Di Pasquale, N.; Carbone, P.; Marchisio, D.L. A novel multiscale model for the simulation of polymer flash nano-precipitation. Chem. Eng. Sci. 2017, 171, 485–494. [Google Scholar] [CrossRef]
- Sperger, T.; Sanhueza, I.A.; Kalvet, I.; Schoenebeck, F. Computational studies of synthetically relevant homogeneous organometallic catalysis involving Ni, Pd, Ir, and Rh: An overview of commonly employed DFT methods and mechanistic insights. Chem. Rev. 2015, 115, 9532–9586. [Google Scholar] [CrossRef]
- Risthaus, T.; Grimme, S. Benchmarking of London Dispersion-Accounting Density Functional Theory Methods on Very Large Molecular Complexes. J. Chem. Theory Comput. 2013, 9, 1580–1591. [Google Scholar] [CrossRef]
- Grimme, S. Comment on: “On the Accuracy of DFT Methods in Reproducing Ligand Substitution Energies for Transition Metal Complexes in Solution: The Role of Dispersive Interactions” by H. Jacobsen and L. Cavallo. ChemPhysChem 2012, 13, 1407–1409. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, M.I.; Nair, J.R.; Pratt, L.R.; Soto, F.A.; Balbuena, P.B.; Rempe, S.B. Scaling atomic partial charges of carbonate solvents for lithium ion solvation and diffusion. J. Chem. Theory Comput. 2016, 12, 5709–5718. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.K.; Balasubramanian, S. Liquid dimethyl carbonate: A quantum chemical and molecular dynamics study. J. Phys. Chem. B 2012, 116, 14892–14902. [Google Scholar] [CrossRef]
- Barnes, T.A.; Kaminski, J.W.; Borodin, O.; Miller, T.F., III. Ab initio characterization of the electrochemical stability and solvation properties of condensed-phase ethylene carbonate and dimethyl carbonate mixtures. J. Phys. Chem. C 2015, 119, 3865–3880. [Google Scholar] [CrossRef]
- Atilhan, M.; Aparicio, S. Properties of dialkylcarbonate + 1-alkanol mixtures at the vacuum interface. J. Phys. Chem. C 2016, 120, 29126–29134. [Google Scholar] [CrossRef]
- Amis, E.S. Solvent Effects on Reaction Rates and Mechanisms; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Amis, E.S.; Hinton, J.F. Solvent influence on rates and mechanisms. In Solvent Effects on Chemical Phenomena; Amis, E.S., Hinton, J.F., Eds.; Academic Press: New York, NY, USA, 1973; Volume 1, pp. 207–449. [Google Scholar]
- Kostal, J.; Jorgensen, W.L. Thorpe-ingold acceleration of oxirane formation is mostly a solvent effect. J. Am. Chem. Soc. 2010, 132, 8766–8773. [Google Scholar] [CrossRef] [PubMed]
- Varghese, J.J.; Mushrif, S.H. Origins of Complex Solvent Effects on Chemical Reactivity and Computational Tools to Investigate Them: A Review. React. Chem. Eng. 2019, 4, 165–206. [Google Scholar] [CrossRef]
- Basdogan, Y.; Maldonado, A.M.; Keith, J.A. Advances and challenges in modeling solvated reaction mechanisms for renewable fuels and chemicals. WIREs Comput. Mol. Sci. 2020, 10, e1446. [Google Scholar] [CrossRef]
- Zhu, Q.S.; Wallentine, S.K.; Deng, G.-H.; Rebstock, J.A.; Baker, L.R. The Solvation-Induced Onsager Reaction Field Rather than the Double-Layer Field Controls CO2 Reduction on Gold. JACS Au 2022, 2, 472–482. [Google Scholar] [CrossRef]
- Sorenson, S.A.; Patrow, J.G.; Dawlaty, J.M. Solvation reaction field at the interface measured by vibrational sum frequency generation spectroscopy. J. Am. Chem. Soc. 2017, 139, 2369–2378. [Google Scholar] [CrossRef] [PubMed]
- Rowley, C.N.; Roux, B. The solvation structure of Na+ and K+ in liquid water determined from high level ab initio molecular dynamics simulations. J. Chem. Theory Comput. 2012, 8, 3526–3535. [Google Scholar] [CrossRef]
- Liu, J.C.; Liu, R.X.; Cao, Y.; Chen, M. Solvation structures of calcium and magnesium ions in water with the presence of hydroxide: A study by deep potential molecular dynamics. Phys. Chem. Chem. Phys. 2023, 25, 983–993. [Google Scholar] [CrossRef]
- Hu, Y.-S.; Pan, H. Solvation Structures in Electrolyte and the Interfacial Chemistry for Na-Ion Batteries. ACS Energy Lett. 2022, 7, 4501–4503. [Google Scholar] [CrossRef]
- Forero-Saboya, J.D.; Marchante, E.; Araujo, R.B.; Monti, D.; Johansson, P.; Ponrouch, A. Cation Solvation and Physicochemical Properties of Ca Battery Electrolytes. J. Phys. Chem. C 2019, 123, 29524–29532. [Google Scholar] [CrossRef]
- Rajput, N.N.; Seguin, T.J.; Wood, B.M.; Qu, X.; Persson, K.A. Elucidating Solvation Structures for Rational Design of Multivalent Electrolytes—A Review. Top. Curr. Chem. 2018, 376, 79–124. [Google Scholar] [CrossRef]
- Ho, T.H.; Do, T.H.; Tong, H.D.; Meijer, E.J.; Trinh, T.T. The Role of Chloride ion in the Silicate Condensation Reaction from ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Trinh, T.T.; Rozanska, X.; Delbecq, F.; Sautet, P. The initial step of silicate versus aluminosilicate formation in zeolite synthesis: A reaction mechanism in water with a tetrapropylammonium template. Phys. Chem. Chem. Phys. 2012, 14, 3369–3380. [Google Scholar] [CrossRef] [PubMed]
- Mai, N.G.; Do, H.T.; Hoang, N.H.; Nguyen, A.H.; Tran, K.Q.; Meijer, E.J.; Trinh, T.T. Elucidating the Role of Tetraethylammonium in the Silicate Condensation Reaction from Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. B 2020, 124, 10210–10218. [Google Scholar] [CrossRef] [PubMed]
- Do, T.H.; Tong, H.D.; Tran, K.-Q.; Meijer, E.J.; Trinh, T.T. Insight into the role of excess hydroxide ions in silicate condensation reactions. Phys. Chem. Chem. Phys. 2023, 25, 12723–12733. [Google Scholar] [CrossRef] [PubMed]
- López Barreiro, D.; Yeo, J.; Tarakanova, A.; Martin-Martinez, F.J.; Buehler, M.J. Multiscale Modeling of Silk and Silk-Based Biomaterials—A Review. Macromol. Biosci. 2019, 19, 1800253. [Google Scholar] [CrossRef] [PubMed]
- Dinjaski, N.; Ebrahimi, D.; Qin, Z.; Giordano, J.E.M.; Ling, S.; Buehler, M.J.; Kaplan, D.L.J. Predicting rates of in vivo degradation of recombinant spider silk proteins. J. Tissue Eng. Regen. Med. 2018, 12, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Finney, J.L. Overview lecture. Hydration processes in biological and macromolecular systems. Faraday Discuss. 1996, 103, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Schoenborn, B.P.; Garcia, A.; Knott, R. Hydration in protein crystallography. Prog. Biophys. Mol. Biol. 1995, 64, 105–119. [Google Scholar] [CrossRef]
- Raschke, T.M. Water structure and interactions with protein surfaces. Curr. Opin. Struct. Biol. 2006, 16, 152–159. [Google Scholar] [CrossRef]
- Mazur, K.; Heisler, I.A.; Meech, S.R. Ultrafast dynamics and hydrogen-bond structure in aqueous solutions of model peptides. J. Phys. Chem. B 2010, 114, 10684–10691. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Mancera, R.L.; Dean, P.M. WaterScore: A novel method for distinguishing between bound and displaceable water molecules in the crystal structure of the binding site of protein-ligand complexes. J. Mol. Model. 2003, 9, 172–182. [Google Scholar] [CrossRef] [PubMed]
- Olano, L.R.; Rick, S.W. Hydration free energies and entropies for water in protein interiors. J. Am. Chem. Soc. 2004, 126, 7991–8000. [Google Scholar] [CrossRef] [PubMed]
- Patel, H.; Grüning, B.A.; Günther, S.; Merfort, I. PyWATER: A PyMOL plug-in to find conserved water molecules in proteins by clustering. Bioinformatics 2014, 30, 2978–2980. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, O.; Kalimeri, M.; Melchionna, S.; Hénin, J.; Sterpone, F. On the Role of Internal Water on Protein, Thermal Stability: The Case of Homologous G-domains. J. Phys. Chem. B 2015, 119, 8939–8949. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, D.; Taly, A.; Sterpone, F. Stay Wet, Stay Stable? How Internal Water Helps Stability of Thermophilic Proteins. J. Phys. Chem. B 2015, 119, 12760–12770. [Google Scholar] [CrossRef] [PubMed]
- Ebbinghaus, S.; Kim, S.J.; Heyden, M.; Yu, X.; Heugen, U.; Gruebele, M.; Leitner, D.M.; Havenith, M. An extended dynamical hydration shell around proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 20749–20752. [Google Scholar] [CrossRef] [PubMed]
- Mattea, C.; Qvist, J.; Halle, B. Dynamics at the Protein-Water Interface from 17O Spin Relaxation in Deeply Supercooled Solutions. Biophys. J. 2008, 95, 2951–2963. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, J. Dynamics of hydration water in proteins. Gen. Physiol. Biophys. 2009, 28, 168–173. [Google Scholar] [CrossRef]
- Born, B.; Kim, S.J.; Ebbinghaus, S.; Gruebele, M.; Havenith, M. The terahertz dance of water with the proteins: The effect of protein flexibility on the dynamical hydration shell of ubiquitin. Faraday Discuss. 2009, 141, 161–173. [Google Scholar] [CrossRef]
- Wallnoefer, H.G.; Handschuh, S.; Liedl, K.R.; Fox, T. Stabilizing of a Globular Protein by a Highly Complex Water Network: A Molecular Dynamics Simulation Study on Factor Xa. J. Phys. Chem. B 2010, 114, 7405–7412. [Google Scholar] [CrossRef] [PubMed]
- Clark, P.L.; Ugrinov, K.G. Measuring Cotranslational Folding of Nascent Polypeptide Chains on Ribosomes. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2009; Volume 466, pp. 567–590. [Google Scholar] [CrossRef]
- Fersht, A.R. Structure and Mechanism in Protein Science, 3rd ed.; W.H. Freeman and Company: New York, NY, USA, 1999. [Google Scholar]
- Jonák, J. Protein folding and misfolding, diseases associated with protein misfolding & aggregation. Curr. Opin. Struct. Biol. 2004, 14, 616–621. [Google Scholar]
- Reynaud, E. Protein Misfolding and Degenerative Diseases. Nat. Educ. 2010, 3, 28. [Google Scholar]
- Matus, S.; Glimcher, L.H.; Hetz, C. Protein folding stress in neurodegenerative diseases: A glimpse into the ER. Curr. Opin. Cell Biol. 2011, 23, 239–252. [Google Scholar] [CrossRef]
- Sweeney, P.; Park, H.; Baumann, M.; Dunlop, J.; Frydman, J.; Kopito, R.; McCampbell, A.; Leblanc, G.; Venkateswaran, A.; Nurmi, A.; et al. Protein misfolding in neurodegenerative diseases: Implications and strategies. Transl. Neurodegener. 2017, 6, 6. [Google Scholar] [CrossRef]
- Fare, C.M.; Shorter, J. (Dis)Solving the problem of aberrant protein states. Dis. Models Mech. 2021, 14, dmm048983. [Google Scholar] [CrossRef]
- Khanam, H.; Ali, A.; Asif, M. Neurodegenerative diseases linked to misfolded proteins and their therapeutic approaches: A review. Eur. J. Med. Chem. 2016, 124, 1121–1141. [Google Scholar] [CrossRef]
- Strodel, B. Amyloid aggregation simulations: Challenges, advances and perspectives. Curr. Opin. Struct. Biol. 2021, 67, 145–152. [Google Scholar] [CrossRef]
- Ochneva, A.; Zorkina, Y.; Abramova, O.; Pavlova, O.; Ushakova, V.; Morozova, A.; Zubkov, E.; Pavlov, K.; Gurina, O.; Chekhonin, V. Protein Misfolding and Aggregation in the Brain: Common Pathogenetic Pathways in Neurodegenerative and Mental Disorders. Int. J. Mol. Sci. 2022, 23, 14498. [Google Scholar] [CrossRef]
- Baker, J.D.; Webster, J.M.; Shelton, L.B.; Koren III, J.; Uversky, V.N.; Blair, L.J.; Dickey, C.A. Neurodegenerative Diseases as Protein Folding Disorders. In The Molecular and Cellular Basis of Neurodegenerative Diseases, Underlying Mechanisms; Elsevier: Amsterdam, The Netherlands, 2018; pp. 243–267. [Google Scholar] [CrossRef]
- Lucent, D.; Vishal, V.; Pande, V.S. Protein folding under confinement: A role for solvent. Proc. Natl. Acad. Sci. USA 2007, 104, 10430–10434. [Google Scholar] [CrossRef]
- Onuchic, J.N.; Luthey-Schulten, Z.; Wolynes, P.G. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef]
- Blanco, F.J.; Rivas, G.; Serrano, L. A short linear peptide that folds into a native stable β-hairpin in aqueous solution. Nat. Struct. Biol. 1994, 1, 584–590. [Google Scholar] [CrossRef]
- Blanco, F.J.; Serrano, L. Folding of protein g b1 domain studied by the conformational characterization of fragments comprising its secondary structure elements. Eur. J. Biochem. 1995, 230, 634–649. [Google Scholar] [CrossRef]
- Munoz, V.; Henry, E.R.; Hofrichter, J.; Eaton, W.A. A statistical mechanical model for β-hairpin kinetics. Proc. Natl. Acad. Sci. USA 1998, 95, 5872–5879. [Google Scholar] [CrossRef]
- Zhou, R.; Berne, B.J. Can a continuum solvent model reproduce the free energy landscape of a β-hairpin folding in water? Proc. Natl. Acad. Sci. USA 2002, 99, 12777–12782. [Google Scholar] [CrossRef]
- Zhou, R. Free energy landscape of protein folding in water: Explicit vs. implicit solvent. Proteins Struct. Funct. Bioinform. 2003, 53, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Freddolino, P.L.; Liu, F.; Gruebele, M.; Schulten, K. Tenmicrosecond MD simulation of a fast-folding WW domain. Biophys. J. 2008, 94, L75–L77. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.; Kim, E.; Shin, S.; Pak, Y. Ab initio folding of helix bundle proteins using molecular dynamics simulations. J. Am. Chem. Soc. 2003, 125, 14841–14846. [Google Scholar] [CrossRef] [PubMed]
- Vaiana, S.M.; Manno, M.; Emanuele, A.; Palma-Vittorelli, M.B.; Palma, M.U. The Role of Solvent in Protein Folding and in Aggregation. J. Biol. Phys. 2001, 27, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Juraszek, J.; Bolhuis, P.G. Sampling the multiple folding mechanisms of Trp-cage in explicit solvent. Proc. Natl. Acad. Sci. USA 2006, 103, 15859–15864. [Google Scholar] [CrossRef]
- Paschek, D.; Hempel, S.; Garcia, A.E. Computing the stability diagram of the Trp-cage miniprotein. Proc. Natl. Acad. Sci. USA 2008, 105, 17754–17759. [Google Scholar] [CrossRef]
- Sanbonmatsu, K.Y.; Garcia, A.E. Structure of Met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins Struct. Funct. Bioinform. 2002, 46, 225–234. [Google Scholar] [CrossRef] [PubMed]
- McKnight, J.C.; Doering, D.S.; Matsudaira, P.T.; Kim, P.S. A Thermostable 35-residue subdomain within villin headpiece. J. Mol. Biol. 1996, 260, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, A.; Shen, M.-Y.; Colubri, A.; Sosnick, T.R.; Berry, R.S.; Freed, K.F. Large-scale context in protein folding: Villin headpiece. Biochemistry 2003, 42, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Duan, Y. Two-stage folding of HP-35 from ab initio simulations. J. Mol. Biol. 2007, 370, 196–206. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.S.; Wallin, S.; Shakhnovich, E.I. Universality and diversity of folding mechanics for three-helix bundle proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Zagrovic, B.; Snow, C.D.; Shirts, M.R.; Pande, V.S. Simulation of folding of a small α-helical protein in atomistic detail using worldwide-distributed computing. J. Mol. Biol. 2002, 323, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Lei, H.; Wu, C.; Liu, H.; Duan, Y. Folding free-energy landscape of villin headpiece subdomain from molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2007, 104, 4925–4930. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Kollman, P.A. Pathways to a protein folding intermediate observed in a 1-ms simulation in aqueous solution. Science 1998, 282, 740–744. [Google Scholar] [CrossRef] [PubMed]
- Kubelka, J.; Eaton, W.A.; Hofrichter, J. Experimental tests of villin subdomain folding simulations. J. Mol. Biol. 2003, 329, 625–630. [Google Scholar] [CrossRef]
- Lei, H.; Deng, X.; Wang, Z.; Duan, Y. The fast-folding HP35 double mutant has a substantially reduced primary folding free energy barrier. J. Chem. Phys. 2008, 129, 155104–155107. [Google Scholar] [CrossRef]
- Freddolino, P.L.; Schulten, K. Common structural transitions in explicit-solvent simulations of villin headpiece folding. Biophys. J. 2009, 97, 2338–2347. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jayachandran, G.; Vishal, V.; Pande, V.S. Using massively parallel simulation and Markovian models to study protein folding: Examining the dynamics of the villin headpiece. J. Chem. Phys. 2006, 124, 164902. [Google Scholar] [CrossRef]
- Oshima, H.; Kinoshita, M. Essential roles of protein-solvent many-body correlation in solvent-entropy effect on protein folding and denaturation: Comparison between hard-sphere solvent and water. J. Chem. Phys. 2015, 142, 145103. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. The contributions of surface charge and geometry to protein-solvent interaction. arXiv 2016, arXiv:1605.01155v1. [Google Scholar]
- Wang, L. The solvent-excluded surfaces of water-soluble proteins. bioRxiv 2018, 294082. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Shao, Q.; Shi, J.; Zhu, W. The effects of organic solvents on the folding pathway and associated thermodynamics of proteins: A microscopic view. Sci. Rep. 2016, 6, 19500. [Google Scholar] [CrossRef] [PubMed]
- van der Vegt, N.F.A.; Nayar, D. The Hydrophobic Effect and the Role of Cosolvents. J. Phys. Chem. B 2017, 121, 9986–9998. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.M.; Gruebele, M.; Sukenik, S. How does solvation in the cell affect protein folding and binding? Curr. Opin. Struct. Biol. 2018, 48, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.; Ranganathan, S.; Jayaram, B.; Sattar, A. Role of solvent accessibility for aggregation-prone patches in protein folding. Sci. Rep. 2018, 8, 12896. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Inoue, M.; Yasuda, S.; Petretto, E.; Škrbić, T.; Giacometti, A.; Kinoshita, M. Universal effects of solvent species on the stabilized structure of a protein. J. Chem. Phys. 2018, 149, 045105. [Google Scholar] [CrossRef]
- Arakawa, T. Protein-solvent interaction. Biophys. Rev. 2018, 10, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Bucciarelli, S.; Sayedi, E.S.; Osella, S.; Trzaskowski, B.; Vissing, K.J.; Vestergaard, B.; Foderà, V. Disentangling the role of solvent polarity and protein solvation in folding and self-assembly of α-lactalbumin. J. Colloid Interface Sci. 2020, 561, 749–761. [Google Scholar] [CrossRef] [PubMed]
- Stöhr, M.; Tkatchenko, A. Quantum mechanics of proteins in explicit water: The role of plasmon-like solute-solvent interactions. Sci. Adv. 2019, 5, eaax0024. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Yang, W.; Meng, Y.Y.; Xiao, X.; Guo, Y.; Pu, X.; Li, M. Effects of organic solvent and crystal water on gamma-chymotrypsin in acetonitrile media: Observations from molecular dynamics simulation and DFT calculation. J. Phys. Chem. B 2012, 116, 3292–3304. [Google Scholar] [CrossRef] [PubMed]
- Roccatano, D. Computer simulations study of biomolecules in non-aqueous or cosolvent/water mixture solutions. Curr. Protein Pept. Sci. 2008, 9, 407–426. [Google Scholar] [CrossRef] [PubMed]
- Micaelo, N.M.; Soares, C.M. Modeling hydration mechanisms of enzymes in nonpolar and polar organic solvents. FEBS J. 2007, 274, 2424–2436. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Dordick, J.S.; Garde, S. Hydration of enzyme in nonaqueous media is consistent with solvent dependence of its activity. Biophys. J. 2004, 87, 812–821. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Yuan, Y.; Zhu, Y.; Guo, Y.; Li, M.; Wang, Z.; Pu, X.; Jiang, L. Effects of organic solvents and substrate binding on trypsin in acetonitrile and hexane media. J. Mol. Model. 2013, 19, 3749–3766. [Google Scholar] [CrossRef]
- Falk, M.; Hartman, K.A.; Lord, R.C. Hydration of deoxyribonucleic acid. I. A gravimetric study. J. Am. Chem. Soc. 1962, 84, 3843–3846. [Google Scholar] [CrossRef]
- Falk, M.; Hartman, K.A.; Lord, R.C. Hydration of deoxyribonucleic acid. II. An infrared study. J. Am. Chem. Soc. 1963, 85, 387–391. [Google Scholar] [CrossRef]
- Falk, M.; Hartman, K.A.; Lord, R.C. Hydration of deoxyribonucleic acid. III. A spectroscopic study of the effect of hydration on the structure of deoxyribonucleic acid. J. Am. Chem. Soc. 1963, 85, 391–394. [Google Scholar] [CrossRef]
- Tunis, M.-J.B.; Hearst, J.E. On the hydration of DNA. I. Preferential hydration and stability of DNA in concentrated trifluoracetate solution. Biopolymers 1968, 6, 1325–1344. [Google Scholar] [CrossRef] [PubMed]
- Tunis, M.-J.B.; Hearst, J.E. On the hydration of DNA. II. Base composition dependence of the net hydration of DNA. Biopolymers 1968, 6, 1345–1353. [Google Scholar] [CrossRef] [PubMed]
- Falk, M.; Poole, A.G.; Goymour, C.G. Infrared study of the state of water in the hydration shell of DNA. Can. J. Chem. 1970, 48, 1536–1542. [Google Scholar] [CrossRef]
- Levy, Y.; Onuchic, J.N. Water mediation in protein folding and molecular recognition. Annu. Rev. Biophys. Biomol. Struct. 2006, 35, 389–415. [Google Scholar] [CrossRef] [PubMed]
- Norberg, J.; Nilsson, L. Solvent Influence on Base Stacking. Biophys. J. 1998, 74, 394–402. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H. DNA Stability in Ionic Liquids and Deep Eutectic Solvents. J. Chem. Technol. Biotechnol. 2015, 90, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Bonner, G.; Klibanov, A.M. Structural stability of DNA in nonaqueous solvents. Biotechnol. Bioeng. 2000, 86, 339–344. [Google Scholar] [CrossRef]
- Shen, X.; Gu, B.; Che, S.A.; Zhang, F.S. Solvent effects on the conformation of DNA dodecamer segment: A simulation study. J. Chem. Phys. 2011, 135, 034509. [Google Scholar] [CrossRef]
- Arcella, A.; Portella, G.; Collepardo-Guevara, R.; Chakraborty, D.; Wales, D.J.; Orozco, M. Structure and Properties of DNA in Apolar Solvents. J. Phys. Chem. B 2014, 118, 8540–8548. [Google Scholar] [CrossRef]
- Nakano, S.I.; Sugimoto, N. The structural stability and catalytic activity of DNA and RNA oligonucleotides in the presence of organic solvents. Biophys. Rev. 2016, 8, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Nan, Z.; Ming-Ru, L.; Feng-Shou, Z. Ethylene glycol solution-induced DNA conformational transitions. Chin. Phys. B 2018, 27, 113102. [Google Scholar]
- Kuzmanov, U.; Emili, A. Protein-protein interaction networks: Probing disease mechanisms using model systems. Genome Med. 2013, 5, 37. [Google Scholar] [CrossRef] [PubMed]
- Garland, W.; Benezra, R.; Chaudhary, J. Chapter Fifteen—Targeting Protein–Protein Interactions to Treat Cancer—Recent Progress and Future Directions. Annu. Rep. Med. Chem. 2013, 48, 227–245. [Google Scholar] [CrossRef]
- Seychell, B.C.; Beck, T. Molecular basis for protein–protein interactions. Beilstein J. Org. Chem. 2021, 17, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, G. Protein–Protein Interaction Interfaces and their Functional Implications. In Protein–Protein Interaction Regulators; Roy, S., Fu, H., Eds.; The Royal Society of Chemistry: London, UK, 2020; pp. 1–24. [Google Scholar]
- Ebel, C. Solvent Mediated Protein-Protein Interactions. In Protein Interactions: Biophysical Approaches for the Study of Complex Reversible Systems; Springer: Boston, MA, USA, 2007; Volume 5, pp. 255–287. [Google Scholar] [CrossRef]
- Vagenende, V.; Han, A.X.; Pek, H.B.; Loo, B.L.W. Quantifying the Molecular Origins of Opposite Solvent Effects on Protein-Protein Interactions. PLoS Comput. Biol. 2013, 9, e1003072. [Google Scholar] [CrossRef] [PubMed]
- Levy, Y.; Cho, S.S.; Onuchic, J.N.; Wolynes, P.G. A survey of flexible protein binding mechanisms and their transition states using native topology based energy landscapes. J. Mol. Biol. 2005, 346, 1121–1145. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Gu, W.; Geyer, T.; Helms, V. Adhesive water networks facilitate binding of protein interfaces. Nat. Commun. 2011, 2, 261. [Google Scholar] [CrossRef]
- Ghanakota, P.; van Vlijmen, H.; Sherman, W.; Beuming, T. Large-Scale Validation of Mixed-Solvent Simulations to Assess Hotspots at Protein–Protein Interaction Interfaces. J. Chem. Inf. Model. 2018, 58, 784–793. [Google Scholar] [CrossRef]
- Mayol, G.F.; Defelipe, L.A.; Arcon, J.P.; Turjanski, A.G.; Martí, M.A. Solvent Sites Improve Docking Performance of Protein–Protein Complexes and Protein–Protein Interface-Targeted Drugs. J. Chem. Inf. Model. 2022, 62, 3577–3588. [Google Scholar] [CrossRef]
- Morriss-Andrews, A.; Shea, J.-E. Computational Studies of Protein Aggregation: Methods and Applications. Annu. Rev. Phys. Chem. 2015, 66, 643–666. [Google Scholar] [CrossRef] [PubMed]
- Kouza, M.; Kolinski, A.; Buhimschi, I.A.; Kloczkowski, A. Explicit-Solvent All-Atom Molecular Dynamics of Peptide Aggregation. In Computational Methods to Study the Structure and Dynamics of Biomolecules and Biomolecular Processes; Liwo, A., Ed.; Springer Series on Bio- and Neurosystems; Springer: Cham, Switzerland, 2019; Volume 8, pp. 541–558. [Google Scholar] [CrossRef]
- Klimov, D.K.; Straub, J.E.; Thirumalai, D. Aqueous urea solution destabilizes A-beta(16–22) oligomers. Proc. Natl. Acad. Sci. USA 2004, 101, 14760–14765. [Google Scholar] [CrossRef] [PubMed]
- Matubayasi, N.; Masutani, K. Energetics of co-solvent effect on peptide aggregation. Biophys. Physicobiol. 2019, 16, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Emperador, A. Accurate Description of Protein–Protein Recognition and Protein Aggregation with the Implicit-Solvent-Based PACSAB Protein Model. Polymers 2021, 13, 4172. [Google Scholar] [CrossRef] [PubMed]
- Stephens, A.D.; Kölbel, J.; Moons, R.; Chung, C.W.; Ruggiero, M.T.; Mahmoudi, N.; Shmool, T.A.; McCoy, T.M.; Nietlispach, D.; Routh, A.F.; et al. Decreased water mobility contributes to increased α-Synuclein aggregation. Angew. Chem. Int. Ed. 2023, 62, e202212063. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorsi, R.; Scrocco, E.; Tomasi, J. Simple theoretical models for biochemical systems, with applications to DNA. J. Biosci. 1985, 8, 627–634. [Google Scholar] [CrossRef]
- Tomasi, J. Effective and practical ways of introducing the effect of the solvent in the theoretical evaluation of conformational properties of biomolecules. In QSAR in Drug Design and Toxicology, Proceedings of the Sixth European Symposium on Quantitative Structure-Activity Relationships, Portorož-Portorose, Yugoslavia, 22–26 September 1986; Hadži, D., Jerman-Blažič, B., Eds.; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Spyrakis, F.; Cozzini, P.; Bertoli, C.; Marabotti, A.; Kellogg, G.E.; Mozzarelli, A. Energetics of the protein-DNA-water interaction. BMC Struct. Biol. 2007, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Serf, S.; Nilsson, I. Structure, interaction, dynamics and solvent effects on the DNA-EcoRI complex in aqueous solution from molecular dynamics simulation. Biophys. J. 1999, 77, 1782–1800. [Google Scholar]
- Schwabe, J.W. The role of water in protein-DNA interactions. Curr. Opin. Struct. Biol. 1997, 7, 126–134. [Google Scholar] [CrossRef]
- Woda, J.; Schneider, B.; Patel, K.; Mistry, K.; Berman, H.M. An analysis of the relationship between hydration and protein-DNA interactions. Biophys. J. 1998, 75, 2170–2177. [Google Scholar] [CrossRef][Green Version]
- Harris, L.F.; Sullivan, M.R.; Popken-Harris, P.D. Molecular dynamics simulations in solvent of the bacteriophage 434 cI repressor protein DNA binding domain amino acids (r1-69) in complex with its cognate operator (OR1) DNA sequence. J. Biomol. Struct. Dyn. 1999, 17, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Suenaga, A.; Yatsu, C.; Komeiji, Y.; Uebeyasi, M.; Meguro, T.; Yamato, I. Molecular dynamics simulation of trp repressor-operator complex. Analysis of hydrogen bond patterns of protein-DNA interactions. J. Mol. Struct. 2000, 526, 209–218. [Google Scholar] [CrossRef]
- Tsui, V.; Radhakrishnan, I.; Wright, P.E.; Case, D.A. NMR and molecular dynamics studies of the hydration of a zinc finger DNA complex. J. Mol. Biol. 2000, 302, 1101–1117. [Google Scholar] [CrossRef] [PubMed]
- Giudice, E.; Lavery, R. Simulations of nucleic acids and their complexes. Acc. Chem. Res. 2002, 35, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Beard, W.A.; Wilson, S.H.; Roux, B.; Broyde, S.; Schlick, T. Local deformations revealed by dynamics simulations of DNA polymerase β with DNA mismatches at the primer terminus. J. Mol. Biol. 2002, 321, 459–478. [Google Scholar] [CrossRef] [PubMed]
- Marco, E.; Garcia-Nieto, R.; Gago, F. Assessment by molecular dynamics simulations of the structural determinants of DNA-binding specificity for transcription factor Sp1. J. Mol. Biol. 2003, 328, 9–32. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jayaram, B.; Jain, T. The role of water in protein-DNA recognition. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 343–361. [Google Scholar] [CrossRef]
- Kriegel, M.; Muller, Y.A. De novo prediction of explicit water molecule positions by a novel algorithm within the protein design software MUMBO. Sci. Rep. 2023, 13, 16680. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.L.; Dill, K.A. Binding of Small-Molecule Ligands to Proteins: “What You See” Is Not Always “What You Get”. Structure 2009, 17, 489–498. [Google Scholar] [CrossRef]
- Mammino, L. Computational chemistry: Studying the properties and behaviours of molecules. In Green Chemistry and Computational Chemistry—Shared Lessons in Sustainability; Mammino, L., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1–40. [Google Scholar]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef]
- Barillari, C.; Taylor, J.; Viner, R.; Essex, J.W. Classification of water molecules in protein binding sites. J. Am. Chem. Soc. 2007, 129, 2577–2587. [Google Scholar] [CrossRef] [PubMed]
- Mancera, R.L. Molecular modeling of hydration in drug design. Curr. Opin. Drug Discov. Dev. 2007, 10, 275–280. [Google Scholar]
- Ross, G.A.; Morris, G.M.; Biggin, P.C. Rapid and accurate prediction and scoring of water molecules in protein binding sites. PLoS ONE 2012, 7, e32036. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Zaniewski, R.P.; Marr, E.S.; Lacey, B.M.; Tomaras, A.P.; Evdokimov, A.; Miller, J.R.; Shanmugasundaram, V. Structural Basis for Effectiveness of Siderophore-Conjugated Monocarbams against Clinically Relevant Strains of Pseudomonas aeruginosa. Proc. Natl. Acad. Sci. USA 2010, 107, 22002–22007. [Google Scholar] [CrossRef] [PubMed]
- Kimura, S.R.; Hu, H.P.; Ruvinsky, A.M.; Sherman, W.; Favia, A.D. Deciphering cryptic binding sites on proteins by mixed-solvent molecular dynamics. J. Chem. Inf. Model. 2017, 57, 1388–1401. [Google Scholar] [CrossRef] [PubMed]
- Arcon, J.P.; Defelipe, L.A.; Modenutti, C.P.; López, E.D.; Alvarez-Garcia, D.; Barril, X.; Turjanski, A.G.; Martí, M.A. Molecular dynamics in mixed solvents reveals protein–ligand interactions, improves docking, and allows accurate binding free energy predictions. J. Chem. Inf. Model. 2017, 57, 846–863. [Google Scholar] [CrossRef] [PubMed]
- Mattos, C.; Ringe, D. Locating and characterizing binding sites on proteins. Nat. Biotechnol. 1996, 14, 595–599. [Google Scholar] [CrossRef] [PubMed]
- Mattos, C.; Bellamacina, C.R.; Peisach, E.; Pereira, A.; Vitkup, D.; Petsko, G.A.; Ringe, D. Multiple solvent crystal structures: Probing binding sites, plasticity and hydration. J. Mol. Biol. 2006, 357, 1471–1482. [Google Scholar] [CrossRef] [PubMed]
- Ghanakota, P.; Carlson, H.A. Driving Structure-Based Drug Discovery through Cosolvent Molecular Dynamics. J. Med. Chem. 2016, 59, 10383–10399. [Google Scholar] [CrossRef]
- Ghanakota, P.; Carlson, H.A. Moving Beyond Active-Site Detection: MixMD Applied to Allosteric Systems. J. Phys. Chem. B 2016, 120, 8685–8695. [Google Scholar] [CrossRef]
- Setny, P.; Wang, Z.; Cheng, L.-T.; Li, B.; McCammon, J.A.; Dzubiella, J. Dewetting-controlled binding of ligands to hydrophobic pockets. Phys. Rev. Lett. 2009, 103, 187801. [Google Scholar] [CrossRef] [PubMed]
- Böhm, H.-J.; Klebe, G. What can we learn from molecular recognition in protein–ligand complexes for the design of new drugs? Angew. Chem. Int. Ed. Engl. 1996, 35, 2588–2614. [Google Scholar] [CrossRef]
- Ahmad, M.; Gu, W.; Helms, V. Mechanism of fast peptide recognition by SH3 domains. Angew. Chem. Int. Ed. Engl. 2008, 47, 7626–7630. [Google Scholar] [CrossRef] [PubMed]
- Schmidtke, P.; Luque, F.J.; Murray, J.B.; Barril, X. Shielded hydrogen bonds as structural determinants of binding kinetics: Application in drug design. J. Am. Chem. Soc. 2011, 133, 18903–18910. [Google Scholar] [CrossRef] [PubMed]
- Dror, R.O.; Pan, A.C.; Arlow, D.H.; Borhani, D.W.; Maragakis, P.; Shan, Y.; Xu, H.; Shaw, D.E. Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc. Natl. Acad. Sci. USA 2011, 108, 13118–13123. [Google Scholar] [CrossRef]
- Setny, P.; Baron, R.; Michael Kekenes-Huskey, P.; McCammon, J.A.; Dzubiella, J. Solvent fluctuations in hydrophobic cavity–ligand binding kinetics. Proc. Natl. Acad. Sci. USA 2013, 110, 1197–1202. [Google Scholar] [CrossRef]
- Young, T.; Abel, R.; Kim, B.; Berne, B.J.; Friesner, R.A. Motifs for molecular recognition exploiting hydrophobic enclosure in protein–ligand binding. Proc. Natl. Acad. Sci. USA 2007, 104, 808–813. [Google Scholar] [CrossRef]
- Fox, J.M.; Kang, K.; Sastry, M.; Sherman, W.; Sankaran, B.; Zwart, P.H.; Whitesides, G.M. Water-Restructuring Mutations Can Reverse the Thermodynamic Signature of Ligand Binding to Human Carbonic Anhydrase. Angew. Chem. Int. Ed. 2017, 56, 3833–3837. [Google Scholar] [CrossRef]
- Mohanty, M.; Mohanty, P.S. Molecular docking in organic, inorganic, and hybrid systems: A tutorial review. Monatsh. Chem. 2023, 154, 683–707. [Google Scholar] [CrossRef]
- Hu, X.; Maffucci, I.; Contini, A. Advances in the treatment of explicit water molecules in docking and binding free energy calculations. Curr. Med. Chem. 2019, 26, 7598–7622. [Google Scholar] [CrossRef]
- Pavlovicz, R.E.; Park, H.; DiMaio, F. Efficient consideration of coordinated water molecules improves computational protein–protein and protein–ligand docking discrimination. PLoS Comput. Biol. 2020, 16, e1008103. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Wang, D.; Shen, Z.; Li, S.; Li, H. Multi-Body Interactions in Molecular Docking Program Devised with Key Water Molecules in Protein Binding Sites. Molecules 2018, 23, 2321. [Google Scholar] [CrossRef] [PubMed]
- Cuzzolin, A.; Deganutti, G.; Salmaso, V.; Sturlese, M.; Moro, S. AquaMMapS: An Alternative Tool to Monitor the Role of Water Molecules During Protein–Ligand Association. ChemMedChem 2018, 13, 522–531. [Google Scholar] [CrossRef] [PubMed]
- Mitusińska, K.; Raczyńska, A.; Bzówka, M.; Bagrowska, W.; Góra, A. Applications of water molecules for analysis of macromolecule properties. Comput. Struct. Biotechnol. J. 2020, 18, 355–365. [Google Scholar] [CrossRef] [PubMed]
- Tuccinardi, T. What is the current value of MM/PBSA and MM/GBSA methods in drug discovery? Expert Opin. Drug Discov. 2021, 16, 1233–1237. [Google Scholar] [CrossRef]
- Stanzione, F.; Giangreco, I.; Cole, J.C. Use of molecular docking computational tools in drug discovery. Prog. Med. Chem. 2021, 60, 273–343. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.T.; Shub, L.; Meiler, J. PlaceWaters: Real-time, explicit interface water sampling during Rosetta ligand docking. PLoS ONE 2022, 17, e0269072. [Google Scholar] [CrossRef]
- Bálint, M.; Zsidó, B.Z.; van der Spoel, D.; Hetényi, C. Binding Networks Identify Targetable Protein Pockets for Mechanism-Based Drug Design. Int. J. Mol. Sci. 2022, 23, 7313. [Google Scholar] [CrossRef] [PubMed]
- Zsidó, B.Z.; Bayarsaikhan, B.; Börzsei, R.; Szél, V.; Mohos, V.; Hetényi, C. The Advances and Limitations of the Determination and Applications of Water Structure in Molecular Engineering. Int. J. Mol. Sci. 2023, 24, 11784. [Google Scholar] [CrossRef]
- Wolfenden, R. Conformational aspects of inhibitor design: Enzyme-substrate interactions in the transition state. Bioorg. Med. Chem. 1999, 7, 647–652. [Google Scholar] [CrossRef]
- Dunn, R.V.; Daniel, R.M. The use of gas-phase substrates to study enzyme catalysis at low hydration. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 1309–1320. [Google Scholar] [CrossRef][Green Version]
- Oleinikova, A.; Smolin, N.; Brovchenko, I.; Geiger, A.; Winter, R. Formation of spanning water networks on protein surfaces via 2D percolation transition. J. Phys. Chem. B 2005, 109, 1988–1998. [Google Scholar] [CrossRef]
- Chianella, I.; Karim, K.; Piletska, E.V.; Preston, C.; Piletsky, S.A. Computational design and synthesis of molecularly imprinted polymers with high binding capacity for pharmaceutical applications-model case: Adsorbent for abacavir. Anal. Chim. Acta 2006, 559, 73–78. [Google Scholar] [CrossRef]
- Teze, D.; Hendrickx, J.; Dion, M.; Tellier, C.; Woods, V.L.; Tran, V.; Sanejouand, Y.-H. Conserved water molecules in family 1 glycosidases: A DXMS and molecular dynamics study. Biochemistry 2013, 52, 5900–5910. [Google Scholar] [CrossRef]
- Dielmann-Gessner, J.; Grossman, M.; Conti Nibali, V.; Born, B.; Solomonov, I.; Fields, G.B.; Havenith, M.; Sagi, I. Enzymatic turnover of macromolecules generates long-lasting protein–water-coupled motions beyond reaction steady state. Proc. Natl. Acad. Sci. USA 2014, 111, 17857–17862. [Google Scholar] [CrossRef]
- UNAIDS. Fact Sheet. Available online: https://www.unaids.org/en/resources/fact-sheet (accessed on 20 December 2023).
- Ribeiro, A.J.M.; Ramos, M.J.; Fernandes, P.A. The catalytic mechanism of HIV-1 integrase for DNA 3′-end processing established by QM/MM calculations. J. Am. Chem. Soc. 2012, 134, 13436–13447. [Google Scholar] [CrossRef]
- Rungrotmongkol, T.; Mulholland, A.J.; Hannongbua, S. Active site dynamics and combined quantum mechanics/molecular mechanics (QM/MM) modelling of a HIV-1 reverse transcriptase/DNA/dTTP complex. J. Mol. Graph. Model. 2007, 26, 1–13. [Google Scholar] [CrossRef]
- Gopal, S.M.; Klumpers, F.; Herrmann, C.; Schäfer, L.V. Solvent effects on ligand binding to a serine protease. Phys. Chem. Chem. Phys. 2017, 19, 10753–10766. [Google Scholar] [CrossRef]
- Urbanowicz, B.R.; Bharadwaj, V.S.; Alahuhta, M.; Peña, M.J.; Lunin, V.V.; Bomble, Y.J.; Wang, S.; Yang, J.Y.; Tuomivaara, S.T.; Himmel, M.E.; et al. Structural, mutagenic and in silico studies of xyloglucan fucosylation in Arabidopsis thaliana suggest a water-mediated mechanism. Plant J. 2017, 91, 931–949. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Huang, X.; Zhu, Y. Using molecular dynamics simulations to evaluate active designs of cephradine hydrolase by molecular mechanics/Poisson–Boltzmann surface area and molecular mechanics/generalized Born surface area methods. RSC Adv. 2019, 9, 13868–13877. [Google Scholar] [CrossRef] [PubMed]
- van der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef]
- Magalhães, R.P.; Fernandes, H.S.; Sousa, S.F. Modelling enzymatic mechanisms with QM/MM approaches: Current status and future challenges. Isr. J. Chem. 2020, 60, 655–666. [Google Scholar] [CrossRef]
- Jedrzejewski, M.; Belza, B.; Lewandowska, I.; Sadlej, M.; Perlinska, A.P.; Augustyniak, R.; Christian, T.; Hou, Y.-M.; Kalek, M.; Sulkowska, J.I. Nucleolar Essential Protein 1 (Nep1): Elucidation of enzymatic catalysis mechanism by molecular dynamics simulation and quantum mechanics study. Comput. Struct. Biotechnol. J. 2023, 21, 3999–4008. [Google Scholar] [CrossRef]
- Gurova, K. New hopes from old drugs: Revisiting DNA-binding small molecules as anticancer agents. Future Oncol. 2009, 5, 1685–1704. [Google Scholar] [CrossRef]
- Misra, V.K.; Honig, B. On the magnitude of the electrostatic contribution to ligand-DNA interactions. Proc. Natl. Acad. Sci. USA 1995, 92, 4691–4695. [Google Scholar] [CrossRef]
- Chaires, J.B. Energetics of drug-DNA interactions. Biopolymers 1997, 44, 201–215. [Google Scholar] [CrossRef]
- Harris, S.A.; Gavathiotis, E.; Searle, M.S.; Orozén, M.; Laughton, C.A. Cooperativity in drug-DNA recognition: A molecular dynamics study. J. Am. Chem. Soc. 2001, 123, 12658–12663. [Google Scholar] [CrossRef]
- Sheng, J.; Gan, J.; Huang, Z. Structure-based DNA-targeting strategies with small molecule ligands for drug discovery. Med. Res. Rev. 2013, 33, 1119–1173. [Google Scholar] [CrossRef]
- Krafcikova, M.; Dzatko, S.; Caron, C.; Granzhan, A.; Fiala, R.; Loja, T.; Teulade-Fichou, M.-P.; Fessl, T.; Hänsel-Hertsch, R.; Mergny, J.-L.; et al. Monitoring DNA–Ligand Interactions in Living Human Cells Using NMR Spectroscopy. J. Am. Chem. Soc. 2019, 141, 13281–13285. [Google Scholar] [CrossRef] [PubMed]
- Ricci, C.G.; Netz, P.A. Docking Studies on DNA-Ligand Interactions: Building and Application of a Protocol To Identify the Binding Mode. J. Chem. Inf. Model. 2009, 49, 1925–1935. [Google Scholar] [CrossRef] [PubMed]
- Carter, E.K.; Laughlin-Toth, S.; Dodd, T.; Wilson, W.D.; Ivanov, I. Small molecule binders recognize DNA microstructural variations via an induced fit mechanism. Phys. Chem. Chem. Phys. 2019, 21, 1841–1851. [Google Scholar] [CrossRef]
- Schuurs, Z.P.; Martyn, A.P.; Soltau, C.P.; Beard, S.; Shah, E.T.; Adams, M.N.; Croft, L.V.; O’Byrne, K.J.; Richard, D.J.; Gandhi, N.S. An Exploration of Small Molecules That Bind Human Single-Stranded DNA Binding Protein 1. Biology 2023, 12, 1405. [Google Scholar] [CrossRef]
- Lang, P.T.; Brozell, S.R.; Mukherjee, S.; Pettersen, E.F.; Meng, E.C.; Thomas, V.; Rizzo, R.C.; Case, D.A.; James, T.L.; Kuntz, I.D. DOCK 6: Combining techniques to model RNA-small molecule complexes. RNA 2009, 15, 1219–1230. [Google Scholar] [CrossRef]
- Panei, F.P.; Gkeka, P.; Bonomi, M. Identifying small-molecules binding sites in RNA conformational ensembles with SHAMAN. bioRxiv, 2023; preprint. [Google Scholar] [CrossRef]
- Yusof, R.; Jumbri, K.; Ahmad, H.; Abdulmalek, E.; Abdul Rahman, M.B. Binding of tetrabutylammonium bromide based deep eutectic solvent to DNA by spectroscopic analysis. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 253, 119543. [Google Scholar] [CrossRef]
- Malola, S.; Matus, M.F.; Häkkinen, H. Theoretical Analysis of the Electronic Structure and Optical Properties of DNA-Stabilized Silver Cluster Ag16Cl2 in Aqueous Solvent. J. Phys. Chem. C 2023, 127, 16553–16559. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Wu, Y.; Jiang, L.; Zhang, W.; Qiao, X.; Yan, H.; Zhou, H.; Tang, B. Removal of trace DNA toxic compounds using a Poly(deep eutectic solvent) @Biomass based on multi-physical interactions. J. Hazard. Mater. 2021, 418, 126369. [Google Scholar] [CrossRef] [PubMed]
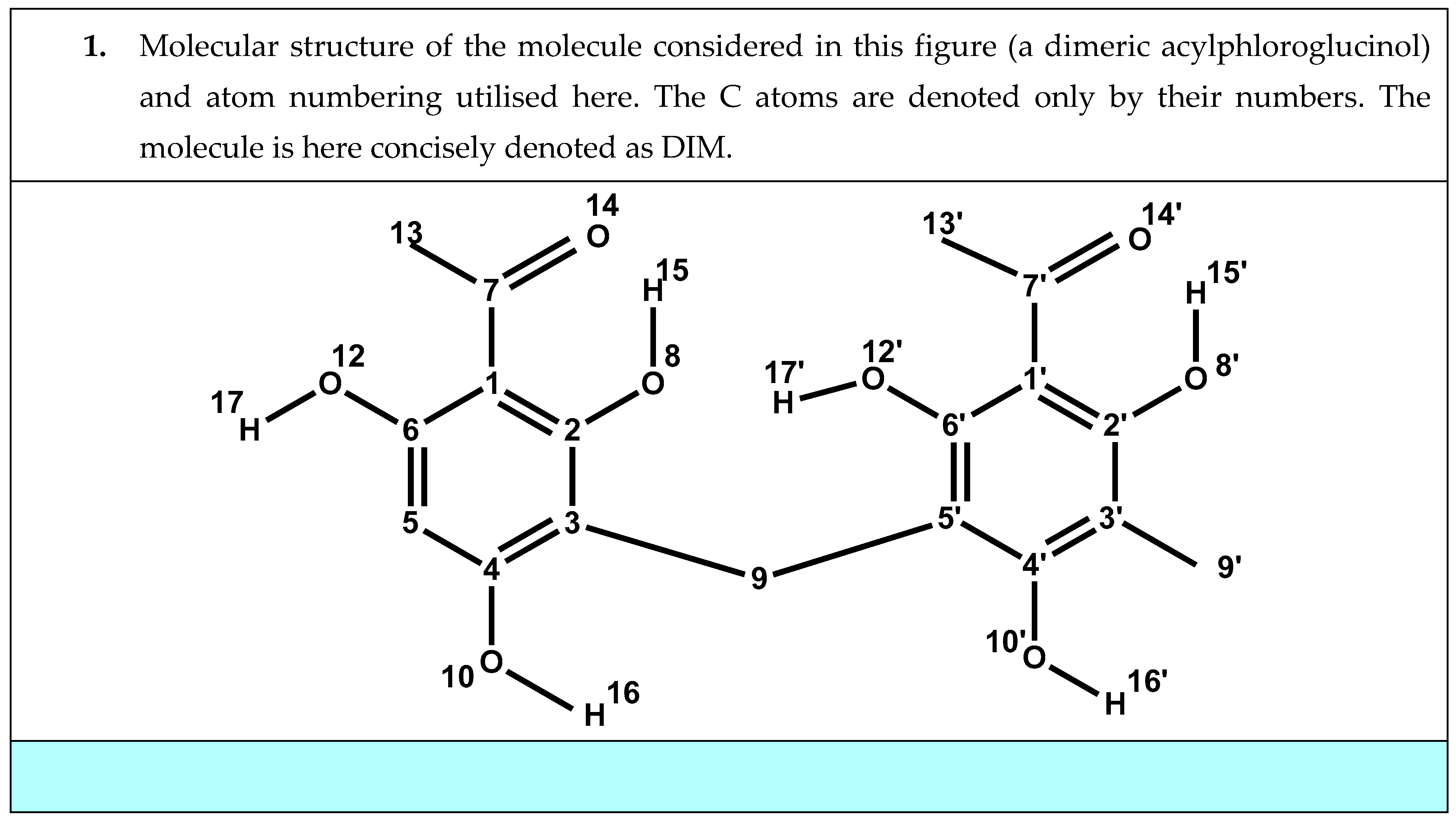
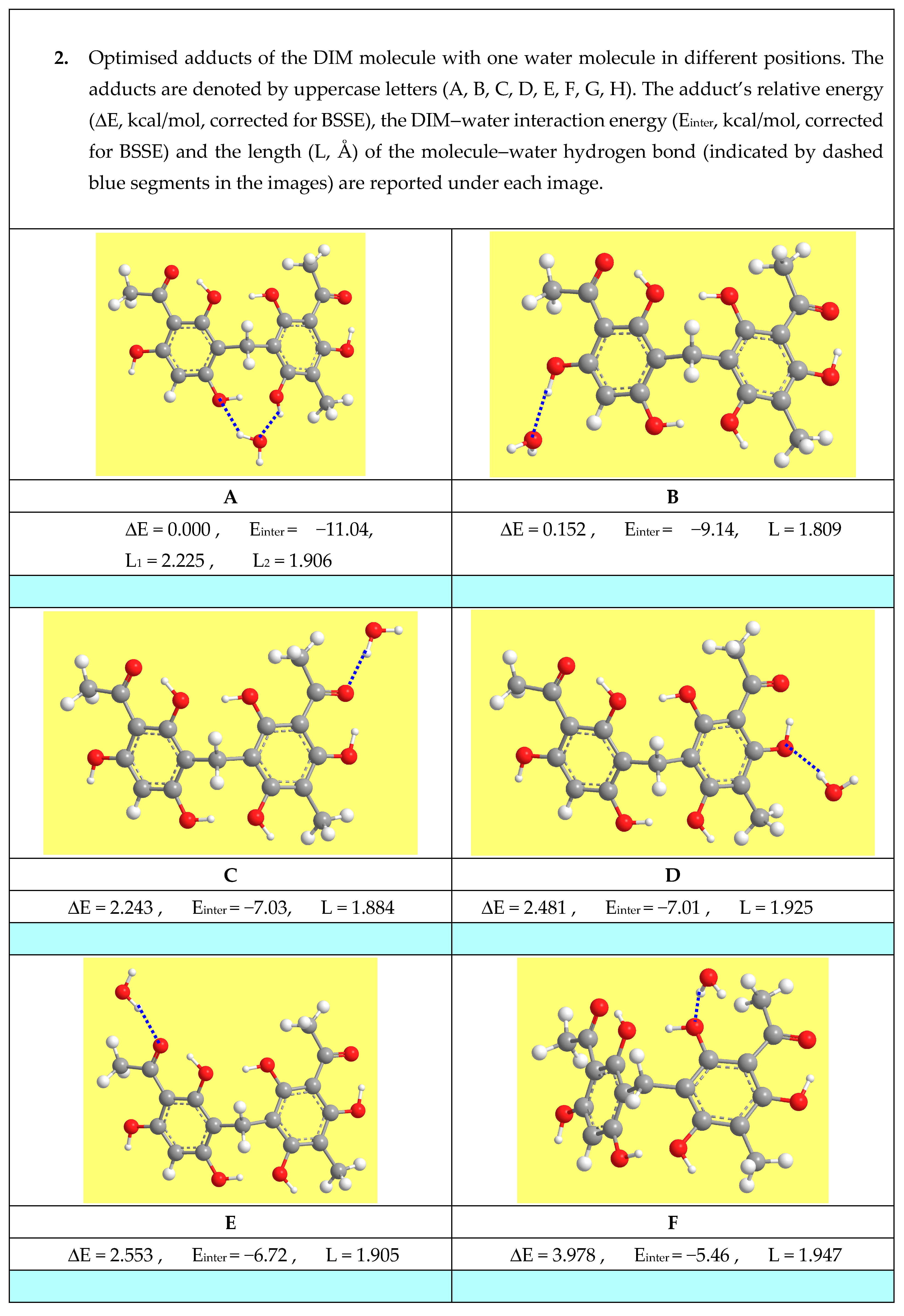
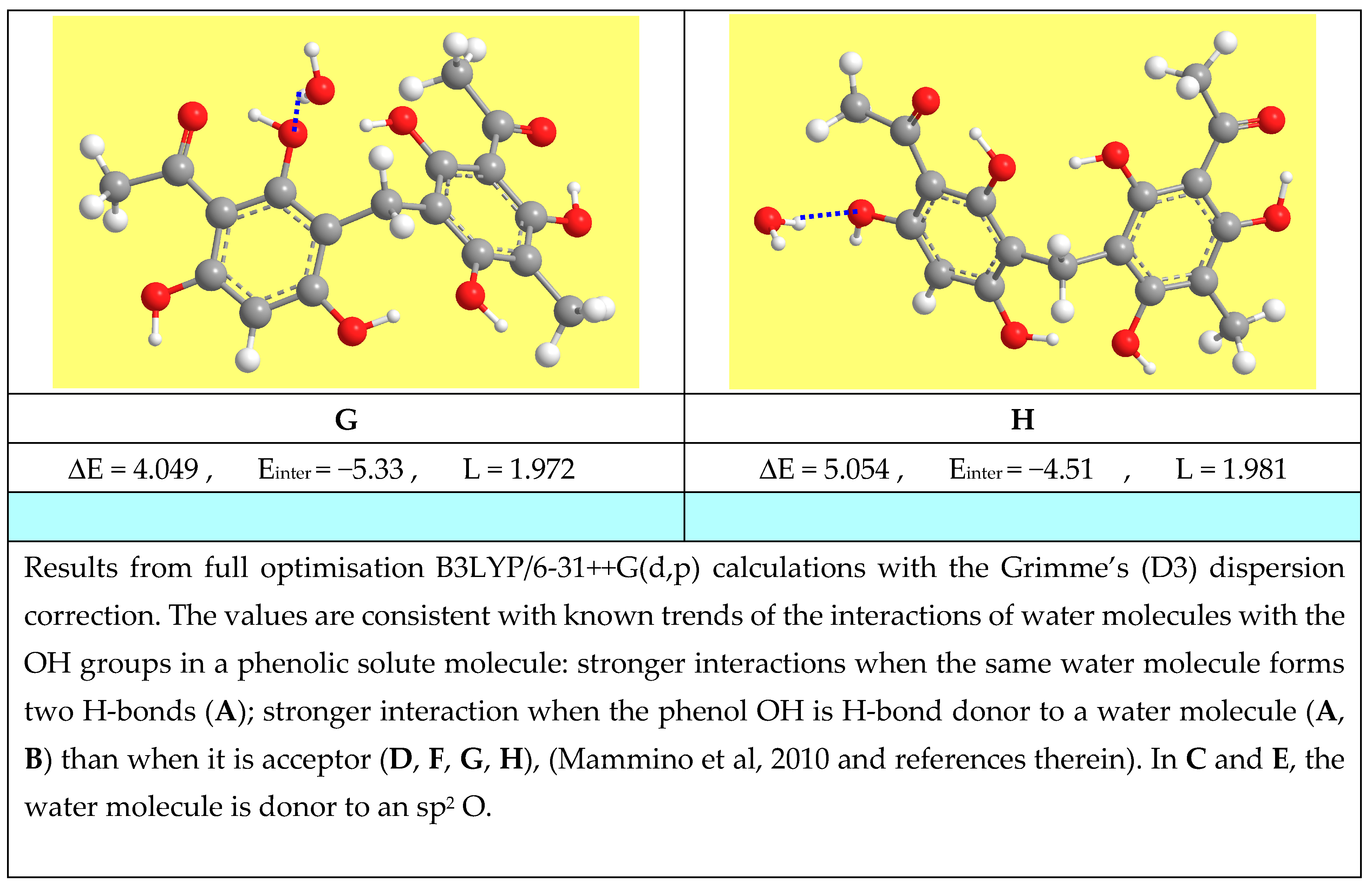

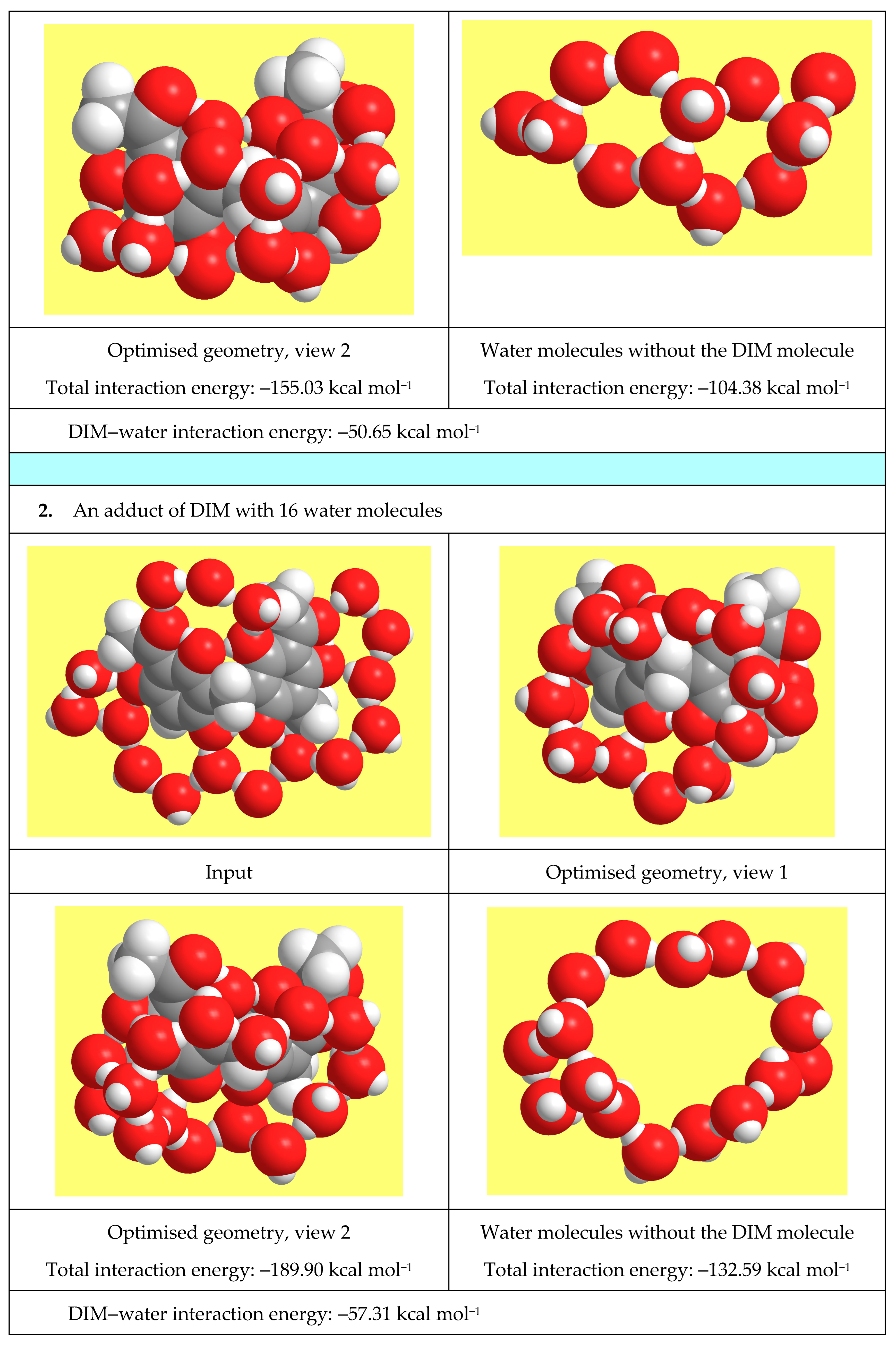

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tshilande, N.; Mammino, L.; Bilonda, M.K. The Study of Molecules and Processes in Solution: An Overview of Questions, Approaches and Applications. Computation 2024, 12, 78. https://doi.org/10.3390/computation12040078
Tshilande N, Mammino L, Bilonda MK. The Study of Molecules and Processes in Solution: An Overview of Questions, Approaches and Applications. Computation. 2024; 12(4):78. https://doi.org/10.3390/computation12040078
Chicago/Turabian StyleTshilande, Neani, Liliana Mammino, and Mireille K. Bilonda. 2024. "The Study of Molecules and Processes in Solution: An Overview of Questions, Approaches and Applications" Computation 12, no. 4: 78. https://doi.org/10.3390/computation12040078
APA StyleTshilande, N., Mammino, L., & Bilonda, M. K. (2024). The Study of Molecules and Processes in Solution: An Overview of Questions, Approaches and Applications. Computation, 12(4), 78. https://doi.org/10.3390/computation12040078





