Application of Smart Condensed H-Adsorption Nanocomposites in Batteries: Energy Storage Systems and DFT Computations
Abstract
1. Introduction
2. Materials and Methods
3. Results
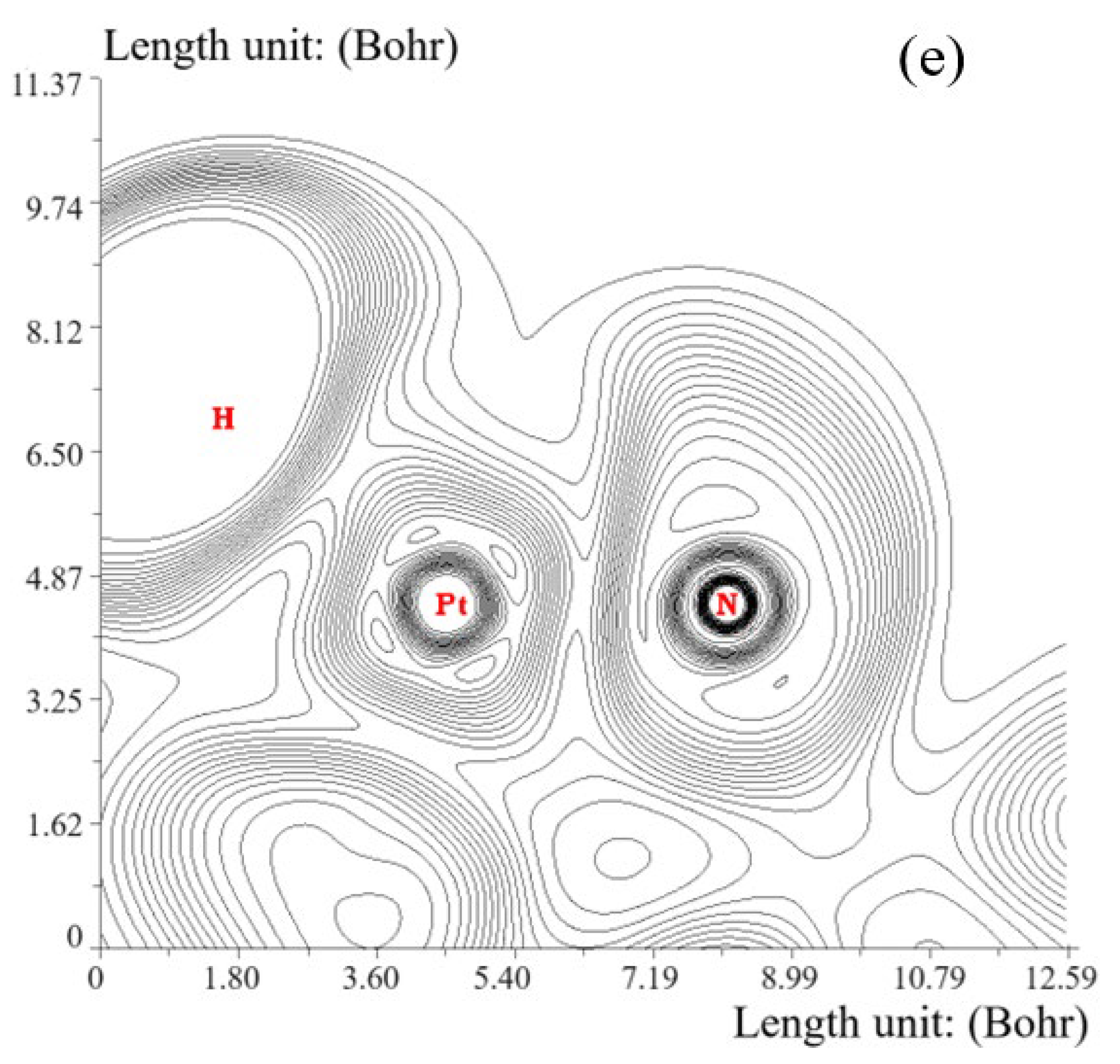
3.1. Elecrton Distribution Analysis
3.2. Charge Transfer, Overlap Integral, and Bond Order Analysis
3.3. Nuclear Magnetic Resonance
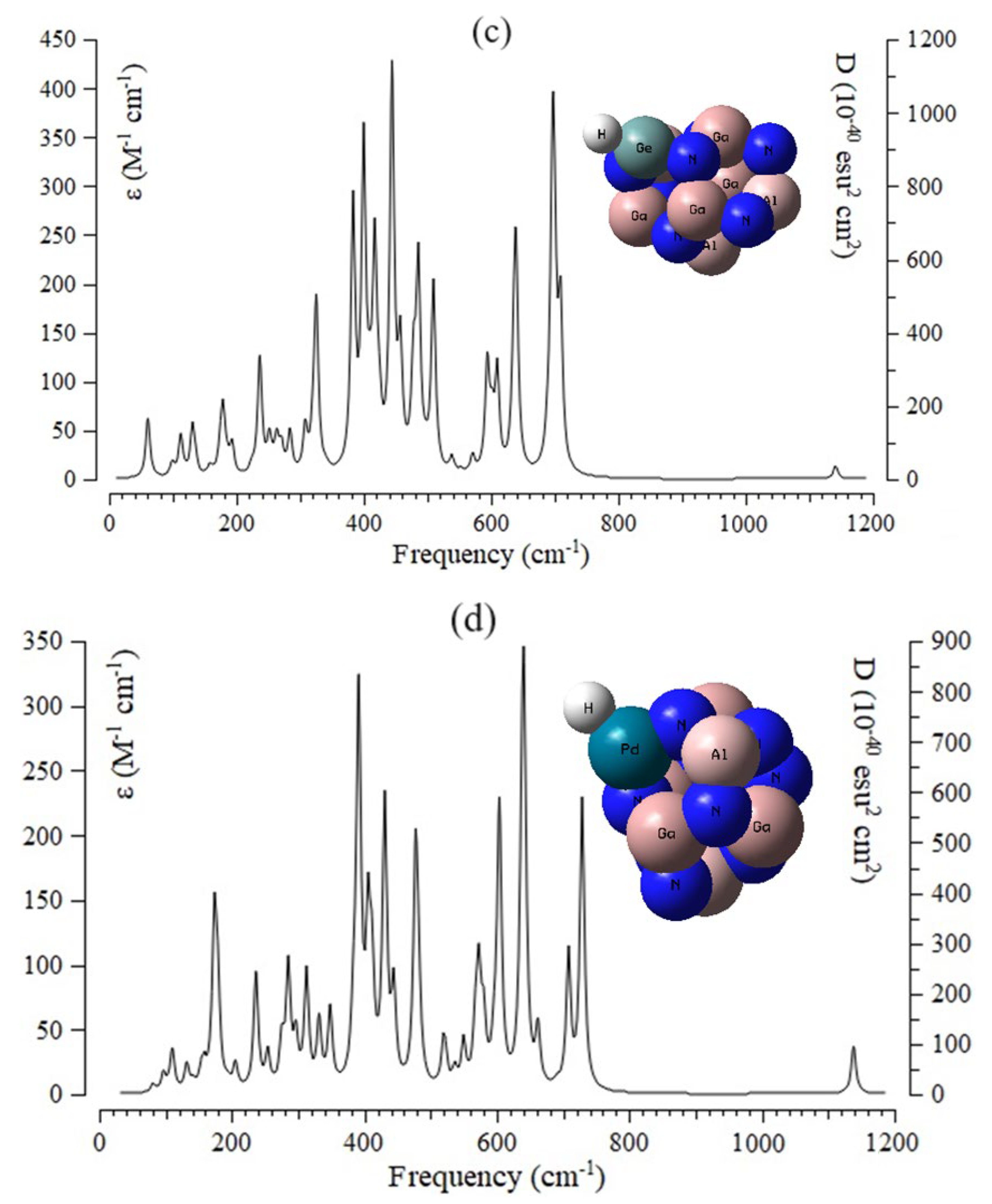
3.4. Insights of Infrared Spectroscopy and Thermochemistry
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Chen, X.; Wang, Z. Review of the AlGaN/GaN High-Electron-Mobility Transistor-Based Biosensors: Structure, Mechanisms, and Applications. Micromachines 2024, 15, 330. [Google Scholar] [CrossRef] [PubMed]
- Bhat, A.M.; Periasamy, C.; Poonia, R.; Varghese, A.; Shaf, N.; Tripathy, S. AlGaN/GaN HEMT Based Ph Detection Using Atomic Layer Deposition of Al2O3 as Sensing Membrane and Passivation. IEEE Trans. Nanotechnol. 2023, 22, 466–472. [Google Scholar] [CrossRef]
- Mollaamin, F. Competitive Intracellular Hydrogen-Nanocarrier Among Aluminum, Carbon, or Silicon Implantation: A Novel Technology of Eco-Friendly Energy Storage using Research Density Functional Theory. Russ. J. Phys. Chem. B 2024, 18, 805–820. [Google Scholar] [CrossRef]
- Sun, R.; Chen, X.; Liu, C.; Chen, W.; Zhang, B. Degradation mechanism of Schottky P-GaN gate stack in GaN power devices under neutron irradiation. Appl. Phys. Lett. 2021, 119, 133503. [Google Scholar] [CrossRef]
- Wang, P.F.; Li, X.; Zhang, E.X.; Jiang, R.; McCurdy, M.W.; Poling, B.S.; Heller, E.R.; Schrimpf, R.D.; Fleetwood, D.M. Worst-Case Bias for High Voltage, Elevated-Temperature Stress of AlGaN/GaN HEMTs. IEEE Trans. Device Mater. Reliab. 2020, 20, 420–428. [Google Scholar] [CrossRef]
- Bashirov, R.J.; Ismayilov, N.E.; Huseynov, R.E.; Muradov, N.M. Quality control methods and models of polymer composite materials. Adv. Phys. Res. 2024, 6, 90–99. [Google Scholar] [CrossRef]
- Noori, A.F.; Ghaleb, A.M.; Salih, A.I. A theoretical study of the physical properties of hexagonal gallium nitrate using density functional theory. Adv. Phys. Res. 2024, 6, 225–238. [Google Scholar] [CrossRef]
- Utamuradova, S.B.; Rakhmanov, D.A.; Tuan, P.L.; Doroshkevich, A.S.; Isayev, R.S.; Abiyev, A.S. Studying the influence of proton irradiation on the distribution profile of Pt and Cr in surface layers n-Si˂Pt˃, n-Si˂Cr˃ using ellipsometric spectroscopy. Adv. Phys. Res. 2024, 6, 83–89. [Google Scholar] [CrossRef]
- Zolotarev, K.V.; Mikhailov, A.N.; Nakhod, V.I.; Sanzhakov, M.A.; Tikhonova, E.G.; Mikhailova, M.V. Characterization and in vivo toxicity assay of uncoated silicon nanoparticles. New Mater. Compd. Appl. 2024, 8, 162–170. [Google Scholar] [CrossRef]
- Utamuradova, S.B.; Matchonov, H.J.; Khamdamov, Z.J.; Utemuratova, H.Y. X-ray diffraction study of the phase state of silicon single crystals doped with manganese. New Mater. Compd. Appl. 2023, 7, 93–99. [Google Scholar]
- Blasco, R.; Ajay, A.; Robin, E.; Bougerol, C.; Lorentz, K.; Alves, L.C.; Mouton, I.; Amichi, L.; Grenier, A.; Monroy, E. Electrical and optical properties of heavily Ge-doped AlGaN. J. Phys. D Appl. Phys. 2019, 52, 125101. [Google Scholar] [CrossRef]
- Wang, D.; Liu, X.; Fang, S.; Huang, C.; Kang, Y.; Yu, H.; Liu, Z.; Zhang, H.; Long, R.; Xiong, Y.; et al. Pt/AlGaN Nanoarchitecture: Toward High Responsivity, Self-Powered Ultraviolet-Sensitive Photodetection. Nano Lett. 2021, 21, 120–129. [Google Scholar] [CrossRef]
- Abdullayeva, L.K.; Hasanov, M.H. Investigation of the role of metal in non-alloy metal-semiconductor (Si) contact. New Mater. Compd. Appl. 2024, 8, 135–141. [Google Scholar] [CrossRef]
- Mollaamin, F.; Shahriari, S.; Monajjemi, M. Influence of Transition Metals for Emergence of Energy Storage in Fuel Cells through Hydrogen Adsorption on the MgAl Surface. Russ. J. Phys. Chem. B 2024, 18, 398–418. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Nanomaterials for Sustainable Energy in Hydrogen-Fuel Cell: Functionalization and Characterization of Carbon Nano-Semiconductors with Silicon, Germanium, Tin or Lead through Density Functional Theory Study. Russ. J. Phys. Chem. B 2024, 18, 607–623. [Google Scholar] [CrossRef]
- Bakhshi, K.; Mollaamin, F.; Monajjemi, M. Exchange and Correlation Effect of Hydrogen Chemisorption on Nano V(100) Surface: A DFT Study by Generalized Gradient Approximation (GGA). J. Comput. Theor. Nanosci. 2011, 8, 763–768. [Google Scholar] [CrossRef]
- Hu, J.; Shen, H.; Jiang, M.; Gong, H.; Xiao, H.; Liu, Z.; Sun, G.; Zu, X. A DFT Study of Hydrogen Storage in High-Entropy Alloy TiZrHfScMo. Nanomaterials 2019, 9, 461. [Google Scholar] [CrossRef]
- Pius, K.K.; Ongwen, N.O.; Mageto, M.; Odari, V.; Gaitho, F.M. Mechanical Properties of Al–Mg–Si Alloys (6xxx Series): A DFT-Based Study. Alloys 2023, 2, 213–226. [Google Scholar] [CrossRef]
- Oreshonkov, A.S. SI: Advances in Density Functional Theory (DFT) Studies of Solids. Materials 2022, 15, 2099. [Google Scholar] [CrossRef]
- Fan, X.; Mi, Z.; Yang, L.; Su, H. Application of DFT Simulation to the Investigation of Hydrogen Embrittlement Mechanism and Design of High Strength Low Alloy Steel. Materials 2023, 16, 152. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Yu, C.-F. A DFT Characterization of Structural, Mechanical, and Thermodynamic Properties of Ag9In4 Binary Intermetallic Compound. Metals 2022, 12, 1852. [Google Scholar] [CrossRef]
- Cruz-Martínez, H.; García-Hilerio, B.; Montejo-Alvaro, F.; Gazga-Villalobos, A.; Rojas-Chávez, H.; Sánchez-Rodríguez, E.P. Density Functional Theory-Based Approaches to Improving Hydrogen Storage in Graphene-Based Materials. Molecules 2024, 29, 436. [Google Scholar] [CrossRef] [PubMed]
- Shelyapina, M.G. Hydrogen Diffusion on, into and in Magnesium Probed by DFT: A Review. Hydrogen 2022, 3, 285–302. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Liu, Y.; Li, Q.; Yang, T.; Jia, H. Crystal Structure Prediction and Performance Assessment of Hydrogen Storage Materials: Insights from Computational Materials Science. Energies 2024, 17, 3591. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Adsorption ability of Ga5N10 nanomaterial for removing metal ions contamination from drinking water by DFT. Int. J. Quantum Chem. 2024, 124, e27348. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Molecular modelling framework of metal-organic clusters for conserving surfaces: Langmuir sorption through the TD-DFT/ONIOM approach. Mol. Simul. 2023, 49, 365–376. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211, Bibcode:1980CaJPh.58.1200V. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6.06.16; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Zavoisky, E. Spin-magnetic resonance in paramagnetics. J. Phys. Ussr 1945, 9, 245. [Google Scholar]
- Xu, Z.; Qin, C.; Yu, Y.; Jiang, G.; Zhao, L. First-principles study of adsorption, dissociation, and diffusion of hydrogen on α-U (110) surface. AIP Adv. 2024, 14, 055114. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 9, 5397–5403. [Google Scholar] [CrossRef]
- Steinmann, S.N.; Mo, Y.; Corminboeuf, C. How do electron localization functions describe π-electron delocalization? Phys. Chem. Chem. Phys. 2011, 13, 20584–20592. [Google Scholar] [CrossRef]
- Tian, L.; Feiwu, C.; Xuebao, W. Meaning and Functional Form of the Electron Localization Function. Acta Phys. Chim. Sin. 2011, 27, 2786–2792. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Mayer, I. Improved definition of bond orders for correlated wave functions. Chem. Phys. Lett. 2012, 544, 83–86. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Trapping of toxic heavy metals from water by GN–nanocage: Application of nanomaterials for contaminant removal technique. J. Mol. Struct. 2024, 1300, 137214. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Bond Order Analysis Based on the Laplacian of Electron Density in Fuzzy Overlap Space. J. Phys. Chem. A 2013, 117, 3100–3108. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Pedrycz, W.; Yang, S.-H.; Boutat, D. Consensus of T-S Fuzzy Fractional-Order, Singular Perturbation, Multi-Agent Systems. Fractal Fract. 2024, 8, 523. [Google Scholar] [CrossRef]
- Anaad, M.A.; Al-Sharuee, I.F. Raman spectroscopy and structural characteristics of fluorescein and coumarin doped silica sol, gel, and aerogel. New Mater. Compd. Appl. 2023, 7, 122–136. [Google Scholar]
- Utamuradova, S.B.; Daliev, S.K.; Bokiyev, B.R.; Zarifbaev, J.S. X-ray spectroscopy of silicon doped with germanium atoms. Adv. Phys. Res. 2024, 6, 211–218. [Google Scholar] [CrossRef]
- Daliev, K.S.; Utamuradova, S.B.; Khamdamov, J.J.; Bahronkulov, Z.E. Electrophysical properties of silicon doped with lutetium. Adv. Phys. Res. 2024, 6, 42–49. [Google Scholar] [CrossRef]
- Mollaamin, F.; Monajjemi, M. Tailoring and functionalizing the graphitic-like GaN and GaP nanostructures as selective sensors for NO, NO2, and NH3 adsorbing: A DFT study. J. Mol. Model. 2023, 29, 170. [Google Scholar] [CrossRef] [PubMed]
- Mamadalimov, A.T.; Isaev, M.S.; Karimov, M.K.; Isaev, F.M.; Muminova, Z.A.; Karimova, S.T.; Kayumova, M.R.; Badalova, G.T.; Abdurazzakov, K.T. Study of infrared quenching in silicide-silicon-silicide structures. Adv. Phys. Res. 2024, 6, 50–55. [Google Scholar] [CrossRef]
- Utamuradova, S.B.; Daliyev, S.K.; Fayzullayev, K.M.; Rakhmanov, D.A.; Zarifbayev, J.S. Raman spectroscopy of defects in silicon doped with chromium atoms. New Mater. Compd. Appl. 2023, 7, 37–43. [Google Scholar]
- Mollaamin, F.; Monajjemi, M. In Silico-DFT Investigation of Nanocluster Alloys of Al-(Mg, Ge, Sn) Coated by Nitrogen Heterocyclic Carbenes as Corrosion Inhibitors. J. Clust. Sci. 2023, 34, 2901–2918. [Google Scholar] [CrossRef]

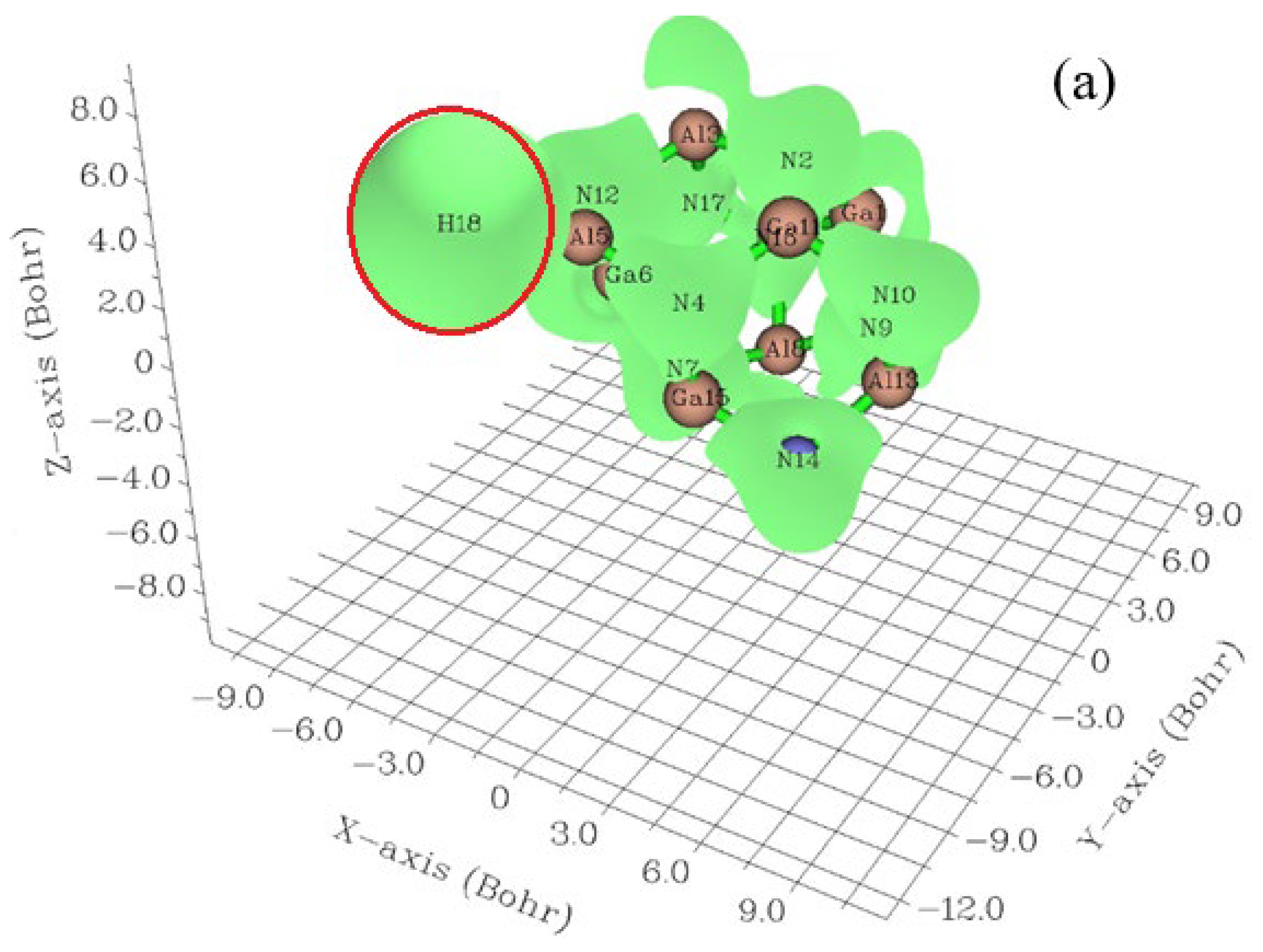
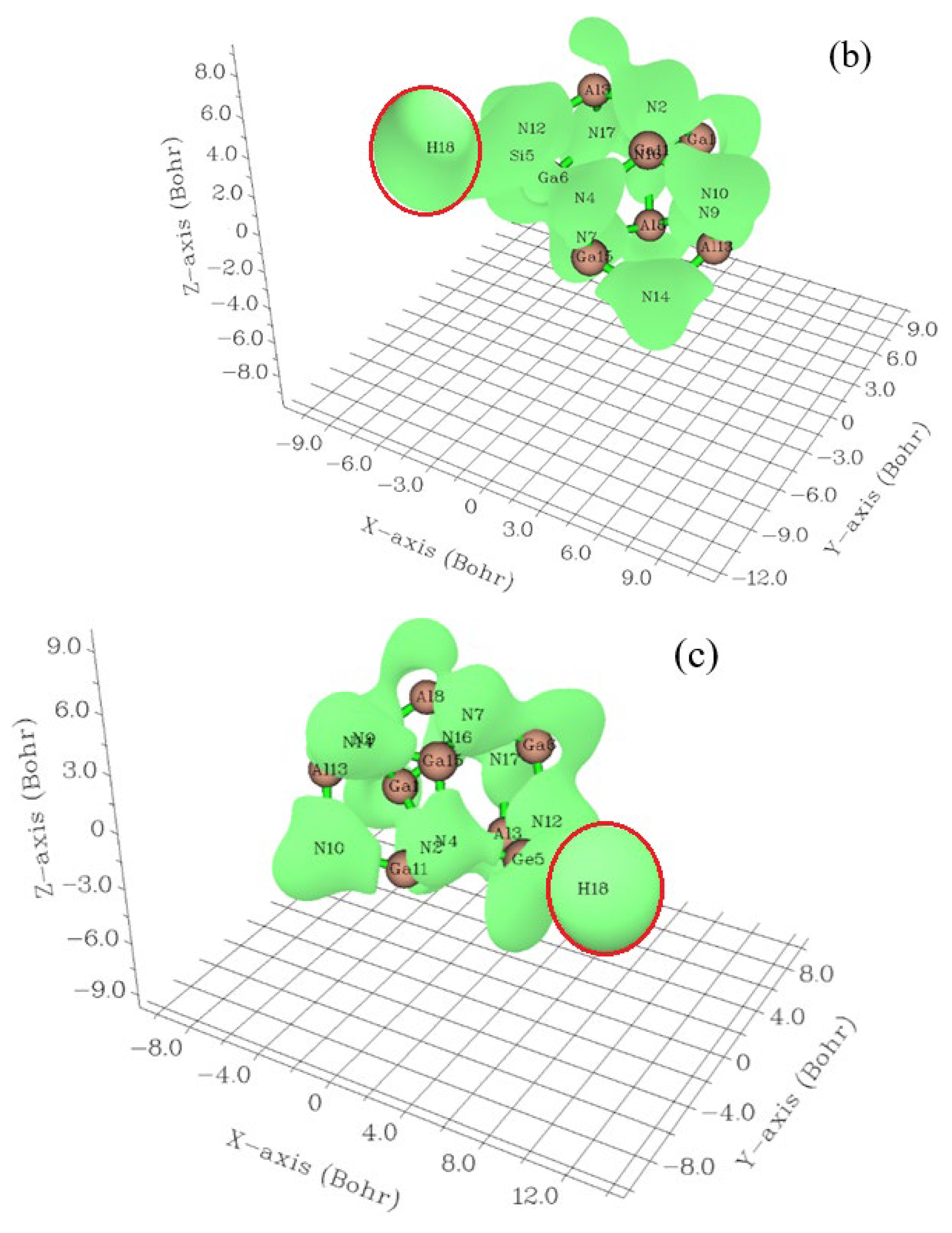

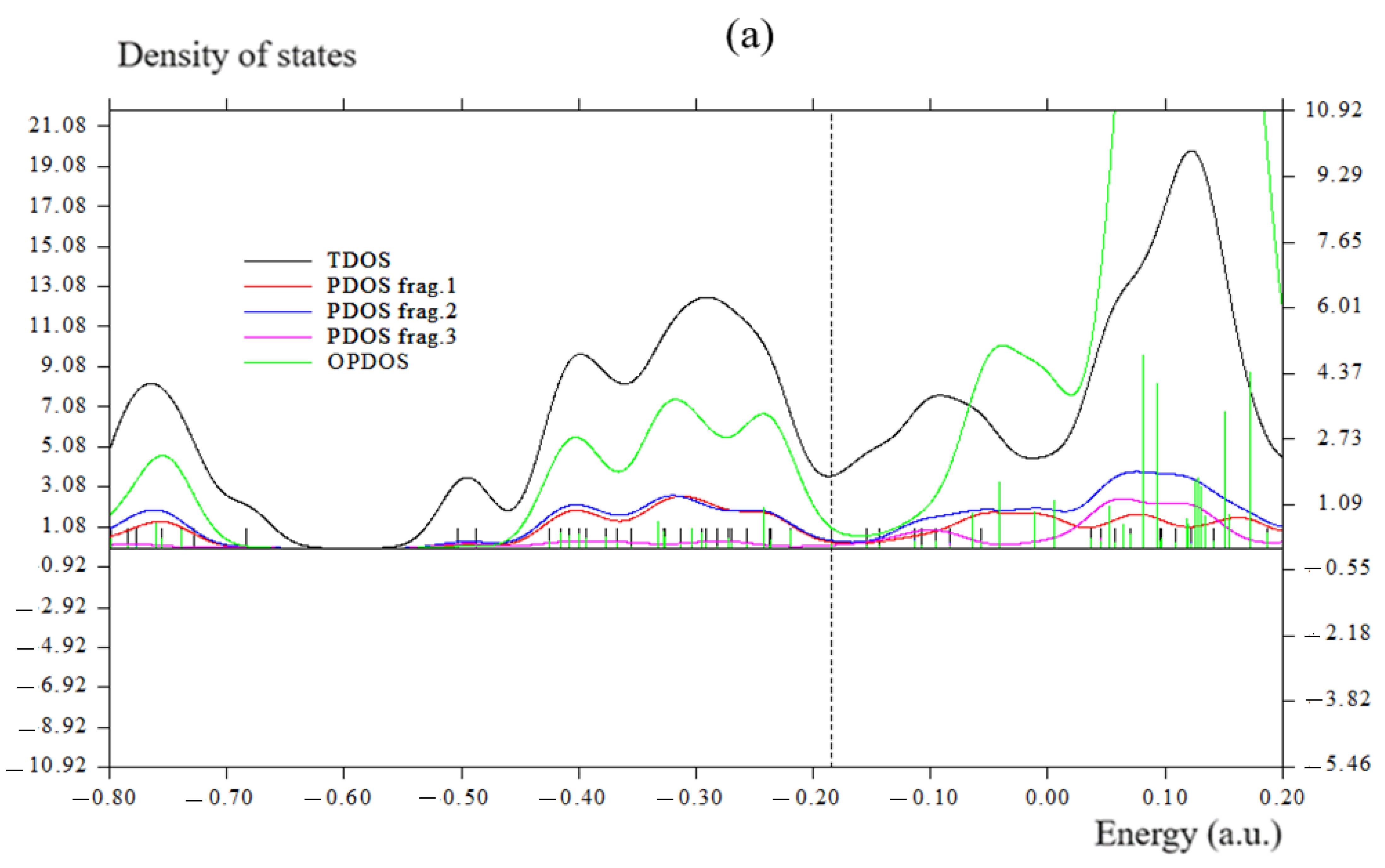
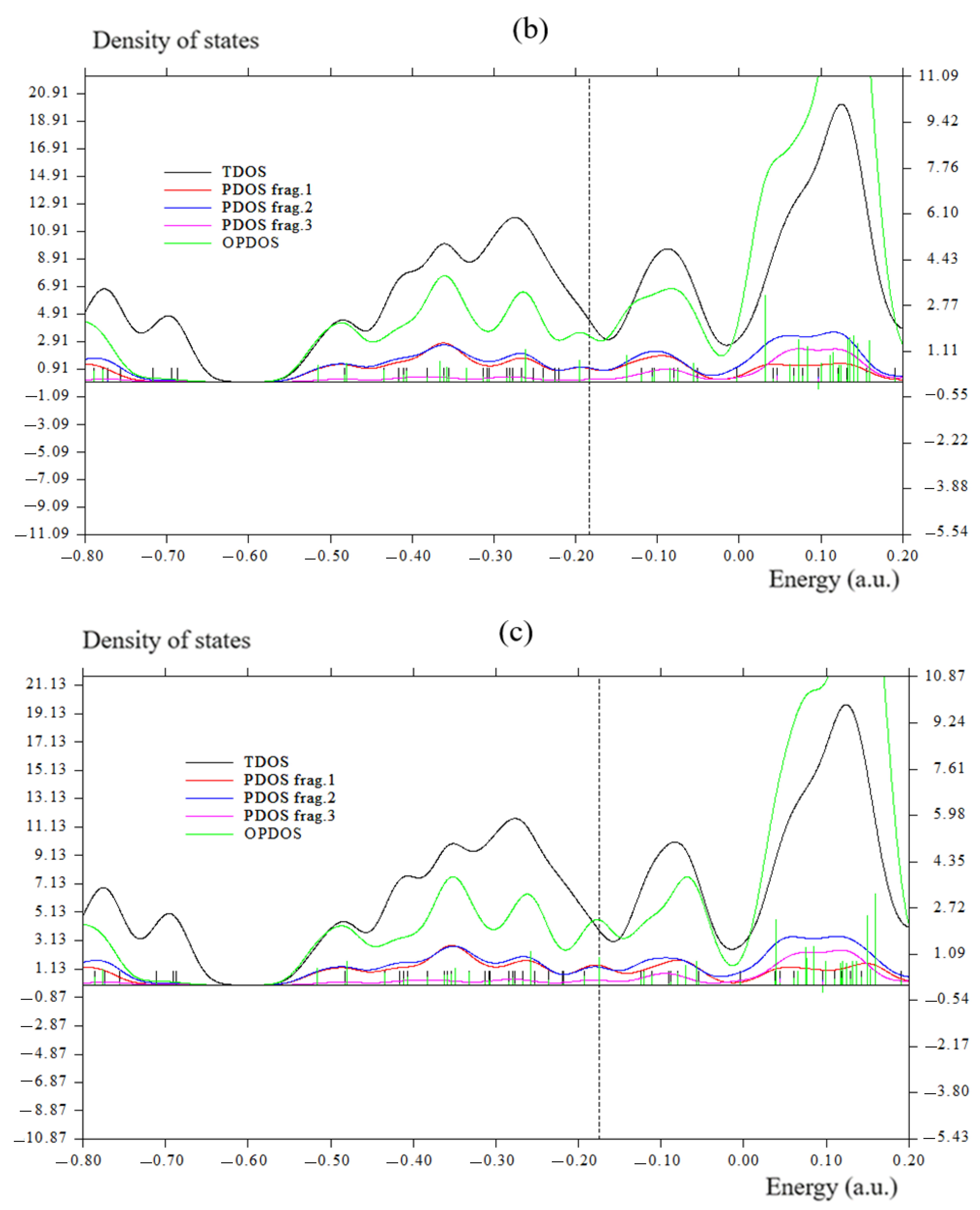







| Si–AlGaN | Si–AlGaN–H | Ge–AlGaN | Ge–AlGaN–H | ||||
|---|---|---|---|---|---|---|---|
| Atom | Q | Atom | Q | Atom | Q | Atom | Q |
| Ga1 | 1.01 | Ga1 | 0.99 | Ga1 | 1.01 | Ga1 | 0.98 |
| N2 | −1.14 | N2 | −1.14 | N2 | −1.14 | N2 | −1.14 |
| Al3 | 1.25 | Al3 | 1.28 | Al3 | 1.24 | Al3 | 1.29 |
| N4 | −1.10 | N4 | −1.07 | N4 | −1.09 | N4 | −1.08 |
| Si5 | 0.75 | Si5 | 0.75 | Ge5 | 0.76 | Ge5 | 0.70 |
| Ga6 | 0.97 | Ga6 | 0.96 | Ga6 | 0.97 | Ga6 | 0.98 |
| N7 | −1.12 | N7 | −1.12 | N7 | −1.12 | N7 | −1.15 |
| Al8 | 1.29 | Al8 | 1.28 | Al8 | 1.28 | Al8 | 1.26 |
| N9 | −1.18 | N9 | −1.18 | N9 | −1.18 | N9 | −1.20 |
| N10 | −0.79 | N10 | −0.77 | N10 | −0.80 | N10 | −0.77 |
| Ga11 | 1.01 | Ga11 | 1.06 | Ga11 | 1.01 | Ga11 | 1.07 |
| N12 | −1.14 | N12 | −1.13 | N12 | −1.12 | N12 | −1.12 |
| Al13 | 1.19 | Al13 | 1.20 | Al13 | 1.19 | Al13 | 1.23 |
| N14 | −0.77 | N14 | −0.83 | N14 | −0.77 | N14 | −0.78 |
| Ga15 | 1.03 | Ga15 | 1.01 | Ga15 | 1.02 | Ga15 | 1.04 |
| N16 | −0.64 | N16 | −0.63 | N16 | −0.64 | N16 | −0.70 |
| N17 | −0.61 | N17 | −0.63 | N17 | −0.61 | N17 | −0.63 |
| - | - | H18 | −0.01 | - | - | H18 | −0.04 |
| Pd–AlGaN | Pd–AlGaN–H | Pt–AlGaN | Pt–AlGaN–H | ||||
| Atom | Q | Atom | Q | Atom | Q | Atom | Q |
| Ga1 | 1.02 | Ga1 | 1.01 | Ga1 | 1.03 | Ga1 | 1.01 |
| N2 | −1.15 | N2 | −1.16 | N2 | −1.15 | N2 | −1.15 |
| Al3 | 1.24 | Al3 | 1.29 | Al3 | 1.26 | Al3 | 1.26 |
| N4 | −0.88 | N4 | −0.91 | N4 | −0.95 | N4 | −1.02 |
| Pd5 | 0.33 | Pd5 | 0.20 | Pt5 | 0.41 | Pt5 | 0.29 |
| Ga6 | 0.96 | Ga6 | 1.00 | Ga6 | 0.97 | Ga6 | 0.99 |
| N7 | −1.13 | N7 | −1.13 | N7 | −1.13 | N7 | −1.15 |
| Al8 | 1.29 | Al8 | 1.31 | Al8 | 1.31 | Al8 | 1.28 |
| N9 | −1.19 | N9 | −1.20 | N9 | −1.19 | N9 | −1.21 |
| N10 | −0.80 | N10 | −0.77 | N10 | −0.81 | N10 | −0.77 |
| Ga11 | 1.04 | Ga11 | 1.07 | Ga11 | 1.06 | Ga11 | 1.08 |
| N12 | −0.93 | N12 | −0.92 | N12 | −1.01 | N12 | −1.00 |
| Al13 | 1.20 | Al13 | 1.22 | Al13 | 1.20 | Al13 | 1.25 |
| N14 | −0.78 | N14 | −0.83 | N14 | −0.78 | N14 | −0.77 |
| Ga15 | 1.04 | Ga15 | 1.06 | Ga15 | 1.06 | Ga15 | 1.09 |
| N16 | −0.64 | N16 | −0.63 | N16 | −0.64 | N16 | −0.63 |
| N17 | −0.61 | N17 | −0.63 | N17 | −0.62 | N17 | −0.62 |
| - | - | H18 | 0.01 | - | - | H18 | 0.04 |
| Hetero-Clusters | ELUMO (a.u.) | EHOMO (a.u.) | ∆E = ELUMO − EHOMO (a.u.) | <S2> |
|---|---|---|---|---|
| AlGaN–H | −0.1550 | −0.1846 | 0.0296 | 1.7500 |
| Si–AlGaN–H | −0.1531 | −0.1833 | 0.0302 | 2.0022 |
| Ge–AlGaN–H | −0.1519 | −0.1822 | 0.0303 | 2.6557 |
| Pd–AlGaN–H | −0.1499 | −0.1780 | 0.0281 | 2.6260 |
| Pt–AlGaN–H | −0.1513 | −0.1791 | 0.0278 | 2.6349 |
| Hetero-Clusters | Mayer | Wiberg | Mulliken | Laplacian | Fuzzy |
|---|---|---|---|---|---|
| AlGaN–H | 0.8987 | 0.8649 | 0.6726 | 0.1671 | 0.8830 |
| Si–AlGaN–H | 0.7382 | 0.7392 | 0.4882 | 0.0962 | 0.7786 |
| Ge–AlGaN–H | 0.7161 | 0.7173 | 0.4637 | 0.0909 | 0.7942 |
| Pd–AlGaN–H | 0.7161 | 0.7173 | 0.4637 | 0.0909 | 0.7942 |
| Pt–AlGaN–H | 0.7092 | 0.7178 | 0.5694 | 0.0909 | 0.8347 |
| Si–AlGaN | Si–AlGaN–H | Ge–AlGaN | Ge–AlGaN–H | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Atom | σiso | σaniso | Atom | σiso | σaniso | Atom | σiso | σaniso | Atom | σiso | σaniso |
| Ga1 | 12.30 | 19.48 | Ga1 | 8.65 | 9.14 | Ga1 | 12.37 | 19.45 | Ga1 | 9.50 | 8.11 |
| N2 | 211.71 | 624.20 | N2 | 139.86 | 203.14 | N2 | 210.74 | 620.27 | N2 | 87.41 | 93.07 |
| Al3 | 11.88 | 23.16 | Al3 | 7.51 | 11.2847 | Al3 | 11.87 | 22.28 | Al3 | 5.73 | 8.07 |
| N4 | 308.10 | 275.86 | N4 | 36.99 | 240.33 | N4 | 319.55 | 305.14 | N4 | 8.23 | 198.17 |
| Si5 | 18.22 | 43.62 | Si5 | 6.82 | 6.97 | Ge5 | 6.40 | 35.07 | Ge5 | 2.03 | 9.00 |
| Ga6 | 12.08 | 12.64 | Ga6 | 9.28 | 9.11 | Ga6 | 12.15 | 12.79 | Ga6 | 5.23 | 6.84 |
| N7 | 228.84 | 504.84 | N7 | 82.75 | 146.76 | N7 | 228.98 | 505.93 | N7 | 16.94 | 207.20 |
| Al8 | 10.79 | 23.46 | Al8 | 8.77 | 9.31 | Al8 | 10.97 | 23.11 | Al8 | 7.55 | 8.10 |
| N9 | 169.84 | 1065.91 | N9 | 33.37 | 201.21 | N9 | 173.76 | 1066.86 | N9 | 113.20 | 124.00 |
| N10 | 4464.28 | 8163.38 | N10 | 842.21 | 996.91 | N10 | 4523.80 | 8361.71 | N10 | 904.78 | 1211.65 |
| Ga11 | 3.61 | 52.52 | Ga11 | 3.40 | 16.40 | Ga11 | 3.31 | 53.53 | Ga11 | 1.33 | 11.40 |
| N12 | 26.94 | 761.34 | N12 | 73.42 | 95.97 | N12 | 24.49 | 753.65 | N12 | 142.53 | 248.75 |
| Al13 | 25.84 | 86.33 | Al13 | 0.36 | 13.3565 | Al13 | 26.69 | 88.23 | Al13 | 3.07 | 21.61 |
| N14 | 4470.40 | 7959.14 | N14 | 600.52 | 810.90 | N14 | 4555.61 | 8140.97 | N14 | 905.21 | 1261.30 |
| Ga15 | 2.00 | 49.70 | Ga15 | 6.30 | 6.26 | Ga15 | 2.23 | 50.43 | Ga15 | 0.63 | 10.75 |
| N16 | 100.42 | 471.67 | N16 | 120.60 | 303.16 | N16 | 82.81 | 452.43 | N16 | 140.98 | 315.61 |
| N17 | 898.88 | 1478.95 | N17 | 155.89 | 373.89 | N17 | 887.57 | 1455.59 | N17 | 158.03 | 386.88 |
| - | - | - | H18 | 19.91 | 7.44 | - | - | H18 | 20.22 | 5.20 | |
| Pd–AlGaN | Pd–AlGaN–H | Pt–AlGaN | Pt–AlGaN–H | ||||||||
| Atom | σiso | σaniso | Atom | σiso | σaniso | Atom | σiso | σaniso | Atom | σiso | σaniso |
| Ga1 | 6.37 | 18.00 | Ga1 | 6.08 | 9.86 | Ga1 | 6.77 | 16.59 | Ga1 | 9.02 | 8.54 |
| N2 | 137.27 | 537.01 | N2 | 119.65 | 355.55 | N2 | 118.06 | 425.22 | N2 | 163.81 | 264.91 |
| Al3 | 7.87 | 8.40 | Al3 | 4.16 | 10.10 | Al3 | 6.66 | 9.20 | Al3 | 6.29 | 8.38 |
| N4 | 142.80 | 640.37 | N4 | 25.36 | 352.27 | N4 | 235.12 | 569.01 | N4 | 53.69 | 313.02 |
| Pd5 | 425.10 | 289.99 | Pd5 | 579.57 | 326.71 | Pt5 | 279.65 | 164.23 | Pt5 | 297.64 | 187.35 |
| Ga6 | 7.57 | 22.45 | Ga6 | 4.55 | 9.98 | Ga6 | 7.06 | 18.41 | Ga6 | 7.25 | 9.06 |
| N7 | 200.06 | 399.43 | N7 | 109.93 | 244.32 | N7 | 174.42 | 304.42 | N7 | 164.67 | 247.81 |
| Al8 | 14.56 | 22.62 | Al8 | 5.76 | 12.80 | Al8 | 11.80 | 15.94 | Al8 | 7.61 | 9.36 |
| N9 | 345.31 | 774.53 | N9 | 21.20 | 292.11 | N9 | 280.20 | 547.55 | N9 | 67.07 | 222.59 |
| N10 | 3220.83 | 6565.74 | N10 | 834.52 | 1372.60 | N10 | 2958.67 | 5956.82 | N10 | 1039.10 | 1580.11 |
| Ga11 | 3.26 | 52.61 | Ga11 | 2.15 | 12.39 | Ga11 | 1.85 | 48.26 | Ga11 | 1.25 | 16.37 |
| N12 | 153.93 | 438.24 | N12 | 19.90 | 433.03 | N12 | 265.17 | 235.40 | N12 | 5.14 | 409.16 |
| Al13 | 31.41 | 41.80 | Al13 | 5.49 | 15.12 | Al13 | 29.24 | 39.10 | Al13 | 6.28 | 23.95 |
| N14 | 2818.52 | 6276.45 | N14 | 753.50 | 1263.81 | N14 | 2596.97 | 5751.33 | N14 | 1043.19 | 1585.44 |
| Ga15 | 7.62 | 51.13 | Ga15 | 1.21 | 9.46 | Ga15 | 6.77 | 46.72 | Ga15 | 1.60 | 17.01 |
| N16 | 795.61 | 2802.93 | N16 | 154.80 | 274.34 | N16 | 471.94 | 1878.49 | N16 | 139.56 | 310.20 |
| N17 | 402.92 | 3204.08 | N17 | 194.62 | 396.81 | N17 | 111.39 | 2245.36 | N17 | 185.56 | 407.10 |
| - | - | - | H18 | 23.76 | 6.07 | - | - | - | H18 | 24.23 | 4.77 |
| Compound | Dipole Moment (Debye) | ∆Eoads × 10–3 (kcal/mol) | ∆Hoads × 10–3 (kcal/mol) | ∆Goads × 10–3 (kcal/mol) | EoH–binding (kcal/mol) |
|---|---|---|---|---|---|
| AlGaN | 4.6672 | −319.178 | −319.178 | −319.219 | - |
| AlGaN–H | 5.5817 | −319.503 | −319.502 | −319.542 | −325 |
| Si–AlGaN | 5.8081 | −320.296 | −320.295 | −320.335 | - |
| Si–AlGaN–H | 5.0608 | −320.656 | −320.656 | −320.697 | −360 |
| Ge–AlGaN | 5.6442 | −320.240 | −320.239 | −320.279 | - |
| Ge–AlGaN–H | 4.3890 | −320.608 | −320.607 | −320.650 | −368 |
| Pd–AlGaN | 5.1550 | −397.327 | −397.327 | −397.368 | - |
| Pd–AlGaN–H | 6.2464 | −397.686 | −397.686 | −397.729 | −359 |
| Pt–AlGaN | 5.5186 | −392.573 | −392.573 | −392.614 | - |
| Pt–AlGaN–H | 5.0840 | −392.956 | −392.956 | −392.999 | −383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mollaamin, F.; Monajjemi, M. Application of Smart Condensed H-Adsorption Nanocomposites in Batteries: Energy Storage Systems and DFT Computations. Computation 2024, 12, 234. https://doi.org/10.3390/computation12120234
Mollaamin F, Monajjemi M. Application of Smart Condensed H-Adsorption Nanocomposites in Batteries: Energy Storage Systems and DFT Computations. Computation. 2024; 12(12):234. https://doi.org/10.3390/computation12120234
Chicago/Turabian StyleMollaamin, Fatemeh, and Majid Monajjemi. 2024. "Application of Smart Condensed H-Adsorption Nanocomposites in Batteries: Energy Storage Systems and DFT Computations" Computation 12, no. 12: 234. https://doi.org/10.3390/computation12120234
APA StyleMollaamin, F., & Monajjemi, M. (2024). Application of Smart Condensed H-Adsorption Nanocomposites in Batteries: Energy Storage Systems and DFT Computations. Computation, 12(12), 234. https://doi.org/10.3390/computation12120234







