Multiple Behavioral Conditions of the Forward Exchange Rates and Stock Market Return in the South Asian Stock Markets During COVID-19: A Novel MT-QARDL Approach
Abstract
1. Introduction
2. Literature Review
3. Research Methodology: Toward a New Multiple Threshold Quantile Autoregressive Distributive Lag (MT-QARDL) Framework
Sign and Location-Based Asymmetries
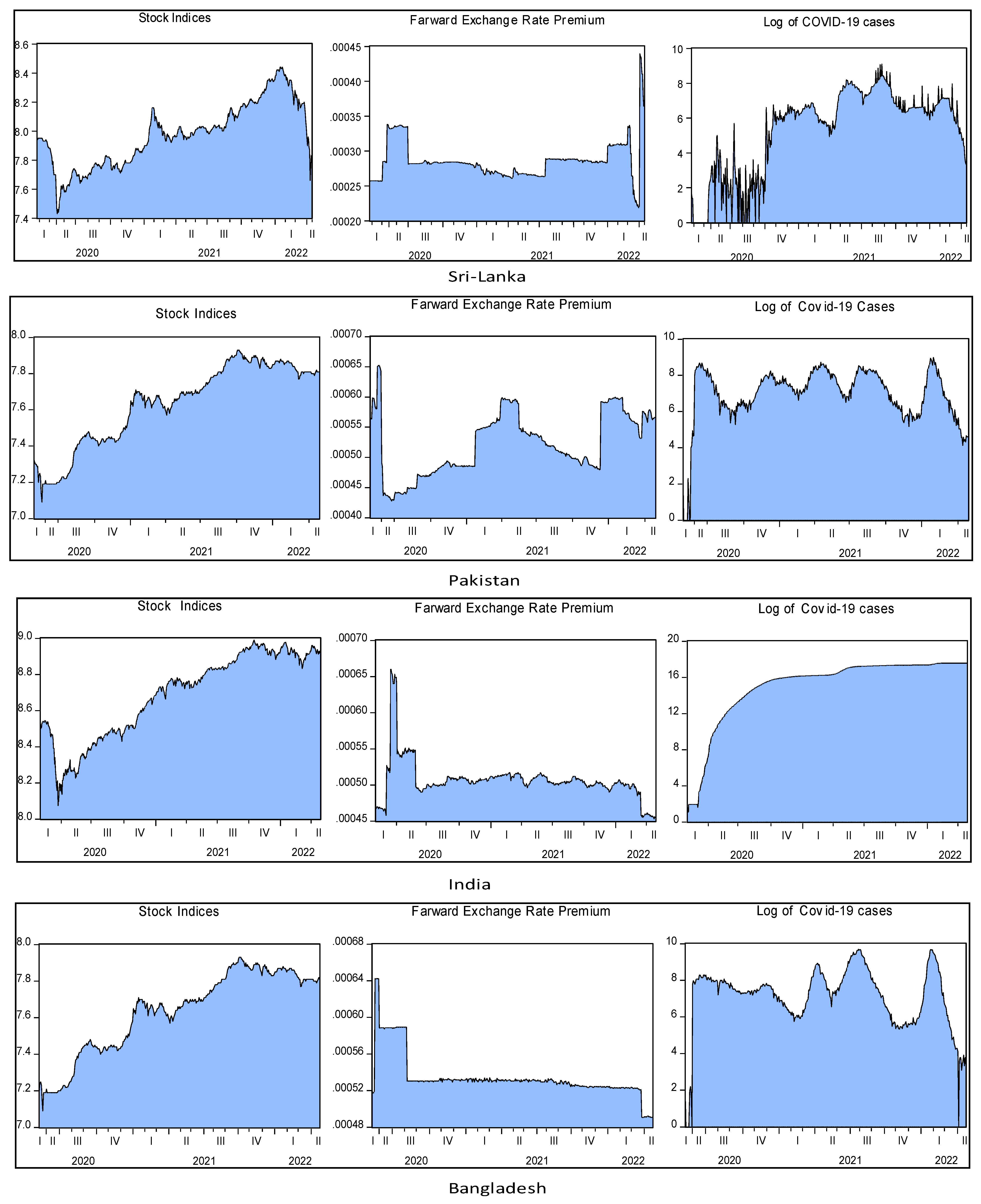
4. Data and Descriptive Statistics
Descriptive Statistics
5. Results with Practical Implications for Short-Run Speculators and Long-Run Shareholders
5.1. QARDL Estimations and Weak Response of South Asian Stock Market (SM) Bullish and Bearish Returns to Forward Exchange Rate Premium (FERP) of 3rd, 6th, 9th, and 12th Months
5.2. MT-QARDL Estimated Results
5.2.1. The Impact of Bearish, Bullish, and Median Quantiles of the Forward Exchange Rate Premium (FERP) on the Lower Quantiles of the Stock Market Returns (SMRs) in the Short and Long Term
5.2.2. The Impact of Bearish, Bullish, and Median Quantiles of the Forward Exchange Rate Premium (FERP) on the Higher Quantiles of the Stock Market Returns (SMRs) in the Short and Long Term
5.2.3. Behavioral Response of the Stock Market to the Bullish, Bearish, and Normal Fluctuations in COVID-19 Cases
5.2.4. Robustness Analysis: A Multivariate Non-Causality Analysis
6. Conclusions with General Policy Guidelines and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Authors | Econometric Model | The Purpose of the Study | Is the Employed Model Possess Asymmetrical Characteristics? | Is the Study Conducted for the Context of South Asian Economies? | Is the Employed Model Effectively Identify Potential Asymmetries? | Is the Employed Model Capable of Estimating ‘Location-Based’ Asymmetries? | Is the Employed Model Capable of Estimating ‘Sign-Based’ Asymmetries? | Does the Model Have the Capability to Estimate for the ‘Short’ and ‘Long-Term’ Investment Periods? |
|---|---|---|---|---|---|---|---|---|
| (Chen and Sun, [85] | Quantile domain Granger causality approach | The asymmetrical interactions between spot-based forex and financial markets | Yes | Yes | Yes | Yes | No | No |
| (Tabash et al. [4] | Panel-based Non-linear Autoregressive Distributive Lag model with pooled mean group approach | The asymmetrical causation from spot values of the exchange rates toward stock returns | Yes | Yes | Yes | No | Yes | Yes |
| (Tian et al. [86] | The GARCH-based copula quantile regression approach | The tail dependency between exchange rates and stock returns | Yes | Yes | Yes | Yes | No | No |
| Suleman et al. [3] | Panel-based Non-linear Autoregressive Distributive Lag model with pooled mean group approach | Asymmetrical impact of stock returns to the inflation and deflation in spot-based currency values | Yes | No | Yes | No | Yes | Yes |
| (Chen et al. [63] | The time-varying parameter factor augmented VAR and non-linear Granger causality approach | The non-linear interactions between stocks and spot-based exchange rates | Yes | Yes | Yes | No | No | No |
| (Hashmi et al. [41] | Quantile Autoregressive Distributive Lag model (QARDL) | The asymmetrical response of stock returns at different quantiles to the fluctuations in spot exchange rate | Yes | Yes | Yes | Yes | No | Yes |
| Salisu et al. [87] | Threshold augmented vector global auto-regression (GVAR) | The impact of COVID-19 on the stock and spot exchange rates | Yes | Yes | Yes | No | No | No |
| Salisu et al. [42] | The panel domain Non-linear Autoregressive Distributive Lag model | The response of U.S. firms’ stock returns to the positive and negative shocks in spot values of the exchange rates | Yes | No | Yes | No | Yes | Yes |
| Zhu et al. [43] | The threshold rolling window quantile regression approach | The response of stock returns of BRICS to the fluctuations in spot exchange rate | Yes | Yes | Yes | Yes | No | No |
| Ding et al. [44] | Ordinary least square regression model | The stock and exchange rate interactions | No | No | No | No | No | No |
| Huang et al. [45] | Time-varying Parameter Vector Auto-regression | The response of stock returns to the fluctuations in spot exchange rate | No | No | No | No | No | No |
| Khan et al. [46] | Autoregressive Distributive Lag model (ARDL) with graphical simulations | The linear response of stock returns to the fluctuations in spot currency values | No | No | No | No | No | Yes |
| Kumar et al. [47] | The Non-Linear Autoregressive Distributive Lag model approach (NARDL) | The response of Indian stock returns to the positive and negative fluctuations in spot exchange rates | Yes | Yes | Yes | No | Yes | Yes |
| Salisu et al. [48] | Panel-based Autoregressive Distributive Lag model | The response of stock returns to the positive and negative fluctuations in exchange rates under different interest rate regimes | No | Yes | No | No | No | Yes |
| Xie et al. [40] | Symmetric and asymmetric panel domain Granger causation approach | The dynamic interaction between stock and exchange rate | Yes | Yes | Yes | No | No | No |
| Ansriansyah and Messins [37] | Granger causality approach | The dynamic interaction between stock and exchange rate | No | Yes | No | No | No | No |
| Current article (contribution with respect to novel method) | Multiple Threshold-based Quantile-based Autoregressive Distributive Lag model approach | The response of stock returns at different quantiles to the bearish, bullish, and moderate fluctuations in forward exchange rate premiums | Yes | No | Yes | Yes | Yes | Yes |
| Pakistan | India | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Absolute | FERP-3M | FERP-9M | FERP-12M | Absolute | FERP-3M | FERP-6M | FERP-9M | FERP-12M | |||
| Returns | Returns | ||||||||||
| Dimension | HWBZ test | HWBZ test | |||||||||
| η = 1 | 0.593 | 0.572 | 0.593 | 0.639 | 0.553 | 0.584 | 0.623 | 0.652 | 0.573 | ||
| η = 1.5 | 0.61 | 0.582 | 0.599 | 0.6083 | 0.57 | 0.573 | 0.599 | 0.66 | 0.58 | ||
| Bangladesh | Sri Lanka | ||||||||||
| Absolute | FERP-3M | FERP-6M | FERP-9M | FERP-12M | Absolute | FERP-3M | FERP-6M | FERP-9M | FERP-12M | ||
| Returns | Returns | ||||||||||
| HWBZ test | HWBZ test | ||||||||||
| η = 1 | 0.573 | 0.58 | 0.592 | 0.61 | 0.67 | 0.593 | 0.688 | 0.581 | |||
| η = 1.5 | 0.55 | 0.5899 | 0.602 | 0.599 | 0.66 | 0.608 | 0.69 | 0.59 | |||
| (a) | ||||||||||||||||||||||||||||
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||||||||||
| FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | |||||||||||||
| Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | Coef. | |||||||||||||
| 0.1 | −0.4250 | −0.4135 | −0.3690 | −0.3578 | 0.0460 | −0.0246 | 0.0546 | −0.0233 | −0.3751 | −0.3520 | −0.2949 | −0.2663 | −0.4969 *** | −0.4782 *** | −0.3844 *** | −0.3712 *** | ||||||||||||
| 0.2 | −0.2376 | −0.2308 | −0.2125 | −0.2065 | −0.1181 | −0.0747 | −0.0598 | −0.0632 | 0.6141 ** | 0.5930 ** | 0.5331 ** | 0.5111 ** | −0.3199 * | −0.3065 * | −0.26020 | −0.24567 | ||||||||||||
| 0.3 | −0.0436 | −0.0428 | −0.0413 | −0.0423 | −0.0740 | −0.0686 | −0.0538 | −0.0476 | −0.1650 | −0.1580 | −0.1324 | −0.1312 | −0.07481 | −0.06874 | −0.05057 | −0.04386 | ||||||||||||
| 0.7 | −0.0582 | −0.0561 | −0.0503 | −0.0482 | 0.3000 | 0.2899 | 0.2740 | 0.2715 | −0.2701 | −0.2603 | −0.1991 | −0.1809 | 0.4144 *** | 0.4092 *** | 0.3807 *** | 0.3688 *** | ||||||||||||
| 0.8 | 0.0099 | 0.0100 | 0.0102 | 0.0103 | 0.2881 | 0.2763 | 0.2576 | 0.2514 | −0.0072 | −0.0065 | −0.0022 | −0.0039 | 0.4828 *** | 0.4730 *** | 0.4392 *** | 0.4249 *** | ||||||||||||
| 0.9 | 0.0809 | 0.0823 | 0.0860 | 0.0874 | 0.4071 | 0.4085 * | 0.3634 | 0.3531 | −0.8694 ** | −0.8356 ** | −0.7372 ** | −0.6930 ** | 0.7959 *** | 0.7660 *** | 0.7010 *** | 0.6799 *** | ||||||||||||
| 0.1 | 0.0034 | 0.0034 | 0.0029 | 0.0029 | −0.0208 | −0.0191 | −0.0208 | −0.0185 | −0.0116 | −0.0116 | −0.0124 | −0.0121 | −0.01209 | −0.01187 | −0.00953 | −0.00952 | ||||||||||||
| 0.2 | −0.0012 | −0.0011 | −0.0011 | −0.0010 | −0.01566 ** | −0.01516 *** | −0.01548 *** | −0.01563 *** | 0.0003 | 0.0003 | 0.0009 | −0.0001 | −0.01237 | −0.012616 * | −0.0128 * | −0.01321 * | ||||||||||||
| 0.3 | 0.0006 | 0.0006 | 0.0007 | 0.0008 | −0.01175 *** | −0.01191 *** | −0.01177 *** | −0.01176 *** | −0.008814 * | −0.008812 * | −0.008669 * | −0.008803 * | −0.01445 ** | −0.01448 ** | −0.01446 ** | −0.01450 ** | ||||||||||||
| 0.7 | −0.0008 | −0.0008 | −0.0008 | −0.0008 | −0.01090 *** | −0.00989 ** | −0.01089 *** | −0.01057 *** | −0.0049 | −0.0049 | −0.0058 | −0.0060 | −0.00797 | −0.00793 | −0.00785 | −0.00788 | ||||||||||||
| 0.8 | −0.0004 | −0.0004 | −0.0004 | −0.0004 | −0.006047 * | −0.0057 | −0.00599 * | −0.0060 | −0.0005 | −0.0005 | −0.0004 | −0.0005 | −0.009091 ** | −0.008965 ** | −0.008964 ** | −0.008829 * | ||||||||||||
| 0.9 | −0.01427 ** | −0.01428 ** | −0.01427 ** | −0.01427 ** | −0.0061 | −0.0061 | −0.0060 | −0.0061 | −0.01987 ** | −0.01987 ** | −0.01964 ** | −0.0191 ** | −0.00109 | −0.00115 | −0.00094 | −0.00083 | ||||||||||||
| 0.1 | −0.0400 | −0.0400 | −0.0390 | −0.0390 | −0.0067 | −0.0134 | −0.0065 | −0.0147 | −0.0484 | −0.0473 | −0.0457 | −0.0434 | −0.05974 *** | −0.0594 *** | −0.05198 *** | −0.05217 *** | ||||||||||||
| 0.2 | −0.02498 * | −0.02502 * | −0.02518 * | −0.02527 * | −0.0243 | −0.0195 | −0.0199 | −0.0213 | 0.07100 ** | 0.07087 ** | 0.07110 ** | 0.06990 ** | −0.04236 ** | −0.04243 ** | −0.04125 ** | −0.04122 ** | ||||||||||||
| 0.3 | −0.0036 | −0.0036 | −0.0037 | −0.0038 | −0.0178 | −0.0179 | −0.0177 | −0.0176 | −0.0242 | −0.0242 | −0.0234 | −0.0241 | −0.01864 | −0.01856 | −0.01820 | −0.01805 | ||||||||||||
| 0.7 | −0.0073 | −0.0073 | −0.0073 | −0.0073 | 0.0231 | 0.0234 | 0.0230 | 0.0239 | −0.0349 | −0.0349 | −0.0315 | −0.0304 | 0.03637 ** | 0.03697 ** | 0.03720 ** | 0.03701 ** | ||||||||||||
| 0.8 | −0.0003 | −0.0003 | −0.0003 | −0.0003 | 0.0250 | 0.0248 | 0.0247 | 0.0248 | −0.0024 | −0.0023 | −0.0020 | −0.0023 | 0.04217 *** | 0.04254 *** | 0.04261 *** | 0.0424 *** | ||||||||||||
| 0.9 | −0.0045 | −0.0045 | −0.0045 | −0.0045 | 0.0372 | 0.03875 * | 0.0369 | 0.0369 | −0.1172 ** | −0.1172 ** | −0.11664 ** | −0.11474 ** | 0.08086 *** | 0.08007 *** | 0.08019 *** | 0.08047 *** | ||||||||||||
| 0.1 | 0.00411 * | 0.004114 * | 0.004023 * | 0.004023 * | 0.0239 | 0.0231 | 0.02388 | 0.02265 | 0.002626 *** | 0.002627 *** | 0.002589 *** | 0.002619 *** | 0.00040 | 0.00040 | 0.00012 | 0.00013 | ||||||||||||
| 0.2 | 0.0020 | 0.0020 | 0.0021 | 0.0021 | 0.01162 * | 0.01170 ** | 0.01189 ** | 0.01202 ** | 0.001163 ** | 0.001158 ** | 0.001089 ** | 0.00112 ** | 0.00037 | 0.00038 | 0.00046 | 0.00049 | ||||||||||||
| 0.3 | 0.000799 * | 0.000805 * | 0.000846 ** | 0.000872 ** | 0.005296 * | 0.005335 * | 0.005325 * | 0.005357 * | 0.001847 ** | 0.001847 ** | 0.001734 ** | 0.001843 ** | 0.000938 ** | 0.000942 ** | 0.000957 ** | 0.000967 ** | ||||||||||||
| 0.7 | 0.001109 * | 0.00111 * | 0.00111 * | 0.001111 * | 0.003473 ** | 0.0024 | 0.003403 ** | 0.003288 ** | 0.0007 | 0.0007 | 0.0008 | 0.000851 * | 0.000999 *** | 0.000993 *** | 0.000974 *** | 0.000966 *** | ||||||||||||
| 0.8 | 0.00004 | 0.00003 | 0.00004 | 0.00004 | −0.0003 | −0.0004 | −0.0004 | −0.0004 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.000727 ** | 0.000743 ** | 0.000726 ** | 0.000725 ** | ||||||||||||
| 0.9 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | −0.0022 | −0.0019 | −0.0023 | −0.0024 | −0.0012 | −0.0012 | −0.0013 | −0.0014 | 0.00078 | 0.00075 | 0.00065 | 0.00060 | ||||||||||||
| 0.1 | −0.0701 | −0.0701 | −0.0665 | −0.0665 | 0.0882 | 0.0520 | 0.0885 | 0.0504 | 0.0156 | 0.0156 | 0.0218 | 0.0163 | 0.4785 *** | 0.4804 *** | 0.4914 *** | 0.4934 *** | ||||||||||||
| 0.2 | 0.0053 | 0.0051 | 0.0039 | 0.0031 | 0.0634 | 0.0773 | 0.0718 | 0.0662 | −0.0419 | −0.0418 | −0.0527 | −0.0408 | 0.3689 *** | 0.3693 *** | 0.3621 *** | 0.3615 *** | ||||||||||||
| 0.3 | 0.0063 | 0.0057 | 0.0025 | 0.0007 | 0.1022 ** | 0.10226 ** | 0.1022 ** | 0.10230 ** | −0.0128 | −0.0128 | −0.0039 | −0.0132 | 0.3591 *** | 0.3593 *** | 0.3592 *** | 0.3581 *** | ||||||||||||
| 0.7 | −0.0659 | −0.0659 | −0.0658 | −0.0658 | −0.0535 | −0.0450 | −0.0533 | −0.0522 | −0.0093 | −0.0092 | −0.0115 | −0.0101 | 0.04572 | 0.04160 | 0.03704 | 0.03466 | ||||||||||||
| 0.8 | −0.0023 | −0.0023 | −0.0023 | −0.0023 | −0.0631 | −0.0581 | −0.0636 | −0.0634 | −0.0029 | −0.0030 | −0.0029 | −0.0030 | 0.00113 | 0.00070 | 0.00031 | 0.00186 | ||||||||||||
| 0.9 | −0.1709 *** | −0.1708 *** | −0.1707 *** | −0.1706 *** | −0.0866 | −0.0868 | −0.0871 | −0.0849 | −0.0924 | −0.0924 | −0.0980 | −0.1011 | −0.07470 | −0.07115 | −0.06676 | −0.06338 | ||||||||||||
| 0.1 | −0.0462 | −0.0462 | −0.0460 | −0.0460 | 0.0455 | 0.0396 | 0.0445 | 0.0344 | −0.3068 *** | −0.30571 *** | −0.3018 *** | −0.2989 *** | −0.01497 | −0.01466 | −0.01148 | −0.01134 | ||||||||||||
| 0.2 | −0.051539 * | −0.05154 * | −0.0516 | −0.0516 | −0.0494 | −0.11042 * | −0.1126 | −0.1122 | −0.3524 *** | −0.35105 *** | −0.3429 *** | −0.3399 *** | −0.0320 *** | −0.03205 *** | −0.03269 *** | −0.03278 *** | ||||||||||||
| 0.3 | −0.0850 *** | −0.0858 *** | −0.08529 *** | −0.08507 *** | −0.0047 | −0.0049 | −0.0045 | −0.0045 | −0.37794 *** | −0.37653 *** | −0.3708 *** | −0.3657 *** | −0.03206 ** | −0.03201 ** | −0.03187 ** | −0.03192 ** | ||||||||||||
| 0.7 | −0.0181 | −0.0181 | −0.0181 | −0.0181 | 0.1470 ** | 0.1209 | 0.1446 ** | 0.1442 ** | −0.2073 | −0.2071 | −0.1922 | −0.2519 | −0.05581 | −0.05368 | −0.05162 | −0.05046 | ||||||||||||
| 0.8 | −0.0352 | −0.0352 | −0.0352 | −0.0352 | −0.0102 | −0.0105 | −0.0106 | −0.0103 | −0.0950 | −0.0950 | −0.0954 | −0.0950 | −0.06687 *** | −0.06577 *** | −0.06344 *** | −0.06134 | ||||||||||||
| 0.9 | −0.1349 *** | −0.1348 *** | −0.1348 *** | −0.1348 *** | 0.0434 | 0.0427 | 0.0431 | 0.0437 | −0.0932 | −0.0932 | −0.0929 | −0.1229 | −0.07808 *** | −0.07810 *** | −0.07750 *** | −0.07711 *** | ||||||||||||
| 0.1 | −0.0051 | −0.0051 | −0.0053 | −0.0053 | −0.1685 | −0.1595 | −0.1686 | −0.1572 | −0.0033 | −0.0033 | −0.0034 | −0.0030 | 0.00266 | 0.00267 | 0.00237 | 0.00239 | ||||||||||||
| 0.2 | −0.0048 | −0.0048 | −0.0048 | −0.0049 | −0.07398 * | −0.07608 *** | −0.07668 *** | −0.07642 *** | −0.00204 *** | −0.00202 *** | −0.0019 *** | −0.00189 *** | 0.002708 ** | 0.002704 ** | 0.002668 ** | 0.002658 ** | ||||||||||||
| 0.3 | −0.0019 | −0.0019 | −0.0019 | −0.0020 | −0.03952 * | −0.03968 * | −0.039437 * | −0.03948 * | −0.0013 | −0.0013 | −0.0012 | −0.0012 | 0.00077 | 0.00078 | 0.00080 | 0.00081 | ||||||||||||
| 0.7 | 0.0020 | 0.0020 | 0.0020 | 0.0020 | −0.00911 * | −0.0053 | −0.00911 * | −0.009274 * | −0.0004 | −0.0004 | −0.0003 | −0.0010 | −0.001775 * | −0.001769 * | −0.001761 * | −0.001746 * | ||||||||||||
| 0.8 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.01315 ** | 0.01311 ** | 0.0132 ** | 0.01324 ** | 0.0003 | 0.0003 | 0.0002 | 0.0003 | −0.00066 | −0.00059 | −0.00061 | −0.00059 | ||||||||||||
| 0.9 | 0.0016 | 0.0016 | 0.0016 | 0.0016 | 0.0299 | 0.0281 | 0.0300 | 0.0299 | 0.0013 | 0.0013 | 0.0013 | 0.0009 | −0.002106 * | −0.002004 * | −0.00178 | −0.00171 | ||||||||||||
| (b) | ||||||||||||||||||||||||||||
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||||||||||
| FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | |||||||||||||
| Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | Restr.Value | |||||||||||||
| 0.1, 0.9 | −0.3440 | −0.3312 | −0.2830 | −0.2704 | 0.3305 | 0.2960 | 0.2892 | 0.2065 | −1.2432 | −1.1864 | −1.0321 | −0.9581 | 0.2990 | 0.2878 | 0.3166 | 0.3088 | ||||||||||||
| −0.0109 | −0.0109 | −0.0114 | −0.0114 | −0.0055 | −0.0045 | −0.0054 | −0.0036 | −0.03147 *** | −0.03146 *** | −0.03206 *** | −0.03120 *** | −0.0132 | −0.0130 | −0.0105 | −0.0104 | |||||||||||||
| −0.0445 | −0.0445 | −0.0435 | −0.0435 | 0.0358 | 0.0339 | 0.0356 | 0.0278 | −0.1654 | −0.1644 | −0.1624 | −0.1579 | 0.0211 | 0.0207 | 0.0282 | 0.0283 | |||||||||||||
| 0.004614 ** | 0.004615 ** | 0.004527 ** | 0.004528 ** | 0.0138 | 0.0133 | 0.0137 | 0.0124 | 0.0014 | 0.0014 | 0.0013 | 0.0013 | 0.0012 | 0.0011 | 0.0008 | 0.0007 | |||||||||||||
| −0.2410 * | −0.2409 * | −0.2372 * | −0.2371 * | 0.0174 | −0.0186 | 0.0172 | −0.0329 | −0.0764 | −0.0765 | −0.0761 | −0.0843 | 0.403839 ** | 0.409285 ** | 0.424734 ** | 0.430117 ** | |||||||||||||
| −0.1811 ** | −0.1811 ** | −0.1808 ** | −0.1808 ** | −0.1800 | −0.1778 | −0.1812 | −0.1886 | −0.0205 | −0.0194 | −0.0133 | 0.0279 | −0.0931 | −0.0928 | −0.0890 | −0.0884 | |||||||||||||
| −0.0035 | −0.0035 | −0.0036 | −0.0036 | −0.1227 | −0.1173 | −0.1227 | −0.1134 | −0.0022 | −0.0021 | −0.0021 | −0.0022 | 0.0006 | 0.0007 | 0.0006 | 0.0007 | |||||||||||||
| 0.2, 0.8 | −0.2277 | −0.2209 | −0.2023 | −0.1962 | 0.0474 | 0.1136 | 0.0689 | 0.0649 | 0.6083 ** | 0.5877 ** | 0.5309 ** | 0.5085 ** | 0.1629 | 0.1666 | 0.1790 | 0.1793 | ||||||||||||
| −0.0015 | −0.0015 | −0.0014 | −0.0014 | −0.0003 | −0.0003 | 0.0000 | −0.0007 | −0.0002 | −0.0002 | 0.0005 | −0.0006 | −0.021463 ** | −0.021581 ** | −0.021852 ** | −0.022047 ** | |||||||||||||
| −0.0253 | −0.0253 | −0.0255 | −0.0256 | 0.0060 | 0.0139 | 0.0100 | 0.0091 | 0.06885 * | 0.06872 * | 0.06915 * | 0.06778 * | −0.0002 | 0.0001 | 0.0014 | 0.0013 | |||||||||||||
| 0.0021 | 0.0021 | 0.0021 | 0.0021 | 0.0035 | 0.0035 | 0.0037 | 0.0038 | 0.001197 * | 0.001192 * | 0.00112 * | 0.00115 * | 0.001098 * | 0.001125 * | 0.001181 ** | 0.001213 ** | |||||||||||||
| 0.0031 | 0.0028 | 0.0016 | 0.0008 | 0.0160 | 0.0354 | 0.0238 | 0.0044 | −0.0445 | −0.0444 | −0.0556 | −0.0434 | 0.370105 *** | 0.370037 *** | 0.362431 *** | 0.363442 *** | |||||||||||||
| −0.0867 | −0.0867 | −0.0867 | −0.0868 | −0.3284 | −0.3810 *** | −0.3920 *** | −0.3891 *** | −0.0680 | −0.0666 | −0.0568 | 0.0148 | −0.0990 | −0.0978 | −0.0961 | −0.0941 | |||||||||||||
| −0.0047 | −0.0047 | −0.0047 | −0.0048 | −0.0449 | −0.04877 * | −0.04751 * | −0.04928 * | −0.0019 | −0.0019 | −0.0017 | −0.0018 | 0.0020 | 0.0021 | 0.0021 | 0.0021 | |||||||||||||
| 0.3, 0.7 | −0.1018 | −0.0989 | −0.0916 | −0.0905 | 0.1034 | 0.1334 | 0.0914 | 0.1006 | −0.4338 | −0.4170 | −0.3315 | −0.3108 | 0.3396 | 0.3405 | 0.3302 | 0.325025 * | ||||||||||||
| −0.0002 | −0.0002 | −0.0001 | −0.0001 | −0.0012 | −0.0012 | −0.0012 | −0.0014 | −0.01366 ** | −0.01365 ** | −0.01451 ** | −0.01479 ** | −0.022424 *** | −0.022383 *** | −0.022311 *** | −0.022391 *** | |||||||||||||
| −0.0109 | −0.0109 | −0.0110 | −0.0111 | 0.0105 | 0.0141 | 0.0105 | 0.0118 | −0.0589 | −0.0589 | −0.0549 | −0.0543 | 0.0177 | 0.0184 | 0.0190 | 0.0190 | |||||||||||||
| 0.001908 *** | 0.001915 *** | 0.001957 *** | 0.001983 *** | 0.0010 | −0.0001 | 0.0009 | 0.0008 | 0.002529 *** | 0.002528 *** | 0.002543 *** | 0.002697 *** | 0.001937 *** | 0.001934 *** | 0.001931 *** | 0.001932 *** | |||||||||||||
| −0.0596 | −0.0602 | −0.0633 | −0.0651 | 0.0645 | 0.0735 | 0.0647 | 0.0517 | −0.0217 | −0.0217 | −0.0154 | −0.0229 | 0.404841 *** | 0.400952 *** | 0.396339 *** | 0.39285 *** | |||||||||||||
| −0.1040 * | −0.1039 * | −0.1034 * | −0.1032 * | −0.1265 | −0.1441 | −0.1287 | −0.1270 | −0.2057 | −0.2042 | −0.1816 | −0.1680 | −0.0879 | −0.0857 | −0.0835 | −0.0824 | |||||||||||||
| 0.00010 | 0.00008 | 0.00005 | 0.00002 | −0.0327 | −0.0308 | −0.0326 | −0.03485 * | −0.0018 | −0.0017 | −0.0015 | −0.0023 | −0.0010 | −0.0010 | −0.0010 | −0.0009 | |||||||||||||
| Pakistan | India | Bangladesh | Sri Lanka | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | ||
| Quantiles | Restr. Value | Restr. Value | Restr. Value | Restr. VALUE | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | Restr. Value | |
| 0.1, 0.9 | 1.436 | 1.628 | 1.572 | 1.579 | 0.0063 *** | 0.2959 | 0.2935 | 0.2957 | 0.5917 *** | 0.5897 *** | 0.5912 *** | 0.5898 *** | 0.1353 | 0.1026 | 0.1241 | 0.1315 | |
| 0.1, 0.9 | −0.1143 ** | −0.1230 ** | −0.1236 ** | −0.123 ** | −0.1558 | −0.0332 | −0.0329 | −0.0332 | −0.07910 *** | −0.07886 *** | −0.07907 *** | −0.0788 *** | −0.0186 | −0.0170 | −0.0174 | −0.0182 | |
| 0.1, 0.9 | 0.073 | 0.090 | 0.091 | 0.096 | −0.0021 *** | 0.0055 | 0.0060 | 0.0063 | 0.0033 | 0.0034 | 0.0038 | 0.0039 | 0.0006 | −0.0015 | 0.0005 | 0.0006 | |
| 0.1, 0.9 | 0.032 | 0.045 | 0.043 | 0.044 | −0.0023 | 0.0164 | 0.0184 | 0.0226 | −0.0017 | −0.0017 | −0.0019 | −0.0019 | 0.0004 | −0.0019 | −0.0002 | 0.0004 | |
| 0.1, 0.9 | 0.076 | 0.094 | 0.096 | 0.100 | −0.0114 | 0.0115 | 0.0114 | 0.0113 | 0.01930 ** | 0.02004 ** | 0.02195 ** | 0.0229 ** | −0.0058 | −0.0116 | −0.0072 | −0.0074 | |
| 0.1, 0.9 | 0.0117 *** | 0.0116 *** | 0.0116 *** | 0.0114 *** | −0.0016 *** | 0.0020 | 0.0020 | 0.0020 | 0.0045 | 0.0046 | 0.0045 | 0.0045 | 0.00675 *** | 0.006642 *** | 0.006656 *** | 0.006744 *** | |
| 0.1, 0.9 | −0.031 | −0.034 | −0.033 | −0.034 | −0.0014 | 0.0082 | 0.0083 | 0.0099 | 0.0011 | 0.0012 | 0.0012 | 0.0012 | 0.0015 | 0.0013 | 0.0009 | 0.0015 | |
| 0.1, 0.9 | 0.017 | 0.018 | 0.018 | 0.018 | −0.0032 | 0.0054 | 0.0049 | 0.0046 | 0.02551 ** | 0.02565 ** | 0.02548 ** | 0.02560 ** | −0.0071 | −0.0121 | −0.0077 | −0.0079 | |
| 0.1, 0.9 | −0.094 | −0.084 | −0.086 | −0.086 | 0.1170 | −0.1123 | −0.1230 | −0.1270 | 0.1571 | 0.1536 | 0.1566 | 0.1539 | 0.2527 | 0.2389 | 0.2500 | 0.2565 | |
| 0.1, 0.9 | −0.044 | −0.036 | −0.032 | −0.036 | 0.1053 | −0.0275 | −0.0469 | −0.0546 | −0.0155 | −0.0158 | −0.0177 | −0.0181 | −0.0125 | −0.0160 | −0.0142 | −0.0148 | |
| 0.1, 0.9 | −0.004 | −0.001 | 0.001 | 0.002 | −0.0148 | −0.0116 | −0.0129 | −0.0176 | −0.0435 | −0.0623 | −0.0716 | −0.0727 | 0.3004 | 0.3507 | 0.3364 | 0.3579 | |
| 0.1, 0.9 | 0.127 | 0.164 | 0.200 | 0.208 | 0.1997 | 0.3184 | 0.2723 | 0.2701 | 0.4710 | 0.4847 * | 0.5350 * | 0.5556 * | −0.0363 | −0.1747 | −0.0583 | −0.0542 | |
| 0.1, 0.9 | 0.1091 *** | 0.1081 *** | 0.1080 *** | 0.1079 *** | 0.0516 | −0.0332 | −0.0379 | −0.0403 | −0.0263 | −0.0260 | −0.0263 | −0.0260 | −0.0261 | −0.0278 | −0.0260 | −0.0262 | |
| 0.1, 0.9 | 0.243 | 0.242 | 0.240 | 0.244 | −0.0066 | −0.0141 | −0.0142 | −0.0176 | 0.0667 | 0.0475 | 0.0447 | 0.0464 | 0.4050 | 0.3828 | 0.3927 | 0.4071 | |
| 0.1, 0.9 | 0.341 | 0.370 | 0.384 | 0.387 | 0.1071 | 0.1547 | 0.1193 | 0.1141 | 0.6171 | 0.6144 | 0.6147 * | 0.6149 * | −0.0703 | −0.3357 | −0.1005 | −0.0899 | |
| 0.2, 0.8 | 2.3726 ** | 2.3062 ** | 2.1775 ** | 2.1560 ** | 0.0039 ** | 0.0949 | 0.0897 | 0.0903 | 0.3924 ** | 0.3922 ** | 0.3880 ** | 0.3874 ** | 0.1838 | 0.1566 | 0.1608 | 0.1790 | |
| 0.2, 0.8 | −0.0954 *** | −0.0950 *** | −0.0953 *** | −0.0953 *** | −0.1064 | −0.0105 | −0.0099 | −0.0100 | −0.0532 ** | −0.05318 ** | −0.05266 ** | −0.05256 ** | −0.0254 | −0.0218 | −0.0225 | −0.0249 | |
| 0.2, 0.8 | 0.1843 * | 0.1835 * | 0.18576 * | 0.1897 * | −0.0013 | 0.003426 * | 0.003781 * | 0.003922 * | 0.0019 | 0.0020 | 0.0021 | 0.0022 | −0.0005 | −0.0004 | −0.0006 | −0.0007 | |
| 0.2, 0.8 | 0.144 | 0.142 | 0.140 | 0.142 | −0.0009 | 0.0106 | 0.0109 | 0.0149 | −0.0037 | −0.0038 | −0.0040 | −0.0041 | −0.0047 | −0.0030 | −0.0059 | −0.0056 | |
| 0.2, 0.8 | 0.1863 * | 0.1848 * | 0.1869 * | 0.19079 * | −0.0047 | 0.0041 | 0.0045 | 0.0047 | 0.01924 *** | 0.01988 *** | 0.02182 *** | 0.02273 *** | −0.0005 | −0.0006 | −0.0015 | −0.0015 | |
| 0.2, 0.8 | 0.001 | 0.001 | 0.001 | 0.001 | −0.00116 * | 0.001473 * | 0.001481 * | 0.001477 * | 0.0037 | 0.0037 | 0.0036 | 0.0036 | 0.003833 ** | 0.003849 ** | 0.003822 ** | 0.003853 ** | |
| 0.2, 0.8 | −0.0427 *** | −0.0423 ** | −0.0425 *** | −0.0427 *** | −0.0006 | 0.0053 | 0.0049 | 0.0065 | −0.0008 | −0.0007 | −0.0005 | −0.0005 | −0.0037 | −0.0016 | −0.0045 | −0.0037 | |
| 0.2, 0.8 | 0.004 | 0.004 | 0.003 | 0.003 | −0.0014 | 0.0017 | 0.0017 | 0.0017 | 0.02548 *** | 0.02547 *** | 0.02536 *** | 0.02541 *** | 0.0022 | 0.0018 | 0.0009 | 0.0011 | |
| 0.2, 0.8 | −0.059 | −0.059 | −0.071 | −0.067 | 0.0779 | 0.0045 | 0.0027 | 0.0008 | 0.0646 | 0.0651 | 0.0588 | 0.0582 | 0.1720 | 0.1635 | 0.1715 | 0.1747 | |
| 0.2, 0.8 | 0.127 | 0.127 | 0.135 | 0.136 | 0.1095 | 0.0564 | 0.0631 | 0.0652 | 0.0007 | 0.0007 | 0.0011 | 0.0012 | −0.0155 | −0.0155 | −0.0176 | −0.0183 | |
| 0.2, 0.8 | 0.127 | 0.126 | 0.132 | 0.130 | −0.0049 | −0.0161 | −0.0174 | −0.0219 | −0.1516 * | −0.1541 * | −0.1594 * | −0.1625 * | 0.1236 | 0.1070 | 0.1442 | 0.1541 | |
| 0.2, 0.8 | 0.385 | 0.396 | 0.447 | 0.460 | 0.2051 | 0.490264 ** | 0.486899 * | 0.4985 | 0.3558 *** | 0.36745 *** | 0.4076 *** | 0.4216 *** | 0.1121 | 0.1177 | 0.1145 | 0.1149 | |
| 0.2, 0.8 | −0.034 | −0.034 | −0.033 | −0.033 | 0.0532 | 0.0054 | 0.0083 | 0.0085 | −0.0031 | −0.0031 | −0.0027 | −0.0026 | −0.0293 | −0.0284 | −0.0290 | −0.0292 | |
| 0.2, 0.8 | 0.077 | 0.077 | 0.079 | 0.078 | −0.0022 | −0.0134 | −0.0129 | −0.0162 | −0.0816 | −0.0789 | −0.0682 | −0.0656 | 0.2463 | 0.2169 | 0.2466 | 0.2499 | |
| 0.2, 0.8 | 0.320 | 0.324 | 0.344 | 0.345 | 0.1081 | 0.244894 ** | 0.22041 * | 0.2174 | 0.4597 *** | 0.4594 *** | 0.4621 *** | 0.46045 *** | 0.2238 | 0.2285 | 0.2035 | 0.1970 | |
| 0.3, 0.7 | 2.8838 *** | 2.7196 *** | 2.5787 *** | 2.5211 *** | 0.0037 ** | −0.0845 | −0.0874 | −0.0815 | 0.3735 *** | 0.3731 *** | 0.3687 *** | 0.37186 *** | 0.0600 | 0.0471 | 0.0533 | 0.0712 | |
| 0.3, 0.7 | −0.0760 *** | −0.0749 *** | −0.0765 *** | −0.0788 *** | −0.1289 | 0.0097 | 0.0101 | 0.0094 | −0.04919 *** | −0.0491 *** | −0.04857 *** | −0.04899 *** | −0.0112 | −0.0096 | −0.0104 | −0.0128 | |
| 0.3, 0.7 | 0.2558 *** | 0.2464 *** | 0.2522 *** | 0.2519 *** | −0.0008 | −0.0006 | −0.0006 | −0.0006 | 0.00492 *** | 0.005077 *** | 0.005574 *** | 0.005786 *** | −0.0020 | −0.0021 | −0.0023 | −0.0025 | |
| 0.3, 0.7 | 0.2368 *** | 0.2277 *** | 0.2312 *** | 0.2295 *** | 0.0048 | 0.0080 | 0.0106 | 0.0148 | 0.0030 | 0.0031 | 0.0035 | 0.0035 | −0.008123 * | −0.009526 ** | −0.009849 ** | −0.00957 * | |
| 0.3, 0.7 | 0.2486 *** | 0.2393 *** | 0.2444 *** | 0.2442 *** | −0.0046 | −0.0037 | −0.0049 | −0.0048 | 0.01752 *** | 0.01811 *** | 0.01981 *** | 0.02074 *** | −0.0049 | −0.0050 | −0.0061 | −0.0060 | |
| 0.3, 0.7 | −0.0006 | −0.0005 | −0.001 | −0.001 | −0.00083 * | −0.0002 | −0.0002 | −0.0002 | 0.007251 *** | 0.007247 *** | 0.007239 *** | 0.00722 *** | 0.003459 *** | 0.003245 ** | 0.00324 ** | 0.003273 ** | |
| 0.3, 0.7 | −0.0238 ** | −0.0226 * | −0.02316 * | −0.0235 * | 0.0023 | 0.0039 | 0.0047 | 0.0064 | 0.003936 * | 0.003918 * | 0.003957 * | 0.003886 * | −0.0073 | −0.008747 * | −0.0080 | −0.0070 | |
| 0.3, 0.7 | −0.01007 * | −0.009 | −0.010 | −0.009 | −0.0014 | −0.0021 | −0.0024 | −0.0023 | 0.02222 *** | 0.02223 *** | 0.02203 *** | 0.02223 *** | −0.0023 | −0.0022 | −0.0029 | −0.0024 | |
| 0.3, 0.7 | −0.025 | −0.024 | −0.026 | −0.041 | 0.0221 | 0.0200 | 0.0087 | 0.0079 | 0.0134 | 0.0128 | 0.0218 | 0.0120 | 0.1958 * | 0.1915 * | 0.1998 ** | 0.2023 ** | |
| 0.3, 0.7 | 0.153 | 0.146 | 0.142 | 0.145 | 0.116 *** | −0.0023 | −0.0095 | −0.0102 | 0.01231 * | 0.01275 * | 0.0136 | 0.01463 * | −0.0140 | −0.0148 | −0.0164 | −0.0171 | |
| 0.3, 0.7 | −0.042 | −0.047 | −0.053 | −0.056 | −0.0107 | −0.0193 | −0.0225 | −0.0269 | −0.0420 | −0.0433 | −0.0479 | −0.0495 | 0.2292 | 0.1956 | 0.2207 | 0.2289 | |
| 0.3, 0.7 | 0.415 | 0.392 | 0.416 | 0.428 | 0.271 ** | 0.3048 | 0.2562 | 0.2613 | 0.2004 | 0.2067 | 0.2211 | 0.2357 | −0.0208 | −0.0164 | −0.0289 | −0.0251 | |
| 0.3, 0.7 | −0.001 | −0.002 | −0.002 | −0.002 | 0.053 ** | −0.0160 | −0.0160 | −0.0160 | 0.0093 | 0.0094 | 0.0088 | 0.0095 | −0.0237 | −0.0244 | −0.0246 | −0.0247 | |
| 0.3, 0.7 | −0.129 | −0.127 | −0.109 | −0.107 | −0.0081 | −0.0138 | −0.0151 | −0.0183 | −0.0036 | −0.0035 | −0.0052 | −0.0036 | 0.3213 | 0.2693 | 0.2709 | 0.2730 | |
| 0.3, 0.7 | 0.371 | 0.337 | 0.340 | 0.338 | 0.142 ** | 0.1554 | 0.1193 | 0.1172 | 0.2497 | 0.2492 | 0.2411 | 0.2481 | −0.0419 | −0.0317 | −0.0508 | −0.0429 |
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | |
| Long-Run Sign-Based Asymmetries | ||||||||||||||||||||
| r = 0.1 | 0.983 | 0.99 | 1.21 | 1.27 | 2.10 ** | 1.76 | 1.83 * | 1.86 * | 1.88 * | 5.98 *** | 2.68 ** | 3.847 *** | 2.94 ** | 2.74 ** | 8.29 *** | 3.12 *** | 2.99 *** | 3.847 *** | 3.63 *** | 8.746 *** |
| r = 0.2 | 1.07 | 1.2 | 1.09 | 0.99 | 2.99 *** | 6.836 *** | 8.19 *** | 7.827 *** | 6.10 *** | 4.10 *** | 5.17 *** | 5.297 *** | 7.10 *** | 11.23 *** | 4.82 *** | 8.286 *** | 11.13 *** | 10.50 *** | 10.012 *** | 5.87 *** |
| r = 0.3 | 0.67 | 0.1 | 0.86 | 0.99 | 1.6 | 4.76 *** | 4.99 *** | 8.19 *** | 8.27 *** | 2.90 *** | 3.88 *** | 4.062 *** | 4.25 *** | 4.88 *** | 1.99 ** | 2.187 ** | 3.32 *** | 8.726 *** | 11.22 *** | 1.87 * |
| r = 0.7 | 1.81 * | 1.69 | 1.37 | 1.79 * | 3.87 *** | 2.01 ** | 1.9 ** | 2.53 *** | 2.91 *** | 1.19 | 3.87 *** | 4.10 *** | 2.10 ** | 3.2 *** | 5.09 *** | 0.19 | 0.1 | 1.53 | 1.244 | 0.71 |
| r = 0.8 | 1.91 ** | 2.01 ** | 2.87 *** | 1.90 ** | 5.28 *** | 3.12 *** | 4.87 *** | 2.37 *** | 3.001 *** | 6.12 *** | 1.28 | 1.75 | 0.87 | 0.22 | 1.1 | 0.65 | 1.72 | 1.66 | 1.01 | 1.002 |
| r = 0.9 | 1.62 | 0.58 | 0.22 | 1.7 | 3.45 *** | 3.72 *** | 5.10 *** | 5.22 *** | 6.09 *** | 2.10 ** | 0.99 | 1.61 | 1.71 | 1.62 | 1.5 | 2.04 *** | 2.6 ** | 1.99 ** | 2.01 ** | 1.90 ** |
| Short-run Sign-based asymmetries | ||||||||||||||||||||
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||
| 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | COVID-19 | |
| r = 0.1 | 2.77 *** | 3.23 *** | 3.78 *** | 4.10 *** | 3.87 *** | 0.22 | 1.09 | 0.81 | 1.65 | 0.19 | 4.89 *** | 6.04 *** | 9.82 *** | 11.92 *** | 3.99 *** | 1.48 | 1.2 | 0.514 | 0.77 | 1.55 |
| r = 0.2 | 1.78 * | 1.67 | 1.89 * | 1.09 | 4.92 *** | 1.63 | 1.34 | 1.62 | 1.66 | 0.55 | 5.21 *** | 7.91 *** | 3.12 *** | 6.38 *** | 5.50 *** | 1.66 | 0.99 | 0.87 | 0.76 | 1.61 |
| r = 0.3 | 1.91 ** | 1.79 * | 1.81 * | 1.01 | 7.10 *** | 0.192 | 0.918 | 1.052 | 1.33 | 1.69 | 7.10 *** | 11.2 *** | 10.5 *** | 8.01 *** | 3.17 *** | 1.027 | 1.61 | 1.23 | 1.44 | 1.4 |
| r = 0.7 | 1.22 | 0.87 | 0.99 | 0.1 | 1.2 | 6.92 *** | 6.5 *** | 6.89 *** | 9.10 *** | 4.78 *** | 0.33 | 1.01 | 1.6 | 1.69 | 0.9 | 1.66 | 0.667 | 0.77 | 0.81 | 1.39 |
| r = 0.8 | 1.99 ** | 2.55 ** | 2.41 ** | 3.8 *** | 1.01 | 8.52 *** | 8.11 *** | 9.22 *** | 11.1 *** | 5.99 *** | 1.22 | 1.35 | 0.99 | 1.01 | 1.01 | 1.88 ** | 2.3 ** | 2.76 *** | 3.6 *** | 5.10 *** |
| r = 0.9 | 4.87 *** | 4.31 *** | 4.72 *** | 4.5 *** | 2.2 ** | 8.34 *** | 5.10 *** | 3.76 *** | 4.22 *** | 6.10 *** | 1.77 | 1.24 | 1.33 | 1.48 | 1.57 | 3.87 *** | 4.10 *** | 5.87 *** | 7.10 *** | 7.2 *** |
| Pakistan | India | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e = 1 | e = 1.5 | e = 1 | e = 1.5 | ||||||||||
| l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | ||
| FERP-3rd month to SMRs | 0.0993 * | 0.736 | 0.019 ** | 0.0192 ** | 0.0027 *** | 0.0019 *** | FERP-3rd month to SMRs | 0.00683 *** | 0.001 *** | 0.002 ** | 0.001 *** | 0.00692 *** | 0.0032 *** |
| FERP-6th month to SMRs | 0.067 * | 0.054 * | 0.0021 *** | 0.032 ** | 0.0099 *** | 0.0082 *** | FERP-6th month to SMRs | 0.055 * | 0.0837 * | 0.015 ** | 0.049 ** | 0.0019 *** | 0.001 *** |
| FERP-9th month to SMRs | 0.071 * | 0.22 | 0.003 *** | 0.0152 ** | 0.0029 *** | 0.0069 *** | FERP-9th month to SMRs | 0.012 ** | 0.099 * | 0.0066 *** | 0.01 ** | 0.002 *** | 0.0083 *** |
| FERP-12th month to SMRs | 0.058 * | 0.001 *** | 0.0092 *** | 0.011 ** | 0.029 ** | 0.002 *** | FERP-12th month to SMRs | 0.034 ** | 0.1 | 0.0882 * | 0.038 ** | 0.00778 *** | 0.00192 *** |
| Bangladesh | Sri Lanka | ||||||||||||
| e = 1 | e = 1.5 | e = 1 | e = 1.5 | ||||||||||
| l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | l = 1 | l = 2 | l = 3 | ||
| FERP-3rd month to SMRs | 0.0538 * | 0.0488 ** | 0.009 *** | 0.0016 ** | 0.082 * | 0.0166 ** | FERP-3rd month to SMRs | 0.0186 ** | 0.0073 *** | 0.00192 *** | 0.00382 ** | 0.0067 *** | 0.0012 *** |
| FERP-6th month to SMRs | 0.0273 ** | 0.0281 ** | 0.049 ** | 0.0079 *** | 0.0019 *** | 0.047 ** | FERP-6th month to SMRs | 0.023 ** | 0.017 ** | 0.0088 *** | 0.012 ** | 0.00182 *** | 0.0019 *** |
| FERP-9th month to SMRs | 0.079 * | 0.036 ** | 0.001 *** | 0.0012 *** | 0.0001 *** | 0.00155 *** | FERP-9th month to SMRs | 0.837 | 0.09 * | 0.012 ** | 0.01 ** | 0.00610 *** | 0.0011 *** |
| FERP-12th month to SMRs | 0.010 ** | 0.008 *** | 0.031 ** | 0.00554 *** | 0.00285 *** | 0.0072 *** | FERP-12th month to SMRs | 0.0192 ** | 0.087 * | 0.0069 *** | 0.02 ** | 0.0049 *** | 0.002 *** |
References
- Dornbusch, R. Expectations and Exchange Rate Dynamics. J. Political Econ. 1976, 84, 1161–1176. [Google Scholar] [CrossRef]
- Dornbusch, R.; Fischer, S. Exchange Rates and the Current Account. Am. Econ. Rev. 1980, 70, 860–971. [Google Scholar]
- Suleman, M.T.; Tabash, M.I.; Sheikh, U.A. Do stock market fluctuations lead to currency deflation in the South Asian region? Evidence beyond symmetry. Int. J. Financ. Econ. 2024, 29, 1432–1450. [Google Scholar] [CrossRef]
- Tabash, M.I.; Sheikh, U.A.; Matar, A.; Ahmed, A.; Tran, D.K. Do Financial Crises Matter for Nonlinear Exchange Rate and Stock Market Cointegration? A Heterogeneous Nonlinear Panel Data Model with PMG Approach. Int. J. Financ. Stud. 2023, 11, 7. [Google Scholar] [CrossRef]
- Demirguc-Kunt, A.; Pedraza, A.; Ruiz-Ortega, C. Banking Sector Performance During the COVID-19 Crisis. J. Bank. Financ. 2021, 133, 106305. [Google Scholar] [CrossRef]
- Kassouri, Y.; Altıntaş, H. Threshold cointegration, nonlinearity, and frequency domain causality relationship between stock price and Turkish Lira. Res. Int. Bus. Financ. 2020, 52, 101097. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Wiseman, R.M.; Gomez-Mejia, L.R. A Behavioral Agency Model of Managerial Risk Taking. Acad. Manag. Rev. 1998, 23, 133–153. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Kyei, C.K.; Gupta, R.; Olson, E. Investor sentiment and dollar-pound exchange rate returns: Evidence from over a century of data using a cross-quantilogram approach. Financ. Res. Lett. 2021, 38, 101504. [Google Scholar] [CrossRef]
- Sheikh, U.A.; Asadi, M.; Roubaud, D.; Hammoudeh, S. Global uncertainties and Australian financial markets: Quantile time-frequency connectedness. Int. Rev. Financ. Anal. 2024, 92, 103098. [Google Scholar] [CrossRef]
- Kayani, U.; Sheikh, U.A.; Khalfaoui, R.; Roubaud, D.; Hammoudeh, S. Impact of Climate Policy Uncertainty (CPU) and global Energy Uncertainty (EU) news on U.S. sectors: The moderating role of CPU on the EU and U.S. sectoral stock nexus. J. Environ. Manag. 2024, 366, 121654. [Google Scholar] [CrossRef] [PubMed]
- Tabash, M.I.; Sheikh, U.A.; Mensi, W.; Kang, S.H. Quantile-based extended joint connectedness between trade policy uncertainty and Gulf Cooperation Council Islamic sectoral volatility. Borsa Istanb. Rev. 2024. [Google Scholar] [CrossRef]
- Suleman, M.T.; Sheikh, U.A.; Galariotis, E.C.; Roubaud, D. The impact of bitcoin fear and greed on good and bad network connectedness: The case of the US sectoral high frequency returns. In Annals of Operations Research; Springer: New York, NY, USA, 2023. [Google Scholar]
- Hashmi, S.M.; Chang, B.H. Asymmetric effect of macroeconomic variables on the emerging stock indices: A quantile ARDL approach. Int. J. Financ. Econ. 2021. [Google Scholar] [CrossRef]
- Ain Shahrier, N. Contagion effects in ASEAN-5 exchange rates during the COVID-19 pandemic. N. Am. J. Econ. Financ. 2022, 62, 101707. [Google Scholar] [CrossRef]
- Aquilante, T.; Di Pace, F.; Masolo, R.M. Exchange-rate and news: Evidence from the COVID pandemic. Econ. Lett. 2022, 213, 110390. [Google Scholar] [CrossRef]
- Narayanan, S.; Raghunathan, K.; Rashid, S.; Winter-Nelson, A. Lessons from a time of upheaval: COVID-19 in South Asia. Appl. Econ. Perspect. Policy 2023, 45, 2078–2093. [Google Scholar] [CrossRef]
- Jabeen, S.; Farhan, M.; Zaka, M.A.; Fiaz, M.; Farasat, M. COVID and World Stock Markets: A Comprehensive Discussion. Front. Psychol. 2022, 12, 763346. [Google Scholar] [CrossRef]
- Rahman, M.A.; Khudri, M.M.; Kamran, M.; Butt, P. A note on the relationship between COVID-19 and stock market return: Evidence from South Asia. Int. J. Islam. Middle East. Financ. Manag. 2022, 15, 359–371. [Google Scholar] [CrossRef]
- Dumitrescu, E.-I.; Hurlin, C. Testing for Granger non-causality in heterogeneous panels. Econ. Model. 2012, 29, 1450–1460. [Google Scholar] [CrossRef]
- Ashraf, B.N. Stock markets’ reaction to COVID-19: Cases or fatalities? Res. Int. Bus. Financ. 2020, 54, 101249. [Google Scholar] [CrossRef]
- Baek, S.; Mohanty, S.K.; Glambosky, M. COVID-19 and stock market volatility: An industry level analysis. Financ. Res. Lett. 2020, 37, 101748. [Google Scholar] [CrossRef] [PubMed]
- Ftiti, Z.; Ben Ameur, H.; Louhichi, W. Does non-fundamental news related to COVID-19 matter for stock returns? Evidence from Shanghai stock market. Econ. Model. 2021, 99, 105484. [Google Scholar] [CrossRef] [PubMed]
- Topcu, M.; Gulal, O.S. The impact of COVID-19 on emerging stock markets. Financ. Res. Lett. 2020, 36, 101691. [Google Scholar] [CrossRef] [PubMed]
- Rouatbi, W.; Demir, E.; Kizys, R.; Zaremba, A. Immunizing markets against the pandemic: COVID-19 vaccinations and stock volatility around the world. Int. Rev. Financ. Anal. 2021, 77, 101819. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.; Levine, R.; Lin, C.; Xie, W. Corporate immunity to the COVID-19 pandemic. J. Financ. Econ. 2021, 141, 802–830. [Google Scholar] [CrossRef]
- Shahbaz, M.; Sheikh, U.A.; Tabash, M.I.; Jiao, Z. Shock transmission between climate policy uncertainty, financial stress indicators, oil price uncertainty and industrial metal volatility: Identifying moderators, hedgers and shock transmitters. Energy Econ. 2024, 107732. [Google Scholar] [CrossRef]
- Iacopini, M.; Poon, A.; Rossini, L.; Zhu, D. Bayesian mixed-frequency quantile vector autoregression: Eliciting tail risks of monthly US GDP. J. Econ. Dyn. Control. 2023, 157, 104757. [Google Scholar] [CrossRef]
- Pal, D.; Mitra, S.K. Asymmetric impact of crude price on oil product pricing in the United States: An application of multiple threshold nonlinear autoregressive distributed lag model. Econ. Model. 2015, 51, 436–443. [Google Scholar] [CrossRef]
- Pal, D.; Mitra, S.K. Asymmetric oil product pricing in India: Evidence from a multiple threshold nonlinear ARDL model. Econ. Model. 2016, 59, 314–328. [Google Scholar] [CrossRef]
- Pal, D.; Mitra, S.K. Asymmetric oil price transmission to the purchasing power of the U.S. dollar: A multiple threshold NARDL modelling approach. Resour. Policy 2019, 64, 101508. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- Sim, N.; Zhou, H. Oil prices, US stock return, and the dependence between their quantiles. J. Bank. Financ. 2015, 55, 1–8. Available online: https://econpapers.repec.org/RePEc:eee:jbfina:v:55:y:2015:i:c:p:1-8 (accessed on 11 July 2024). [CrossRef]
- Cho, J.S.; Kim, T.; Shin, Y. Quantile cointegration in the autoregressive distributed-lag modeling framework. J. Econom. 2015, 188, 281–300. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Koenker, R.; Xiao, Z. Quantile Autoregression. J. Am. Stat. Assoc. 2006, 101, 980–990. [Google Scholar] [CrossRef]
- Andriansyah, A.; Messinis, G. Stock prices, exchange rates and portfolio equity flows: A Toda-Yamamoto Panel Causality Test. J. Econ. Stud. 2019, 46, 399–421. [Google Scholar] [CrossRef]
- Anisak, N.; Mohamad, A. Foreign Exchange Exposure of Indonesian Listed Firms. Glob. Bus. Rev. 2019, 21, 918–936. [Google Scholar] [CrossRef]
- Wei, Y.; Qin, S.; Li, X.; Zhu, S.; Wei, G. Oil price fluctuation, stock market and macroeconomic fundamentals: Evidence from China before and after the financial crisis. Financ. Res. Lett. 2019, 30, 23–29. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, S.-W.; Wu, A.-C. The foreign exchange and stock market nexus: New international evidence. Int. Rev. Econ. Financ. 2020, 67, 240–266. [Google Scholar] [CrossRef]
- Hashmi, S.M.; Chang, B.H.; Huang, L.; Uche, E. Revisiting the relationship between oil prices, exchange rate, and stock prices: An application of quantile ARDL model. Resour. Policy 2022, 75, 102543. [Google Scholar] [CrossRef]
- Salisu, A.A.; Isah, K.; Ogbonnaya-Orji, N. A firm level analysis of asymmetric response of U.S. stock returns to exchange rate movements. Int. J. Financ. Econ. 2022, 27, 1220–1239. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, D.; Hau, L.; Wu, H.; Ye, F. Time-frequency effect of crude oil and exchange rates on stock markets in BRICS countries: Evidence from wavelet quantile regression analysis. N. Am. J. Econ. Financ. 2022, 61, 101708. [Google Scholar] [CrossRef]
- Ding, L. Conditional correlation between exchange rates and stock prices. Q. Rev. Econ. Financ. 2021, 80, 452–463. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, X.; Zhang, S. The effects of exchange rate fluctuations on the stock market and the affecting mechanisms: Evidence from BRICS countries. N. Am. J. Econ. Financ. 2021, 56, 101340. [Google Scholar] [CrossRef]
- Khan, M.K.; Teng, J.-Z.; Khan, M.I.; Khan, M.F. Stock market reaction to macroeconomic variables: An assessment with dynamic autoregressive distributed lag simulations. Int. J. Financ. Econ. 2021, 28, 2436–2448. [Google Scholar] [CrossRef]
- Kumar, S.; Choudhary, S.; Singh, G.; Singhal, S. Crude oil, gold, natural gas, exchange rate and indian stock market: Evidence from the asymmetric nonlinear ARDL model. Resour. Policy 2021, 73, 102194. [Google Scholar] [CrossRef]
- Salisu, A.A.; Vo, X.V. The behavior of exchange rate and stock returns in high and low interest rate environments. Int. Rev. Econ. Financ. 2021, 74, 138–149. [Google Scholar] [CrossRef]
- Wong, H.T. Real exchange rate returns and real stock price returns. Int. Rev. Econ. Financ. 2017, 49, 340–352. [Google Scholar] [CrossRef]
- Cho, J.S.; Greenwood-Nimmo, M.; Shin, Y. Recent developments of the autoregressive distributed lag modelling framework. J. Econ. Surv. 2021, 37, 7–32. [Google Scholar] [CrossRef]
- Shin, Y.; Yu, B.; Greenwood-Nimmo, M. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications; Springer: New York, NY, USA, 2014; pp. 281–314. [Google Scholar]
- Chang, H.-W.; Chang, T.; Wang, M.-C. Revisit the impact of exchange rate on stock market returns during the pandemic period. N. Am. J. Econ. Financ. 2024, 70, 102068. [Google Scholar] [CrossRef]
- Xiong, Y.; Shen, J.; Yoon, S.-M.; Dong, X. Macroeconomic determinants of the long-term correlation between stock and exchange rate markets in China: A DCC-MIDAS-X approach considering structural breaks. Financ. Res. Lett. 2024, 61, 105020. [Google Scholar] [CrossRef]
- Branson, W.H. A Model of Exchange-Rate Determination with Policy Reaction: Evidence From Monthly Data; National Bureau of Economic Research: Cambridge, MA, USA, 1983. [Google Scholar]
- Sokhanvar, A.; Çiftçioğlu, S.; Hammoudeh, S. Comparative analysis of the exchange rates-stock returns nexus in commodity-exporters and -importers before and during the war in Ukraine. Res. Int. Bus. Financ. 2024, 67, 102152. [Google Scholar] [CrossRef]
- Tabash, M.I.; Sheikh, U.A.; Asad, M.; Khan, A.A. Do positive and negative variations in stock indexes lead to depreciation in local currencies? A beyond symmetrical evidence from ASEAN-5 region. Econ. Res.-Ekon. Istraživanja 2023, 36, 2208635. [Google Scholar] [CrossRef]
- Evans, M.D.D.; Lyons, R.K. Order flow and exchange rate dynamics. J. Political Econ. 2002, 110, 170–180. [Google Scholar] [CrossRef]
- Mohamed Dahir, A.; Mahat, F.; Ab Razak, N.H.; Bany-Ariffin, A.N. Revisiting the dynamic relationship between exchange rates and stock prices in BRICS countries: A wavelet analysis. Borsa Istanb. Rev. 2018, 18, 101–113. [Google Scholar] [CrossRef]
- Areli Bermudez Delgado, N.; Bermudez Delgado, E.; Saucedo, E. The relationship between oil prices, the stock market and the exchange rate: Evidence from Mexico. N. Am. J. Econ. Financ. 2018, 45, 266–275. [Google Scholar] [CrossRef]
- Roubaud, D.; Arouri, M. Oil prices, exchange rates and stock markets under uncertainty and regime-switching. Financ. Res. Lett. 2018, 27, 28–33. [Google Scholar] [CrossRef]
- Blau, B.M. Exchange rate volatility and the stability of stock prices. Int. Rev. Econ. Financ. 2018, 58, 299–311. [Google Scholar] [CrossRef]
- Wen Chang, H.; Chang, T. How oil price and exchange rate affect stock price in China using Bayesian Quantile_on_Quantile with GARCH approach. N. Am. J. Econ. Financ. 2023, 64, 101879. [Google Scholar] [CrossRef]
- Chen, L.; Wen, F.; Li, W.; Yin, H.; Zhao, L. Extreme risk spillover of the oil, exchange rate to Chinese stock market: Evidence from implied volatility indexes. Energy Econ. 2022, 107, 105857. [Google Scholar] [CrossRef]
- Xu, X.; Huang, S.; An, H. The dynamic moderating function of the exchange rate market on the oil-stock nexus. Int. Rev. Financ. Anal. 2022, 81, 102126. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A.; Ugolini, A. Downside and upside risk spillovers between exchange rates and stock prices. J. Bank. Financ. 2016, 62, 76–96. [Google Scholar] [CrossRef]
- Asadi, M.; Sheikh, U.A.; Balcilar, M.; Roubaud, D.; Ghasemi, H.R. Are there inextricable connections among automobile stocks, crude oil, steel, and the US dollar? Energy Econ. 2023, 128, 107176. [Google Scholar] [CrossRef]
- El-Masry, A.A.; Badr, O.M. Stock market performance and foreign exchange market in Egypt: Does 25th January revolution matter? Int. J. Emerg. Mark. 2021, 16, 1048–1076. [Google Scholar] [CrossRef]
- Nusair, S.A.; Olson, D. Dynamic relationship between exchange rates and stock prices for the G7 countries: A nonlinear ARDL approach. J. Int. Financ. Mark. Inst. Money 2022, 78, 101541. [Google Scholar] [CrossRef]
- Kim, T.-H.; White, H. Estimation, Inference, and Specification Testing for Possibly Misspecified Quantile Regression; Emerald Group Publishing Limited: Leeds, UK, 2003. [Google Scholar]
- Newey, W.K.; Powell, J.L. Asymmetric least squares estimation and testing. Econom. J. Econom. Soc. 1987, 55, 819–847. [Google Scholar]
- Daniels, J.P.; VanHoose, D.D. Global Economic Issues and Policies; Routledge: London, UK, 2014. [Google Scholar]
- Stephens, J.J. Managing Currency Risk: Using Financial Derivatives; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Shapiro, A.C.; Hanouna, P. Multinational Financial Management; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Liao, J.; Zhu, X.; Chen, J. Dynamic spillovers across oil, gold and stock markets in the presence of major public health emergencies. Int. Rev. Financ. Anal. 2021, 77, 101822. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Brock, W.A.; Dechert, W.; Scheinkman, J.A.; LeBaron, B. A test for A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Hui, Y.; Wong, W.-K.; Bai, Z.; Zhu, Z.-Z. A new nonlinearity test to circumvent the limitation of Volterra expansion with application. J. Korean Stat. Soc. 2017, 46, 365–374. [Google Scholar] [CrossRef]
- Chaudhry, A.; Bukhari, S.K.H. A structural VAR analysis of the impact of macroeconomic shocks on Pakistan’s textile exports. Econ. Model. 2013, 32, 302–315. [Google Scholar] [CrossRef]
- Al-Awadhi, A.M.; Alsaifi, K.; Al-Awadhi, A.; Alhammadi, S. Death and contagious infectious diseases: Impact of the COVID-19 virus on stock market returns. J. Behav. Exp. Financ. 2020, 27, 100326. [Google Scholar] [CrossRef] [PubMed]
- Chebbi, K.; Ammer, M.A.; Hameed, A. The COVID-19 pandemic and stock liquidity: Evidence from S&P 500. Q. Rev. Econ. Financ. 2021, 81, 134–142. [Google Scholar] [CrossRef]
- Bai, Z.; Hui, Y.; Jiang, D.; Lv, Z.; Wong, W.-K.; Zheng, S. A new test of multivariate nonlinear causality. PLoS ONE 2018, 13, e0185155. [Google Scholar] [CrossRef]
- Tabash, M.I.; Sheikh, U.A.; Roubaud, D.; Galariotis, E.; Aytaç, B. Exploring the influence of Silicon Valley Bank default and U.S. financial stress on sectoral interactions and effective hedging strategies. Appl. Econ. 2024, 1–25. [Google Scholar] [CrossRef]
- Chen, B.; Sun, Y. Financial market connectedness between the U.S. and China: A new perspective based on non-linear causality networks. J. Int. Financ. Mark. Inst. Money 2024, 90, 101886. [Google Scholar] [CrossRef]
- Tian, M.; El Khoury, R.; Alshater, M.M. The nonlinear and negative tail dependence and risk spillovers between foreign exchange and stock markets in emerging economies. J. Int. Financ. Mark. Inst. Money. 2023, 82, 101712. [Google Scholar] [CrossRef]
- Salisu, A.A.; Ayinde, T.O.; Gupta, R.; Wohar, M.E. Global evidence of the COVID-19 shock on real equity prices and real exchange rates: A counterfactual analysis with a threshold-augmented GVAR model. Financ. Res. Lett. 2022, 47, 102519. [Google Scholar] [CrossRef]
| Pakistan | India | Bangladesh | Sri Lanka | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LNSI | Ln (FERP3M) | Ln (FERP6M) | Ln (FERP9M) | Ln (FERP12M) | LNSI | Ln (FERP3M) | Ln (FERP6M) | Ln (FERP9M) | Ln (FERP12M) | LNSI | Ln (FERP3M) | Ln (FERP6M) | Ln (FERP9M) | Ln (FERP12M) | LNSI | Ln (FERP3M) | Ln (FERP6M) | Ln (FERP9M) | Ln (FERP12M) | ||||
| Mean | 7.63 | −8.95 | −8.65 | −7.849 | −7.56 | 8.68 | −8.97 | −8.68 | −7.87 | −7.58 | 7.632494 | −8.91 | −8.63 | −7.821 | −7.53 | 7.973 | −9.54 | −9.27 | −8.45 | −8.16 | |||
| Median | 7.69 | −8.95 | −8.66 | −7.85 | −7.56 | 8.74 | −8.97 | −8.691 | −7.88 | −7.59 | 7.69 | −8.92 | −8.63 | −7.82 | −7.54 | 7.97 | −9.55 | −9.26 | −8.45 | −8.16 | |||
| Maximum | 7.93 | −8.72 | −8.43 | −7.62 | −7.33 | 8.99 | −8.70 | −8.42 | −7.60 | −7.32 | 7.93 | −8.73 | −8.44 | −7.63 | −7.35 | 8.44 | −9.113 | −8.82 | −8.01 | −7.73 | |||
| Minimum | 7.09 | −9.14 | −8.85 | −8.043 | −7.75 | 8.07 | −9.081 | −8.79 | −7.98 | −7.69 | 7.09 | −9.002 | −8.715 | −7.907 | −7.61 | 7.43 | −9.81 | −9.52 | −8.71 | −8.42 | |||
| Std. Dev. | 0.23 | 0.099 | 0.099 | 0.099 | 0.099 | 0.23 | 0.052 | 0.052 | 0.052 | 0.052 | 0.22 | 0.043 | 0.0433 | 0.043 | 0.043 | 0.219 | 0.088 | 0.088 | 0.089 | 0.089 | |||
| Skewness | −0.62 | 0.020 | 0.020 | 0.021 | 0.022 | −0.547 | 2.255 | 2.240 | 2.16 | 2.124 | −0.63 | 1.993 | 1.989 | 1.972 | 1.956 | 0.113 | 1.31 | 1.30 | 1.27 | 1.26 | |||
| Kurtosis | 2.19 | 2.045 | 2.045 | 2.051 | 2.054 | 2.09 | 13.38 | 13.28 | 13.05 | 12.88 | 2.250 | 8.12 | 8.11 | 8.089 | 8.056 | 2.367 | 7.98 | 7.964 | 7.85 | 7.78 | |||
| Jarque–Bera | 36.72 | 15.20 | 15.16 | 14.99 | 14.89 | 46.84 | 2974.09 | 2919.60 | 2783.06 | 2686.41 | 34.95 | 676.02 | 673.85 | 665.36 | 655.73 | 9.516 | 668.01 | 662.51 | 633.09 | 616.06 | |||
| Probability | 0.000 | 0.0005 | 0.0005 | 0.0005 | 0.000 | 0.000 | 0.000 | 0.0000 | 0.000 | 0.000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.000 | 0.008 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |||
| Sum | 3044.91 | −3569.54 | −3454.85 | −3131.77 | −3017.28 | 4846.6 | −4997.89 | −4837.97 | −4386.9 | −4227.17 | 2938.51 | −3433.82 | −3323.15 | −3011.42 | −2900.88 | 4026.71 | −4821.55 | −4676.4 | −4267.63 | −4122.78 | |||
| Sum Sq. Dev. | 19.99 | 3.97 | 3.96 | 3.95 | 3.945 | 30.108 | 1.506 | 1.515 | 1.534 | 1.550 | 19.03 | 0.72 | 0.723 | 0.728 | 0.72 | 24.38 | 3.95 | 3.96 | 3.99 | 4.009 | |||
| Observations | 399 | 399 | 399 | 399 | 399 | 558 | 557 | 557 | 557 | 557 | 385 | 385 | 385 | 385 | 385 | 505 | 505 | 505 | 505 | 505 | |||
| ADF (1st diff) | −20.98 *** | −11.89 *** | −12.10 *** | −9.83 *** | −10.50 *** | −7.17 *** | −8.09 *** | −8.11 *** | −8.13 *** | −8.96 *** | −23.90 *** | −19.55 *** | −22.80 ** | −22.90 *** | −25.90 *** | −27.90 *** | −18.75 *** | −18.90 *** | −18.92 *** | −20.10 *** | |||
| PP (1st diff) | −21.1 *** | −19.90 *** | −21.50 *** | −20.90 *** | −22.60 *** | −25.43 *** | −23.17 *** | −23.52 *** | −25.83 *** | −23.10 *** | −25.80 *** | −19.50 *** | −21.73 *** | −22.4 *** | −26.90 *** | −27.1 *** | −19.10 *** | −19.15 *** | −20.80 *** | −21.60 *** | |||
| KPSS (1st diff) | 0.15 | 0.11 | 0.18 | 0.15 | 0.30 | 0.12 | 0.06 | 0.05 | 0.023 | 0.030 | 0.015 | 0.05 | 0.068 | 0.090 | 0.095 | 0.045 | 0.015 | 0.095 | 0.011 | 0.05 | |||
| Variables | Pakistan | India | Bangladesh | Sri Lanka | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | FERP-3M | FERP-6M | FERP-9M | FERP-12M | |||
| −0.270 ** | −0.2627 *** | −0.2414 *** | −0.2340 *** | 0.0953 | 0.089468 | 0.09788 | 0.09757 | −0.11182 | −0.10589 | −0.08773 | −0.08208 | 0.162565 | 0.161059 | 0.157351 | 0.156171 | |||
| 0.0024 | 0.002501 | 0.00251 | 0.002525 | −0.0143 *** | −0.01435 *** | −0.01431 *** | −0.01432 *** | −0.00796 | −0.00795 | −0.0079 | −0.0079 | −0.0138 ** | −0.0138 *** | −0.01382 *** | −0.01381 | |||
| −0.0269 | −0.027 | −0.0269 | −0.02702 | −0.00205 | −0.00284 | −0.00201 | −0.00215 | −0.01894 | −0.01888 | −0.01846 | −0.01841 | 0.006179 | 0.006207 | 0.006384 | 0.006475 | |||
| 0.001668 ** | 0.001669 ** | 0.001675 *** | 0.00167 *** | 0.00078 ** | 0.000787 ** | 0.000788 *** | 0.000788 *** | 0.00072 | 0.00072 | 0.000722 | 0.00072 | 0.00126 *** | 0.00126 *** | 0.00126 *** | 0.00126 | |||
| −0.1127 ** | −0.1127 ** | −0.1126 ** | −0.1125 *** | −0.1128 *** | −0.1117 *** | −0.1130 ** | −0.1125 *** | 0.1350 *** | 0.1350 *** | 0.1350 *** | 0.135059 | |||||||
| −0.1047 *** | −0.1049 *** | −0.105 *** | −0.1064 *** | 0.030759 | −0.1472 *** | −0.1432 ** | −0.1408 *** | −0.3484 *** | −0.3475 *** | −0.3410 *** | −0.3412 *** | −0.04226 | −0.04218 | −0.04185 | −0.04168 | |||
| 0.009251 | 0.009 | 0.00106 | 0.001056 | −0.0351 *** | −0.0340 *** | −0.0350 *** | −0.0349 *** | −0.00294 ** | −0.00294 ** | −0.0028 ** | −0.0005 ** | −0.0004 ** | −0.0035 *** | −0.00046 ** | −0.0035 | |||
| 0.0024 | 0.002 | 0.0025 | 0.0025 | −0.01 | −0.0143 *** | −0.01431 *** | −0.01432 *** | −0.007 | −0.0079 | −0.0079 | −0.007 | −0.013 ** | −0.013 *** | −0.00138 ** | −0.0138 ** | |||
| DW | 1.99 | 2.01 | 1.89 | 1.95 | 2.001 | 2.05 | 2.12 | 2.15 | 1.99 | 2.1 | 1.8 | 2.2 | 1.9 | 2.1 | 2.2 | 2.3 | ||
| BP test | 9.62 *** | 11.625 *** | 8.73 *** | 10.21 *** | 7.32 *** | 8.62 *** | 9.12 *** | 9.10 *** | 6.63 *** | 6.87 *** | 7.7 *** | 8.9 *** | 11.2 *** | 12.3 *** | 11.90 *** | 12.50 *** | ||
| CUSUM | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | Stable | ||
| RR test | 2.63 *** | 2.2 *** | 3.15 *** | 2.21 *** | 2.4 *** | 3.39 *** | 2.1 *** | 2.55 *** | 2.2 *** | 2.76 *** | 2.75 *** | 2.6 *** | 2.1 *** | 2.33 *** | 2.5 *** | 2.2 *** | ||
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Absolute Returns | FERP-3M | FERP-6M | FERP-9M | FERP-12M | Absolute Returns | FERP-3M | FERP-6M | FERP-9M | FERP-12M | Absolute Returns | FERP-3M | FERP-6M | FERP-9M | FERP-12M | Absolute Returns | FERP-3M | FERP-6M | FERP-9M | FERP-12M | |
| Dimension | BDS Statistic | BDS Statistic | BDS Statistic | BDS Statistic | ||||||||||||||||
| 2 | 0.029 *** | 0.193 *** | 0.193 *** | 0.192 *** | 0.192 *** | 0.032 *** | 0.194 *** | 0.197 *** | 0.1945 *** | 0.1938 *** | 0.032 *** | 0.1853 *** | 0.185 *** | 0.190 *** | 0.1943 *** | 0.0474 *** | 0.189 *** | 0.189 *** | 0.189 *** | 0.188 *** |
| 3 | 0.046 *** | 0.325 *** | 0.325 *** | 0.324 *** | 0.324 *** | 0.060 *** | 0.329 *** | 0.333 *** | 0.329 *** | 0.328 *** | 0.049 *** | 0.313 *** | 0.314 *** | 0.323 *** | 0.329 *** | 0.0881 *** | 0.318 *** | 0.318 *** | 0.317 *** | 0.317 *** |
| 4 | 0.0613 *** | 0.417 *** | 0.417 *** | 0.416 *** | 0.414 *** | 0.0716 *** | 0.423 *** | 0.426 *** | 0.423 *** | 0.422 *** | 0.0656 *** | 0.401 *** | 0.402 *** | 0.412 *** | 0.421 *** | 0.113 *** | 0.405 *** | 0.405 *** | 0.405 *** | 0.404 *** |
| 5 | 0.0703 *** | 0.47 *** | 0.479 *** | 0.478 *** | 0.476 *** | 0.0782 *** | 0.488 *** | 0.491 *** | 0.4879 *** | 0.486 *** | 0.0762 *** | 0.462 *** | 0.463 *** | 0.473 *** | 0.485 *** | 0.127 *** | 0.464 *** | 0.464 *** | 0.464 *** | 0.462 *** |
| 6 | 0.072 *** | 0.521 *** | 0.5211 *** | 0.519 *** | 0.517 *** | 0.079 *** | 0.532 *** | 0.535 *** | 0.532 *** | 0.53 *** | 0.076 *** | 0.506 *** | 0.506 *** | 0.517 *** | 0.531 *** | 0.136 *** | 0.503 *** | 0.504 *** | 0.503 *** | 0.501 *** |
| (a) | ||||||||||||||||||||||||||||||
| Pakistan | India | Bangdladesh | Sri Lanka | |||||||||||||||||||||||||||
| 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | |||||||||||||||
| Quantile | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | ||||||||||||||
| 0.1 | 0.5324 | 0.6939 | 0.6807 | 0.6756 | 0.1225 | 0.1388 | 0.12343 | 0.1167 | 0.4783 *** | 0.4782 *** | 0.4780 *** | 0.4781 *** | −0.1566 | −0.1661 | −0.1499 | −0.1611 | ||||||||||||||
| 0.2 | 1.1940 | 1.1556 | 1.1011 | 1.0819 | 0.2175 | 0.2175 | 0.21697 | 0.2139 | 0.3636 *** | 0.3637 *** | 0.3593 *** | 0.3588 *** | −0.0122 | −0.0106 | −0.0146 | −0.0158 | ||||||||||||||
| 0.3 | 1.0972 | 1.0632 | 1.0207 | 0.9754 | 0.1277 | 0.1273 | 0.12914 | 0.1291 | 0.2604 *** | 0.2603 *** | 0.2564 *** | 0.2601 *** | −0.0517 | −0.0495 | −0.0496 | −0.0509 | ||||||||||||||
| 0.7 | 1.942 *** | 1.800 *** | 1.663 *** | 1.622 *** | 0.3704 *** | 0.3711 *** | 0.3708 *** | 0.3734 *** | 0.11310 | 0.11276 | 0.11232 | 0.11175 | 0.3192 *** | 0.3328 *** | 0.33085 *** | 0.3299 *** | ||||||||||||||
| 0.8 | 1.334 ** | 1.294 ** | 1.181 * | 1.151 * | 0.4597 *** | 0.4602 *** | 0.4602 *** | 0.46044 *** | 0.02881 | 0.02859 | 0.02867 | 0.02854 | 0.4035 *** | 0.4033 *** | 0.4034 *** | 0.4027 *** | ||||||||||||||
| 0.9 | 1.0602 | 1.0785 | 0.9970 | 0.9802 | 0.7493 * | 0.7400 | 0.7575 * | 0.7631 * | 0.11346 | 0.11146 | 0.11324 | 0.11164 | 0.4994 *** | 0.5049 *** | 0.5021 *** | 0.5004 *** | ||||||||||||||
| 0.1 | −0.088 ** | −0.092 ** | −0.0928 ** | −0.0927 ** | −0.0144 | −0.0163 | −0.01454 | −0.0138 | −0.06933 *** | −0.06937 *** | −0.06936 *** | −0.0699 *** | 0.0233 | 0.0219 | 0.0222 | 0.0239 | ||||||||||||||
| 0.2 | −0.0690 *** | −0.0687 *** | −0.0689 *** | −0.0689 *** | −0.0248 | −0.0248 | −0.02470 | −0.0244 | −0.05275 *** | −0.05275 *** | −0.05221 *** | −0.05214 *** | 0.0072 | 0.0070 | 0.0074 | 0.0076 | ||||||||||||||
| 0.3 | −0.0389 ** | −0.0386 ** | −0.0396 ** | −0.0390 ** | −0.0145 | −0.0145 | −0.01470 | −0.0147 | −0.03701 *** | −0.03701 *** | −0.03649 *** | −0.03697 *** | 0.0117 | 0.0114 | 0.0114 | 0.0116 | ||||||||||||||
| 0.7 | −0.0431 *** | −0.0421 *** | −0.0422 *** | −0.0451 *** | −0.04148 *** | −0.04149 *** | −0.0414 *** | −0.04174 *** | −0.01218 | −0.01213 | −0.01207 | −0.01200 | −0.03925 *** | −0.0410 *** | −0.04078 *** | −0.04073 *** | ||||||||||||||
| 0.8 | −0.0323 * | −0.0322 * | −0.0318 | −0.0318 | −0.05141 *** | −0.05146 *** | −0.0514 *** | −0.05148 *** | −0.00046 | −0.00043 | −0.00045 | −0.00043 | −0.04905 *** | −0.04897 *** | −0.04899 *** | −0.04889 *** | ||||||||||||||
| 0.9 | −0.0321 | −0.0360 | −0.0361 | −0.0363 | −0.08370 * | −0.0827 | −0.08463 * | −0.08525 * | −0.00973 | −0.00949 | −0.00971 | −0.00951 | −0.05832 *** | −0.05900 *** | −0.05865 *** | −0.05848 *** | ||||||||||||||
| 0.1 | −0.0022 | 0.0122 | 0.0119 | 0.0117 | 0.006436 * | 0.006764 * | 0.007332 * | 0.007557 * | 0.001925 | 0.001988 | 0.002177 | 0.002274 | 0.004987 | 0.002915 | 0.005441 | 0.0058 | ||||||||||||||
| 0.2 | 0.0783 | 0.0768 | 0.0776 | 0.0779 | 0.00536 *** | 0.005534 *** | 0.006098 *** | 0.006304 *** | 0.00022 | 0.00022 | 0.00018 | 0.00020 | 0.006128 *** | 0.006353 *** | 0.006844 *** | 0.007069 *** | ||||||||||||||
| 0.3 | 0.0901 | 0.0894 | 0.0922 | 0.0904 | 0.0017 | 0.0018 | 0.00195 | 0.0020 | 0.00137 | 0.00142 | 0.00155 | 0.00162 | 0.005293 *** | 0.005466 *** | 0.005973 *** | 0.006179 *** | ||||||||||||||
| 0.7 | 0.1782 *** | 0.1687 *** | 0.1685 *** | 0.1668 *** | 0.001392 * | 0.001437 * | 0.001584 * | 0.001654 * | 0.003549 *** | 0.003661 *** | 0.004029 *** | 0.004167 *** | 0.0008 | 0.0007 | 0.0008 | 0.0007 | ||||||||||||||
| 0.8 | 0.1190 * | 0.1184 * | 0.1166 * | 0.1170 * | 0.001635 * | 0.001691 * | 0.001864 * | 0.001935 ** | 0.00168 | 0.00174 | 0.00192 | 0.00199 | 0.0014 | 0.0015 | 0.0016 | 0.0017 | ||||||||||||||
| 0.9 | 0.0877 | 0.0894 | 0.0882 | 0.0891 | 0.0025 | 0.0025 | 0.00288 | 0.0030 | 0.00141 | 0.00143 | 0.00159 | 0.00164 | 0.0037 ** | 0.003838 ** | 0.004185 ** | 0.00429 ** | ||||||||||||||
| 0.1 | −0.0202 | −0.0082 | −0.0103 | −0.0112 | −0.0119 | −0.0119 | −0.01274 | −0.0124 | −0.00393 | −0.00405 | −0.00444 | −0.00457 | −0.01193 ** | −0.01396 *** | −0.0133 ** | −0.01378 ** | ||||||||||||||
| 0.2 | 0.0636 | 0.0617 | 0.0605 | 0.0602 | −0.02065 *** | −0.02089*** | −0.02150 *** | −0.02174 *** | −0.005228 * | −0.005378 * | −0.005666 * | −0.00585 * | −0.009856 *** | −0.007222 ** | −0.01099 *** | −0.01143 *** | ||||||||||||||
| 0.3 | 0.0899 | 0.0893 | 0.091737 * | 0.0901 | −0.02438 *** | −0.02453 *** | −0.02546 *** | −0.025745 *** | 0.00202 | 0.00209 | 0.00238 | 0.00237 | −0.009353 *** | −0.009613 *** | −0.01046 *** | −0.01082 *** | ||||||||||||||
| 0.7 | 0.1575 *** | 0.1482 *** | 0.1460 *** | 0.1430 *** | 0.0102 | 0.0094 | 0.0110 | 0.0112 | 0.00100 | 0.00102 | 0.00111 | 0.00115 | −0.0008 | −0.0010 | −0.0010 | −0.0011 | ||||||||||||||
| 0.8 | 0.0912 | 0.0900 | 0.0858 | 0.0853 | 0.0079 | 0.0083 | 0.0073 | 0.0073 | 0.00149 | 0.00154 | 0.00166 | 0.00174 | 0.0031 | 0.0031 | 0.0034 | 0.0035 | ||||||||||||||
| 0.9 | 0.0628 | 0.0630 | 0.0595 | 0.0593 | 0.0058 | 0.0052 | 0.0061 | 0.0057 | 0.00225 | 0.00235 | 0.00257 | 0.00265 | 0.01022 *** | 0.01095 *** | 0.01154 *** | 0.011797 *** | ||||||||||||||
| 0.1 | 0.0077 | 0.0228 | 0.0235 | 0.0238 | 0.0159 | 0.0172 | 0.0182 | 0.0184 | 0.02763 *** | 0.02854 *** | 0.03142 *** | 0.03267 *** | 0.0023 | −0.00310 | 0.0025 | 0.0026 | ||||||||||||||
| 0.2 | 0.0876 | 0.0862 | 0.0878 | 0.0885 | 0.0094 | 0.0098 | 0.0107 | 0.0110 | 0.02126 *** | 0.02196 *** | 0.02416 *** | 0.02510 *** | 0.0050 | 0.0053 | 0.0054 | 0.0055 | ||||||||||||||
| 0.3 | 0.0947 | 0.0944 | 0.0976 | 0.0958 | 0.0024 | 0.0029 | 0.0027 | 0.0028 | 0.01583 *** | 0.01636 *** | 0.01791 *** | 0.01872 *** | 0.0006 | 0.0007 | 0.0008 | 0.0008 | ||||||||||||||
| 0.7 | 0.1660 *** | 0.1563 *** | 0.1551 *** | 0.1536 *** | 0.007855 * | 0.008125 * | 0.008944 * | 0.009427 * | 0.00169 | 0.00175 | 0.00190 | 0.00203 | 0.0038 | 0.0040 | 0.0043 | 0.0046 | ||||||||||||||
| 0.8 | 0.1108 * | 0.1100 * | 0.1074 * | 0.1074 * | 0.008898 ** | 0.00913 ** | 0.01030 ** | 0.01070 ** | −0.00202 | −0.00208 | −0.00234 | −0.00238 | 0.0037 | 0.0039 | 0.0042 | 0.0044 | ||||||||||||||
| 0.9 | 0.0804 | 0.0823 | 0.0805 | 0.0811 | 0.0085 | 0.00902 | 0.0098 | 0.0100 | −0.00832 | −0.00850 | −0.00947 | −0.00975 | 0.0012 | 0.0013 | 0.0014 | 0.0014 | ||||||||||||||
| 0.1 | 0.0152 *** | 0.0150 *** | 0.0150 *** | 0.01508 *** | 0.003287 ** | 0.003314 ** | 0.003285 ** | 0.003274 ** | 0.007411 *** | 0.00741 *** | 0.007413 *** | 0.007403 *** | 0.004186 *** | 0.004052 *** | 0.004075 *** | 0.004139 *** | ||||||||||||||
| 0.2 | 0.00315 * | 0.00316 * | 0.00316 * | 0.00315 * | 0.00231 *** | 0.002315 *** | 0.002313 *** | 0.002309 *** | 0.003696 *** | 0.003696 *** | 0.003675 *** | 0.003672 *** | 0.002609 ** | 0.002608 ** | 0.00259 ** | 0.002588 ** | ||||||||||||||
| 0.3 | 0.0006 | 0.0007 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.004193 *** | 0.004192 *** | 0.004197 *** | 0.004187 *** | 0.002613 ** | 0.002592 ** | 0.002574 ** | 0.002569 ** | ||||||||||||||
| 0.7 | −0.0010 | −0.0008 | −0.0009 | −0.0008 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.003058 * | 0.003054 * | 0.003042 * | 0.003033 * | 0.0002 | 0.0000 | 0.0000 | 0.0000 | ||||||||||||||
| 0.8 | −0.0016 | −0.0016 | −0.0017 | −0.0017 | −0.0001 | −0.0001 | −0.0001 | −0.0001 | −0.00003 | −0.00003 | −0.00004 | −0.00004 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | ||||||||||||||
| 0.9 | −0.0032 | −0.0032 | −0.0031 | −0.0031 | −0.000518 * | −0.00053 * | −0.000525 * | −0.000518 * | −0.00286 | −0.00286 | −0.00287 | −0.00287 | 0.001905 ** | 0.001944 ** | 0.001923 ** | 0.001911 ** | ||||||||||||||
| 0.1 | −0.0035 | −0.0055 | −0.0052 | −0.0051 | −0.0064 | −0.0062 | −0.0060 | −0.0056 | 0.00187 | 0.00188 | 0.00192 | 0.00194 | −0.02335 *** | −0.02243 *** | −0.02286 *** | −0.02315 *** | ||||||||||||||
| 0.2 | −0.0120 | −0.0119 | −0.0123 | −0.0122 | −0.01080 *** | −0.010584 *** | −0.009883 *** | −0.009632 *** | −0.00057 | −0.00054 | −0.00029 | −0.00028 | −0.02110 *** | −0.01733 *** | −0.02086 *** | −0.02092 *** | ||||||||||||||
| 0.3 | −0.0001 | 0.0000 | −0.0004 | −0.0002 | −0.01261 *** | −0.01229 *** | −0.011562 *** | −0.01126 *** | 0.004915 ** | 0.004911 ** | 0.004963 ** | 0.004893 ** | −0.01931 *** | −0.01928 *** | −0.01919 *** | −0.01917 *** | ||||||||||||||
| 0.7 | −0.0255 *** | −0.02436 *** | −0.0241 *** | −0.0243 *** | 0.0056 | 0.0050 | 0.0053 | 0.0052 | −0.00098 | −0.00099 | −0.00101 | −0.00101 | 0.0003 | 0.0004 | 0.0005 | 0.0005 | ||||||||||||||
| 0.8 | −0.0325 *** | −0.03226 *** | −0.0317 *** | −0.0314 *** | 0.0046 | 0.0047 | 0.0038 | 0.0037 | −0.00019 | −0.00020 | −0.00024 | −0.00023 | 0.0057 | 0.0057 | 0.0056 | 0.0056 | ||||||||||||||
| 0.9 | −0.02951 ** | −0.030053 ** | −0.02944 ** | −0.02956 ** | 0.0036 | 0.0032 | 0.0034 | 0.0031 | −0.00077 | −0.00070 | −0.00073 | −0.00075 | 0.01310 *** | 0.01363 *** | 0.01310 *** | 0.01295 *** | ||||||||||||||
| 0.1 | 0.0274 ** | 0.02775 * | 0.02766 * | 0.02762 * | 0.0082 | 0.0086 | 0.0082 | 0.0080 | 0.03842 *** | 0.03842 *** | 0.03836 *** | 0.03839 *** | −0.0038 | −0.0085 | −0.0036 | −0.0040 | ||||||||||||||
| 0.2 | 0.0152 ** | 0.01493 ** | 0.01480 ** | 0.01471 ** | 0.0047 | 0.0047 | 0.0046 | 0.0046 | 0.02991 *** | 0.02991 *** | 0.02984 *** | 0.02984 *** | −0.0012 | −0.0011 | −0.0015 | −0.0016 | ||||||||||||||
| 0.3 | 0.0060 | 0.0062 | 0.0060 | 0.0058 | 0.0012 | 0.0014 | 0.0012 | 0.0012 | 0.02155 *** | 0.02154 *** | 0.02137 *** | 0.02152 *** | −0.0065 | −0.0063 | −0.0063 | −0.0064 | ||||||||||||||
| 0.7 | −0.0161 *** | −0.01574 *** | −0.01541 *** | −0.01448 *** | 0.004097 * | 0.004103 * | 0.004095 * | 0.004158 * | 0.00067 | 0.00069 | 0.00066 | 0.00071 | 0.0060 | 0.0064 | 0.0062 | 0.0065 | ||||||||||||||
| 0.8 | −0.0113 ** | −0.01132 ** | −0.01130 ** | −0.01131 ** | 0.004665 ** | 0.004633 ** | 0.004742 ** | 0.004745 ** | −0.00443 | −0.00443 | −0.00447 | −0.00443 | 0.0052 | 0.0052 | 0.0052 | 0.0052 | ||||||||||||||
| 0.9 | −0.0104 | −0.0098 | −0.0095 | −0.0096 | 0.0043 | 0.00441 | 0.0043 | 0.0042 | −0.01291 | −0.01277 | −0.01288 | −0.01279 | −0.0014 | −0.0014 | −0.0014 | −0.0014 | ||||||||||||||
| (b) | ||||||||||||||||||||||||||||||
| Pakistan | India | Bangladesh | Sri Lanka | |||||||||||||||||||||||||||
| 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | 3M-FERP | 6M-FERP | 9M-FERP | 12M-FERP | |||||||||||||||
| Quantile | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | Coeff. | ||||||||||||||
| 0.1 | 0.0260 | 0.0333 | 0.0331 | 0.0331 | 0.0236 | 0.01443 | 0.0228 | 0.0259 | 0.17361 * | 0.17360 * | 0.1731 * | 0.17356 * | 0.3518 *** | 0.3347 *** | 0.34576 *** | 0.3518 *** | ||||||||||||||
| 0.2 | 0.0545 | 0.0543 | 0.0512 | 0.0538 | 0.0819 | 0.08235 | 0.0817 | 0.0808 | 0.0729 | 0.07301 | 0.06674 | 0.06614 | 0.2865 *** | 0.2854 *** | 0.28845 *** | 0.2883 *** | ||||||||||||||
| 0.3 | 0.0105 | 0.0104 | 0.0109 | 0.0106 | 0.0986 | 0.09872 | 0.0987 | 0.0988 | 0.0254 | 0.02540 | 0.03510 | 0.02544 | 0.2440 *** | 0.2452 *** | 0.24591 *** | 0.2454 *** | ||||||||||||||
| 0.7 | −0.0389 | −0.0387 | −0.0391 | −0.0556 | 0.0041 | 0.00426 | 0.0042 | 0.0051 | −0.0120 | −0.01263 | −0.01327 | −0.01343 | 0.0444 | 0.0467 | 0.0491 | 0.0493 | ||||||||||||||
| 0.8 | −0.1165 | −0.1175 | −0.1246 | −0.1246 | 0.0061 | 0.00513 | 0.0152 | 0.0161 | −0.0083 | −0.00791 | −0.00797 | −0.00790 | −0.0220 | −0.0215 | −0.0219 | −0.0213 | ||||||||||||||
| 0.9 | −0.1234 | −0.1212 | −0.1221 | −0.1223 | −0.0510 | −0.04378 | −0.0515 | −0.0568 | −0.0165 | −0.02002 | −0.01653 | −0.01962 | −0.0066 | 0.0045 | −0.0007 | −0.0030 | ||||||||||||||
| 0.1 | 0.2470 | 0.2542 | 0.2540 | 0.2539 | −0.0551 | −0.05715 | −0.0615 | −0.0629 | 0.0021 | 0.00219 | 0.00246 | 0.00253 | 0.0051 | 0.0021 | 0.0056 | 0.0058 | ||||||||||||||
| 0.2 | 0.3095 *** | 0.3097 *** | 0.3098 *** | 0.3096 *** | 0.0415 | 0.04253 | 0.0475 | 0.0500 | 0.0079 | 0.00815 | 0.00935 | 0.00974 | −0.0005 | −0.0003 | −0.0007 | −0.0008 | ||||||||||||||
| 0.3 | 0.2804 ** | 0.2805 * | 0.2804 | 0.2805 | −0.0100 | −0.01015 | −0.0115 | −0.0119 | 0.01055 ** | 0.01091 ** | 0.01154 ** | 0.01249 ** | −0.0015 | −0.0017 | −0.0019 | −0.0019 | ||||||||||||||
| 0.7 | 0.2069 ** | 0.1956 ** | 0.1669 | 0.1667 | −0.0036 | −0.00370 | −0.0041 | −0.0039 | 0.0062 | 0.00647 | 0.00716 | 0.00744 | −0.0051 | −0.0058 | −0.0063 | −0.0066 | ||||||||||||||
| 0.8 | 0.1524 | 0.1474 | 0.1306 | 0.1282 | 0.0033 | 0.00232 | 0.0095 | 0.0097 | −0.0027 | −0.00283 | −0.00313 | −0.00325 | −0.007596 * | −0.007819 * | −0.008596 * | −0.00886 * | ||||||||||||||
| 0.9 | 0.0434 | 0.0400 | 0.0190 | 0.0123 | 0.0099 | 0.01809 | 0.0086 | 0.0027 | −0.0132 | −0.01336 | −0.01501 | −0.01534 | −0.01016 *** | −0.01071 *** | −0.01156 *** | −0.0119 *** | ||||||||||||||
| 0.1 | 0.1696 | 0.1687 | 0.1605 | 0.1571 | 0.0188 | 0.01851 | 0.0186 | 0.0180 | −0.0009 | −0.00105 | −0.00151 | −0.00178 | 0.0168 | 0.0501 | 0.0138 | 0.0221 | ||||||||||||||
| 0.2 | 0.2282 *** | 0.2256 *** | 0.2193 *** | 0.21518 *** | 0.0045 | 0.00438 | 0.0035 | 0.0032 | −0.0607 | −0.06284 | −0.06761 | −0.07026 | −0.0380 | −0.0569 | −0.0393 | −0.0386 | ||||||||||||||
| 0.3 | 0.0800 | 0.0738 | 0.0528 | 0.0445 | −0.0156 | −0.0156 | −0.0168 | −0.0171 | −0.0442 | −0.04571 | −0.05079 | −0.05235 | 0.0063 | 0.0061 | 0.0072 | 0.0061 | ||||||||||||||
| 0.7 | 0.1949 *** | 0.1929 *** | 0.1884 *** | 0.1897 *** | −0.1173 *** | −0.1152 *** | −0.11733 *** | −0.1162 *** | 0.0000 | 0.00014 | 0.00029 | 0.00019 | 0.1072 | 0.0732 | 0.0817 | 0.0841 | ||||||||||||||
| 0.8 | 0.2160 *** | 0.2142 *** | 0.2067 *** | 0.2047 *** | −0.1340 *** | −0.13207 *** | −0.13262 *** | −0.1315 *** | −0.09323 * | −0.09362 * | −0.09442 * | −0.09493 * | 0.0459 | 0.0476 | 0.0517 | 0.0541 | ||||||||||||||
| 0.9 | 0.1439 ** | 0.1438 ** | 0.13544 ** | 0.1354 ** | −0.1438 *** | −0.1417 *** | −0.14318 *** | −0.1421 *** | −0.0449 | −0.06358 | −0.07265 * | −0.07355 * | 0.1679 | 0.1844 | 0.1909 | 0.1971 | ||||||||||||||
| 0.1 | 0.5122 *** | 0.5333 *** | 0.5621 *** | 0.5738 *** | 0.0580 | 0.0603 | 0.0658 | 0.0651 | 0.3380 *** | 0.3492 *** | 0.38524 *** | 0.3999 *** | 0.0154 | −0.1160 | 0.0104 | 0.0168 | ||||||||||||||
| 0.2 | 0.5472 *** | 0.559 *** | 0.5881 *** | 0.5972 *** | 0.1437 | 0.1466 | 0.1638 | 0.1710 | 0.2316 *** | 0.2393 *** | 0.2651 *** | 0.2751 *** | 0.0805 | 0.0846 | 0.0852 | 0.0869 | ||||||||||||||
| 0.3 | 0.4854 *** | 0.4919 *** | 0.5120 ** | 0.5228 ** | 0.0212 | 0.0243 | 0.0238 | 0.0255 | 0.1535 * | 0.15866 * | 0.1766 * | 0.18163 * | −0.0146 | −0.0129 | −0.0142 | −0.0149 | ||||||||||||||
| 0.7 | 0.2811 ** | 0.2470 ** | 0.2173 * | 0.2144 | −0.0081 | −0.0078 | −0.0092 | −0.0065 | 0.0446 | 0.04568 | 0.04188 | 0.05144 | −0.0049 | −0.0029 | −0.0069 | −0.0006 | ||||||||||||||
| 0.8 | 0.1894 | 0.1823 | 0.1724 | 0.1715 | 0.0566 | 0.0554 | 0.0815 | 0.0852 | 0.1219 | 0.12580 | 0.13997 | 0.14386 | 0.0330 | 0.0336 | 0.0372 | 0.0376 | ||||||||||||||
| 0.9 | −0.0334 | −0.0222 | −0.0487 | −0.0570 | −0.0294 | −0.0302 | −0.0351 | −0.0373 | 0.1307 | 0.13317 | 0.14729 | 0.15302 | −0.0503 | −0.0582 | −0.0607 | −0.0614 | ||||||||||||||
| 0.1 | 0.0125 *** | 0.01256 *** | 0.0125 *** | 0.0125 *** | −0.0384 | −0.0386 | −0.0378 | −0.0371 | −0.0081 | −0.00811 | −0.00805 | −0.00808 | −0.0059 | −0.0076 | −0.0059 | −0.0061 | ||||||||||||||
| 0.2 | −0.0320 ** | −0.0320 ** | −0.0323 ** | −0.0321 ** | 0.0136 | 0.0135 | 0.0137 | 0.0140 | 0.0037 | 0.00371 | 0.00416 | 0.00420 | −0.0166 | −0.0163 | −0.0167 | −0.0167 | ||||||||||||||
| 0.3 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | −0.0076 | −0.0076 | −0.0076 | −0.0076 | 0.0070 | 0.00698 | 0.00637 | 0.00699 | −0.0153 | −0.0156 | −0.0157 | −0.0156 | ||||||||||||||
| 0.7 | −0.0024 | −0.0026 | −0.0026 | −0.0028 | −0.0009 | −0.0010 | −0.0009 | −0.0009 | 0.0024 | 0.00241 | 0.00246 | 0.00247 | −0.0102 | −0.0112 | −0.0111 | −0.0111 | ||||||||||||||
| 0.8 | −0.0026 | −0.0025 | −0.0014 | −0.0014 | −0.0001 | −0.0005 | 0.0021 | 0.0020 | −0.0068 | −0.00685 | −0.00685 | −0.00685 | −0.01452 * | −0.01453 * | −0.01453 * | −0.01450 * | ||||||||||||||
| 0.9 | 0.0961 *** | 0.09519 *** | 0.0950 *** | 0.0950 *** | 0.0086 | 0.0129 | 0.0073 | 0.0043 | −0.0182 | −0.01790 | −0.01822 | −0.01794 | −0.02196 *** | −0.02261 *** | −0.02227 *** | −0.02217 *** | ||||||||||||||
| 0.1 | 0.0189 | 0.0162 | 0.0174 | 0.0178 | 0.0165 | 0.0159 | 0.0149 | 0.0140 | 0.0848 | 0.08465 | 0.08425 | 0.08410 | 0.0652 | 0.0336 | 0.0545 | 0.0674 | ||||||||||||||
| 0.2 | −0.0419 | −0.0408 | −0.0373 | −0.0377 | 0.0133 | 0.0130 | 0.0117 | 0.0112 | −0.0067 | −0.00686 | −0.00518 | −0.00524 | 0.0221 | −0.0054 | 0.0235 | 0.0255 | ||||||||||||||
| 0.3 | −0.1679 *** | −0.1674 *** | −0.1664 *** | −0.1656 *** | 0.0046 | 0.0046 | 0.0040 | 0.0039 | −0.0146 | −0.01456 | −0.01457 | −0.01453 | 0.0257 | 0.0264 | 0.0269 | 0.0251 | ||||||||||||||
| 0.7 | 0.0283 | 0.0313 | 0.0540 | 0.0535 | −0.06651 *** | −0.06297 *** | −0.05879 *** | −0.05627 *** | 0.0110 | 0.01105 | 0.00935 | 0.01092 | 0.1525 | 0.1019 | 0.1018 | 0.1046 | ||||||||||||||
| 0.8 | 0.1087 | 0.1091 | 0.1127 | 0.1101 | −0.07421 *** | −0.07105 *** | −0.064285 *** | −0.06151 *** | −0.0749 | −0.07201 | −0.06301 | −0.06039 | 0.0810 | 0.0812 | 0.0809 | 0.0812 | ||||||||||||||
| 0.9 | 0.2133 | 0.2173 | 0.2186 | 0.2208 | −0.07843 *** | −0.07456 *** | −0.068771 *** | −0.06563 *** | −0.0180 | −0.03719 | −0.03951 | −0.03770 | 0.1967 | 0.2081 | 0.1961 | 0.1965 | ||||||||||||||
| 0.1 | 0.3710 *** | 0.3774 *** | 0.3781 *** | 0.37838 *** | 0.0216 | 0.0215 | 0.0215 | 0.0203 | 0.4256 *** | 0.4256 *** | 0.4255 *** | 0.4255 *** | 0.0379 | −0.2173 | 0.0252 | 0.0361 | ||||||||||||||
| 0.2 | 0.2883 *** | 0.2945 *** | 0.2977 *** | 0.2967 *** | 0.0698 | 0.0688 | 0.0699 | 0.0703 | 0.2889 *** | 0.2889 *** | 0.2902 *** | 0.2901 *** | 0.1675 | 0.1706 | 0.1577 | 0.1555 | ||||||||||||||
| 0.3 | 0.2812 *** | 0.2806 *** | 0.2790 *** | 0.2817 *** | 0.0097 | 0.0107 | 0.0096 | 0.0099 | 0.1896 * | 0.1896 * | 0.1917 * | 0.1895 * | −0.0211 | −0.0171 | −0.0172 | −0.0175 | ||||||||||||||
| 0.7 | 0.1159 | 0.0816 | 0.0738 | 0.0672 | −0.0080 | −0.0077 | −0.0080 | −0.0067 | 0.06009 | 0.05956 | 0.04939 | 0.05853 | −0.0155 | −0.0116 | −0.0180 | −0.0070 | ||||||||||||||
| 0.8 | 0.0584 | 0.0548 | 0.0591 | 0.0591 | 0.0252 | 0.0237 | 0.0329 | 0.0331 | 0.17076 | 0.17054 | 0.17198 | 0.17029 | 0.0616 | 0.0608 | 0.0614 | 0.0599 | ||||||||||||||
| 0.9 | −0.0037 | 0.0178 | 0.0187 | 0.0196 | −0.0191 | −0.01911 | −0.01986 | −0.02014 | 0.19138 | 0.18871 | 0.18923 | 0.18931 | −0.1029 | −0.1155 | −0.1100 | −0.1076 | ||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabash, M.I.; Ahmed, A.; Issa, S.S.; Mansour, M.; Varma, M.; Al-Absy, M.S.M. Multiple Behavioral Conditions of the Forward Exchange Rates and Stock Market Return in the South Asian Stock Markets During COVID-19: A Novel MT-QARDL Approach. Computation 2024, 12, 233. https://doi.org/10.3390/computation12120233
Tabash MI, Ahmed A, Issa SS, Mansour M, Varma M, Al-Absy MSM. Multiple Behavioral Conditions of the Forward Exchange Rates and Stock Market Return in the South Asian Stock Markets During COVID-19: A Novel MT-QARDL Approach. Computation. 2024; 12(12):233. https://doi.org/10.3390/computation12120233
Chicago/Turabian StyleTabash, Mosab I., Adel Ahmed, Suzan Sameer Issa, Marwan Mansour, Manishkumar Varma, and Mujeeb Saif Mohsen Al-Absy. 2024. "Multiple Behavioral Conditions of the Forward Exchange Rates and Stock Market Return in the South Asian Stock Markets During COVID-19: A Novel MT-QARDL Approach" Computation 12, no. 12: 233. https://doi.org/10.3390/computation12120233
APA StyleTabash, M. I., Ahmed, A., Issa, S. S., Mansour, M., Varma, M., & Al-Absy, M. S. M. (2024). Multiple Behavioral Conditions of the Forward Exchange Rates and Stock Market Return in the South Asian Stock Markets During COVID-19: A Novel MT-QARDL Approach. Computation, 12(12), 233. https://doi.org/10.3390/computation12120233









