Abstract
Platooning of vehicular systems has been considered an effective solution for alleviating traffic congestion and reducing energy consumption. Because of limitations in onboard sensors, the measurement system inevitably suffers from measurement delays and noise, yet it receives insufficient attention. In this article, to deal with the measurement delays and noise while improving convergence performance, the platoon control problem of vehicular systems is studied under the nonsingular terminal sliding mode control (NTSMC) framework. A sliding mode observer (SMO) is proposed to estimate the states affected by measurement delays and noise. A distributed NTSMC scheme is developed for the platooning of the vehicular systems and ensures the convergence of the sliding mode surface affected by measurement delays and noise. One salient feature of the proposed SMO is that it can handle time-varying measurement delays rather than constant ones. Moreover, the control law is free of initial spacing error conditions under the employed coupled spacing policy. Numerical simulations are finally provided to demonstrate the effectiveness and efficiency of the proposed algorithm.
1. Introduction
In recent years, platooning of vehicular systems has attracted widespread attention from industry and academia in solving severe urban traffic congestion [,]. Vehicle platoon control can improve road capacity by reducing the distance between vehicles, which reduces air resistance to improve energy efficiency [,]. A qualified vehicular platoon controller can increase the velocity of the system while ensuring passenger safety []. However, the increased velocity and decreased distance have brought higher requirements for driving safety and measurement systems.
Feedback is a basic component of the automation system [,]. However, because of the imperfection of sensors, there is usually a certain measurement delay and noise in the measurement system []. If it is not reasonably solved, it leads to poor control effect and even undermines the system safety []. To handle the delayed measurement, ref. [] utilized a hybrid sampled data observer to estimate the state while guaranteeing the exponential convergence of the estimation error system. Considering measurement delay and noise at the same time, ref. [] used a sliding mode observer and Lyapunov–Razumikhin approach to estimate the state of Lipschitz systems. Because of the physical limitations of sensors, time-varying delay and noise also corrode the sensory signals of the vehicle []. Ref. [] proposed a multisensor fusion algorithm and measurement reconstruction method to estimate lateral vehicle state by means of a multi-rate Kalman filter. Combining a deep recurrent neural network and unscented Kalman filter, a brain-inspired system was proposed in [] to deal with the measurement delays and noise in autonomous electric vehicles. However, as far as the author knows, there is no research that considers measurement delays and noise in vehicular platoon systems. The motivation that inspired this article was to design a sliding mode observer to estimate the corrupted vehicle states.
In recent years, researchers have developed many control strategies to achieve platooning of vehicular systems, e.g., PID control [,,], fuzzy control [,], model predictive control [,,], and sliding-mode control. Considering the uncertainty, a hierarchical fuzzy logic model was proposed in [] for vehicle platooning, whereas it depends on available experience and has poor learning ability. In [], a centralized model predictive control was constructed to improve the energy efficiency of hybrid electric vehicular platoon systems. Unfortunately, this method uses a centralized control strategy, which increases the difficulty of communication and is difficult to apply to large-scale vehicle systems. To alleviate communication pressure and improve reliability, a decentralized sliding mode algorithm was applied in [] to the vehicular platoon systems, but it ignored the non-zero initial spacing error conditions. To relax the zero initial spacing condition, in [], an integrated sliding mode control (ISMC) method based on a modified constant time headway (MCTH) policy was proposed to guarantee the finite time stability and string stability of vehicular platoon systems. Based on the above two articles, many scholars conducted in-depth research from the perspectives of error convergence efficiency [], anti-interference ability [], fault-tolerant control [], and input saturation []. However, the above-mentioned articles required the initial spacing error messages of the system, which is hard to obtain in the rapidly changing platoon. Therefore, this article utilizes the coupled spacing error to solve this problem.
In addition to measurement delays and noise, external disturbances are challenges that the vehicular platoon system should overcome because of inevitable air resistance and mechanical friction [,]. Sliding mode control is a crucial technique for handling disturbances because its inherent reaching law allows the system states to converge to the designated sliding surface. Once on this surface, the closed-loop system exhibits strong robustness and becomes insensitive to disturbances [,]. Combining a finite-time estimator, an integral sliding mode control strategy was applied to the bi-directional platoon system and achieved vehicle platooning control without acceleration information []. A discrete sliding mode controller was deployed in heterogeneous discrete connected autonomous vehicles and achieved longitudinal control of the vehicles under switching topologies []. By constructing the sliding mode surface using a prescribed performance function, the transient and steady-state performances of the platoon system were ensured to meet the prescribed requirements in the presence of external disturbances []. However, there are two shortcomings in the aforementioned research: 1. The traditional SMC can only achieve asymptotic stability, and the error of the closed-loop system cannot converge to the origin within a finite time, which reduces the operational efficiency of the system. 2. Existing sliding mode-based platoon systems usually employ real-time states to construct the sliding mode surfaces and controllers and allow the system states to reach the ideal sliding mode surface . Unfortunately, this is difficult to achieve in systems with measurement delays and noise, as the real states cannot be obtained. The first issue is tractable and can be directly utilized with the more established NTSMC method. The critical issue is the second one, for which this paper rigorously analyzes the dynamics of the state estimate-based sliding mode system and ensures that it converges to a neighborhood of the ideal sliding mode surface.
In summary, there are still the following shortcomings in the existing research on vehicular platoon systems: 1. How to estimate the state information of vehicular platoons affected by measurement noise and delays is the primary issue that this paper aims to address. 2. Given that estimation errors in state information are inevitable, how to achieve string stability in a sliding mode-based platoon system that incorporates estimation errors is a crucial problem that this paper seeks to resolve.
In order to overcome the measurement delay and noise while being independent of initial spacing errors, this work studies the platoon control of vehicular systems based on a distributed NTSMC. The main contributions of this work are as follows:
- (1)
- The first contribution lies in the design of an SMO for estimating the vehicle states subject to the time-varying measurement delays and noise. Using the Lyapunov–Razumikhin method, the estimation error of SMO achieves uniform ultimate boundedness as long as the varying measurement delays and noise are bounded. Specifically, both the velocity and acceleration of the vehicle are accurately estimated, relying solely on position value subject to measurement delay and noise.
- (2)
- Using the states estimated by an SMO, a disturbed NTSMC is developed to allow the closed-loop system to converge to a neighborhood of the origin in finite time. Sliding mode dynamics composed of state estimates are rigorously analyzed to ensure that the state of the system is maintained in the neighborhood of the ideal sliding mode surface.
- (3)
- A coupled spacing policy is employed in the platoon controller to guarantee string stability of the vehicular platoon system and is independent of initial spacing errors.
The remainder of this paper is organized as follows. Section 2 models the vehicular platoon system and formulates the platoon control problem. In Section 3, an SMO is proposed to estimate the states affected by measurement delays and noise, and the NTSMC is synthesized based on the CTH policy. Simulation studies are conducted to demonstrate the effectiveness and efficiency of the proposed algorithm in Section 4. Finally, the conclusion and future work are presented in Section 5.
2. System Description and Problem Formulation
2.1. System Description
In this article, a heterogeneous vehicle platoon system consisting of vehicles is considered, as illustrated in Figure 1 and the bold dots represent vehicles that have been omitted due to space constraints. The leading vehicle of the platoon is denoted as 0, and the remaining vehicles are follower vehicles. Each vehicle can measure its own velocity and acceleration, as well as the distance to the front vehicle, using onboard radar. These measurements are typically obtained through data fusion from various sensors, which may involve measurement delays and noise. Once the measurement system acquires the relevant data, vehicle i can broadcast this information to its neighbors via the Vehicular Ad Hoc Networks (VANETs) []. The longitudinal kinematic model of the leading vehicle can be expressed as [,]
where , , and represent the position, velocity, and acceleration of the leading vehicle, respectively, and are considered as known reference inputs. The leader serves as a reference signal/reference trajectory, and there is no need to design its controller. Thus, this article employs a second-order model for the leader to simplify the analysis. The dynamics for the follower vehicles can be expressed as
where and represent the position and velocity, respectively, of the i-th follower vehicle; represents external disturbances such as road resistance and gusts; is the engine time constant; is the control input; and represents the measurement data affected by the measurement delay and noise .
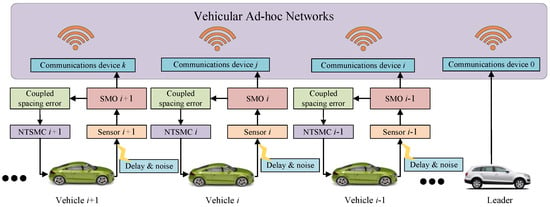
Figure 1.
Nonsingular terminal sliding mode control for vehicular platoon systems with measurement delays and noise.
2.2. Problem Formulation
To ensure driving safety, the desired distance between vehicles is
where represents the constant standstill distance, is a positive constant, and the spacing error between two adjacent vehicles is defined as
This article addresses a platoon system consisting of a leader (1) and N follower vehicles (2) by designing an SMO to estimate vehicle states affected by measurement delays and noise. Then, a distributed nonsingular terminal sliding mode controller is constructed, and the following control objectives are achieved: (1) finite-time stability, ensuring that the single vehicle in the platoon reaches stability within a finite time, i.e., the distance error between vehicles converges to 0 within a finite time, and (2) string stability, i.e., to suppress the propagation of spacing errors along the platoon, the spacing error of vehicle i should not exceed the spacing error of vehicle . This means that the transfer function of spacing error satisfies the inequality .
3. Distributed NTSMC Scheme with Sliding Mode Observer
In this section, an SMO is constructed to estimate the states affected by measurement delays and noise, and the boundedness of the estimation errors is analyzed by constructing a Lyapunov–Rzumikhin function. Subsequently, a distributed NTSMC is designed based on the coupled error while ensuring finite-time convergence of the tracking error for each individual vehicle and string stability of the whole platoon system.
3.1. Design of SMO
Before designing the SMO, the system model (2) is rewritten in the following compact form:
where , and . For the system (2) with measurement delays and noise, the following SMO is designed as
where is the parameter matrix to be designed, , and
where , is a positive definite matrix, J is a preset matrix with suitable dimensions to enhance the degrees of freedom in the design, and represents the magnitude of the boundary layer.
The following lemma is necessary to prove the convergence of the estimation error.
Lemma 1 ([]).
Consider the following matrix inequality
where λ is a constant and and are square matrices of dimension 3. Then, for any positive λ and positive definite matrix , it is possible to choose such that there exists a positive definite matrix satisfying the linear matrix inequality (LMI) (8).
Furthermore, since the proof of the convergence results for the observer is based on the Razumikhin theorem, we now introduce the concept of this theorem briefly.
Lemma 2 ([]).
It is sufficient to show that if for some , the inequality holds ; then, it follows that , with , continuous, positive definite, and non-decreasing.
Next, the following theorem addresses the convergence of the observer (6).
Theorem 1.
Proof of Theorem 1.
Before the proof begins, the estimation error is defined as
Then, for , combining Equations (5), (6) and (9), one has
It can be derived from (2) that
where . For , one has ; then,
with . Combining Equations (11) and (12), it can be derived that
Now, the Lyapunov–Rzumikhin function candidate is introduced as
where is defined in Lemma 1. The derivative of can be derived as
where and . The last two terms of the above formula satisfy
Now, according to the Razumikhin theorem condition and Young’s inequality, one has
where . When , according to (7), one has
When , according to (7) and , one has
According to the Young’s inequality, it can be derived that
where and . Based on , it can be obtained that
Substituting Equations (16), (17) and (21) into (15) and combining with Lemma 1, one can obtain
Next, consider two cases based on the relationship between and .
- 1.
- When ,where . Defining , if , one has
- 2.
To sum up, if the measurement delay satisfies , the estimation error of the SMO is uniformly ultimately bounded with . The proof is complete. □
3.2. SMO-Based Distributed Nonsingular Terminal Sliding Mode Control
To achieve the string stability, the coupled spacing error is designed as follows:
where is a positive constant. The coupled spacing error depicts the relationship between the errors of two consecutive vehicles. It is not difficult to find that the string stability can be guaranteed if the term holds. The following lemma shows the relationship between and .
Lemma 3.
Equation is equivalent to for .
Proof of Lemma 2.
Writing and in the vector form and yields
where
Since , are positive constants, we have that matrix is a nonsingular matrix, which directly deduces the conclusion. The proof is thus complete. □
Because of the outstanding capability in anti-interference, SMC, especially terminal sliding mode control, has been extensively applied in vehicular platoon systems. This article considers a nonsingular terminal sliding mode surface
where and are positive constants, , and and are two assigned odd integers. Before designing the controller, it should be clarified that because of measurement delays and noise, the controller can only use estimated states. In other words, the coupling error should be rewritten as
where . Subsequently, the controller based on the estimated states is designed as
where and
is to replace all states in with the corresponding estimates.
In the following theorem, a sufficient condition is given to guarantee that the state trajectories of the system will reach within the neighborhood of the sliding mode surface .
Theorem 2.
Consider the vehicular platoon system described by (1) and (2) with the SMO (6). If the switching gain satisfies
where and are corresponding Lipschitz constants, and are bounds related to the estimation errors of the observer, and is the upper bound of . Then, the controller (31) assures that the state trajectories of the system can reach within the following neighborhood of the sliding mode surface ,
where and are Lipschitz constants described later and is the bound related to the estimation errors of the observer.
Proof of Theorem 2.
For each vehicle, consider the Lyapunov function candidate . Differentiating with respect to time derives
Substituting the control law (31), one obtains
Since and are odd integers, both and are positive. Considering and are Lipschitz continuous, the following inequalities can be obtained:
Now, Theorem 2 can be proved in two steps: (i) and (ii) .
Since the estimation error is bounded, we have
Then, the maximal size of the neighborhood can be obtained as
Thus the proof is complete. □
In the following, the stability of the closed-loop vehicular platoon system is studied. According to the sliding mainfold (29), it yields . Then, by means of (34), the uniform ultimate boundedness of coupled spacing error can be derived in the following theorem.
Theorem 3.
Proof of Theorem 3.
Consider a Lyapunov function candidate . According to (34), the derivative of can be obtained as . It is seen that when the coupled spacing error stays in the two domains: and . This means that the coupled spacing error is attracted to the domain . By sorting to (34), one can yield that converges to defined in (41). The proof is thus complete. □
From (41), the coupled spacing error converges to a small region around the origin by setting appropriate parameters, and then, the string stability of the closed-loop system can be proved in the following theorem.
Theorem 4.
Proof of Theorem 4.
From Theorem 3, we know that can converge to a small region around the origin by setting appropriate parameters. Since for , the following can be obtained:
If holds, one has
Thus, we can obtain , which implies that the closed-loop system has strong string stability. The proof is thus complete. □
4. Simulation Results
In this section, the control scheme proposed in the above section is applied to a heterogeneous vehicle platoon system. The platoon consists of seven vehicles that travel along a straight path on a horizontal road. The lead vehicle in the platoon is labeled as 0 and has an initial position and velocity configured to 220 m and 10.1 m/s, respectively. The acceleration of the leader varies according to the following function:
The engine constants and initial states of the other followers are shown in Table 1. The relevant parameters in Table 1 are referenced from the literature []. Based on the dynamic characteristics of the vehicle and considering the heterogeneous vehicular platoon systems, the engine time constants are set between 0.12 and 0.15. The initial positions in the simulation create non-zero initial position errors, and the initial velocities are set to different values, making the simulation more representative of real traffic scenarios.

Table 1.
The engine tag and initial states of vehicle i.
To better simulate the measurement system of the vehicle, the measurement delay is set as a varying random function, ranging from s to s. Measurement noise is also a random function, varying between m and m, because of the inevitable errors in radar. The parameters of the SMO are chosen as ,
and is chosen as to alleviate the chattering phenomenon in the sliding mode observer. The matrix P is set as
which satisfies the requirements in Lemma 1, ensuring that the estimation error of the sliding mode observer achieves uniform ultimate boundedness. For the coupled spacing policy, the constant standstill distance is set as , the headway constant is , and the coupled gain is chosen as to achieve string stability of the platoon system. For the disturbed NTSMC, the parameter are set as , , and , which can avoid singularity in the control input. The external distance is set as .
According to the proposed observer (6) and controller (31), if the parameters are set as described above, the state trajectory of the closed-loop vehicle platoon system is shown in Figure 2. Figure 2a shows the positions of vehicles during the traveling process. From 0–6 s, the spacing between the vehicles is small, and the spacing grows when acceleration occurs. This is due to the spacing strategy (3), which is influenced by the velocity and is more favorable to driving safety. In addition, the lines in Figure 2a do not cross or overlap, which indicates that there is no collision among the vehicles. Figure 2b,c represent the velocities and spacing errors, respectively. It can be seen that all the spacing errors converge in the neighborhood of origin in a short time and satisfy string stability at steady state, i.e., . Figure 2d shows that there is no violent acceleration and deceleration, which ensures the comfort of the travelers. Figure 2e indicates that no chattering phenomenon occurs, thus avoiding excessive wear on the actuators. Figure 2f–h show the estimation results of the SMO subject to measurement delays and noise, indicating that the estimation errors converge to the neighborhood of the origin in about 1–5 s. This demonstrates that the proposed SMO can effectively handle time-varying measurement delays and noise.
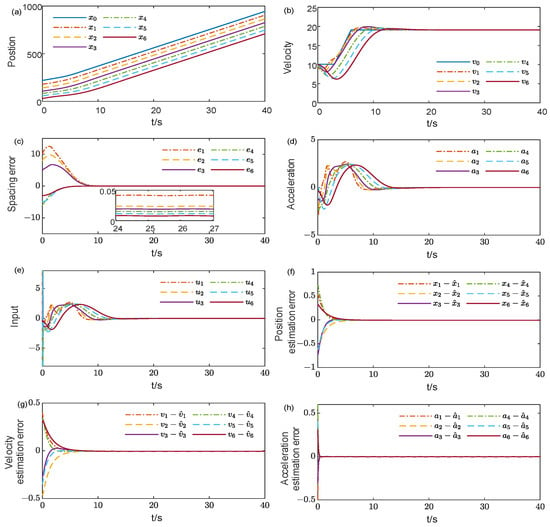
Figure 2.
System trajectories under the SMO-based distributed NTSMC. (a,b,d,e) represent the position, velocity, acceleration, and control input of each vehicle, respectively. (c) shows the error between the actual inter-vehicle distance and the desired distance. (f–h) present the estimates from the observer, namely the estimation errors of position, velocity, and acceleration, respectively.
To be more convincing, a comparative simulation of the NTSMC without an SMO is conducted, as shown in Figure 3. Figure 3c shows that the control performance of the closed-loop system is not satisfactory and violates the string stability criteria in steady state. As the platoon scale increases, the string unstable platoon can reduce traffic efficiency. The above content thoroughly demonstrates the importance of addressing measurement delays and noise. Other results are similar to those in Figure 2 and are not discussed further here.
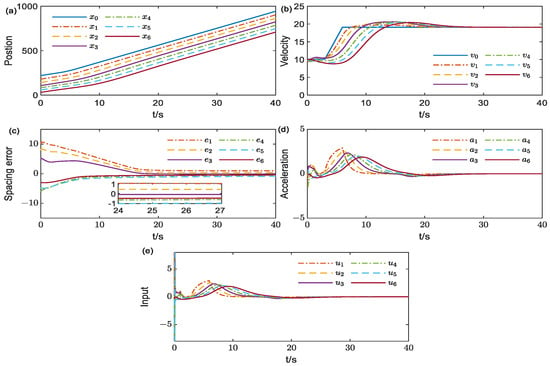
Figure 3.
System trajectories under the distributed NTSMC without SMO. (a,b,d,e) represent the position, velocity, acceleration, and control input of each vehicle, respectively. (c) shows the error between the actual inter-vehicle distance and the desired distance.
In order to illustrate that the convergence speed of the SMO in this paper is acceptable, we conducted a comparative simulation, as shown in Figure 4, referencing the literature []. From Figure 4, it can be seen that the results of position, velocity, and acceleration in the comparative simulation are similar to those of the method proposed in this paper, while the convergence speed of the spacing error is noticeably slower. Meanwhile, the estimation error convergence speed in [] is also slow, which contributes to the delayed convergence speed of the spacing error Figure 4c. Therefore, it can be concluded that the convergence speed of the observer in this paper is significantly faster than that in the referenced literature [].
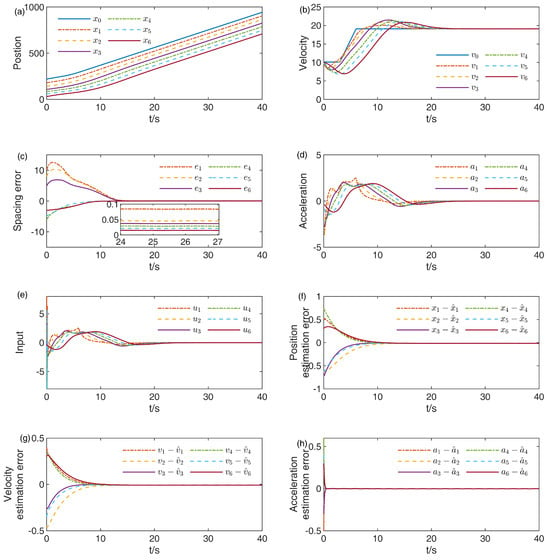
Figure 4.
System trajectories under the distributed NTSMC with Observer []. (a,b,d,e) represent the position, velocity, acceleration, and control input of each vehicle, respectively. (c) shows the error between the actual inter-vehicle distance and the desired distance. (f–h) present the estimates from the observer, namely the estimation errors of position, velocity, and acceleration, respectively.
5. Conclusions
Robust platoon control of heterogeneous vehicles with measurement delays and noise is achieved in this article. Relying only on position data affected by time-varying measurement delays and noise, the proposed SMO accurately estimates the state of the vehicle. In addition, by applying the distributed NTSMC method to the vehicular platoon, the closed-loop error can converge to a neighborhood of the origin in a finite time. Though the real state is unavailable, the estimation-based controller still ensures the system state arrives within a neighborhood of the ideal sliding mode surface. With the coupled error strategy, the string stability of the platoon can be achieved, and the propagation of disturbances is effectively suppressed. Besides the limitations of the measurement system, the vehicular communication system can be eroded by delays and packet loss. Thus, the weaknesses of the communication system are the focus of our future work.
Author Contributions
Writing the original draft: M.L.; methodology: S.L. and X.L.; supervision: X.L.; funding acquisition: X.L.; simulations: M.L. and Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the Iconic Specialized Cultivation Project of Yanshan University (Grant No. 2022BZZD005), in part by the Hebei Natural Science Foundation Grant No. F2024203083, and in part by the Science Research Project of Hebei Education Department No. BJK2024173.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, S.E.; Zheng, Y.; Li, K.; Wu, Y.; Hedrick, J.K.; Gao, F.; Zhang, H. Dynamical Modeling and Distributed Control of Connected and Automated Vehicles: Challenges and Opportunities. IEEE Intell. Transp. Syst. Mag. 2017, 9, 46–58. [Google Scholar] [CrossRef]
- Xu, L.; Wang, L.Y.; Yin, G.; Zhang, H. Communication information structures and contents for enhanced safety of highway vehicle platoons. IEEE Trans. Veh. Technol. 2014, 63, 4206–4220. [Google Scholar] [CrossRef]
- van de Hoef, S.; Johansson, K.H.; Dimarogonas, D.V. Fuel-Efficient En Route Formation of Truck Platoons. IEEE Trans. Intell. Transp. Syst. 2018, 19, 102–112. [Google Scholar] [CrossRef]
- Li, M.; Li, S.; Luo, X.; Zheng, X.; Guan, X. Distributed periodic event-triggered terminal sliding mode control for vehicular platoon system. Sci. China Inf. Sci. 2023, 66, 229203. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Shen, Z.; Wang, L.; Du, H.; Yin, C. Distributed multilane merging for connected autonomous vehicle platooning. Sci. China Inf. Sci. 2021, 64, 212202. [Google Scholar] [CrossRef]
- Chang, R.; Hou, T.T.; Bai, Z.Z.; Sun, C.Y. Event-triggered adaptive tracking control for nonlinear systems with input saturation and unknown control directions. Int. J. Robust Nonlinear Control 2024, 34, 3891–3911. [Google Scholar] [CrossRef]
- Chang, R.; Bai, Z.Z.; Zhang, B.Y.; Sun, C.Y. Adaptive finite-time prescribed performance tracking control for unknown nonlinear systems subject to full-state constraints and input saturation. Int. J. Robust Nonlinear Control 2022, 32, 9347–9362. [Google Scholar] [CrossRef]
- Li, Y.; Yin, G.; Zhuang, W.; Zhang, N.; Wang, J.; Geng, K. Compensating delays and noises in motion control of autonomous electric vehicles by using deep learning and unscented Kalman predictor. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4326–4338. [Google Scholar] [CrossRef]
- Germani, A.; Manes, C.; Pepe, P. A new approach to state observation of nonlinear systems with delayed output. IEEE Trans. Autom. Control 2002, 47, 96–101. [Google Scholar] [CrossRef]
- Ahmed-Ali, T.; Karafyllis, I.; Lamnabhi-Lagarrigue, F. Global exponential sampled-data observers for nonlinear systems with delayed measurements. Syst. Control Lett. 2013, 62, 539–549. [Google Scholar] [CrossRef]
- He, Q.; Liu, J. Sliding mode observer for a class of globally Lipschitz non-linear systems with time-varying delay and noise in its output. IET Control Theory Appl. 2014, 8, 1328–1336. [Google Scholar] [CrossRef]
- Ryu, J.; Gerdes, J.C. Integrating inertial sensors with global positioning system (GPS) for vehicle dynamics control. J. Dyn. Sys. Meas. Control 2004, 126, 243–254. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Fujimoto, H.; Hori, Y. Vision-Based Lateral State Estimation for Integrated Control of Automated Vehicles Considering Multirate and Unevenly Delayed Measurements. IEEE/ASME Trans. Mechatron. 2018, 23, 2619–2627. [Google Scholar] [CrossRef]
- Fiengo, G.; Lui, D.G.; Petrillo, A.; Santini, S.; Tufo, M. Distributed Robust PID Control For Leader Tracking in Uncertain Connected Ground Vehicles with V2V Communication Delay. IEEE/ASME Trans. Mechatron. 2019, 24, 1153–1165. [Google Scholar] [CrossRef]
- Dasgupta, S.; Raghuraman, V.; Choudhury, A.; Teja, T.N.; Dauwels, J. Merging and splitting maneuver of platoons by means of a novel PID controller. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Tiganasu, A.; Lazar, C.; Caruntu, C.F. Cyber Physical Systems-Oriented Design of Cooperative Control for Vehicle Platooning. In Proceedings of the International Conference on Control Systems & Computer Science, Bucharest, Romania, 29–31 May 2017; pp. 21–27. [Google Scholar]
- Ma, Y.; Li, Z.; Malekian, R.; Zhang, R.; Song, X.; Sotelo, M.A. Hierarchical Fuzzy Logic-Based Variable Structure Control for Vehicles Platooning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1329–1340. [Google Scholar] [CrossRef]
- Lin, Y.C.; Nguyen, H.L.T. Adaptive Neuro-Fuzzy Predictor-Based Control for Cooperative Adaptive Cruise Control System. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1054–1063. [Google Scholar] [CrossRef]
- Ibrahim, A.; Goswami, D.; Li, H.; Soroa, I.M.; Basten, T. Multi-layer multi-rate model predictive control for vehicle platooning under IEEE 802.11p. Transp. Res. Part C Emerg. Technol. 2021, 124, 102905. [Google Scholar] [CrossRef]
- Yu, K.; Yang, H.; Tan, X.; Kawabe, T.; Guo, Y.; Liang, Q.; Fu, Z.; Zheng, Z. Model Predictive Control for Hybrid Electric Vehicle Platooning Using Slope Information. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1894–1909. [Google Scholar] [CrossRef]
- Liu, P.; Kurt, A.; Ozguner, U. Distributed Model Predictive Control for Cooperative and Flexible Vehicle Platooning. IEEE Trans. Control Syst. Technol. 2019, 27, 1115–1128. [Google Scholar] [CrossRef]
- Kwon, J.W.; Chwa, D. Adaptive Bidirectional Platoon Control Using a Coupled Sliding Mode Control Method. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2040–2048. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J.; Liao, F.; Teo, R.S.H. Distributed Adaptive Integrated-Sliding-Mode Controller Synthesis for String Stability of Vehicle Platoons. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2419–2429. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Yan, J.; Guan, X. Distributed Integrated Sliding Mode Control for Vehicle Platoons Based on Disturbance Observer and Multi Power Reaching Law. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3366–3376. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Wang, L.; Zuo, Z.; Guan, X. Integral Sliding Mode Control Using a Disturbance Observer for Vehicle Platoons. IEEE Trans. Ind. Electron. 2020, 67, 6639–6648. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. Adaptive Fault-Tolerant Control of Platoons with Guaranteed Traffic Flow Stability. IEEE Trans. Veh. Technol. 2020, 69, 6916–6927. [Google Scholar] [CrossRef]
- Guo, X.G.; Wang, J.L.; Liao, F.; Teo, R.S.H. CNN-Based Distributed Adaptive Control for Vehicle-Following Platoon With Input Saturation. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3121–3132. [Google Scholar] [CrossRef]
- Li, M.; Li, S.; Luo, X.; Fan, Y.; Guan, X. Distributed recursive terminal sliding mode control for vehicular platoon systems with mismatched disturbances. Trans. Inst. Meas. Control, 2024; early access. [Google Scholar] [CrossRef]
- Zheng, X.; Li, S.; Luo, X.; Zhang, Y.; Li, X.; Guan, X. Fast Distributed Platooning of Connected Vehicular Systems With Inaccurate Velocity Measurement. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5996–6006. [Google Scholar] [CrossRef]
- Chang, S.; Wang, Y.; Zuo, Z. Fixed-Time Active Disturbance Rejection Control and Its Application to Wheeled Mobile Robots. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7120–7130. [Google Scholar] [CrossRef]
- Boo, J.; Chwa, D. Integral sliding mode control-based robust bidirectional platoon control of vehicles with the unknown acceleration and mismatched disturbance. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10881–10894. [Google Scholar] [CrossRef]
- Yan, Y.; Du, H.; Han, Q.L.; Li, W. Discrete multi-objective switching topology sliding mode control of connected autonomous vehicles with packet loss. IEEE Trans. Intell. Veh. 2022, 8, 2926–2938. [Google Scholar] [CrossRef]
- Lin, M.F.; Liu, C.L.; Zhang, Y.; Chen, Y.Y. Distributed adaptive sliding-mode control for 2-D plane vehicle platoon with prescribed performance and angle constraint. ISA Trans. 2024, 145, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Luo, X.; Zhang, Y.; Guan, X. Distributed integrated sliding mode control via neural network and disturbance observer for heterogeneous vehicle systems with uncertainties. Trans. Inst. Meas. Control 2023, 45, 2204–2215. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J.; Liao, F. Neuroadaptive quantized PID sliding-mode control for heterogeneous vehicular platoon with unknown actuator deadzone. Int. J. Robust Nonlinear Control 2019, 29, 188–208. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. A new quadratic spacing policy and adaptive fault-tolerant platooning with actuator saturation. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1200–1212. [Google Scholar] [CrossRef]
- Cacace, F.; Germani, A.; Manes, C. An observer for a class of nonlinear systems with time varying observation delay. Syst. Control Lett. 2010, 59, 305–312. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).