1. Introduction—Induction Motors
Electric motors are used in a variety of industries, ranging from home electronics to aviation and including automotive and aerospace. Highly efficient motors can bring substantial advantages, such as minimizing energy expenditures and lessening greenhouse gas emissions. Thanks to its high starting torque, sufficient speed control, and fair overload power, a particular form of motor known as an induction motor has gained popularity in recent years [
1]. The interactions between the magnetic field formed by the stator winding and the cage bar generate mechanical power [
2]. Furthermore, since rare-earth metals are in short supply, induction motors, which are a form of non-magnetic motor, are emerging as a promising choice. However, a major downside of induction motors is their underlying high heat factor, which affects their lifetime and performance.
On the other hand, it is crucial to understand the rotor temperature of squirrel-cage induction motors (SCIMs) to guarantee their steady and stable operation. Rotor overheating seriously affects the end rings and rotor bars [
3]. SCIMs are mainly used in cases where the motor needs to operate at a constant speed and should start by itself. Squirrel-cage induction motors also have many applications in the industrial sector. These motors need a very low level of maintenance, so most industries prefer the usage of SCIMs in these types of situations. Three-phase induction motors (IMs) are used in woodworking machines, compressors, elevators, and conveyors in the mining industry, the chemical industry, the automotive industry, and in railway applications [
4,
5]. The widespread use of squirrel-cage induction motors in various applications can be attributed to their simple structure, high reliability, and affordability. As electric motors continue to expand their reach in various industries, it becomes crucial to monitor their conditions and diagnose unforeseen problems and faults that may occur during operation, such as overheating of the rotor and stator or different types of faults in these components [
6,
7,
8].
Figure 1 shows the structure of an SCIM and its squirrel-cage rotor. Under normal operation, most of the heat generated by the motor’s losses is dissipated through heat transfer to the surrounding environment. However, factors such as heavy overloading, prolonged starting, or impaired cooling conditions during operation (due to a broken cooling fan or clogged motor casing) can affect the motor’s cooling capability [
9]. When the cooling capacity of an SCIM is compromised, the temperature of the rotor bars and end rings, stator windings, and their insulation can surpass their maximum thresholds [
10]. Therefore, the real-time and accurate thermal monitoring of the SCIM’s temperature is critical in order to minimize thermal damage and ensure reliable and safe operation [
7].
Estimating an SCIM’s rotor temperature is carried out by the thermal monitoring technique, which involves three methods. The first method estimates the rotor temperature using SCIM parameters such as the rotor resistance. The second method uses estimators that predict the rotor temperature according to the SCIM’s thermal model. The third method combines the first and second methods. However, since the temperature estimation methods consider large parts of the SCIM, they cannot identify the rotor’s local hotspots. Therefore, methods of directly measuring the rotor temperature are superior to estimation methods in this regard [
11].
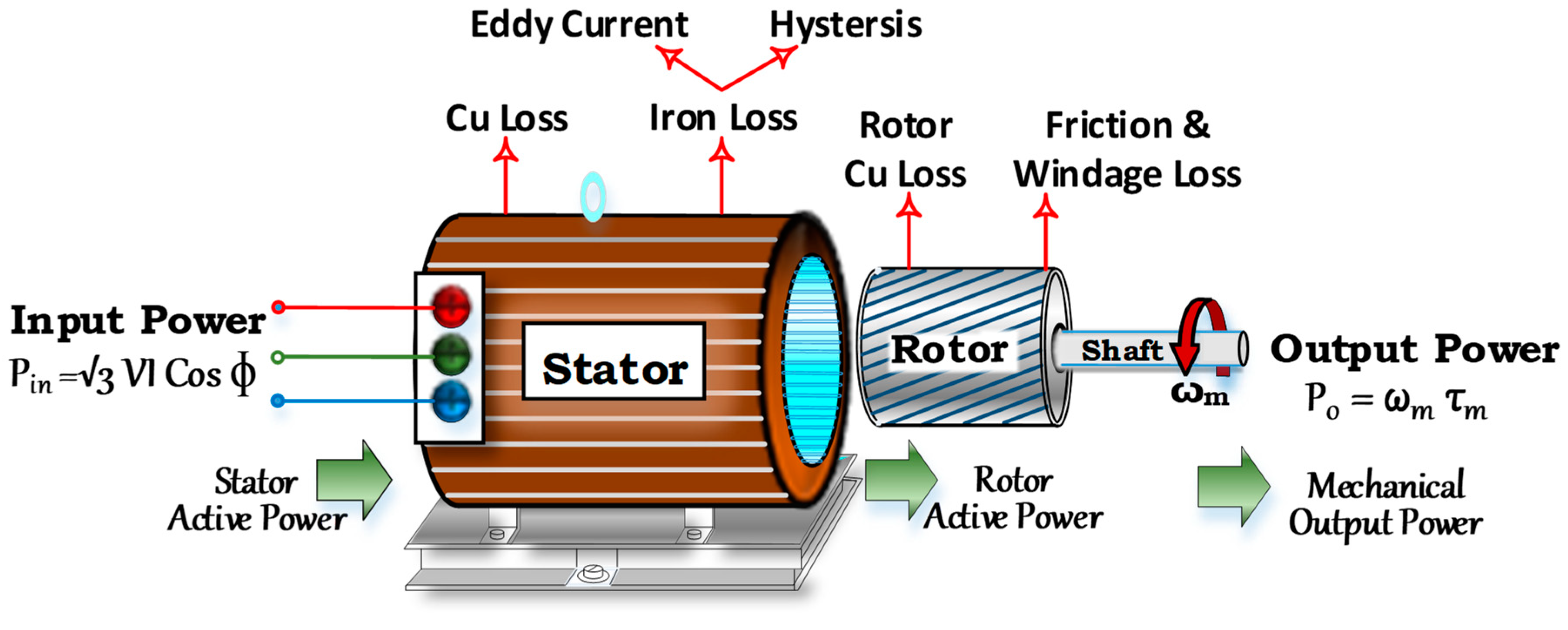
In this paper, the losses and hotspots in a squirrel-cage induction motor are listed and briefed. The high temperatures caused by these losses and hotspots and their influence on the performance of the induction motor are briefed. A steady-state analysis of a three-phase IM using a popular computation approach, the lumped-parameter thermal network (LPTN) modeling method, is explained as it is super-fast, mathematically super-simple, and easy to implement, and this method is used to model the main heat transfer paths. The applicability of the thermal investigation through another outstanding computation technique, the finite element method (FEM), is also discussed, as induction machines with components with large temperature gradients take time to process, unlike with thermal network modeling. Various experimental works on the motor efficiency of copper and aluminum rotors are discussed. Various cooling schemes such as water cooling and oil cooling employed for the cooling of the induction motor are highlighted. Also, methods for improving the efficiency, such as introducing nano-fluids into the coolant pipes and changing the material of the casing, the stator, and the rotor, are presented.
1.1. Losses in a Squirrel-Cage Induction Motor
Every electrical machine has losses in the form of heat. These losses can be separated into I
2R losses, iron core losses, eddy-current losses, hysteresis losses, surface losses, losses because of flux pulsation, and mechanical losses [
12,
13,
14]. Mechanical losses cannot be estimated analytically, so these losses will not be considered in the following simulations.
I
2R losses in the stator and rotor windings can be represented with Equation (1).
where
R1 and
R2 represent the winding resistance,
m represents the number of phases, and
I is the supply current.
Iron core losses can be calculated by Equation (2).
The
β coefficient depends on the lamination used,
P1,0 represents the specific losses of the iron used,
f represents the frequency of the supply,
kdj represents the coefficient of heterogeneous distribution of the FD,
Bj is the average FD, and m
j represents the magnetic circuit weight of division. The surface losses of the iron core in the air gap are described by:
D1 represents the inner diameter of the stator, α is the coverage coefficient of poles,
le is the stator/rotor packet length,
K0 is the surface loss factor,
Q1,2 is the number of slots,
n is the RPM,
td1 is the slot pitch, and
βδ is the pulsation in air gap FD.
β0x depends on the ratio of slots opening and the air gap length in the stator teeth. The pulsating-magnetic-flux-caused set teeth losses are described by:
n is the RPM, mj1,2 is the stator/rotor teeth weight, Bp1,2 is the FD magnitude of the saturating stator/rotor teeth, and Q1,2 is the number of slots.
1.2. Hotspots in a Squirrel-Cage Induction Motor
An induction motor is designed to work according to industrial standards; sometimes, it produces heat more than what is predicted, necessitating experimental research on the heat development in the motor, as shown in
Figure 2. In general, heat is produced everywhere in the motor, but some specific parts play a vital role in producing the energy, and studying those parts (as different parts will have different temperature limits) could result in a new analysis and scope of improvement in that area, which could increase the efficiency of the electric motor as a whole. Bearings and stator windings are very important for a motor to work efficiently [
13,
15]. Since the winding is a major source of heat and its insulation is thermally sensitive, lowering the winding temperature is critical to improving the motor’s stability. An enhanced power loading and a high torque density necessitate a wide-end winding. The losses in the system are controlled by those from the winding owing to the reduced speed and application of high torque [
13].
Increased temperature is the largest influencing factor of the efficiency of induction motors, as shown in
Figure 3. An elevated temperature has a consequence on numerous elements of motor function. An induction motor’s efficiency declines as the winding temperature increases. As the winding temperature is raised, the input energy consumption increases. Raising the winding temperature of the motor induces the motor torque to fall and the motor efficiency to deteriorate. The stator winding temperature is critical to understand, as it damages the insulation system since high temperatures affect the life span of the stator. The temperature affects the winding impedance and the magnetic flux density. Whenever the temperature of the motor rises, the winding impedance increases. This may harm the motor’s maximum torque potential at maximum speed as well as its efficiency. Whenever the temperature of the material rises, atomic oscillations cause previously oriented magnetic dipoles to “dynamically resize”, resulting in a drop in the intensity of the magnetic flux. Hence, the flux density of the magnetic materials will diminish as the temperature rises. The torque falls as the magnetic field intensity decreases. As a result, a drop in the magnetic flux and an increase in the inductance will have a substantial influence on the motor’s efficiency. The operating temperature of the motor has the highest influence on the element durability for both the bearings and the stator winding. An excessive bearing temperature will degrade the lubrication system, leading to the need for frequent lubrication, as shown in
Figure 3 [
17,
18].
To remove heat from the motor, the forced convection method is used with fan-cooled motors. Various factors like the speed of the motor, the air temperature around it, and tribology factors impact the bearing temperature loss. However, the primary loss of heat dissipation is produced at the stator of the motor. The temperatures at different parts of the squirrel-cage induction motor examined in this study at different operation times are listed in
Table 1.
As depicted in
Table 1, the highest temperature, i.e., 43.8 °C, was recorded at the rotor tooth region, and the lowest temperature, i.e., 40.8 °C, was recorded at the shaft surface. The temperature at the majority of the components was recorded in the range of from 40.6 °C to 46 °C. The recorded temperatures were quite low because they were recorded after a short time interval. Nevertheless, these temperatures would be bound to increase as the time of the operation increases. Hence, the thermal management of an electric machine is vital to safeguarding the machine and its efficiency. An analysis of the temperature rise under various cooling settings makes it simple to select an appropriate cooling strategy [
18].
2. Thermal Analysis of High-Efficiency Three-Phase Cage Induction Motors
2.1. LPTN—Lumped-Parameter Thermal Network Modeling Method, a Computational Approach
Thermal network modeling divides the motor into simple thermal elements comprising combinations of modes of heat transfer, such as radiation, convection, and conduction [
19]. The thermal network of an IM is not much different if we think of the electric resistance as thermal resistance, current sources as power sources, electric capacitors as thermal capacitors, voltage as nodal temperatures, and the current flowing through resistance as the power flow. All these thermal resistances, thermal capacitance, and component geometries of a motor can be determined mathematically. These parameters and associated losses are fitted into thermal networks to obtain the temperature distributions across the motor at different operating conditions [
16,
20].
A steady-state analysis of a three-phase IM can be carried out using thermal resistance and thermal sources amid the motor component nodes; however, with transient analysis, the thermal capacitance is used to observe the internal energy change in the components over time. To find the temperatures of various components, a network founded on a lumped-parameter thermal network could be established, and the geometry of the components and their thermal properties could be used to express the developed model [
21,
22]. This would have the advantages of being super-fast, mathematically super-simple, and easy to implement, but it would need some experience to model the main heat transfer paths accurately. This method assumes that the temperature gradient within a solid is negligible [
23]. The model could be upgraded by increasing the number of nodes and accurately designing heat flow directions [
24]. Motor-CAD and Open Modelica are some of the software programs used to model thermal networks [
19,
25].
Badran et.al. [
26] used a Y 90S-2 three-phase squirrel-cage rotor induction motor and produced a thermal network with 10 nodes and 14 thermal resistances. The stator of the motor had networks for the stator iron, stator windings, and end windings. The heat transfer to the stator from the rotor windings through the air gap occurred immediately with an insignificant effect on the stator teeth. Finally, the rotor, stator, and frame were connected through thermal resistances. The following components are those that were considered for modeling the thermal networks in this study: the rotor bars, slot stator windings, stator core, right end windings, right end-cap air, left end windings, left end-cap air, round frame, right side frame, and left side frame. The models were made based on the main heat flow paths as represented in the motor shown in
Figure 4 and
Figure 5.
The heat flow can be written as the induced heat transferred from the rotor bars to the stator windings through the air gap. This heat would then flow to the stator iron followed by the round frame via convection to the atmosphere. There is heat transfer from the stator end windings and rotor bar sides to the end-cap air by convection, and, finally, the side frame passes it on to the atmosphere by convection. The heat sources are the losses generated in the induction motor [
26]. The thermal behavior of a node in an induction motor can be represented by the following equation:
In other words, the rate of energy stored within the system is the difference between the heat inflow rate to the system and the heat outflow rate from the system plus the rate of heat generation within the system [
26,
27].
- (i)
Conduction
- (ii)
Convection
Heat transfer through the air gaps can be described by Taylor’s number and can be used to find the convection coefficient [
28,
29].
- (iii)
Radiation
2.2. Thermal Investigation through Finite Element Method (FEM), a Computational Approach
In finite element examination, the governing equations contain finite elements that are joined to a large group of equations that represent the physics of the problem. This method is usually used for machines with components with large temperature gradients and takes time to process compared to thermal network modeling [
19]. The capacity to solve nonlinear, circular geometry, and time-dependent problems make FEA superior to other numerical methods. ANSYS is one of the software programs used for finite element analysis. The Biot–Fourier equation is used assuming the heat flow is transient.
T is the temperature, c is the specific heat capacity, t is the time, ρ is the density, and Q is the internal heat generation.
Usually, there are two kinds of boundary conditions in thermal analysis, namely, Dirichlet’s condition and Neuman’s condition. A constant temperature is set for a solid body surface using Dirichlet’s condition. Neuman’s condition is presented at the cooling surface through the heat transfer coefficient. The HTC can be calculated analytically from Newton’s law in the following equation [
12]:
The HTC can be determined through CFD:
where
λ is the fluid thermal conductivity,
d is the specific diameter of the solid at the boundary,
q is the heat flux,
Ts is the solid body temperature,
Tf is the fluid temperatures, and
Nu is the Nusselt number, which is represented as:
µ is the viscosity, and c is the specific heat of the fluid.
The thermal utilization of an induction machine can also be found using CFD. To make sure that CFD simulations are trustworthy, the results obtained by these simulations need to be validated properly [
30].
2.3. Experimental Analysis to Compare the Motor Efficiency of Copper and Aluminum Rotors
Cheng et al. [
31] performed certain calculations comparing the efficiency of copper and aluminum rotors for induction motors. To validate their results, certain experiments were carried out involving both of the induction motors (aluminum and copper) along with other test equipment items like a MagtrolHD-825 Dynamometer, a YASKAWA Varispeed G7 Inverter, and so on.
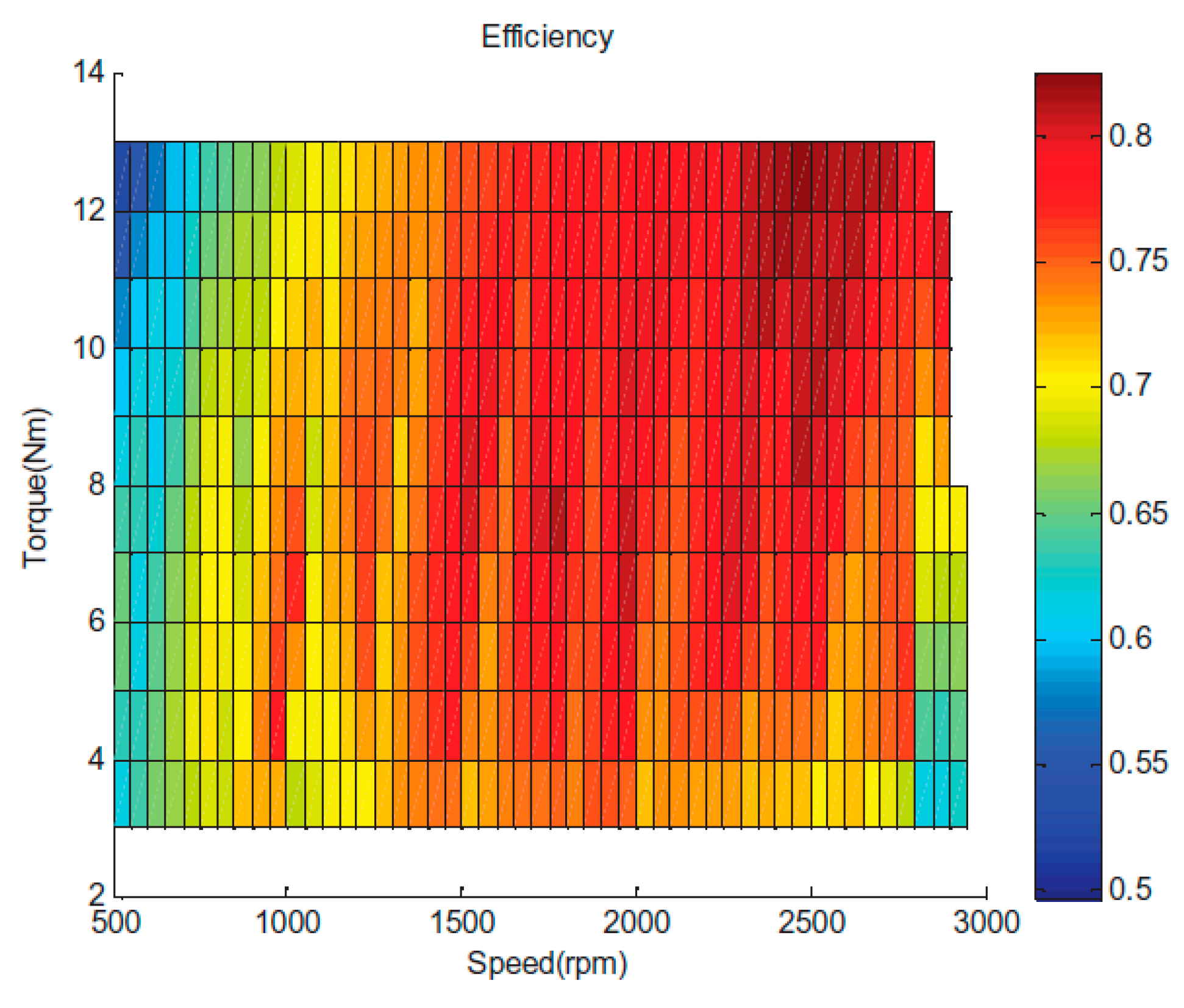
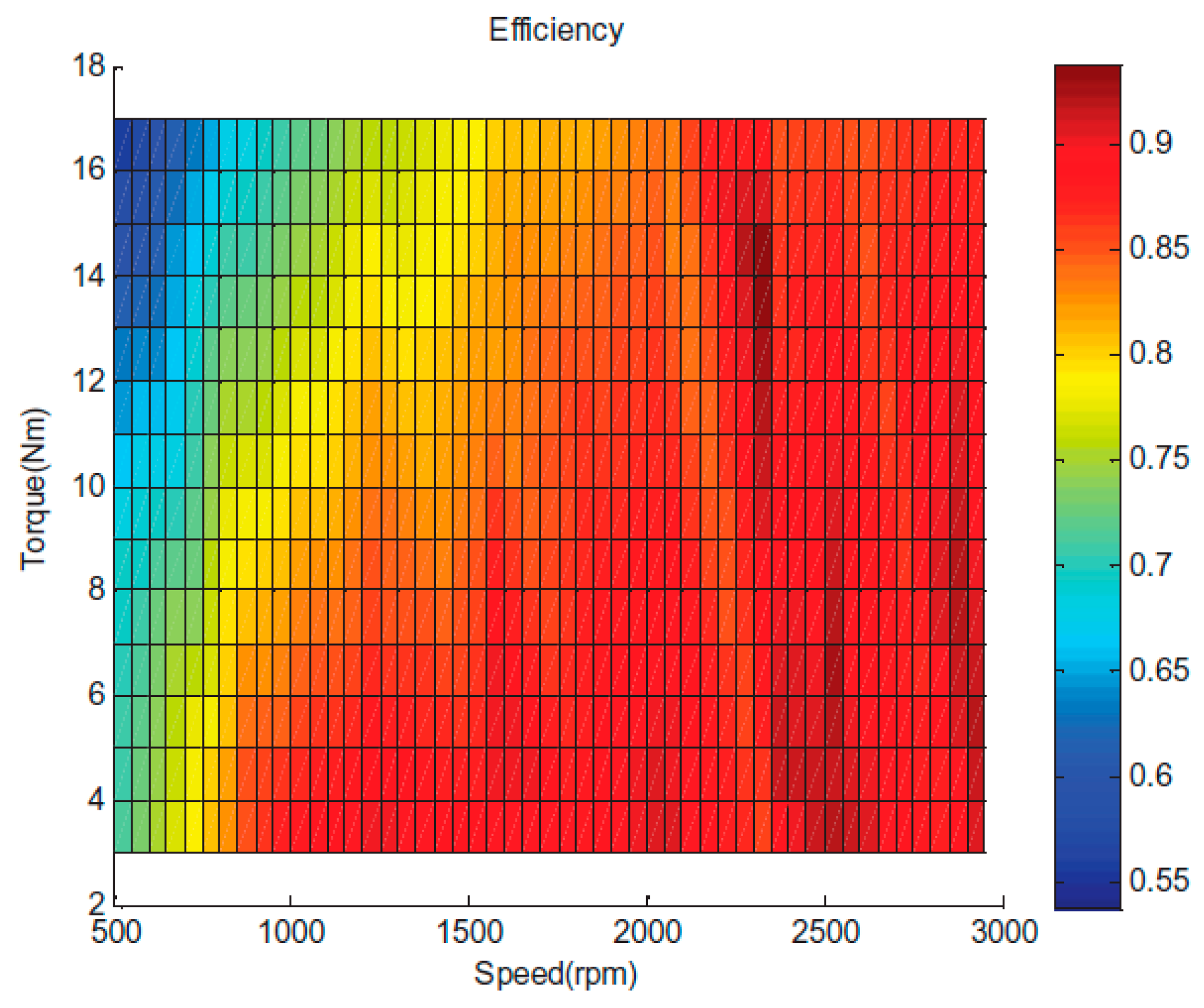
The color indicator for efficiency was mentioned in
Figure 6 and
Figure 7. The brightness of the red color indicates a higher efficiency of the rotor. So, it is quite evident that the area of red color in the copper graph,
Figure 7, is visibly greater than that of the aluminum graph. For example, with the rotor speed set at 2500 rpm and at 10 Nm torque, the copper rotor was 15% more efficient compared to the aluminum rotor. This ultimately suggests that the efficiency of a motor with a copper rotor is higher in comparison to a motor with an aluminum rotor [
31].
The peak efficiency of the motor with an aluminum rotor was obtained at 2500 RPM and 13 Nm torque, whereas the peak efficiency of the motor with a copper rotor was obtained at 2300 RPM and 15 Nm torque. So, clearly, the speed is directly proportional to the efficiency of the motor. The lowest efficiencies were achieved at both the extremes of the experiment, i.e., at high torque and low speed. The lowest efficiency of the motor with an aluminum rotor was obtained at 500 RPM and 13 Nm torque. In the same way, the lowest efficiency of the motor with a copper rotor was obtained at 550 RPM and 17 Nm torque. So, clearly, high torque is indirectly proportional to the efficiency of the motor.
One more major statistical inference from
Figure 6 and
Figure 7 is that the effectiveness of the IM with a copper rotor was 87% at a higher RPM. This percentage could even reach 90% at some discrete points in the graph [
31], whereas for the aluminum rotor, the efficiency was 76%. The utilization of steel and copper in an effective manner, improving the topology and the geometry of the motor, and enhancing the design along with the cooling properties are the main aspects for achieving the optimum design of an induction motor, which ultimately leads to an increase in the efficiency of the whole system [
32].
The efficiency of a squirrel-cage induction motor with a copper rotor and one with an aluminum rotor depends on several factors, including the torque and speed, as mentioned in the above experimental statistics. The efficiency in an electric motor is a measure of how effectively it converts electrical power into mechanical power. In general, the efficiency can be influenced by losses in the motor, including copper losses (also known as I2R losses) and core losses. As the torque and speed increase, the mechanical power output increases, and the copper losses also increase due to the higher current, reducing the motor’s efficiency. However, the effect of the torque and speed on the efficiency depends on the load conditions and the design of the motor. Different motors may have different efficiency profiles.
Comparing copper and aluminum rotors:
− Copper rotors typically have a lower resistance than aluminum rotors, which can lead to lower copper losses and a potentially higher efficiency under heavy loads.
− Aluminum rotors are lighter, which can reduce the moment of inertia and improve the acceleration performance. This can be advantageous in certain applications.
In summary, the efficiency of squirrel-cage induction motors, whether they have copper or aluminum rotors, is influenced by various factors, including the load conditions, design, and materials used. Copper rotors may have an advantage in terms of lower copper losses, but other factors, like the motor size and application, also play a significant role in determining the overall efficiency.
2.4. Experimental Analysis of the Stator of an Induction Motor
Table 2 shows the temperatures corresponding to the slot windings, end windings, and the yoke of the iron core of the stator at a 2880 RPM rotor speed and a torque of 10 N-m. The temperature of the end windings of the water-cooled motor is represented by WaterEW, the temperature of the slot windings is represented by WaterSW, and the temperature at the yoke of the iron core of the stator is represented by WaterYoke. For the air-cooled motor, the temperature of the end windings is represented by WindEW, the temperature of the slot windings is represented by WindSW, and the temperature at the yoke of the iron core of the stator is represented by WaterYoke [
31].
Table 2 and
Table 3 suggest that the temperature was decreased by 39.49% at the end windings, 41.67% at the side windings, and by a huge margin of 56.95% at the yoke of the induction motor with the usage of water as a coolant instead of air as a coolant. It is also noted that almost equal temperatures (79 °C) were recorded at the end windings and the slot windings when water was used as a coolant. As far as the water-cooling motor is concerned, the end windings had the highest temperature, and the yoke region experienced the highest temperature change [
31]. From the above analysis, it was deduced that for greater efficiency, copper rotors should be used, and when it comes to achieving better reliability, water-cooled motors are the best compared to air-cooled motors [
33].
2.5. Materials for Parts of Squirrel-Cage Motor
Kim et al. (2002) designed and investigated a composite squirrel-cage rotor made of composites. Fiber-reinforced composite materials were used for making the spindle shaft, and an epoxy composite containing magnetic powder was used for the squirrel-cage rotor. The thermal coefficient, thermal conductivity, magnetization properties, and storage modulus were measured, and the optimal design conditions of the squirrel-cage rotor were proposed. Iron powders and ferrite powders were used in the composites and were tested. Both powders were suitable at low temperatures, and the ferrite powder was not suitable at high temperatures. An air-cooling system had to be provided for high-temperature driving conditions, as shown in
Figure 8 [
34].
Usha S. et.al. [
35] investigated aluminum for the casing, rotor bars, and end ring material, Nomex 430 for the stator liner, and silicon steel for the stator slot. It was found that iron could make the motor light and had an improved efficiency at high-speed conditions. Their experimental results indicated that the overall efficiency of the motor was increased by 5%.
Karnavas and Chasiotis (2017) studied the influence of the application of soft magnetic materials on the design and performance of a squirrel-cage induction motor. A total of twenty-two different materials were examined, which included silicon steel, nickel-iron, cobalt iron, amorphous metallic alloys, permalloy powder, sendust powder, and iron powder [
33]. Marfoli et al. (2021) compared the design of squirrel-cages made of aluminum and copper. Copper cages reduced the motor losses but required a higher starting torque. The advantages and disadvantages of using a copper cage were analyzed under different operating conditions [
36].
Kim (2015) analyzed the speed characteristics and starting torque for a squirrel-cage induction motor related to the material properties of the rotor. The results of the transient characteristics were given to a three-phase, four-pole, 5 hp induction motor for calculating the speeds, starting torque, and rotation angle of the rotors. The materials of the model were changed to copper and silicon copper [
37]. Wijaya et al. (2021) studied the effect of different core materials in very-low-voltage induction motors for electric vehicles. The core materials affected the performance of the motor significantly. The performance of the motor was studied with the following three materials: Arnon7, nickel steel carpenter, and M19_24G. It was found that the product cost was the lowest when Arnon7 was used. The efficiency of the motor was 83.27% when nickel steel carpenter was used and 83.10% when M19-24G was used. A power density of 0.37 kW/kg was achieved with M19_24G, and a power density of 0.38 kW/kg was achieved with Arnon7 [
38].
The performance of the motor can also be improved by changing the material used for casing the stator and rotor [
22,
39]. Aluminum 61% IACS was used to make the housing of a motor and for the rotor bars and end ring instead of cold-rolled steel. The losses that occur in various parts of the motor could be minimized by using aluminum, resulting in an improvement in the cooling performance. Silicon steel has good electrical resistivity and is very useful for reducing eddy currents, hence it being used for stator back iron instead of M-19 Ga steel [
20]. After modifying the material and comparing it to a standard motor, there was an increase of up to 5% in terms of efficiency. A comparison of a selection of materials that can be used for the components of SCIMs is listed in
Table 4.
3. Cooling Strategies of High-Efficiency Three-Phase Cage Induction Motors
A cooling system is essential for minimizing the energy losses due to heat spots formed in all electric motors [
40]. Cooling is mostly carried out based on the slot conduction and end windings in the motor. A cooling jacket is also helpful for the cooling process. A system with a good efficiency is crucial to minimizing the working temperature of the hotspots in a motor, especially in the copper windings. Therefore, reliable and precise modeling of the cooling system and the design of the motor is very important for the optimization of the thermal management of the motor [
13,
41].
Different types of cooling methods are available, but the water-jacket-cooling scheme dissipates >99% of the heat formed. The residual heat is dissipated in the form of a convection process, where the heat converts solids to either gas or liquids, which can be emitted naturally or by force. In a liquid-cooling system, a mixture of water and glycol in an equal ratio is generally used, and the air formed after absorbing the heat can be forcibly removed employing a fan. Oil cooling takes place by a spraying method, and it is used for cooling the magnets that are inside the rotor [
42].
Liquid cooling is required to keep the temperature in the windings under the permissible limits in greater-power-density motors [
43]. Experiments were conducted on the prototype of an electric motor to calculate the effectiveness of a heat pipe thermal management scheme. The temperature of the exterior surface of the IM was reduced to 84.05 °C, or from 162.11 °C to 78.06 °C, with a thermal resistance of 0.21 °C/W and at a heat load of 120 W. The best pulsating heat pipe effectiveness was indicated at a heat load above 60W [
44].
In general, the most commonly used cooling methods applied in motors are air cooling and water cooling. Air cooling generally involves a forced-convection method, in which air is forced into the motor to cool the rotor and stator. When the air is forced through the rotor, the air gets heated up (the temperature would be higher than the stator, thus providing extra heat to the stator) resulting in a poor motor performance [
42].
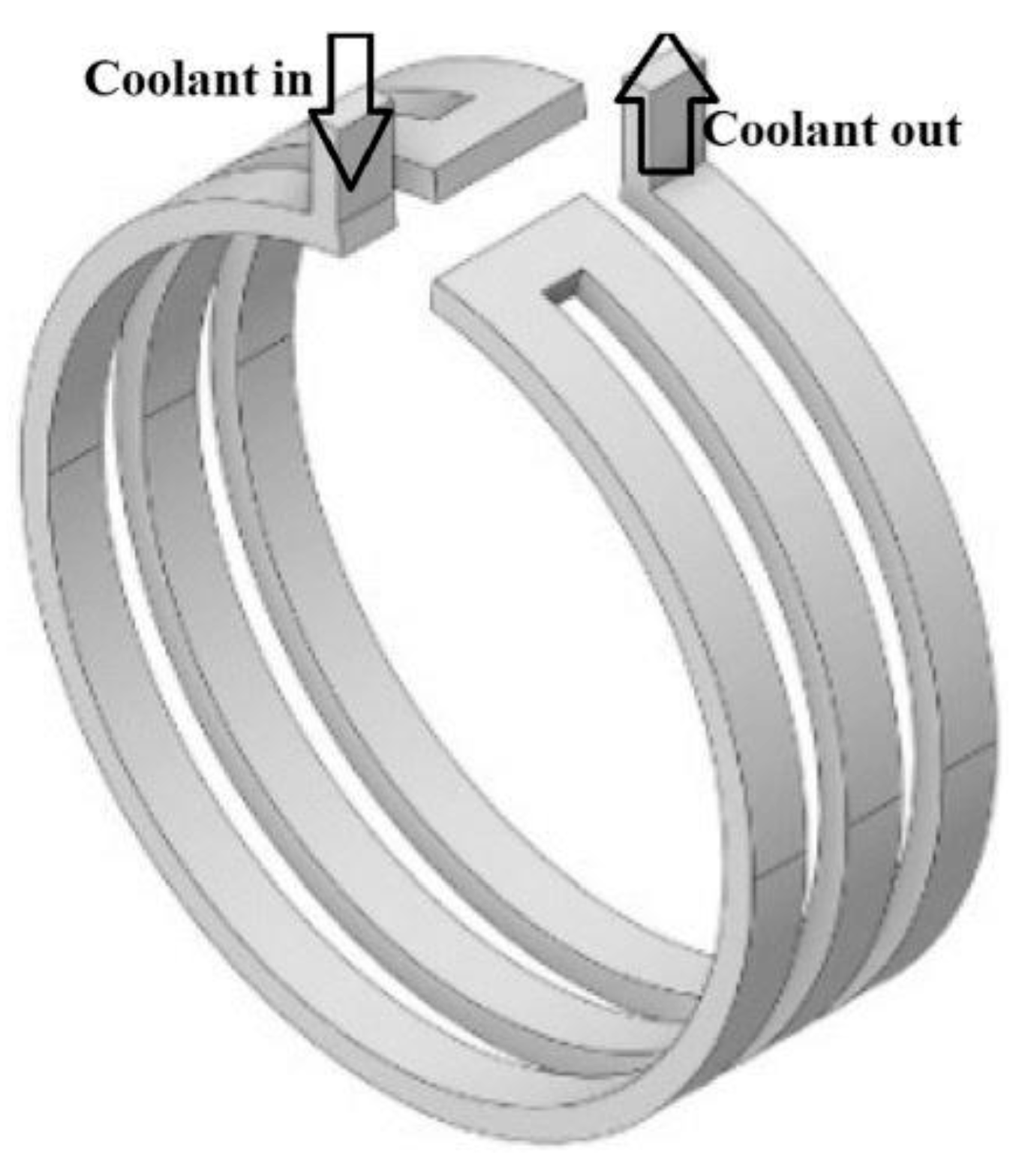
3.1. Water-Cooling System
The basic principle of a water-cooling system is conduction. Water flows in a pattern that is combined with the housing of the induction motor. The flowing water absorbs heat from the stator, thus enabling the cooling of the motor. Two types of water flow systems have been examined, namely axial water flow and tangential water flow, as shown in
Figure 9 and
Figure 10. The water quantity and velocity influence the heat transfer between the frame and the water. Under simulation conditions, heat spots generated by water turbulence can be calculated [
45].
Reynold’s average Navier–Stokes equation is used to describe the flow of a non-compressible liquid [
46].
η is the dynamic viscosity, U is the averaged velocity field,
ρ is the density of the fluid, U is the velocity vector, and f is the volumetric force vector. The physics of transient heat conduction are given below:
ρ is the mass density, cp is tie specific heat capacity, T is the temperature, λ is the heat conductivity, and P is the heat generation rate.
The boundary conditions of convection and radiation for the water-cooled thermal field are given by:
Tf is the frame temperature, Tw is the water temperature, h is the frame, and HTC is the fluid convective heat transfer coefficient.
Submersible motor pumps are generally squirrel-cage motors that are submerged for performing cooling through the motor housing, which results in a high power density but a lower efficiency, as shown in
Figure 11 [
47,
48].
3.2. Oil-Cooling Systems
The performance of an electric motor is essentially restricted by the magnitude of heat that can be successfully dissipated. The oil-cooling technique involves the spraying of oil onto the copper coils that cannot be cooled using water-cooling techniques, as the direct cooling method is required to cool the inside of the motor according to research carried out in the past. It helps to maintain the average temperature of the coil. Even though various research works have been conducted on this process, there is no exact conclusion indicating the ideal method to use [
22,
49]. Current signs of progress in IM thermal management include using direct oil spraying or splash-based cooling to improve efficiency [
50,
51].
At present, a direct method is used where a groove is made between the stator and the rotor and oil is sent to cool the coil. Experiments have been conducted where the coil is immersed in the oil. This method results in friction losses between the cooling coil and the rotor. Another method is an injection method where the oil is directly sprayed onto the coil using injectors. Different shapes of injectors have been experimented with to find better spraying characteristics, such as a full-cone nozzle, a flat jet nozzle, dripping, and multi-jets. When a dripping injector is used, the best cooling performance is achieved.
Other methods, like optimizing the copper windings, have shown good improvements in terms of heat generation and the efficiency of the motor itself. The hairpin winding method is the latest modification, which has the benefit of a high efficiency and a high power density in the IM due to the high space factor. The hairpin winding method is shown in
Figure 12, where hairpin-shaped square coils are inserted into the stator slots and are welded at the end turns. This helps in decreasing the gap between the coil windings and also the size of the motor. The cooling performance is also improved with this method, resulting in a high efficiency [
52].
In general, induction motors are cooled by airflow around the housing. Even though this method is cheap, the cooling performance is not good enough for motors being used at high speeds. Therefore, some modifications were made to the existing totally enclosed fan-cooled (TEFC) prototype by inserting holes into the machine, where and oil-cooling circuit is used, as shown in
Figure 13. These holes let the oil flow inside the motor on the active hotspots of the motor such as the stator end-windings and rotor end-rings [
46]. An enclosed water-cooled motor thermal model was also developed and analyzed. A water-cooling jacket was also investigated for radial and axial water flow directions. The measurement and simulation results indicated that the temperatures of the stator winding and the rotor were compared and showed good improvement [
53].
3.3. Natural Water-Cooling Capillaries (NWCC) Method
Cooling through the NWCC approach does not need a large external heat exchanger and external energy. In this method, water is absorbed by capillaries, which are usually made of cotton or jute natural ventilation systems and are mounted to reduce the surrounding temperature of the motor, as shown in
Figure 14. The NWCC scheme is used to decrease the temperature and to protect the shielding of the insulation material. This in turn increases the thermal resisting capacity of the motor, which results in a long life span of the motor. This technique is useful in reducing the neighboring temperatures of the motor [
55].
Needless to say, the above-mentioned methods have their advantages and disadvantages. Water cooling is advantageous in some scenarios because it can absorb a significant amount of heat before reaching its boiling point, making it a reliable cooling medium. It also generally requires less maintenance compared to some other methods. However, there is a potential risk of water leakage, which could damage the motor and the surrounding equipment.
Oil cooling exhibits better heat transfer properties and can efficiently cool the motor windings. In addition, oil cooling offers improved dielectric properties, and the oil can help to insulate the motor windings and protect them from contaminants. However, there is a risk attached to it, as some cooling oils can be flammable, posing a safety risk in certain environments. Setting up oil cooling is comparatively more expensive than air cooling, which sometimes can be a limitation for economical scenarios.
The natural water-cooling capillaries method (NWCC) also has its advantages and disadvantages. It perfectly suits situations where available energy is limited to an extent. Since it relies on natural convection, it consumes less energy compared to forced water-cooling systems. This method can efficiently cool the motor through natural convection without the need for a pump. However, the downside is its limited applicability, as this method may not be suitable for all motor configurations and applications. Designing and implementing capillaries within the motor can be complex and may require custom solutions. The cooling capacity of this method may be limited compared to other active cooling methods like water cooling.
In summary, the choice of cooling method for a squirrel-cage induction motor depends on various factors, including the specific application, operating conditions, and safety considerations. Water and oil cooling are more common in industrial settings, while the natural water-cooling capillaries method is more specialized and may be suitable for certain niche applications.
3.4. Energy Harvesting and Self-Powered Induction Motor with Thermal Analysis
The process of energy harvesting involves the collection and storage of several forms of energy, including solar, thermal, mechanical, and electromagnetic [
56]. Induction motors that are self-powered generate electricity from the rotational energy they store. This is accomplished with a motor-integrated generator [
19]. The rotation of the motor causes the generator to produce electricity, which may then be used to power the electronic devices. The efficiency, dependability, and ease of maintenance are all improved with self-powered induction motors [
57]. Engineers can make accurate predictions about the thermal behavior of the system under a variety of conditions of operation and locate hotspots as well as thermal stress using these methods.
Self-powered induction motors and their surrounding environments are modeled mathematically as part of the thermal modeling process [
58]. This model takes into account the heat produced by the motor as well as the heat that is transferred through the air and the components. By testing the model under a variety of different operating situations, engineers can forecast the temperature distribution across the motor and locate any hotspots. The thermal behavior of these motors can be simulated through computation using appropriate computer software. Engineers can input several running situations into the software to the test and discover any potential thermal problems [
3]. Engineers can evaluate their thermal models and simulations and find inconsistencies between the measured and expected temperature distributions [
32]. Testing can uncover any thermal concerns that are not accounted for by the models and simulations. Both the dependability and the efficiency of self-powered induction motors are dependent on thermal analysis [
59].
The collection of energy is an intriguing potential source of renewable energy. Induction motors that are self-powered can obtain their power from energy harvesting [
60]. Engineers can optimize the thermal behavior of these systems to ensure their continued effectiveness and dependability over the long term. As the need for environmentally friendly power sources grows, technologies like energy harvesting and self-powered induction motors may gain increasing traction [
61]. Thermal analysis is necessary for designing, developing, and perfecting these systems to achieve long-term success, such as lowering both the energy consumption and operational expenses.
3.5. Miscellaneous Methods of Thermal Management
Various schemes of cooling have been researched. One of them involves using baffles inside the coolant pipes as well as introducing nano-fluids into the coolant pipe, which could improve the efficiency of an air-cooled motor [
13]. This might help in achieving effective cooling using a fan. Using different coolants or a mixture of coolants instead of water might also help in achieving effective cooling. Experimenting and changing the liquid flow pattern attached to the housing of the motor that is used for water cooling can also present advantages. At present, the thermal management of mobile and electronic devices is maintained by heat pipes, and there has been a drastic increase in the usage of these pipes in current appliances and devices, and some have even received patent rights. Different types of heat pipes are used for cooling different electronic gadgets. In certain IM cooling devices, the evaporator part of the heat pipe is mounted inside the motor housing. But in some other cases, it is placed within the shaft and the condenser, which is cooled either by a liquid or air is placed outside the housing of the motor [
62].
Numerical results have shown drastic effects of the estimations of the intricate thermal physics occurring in the end region of a more porous end winding geometry; here, the heat removal percentage through the outer frame surges by up to 35%. Furthermore, a lessening of the total internal convective thermal resistance between the end windings and the external frame of about 28% is realized [
63]. A comparison of the existing cooling schemes is listed in
Table 5.
5. Summary
Technologies like energy harvesting and self-powered induction motors may gain more popularity as the demand for greener power sources rises. The thermal behavior of these systems may be optimized to guarantee their long-term reliability and efficiency. The sole objective could be to eliminate thermal issues with the use of modeling and testing, which would enhance the system’s overall performance and reliability. Overheating due to motor losses has a substantial impact on the power coefficient, efficiency, and the insulating glass and components required for the magnetic materials. As a result, the thermal management of an electrical motor is critical to the equipment’s safety and efficiency.
The thermal analysis could be carried out with two computation methods, the lumped-parameter circuit method and the finite element analysis method. LPCM is used for assemblies in which the components have no big temperature gradients, i.e., the temperature is constant at every single point within a particular component. LPCM is fast and needs experience in order to understand the direction of the flow of heat between components. Finite element analysis is used for understanding bodies that have large temperature gradients. FEA is slow and complicated to solve, and it is difficult to take the convective and radiative heat transfer of the cooling fluids into account.
In this paper, aluminum and copper rotors were compared based on their efficiency. From the experimental tests, it was quite evident that the copper rotors were more efficient when compared to the aluminum rotors. At 2300 RPM and 15 Nm torque, the efficiency of the copper rotor came out to be 87%, which was 11% greater than the aluminum rotor. So, in all senses, copper rotors are more efficient compared to aluminum rotors.
The analysis also indicated that the usage of water as a coolant helped the system to decrease the working temperature by 39.49% at the end windings, 41.67% at the side windings, and by a huge margin of 56.95% at the yoke of the induction motor. Cooling the motor could be achieved using many techniques, but the effectiveness of the cooling system depends on the type and size of the motor. After finding the hotspots, the cooling system should be selected based on the part that needs to be cooled. Various cooling techniques are adopted to cool different parts of motors individually.