A New Mixed Fractional Derivative with Applications in Computational Biology
Abstract
1. Introduction
2. The New Mixed Fractional Derivative
- When and , we obtain the Caputo fractional derivative [3] with singular kernel, as follows:
- When and , we obtain the CF fractional derivative [4] with non-singular kernel, as follows:where .
- When , , and , we obtain the AB fractional derivative [5], as follows:
- When and , we find the weighted-AB fractional derivative [6], as follows:
- When , we obtain the GHF derivative [7], as follows:
- When , and (with ), we obtain the power fractional derivative [13], as follows:
- When , , and , we obtain the fractional derivative introduced in [14], as follows:
3. Laplace Transform of the New Mixed Fractional Derivative
- (i)
- The Laplace transform of is given by the following:In particular, we find the following:
- (ii)
- The Laplace transform of is given by the following:In particular, we have the following:
4. The Associated Fractional Integral
- When , we had the following:By taking the inverse Laplace, we obtained the following:Hence,
- When , we had the following:By passage to the inverse Laplace, we obtained the following:which led to:
- (i)
- (ii)
- (iii)
- If , then (15) reduced to the standard weighted Riemann–Liouville fractional integral of order r and to the ordinary integral when and .
5. Fundamental Properties of the New Differential and Integral Operators
6. Numerical Scheme
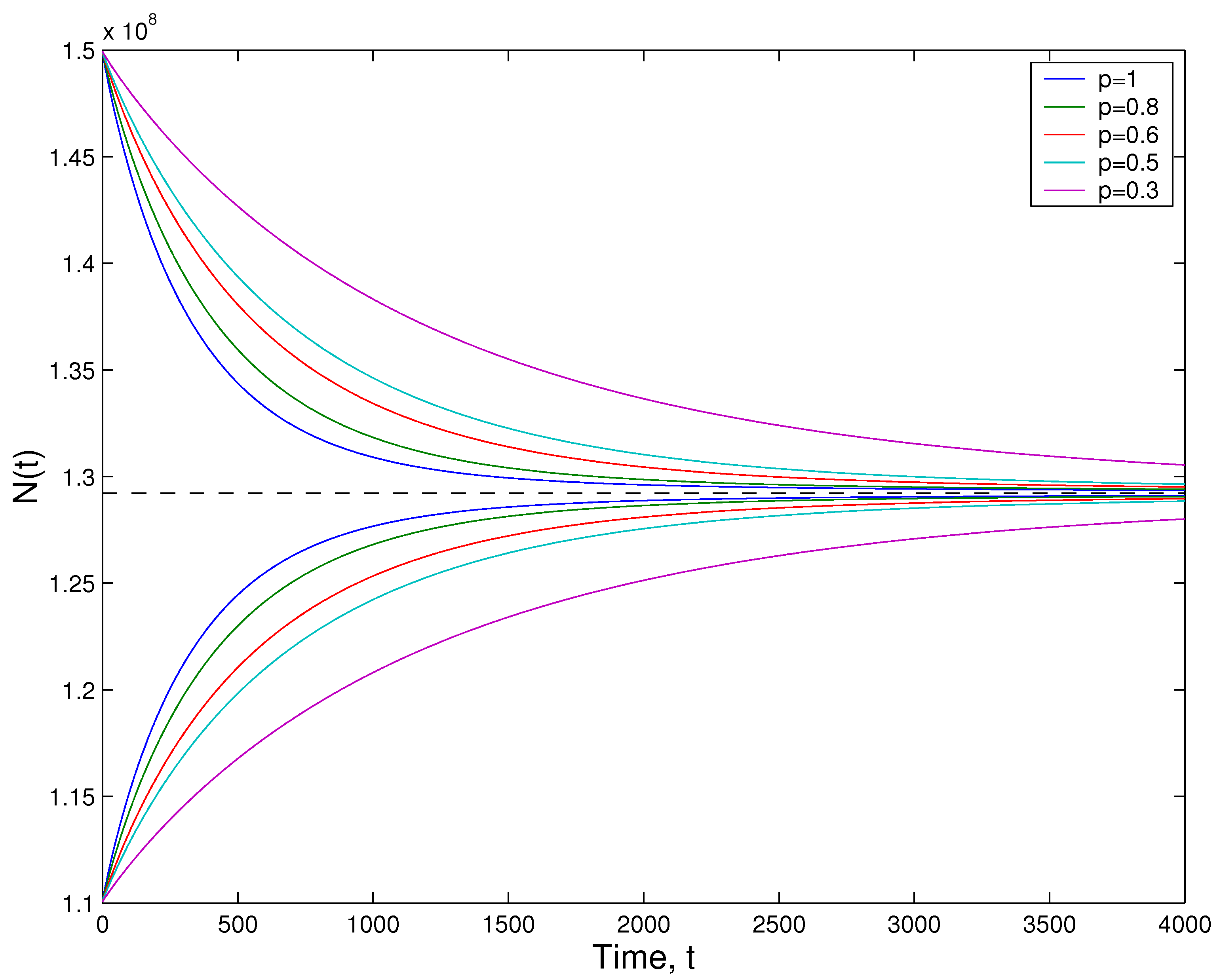
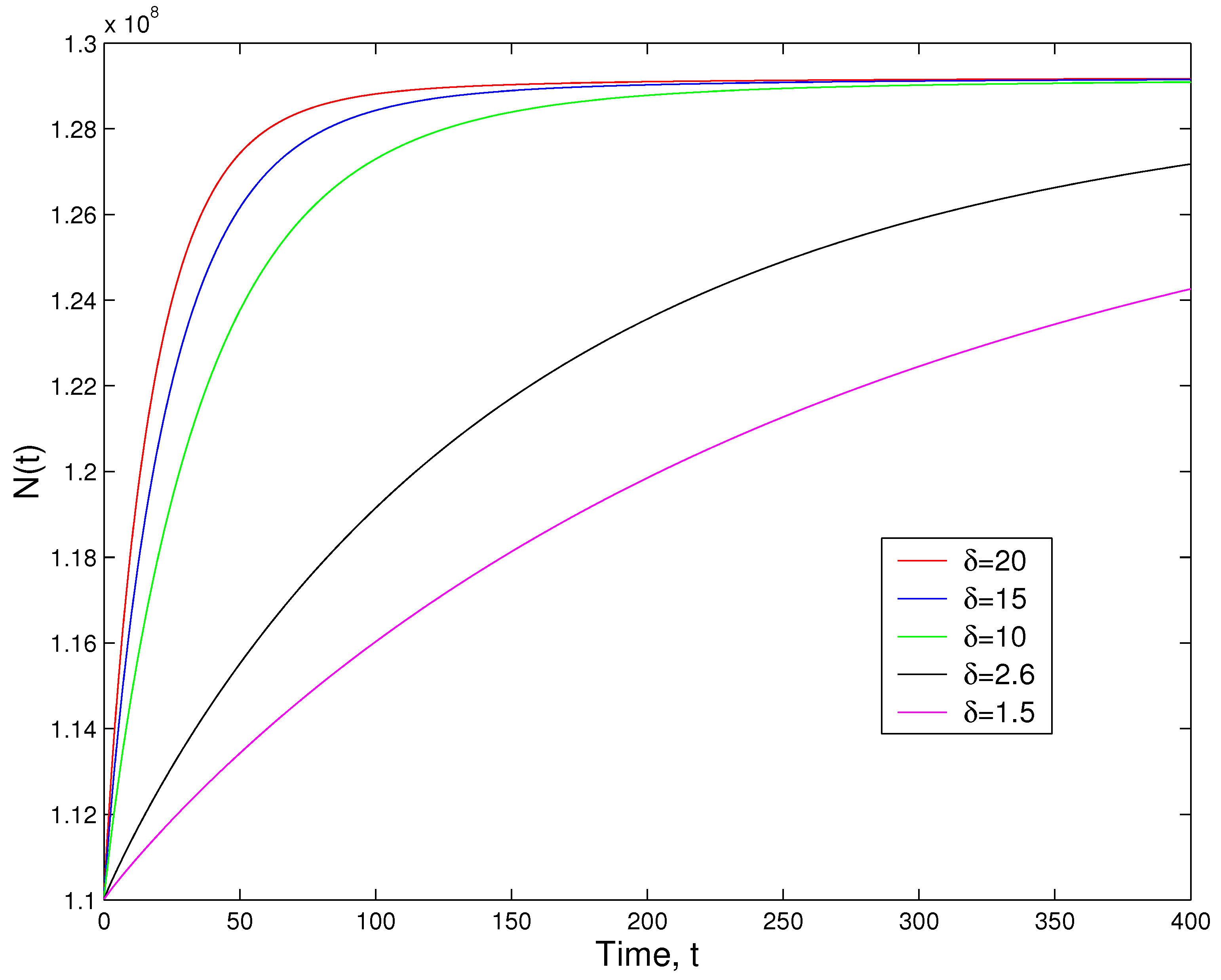
7. Application in Computational Biology
8. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Al-Refai, M. On weighted Atangana-Baleanu fractional operators. Adv. Differ. Equ. 2020, 2020, 3. [Google Scholar] [CrossRef]
- Hattaf, K. A new generalized definition of fractional derivative with non-singular kernel. Computation 2020, 8, 49. [Google Scholar] [CrossRef]
- Hattaf, K. A new class of generalized fractal and fractal-fractional derivatives with non-singular kernels. Fractal Fract. 2023, 7, 395. [Google Scholar] [CrossRef]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Solitons Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Asma, M.Y.; Afzaal, M.; DarAssi, M.H.; Khan, M.A.; Alshahrani, M.Y.; Suliman, M. A mathematical model of vaccinations using new fractional order derivative. Vaccines 2022, 10, 1980. [Google Scholar] [CrossRef]
- Cheneke, K.R.; Rao, K.P.; Edesssa, G.K. A new generalized fractional-order derivative and bifurcation analysis of cholera and human immunodeficiency co-infection dynamic transmission. Int. J. Math. Math. Sci. 2022, 2022, 7965145. [Google Scholar] [CrossRef]
- Lemnaouar, M.R.; Taftaf, C.; Louartassi, C.Y. On the controllability of fractional semilinear systems via the generalized Hattaf fractional derivative. Int. J. Dyn. Control 2023, 1–8. [Google Scholar] [CrossRef]
- Lotfi, E.M.; Zine, H.; Torres, D.F.M.; Yousfi, N. The power fractional calculus: First definitions and properties with applications to power fractional differential equations. Mathematics 2022, 10, 3594. [Google Scholar] [CrossRef]
- Chinchole, S.M.; Bhadane, A.P. A new definition of fractional derivatives with Mittag–Leffler kernel of two parameters. Commun. Math. Appl. 2022, 13, 19–26. [Google Scholar] [CrossRef]
- Hattaf, K. On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology. Computation 2022, 10, 97. [Google Scholar] [CrossRef]
- Hattaf, K.; Hajhouji, Z.; Ichou, M.A.; Yousfi, N. A Numerical Method for Fractional Differential Equations with New Generalized Hattaf Fractional Derivative. Math. Probl. Eng. 2022, 2022, 3358071. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Zitane, H.; Torres, D.F.M. A class of fractional differential equations via power non-local and non-singular kernels: Existence, uniqueness and numerical approximations. Phys. D Nonlinear Phenom. 2024, 457, 133951. [Google Scholar] [CrossRef]
- Wiman, A. Über den fundamental satz in der theorie der funktionen Ea(x). Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A. On some new properties of fractional derivatives with Mittag–Leffler kernel. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 444–462. [Google Scholar] [CrossRef]
- Eikenberry, S.; Hews, S.; Nagy, J.D.; Kuang, Y. The dynamics of a delay model of HBV infection with logistic hepatocyte growth. Math. Biosci. Eng. 2009, 6, 283–299. [Google Scholar]
- Zhou, J.C.; Salahshour, S.; Ahmadian, A.; Senu, N. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef]
- Hendy, M.H.; Amin, M.M.; Ezzat, M.A. Two-dimensional problem for thermoviscoelastic materials with fractional order heat transfer. J. Therm. Stress. 2019, 42, 1298–1315. [Google Scholar] [CrossRef]
- Shymanskyi, V.; Sokolovskyy, I.; Sokolovskyy, Y.; Bubnyak, T. Variational Method for Solving the Time-Fractal Heat Conduction Problem in the Claydite-Block Construction. In Proceedings of the International Conference on Computer Science, Engineering and Education Applications, Kyiv, Ukraine, 21–22 February 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 97–106. [Google Scholar]
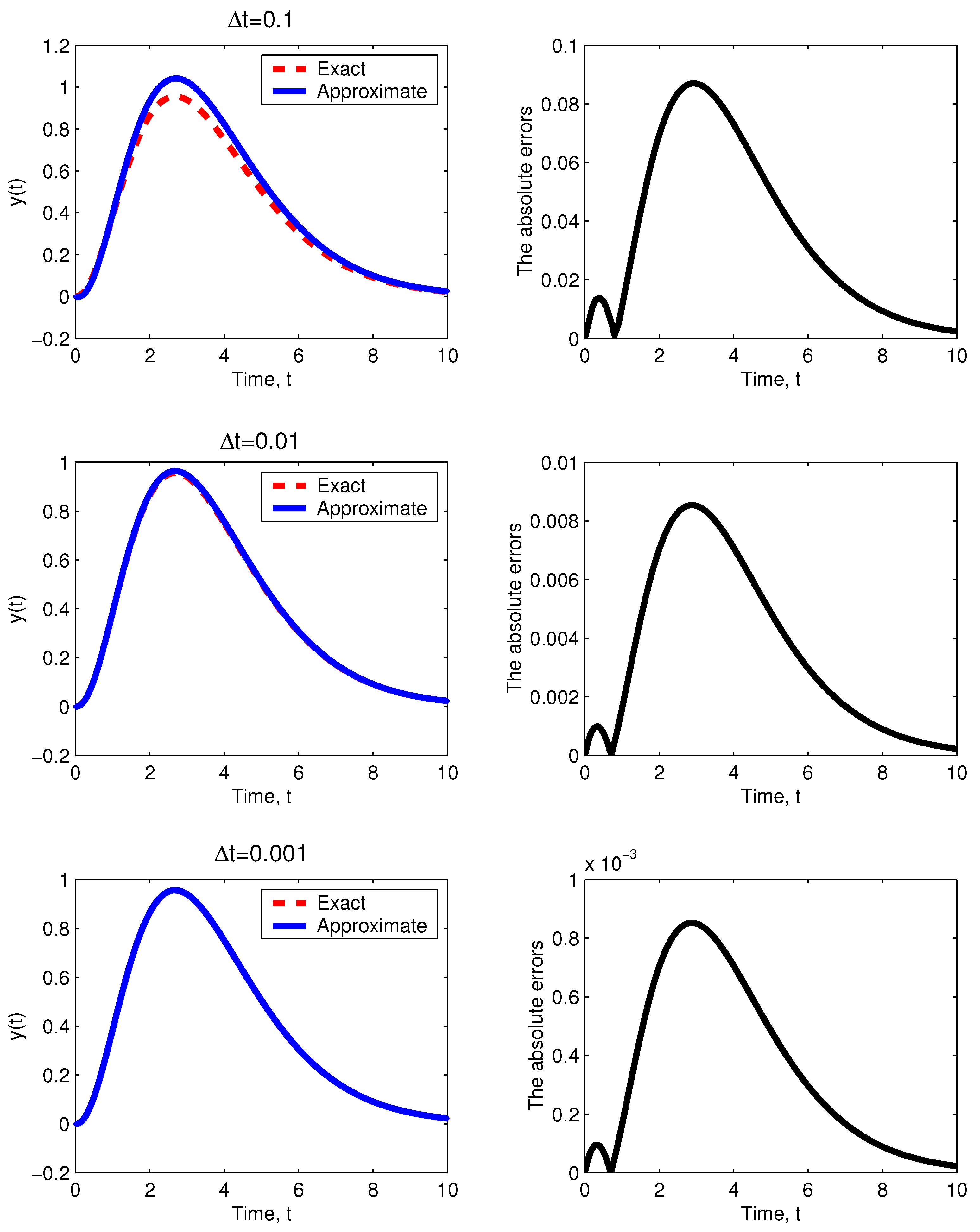
| Discretization Step () | Error |
|---|---|
| 0.1 | |
| 0.01 | |
| 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hattaf, K. A New Mixed Fractional Derivative with Applications in Computational Biology. Computation 2024, 12, 7. https://doi.org/10.3390/computation12010007
Hattaf K. A New Mixed Fractional Derivative with Applications in Computational Biology. Computation. 2024; 12(1):7. https://doi.org/10.3390/computation12010007
Chicago/Turabian StyleHattaf, Khalid. 2024. "A New Mixed Fractional Derivative with Applications in Computational Biology" Computation 12, no. 1: 7. https://doi.org/10.3390/computation12010007
APA StyleHattaf, K. (2024). A New Mixed Fractional Derivative with Applications in Computational Biology. Computation, 12(1), 7. https://doi.org/10.3390/computation12010007






