Abstract
Due to their excellent properties, triply periodic minimal surfaces (TPMS) have been applied to design scaffolds for bone tissue engineering applications. Predicting the mechanical response of bone scaffolds in different loading conditions is vital to designing scaffolds. The optimal mechanical properties can be achieved by tuning their geometrical parameters to mimic the mechanical properties of natural bone. In this study, we designed gyroid scaffolds of different user-specific pore and strut sizes using a combined TPMS and signed distance field (SDF) method to obtain varying architecture and porosities. The designed scaffolds were converted to various meshes such as surface, volume, and finite element (FE) volume meshes to create FE models with different boundary and loading conditions. The designed scaffolds under compressive loading were numerically evaluated using a finite element method (FEM) to predict and compare effective elastic moduli. The effective elastic moduli range from 0.05 GPa to 1.93 GPa was predicted for scaffolds of different architectures comparable to human trabecular bone. The results assert that the optimal mechanical properties of the scaffolds can be achieved by tuning their design and morphological parameters to match the mechanical properties of human bone.
1. Introduction
Diseases, injuries, and trauma damage and degenerate tissues in the human body, requiring repair, replacement, and regeneration treatments. After blood, bone is the most common transplanted tissue, and the standard treatment for bone grafts, including the golden standard of autologous grafts, has risks associated with limited donors, donor-site morbidity, contamination, germ transmission, and immune reactions [1]. Bone tissue engineering using three-dimensional (3D) temporary biodegradable or biocompatible porous scaffolds manufactured through additive manufacturing (AM) is developing as a potential replacement for using bone grafts to cure bone injury and recover damaged bone tissues [2,3]. Scaffolds improve stem cells’ adhesion, proliferation, and differentiation to form new tissues in the injured or diseased organs [4]. It also facilitates the flow of waste and nutrients, has a degradation rate that matches neo-tissue growth, and has mechanical properties equivalent to host tissues [5]. Apart from the materials of scaffolds, the architecture of scaffolds is crucial to influencing the mechanical and degradation properties to help bone tissue regeneration and repair the injury [6]. The scaffold architecture has an interconnected pore–strut network of different porosities, which can be achieved by tuning its morphological parameters, such as relative density or volume fraction (Figure 1). Morphological parameters of scaffolds, such as pore and strut sizes, can affect cell behaviour, neo-tissues’ function, and their mechanical stability in tissue regeneration applications [7]. Earlier research showed that a minimum pore size of 100 µm helps transport metabolic wastes, and pore sizes greater than 300 µm enhance the formation of neo-capillaries and neo-bone tissues. Tiny pores induce cell attachment before osteogenesis, and large pores help support vascularisation for successful bone growth [8]. A scaffold design involving pore size, geometry, volume fraction, and its related porosity influences the mechanical performance of scaffolds, especially in terms of stiffness and strength relative to that of natural bone, so that they can withstand different loading conditions [9]. For designing tissue scaffolds without adverse effects on nearby surrounding bone tissues, a close value of effective elastic modulus to that of bone is needed.
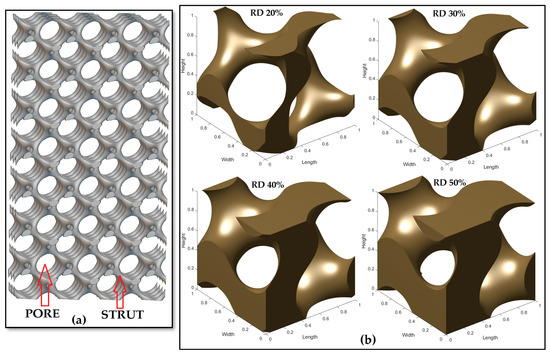
Figure 1.
(a) A triply periodic minimal surface-based gyroid scaffold of pore size 1000 µm and strut size of 200 µm with a well-interconnected network of pores and struts helping the movement of oxygen, nutrients, and waste materials. (b) Illustration of how relative density affects volume fraction and influences the morphology of a unit cell. (c) Representative of a gyroid unit cell’s pore size (red) and strut size (black) [6].
Traditional chemical methods to fabricate scaffolds of required pore sizes have limitations in controlling the spatial and temporal qualities of 3D microarchitecture and are restricted to fabricating scaffolds of simple macro-architecture, which may not achieve the purpose of regeneration of complex functional tissues [10]. AM such as 3D printing combined with computer-aided design (CAD) can now fabricate scaffolds of complex and patient-specific geometries with controllable architecture and desired properties. The conventional lattice scaffold designs have anti-biomorphic and anti-machinable pore microarchitectures of sharp twisting straight corners, thus making an unsuitable environment for cell attachment and growth [11,12]. Therefore, more focus is turned on the scaffold designs to achieve an integrated hierarchical porous architecture and intricate anatomical shapes to perform the required mechanical stability, diffusion, and permeability functions to regenerate biological tissues. TPMS, accurately described by implicit mathematical functions, are minimal surfaces of zero mean curvature with structures repeating in three dimensions [13]. The scaffold geometries based on TPMS improve cell proliferation and increase augmentation of tissue growth by using smooth, non-tortuous pores [14,15]. TPMS-based scaffolds have proven to have better structural rigidity, high fatigue resistance, porosity, and elastic modulus similar to those of bones [16,17]. The designs of 3D scaffolds based on TPMS have been demonstrated recently with an SDF method by Yoo et al. to create a complex internal micro-structure of well-connected pore networks and external surface features like that of an anatomical model [18,19,20]. Lee et al. designed functionally graded scaffolds (FGSs) by developing mathematical filtering to modify the SDF distribution to change the morphology of a TPMS structure [21]. Walker et al. utilised the SDF method with gyroid architecture to design porous poly(propylene fumarate) scaffolds of user-defined pore and strut sizes and porosity to achieve optimal mechanical properties, degradation, and tissue growth [6]. Yanez et al. designed normal and deformed gyroid porous titanium structures with different porosities, which have good stiffness and strength under other compressive loads for bone defect applications [22].
FEM is vastly used when traditional analytical and experimental methods cannot solve the problems of domains with complex geometries, different loading situations, and material properties. The advantages of FEM include lessening project development time, reducing trial-and-error testing needs, and enhancing product safety [23]. In total hip arthroplasty, Mehboob et al. utilised 3D FE models of solid CoCr alloy and porous titanium stems to predict stem stiffness on periprosthetic bone formation and stress shielding [24]. Yue et al. employed FEM for the prediction of mechanical behaviour, the permeability of Voronoi tessellation-based irregular porous scaffolds, and cube/diamond/rhombic/dodecahedron/octahedron unit-cell based lattice scaffolds for investigation of the relationship between structural properties, mechanical strength, and fluid flow [25]. FEM is also applied in different research works involving scaffolds of various geometries and materials in bone tissue engineering applications for the prediction of mechanical properties under compressive loading, stiffness, deformation behaviour, permeability, a mechanical stimulus at a cellular level, and bone remodelling required for bone ingrowth inside the scaffolds [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45].
In this research, five uniform scaffolds of gyroid architecture with user-specified inputs of pore size (200 µm to 1000 µm) and strut size (200 µm) were designed based on TPMS and the SDF to achieve the required porosities (approximately 50 to 90%) for bone tissue engineering. Tissue engineering users can specify the precise feature dimensions of a scaffold architecture with this method, and different architectures can be achieved by varying these feature dimensions. Additionally, a computational simulation based on the FEM was performed on these designed scaffolds to evaluate their mechanical behaviours under compressive loading with insight into how the morphological properties affect the mechanical properties, as illustrated by the workflow structure (Figure 2). These given TPMS scaffolds were modelled such that the predicted effective elastic moduli were in the preferable range of human trabecular bone.

Figure 2.
Workflow of the given research project for the design of scaffolds and FEM-based compressive loading simulation. The nTop notebooks for design of scaffolds (Appendix A and Appendix D), creation of FE volume mesh (Appendix C) and static structural analysis (Appendix D) can be seen.
2. Materials and Methods
nTopology (Version 3.27.2, non-commercial license) software was used to design scaffolds and perform numerical FE simulation in a Z2-G4 workstation (128 GB RAM, i7-9700 CPU @3 GHz, 8 Cores). The gyroid scaffolds were designed using TPMS with the SDF method. LabVIEW was used to find the periodic coefficient and level constant values needed for the design of gyroid scaffolds of dimensions of 5 × 5 × 10 mm3. In the FE simulation, two plates (5.5 × 5.5 × 0.5 mm3) were kept above and below the scaffolds for uniform compression.
2.1. Design of Scaffolds
2.1.1. Implicit Description of TPMS
The gyroid surface can be represented by an implicit mathematical equation based on Level-set methods (LSM). In the LSM, a surface or shape is divided into two specific phases, separated by an iso-surface boundary: a solid network of interconnected struts and void pores.
where F(G) is the implicit equation to design the gyroid scaffold; N = 2πn/L; n is the number of repeated cells in each direction; L is the unit cell length; N is the period coefficient for angular frequencies in x, y, and z directions; and C is the level constant. The relative density and the volume fraction of the porous structure (Table 1) are varied by the parameter C, and the size of unit cells is determined by the parameter N in every direction. The parameter N is like angular waves, and modifying the N alters the number and size of pores in the gyroid structure. At the value C = 0, the iso-surface divides the space into two equal volumes of solids and voids. By having either F(G) > C or F(G) < C, the relative densities of the surfaces are modified to create lattice structures. Thus, varying these parameters form a well-interconnected network of pores (voids) and struts (solids) resembling a biomimetic geometry to have a complex geometry.
F(G) = Sin (Nx) Cos (Ny) + Sin (Ny) Cos (Nz) + Sin (Nz) Cos (Nx) − C

Table 1.
Formula for Porosity, Volume Fraction, and Relative Density.
2.1.2. Signed Distance Field
An SDF is a constructive depiction of a shape. It measures distance values to the iso–boundary of a shape (Figure 3) from defined points in 3D space. The positive and negative values of the distances indicate the outside and inside of the boundary of the given shape [19]. The SDF values provide an accurate distance to the zero-level set and define whether the points in the given space are on, outside, or inside the iso-surface [6].
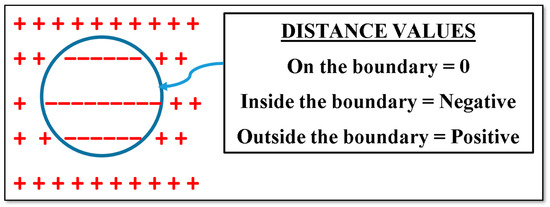
Figure 3.
An illustrative concept of an SDF in 2D.
2.1.3. Design of a Scaffold with an External Shape
The SDF was applied using a Boolean operation (intersection) between the obtained large gyroid surface and the cuboid shape (Figure 4). Due to this intersection, we can obtain a porous cuboid-shaped scaffold of gyroid architecture. This architecture is achieved by picking the highest scalar value at every point in the space between both implicit surfaces and recreating the gyroid surface beside the newly formed zero-level set. This concept can be extended to any arbitrary shape or anatomical model.
where F(Gc) is the newly formed implicit gyroid surface in cuboid shape and F(G) and F(C) are the implicit functions to denote gyroid and cuboid surfaces, respectively.
F(Gc) = Max (F(G), F(C))
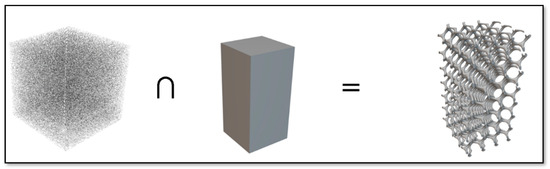
Figure 4.
The Boolean intersection between the gyroid implicit surface and the required shape (cuboid) of 5 × 5 × 10 mm3 to obtain a cuboid gyroid scaffold of 5 × 5 × 10 mm3.
2.1.4. Design of Scaffolds Based on User-Desired Pore Size (PS) and Strut Size (SS)
All of the parameters involved in the design of scaffolds were performed employing the following formulae [6]:
- (i.)
- Calculate level constant (C) based on PS and SS:
C = −0.0006 (PSR)5 + 0.0162 (PSR)4 − 0.1722 (PSR)3 + 0.9142 (PSR)2 − 2.5329 (PSR) + 1.7889
- (ii.)
- Calculate pore size (P2π) and strut size (S2π) for the period coefficient No = 2π:
P2π = −11.7311 C5 − 0.1307 C4 − 1.7987 C3 + 0.2070 C2 − 186.9928 C + 433.0114
S2π = −11.7311C5 − 0.0466 C4 + 1.7987 C3 + 0.0175 C2 − 186.9928 C + 433.0937
- (iii.)
- Calculate the scale factor (SF) from either giving the desired pore or strut size;
- (iv.)
- Calculate suitable period coefficient (N).
N = SF × No = SF × 2π
Five scaffolds with different user inputs of pore size (PS) and strut size (SS) were designed (Figure 5). The logical reason for keeping the strut size constant is to show how the architecture of the design varies by varying the pore sizes (refer to Appendix B).

Figure 5.
Uniform Gyroid Scaffolds of different pore sizes (PS) ranging from 200 µm to 1000 µm with a constant strut size (SS) of 200 µm.
- (i.)
- PS200 (Pore Size 200 µm and Strut Size 200 µm);
- (ii.)
- PS350 (Pore Size 350 µm and Strut Size 200 µm);
- (iii.)
- PS550 (Pore Size 550 µm and Strut Size 200 µm);
- (iv.)
- PS750 (Pore Size 750 µm and Strut Size 200 µm);
- (v.)
- PS1000 (Pore Size 1000 µm and Strut Size 200 µm).
2.2. Creation of FE Volume Meshes
2.2.1. Meshing
The concept of meshing is that it divides the given structure into expectably shaped and mathematically described elements. These divisions help computing machines simulate real-world problems by numerically solving the related governing equations. The meshing process influences the speed and precision of simulation results, hence a trade-off between a simulation project’s mesh quality and computation time [46].
The meshing for simulation involves three types of meshing (Figure 6):
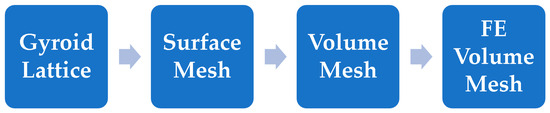
Figure 6.
Workflow of the conversion process of different meshes for simulation.
2.2.2. Converting the Implicit Body (Gyroid Lattice) into the Surface Mesh
The surface meshes (Figure 7) are technically two-dimensional elements, which are triangles in this case, used to approximate the external surface of the gyroid scaffold. The surface meshes can be exported as 3D printing files such as STL, OBJ, and 3MF for manufacturing. However, simulation does not accept a surface mesh, as this type of mesh does not have volume elements. The obtained surface meshes have closed, manifold, and non-self-intersecting elements. A tolerance of 0.1 mm was used in this conversion to balance between the mesh of reasonable size and computation time. A lower tolerance leads to finer meshes but demands more computation time. A minimum feature size of 0.1 mm was used to clean the mesh. The tolerance value was applied in meshing to discretise the implicit body into smaller elements.

Figure 7.
A surface mesh having triangular elements.
2.2.3. Converting the Surface Mesh into a Volume Mesh
In this process, the surface mesh having triangular elements can be converted into a three-dimensional solid volume mesh of tetrahedral elements (Figure 8a). A tolerance of 0.1 mm, minimum feature size of 0.1 mm, an edge length of 0.1 mm, and a growth rate of value 1.005 were used for generating volume elements. Mesh convergence was achieved by varying the values of tolerance from 2 mm to 0.1 mm (Figure 9). A numerical simulation solves the given lattice or structure decomposing into a series of discrete finite elements to obtain accurate results for complex FE models. Every FE sums the degree of freedom (DOF) in each FE model, and more DOFs ensure better obtainment of the structural behaviour, such as displacement and von Mises stress in this case. Establishing convergence and determining mesh independence lead to an accurate model. Mesh convergence is performed on each FE model to resolve how many FEs are needed to ensure that the predicted mechanical result converges to higher accuracy irrespective of decreased element size or an increased number of FEs [47].

Figure 8.
(a) A volume mesh having tetrahedral elements, which are 3D solid volume elements, different from a surface mesh of 2D elements; (b) A FE volume mesh having integration points of a geometric order added to a volume mesh.
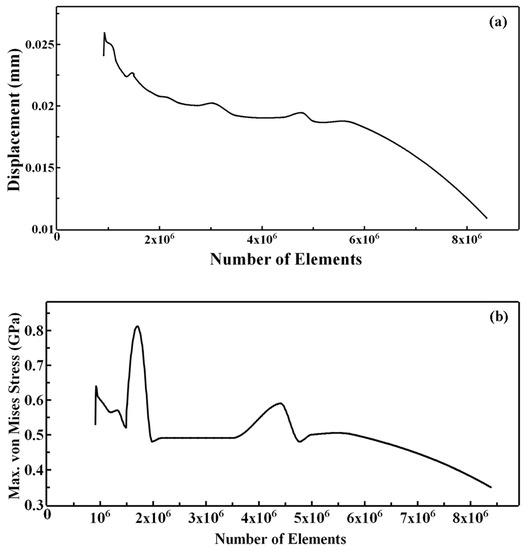
Figure 9.
Convergence plots of PS350 for (a) displacement and (b) Max. von Mises Stress (Remaining plots can be viewed in Supplementary Materials Figure S1).
2.2.4. Converting the Volume Mesh into a FE Volume Mesh
The volume mesh can be converted into an FE mesh, which involves adding the integration points of the desired geometric order (quadratic) to each element within the given volume mesh at the midpoint of the mesh edges (Figure 8b). This conversion allows the FE mesh to be used for static structural analysis. The properties of the FE mesh, such as counts of elements, nodes, edges, and vertices, are given below (Table 2).

Table 2.
Properties of FE volume mesh of scaffolds with top and bottom plates.
2.3. Simulation
2.3.1. FE Model
The material Ti-6Al-4V is assumed as a linear elastic isotropic material for the simulation (Table 3). The FE model uses all of the FE components (FE volume mesh and material properties) with boundary conditions needed to run a static analysis (Figure 10). The boundary conditions are a compressive force of value 300N applied on the top plate (movable) and a displacement restraint applied on the bottom plate (fixed).

Table 3.
Material Properties used in the simulation [48].

Figure 10.
Frontal and isometric views of an FE model, which is a combination of FE volume mesh with boundary conditions—a uniform force (Yellow) is applied on a top plate (movable), and a displacement restraint (red) is applied on a bottom plate (fixed).
2.3.2. Simulation Method and Static Analysis
This project used the method of solid elements to simulate the given lattices (Appendix D). The advantages of using this method are that it gives high accuracy of results with consideration of edge effects and with finding the maximum stress point [49]. The solid elements use the FE volume meshes of the whole lattice. The static structural analysis was performed to calculate displacements, strains, stresses, and reaction forces on the given FE model according to the applied boundary conditions. The relationship between the compressive loads and the displacements was considered linear, with an assumption of load used slowly on the model to reach the equilibrium state and neglecting all damping and inertial forces. Compressive force, compressive strain, effective or compressive elastic modulus, relative elastic modulus, stiffness, and elastic strain energy were calculated from the reactive force and the maximum deformation values obtained from FE simulation (Table 4). The maximum von Mises stress and the maximum deformation values were obtained from the von Mises and the maximum displacement contours from the static analysis.

Table 4.
Formula for calculating mechanical properties.
Values of reactive force (Figure 11a), deformation, and von Mises stress were predicted from FE simulation. The equivalent area of the scaffold is 5 × 5 mm2 (Figure 11b), which is required to calculate the compressive stress.
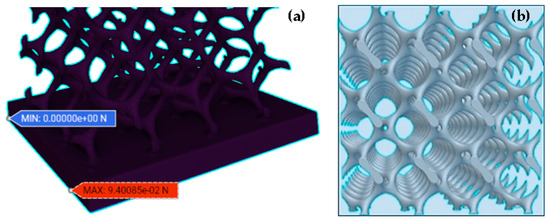
Figure 11.
(a) Reactive force. (b) Equivalent area of a scaffold.
3. Results and Discussion
3.1. Design and Morphological Parameters
The gyroid scaffolds with different pore sizes of 200 µm, 350 µm, 550 µm, 750 µm, and 1000 µm were designed using TPMS and implemented with SDF. The sizes of pores and struts are controlled by the parameter level constant (C), which then influences the structure of the gyroid lattice (Table 5). When the pore size increases, the pore/strut ratio increases and the level constant value drops (Figure 12b,f). As the pore size increases, the surface area decreases, which means that the mobility of cells increases and leads to more transfer of nutrients and more removal of waste materials (Figure 12a). However, this may also restrict cell attachment due to reduced surface area.

Table 5.
Design of Uniform Gyroid scaffolds based on user-specific inputs (Pore and Strut sizes).
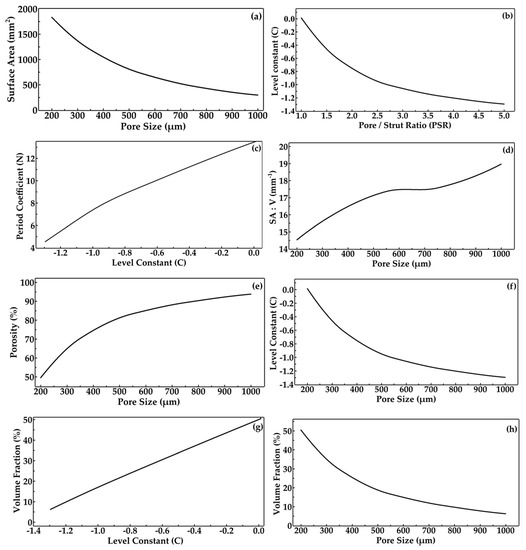
Figure 12.
Graph of Design and Morphological Properties: variations of (a) surface area with poresize, (b) level constant with pore / strut ratio, (c) period coefficient with level constant, (d) surface area to volume ration with pore size, (e) porosity with pore size, (f) level constant with pore size, (g) volume fraction with level constant, and (h) volume fraction with pore size.
The SA: V ratio increases with the increase in pore size (Figure 12d). The high surface area to volume of gyroid architecture provides enough space to transfer oxygen and nutrients and, in turn, more communication with the surrounding environment. The incoming cells to the scaffolds need a large surface area to attach, grow, and multiply due to the enlargement of their cell membrane volumes. The cells do not grow or multiply if less SA: V [16]. Previous research by Arabnejad et al. shows that the porosity is varied by adjusting strut sizes of scaffolds with constant pore size. Contrary to that, this study shows that variation in porosities is achieved by altering different pore sizes with constant strut size. The scaffolds exhibit different porosities from 49.56% to 93.78% (Figure 12e), like that of cancellous bone, which has a porosity between 50% to 90% [50]. The higher pore sizes can lead to higher permeability. Pore sizes higher than 200 µm can have porosities higher than 50%. When C ≤ 0, the parts are solid; when C > 0, the parts are pores. Thus, the varying C changes the boundary of the solid and pore, which means a change in volume fraction (Figure 12h). When the pore size increases, the density of the lattice structure decreases and the volume fraction decreases (Figure 12g), and vice-versa (Table 6).

Table 6.
Effects of pore size on relative density and volume fraction.
3.2. FE Simulation—Von Mises Stress and Deformation Prediction
The mechanical response of non-identical gyroid architectured scaffolds with different pore sizes under compressive loading was studied using FEM simulation in this research. The simulated results report the association between the applied load (300 N force) and the deformations caused by the load. The boundary conditions given in the FE models from the simulation evolved to give the distributions of stress and deformation. The visual results of the von Mises stress contour and the deformation are given (Figure 13 and Figure 14, respectively). The maximum compressive stress is found in the red colour of the contour, and the minimum compressive stress is denoted by its violet colour. The maximum von Mises stress is when the scaffold starts to yield or fracture beyond that point. The von Mises stress and deformation are found to increase once the pore sizes tend to increase. The maximum von Mises stress and maximum deformation are found in the scaffold PS1000 (Table 7).
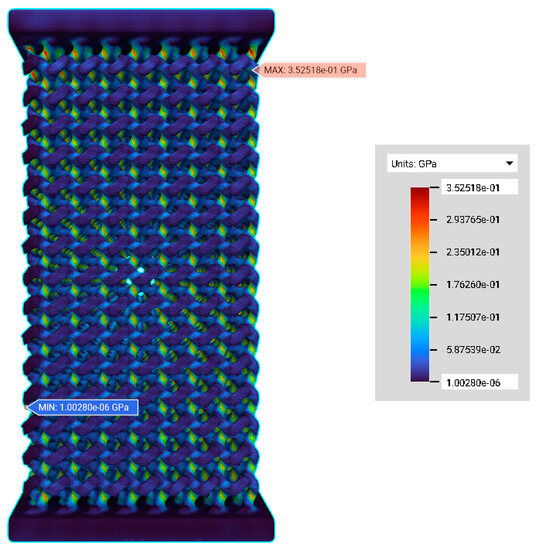
Figure 13.
FE models under compressive loading—the von Mises distribution of gyroid scaffold PS350. The stress values increment from violet (minimum value) to red colour (maximum value). The von Mises contours of other FE models can be seen in Supplementary Materials Table S2.
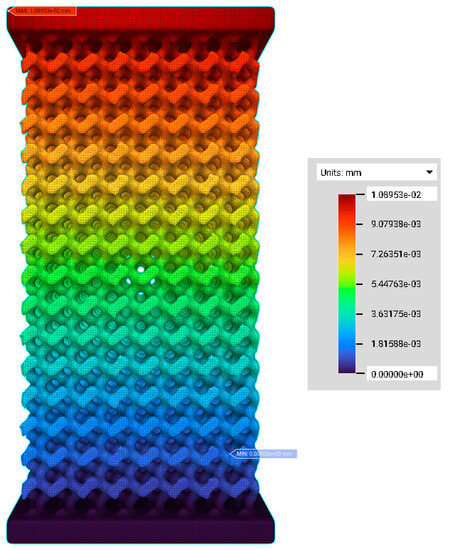
Figure 14.
FE models under compressive loading. Displacement distribution of gyroid scaffold PS350. The displacement values increment from violet (minimum value) to red colour (maximum value). The displacement contours of other FE models can be seen in Supplementary Materials Table S3.

Table 7.
Mechanical Properties under compressive loading obtained from FE simulation.
The two crucial mechanical parameters, stress (σ) and strain (ε), are vital for assessing the relationship between the mechanical behaviour of the given scaffold material and the loads applied to it [51]. The mechanical properties of the scaffolds diminish when the porosity increases and the effective elastic modulus decreases due to increased porosity and pore size, which meet the prerequisites of human trabecular bones [52]. According to Gibson & Ashby et al. [53], the effective elastic modulus (Eeff) of a structure varies if the volume fraction of the structure changes, which is mentioned by the given formula:
where Eeff = (elastic modulus of a lattice structure)/(elastic modulus of the given material). The constant K ranges from 0.1 to 4.0, and n~2 in deformation happening in a structure.
Eeff = K × (Volume fraction)n
Thus, the effective elastic modulus can be tuned by altering the volume fraction of the scaffold architecture. When the volume fraction increases, the effective elastic modulus increases (Figure 15c). The higher porosity and pore size lead to decreased stiffness and effective elastic modulus (Figure 15a,b). This factor may lead to increased bone regeneration through high permeability of nutrients and increased cell growth. However, it may result in decreased mechanical stability due to increased pore volume. With an increase in volume fraction, the effective elastic modulus is found to increase in its values. The effective elastic moduli of the structures were found in the 0.05 GPa to 1.93 GPa range, matching the effective elastic modulus range of trabecular bone [54,55] (Table 7).
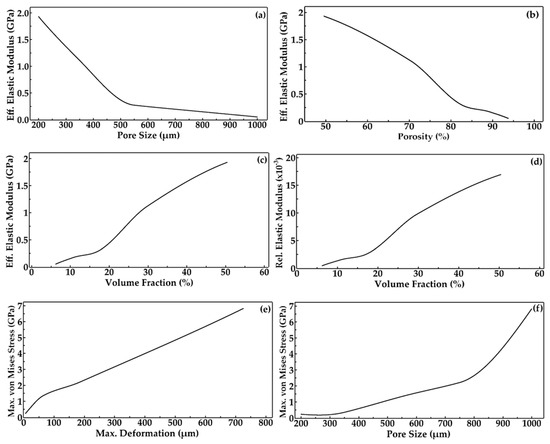
Figure 15.
Graph of mechanical properties predicted from FE simulation: variations of effective elastic modulus with (a) pore size, (b) porosity, and (c) volume fraction; variations of (d) relative elastic modulus with volume fraction, (e) maximum von Mises stress with maximum deformation and (f) maximum von Mises stress with pore size.
3.3. Discussion
Several research works have demonstrated that modifying mechanical structures’ design and morphological parameters enables their elastic properties to match bone-related properties. Barba et al. varied the solid fraction (15 to 85%) of TPMS to achieve the elastic properties of porous titanium for implant applications. The 300 to 600 µm pore size range is critical for osseointegration [56]. Naghavi et al. designed TPMS-based gyroid and diamond Ti6Al4V scaffolds for load-bearing orthopaedic implants to imitate mechanical properties of cortical bone, such as stiffness and strength, which were predicted numerically through FEM. It was established that the stiffness and strength of gyroid scaffolds with a pore size lower than 800 µm are inside the range of mechanical properties of cortical bone in compression [57]. Verma et al. developed TPMS structures and combined their morphological evaluation with the numerical findings of mechanical properties using FEM to achieve the requirements of using these structures as bone implants. It was calculated that the effective elastic modulus of the gyroid structure was 3.565 GPa, matching the properties of a trabecular bone [58]. Verma et al. again designed gyroid-based Ti6Al4V scaffolds with a range of porosities from 40% to 80% and found that the range of effective elastic modulus of 7.16 to 29.63 GPa is favourable for cortical bone implants [59]. Peng et al. designed anisotropic gyroid cellular structures of titanium alloys and applied FEM to find their elastic responses under compressive loading. Their effective elastic moduli ranged from 0.03 to 5.6 GPa, matching the elastic modulus of human trabecular bone [60]. Zaharin et al. examined the effects of gyroid Ti6Al4V unit cell scaffolds of pore size 300 to 600 µm. It was investigated that increased porosity decreased the yield strength and elastic modulus. It was concluded that the mechanical properties of scaffolds with a pore size of 300 µm only matched the bone properties [61].
3.4. Limitations
The main limitation of this research study is that the linear elastic model works well for small strains or deformations and considers a linear relationship between stress and strain components. The linear elasticity applies to situations where the yielding does not occur. A non-linear elastic model must be used if the deformation is large. The choice of a model depends on the material properties such as linear elastic, non-linear elastic, plastic, and viscoelasticity. Another limitation is that the designed scaffolds were not manufactured and have not undergone mechanical or permeability testing. Due to divergence generated by internal defects in additive manufacturing, considerable differences always exist between the mechanical properties predicted from FE simulation and that of parts manufactured. Any scaffold design must be optimised by increasing the relative density to minimise manufacturing issues [62]. This kind of FE simulation project requires high computational power to decrease the computation time due to a vast number of finite elements for obtaining an accurate geometric representation of the scaffold shape and accurate results.
4. Conclusions
This study used TPMS and SDF methods to design a gyroid architecture scaffold with different user-specific inputs (pore and strut sizes). FE simulation was applied to study the mechanical properties affected by morphology parameter variation of pore sizes. These five scaffolds with various pore sizes achieved a wide range of porosities (49% to 94%). The comparison of morphological properties from the design and the mechanical properties from FE simulation leads to the following conclusions.
- (i.)
- The advantage of having TPMS with the SDF method is that the end user can give the desired pore and strut sizes and porosity to achieve the required architecture of scaffolds for effective mechanical and degradation properties.
- (ii.)
- In the design of scaffolds, the level constant plays a vital role in tuning their interconnected architecture by deciding how many parts are to be solid (strut) or void (pores). This level constant influences the morphological parameters such as pore and strut sizes so that the pore–strut ratio decides the level constant variation, whereby a positive value results in more solid regions and a decrease in the level constant results in more solid regions and large pore sizes.
- (iii.)
- The porosity of scaffolds can be controlled by modifying the pore size of the scaffolds, keeping a constant strut size. Thus, these morphological properties affect the architecture of the lattice, which in turn alters the total mechanical properties.
- (iv.)
- The visual stress and deformation distributions are achieved using FE simulations, from which the values of mechanical responses are predicted.
- (v.)
- The maximum von Mises stress and the maximum deformation increase due to decreased volume fraction and increased porosity.
- (vi.)
- The effective elastic modulus of the scaffolds decreases with increased pore size and porosity. It was also predicted that the effective elastic moduli were in the 0.05 to 1.93 GPa range, matching that of trabecular bone.
The readers can reproduce the results by referring to the appendices, which show clear and understandable ‘how to do’ workflows. These workflows can also be applied to other geometrical designs of scaffolds on their own or by importing a mesh (.stl file) or cad file of any scaffold.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation11090181/s1; Table S1: Convergence values; Figure S1: Convergence plots; Table S2: Von mises contours; Table S3: Deformation contours.
Author Contributions
Conceptualisation (FEM), data curation, formal analysis, investigation, methodology, project administration, software, and writing—original draft, H.-S.N.M.; Conceptualisation (Design), J.W.; Funding acquisition, Resources, and Supervision, D.V.; Writing—Review and Editing, D.V., T.R., A.B., K.M., and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data from this research project are found within the article, the appendices, and the Supplementary Materials. The data file containing the design of a scaffold, meshing, and the static structural analysis using FEM in this study is available for the benefit of the scientific community in the Zenodo repository at https://zenodo.org/record/8276799, accessed on 12 July 2023.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Calculate level constant and suitable periodic coefficient to design TPMS-based scaffolds.
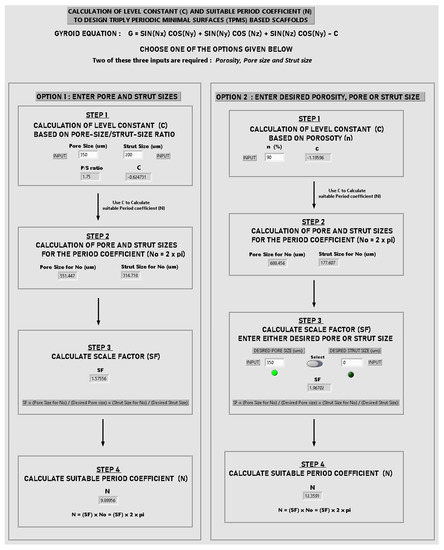
Figure A1.
Front Panel of Virtual Instrument (vi) for calculating C and N.
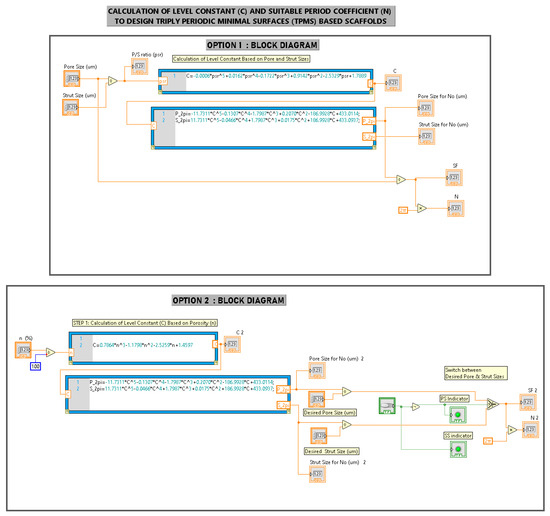
Figure A2.
Block diagrams of vi.
Appendix B. Creation of a Gyroid Scaffold in nTopology Software
The obtained values of C and N from vi (Appendix A) are fed into the gyroid equation, and the scaffold of required pore and strut sizes is created using mathematical operations. The obtained implicit body of the gyroid is large and can be trimmed into the required shape (5 × 5 × 10 mm cuboid shape in this project) using Boolean intersect (Figure A3). Suppose a user needs an anatomical shape of gyroid architecture with the required pore and strut sizes. The “Boolean intersect” operation must be used between the large implicit gyroid body and the anatomical shape (Figure A3).
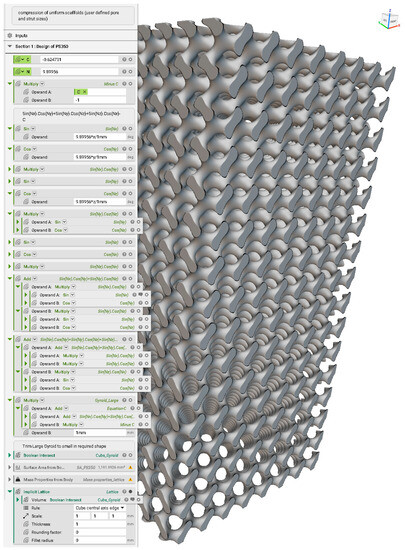
Figure A3.
Design of a gyroid scaffold PS350 in nTopology.
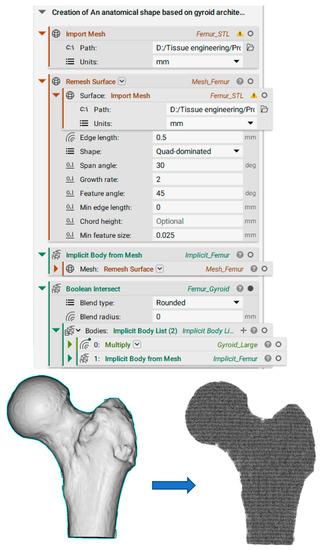
Figure A4.
Conversion of Femur shape into PS350 gyroid architecture.
Appendix C. Creation of FE Volume Mesh in nTopology
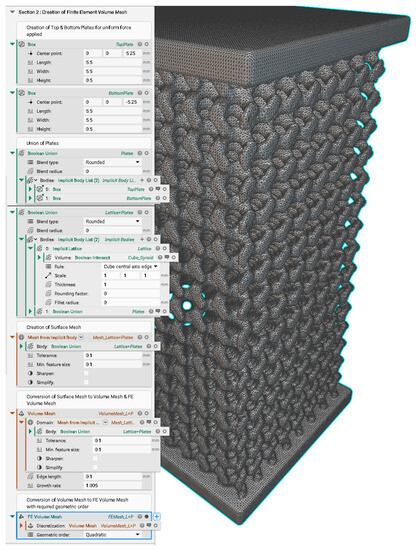
Figure A5.
Different stages of meshing from surface mesh to FE volume mesh.
The quadratic geometric order-based FE volume mesh is preferred over the linear geometric order-based FE volume mesh to obtain the maximum accuracy in results. However, the linear geometric order-based FE volume mesh gives faster computation time.
Appendix D. Static Structural Analysis
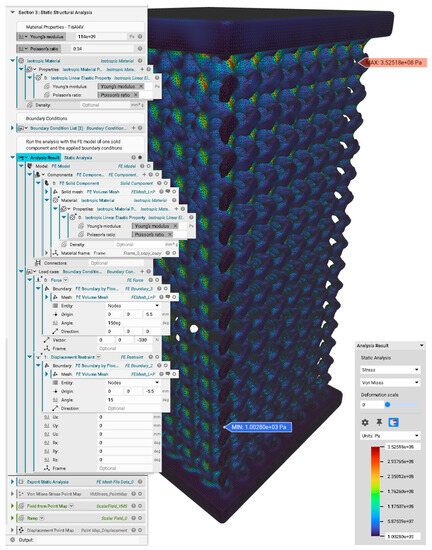
Figure A6.
A FE model of PS350 and its related static structural analysis.
References
- Shegarfi, H.; Reikeras, O. Review Article: Bone Transplantation and Immune Response. J. Orthop. Surg. 2009, 17, 206–211. [Google Scholar] [CrossRef]
- Musthafa, H.S.N.; Velauthapillai, D.; Rahman, T.; Bjørkum, A.; Mustafa, K.; Walker, J. Design of 3D Porous Bone Scaffolds Architecture Based on Tpms and Signed Distance Field Method. In National Conference for Material Technology; NTNU: Trondheim, Norway, 2020; p. 25. [Google Scholar]
- Amini, A.R.; Laurencin, C.T.; Nukavarapu, S.P. Bone Tissue Engineering: Recent Advances and Challenges. Crit. Rev. Biomed. Eng. 2012, 40, 363–408. [Google Scholar] [CrossRef]
- Kafi, M.A.; Khudishta Aktar, M.; Phanny, Y.; Mitsugu, T. Adhesion, Proliferation and Differentiation of Human Mesenchymal Stem Cell on Chitosan/Collagen Composite Scaffold. J. Mater. Sci. Mater. Med. 2019, 30, 131. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Vahabzadeh, S.; Bandyopadhyay, A. Bone Tissue Engineering Using 3D Printing. Mater. Today 2013, 16, 496–504. [Google Scholar] [CrossRef]
- Walker, J.M.; Bodamer, E.; Kleinfehn, A.; Luo, Y.; Becker, M.; Dean, D. Design and Mechanical Characterization of Solid and Highly Porous 3D Printed Poly(Propylene Fumarate) Scaffolds. Prog. Addit. Manuf. 2017, 2, 99–108. [Google Scholar] [CrossRef]
- van Bael, S.; Chai, Y.C.; Truscello, S.; Moesen, M.; Kerckhofs, G.; van Oosterwyck, H.; Kruth, J.P.; Schrooten, J. The Effect of Pore Geometry on the in Vitro Biological Behavior of Human Periosteum-Derived Cells Seeded on Selective Laser-Melted Ti6Al4V Bone Scaffolds. Acta Biomater. 2012, 8, 2824–2834. [Google Scholar] [CrossRef]
- Karageorgiou, V.; Kaplan, D. Porosity of 3D Biomaterial Scaffolds and Osteogenesis. Biomaterials 2005, 26, 5474–5491. [Google Scholar] [CrossRef]
- Murphy, C.M.; O’Brien, F.J. Understanding the Effect of Mean Pore Size on Cell Activity in Collagen-Glycosaminoglycan Scaffolds. Cell Adh. Migr. 2010, 4, 377–381. [Google Scholar] [CrossRef]
- Lu, T.; Li, Y.; Chen, T. Techniques for Fabrication and Construction of Three-Dimensional Scaffolds for Tissue Engineering. Int. J. Nanomed. 2013, 8, 337–350. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply Periodic Minimal Surface (TPMS) Porous Structures: From Multi-Scale Design, Precise Additive Manufacturing to Multidisciplinary Applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Robb, R.A. Cosmology Inspired Design of Biomimetic Tissue Engineering Templates with Gaussian Random Fields. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2006; Larsen, R., Nielsen, M., Sporring, J., Eds.; Springer: Berlin/Heidelberg, 2006; pp. 544–552. [Google Scholar]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional Mechanical Metamaterials Based on Triply Periodic Minimal Surface Lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, T.; Bei, H.-P.; Zhang, L.; Tang, C.-Y.; Zhang, M.; Xu, C.; Bian, L.; Yeung, K.W.-K.; Fuh, J.Y.H.; et al. Gaussian Curvature–Driven Direction of Cell Fate toward Osteogenesis with Triply Periodic Minimal Surface Scaffolds. Proc. Natl. Acad. Sci. USA 2022, 119, e2206684119. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, J.; Jiang, S.; Zhong, C.; Zhao, C.; Jiao, Y.; Shen, J.; Chen, H.; Ye, M.; Zhou, J.; et al. The Design of Strut/TPMS-Based Pore Geometries in Bioceramic Scaffolds Guiding Osteogenesis and Angiogenesis in Bone Regeneration. Mater. Today Bio 2023, 20, 100667. [Google Scholar] [CrossRef] [PubMed]
- Yoo, D.J. Advanced Porous Scaffold Design Using Multi-Void Triply Periodic Minimal Surface Models with High Surface Area to Volume Ratios. Int. J. Precis. Eng. Manuf. 2014, 15, 1657–1666. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti-6Al-4V Triply Periodic Minimal Surface Structures for Bone Implants Fabricated via Selective Laser Melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef]
- Yoo, D.J. Porous Scaffold Design Using the Distance Field and Triply Periodic Minimal Surface Models. Biomaterials 2011, 32, 7741–7754. [Google Scholar] [CrossRef] [PubMed]
- Yoo, D.J. Computer-Aided Porous Scaffold Design for Tissue Engineering Using Triply Periodic Minimal Surfaces. Int. J. Precis. Eng. Manuf. 2011, 12, 61–71. [Google Scholar] [CrossRef]
- Yoo, D. Heterogeneous Minimal Surface Porous Scaffold Design Using the Distance Field and Radial Basis Functions. Med. Eng. Phys. 2012, 34, 625–639. [Google Scholar] [CrossRef]
- Lee, J.-W.; Oh, S.-H.; Jeon, E.; Kim, J.; Park, K. Local Morphology Change of Tpms Structure for the Design of Functionally Graded Porous Media. SSRN 2022, 224, 4229842. [Google Scholar] [CrossRef]
- Yánez, A.; Cuadrado, A.; Martel, O.; Afonso, H.; Monopoli, D. Gyroid Porous Titanium Structures: A Versatile Solution to Be Used as Scaffolds in Bone Defect Reconstruction. Mater. Des. 2018, 140, 21–29. [Google Scholar] [CrossRef]
- What is Finite Element Analysis? Why to do FEA? Available online: https://www.graspengineering.com/hello-world-2/ (accessed on 24 August 2022).
- Mehboob, H.; Ahmad, F.; Tarlochan, F.; Mehboob, A.; Chang, S.H. A Comprehensive Analysis of Bio-Inspired Design of Femoral Stem on Primary and Secondary Stabilities Using Mechanoregulatory Algorithm. Biomech. Model. Mechanobiol. 2020, 19, 2213–2226. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Finite Element Analysis of Mechanical Behavior, Permeability of Irregular Porous Scaffolds and Lattice-Based Porous Scaffolds. Mater. Res. Express 2019, 6, 105407. [Google Scholar] [CrossRef]
- Lacroix, D.; Planell, J.A.; Prendergast, P.J. Computer-Aided Design and Finite-Element Modelling of Biomaterial Scaffolds for Bone Tissue Engineering. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 1993–2009. [Google Scholar] [CrossRef] [PubMed]
- Eshraghi, S.; Das, S. Micromechanical Finite-Element Modeling and Experimental Characterization of the Compressive Mechanical Properties of Polycaprolactone-Hydroxyapatite Composite Scaffolds Prepared by Selective Laser Sintering for Bone Tissue Engineering. Acta Biomater. 2012, 8, 3138–3143. [Google Scholar] [CrossRef]
- Hawker, M.; Wang, F.; Sala, R.; Regondi, S.; Pugliese, R. Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior. Eng 2021, 3, 9–23. [Google Scholar] [CrossRef]
- Schipani, R.; Nolan, D.R.; Lally, C.; Kelly, D.J. Integrating Finite Element Modelling and 3D Printing to Engineer Biomimetic Polymeric Scaffolds for Tissue Engineering. Connect Tissue Res. 2020, 61, 174–189. [Google Scholar] [CrossRef]
- Vozzi, G.; Koc, B.; Moroni, L.; Hendrikson, W.J.; van Blitterswijk, C.A.; Rouwkema, J.; Moroni, L. The Use of Finite Element Analyses to Design and Fabricate Three-Dimensional Scaffolds for Skeletal Tissue Engineering. Front. Bioeng. Biotechnol. 2017, 5, 30. [Google Scholar] [CrossRef]
- Soro, N.; Brassart, L.; Chen, Y.; Veidt, M.; Attar, H.; Dargusch, M.S. Finite Element Analysis of Porous Commercially Pure Titanium for Biomedical Implant Application. Mater. Sci. Eng. A 2018, 725, 43–50. [Google Scholar] [CrossRef]
- Olivares, A.L.; Marsal, È.; Planell, J.A.; Lacroix, D. Finite Element Study of Scaffold Architecture Design and Culture Conditions for Tissue Engineering. Biomaterials 2009, 30, 6142–6149. [Google Scholar] [CrossRef]
- Sun, K.; Li, R.; Li, H.; Fan, M.; Li, H. Analysis and Demonstration of a Scaffold Finite Element Model for Cartilage Tissue Engineering. ACS Omega 2020, 5, 32411–32419. [Google Scholar] [CrossRef]
- Patel, R.; Lu, M.; Diermann, S.H.; Wu, A.; Pettit, A.; Huang, H. Deformation Behavior of Porous PHBV Scaffold in Compression: A Finite Element Analysis Study. J. Mech. Behav. Biomed. Mater. 2019, 96, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Bin Noordin, M.A.; Saad, A.P.B.; Ngadiman, N.H.A.; Mustafa, N.S.; Yusof, N.B.; Ma’aram, A. Finite Element Analysis of Porosity Effects on Mechanical Properties for Tissue Engineering Scaffold. Biointerface Res. Appl. Chem. 2021, 11, 8836–8843. [Google Scholar]
- Kakarla, A.B.; Kong, I.; Guha Nukala, S.; Kong, W. Mechanical Behaviour Evaluation of Porous Scaffold for Tissue-Engineering Applications Using Finite Element Analysis. J. Compos. Sci. 2022, 6, 46. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. Comparative Analysis between the Mechanical Behaviour of Gradient and Uniform Lattice Structures Using Finite Element Analysis. J. Eng. Sci. Technol. 2019, 14, 2779–2791. [Google Scholar]
- Sahai, N.; Gogoi, M. Computer Aided Designing and Finite Element Analysis for Development of Porous 3D Tissue Scaffold—A Review. Int. J. Biomed. Eng. Technol. 2020, 33, 174–197. [Google Scholar] [CrossRef]
- Soufivand, A.A.; Abolfathi, N.; Hashemi, S.A.; Lee, S.J. Prediction of Mechanical Behavior of 3D Bioprinted Tissue-Engineered Scaffolds Using Finite Element Method (FEM) Analysis. Addit. Manuf. 2020, 33, 101181. [Google Scholar] [CrossRef]
- Quevedo González, F.J.; Nuño, N. Finite Element Modelling Approaches for Well-Ordered Porous Metallic Materials for Orthopaedic Applications: Cost Effectiveness and Geometrical Considerations. Comput. Methods Biomech. Biomed. Engin. 2016, 19, 845–854. [Google Scholar] [CrossRef]
- Hashemi, S.A.; Esmaeili, S.; Ghadiri Nejad, M.; Saber Samandari, S.; Sheikhbahaei, E.; Kordjamshidi, A.; Khandan, A. Micro-Finite Element Model to Investigate the Mechanical Stimuli in Scaffolds Fabricated via Space Holder Technique for Cancellous Bone. Int. J. Adv. Des. Manuf. Technol. 2020, 13, 51–58. [Google Scholar]
- Bagde, A.D.; Kuthe, A.M.; Nagdeve, S.R.; Dahake, S.W.; Sapkal, P.S.; Daronde, S.B.; Lande, N.H.; Sarode, B.D. Geometric Modeling and Finite Element Simulation for Architecture Design of 3D Printed Bio-Ceramic Scaffold Used in Bone Tissue Engineering. J. Indian Inst. Sci. 2019, 99, 361–374. [Google Scholar] [CrossRef]
- Baggi, L.; Cappelloni, I.; di Girolamo, M.; Maceri, F.; Vairo, G. The Influence of Implant Diameter and Length on Stress Distribution of Osseointegrated Implants Related to Crestal Bone Geometry: A Three-Dimensional Finite Element Analysis. J. Prosthet. Dent. 2008, 100, 422–431. [Google Scholar] [CrossRef]
- Idhammad, A.; Abdali, A.; Alaa, N. Computational Simulation of the Bone Remodeling Using the Finite Element Method: An Elastic-Damage Theory for Small Displacements. Theor. Biol. Med. Model. 2013, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Daver, A.L.I. Mimicking Bone Anisotropic Structure with Modified Gyroid Scaffolds; A Finite Element Analysis. Politek. Derg. 2021, 24, 1637–1646. [Google Scholar]
- Alkaios Bournias Varotsis. Meshing in FEA, CFD & Manufacturing. Available online: https://ntopology.com/blog/meshing-in-fea-cfd-manufacturing/ (accessed on 5 March 2023).
- Finite Element Analysis Convergence and Mesh Independence. Available online: https://www.xceed-eng.com/finite-element-analysis-convergence-and-mesh-independence/ (accessed on 25 August 2023).
- ProtoXYZ. Titanium Grade 5 (Ti6Al4V). Available online: https://protoxyz.com/materials/Metal/Titanium_Grade_5_(Ti6Al4V) (accessed on 27 January 2023).
- Blake Johnson. What are the Options for Simulating Lattices? Available online: https://support.ntopology.com/hc/en-us/articles/360051081633 (accessed on 5 March 2023).
- Zhang, X.Y.; Fang, G.; Xing, L.L.; Liu, W.; Zhou, J. Effect of Porosity Variation Strategy on the Performance of Functionally Graded Ti-6Al-4V Scaffolds for Bone Tissue Engineering. Mater. Des. 2018, 157, 523–538. [Google Scholar] [CrossRef]
- Medori, E. Mechanical Behaviour of Fdm Printed Latice Structures with Potential for Biomedical Applications. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2021. [Google Scholar]
- Ma, S.; Tang, Q.; Han, X.; Feng, Q.; Song, J.; Setchi, R.; Liu, Y.; Liu, Y.; Goulas, A.; Engstrøm, D.S.; et al. Manufacturability, Mechanical Properties, Mass-Transport Properties and Biocompatibility of Triply Periodic Minimal Surface (TPMS) Porous Scaffolds Fabricated by Selective Laser Melting. Mater. Des. 2020, 195, 109034. [Google Scholar] [CrossRef]
- Gibson, I.J.; Ashby, M.F. The Mechanics of Three-Dimensional Cellular Materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Sun, Y.; Yang, J.; Chen, R.; Xiong, Y.; Hou, W.; Bai, L. Design of a Biomimetic Graded TPMS Scaffold with Quantitatively Adjustable Pore Size. Mater. Des. 2022, 218, 110665. [Google Scholar] [CrossRef]
- Li, J.; Chen, M.; Fan, X.; Zhou, H. Recent Advances in Bioprinting Techniques: Approaches, Applications and Future Prospects. J. Transl. Med. 2016, 14, 271. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Reed, R.C. Synthetic Bone: Design by Additive Manufacturing. Acta Biomater. 2019, 97, 637–656. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Bahrami Babam-Iri, B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering 2022, 2022, 504. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; Kumta, S.; Sehgal, S.; Saxena, K. Low Elastic Modulus and Highly Porous Triply Periodic Minimal Surfaces Architectured Implant for Orthopedic Applications. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089221111258. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; Saxena, K.K.; Xu, J.; Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; et al. Design and Analysis of Biomedical Scaffolds Using TPMS-Based Porous Structures Inspired from Additive Manufacturing. Coatings 2022, 12, 839. [Google Scholar] [CrossRef]
- Peng, X.; Huang, Q.; Zhang, Y.; Zhang, X.; Shen, T.; Shu, H.; Jin, Z. Elastic Response of Anisotropic Gyroid Cellular Structures under Compression: Parametric Analysis. Mater. Des. 2021, 205, 109706. [Google Scholar] [CrossRef]
- Zaharin, H.A.; Abdul Rani, A.M.; Azam, F.I.; Ginta, T.L.; Sallih, N.; Ahmad, A.; Yunus, N.A.; Zulkifli, T.Z.A. Effect of Unit Cell Type and Pore Size on Porosity and Mechanical Behavior of Additively Manufactured Ti6Al4V Scaffolds. Materials 2018, 11, 2402. [Google Scholar] [CrossRef] [PubMed]
- Nagamoto, H. Yamaha Pairing Topology Optimization with Graded Lattices. Available online: https://ntopology.com/blog/user-spotlight-yamaha-pairing-topology-optimization-with-graded-lattices/ (accessed on 10 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).