Numerical Computation of Hydrodynamic Characteristics of an Automated Hand-Washing System
Abstract
:1. Introduction
2. Methodology
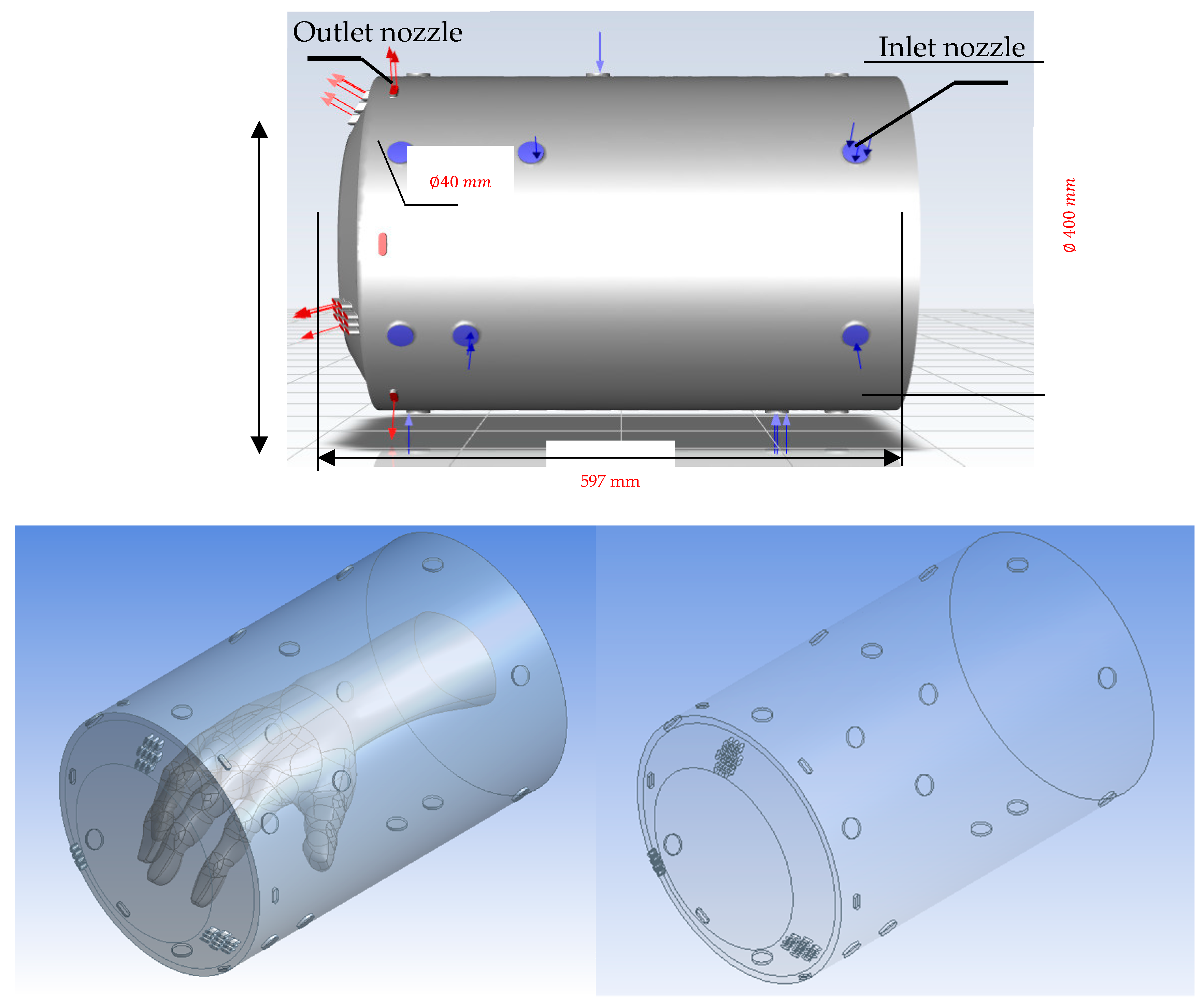
2.1. Physical Model
2.2. Numerical Methods
2.3. Boundary Layer
2.4. Boundary Conditions for Rotatory Simulations
2.5. Mesh Generation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wickramatillake, A.; Kurukularatne, C. SARS-CoV-2 human disinfection chamber: A critical analysis. Occup. Med. 2020, 70, 330–334. [Google Scholar] [CrossRef] [PubMed]
- Riedel, S.; Edward, J.J. The History of Smallpox and Vaccination, Baylor University Medical Center Proceedings. Med. Cent. Proc. 2005, 18, 21–25. [Google Scholar]
- Allegranzi, B.; Pittet, D. Role of Hand Hygiene in Healthcare-Associated Infection Prevention. J. Hosp. Infect. 2009, 73, 305–315. [Google Scholar] [CrossRef]
- Conover, D.M.; Gibson, K.E. A Review of methods for the evaluation of handwashing efficacy. Food Control 2016, 63, 53–64. [Google Scholar] [CrossRef]
- Kukkala, K.B.; Hough, C.; Jasinski, V.A.; Gill, N.; Alhouti, N.; Ceballos, M. WashBot™ An Automatic Hand Washing Machine. ASAIO J. 2022, 68, 105. [Google Scholar] [CrossRef]
- Jolan, B.S.; Marlon, G.R.; Eunelfa, R.C.; Alain, V.C.; Wubishet, D.; Assefa, S.Y. Multi-Station Automated Hand Washing System. Int. J. Recent Technol. Eng. 2020, 9, 36–43. [Google Scholar]
- Le, T.-L.; Chen, J.-C.; Shen, B.-C.; Hwu, F.-S.; Nguyen, H.-B. Numerical investigation of the thermocapillary actuation behavior of a droplet in a microchannel. Int. J. Heat Mass Transf. 2015, 83, 721–730. [Google Scholar] [CrossRef]
- Le, T.-L.; Chen, J.-C.; Hwu, F.-S.; Nguyen, H.-B. Numerical study of the migration of a silicone plug inside a capillary tube subjected to an unsteady wall temperature gradient. Int. J. Heat Mass Transf. 2016, 97, 439–449. [Google Scholar] [CrossRef]
- Le, T.-L.; Chen, J.-C.; Nguyen, H.-B. Numerical study of the thermocapillary droplet migration in a microchannel under a blocking effect from the heated wall. Appl. Therm. Eng. 2017, 122, 820–830. [Google Scholar] [CrossRef]
- Le, T.-L.; Chen, J.-C.; Nguyen, H.-B. Numerical investigation of the forward and backward thermocapillary motion of a water droplet in a microchannel by two periodically activated heat sources. Numer. Heat Transf. Part A Appl. 2021, 79, 146–162. [Google Scholar] [CrossRef]
- Le, T.L.; Hong, T.D. Computational fluid dynamics study of the hydrodynamic characteristics of a torpedo-shaped underwater glider. Fluids 2021, 6, 252. [Google Scholar] [CrossRef]
- Le, T.L.; Nghia, T.T.; Thong, H.D.; Son, M.H.K. Numerical study of aerodynamic performance and flow characteristics of a centrifugal blower. Int. J. Intell. Unmanned Syst. 2022, 11, 396–406. [Google Scholar] [CrossRef]
- Tran, T.-H.; Le, T.-L.; Hong, D.-T.; Nguyen, T.-P. The effect of inlet velocities on the droplet size in T-junction microfluidic devices. JP J. Heat Mass Transf. 2022, 28, 1–14. [Google Scholar] [CrossRef]
- Le, T.-L.; Nguyen, T.T.; Kieu, T.T. A CFD Study on the Design Optimization of Airborne Infection Isolation Room. Math. Probl. Eng. 2022, 2022, 5419671. [Google Scholar] [CrossRef]
- Feurhuber, M.; Magno, M.; Miranda, M.; Prieler, R.; Hochenauer, C. CFD Investigation of Non-Condensable Gases in Vacuum and Non-Vacuum Steam Sterilizers. Chem. Ing. Tech. 2019, 91, 502–513. [Google Scholar] [CrossRef]
- Lewinski, N.A.; Berthet, A.; Maurizi, L.; Eisenbeis, A.; Hopf, N.B. Effectiveness of Hand-Washing on the Removal of Iron Oxide Nanoparticles from Human Skin ex vivo. J. Occup. Evironmental Hyg. 2017, 14, 115–117. [Google Scholar] [CrossRef] [PubMed]
- Vuai, S.A.H.; Sahini, M.G.; Sule, K.S.; Ripanda, A.S.; Mwanga, H.M. A comparative in-vitro study on antimicrobial efficacy of on-market alcohol-based hand washing sanitizers towards combating microbes and its application in combating Covid-19 global outbreak. Heliyon. 2022, 8, 11689. [Google Scholar] [CrossRef]
- Huang, L.Y.; Chen, Z.S. Effect of Technological Parameters on Hydrodynamic Performance of Ultra-High-Pressure Water-Jet nozzle. Appl. Ocean Res. 2022, 129, 103410. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, C.-L.; Song, X.-F.; Yu, J.-G. Computational fluid dynamics simulation as a tool for optimizing the hydrodynamic performance of membrane bioreactors. RSC Adv. 2019, 9, 32034–32046. [Google Scholar] [CrossRef]
- Feurhuber, M.; Cattide, A.; Magno, M.; Miranda, M.; Prieler, R.; Hochenauer, C. Prediction of the fluid flow, heat transfer and inactivation of microorganism at medical devices in modern steam sterilizers using computational fluid dynamics. Appl. Therm. Eng. 2017, 127, 1391–1403. [Google Scholar] [CrossRef]
- Feurhuber, M.; Magno, M.; Miranda, M.; Hochenauer, C. CFD investigations of steam penetration, air-removal and condensation inside hollow loads and cavities. Appl. Therm. Eng. 2019, 147, 1070–1082. [Google Scholar] [CrossRef]
- Brauer, M.; Zhao, J.T.; Bennitt, F.B.; Stanaway, D. Global Access to Hangwashing: Implicatuons for Covid-19 control in Low-income Countries. Environ. Health Perspect. 2020, 128, 069001. [Google Scholar] [CrossRef] [PubMed]
- Phillips, A.B.; Turnock, S.R.; Furlong, M. The Use of Computational Fluid Dynamics to Aid Cost-Effective Hydrodynamic Design of Autonomous Underwater Vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2010, 224, 239–254. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-L.; Vuong, T.-H.-N.; Phung, T.-H. Numerical Computation of Hydrodynamic Characteristics of an Automated Hand-Washing System. Computation 2023, 11, 167. https://doi.org/10.3390/computation11090167
Le T-L, Vuong T-H-N, Phung T-H. Numerical Computation of Hydrodynamic Characteristics of an Automated Hand-Washing System. Computation. 2023; 11(9):167. https://doi.org/10.3390/computation11090167
Chicago/Turabian StyleLe, Thanh-Long, Thi-Hong-Nhi Vuong, and Tran-Hanh Phung. 2023. "Numerical Computation of Hydrodynamic Characteristics of an Automated Hand-Washing System" Computation 11, no. 9: 167. https://doi.org/10.3390/computation11090167
APA StyleLe, T.-L., Vuong, T.-H.-N., & Phung, T.-H. (2023). Numerical Computation of Hydrodynamic Characteristics of an Automated Hand-Washing System. Computation, 11(9), 167. https://doi.org/10.3390/computation11090167





