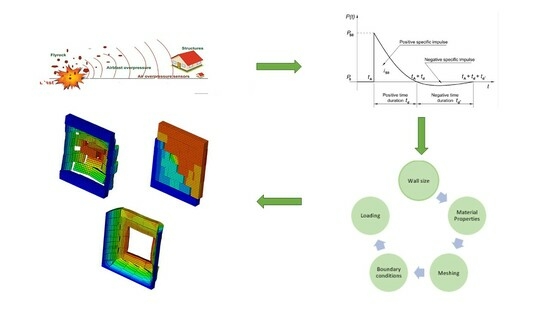
Investigation of the Failure Response of Masonry Walls Subjected to Blast Loading Using Nonlinear Finite Element Analysis
Abstract
1. Introduction
2. Failure Modes and Modeling Approaches of Masonry Walls
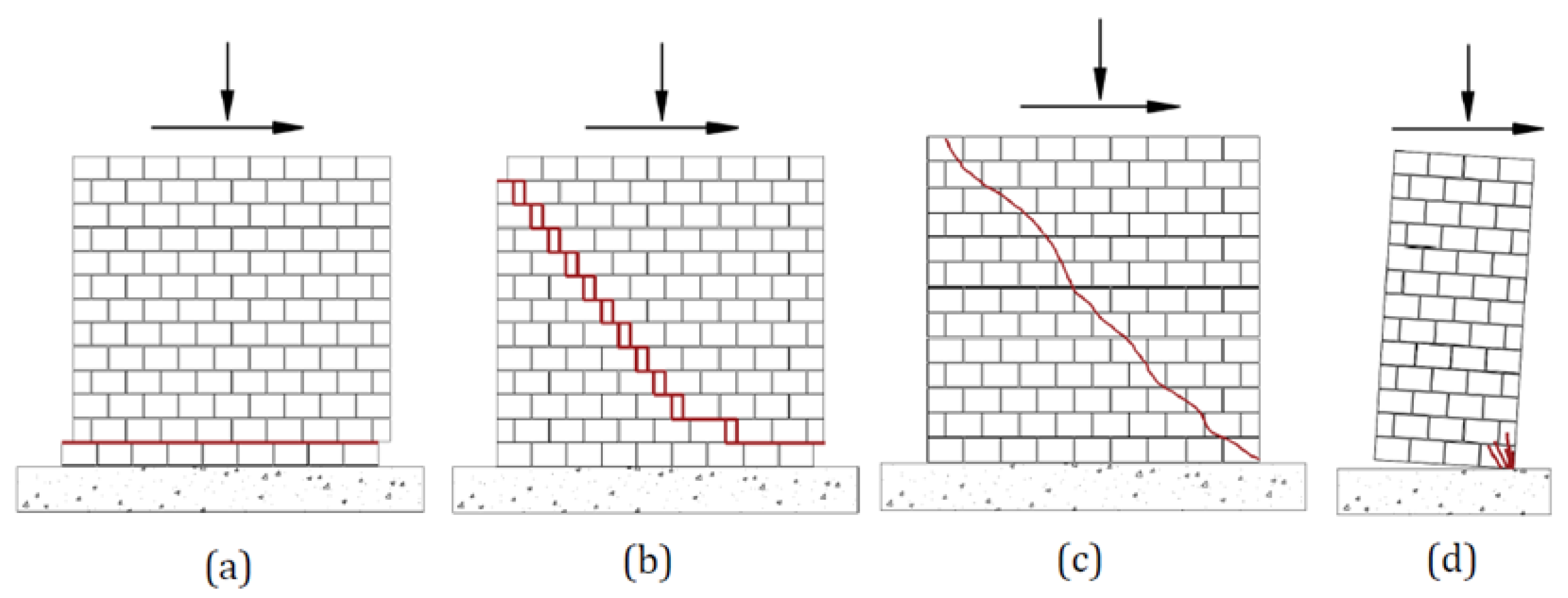
2.1. In-Plane Response of Masonry Walls
2.2. Out-of-Plane Response of Masonry Walls
2.3. General Modeling Approaches for Masonry Structures
3. The Numerical Model Proposed in the Present Article
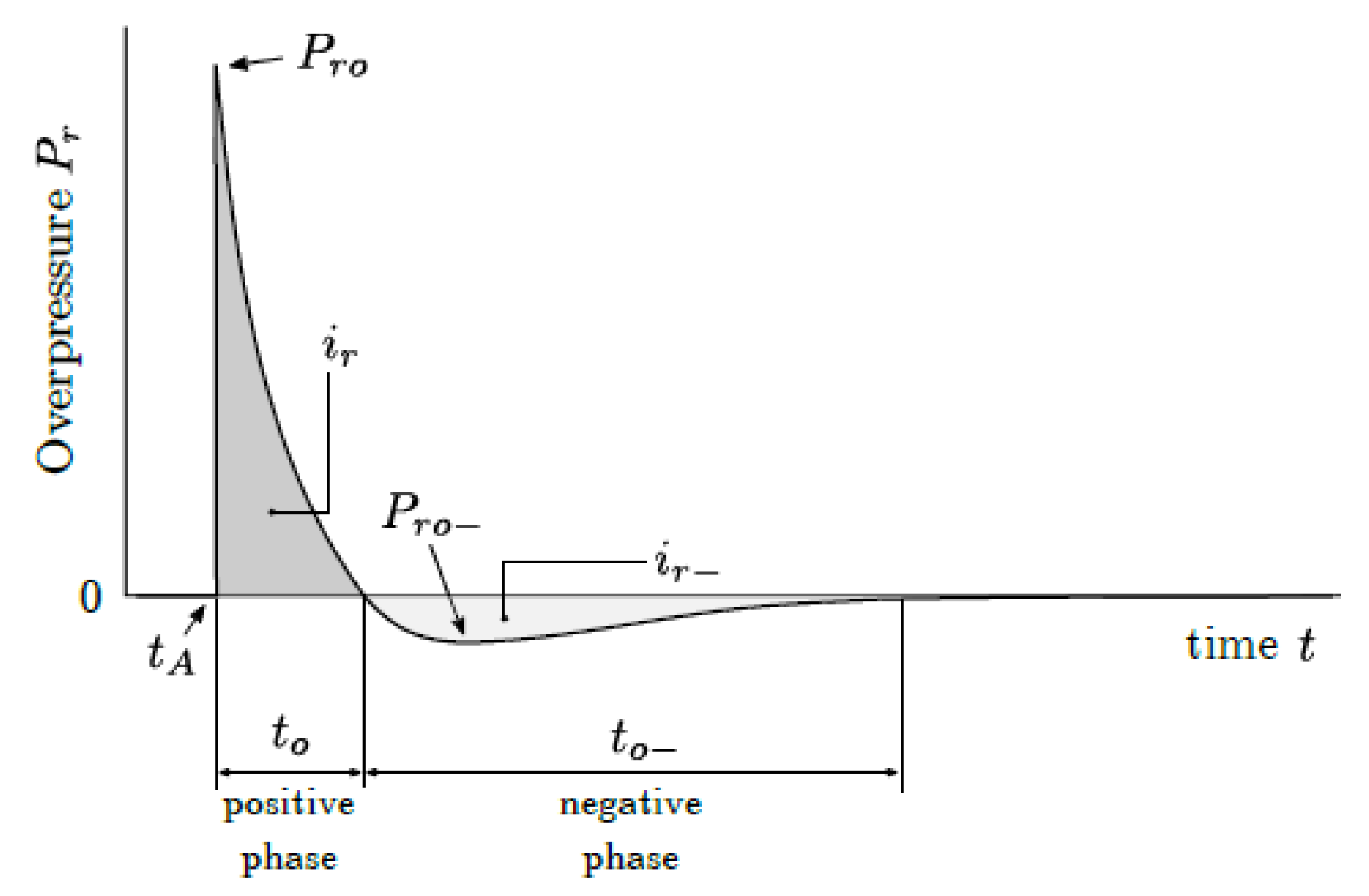
3.1. Blast Shock Wave Modeling
3.2. Continuum Damage Law for the Masonry Units
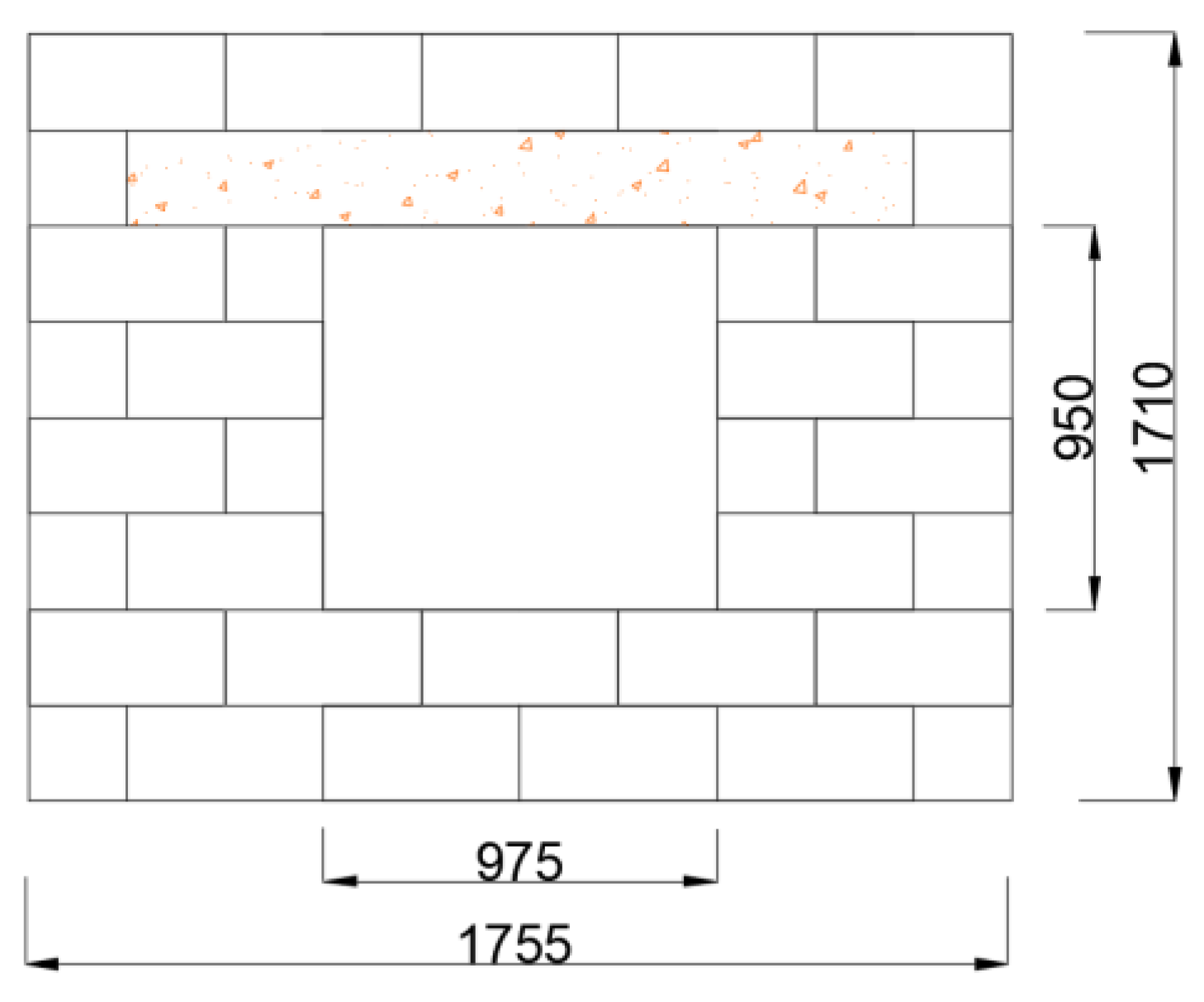
3.3. The Geometry of the Masonry Walls
- -
- A single-leaf wall is considered, and the wall is unreinforced.
- -
- Category 1 buildings [40].
3.4. Details of the Finite Element Model
4. Validation of the Proposed Model
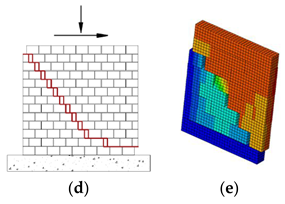
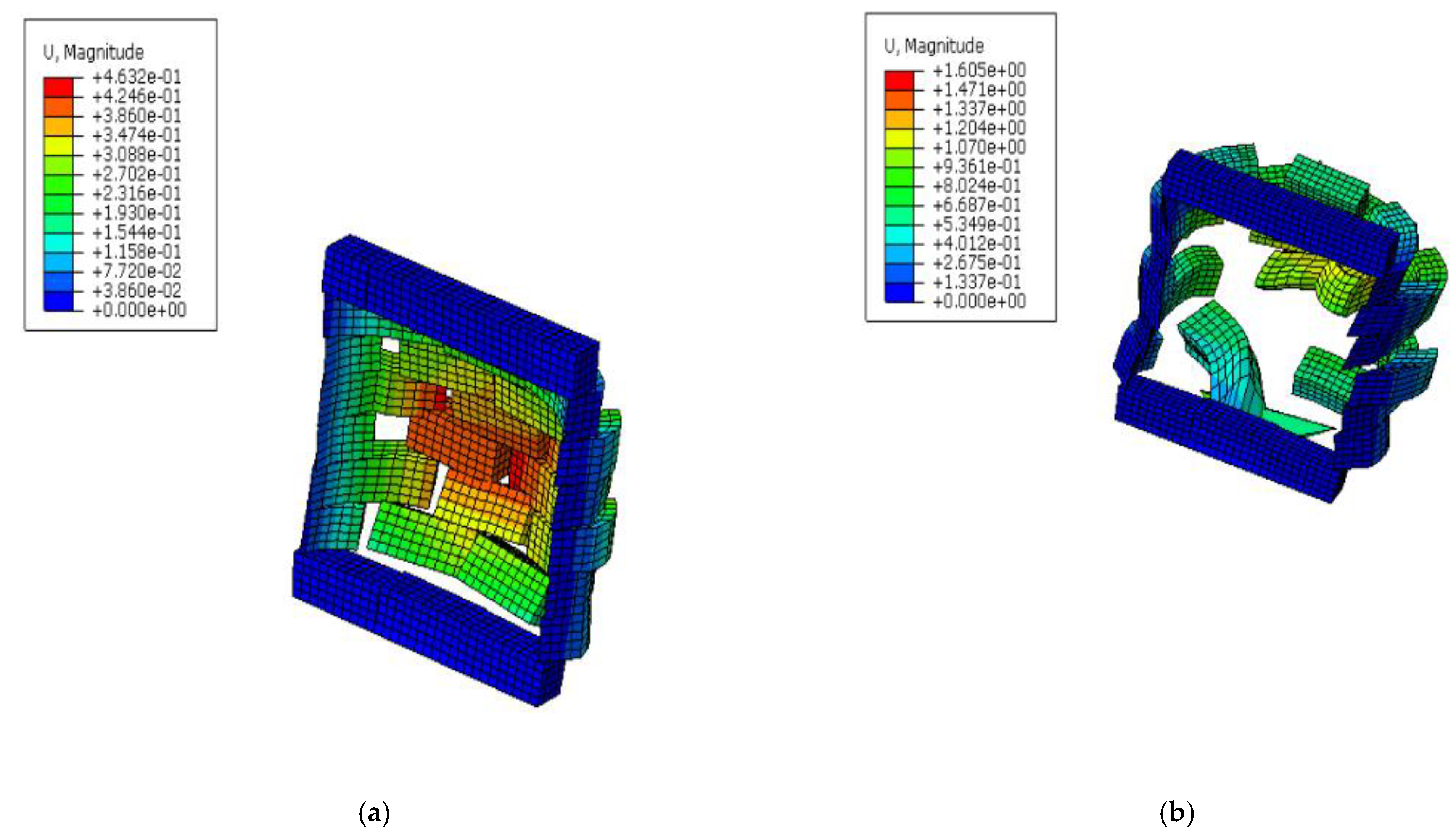
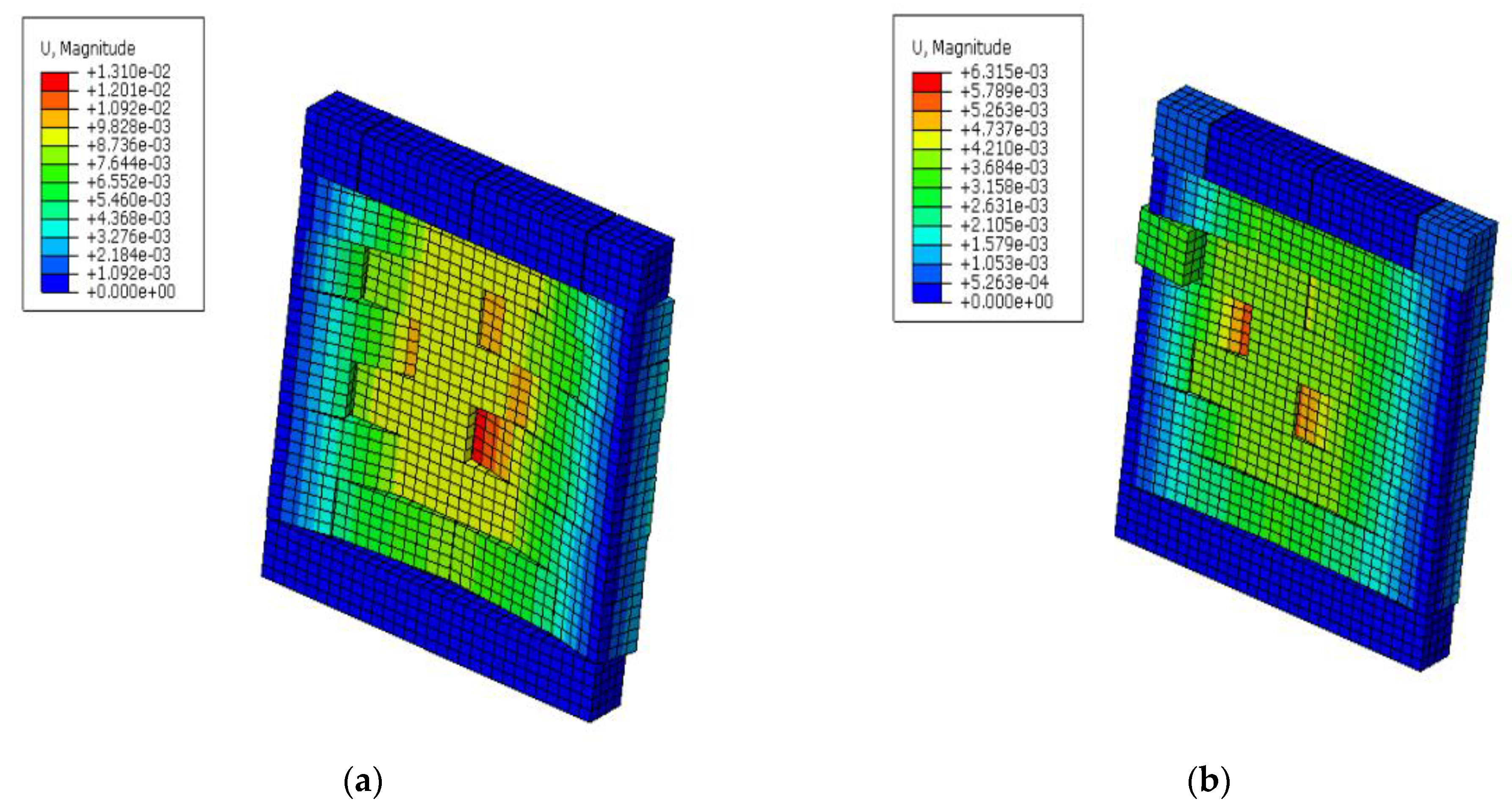
- Masi et al. [13] depicted complete failure, indicating that after a wall is damaged close to the boundary, it comes out in one piece in the middle portion. The explosive weight was 810 kg at 37 m standoff distances (Figure (a)). Out-of-plane experiments conducted by Du et al. [41] depicted complete failure in the middle of a real wall (Figure (b)).

- Salmanpour [21] predicted sliding failure along staircase-shaped cracks as mode of failure for a wall subjected to vertical pressure and shear displacement loading. The damage to buildings during the 2002 Molise earthquake in Italy, as reported in [42], resembles the crack pattern shown below in Figure (d).
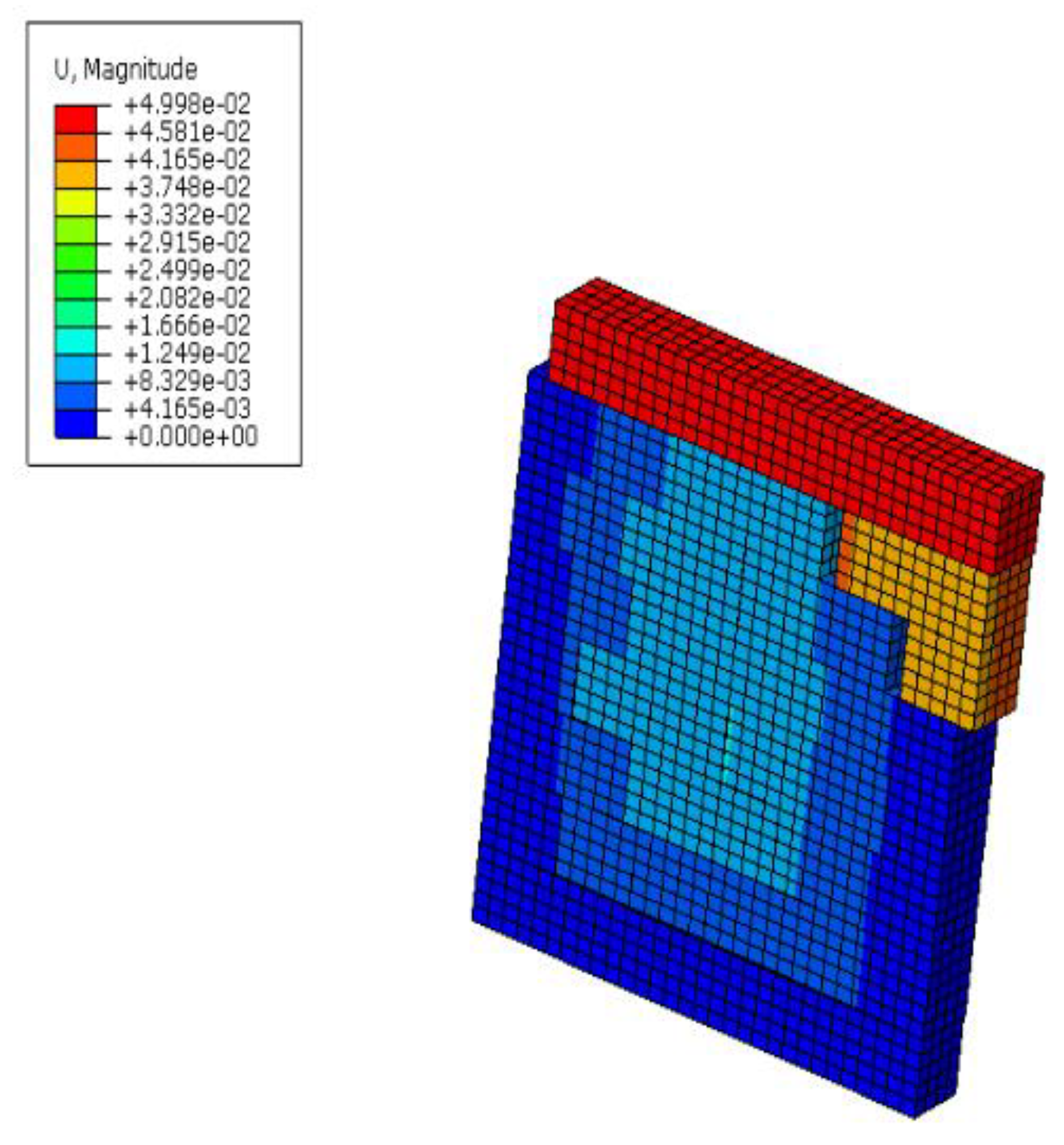
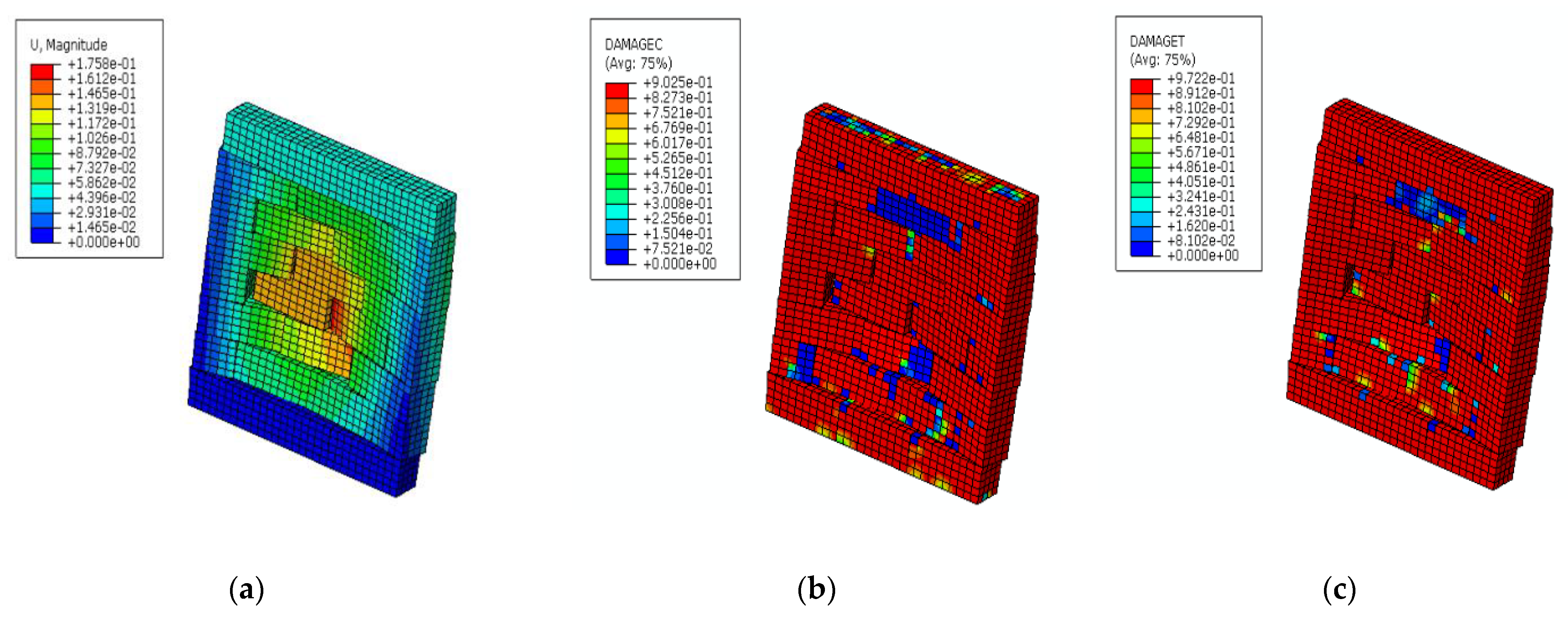
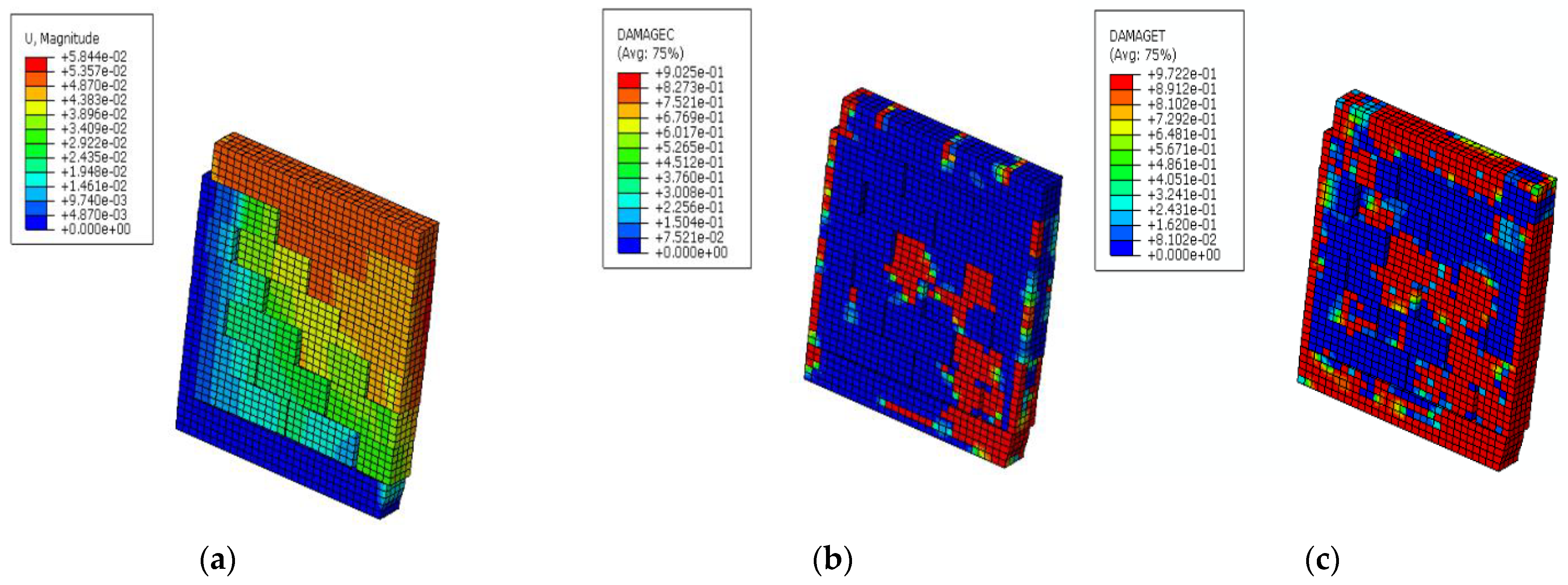
5. Results Obtained from the Proposed Numerical Scheme
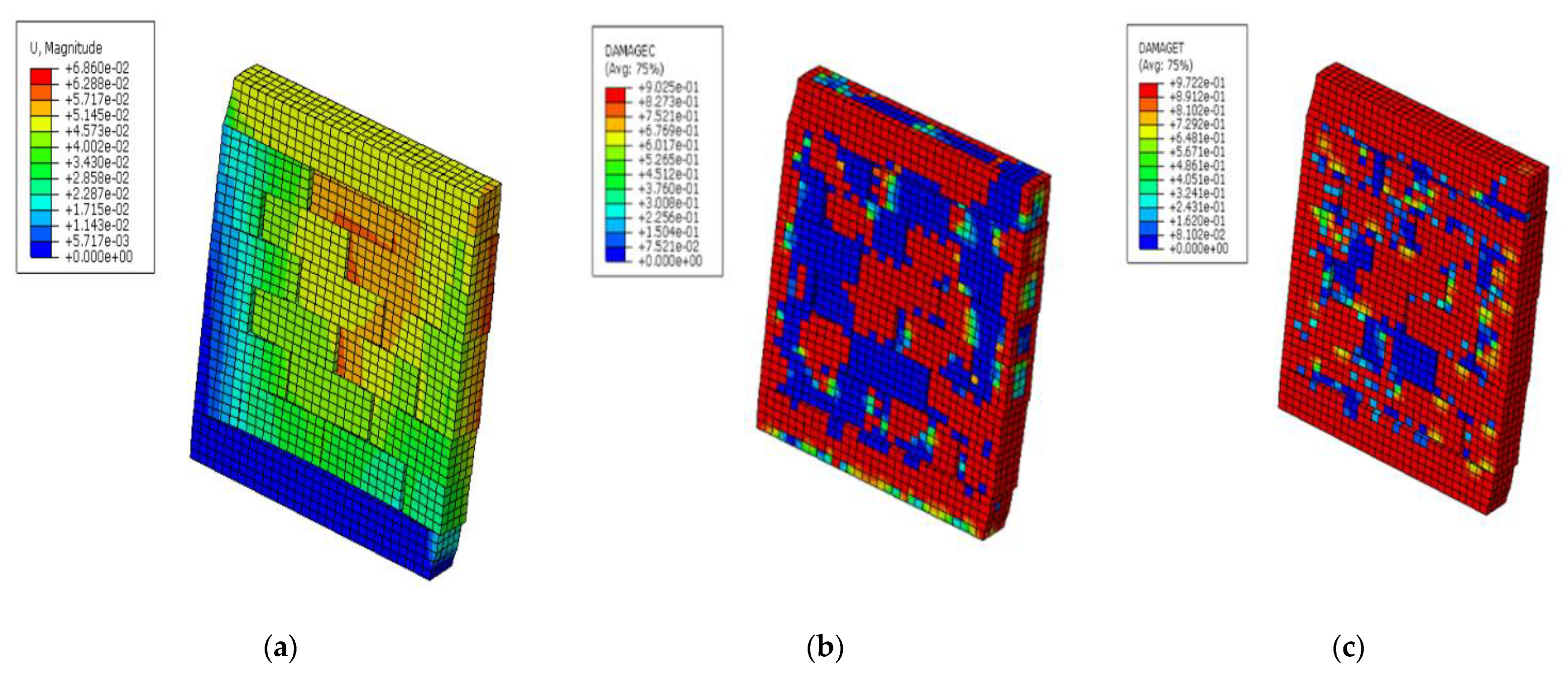
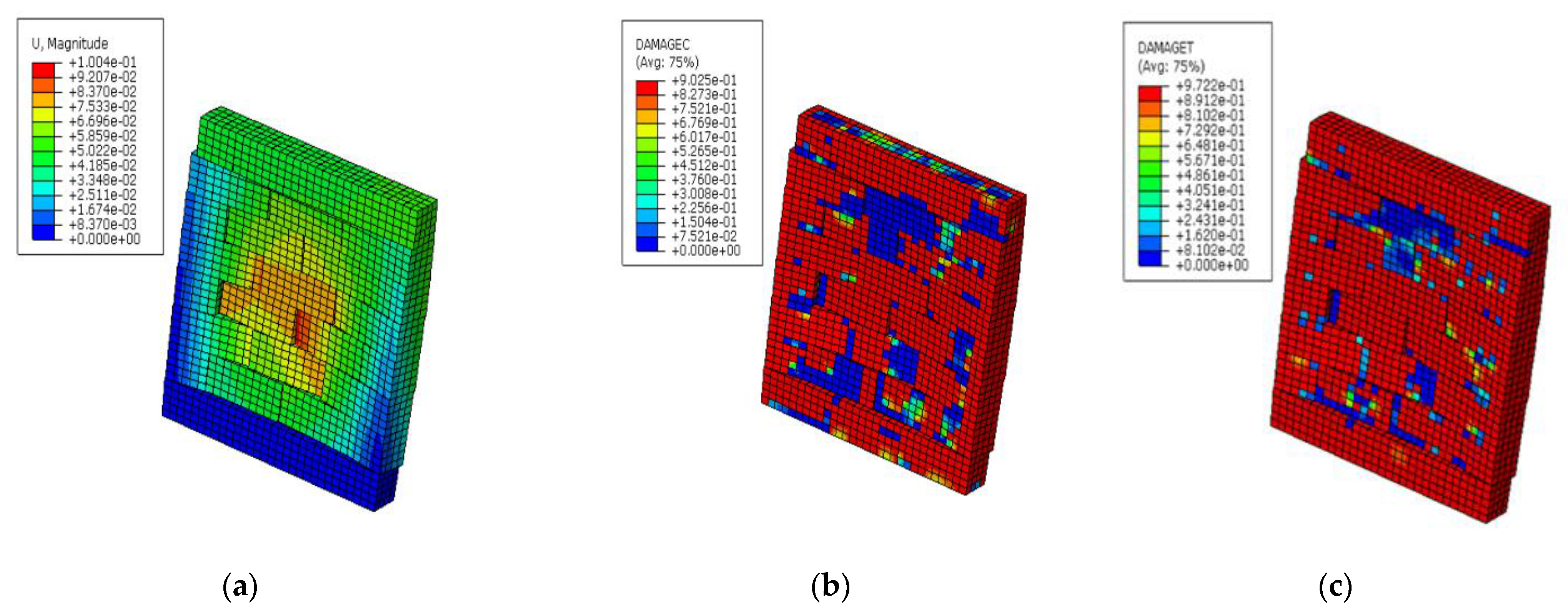
5.1. Case 1: Solid Masonry Wall Loaded with Vertical Pressure, Shear Displacement, and Blast Load
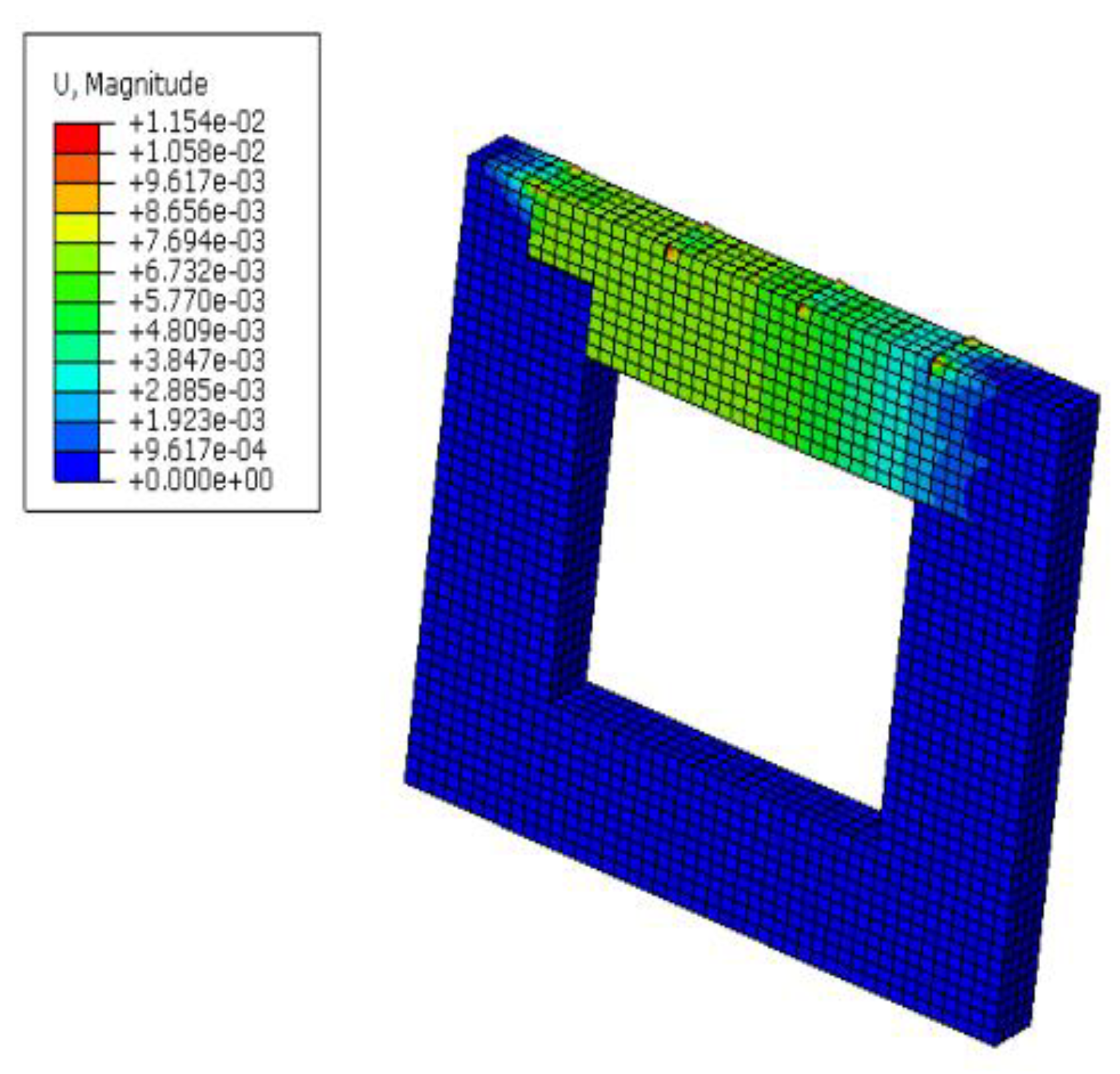
5.2. Case 2: Masonry Wall with an Opening Loaded with Vertical Pressure, Shear Displacement, and Blast Load
5.3. Case 3: Solid Masonry Wall Loaded with Vertical Pressure and Blast Load
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, S.; Elahi, A.; Pervaiz, H.; Rahman, A.G.A.; Barbhuiya, S. Experimental study of masonry wall exposed to blast loading. Mater. Constr. 2014, 64, 2–6. [Google Scholar] [CrossRef]
- Gertsch, L.; Baird, J. A Phased Array Approach to Rock Blasting; University of North Texas, UNT Digital Library: Denton, TX, USA, 2006; pp. 13–40. Available online: https://digital.library.unt.edu (accessed on 22 March 2022).
- Aloui, M.; Bleuzen, Y.; Essefi, E.; Abbes, C. Ground Vibrations and Air Blast Effects Induced by Blasting in Open Pit Mines: Case of Metlaoui Mining Basin, Southwestern Tunisia. J. Geol. Geophys. 2016, 5, 5–7. [Google Scholar] [CrossRef]
- Ipmawati, M.R.; Nainggolan, D.R.; Wiyono, B.; Sunary, R. Effect double-primer placement for improving the fragmentation on harder material in stemming column: A case study. IOP Conf. Ser. Earth Environ. Sci. 2018, 212, 012064. [Google Scholar] [CrossRef]
- Hao, D. Numerical Modelling of Masonry Wall Response to Blast Loads. Aust. J. Struct. Eng. 2009, 10, 37–52. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, D.; Fangyun, L.; Wang, S.C.; Tang, T. Experimental study and numerical simulation of the damage mode of a square reinforced concrete slab under close-in explosion. Eng. Fail. Anal. 2013, 27, 41–51. [Google Scholar] [CrossRef]
- Zhao, C.F.; Chen, J.Y. Damage mechanism and mode of square reinforced concrete slab subjected to blast loading. Theor. Appl. Fract. Mech. 2013, 63–64, 54–62. [Google Scholar] [CrossRef]
- Macorini, L.; Izzuddin, B.A. Nonlinear Analysis of Unreinforced Masonry Walls under Blast Loading Using Mesoscale Partitioned Modeling. J. Struct. Eng. 2014, 140, A4014002. [Google Scholar] [CrossRef]
- Kernicky, T.P.; Whelan, M.J.; Weggel, D.C.; Rice, C.D. Structural Identification and Damage Characterization of a Masonry Infill Wall in a Full-Scale Building Subjected to Internal Blast Load. J. Struct. Eng. 2015, 141, D4014013. [Google Scholar] [CrossRef]
- Jia, H.; Yu, L.; Wu, G. Damage Assessment of Two-Way Bending RC Slabs Subjected to Blast Loadings. Publ. Corp. Sci. World J. 2014, 2014, 718702. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Miranda, S.; Castellazzi, G.; Sarhosis, V. A 3D Detailed Micro-Modelling Approach for the In-Plane and Out-Of-Plane Analysis of Masonry Structures. Comput. Struct. 2018, 206, 18–30. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Rots, J.G.; Blaauwendraad, J. Two Approaches for the Analysis of Masonry Structures: Micro and Macro-Modeling. Heron 1995, 40, 313–338. [Google Scholar]
- Masi, F.; Stafanou, I.; Maffi-Berthier, V.; Vannucci, P. A Discrete Element Method based-approach for arched masonry structures under blast loads. Eng. Struct. 2020, 216, 110721. [Google Scholar] [CrossRef]
- Shamim, S.; Shamd, S.; Khan, A. Finite element analysis of masonry wall subjected to blast loading. Int. J. Adv. Mech. Civ. Eng. 2019, 6, 50–53. [Google Scholar]
- Shamim, S.; Shamd, S.; Khan, A. Numerical Modelling of Masonry Panel Subjected to Surface Blast Loading. J. Xi’an Univ. Archit. Technol. 2020, 12, 846–856. [Google Scholar]
- Abdulla, K.; Cunningham, L.; Gillie, M. Non-linear simulation of masonry behaviour under cyclic loads. In Proceedings of the 2017 MACE PGR Conference, Manchester, UK, 3 April 2017; pp. 20–22. [Google Scholar]
- Anas, S.M.; Alam, M.; Umair, M. Strengthening of braced unreinforced brick masonry wall with (i) C-FRP wrapping, and (ii) steel angle-strip system under blast loading. Mater. Today Proc. 2022, 58, 1181–1198. [Google Scholar] [CrossRef]
- Shariq, M.; Alam, M.; Husain, A.; Islam, N. Response of strengthened unreinforced brick masonry wall with (1) mild steel wire mesh and (2) CFRP wrapping, under close-in blast. Mater. Today Proc. 2022, 64, 643–654. [Google Scholar] [CrossRef]
- Shamim, S.; Khan, R.A.; Ahmad, S. Fragility analysis of masonry wall subjected to blast loading. Structures 2022, 39, 1016–1030. [Google Scholar] [CrossRef]
- Yu, Q.; Zeng, D.; Xu, X.; Li, S.; Dong, W.; Dai, L. Experimental and numerical investigation of polymer-reinforced and normal autoclaved aerated concrete masonry walls under large TNT explosive loads. Int. J. Impact Eng. 2022, 164, 104188. [Google Scholar] [CrossRef]
- Salmanpour, A.H. Displacement Capacity of Structural Masonry. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2017. [Google Scholar]
- De Villiers, W.I. Computational and Experimental Modelling of Masonry Walling towards Performance-Based Standardisation of Alternative Masonry Units for Low-Income Housing. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2019. [Google Scholar]
- Kömürcü, S.; Gedikli, A. Macro and Micro Modeling of the Unreinforced Masonry Shear Walls. Eur. J. Eng. Nat. Sci. 2019, 3, 116–123. [Google Scholar]
- Ranji, A.R.; Esmaeli, A. Blast load response of one-way reinforced concrete slabs retrofitted with Fiber reinforced plastic. Proc. Odessa Polytech. Univ. 2018, 2, 49–58. [Google Scholar] [CrossRef]
- Tan, W.A.; Tingatinga, E.A.; Alvarez, V. Blast load analysis and simulation of unreinforced concrete masonry. J. Phys. Conf. Ser. 2019, 1264, 012008. [Google Scholar] [CrossRef]
- Weggel, D.C. Blast threats and blast loading. In Blast Protection of Civil Infrastructures and Vehicles Using Composites; Series in Civil and Structural Engineering; Woodhead Publishing: Swaston, UK, 2010; pp. 3–43. [Google Scholar] [CrossRef]
- Botez, M.D.; Bredean, L.A. Numerical Study of a RC Slab Subjected to Blast: A Coupled Eulerian-Lagrangian Approach. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 2–5. [Google Scholar] [CrossRef]
- Rigby, S.E.; Tyas, A.; Bennett, T.; Clarke, S.D.; Fay, S.D. The Negative Phase of the Blast Load. Int. J. Prot. Struct. 2014, 5, 1–19. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Elsanadedy, H.M.; Al-Zaheri, Z.M.; Salloum, Y.A.; Abbas, H. Blast response of GFRP strengthened, infill masonry walls. Constr. Build. Mater. 2016, 115, 438–451. [Google Scholar] [CrossRef]
- Bolhassani, M.; Hamid, A.A.; Lau, A.C.W.; Moon, F. Simplified micro modelling of partially grouted masonry assemblages. Constr. Build. Mater. 2015, 83, 159–173. [Google Scholar] [CrossRef]
- Draganić, H.; Sigmund, V. Blast Loading On Structures. Tech. Gaz. 2012, 19, 643–652. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–329. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Tapkin, S.; Tercan, E.; Motsa, S.; Drosopoulos, G.; Stavroulaki, M.; Maravelakis, E.; Stavroulakis, G. Structural Investigation of Masonry Arch Bridges Using Various Nonlinear Finite-Element Models. J. Bridge Eng. 2022, 27, 04022053. [Google Scholar] [CrossRef]
- Daniel, J.; Dubey, R. Finite Element Simulation of Earthquake Resistant Brick Masonry Building Under Shock Loading. Adv. Struct. Eng. 2014, 81, 1027–1038. [Google Scholar] [CrossRef][Green Version]
- Dogu, M.; Menkulasi, F. A flexural design methodology for UHPC beams posttensioned with unbonded tendons. Eng. Struct. 2020, 207, 110193. [Google Scholar] [CrossRef]
- Hognestad, E. A Study of Combined Bending and Axial Load in Reinforced Concrete Members; Bulletin Series No.399; University of Illinois, Engineering Experiment Station: Chicago, IL, USA, 1951; pp. 32–54. [Google Scholar]
- Iuorio, O.; Dauda, J.A. Retrofitting Masonry Walls against Out-Of-Plane Loading with Timber Based Panels. Appl. Sci. 2021, 11, 5443. [Google Scholar] [CrossRef]
- Concrete Manufactures Association. Concrete Masonry Manual, 9th ed.; Concrete Manufactures Association: Menlo Park, CA, USA, 2011; Available online: https://www.cma.org.za/Portals/0/Docs/brickasandblocks (accessed on 22 April 2022).
- SANS 10400-A 2010; The Application of the National Building Regulations Part A: General Principles and Requirements, 3rd ed. SABS Standards Division: Pretoria, South Africa, 2010; ISBN 978-0-626-25157-4.
- Wei, J.; Du, Z.; Zheng, Y.; Ounhueane, O. Research on Damage Characteristics of Brick Masonry under Explosion Load. Shock Vib. 2021, 2021, 5519231. [Google Scholar] [CrossRef]
- Decanini, L.; De Sortis, A.; Goretti, A.; Langenbach, R.; Mollaioli, F.; Rasulo, A. Performance of masonry buildings during the 2002 Molise, Italy, earthquake. Earthq. Spectra 2004, 20 (Suppl. S1), 191–220. [Google Scholar] [CrossRef]
- Raza, I.; Shamim, S.; Ahmad, S.; Khan, R.A. Analysis of two-storey masonry structure under blast loading. Mater. Today Proc. 2023, 80, 1605–1610. [Google Scholar] [CrossRef]
- ABAQUS v. 6.14.2 Users Manual. Available online: http://130.149.89.49:2080/v2016/index.html (accessed on 13 March 2022).


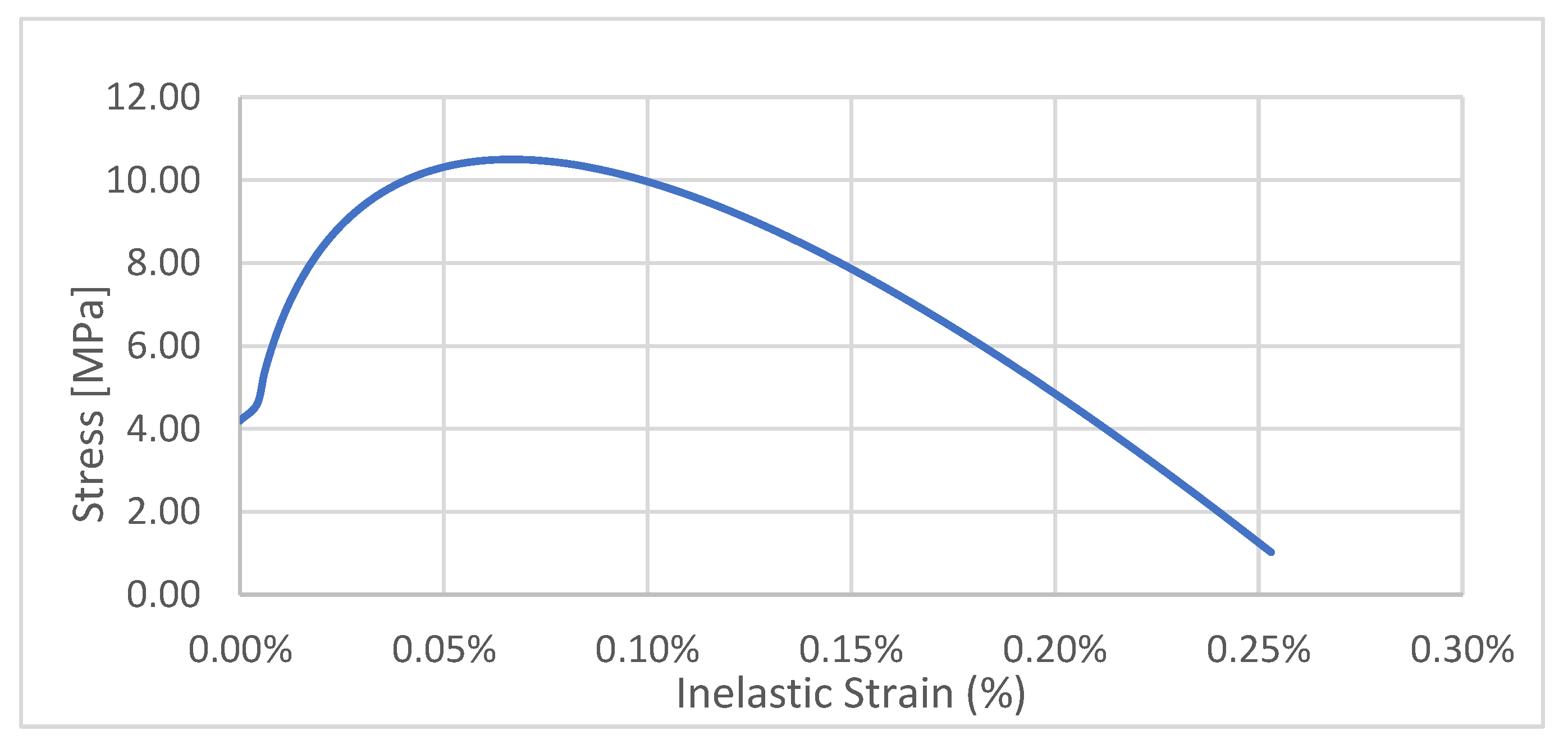
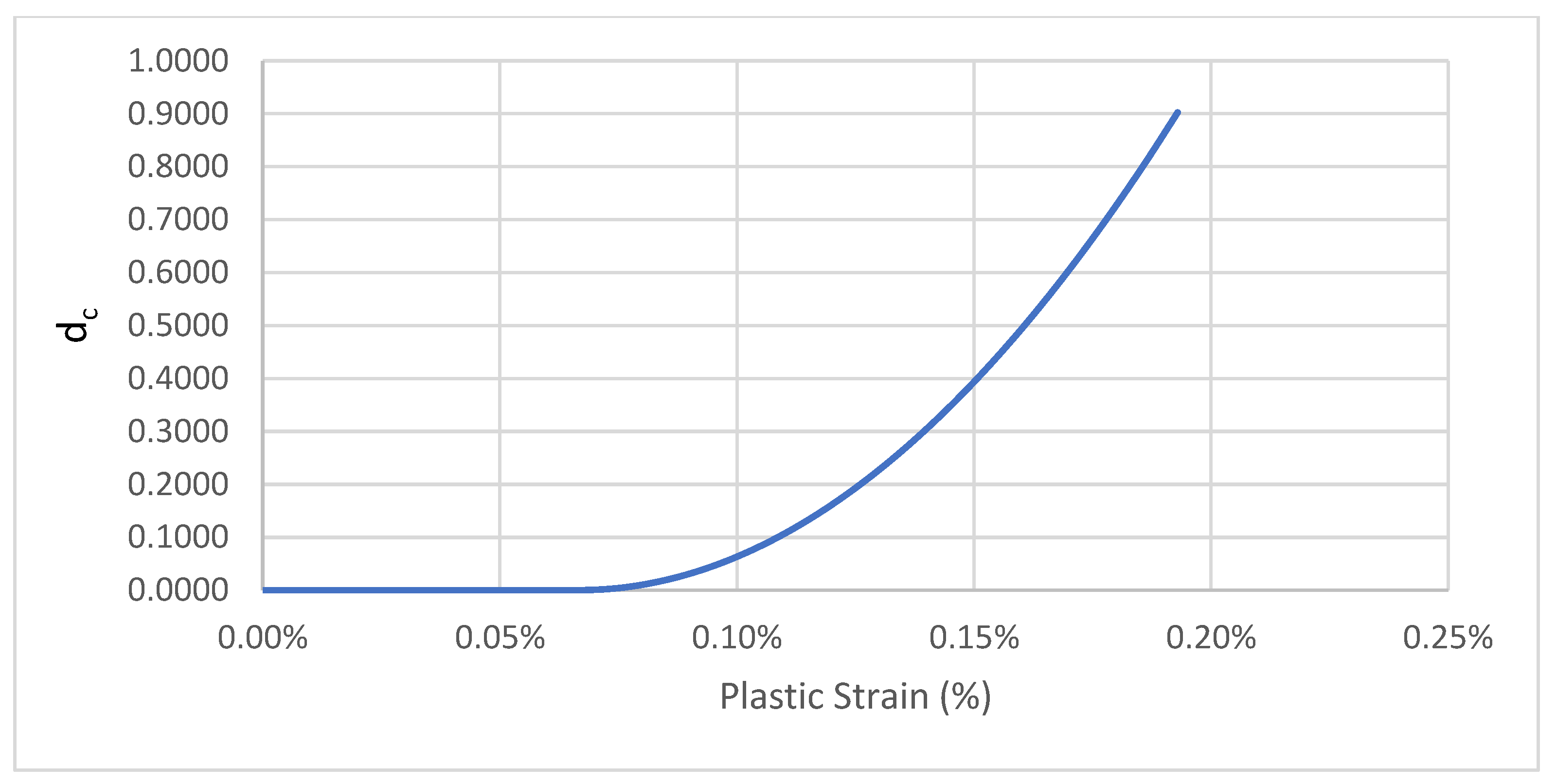
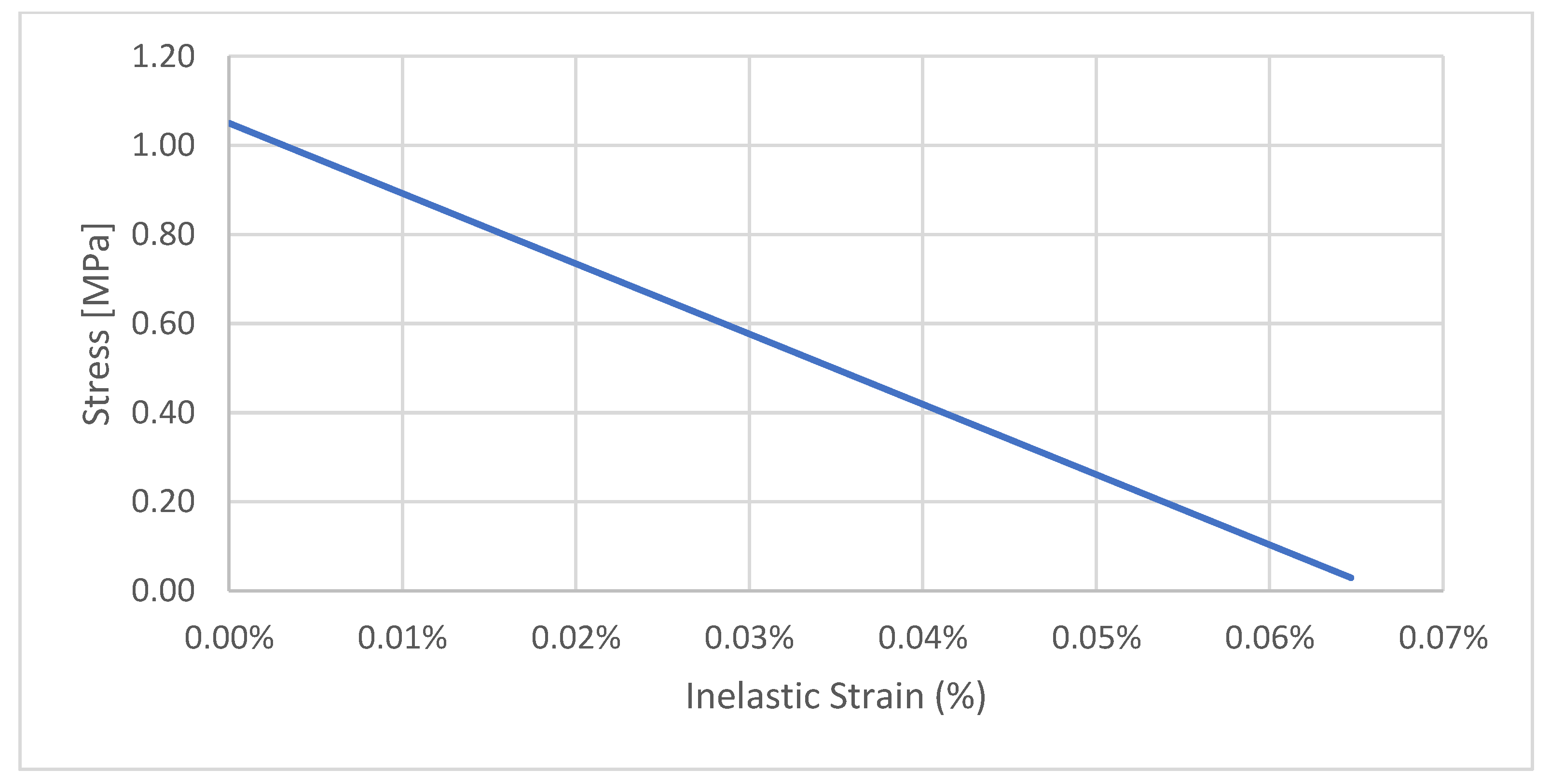

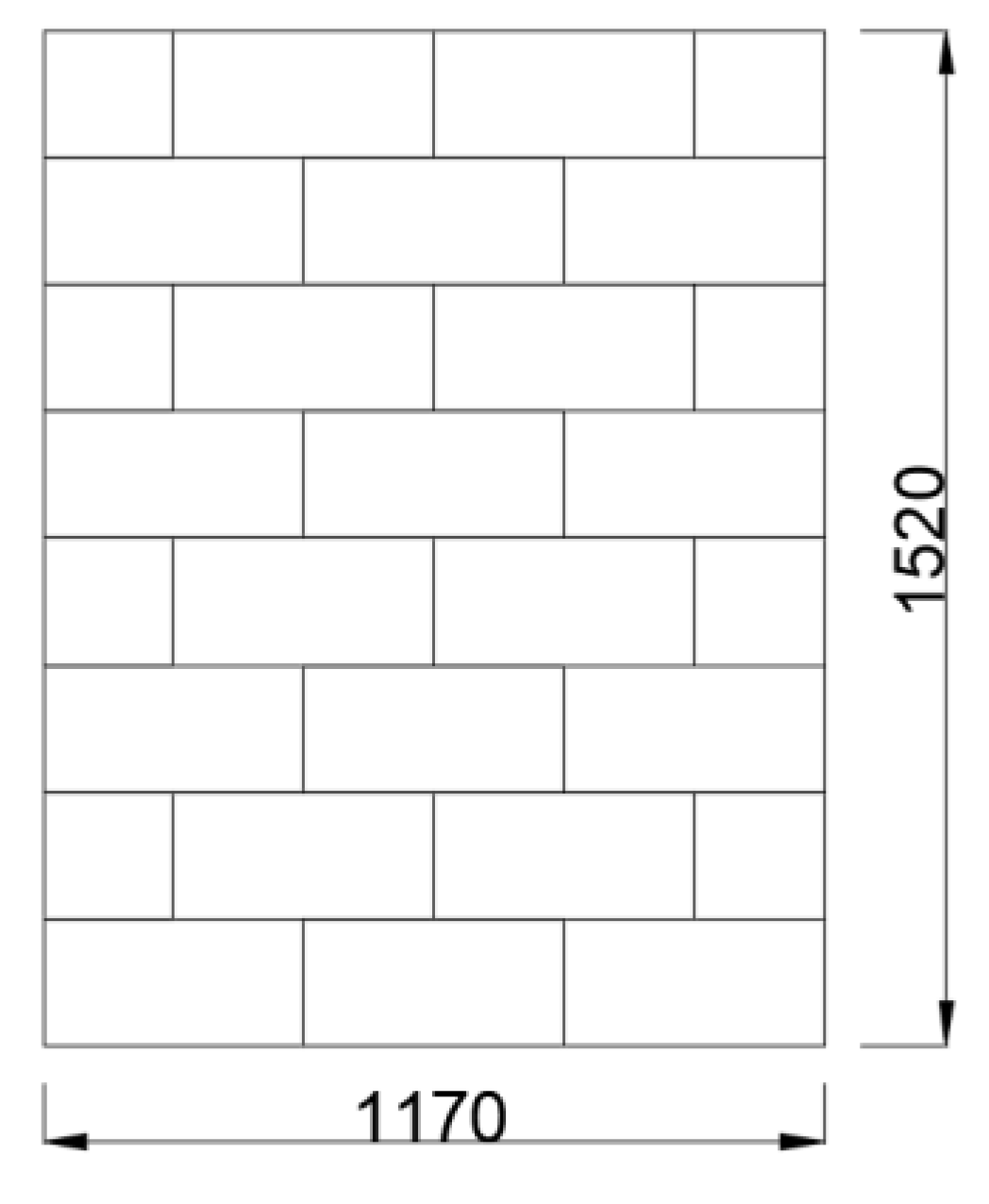





| Plasticity Parameter | Value |
|---|---|
| Dilation angle | 30 |
| Eccentricity parameter | 0.1 |
| Bi- and uni-directional compressive strength ratio | 1.16 |
| Stress ratio in tensile meridian | 0.67 |
| Viscosity parameter | 0.001 |
| Material | Modulus of Elasticity (MPa) | Poisson’s Ratio | Tensile Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|
| Masonry Unit | 15,500 | 0.15 | 1.05 | 10.5 |
| Case Description | Blast Load | Standoff Distance |
|---|---|---|
| Case 1 (solid wall loaded with vertical pressure, horizontal shear displacement, and blast load). | 100 kg TNT | 20 m, 50 m |
| 200 kg TNT | 20 m, 50 m | |
| 1150 kg TNT | 20 m, 50 m, 100 m | |
| Case 2 (wall with an opening loaded with vertical pressure, horizontal shear displacement, and blast load). | 1150 kg TNT | 50 m |
| 2000 kg TNT | 5 m | |
| 3500 kg TNT | 10 m | |
| Case 3 (solid wall loaded with vertical pressure and blast load). No horizontal shear displacement is considered. | 100 kg TNT | 50 m |
| 200 kg TNT | 100 m | |
| 1150 kg TNT | 100 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thango, S.G.; Stavroulakis, G.E.; Drosopoulos, G.A. Investigation of the Failure Response of Masonry Walls Subjected to Blast Loading Using Nonlinear Finite Element Analysis. Computation 2023, 11, 165. https://doi.org/10.3390/computation11080165
Thango SG, Stavroulakis GE, Drosopoulos GA. Investigation of the Failure Response of Masonry Walls Subjected to Blast Loading Using Nonlinear Finite Element Analysis. Computation. 2023; 11(8):165. https://doi.org/10.3390/computation11080165
Chicago/Turabian StyleThango, Sipho G., Georgios E. Stavroulakis, and Georgios A. Drosopoulos. 2023. "Investigation of the Failure Response of Masonry Walls Subjected to Blast Loading Using Nonlinear Finite Element Analysis" Computation 11, no. 8: 165. https://doi.org/10.3390/computation11080165
APA StyleThango, S. G., Stavroulakis, G. E., & Drosopoulos, G. A. (2023). Investigation of the Failure Response of Masonry Walls Subjected to Blast Loading Using Nonlinear Finite Element Analysis. Computation, 11(8), 165. https://doi.org/10.3390/computation11080165