Abstract
The Reissner–Nordstrom spacetimes and some generalised Reissner–Nordstrom spacetimes are analysed. The blackhole solutions are considered. The generalised Reissner–Nordstrom spacetimes with a cosmological-constant term, endowed with a Schwarzschild solid-angle element, are analytically delineated: the radii of the blackholes are analytically calculated and newly parameterised; the coordinate-singularity-avoiding coordinate extension is newly found, i.e., such that the tortoise-coordinate transformation can therefore be applied; the new conditions for merging the solutions as the physical horizons are analytically outlined; the new parameter space of the model is set and constrained; the new role of the cosmological-constant term in designating the Schwarzschild radius is demonstrated; the Reissner–Nordstrom–deSitter case and in the Reissner–Nordstrom–anti-deSitter one are newly demonstrated to be characterised in a different analytical manner. Furthermore, a new family of solutions is found, qualified after the cosmological-constant term. The generalised Reissner–Nordstrom spacetimes with a linear term, endowed with a Schwarzschild solid-angle element, are analytically studied: the radii are enumerated and newly parameterised; the new conditions for the merging of the radii as the physical horizons are set; the new parameter space of the system is arranged and constrained; the role of the linear-term parameter in the delineation of the Schwarzschild radius is newly proven to be apt to imply a small modification only. The generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild solid-angle element, with a linear term and a cosmological-constant term are newly inspected: the radii are analytically calculated and newly parameterised; the new conditions for the merging of the radii as the physical horizons are prescribed; the new parameter space of the scheme is appointed and constrained; the roles of the parameters are newly scrutinised in their application to modify the physical interpretation of the Reissner–Nordstrom parameters only in a small manner; the coordinate-singularity-avoiding coordinate extensions are newly found, i.e., such that the tortoise-coordinate transformation can therefore be applied; the definition of the physical radii is newly found; the results are newly demonstrated in both cases of a positive value of the cosmological constant and in the case of a negative value of the cosmological constant in a different manner; the role of the linear-term parameter is also newly enunciated. More over, a new family of solutions is found, which is delineated after particular values of the linear term and of the cosmological-constant one. The quantum implementation of the models is prospectively envisaged.
1. Introduction
Reissner–Nordstrom blackholes are constituted of one singularity point and two horizons, i.e., an inner Cauchy horizon and an event horizon. The embedding diagram of the Reissner–Nordstrom blackhole for a constant-angle section is obtained as in [1]
Differently from single-horizon blackholes and so, in particular, from asymptotically flat spacetime blackhole solutions [2], for a Reissner–Nordstrom spacetime blackhole solution, it is possible to provide a tortoise-coordinate extension, i.e., an extension of the radial coordinate r into the complex plane as a function of the real component and of the imaginary one. In more detail, let be x the real component and y the imaginary one: the tortoise-coordinate z is defined as
An analytical discussion leads to the definition of and as tow surfaces, respectively. Two groups of contours on each surface are possible, i.e.,
with
i.e., such that and are two surfaces. The Stokes lines are defined as
on from [3]; the horizons must stay within the closed lines of the Stokes lines.
The numerical calculation of the Stokes lines of a Reissner–Nordstrom blackhole (in four spacetime dimensions) is depicted in ([4] Figure 4), leftmost panel.
It is therefore necessary to outline that the singularity, the inner horizon and the event horizon correspond, respectively, to the three poles of the variable z from Equation (2).
This analysis is complemented after the study of [5], in which the imaginary part of the frequency is found to be not periodic.
The Stokes portraits of regular blackholes are introduced in [6].
The generalised Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element and a cosmological-constant term were pointed out as enjoying innovative characterisations.
The stability properties of the generalised Reissner–Nordstrom spacetimes with a cosmological-constant term both in the deSitter case and in the anti-deSitter case have been studied in [7].
The Minkowski inequality of the Reissner–Nordstrom–anti-deSitter spacetimes is presented in [8].
The generalised Reissner–Nordstrom spacetimes endowed with a schwarzschild solid-angle element and a linear term were delineated after the following interesting properties.
In [9], a Reissner–Nordstrom spacetime endowed with a linear term was presented and the three horizons were hinted at; the possibility of merging of the horizons was not included in the analysis.
In [10], the features of a Reissner–Nordstrom spacetime endowed with a ‘quintessential’ component is qualitatively analysed as the mass and the charge are assumed as small quantities; ‘approximate Lie symmetries’ are implemented.
The generalised Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element, a linear term and a cosmological constant were delineated to exhibit crucial features.
In [11], different types of spacetimes are qualitatively depicted and the features of the horizons are qualitatively described.
Some of the features of the generalised Kottler spacetimes and their parameter spaces were studied in [12,13].
In the present study, we analyse the generalised Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element, a cosmological constant; the generalised Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element, a linear term; and the generalised Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element, a linear term and a cosmological constant.
The analytical expressions of the radii are spelled out within a new parameterisation.
The well-posedness of the new analytical expressions of the radii is discussed.
The coordinate-singularity-avoiding coordinate extensions are newly found and provided in the instances where the cosmological-constant term is present: the tortoise-coordinate transformation is newly demonstrated to apply to the generalised Reissner–Nordstrom spacetimes, thus giving rise to new understanding of the geometries.
In the case of a generalised Reissner–Nordstrom spacetime with a linear-term parameter, the conditions for the vanishing of the explicit imaginary part of the radii are set.
In the three instances, the parameter space of the models is newly set and newly fully constrained.
The manuscript is aimed at examining the physical features of these spacetimes; the spacetimes endowed with a deSittter-like case and those endowed with an anti-deSitter-like term are newly demonstrated to exhibit very different intrinsic geometrical properties. The geometrical role of the linear term is newly explored within the Reissner–Nordstrom generalised spacetimes.
The paper is organised as follows.
In Section 1, some features of the Reissner–Nordstrom spacetimes are recalled; in particular, the implementation of the tortoise-coordinate transformation and the study of the horizons is recapitulated.
In Section 2, the generalised Reissner–Nordstrom spacetimes chosen are described; a comparison with the studies of the phenomenological parameters involved in the schemes is summarised.
In Section 3, the generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild solid-angle element, with a cosmological-constant term, are newly studied: the expressions of the analytical radii are spelled out in a new characterisation; the coordinate-singularity-avoiding coordinate extensions are newly found, to which the tortoise-coordinate transformation is therefore newly demonstrated to apply; the parameter space of the model is newly established and constrained. The results newly significantly reveal that the deSitter case and the anti-deSitter case are denoted after new significantly distinct properties.
In Section 4, the generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild solid-angle element, with a linear term, are newly investigated: the expressions of the radii are spelled out in a new parameterisation; the physical radii are newly individuated; the parameter space of the model is newly set and constrained.
In Section 5, the generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild solid-angle element, with a linear term and a cosmological-constant term, are newly examined: the expressions of the radii are written in a new parameteirsation, the coordinate-singularity-avoiding coordinate extensions are newly found, for which the tortoise-coordinate transformation is thus newly revealed to apply; the parameter space of the model is newly indicated and constrained. The results newly demonstrate that the deSitter-like case and the anti-deSitter-like one exhibit very different, non-trivial properties; the presence of the linear term is newly demonstrated to be qualified after intrinsic geometrical properties.
In Section 7, the quantum features of Reissner–Nordstrom spacetimes are recalled with the aim of comparison with the perturbation approach presented in Section 1.
In Section 8, remarks about the newly found results are presented.
2. The Generalised Reissner–Nordstrom Spacetimes
A generalisation of the Reissner–Nordstrom spacetimes endowed with a Schwarzschild solid-angle element is presented in [14] as
Particular values of the summation in Equation (6) are to be chosen.
The ranges of the parameters of the metrics were studied in [15] as
and analysed in [16,17,18].
The spacetimes are discussed in [19] as far as their geometrical features are concerned.
In [14], two particular solutions of the Reissner–Nordstrom–deSitter blackhole spacetime
corresponding to a Reissner–Nordstrom–deSitter spacetime
were found to have an outer horizon of deSitter kind at with , and an inner horizon of the blackhole kind was found at with .
In the present study, the generalisation
is chosen. In more detail, the parameters selected will allow one to describe generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild sold-angle element, with a cosmological-constant term ; generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild sold-angle element, with a linear-term parameter term ; and generalised Reissner–Nordstrom spacetimes, endowed with a Schwarzschild sold-angle element, with a linear-term parameter and with a cosmological-constant term . The linear-term-parameter generalisation will be confirmed to be consistent as a small modification of the Schwarzschild radius. The deSitter cases and the anti-deSitter cases will be newly found to qualify the generalised spacetimes in a different manner, according to the two different instances.
3. The Generalised Reissner–Nordstrom Spacetimes with a Cosmological Constant
The generalised Reissner–Nordstrom spacetimes with a cosmological-constant term, endowed with a Schwarzschild solid-angle element, are written after the square line element
with being the cosmological-constant term; i.e., a generalised Reissner–Nordstrom–deSitter spacetime is obtained in the case , while a generalised Reissner–Nordstrom–anti-deSitter spacetime is described in the case .
The equation is solved as the formal expressions of the four radii
with the functions m and n defined as
and
3.1. Discussion of the Solutions of the Generalised Reissner–Nordstrom Spacetimes with a Cosmological-Constant Term
The well-posedness of the solutions of Equation (12) are discussed in the following.
The non-vanishing nature of the denominators m in the summands of the radii of Equation (12) is as follows
This way, the new following physically consistent constraints are obtained
From Equation (16), one newly learns that the limit to a vanishing cosmological constant is non-trivial.
Furthermore, differently, one newly learns also that the limit to a vanishing parameter is well posed: its physical implementation is the restoration of the Schwarzschild radius in the presence of a cosmological constant; this role is modified after the definition of the new coordinate-singularity-avoiding coordinate extension.
In particular, Equation (16d) defines the modifications to the physical meaning of the Schwarzschild radius, which, in their turn, further constrain the parameter space.
The conditions in Equation (16d) are plotted in Figure 1.
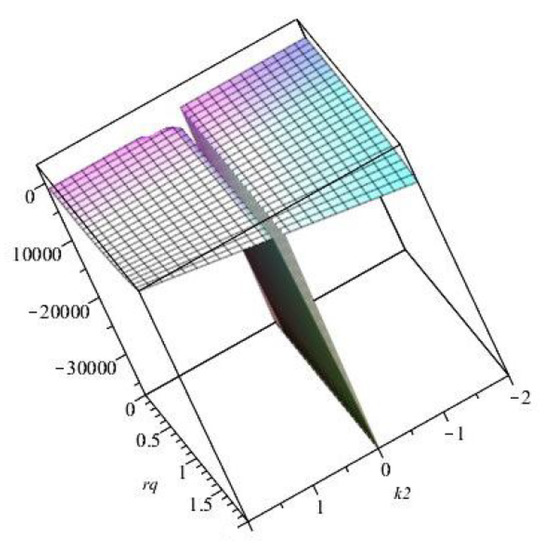
Figure 1.
The modifications of the Schwarzschild-radius parameter after the conditions of the parameter space Equation (19).
The new constraints from Equation (16) imply that there is a profound difference between the geometries of the deSitter characterisation and those of the anti-deSitter one, as can be seen in Figure 1.
Moreover, one new region of the parameter space of the scheme is delineated, which is already ruled out.
The non-vanishing nature of the denominators m is formulated as follows
Requesting , i.e., requesting the most general scheme, further implies
From Equation (18), a new constraint on the parameter space is found, which involves the possible values of .
The choice of an equality in Equation (18) delineates a new particular family of generalised Reissner–Nordstrom spacetimes with a cosmological constant, which has not been explored yet. More specifically, the new family of generalised Reissner–Nordstrom spacetimes with a cosmological constant admits two new physically different cases, in which the cosmological-constant term acts in a different manner and whose geometric properties have not been investigated yet.
Furthermore, Equation (16d) automatically further implies the new following constraint on the parameter space which newly relates and in a new non-trivial manner; i.e.,
for which, in more detail, one demonstrates that the limit to a Schwarzschild spacetime or to a generalised Schwarzschild spacetime are not only highly non-trivial, but also depend momentously on the sign of the cosmological constant; i.e., the generalised Reissner–Nordstrom geometries are found to admit a representation characterised after the new constraints.
More specifically, the request (where the inequality is learnt from the analysis in the above) implies a new lower bound of in the deSitter case.
Requesting , i.e., requesting the most general scheme, further implies possible modifications of the roles and of the values of the square length : form the new definition of the new coordinates-singularity avoiding coordinates extension, one will learn that the modifications of the square length are only small; furthermore, one will learn that such modifications are intrinsically related with the (small) modifications of the value of the Schwarzschild radius.
The generalised Reissner–Nordstrom spacetimes with a cosmological constant therefore are distinguished in a different manner; more specifically, the role of the cosmological constant is that of modifying the expression of the Schwarzschild radius and that of the length in a new non-trivial manner, which, furthermore, act differently in the deSitter case and in the anti-deSitter case.
The numerator of the summands in Equation (12) is studied as follows.
3.2. Merging of the Radii
For the sake of comparison with the more general results of Section 5, the solutions of Equation (12) are simplified and the four radii are demonstrated to become the two horizons as follows
with the functions
and
Indeed, the first summand is calculated to vanish for real values of all the parameters but that of the cosmological-constant term; i.e., it vanishes for consisting of a real part and a (positive) imaginary one: the differences between the deSitter case and the anti-deSitter case are here newly understood also as far as the multivaluedness of the tortoise-coordinate extension is concerned. It is therefore newly verified that the tortoise-coordinate extension is here well posed.
3.3. New Coordinate-Singularity-Avoiding Coordinate Extension of the Generalised Reissner–Nordstrom Spacetimes with a Cosmological Constant
The new coordinate-singularity-avoiding coordinate extension is found to be
with
Indeed, it is crucial to remark that
The coordinate-extension Equation (24) is valid for small values of only; the cosmological-constant term is therefore newly demonstrated to modify the value of the Schwarzschild radius only slightly.
It is thus possible to implement the tortoise-coordinate transformation to study the radii.
4. The Generalised Reissner–Nordstrom Spacetimes with a Linear Term
The generalised Reissner–Nordstrom spacetimes with a linear term, endowed with a Schwarzschild solid angle, are written after the square line element
with being the parameter qualifying the linear term generalising the studied spacetimes. The sign of the parameter is not specified, in order to let one appreciate the geometrical qualifications of the linear term.
The equation of the spacetime Equation (27) is fulfilled after the analytical radii
where the quantity d is defined as
From Equation (28), the conditions
and
are found.
Equation (31) imposes the new condition on the Schwarzschild radius as a constraint of the parameter space
Condition Equation (30) is relevant in establishing the new non-trivial limit to a vanishing ‘linear-term’ component.
The limit procedure is nevertheless comprehended within the analysis of the physical characterisation of the ranges of the ‘linear-term’ parameter. It is crucial to remark that the condition is highly non-trivial, as the term does not define the grade of the equation characterising the blackhole solution.
Furthermore, Equation (32) sheds light of the non-trivial geometry of the generalised Reissner–Nordstrom spacetimes with a linear term, as such geometry is manifested as modifying the Schwarzschild radius but not the parameter in this specific instance.
4.1. Merging of the Radii
The two radii and merge at the vanishing of the square root multiplying the imaginary unit
where the condition Equation (33) is solved as the new constraint of the parameter space
The physical radii and are defined and therefore newly parameterised as
As an example of the conditions imposed on the phase space from Equation (35a), the function from Equation (35a) is illustrated a function of and in Figure 2, in which one part of the new non-trivial conditions imposed on the parameter space can be visualised.
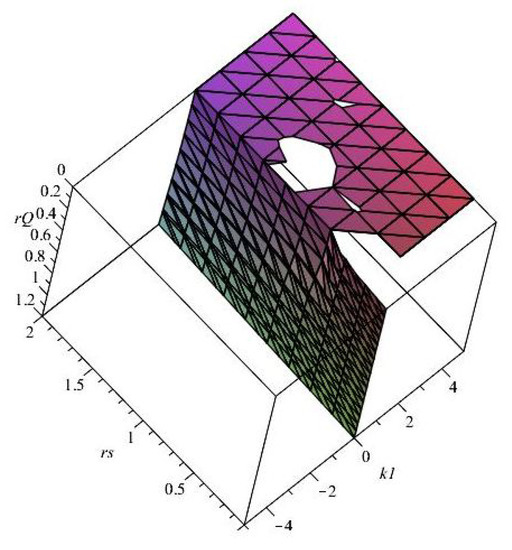
Figure 2.
The new conditions imposed on the parameter space of the generalised Reissner–Nordstrom spacetimes with a linear term after the definition of the new function from Equation (35a) as a function of the Schwarzschild radius and of the parameter qualifying the generalisation of the studied spacetime.
4.2. Merging(s) of the Solution(s)
The function Equations (28b) and (28c) are found to merge and to give rise to the physical horizons following the new condition
for which Equation (36) is solved as
within the constraint of the parameter space
The available portion of parameter space avaialable for the solution of Equation (33) is plotted in Figure 3 as a function of the Schwarzschild radius and of the parameter .
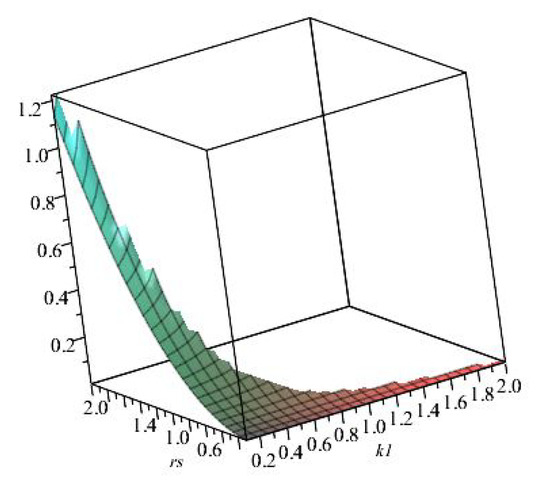
Figure 3.
The function from Equation (33) is plotted as a function of and , from which the full constraints imposed on the parameter space from this condition are delineated.
The two horizon Equations (28b) and (28c) therefore merge at the new condition (37). The new conditions must therefore be imposed on the parameter space of the two-horizon solution of the scheme; it is important to remark that the positive-valued- linear term generalised spacetimes and those qualified after a negative value of the linear term are newly found to be analytically described as with very different geometrical properties newly indicated after the new parameterisation is chosen.
5. Generalised Reissner–Nordstrom Spacetimes with a Linear Term and a Cosmological-Constant Term
The generalised Reissner–Nordstrom spacetimes with a linear term and a cosmological-constant term, endowed with a Schwarzschild solid-angle element, are written after the square line element
where is the parameter characterising the linear term and is the cosmological-constant term, which is, for the moment, not specified as having positive values or as having negative values. The equation of the spacetime (39) is calculated to admit the analytical solutions, which are here newly parameterised as
where the following definitions have been taken:
and
5.1. Discussion of the Radii Solutions
The denominators of the radii solutions of Equation (40) are well posed when
The equation is discussed as
which is solved after the values
which is well posed for
The discussion of the equality in the latter shows that there are regions of the parameter space which have to be excluded since their expression is multiplied by the imaginary unit.
In particular, from the discussion of Equation (45) with respect to the square length , the region to be excluded is depicted in Figure 4.
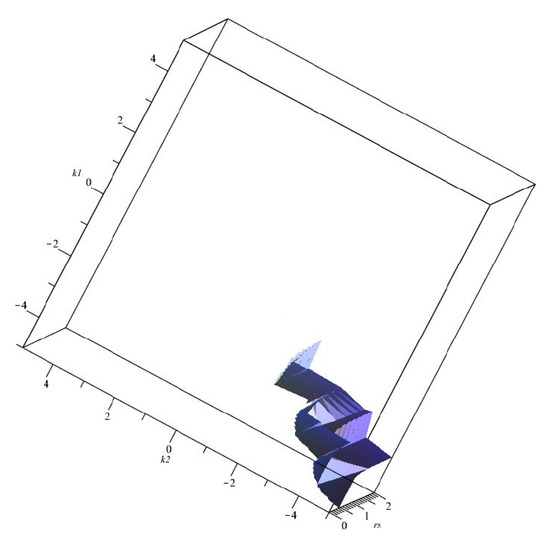
Figure 4.
The region of the parameter space to be excluded after the discussion of Equation (45).
Furthermore, the value has to be excluded from the investigation, as will be explained after the explanations of the roles of the parameters and with respect to the definition of the Schwarzschild radius, for the implementation of the tortoise coordinates, for the study of the blackhole spacetime in a non-perturbation way.
A new particular family of solutions from Equation (40) is
which is solved after the relation for the Reissner–Nordstrom squared length
when evaluated at ; Equation (49) therefore becomes
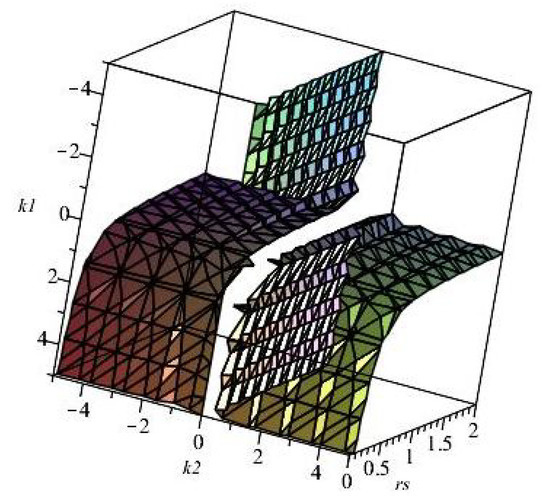
Figure 5.
The parameter space of in Equation (49).
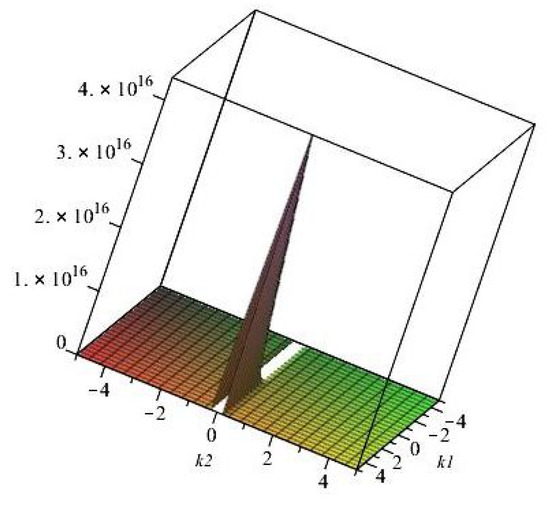
Figure 6.
The parameter space of in Equation (50) in units ().
Furthermore, one must stipulate
5.2. The Physical Horizons
The two physical horizons are obtained from Equation (40) after stipulating that the opportune quantities vanish, i.e.,
and
because of Equation (51).
It is important to remark that the condition Equation (53) does not depend on the square length .
Equation (53) is solved as
Imposing is realised in the instances
The horizons are therefore found as
From Equation (54) and from Equation (55), the new constraints on the Schwarzscihld radius, on and on are obtained.
Furthermore, the new roles of the parameters characterising the value of the Schwarzshild radius are outlined.
The parameter space is therefore studied at the realness of the square roots.
It is possible to remark that the two horizons of Equation (56) exhibit different properties in the deSitter case and in the anti-deSitter case.
The different properties exhibited in the deSitter case and those demonstrated in the anti-deSitter case also involve the linear-term parameter
The method presented in [20] applies only to a Schwarzschild–deSitter spacetime.
In [21], the ‘trapping horizons’ are described only for Reissner–Nordstrom–deSitter spacetimes in the special case of and in the special case .
In the present analysis, the manner of merging of the radii to create the two horizons is newly defined according to the ratio . The new constraints of the new functions a and f on the parameter space further complete the new establishment of the parameter space of the model.
5.3. New Coordinate-Singularity-Avoiding Coordinate Extension of the Generalised Reissner–Nordstrom Spacetimes with a Linear Term and with a Cosmological Constant
The new coordinate-singularity-avoiding coordinate extensions are written as
with the value of being
This way, the expansion is balanced after the newly found initial value of the new radial variable as
The new coordinate-extension Equation (57) is apt for small values of and only; the linear-term parameter and the cosmological-constant term are thus demonstrated to modify the value of the Schwarzschild radius in a new manner. The newly found generalised Reissner–Nordstrom–deSitter geometry and the generalised Reissner–Nordstrom–anti-deSitter one are newly explored; the two geometries are found to be different, the difference being highly non-trivial due to the non-linearity of the Einstein field equations.
One therefore newly learns that the limit to a vanishing cosmological constant is non-trivial.
Moreover, in a different manner, it is also possible to infer the well-posed-ness of the limit to a vanishing value of the parameter; indeed, its physical understanding is the accomplishment in the restoration of the role of the Schwarzschild radius in the presence of a cosmological- constant term; this interpretation is modified after the implementation of the new coordinate-singularity-avoiding coordinate extension.
It is therefore possible to apply the tortoise-coordinate transformation to analyse the radii.
6. Outlook
The present work is aimed at studying some particular features of the generalised Reissner–Nordstrom blackhole spacetimes. The new methodology used is the findings of the analytical radii, the discussion of their well-posedness and the conditions for the obtention of the physical horizons; from the study, new features of the generalised spacetimes are found and new constraints on the parameter spaces of the models are established.
Three particular cases of interest have been investigated.
Concerning the generalised cosmological Reissner–Nordstrom spacetime with a cosmological constant, endowed with a Schwarzschild solid-angle element, the results found complete studies in the literature by adding new qualifications and new relationships among the Reissner–Nordstrom parameters and the cosmological constant; the findings far and away generalise the pioneering work [21], in which only particular aspects of the Schwarzschild–deSitter spacetime were outlined; the study was not followed after further investigations. Furthermore, the present analysis of this spacetimes is complemented with the new definition of the coordinate-singularity-avoiding coordinate extensions, which allows one to implement the tortoise-coordinate transformation; the new coordinate extensions generalise the Nairai transformation for the considered case: in particular, the role of the cosmological constant in modifying the other parameters only slightly is newly found. A new particular family of generalised Reissner–Nordstrom spacetimes with a cosmological constant is found and studied. All the results are demonstrated to hold in the Reissner–Nordstrom–deSitter case and in the Reissner–Nordstrom–anti-deSitter case in a new different non-trivial manner, which further clarifies new features of the generalised deSitter spaces and those of the generalised anti-deSitter spaces.
The exploration of the generalised Reissner–Nordstrom spacetimes with a linear term is motivated by a particular case in [14] and the related literature. In this case, the analytical radii are found and discussed and the expressions of the physical horizons are presented. The analysed generalised spacetime is therefore qualified after new relations among the parameters characterising the solution, as well as new constraints of the parameter space of the model.
The generalised Reissner–Nordstrom spacetimes with a linear term and a cosmological constant, endowed with a Schwarzschild solid-angle element, are studied analytically after [14]. As a result, the analytical expressions of the radii are found and their well-posedness is discussed; the expressions of the physical horizons are presented. The new aspects of the relations among the parameters qualifying the solution are investigated and the new parameter space is set. A new particular family of solutions is found and explored. The new coordinate-singularity-avoiding coordinate extension is newly found to be consistent with the Nairai transformation and allows one to further apply the tortoise-coordinate transformation; the coordinate-singularity-avoiding coordinate extensions newly characterise the role of the parameters of the generalised model in modifying the Reissner–Nordstrom parameters only slightly: furthermore, differently from the case of the generalised Reissner–Nordstrom spacetimes with a cosmological-constant term, the initial values of the coordinates are calculated to be non-trivial.
The specificities of the newly introduced methodology consist also in analysing the physical spacetimes non-perturbatively.
The gathering of the results allows one to implement further qualifications and further investigations.
7. Perspectives
Quantum effects in the present literature about the Reissner–Nordstrom geometry are presented in two issues: one being the perturbative approach after the application of the tortoise-coordinate transformation; the other being the calculation of the Hawking temperature, which is evaluated after the knowledge of the surface of the blackhole object (the surfaces of the generalised Reissner–Nordstrom blackhole objects being determined after the physical radii here found).
7.1. Geometrical Settings
Another aspect which might be considered is therefore the geometrical definition of the radii in the case of non-Riemannian geometries; the most general classification of non-Riemannian geometries was given in the Schouten classification [22,23] and in the extended Schouten classification [24], in which the metric-asymmetricity object, the generalised contortion tensor and non-metricity object are comprehended.
Within this framework, there is room for investigation of different realisations of Reissner–Nordstrom-related spacetimes, for which , with . According to this scheme, it is possible to consider also the spinning features of the spacetime realisation [25], for which already the properties of the analytical radii offer different interpretations.
Differently, in [26,27], a cosmological implementation of mass-inflation and kink instabilities can also be considered.
From a different viewpoint, the Petrov classification can be taken into account for analysis of the geometric properties of the generalised spacetimes, i.e., also to improve the investigation of [21], which was only partially developed in the case of the Schwarzschild–deSitter spacetime and no further investigations have followed ever since.
Within the Petrov classification [28], the action of the 4-rank tensors on bivectors are analysed as those of operators (of which the bivectors are the eigenvectors, bringing the proper eigenvalues), such as the Weyl tensor.
In [29], the characterisation of algebraic types in four-dimensional Lorentzian space is presented. According to the study, the Schwarzschild spacetime is the only spacetime whose asymptotic limit is Minkowski; the geometric asymptotic limit of the other possible generalised spacetimes can be correspondingly analysed. As a result, according to the analysis in [29], the study of the causal character of the corresponding eigenspaces can be compared to the suited analysis of the Schwarzschild case in order to gain items of information about the asymptotical features from an algebraic point of view as well as from a differential-geometry point of view in a new manner.
In [30], Weyl–Cartan spaces are studied as far as the Lorentzian transformations are concerned, for the sake of a classification of the curvature tensor within the framework of Weyl–Cartan geometry: also in this case, from the classification of the Weyl tensor, it is possible to compare the analysed spaces with the Schwarzschild case as far as the asymptotical behaviour is concerned.
7.2. Further Implementations
The quantum instability of the Cauchy horizon in Reissner–Nordstrom–deSitter spacetime was described in [31].
The entropy of the Reissner–Nordstrom–anti-deSitter spacetimes was investigated in [32]. The quantum version of Reissner–Nordstrom–deSitter spacetimes and that of Reissner–Nordstrom–anti-deSitter spacetimes were described in [33]; the quantum feature of the radial coordinate was implemented.
Kerr–deSitter spacetimes were envisaged in [34]; in this case, only three horizons were shown to be physically relevant (i.e., defined with positive sign).
The Gibbons–Hawking temperature of the Reissner–Nordstrom spacetime with a cosmological constant was calculated in [35].
The Reissner–Nordstrom–deSitter blackhole with a linear term and the Reissner–Nordstrom–anti-deSitter blackhole with a linear term have different thermodynamical properties, as scrutinised in [36] and the references therein.
Reissner–Nordstrom spacetimes with cosmological constant were investigated in [37], where different thermodynamical properties were described in the cases of a positive value of the cosmological constant and in those of a negative value of the cosmological constant; the thermodynamical system is investigated within the comparison of the role of the cosmological horizon and that of the blackhole horizon.
Some thermodynamical properties derived from the definition of the Gibbons–Hawking temperature are delineated in [35].
In [38], a temperature which does not match that of a Reissner–Nordstrom–deSitter spacetime was outlined as far as the outer horizon is concerned.
The study of a family of spacetimes which generalise the Reissner–Nordstrom spacetime after the definition of a linear term and a cosmological constant is presented in [39].
An uncharged, rotating Kerr–deSitter solution is examined in [40].
Reissner–Nordstrom blackhole solutions are considered in [41] as far as the ‘quintessential’ component is concerned; in more detail, the variation of the temperature is plotted for different values of the parameter of state related to the quintessence and, for increasing density, the blackhole temperature is shown to decrease.
The temperature of the Schwarzschild ‘quintessential’ blackhole and the Reissner–Nordstrom one with a linear term are defined in [42].
The study of the quantum presentation of the possible realisations of the generalisations of the Reissner–Nordstrom geometries allows for possible cosmological implementations; these geometries can shed light on the mechanisms of celestial-object formations. A comparison with the Bardeen picture is presented in [43].
8. Remarks
In the present paper, the generalised Reissner–Nordstrom spacetimes have been analysed in three particular instances: the generalised Reissner–Nordstrom spacetimes with a cosmological constant, the generalised Reissner–Nordstrom spacetimes with a linear term and the Reissner–Nordstrom spacetimes with a linear term and a cosmological-constant term.
The generalised Reissner–Nordstrom spacetime with a cosmological constant helped us reveal the highly non-trivial differences between the deSitter case and the anti-deSitter case. The differences are outlined not only in the definition of the radii, but also as far as the coordinate-singularity-avoiding coordinate extension is concerned. A comparison with the perturbation approach is accomplished after exploring the features of the cosmological-constant term . A particular new specific family of such spacetime blackhole solutions, corresponding to , is found. The analytical expressions of the physical horizons are set within the appropriate constraints of the parameter space.
The generalised Reissner–Nordstrom spacetimes with a linear term have been analysed. The three radii are found, which are determined after the reduced quartic equation, and the conditions for the description of the physical spacetime two physical horizons are displayed. The geometry role of the linear term, , is here newly investigated with respect to the previous interpretations as quintessence and as non-dynamical dark energy.
Cases of generalised Reissner–Nordstrom spacetime with a linear term and a cosmological constant have been explored. The well-posedness of the four radii is discussed, as well as the description of the two physical horizons. A new family of particular solutions is newly found, according to the new parameterisation of the blackhole spacetime radii and horizons, and the parameter space of these solutions is newly inspected. The coordinate-singularity-avoiding coordinate extension is found; in particular, the non-trivial value of the initial conditions of the radial variable is studied. The comparison with the generalised Reissner–Nordstrom spacetimes with a cosmological-constant term is therefore accomplished after the recognition of the features which are exhibited within the discussion of the physical conditions.
The analysis of the role of the lienar.term parameter and of that of the cosmological term parameter in the modifications of the physical implementation of the Schwarzschild radius open the way to the comparison with analysis of the comparison with [44], which was developed for the sake of possible descriptions of particular types of galaxy rotation curves.
The paper is organised as follows.
In Section 1, the generalised Reissner–Nordstrom spacetimes are introduced; in particular, the perturbation approach is presented, also with respect to the definition of the tortoise-coordinate system.
In Section 2, the generalised Reissner–Nordstrom spacetimes are present from a geometrical point of view. Among the generalisations possible, three of them were taken into account, whose physical expression is straightforwardly juxtaposed with the generalised Schwarzschild spacetimes within the same instances of physical definition.
In Section 3, the generalised Reissner–Nordstrom spacetimes with a cosmological-constant term are newly studied. The two physical horizons are exhibited as analytically descending from the non-trivial four radii, which are the solutions of the equation. The parameter space of the model is set and constrained. The coordinate-singularity-avoiding coordinate extension is found. The results are demonstrated to hold in a different manner in the deSitter case and in the anti-deSitter case, whose specific aspects are found to be significantly different. The solutions are also rewritten in a manner so as to render easy the comparison with the case of a generalised Reissner–Nordstrom spacetime with a linear term and a cosmological-constant term.
In Section 4, generalised Reissner–Nordstrom spacetimes with a linear term are investigated. The particular features of the reduced-quartic equation are outlined as implying three radii; the constraints for the obtention of the two physical radii are discussed. The parameter space of the scheme is established and constrained. The role of the linear term is here contrasted with that of the case of the generalised Schwarzschild spacetimes, in which such a role is straightforwardly interpreted as a small modification of the Schwarzschild radius.
In Section 5, the generalised Reissner–Nordstrom spacetimes with a linear term and a cosmological-constant term are examined. The four radii are found; the well-posedness of the solutions is scrutinised and the conditions of the definition of the two physical radii are researched. The parameter space of the model is defined and constrained and also compared with the cases of the generalised Reissner–Nordstrom spacetimes with a cosmological-constant term. The differences between the deSitter case and the anti-deSitter case are set for comparison. A prospective systematic study of the possible quantum implementations of the geometries allows for the definitions of new cosmological settings also at the semiclassicalisation epoch.
In Section 7, some features of the (generalised) Reissner–Nordstrom spacetimes, such as the Minkowski inequality, are reviewed for the sake of comparison with the Schouten classification and the Petrov classification within the framework of an analysis of asymptotical behaviour; furthermore, the quantum features of generalised Reissner–Nordstrom spacetimes are recalled for comparison with the perturbation approach as well as for prospective studies.
In Section 8, the main features of the generalised chosen Reissner–Nordstrom spacetimes are compared with further examples.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Calculation done by the Author.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Calculations are available from the author.
References
- Brauer, O.; Socolovsky, M. On Schwarzschild anti De Sitter and Reissner–Nordstrom wormholes. arXiv 2019, arXiv:1911.10911. [Google Scholar] [CrossRef]
- Daghigh, R.G.; Kunstatter, G. Highly damped quasinormal modes of generic single-horizon black holes. Class. Quantum Grav. 2005, 22, 4113. [Google Scholar]
- Motl, L.; Neitzke, A. Asymptotic black hole quasinormal frequencies. Adv. Theor. Math. Phys. 2003, 7, 307–330. [Google Scholar] [CrossRef]
- Natario, J.; Schiappa, R. On the Classification of Asymptotic Quasinormal Frequencies for d–Dimensional Black Holes and Quantum Gravity. Adv. Theor. Math. Phys. 2004, 8, 1001–1131. [Google Scholar] [CrossRef]
- Andersson, N.; Howls, C.J. The asymptotic quasinormal mode spectrum of non-rotating black holes. Class. Quantum Grav. 2004, 21, 1623. [Google Scholar] [CrossRef]
- Lan, C.; Wang, Y.-F. Singularities of regular black holes and the monodromy method for asymptotic quasinormal modes. Chin. Phys. C 2023, 47, 025103. [Google Scholar] [CrossRef]
- Costa, J.L.; Girão, P.M. Higher order linear stability and instability of Reissner–Nordstrom Cauchy horizon. Anal. Math. Phys. 2020, 10, 40. [Google Scholar] [CrossRef]
- Chen, D.; Li, H.; Zhou, T. A Penrose type inequality for graphs over Reissner–Nordström-anti-deSitter manifold. J. Math. Phys. 2019, 60, 043503. [Google Scholar] [CrossRef]
- Wei, Y.-H.; Chu, Z.-H. Thermodynamic Properties of a Reissner–Nordstrom Quintessence Black Hole. Chin. Phys Lett. 2011, 28, 100403. [Google Scholar] [CrossRef]
- Hussain, I.; Ali, S. Effect of a quintessence model on the energy of the Reissner–Nordstrom black hole. Gen. Relativ. Grav. 2015, 47, 34. [Google Scholar] [CrossRef]
- Dariescu, M.A.; Dariescu, C. Reissner–Nordstrom black holes with quintessence. Eur. Phys. J. Plus 2021, 136, 375. [Google Scholar] [CrossRef]
- Riojas, M.; Sun, H.Y. The Photon Sphere and the AdS/CFT Correspondence. arXiv 2023, arXiv:2307.06415. [Google Scholar]
- Nieto, J.A.; León, E.A.; García-Quintero, C. Cosmological-static metric correspondence and Kruskal type solutions from symmetry transformations. Rev. Mex. de Fís. 2022, 68, 040701. [Google Scholar] [CrossRef]
- Kiselev, V.V. Quintessence and black holes. Class. Quantum Gravity 2003, 20, 1187–1198. [Google Scholar] [CrossRef]
- Wang, L.M.; Caldwell, R.R.; Ostriker, J.P.; Steinhardt, P.J. Cosmic Concordance and Quintessence. Astrophys. J. 2000, 530, 17. [Google Scholar] [CrossRef]
- Chiba, T. Quintessence, the gravitational constant, and gravity. Phys. Rev. D 1999, 60, 083508. [Google Scholar] [CrossRef]
- Bahcall, N.A.; Ostriker, J.P.; Perlmutter, S.; Steinhardt, P.J. The cosmic triangle: Revealing the state of the universe. Science 1999, 284, 1481. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.M.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Visser, M. The Kiselev black hole is neither perfect fluid, nor is it quintessence. Class. Quantum Grav. 2020, 37, 045001. [Google Scholar] [CrossRef]
- Guven, J.; Nunez, D. Schwarzschild-de Sitter space and its perturbations. Phys. Rev. D 1990, 42, 2577–2584. [Google Scholar] [CrossRef]
- Hayward, S.A.; Nakao, K.; Shiromizu, T. A cosmological constant limits the size of black holes. Phys. Rev. 1994, 49, 5080. [Google Scholar] [CrossRef] [PubMed]
- Schouten, J.A.; Calculus, R. An Introduction to Tensor Analysis and Its Geometrical Applications; Springer: Berlin/Heidelberg, Germany, 1954. [Google Scholar]
- Schouten, J.A.; Struik, D.J. Einführung in die neueren Methoden der Differentialgeometrie. I. Algebra und Übertragungslehre. By Schouten JA and Struik DJ. Pp. xii, 202. RM. 10; geb. RM. 11.50. 1935.(Noordhoff, Groningen). Math. Gaz. 1936, 20, 60–61. [Google Scholar]
- Casanova, S.; Lecian, O.M.; Montani, G.; Ruffini, R.; Zalaletdinov, R. Extended Schouten classification for non-Riemannian geometries. Mod. Phys. Lett. A 2008, 23, 17–23. [Google Scholar] [CrossRef]
- Bahamonde, S.; Valcarcel, J.G. Observational constraints in metric-affine gravity. Eur. Phys. J. C 2021, 81, 495. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Internal structure of black holes. Phys. Rev. D 1990, 41, 1796. [Google Scholar] [CrossRef] [PubMed]
- Maeda, H.; Torii, T.; Harada, T. Novel Cauchy-horizon instability. Phys. Rev. D 2005, 71, 064015. [Google Scholar] [CrossRef]
- Petrov, A.Z. The classification of spaces defining gravitational fields. Gen. Rel. Grav. 2000, 32, 1665–1685. [Google Scholar] [CrossRef]
- Bona, C.; Coll, B.; Morales, J.A. Intrinsic characterization of space-time symmetric tensors. J. Math. Phys. 1992, 33, 670. [Google Scholar] [CrossRef][Green Version]
- Bahamonde, S.; Valcarcel, J.G. On the algebraic classification of the gravitational field in Weyl–Cartan space-times. arXiv 2023, arXiv:2305.05501. [Google Scholar]
- Hollands, S.; Wald, R.M.; Zahn, J. Quantum instability of the Cauchy horizon in Reissner–Nordström–deSitter spacetime. Class. Quantum Gravity 2020, 37, 115009. [Google Scholar] [CrossRef]
- Narasimhamurthy, S.K.; Nekouee, Z.; Manjunatha, H.M. Thermodynamic product formulae for Reissner–Nordström-de Sitter black hole. Indian J. Phys. 2023, 97, 279–284. [Google Scholar] [CrossRef]
- González, C.; Koch, B. Improved Reissner–Nordstrom (A)dS black hole in asymptotic safety. Int. J. Mod. Phys. A 2016, 31, 1650141. [Google Scholar] [CrossRef]
- Wanga, C.; Panga, C.; Weia, S. Extracting energy via magnetic reconnection from Kerr-de Sitter black holes. Phys. Rev. D 2022, 106, 124050. [Google Scholar] [CrossRef]
- Ghaffarnejad, H.; Yaraie, E.; Farsam, M. Quintessence Reissner Nordström anti de Sitter black holes and Joule Thomson effect. Int. J. Theor. Phys. 2018, 57, 671–1682. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, Y.B.; Du, Y.Z.; Li, H.F.; Zhang, L.C. Thermodynamics of the Reissner–Nordstrom-de Sitter Spacetime with Quintessence. Eur. Phys. J. C 2022, 82, 770. [Google Scholar] [CrossRef]
- Li, X.P.; Ma, Y.B.; Zhang, Y.; Zhang, L.C.; Li, H.F. Thermodynamics of phase transition in Reissner–Nordstrom-de Sitter spacetime. Chin. J. Phys. 2023, 83, 123–135. [Google Scholar] [CrossRef]
- Singha, C. Thermodynamics of multi-horizon spacetimes. Gen. Rel. Grav. 2022, 54, 38. [Google Scholar] [CrossRef]
- Patino, A.; Rago, H. A family of Coordinate Systems for Reissner–Nordstrom Geometry. Astrophys. Space Sci. 2001, 278, 305–309. [Google Scholar] [CrossRef]
- Akcay, S.; Matzner, R.A. Kerr-de Sitter Universe. Class. Quantum Gravity 2011, 28, 085012. [Google Scholar] [CrossRef]
- Thomas, B.B.; Saleh, M.; Kofane, T.C. Thermodynamics and phase transition of the Reissner–Nordström black hole surrounded by quintessence. Gen. Rel. Grav. 2012, 44, 2181–2189. [Google Scholar] [CrossRef]
- Ghaderi, K.; Malakolkalami, B. Thermodynamics of the Schwarzschild and the Reissner–Nordstrom black holes with quintessence. Nucl. Phys. B 2016, 903, 10–18. [Google Scholar] [CrossRef]
- Ghaderi, K.; Malakolkalami, B. Effects of quintessence on thermodynamics of the black holes. Astrophys. Space Sci. 2016, 361, 161. [Google Scholar] [CrossRef]
- Mannheim, D.P.; Kazanas, D. Exact vacuum solution to conformal Weyl gravity and galactic rotation curves. Astrophys. J. 1989, 342, 635–638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).