Abstract
We examine the main effects of ICT penetration and the shadow economy on sovereign credit ratings and the cost of debt, along with possible second-order effects between the two variables, on a dataset of 65 countries from 2001 to 2016. The paper presents a range of machine-learning approaches, including bagging, random forests, gradient-boosting machines, and recurrent neural networks. Furthermore, following recent trends in the emerging field of interpretable ML, based on model-agnostic methods such as feature importance and accumulated local effects, we attempt to explain which factors drive the predictions of the so-called ML black box models. We show that policies facilitating the penetration and use of ICT and aiming to curb the shadow economy may exert an asymmetric impact on sovereign ratings and the cost of debt depending on their present magnitudes, not only independently but also in interaction.
Keywords:
credit ratings; sovereign debt; shadow economy; NRI index; CART; random forest; bagging; gradient boosting; recurrent neural network JEL Classification:
C14; C53; E44; F44; G15; H63; O17; O33
1. Introduction
The primary factors that influence sovereign bond yields are typically domestic macroeconomic and financial fundamentals, as well as global factors such as international risk appetite and global liquidity [1], as indicated by a substantial body of literature (see, among others, [2,3]). Credit ratings are widely regarded as a standard means of measuring a country’s financial risk and play a critical role in assessing its overall risk profile [4]. Furthermore, international investors seeking to realize higher returns inevitably face higher risk and volatility and scarce relevant information when focusing on emerging markets [5]. As a result, they turn to credit ratings as valuable indicators of a country’s capacity or willingness to meet its financial obligations. Hence, credit ratings can also be seen, as Cantor and Packer (1996) suggest, as a reflection or proxy of domestic macroeconomic and financial indicators. If a financial market is fully efficient (in the strong sense) and there are no delays in the dissemination of information, rational market participants (as suggested by [1,2]) would have already factored in any changes in a country’s fundamentals since the information is considered to be available to participants at the time of the credit issuance. Nevertheless, especially concerning emerging markets, information, in reality, is scarce, and as literature suggests [6], credit ratings convey some kind of extra information to markets and do have an effect on spreads [7]. Multiple studies [1,8] have yielded consistent results indicating that yield changes are more strongly impacted by negative rate changes, particularly shifts from investment grade to speculative grade, as opposed to upgrades. It should not be forgotten, though, that there is also a regulatory (Basel III Accord) reliance on credit ratings or sometimes an internal corporate policy that forces institutional investors, such as retirement and insurance funds [1], to invest exclusively in securities that enjoy an investment grade.
The objective of this study is to evaluate two complex economic and social phenomena that have not been adequately explored in previous research as potential influencers of sovereign credit ratings and bond yields. The two phenomena under consideration are the prevalence of information and communication technologies and the market-driven economic changes arising from the existence of a shadow economy. The motivation for this study should be attributed to the work of Elgin and Uras [9] concerning the shadow economy and Bissoondoyal-Bheenick et al. [10] regarding ICT, which, to the best of our knowledge, first introduced the two phenomena in the relative literature.
Elgin and Uras [9] (see also Markellos et al. [11]) provided empirical evidence that economies with large informal sectors have a greater propensity to default. Inevitably, diminished public revenues lead to fiscal deficits that a government has three ways to finance: increase tax rates, posing the risk of prompting more businesses to shift to the shadow economy, resulting in reduced overall revenues; cutting down on public expenditures, running the risk of compromising the quality and range of public goods and services offered to citizens; and issue and sell more debt, risking an increase in its cost [12].
The link between the transformation of economies to economies of knowledge through ICT was intuitively recognized by Bissoondoyal-Bheenick et al. [10], who claimed that given that the diffusion of ICT (the informational technological capacity was proxied by the use of mobile phones) shapes the future, the assessment of future creditworthiness should be determined to a certain degree by the level of ICT use. In this line, although no direct effect was found, Kotzinos et al. [13] proposed that ICT is an important indirect driver of sovereign ratings and interest rates by facilitating economic growth and improving labor productivity, while the indirect effect seems to be larger for the leapfrogging developing countries.
Interestingly, some researchers [14,15] have shown academic interest in the link between internet penetration (which forms a significant aspect of the ICT revolution) and the size of the shadow economy. Their research has revealed a negative correlation that is particularly pronounced in the developing stage (as indicated by GDP per capita). In this paper, we undertake a comprehensive examination, for the first time, of the relationship between ICT and the shadow economy with respect to both sovereign ratings and the cost of debt, both separately and in conjunction. We attempt to form an understanding of the aforementioned links through a series of non-parametric machine-learning approaches. Machine learning algorithms, while an established workhorse (along with logistic regression) method concerning financial institution decision processes have not seen a proportional spread in academic literature related to the sovereign cost of debt. This is mainly because the focus of this literature is on comprehending the underlying mechanism rather than solely on prediction. Most machine learning algorithms have long been considered “black boxes” [16] and therefore unsuitable for providing information on the structure of the relationship between dependent and independent variables. The evolution of model intrinsic and model agnostic interpretability methods [17] allows the shedding of light on the underlying mechanism of machine learning algorithmic predictions.
Our analysis offers a continuation of the current empirical literature by providing additional insights into the significance of ICT diffusion and the size of the informal economy as factors influencing ratings and rates. Furthermore, it is the first to explicitly examine the potential additional impacts of these two variables while considering their primary effects. Secondly, our study suggests the utilization of recurrent neural networks, which are highly flexible, able to approximate non-linear relationships and deliver very promising results. Thirdly, we utilize state-of-the-art methods that make the behavior of the machine learning models somewhat explainable, enabling us to describe and quantify the effects being studied. Fourthly, this research adds to the crucial discussion regarding the significant role that ICT and the informal economy play in contemporary societies.
The rest of the paper is organized as follows: Section 2 reviews the literature, focusing especially on the economic repercussions of the two phenomena that rating agencies and markets might take into consideration. Section 3 presents the empirical analysis. Section 6 provides some discussion on findings and policy implications, and finally, Section 7 concludes.
2. Related Literature
2.1. Shadow Economy: Definition, Causes, and Effects
The traditional view of the shadow economy as a parasitic phenomenon [18] plagued with meager wages and poor working conditions [19] undoubtedly remains dominant among scholars and policymakers. A considerable amount of literature extensively discusses the negative impacts of the informal economy. One of the apparent consequences of this type of economy is the reduction of a government’s capability to generate revenue through taxation. Since the primary focus of the informal sector is to avoid paying taxes, a large informal sector severely limits government revenues [20]. The impact of the shadow economy extends beyond just reduced public revenues; it also distorts important economic indicators, which can hamper the effectiveness of macroeconomic policies, as stated in previous literature [21]. Additionally, informal firms face limitations in accessing funding due to their hidden nature and avoidance of accumulating physical capital to avoid detection by tax authorities, which reduces their ability to operate on a larger scale and adopt technological innovations [22]. Therefore, because shadow activities tend to be concentrated in sectors of the economy that involve small-scale labor-intensive production with short cycles, the employment of low-skilled and less-experienced workers becomes unavoidable. Such sectors are usually agriculture, trade, construction, and low-added-value services. Therefore, it should be expected that in countries with large shadow economies, the above segments would become rather inflated, composing a large part of national output.
Additionally, there is a body of literature that challenges the conventional notion that the shadow economy has only negative impacts on economic growth. Instead, some studies suggest that, under certain circumstances, the shadow economy can have positive effects. One significant effect of the shadow economy is its potential to create employment opportunities [23] and ‘protect’ household incomes. According to Gutierrez-Romero [24], there is also evidence to suggest that in developing countries, there is a negative relationship between the informal economy and income inequality. Moreover, a large part of shadow activity earnings is eventually spent in the official sector [21,25], providing a significant positive stimulus effect on the formal economy and tax revenues [23]. It has also been proposed [26,27] that the informal sector may act as a buffer over business cycles since total employment, formal and informal, as a sum, is less volatile than each of them separately. Interestingly, while informal output seems to behave pro-cyclically and in tandem with official output, informal employment seems, in broad terms, to behave acyclically, meaning that it probably adjusts to economic cycles through changes in the level of wages and working hours and not in the number of employed [22]. From a neoclassical perspective [19], the informal economy is considered the optimal solution for fulfilling the demand for small-scale goods and personal or household services that maximize consumers’ utility. Thus, individuals who are willing to take higher risks and offer goods and services in the shadow economy are likely to have an entrepreneurial mindset, which can boost economic growth by increasing overall competitiveness, according to Eilat and Zinnes [21]. This may also compel firms operating in the formal sector to improve their productivity or exit the market [26].
2.2. Diffusion of ICT and Transformations of the Economy
Although scholars do not fully agree on the causal relationship between ICT and economic growth [28], a significant body of empirical research published since the early 2000s suggests that the accumulation of ICT capital, or capital deepening, promotes economic growth by increasing productivity. This is due to the availability of more and better capital equipment for workers [29]. The substantial drop in the cost of ICT equipment has resulted in two significant changes. Firstly, it led to the replacement of labor and non-ICT capital with ICT capital in ICT-using sectors. Secondly, changes in the organization of the ICT-producing sector have led to total factor productivity (TFP) gains across the industry [30]. According to Vu et al. [31], the theoretical bases for the positive impact of ICT on economic growth are the diffusion of knowledge, constant innovation, better-informed decision-making by economic agents, reduced costs of transportation, communication, and trading, and increased efficiency in logistics. However, to fully realize the positive effects of ICT, organizational transformation is also necessary.
The benefits of ICT are not limited to advanced economies. Developing nations provide internet and telephone services primarily through inexpensive and easy-to-implement mobile networks. Rather than using a closed-off approach, they focus on learning through experience and aim to entice foreign ICT investments, including capital and expertise. It is indicative that, concerning 2021 and according to the latest ITU estimations, mobile-cellular telephone subscriptions reached a penetration rate of 105.1% (it is remarkable that, as the World Bank (World Development Report, 2016) [32] highlights, in developing countries, more households possess a cellphone than have access to electricity or clean water) for developing countries as opposed to a rate of 134.8% for developed ones, both approaching saturation, while the penetration rate of fixed-broadband subscriptions reached 13% versus a 35.7% rate, respectively. Mobile telecommunications brought radical changes to a wide range of crucial areas for economic growth, introducing mobile platforms, mobile money, microfinance or microinsurance, m-government, m-health, and boosting education and women’s entrepreneurship. The above functions affect economic development in a number of ways. Naming a few, digital ID alleviates severe weaknesses in civil registration systems that left millions of people without official registration documents, depriving them of opening bank accounts, registering property, or receiving social benefits [32]. Moreover, the implementation of a digital ID system permits the removal from the government payroll of “ghost” civil servants and strengthens electoral integrity. Mobile money, which started as an exchange of airtime credit, evolved in order to store credit on the SIM card [32] and became the most influential ICT enabler of financial inclusion [33] for millions of unbankable people. Such schemes made possible safe, low-cost transfers of small amounts of money to or from tiny or informal enterprises and women entrepreneurs with limited mobility due to cultural, religious, or practical reasons. M-health by providing disease surveillance and telemedicine; m-education by facilitating text message exchange between teacher and students or dispatching class tips to young and inexperienced teachers in rural areas; and m-platforms concerning the primary sector by providing information on prices, crop diseases, and potential buyers enable governments to provide innovative, low-cost solutions to long-standing deficiencies that undermine growth potential.
Conversely, there are worries about the negative consequences of ICT, particularly in terms of widening the digital gap between workers, which can negatively impact social unity and economic progress. Specifically, the increased use of ICT can lead to the replacement of unskilled labor with ICT capital and automation, which is likely to result in lower wages and job insecurity for low-skilled, low-paying, and less-educated workers [28]. As a result, opportunities for these individuals and their families are expected to diminish, leading to a reduction in social mobility.
2.3. The Impact of ICT Diffusion on the Shadow Economy and Their Possible Interactions’ Effects on Sovereign Ratings and the Cost of Debt
There is a relationship that has not been fully explored, which is the connection between the spread of ICT and the prevalence of the underground economy at a macro level [34]. This link has only recently been examined in academia, as seen in works such as in [9,15,35]. The literature is still inconclusive about how different types of ICT interact with the underground economy, how their effects vary across different regions of the world, and the direction of Granger causality between ICT and the underground economy [36] suggests that the Granger causality is bidirectional for both high- and low-income countries).
Veiga and Rohman, Garcia-Murillo and Velez-Ospina [34,35] argue that cell phones rather exacerbate the shadow economy, particularly in developing countries where broadband access is still scarce. On the contrary, high-speed internet connections seem to deter the phenomenon by enabling re-entry into formality through a greater positive productivity effect. The dual role that ICTs might play in the shadow economy also emanates from a sequence of other research papers [15] that provide mixed evidence.
Despite the potential risks associated with the underground economy, ICT presents clear opportunities for governments worldwide to combat the various factors that contribute to it (outlined in Section 2.1). Governments can leverage ICT to reduce regulatory hurdles, enhance tax administration by adopting a more client-focused approach toward taxpayers, identify tax evasion schemes, and streamline the process of formalizing employment [37]. There is an abundance of such successful governmental policy measures; in Georgia tax reforms accompanied by a new electronic tax filing system led to an impressive 2.5 percent of GDP a year gain on tax revenues [38]; in Costa Rica, the digitization of tax registration records and company books was followed by a considerable decrease in informal employment and estimated informal output [26]; in Brazil, Peru and Estonia initiatives to enable the electronic registration of workers and the unification of data declarations to internal revenue service and ministry of labor were accompanied by increased registrations of first time workers and improved labor tax collections. In Section 2.2, we discussed how ICT can facilitate financial inclusion. As the financial sector continues to evolve and more intermediaries enter the market, the cost of credit will decrease. This, in turn, increases the opportunity cost for businesses that operate underground and are therefore excluded from official credit. Additionally, in the absence of access to formal banks, microfinance through mobile “accounts” can provide legitimate credit and security to those who have been excluded from traditional banking systems. Consequently, the financial development enabled by ICT can reduce barriers to obtaining credit and help transition informal businesses towards legitimacy [39].
Furthermore, ICT can promote transparency in government action in various ways. Firstly, internet-enabled technologies have allowed individuals to become providers of news and information, transforming the way information is consumed, created, and distributed, which enables whistleblowing and independent exposure to corruption incidents. Secondly, open government data have the potential, although not yet fully explored, to encourage collaboration between the government and stakeholders (citizens and businesses) to extract value from their use. Thirdly, technologies such as blockchain, which are tamper-evident and tamper-resistant by definition, are suitable for secure document handling and identity management, which are crucial for reliable access to government e-services. Improved transparency in public administration, enabled by technological advancements, is a key factor in enhancing overall governance quality. Evidence shows that improving governance quality may help reduce the growth of the underground economy [18,36].
3. Empirical Application-Data and Sources
Our credit risk sample consists of 1029 (there are 11 country-year credit ratings missing, more specifically ratings concerning Moldova and Nicaragua and years 2011–2016). If no missing ratings existed in the sample, observations would amount to 1040 annual (end of the calendar year) observations of long-term foreign currency credit ratings of sovereign bonds assigned by Standards and Poor’s rating of sixty-five countries (countries comprising our sample classified by region and development stage can be found in Table A5 of Appendix A.) for a time period of 16 years (2001–2016). Qualitative letter ratings are linearly transformed to numerical equivalents, with 1 representing the highest score (triple A) and 21 the lowest (default). As a result, a rise in the rating indicates a country’s downgrading. We opt for Standard and Poor’s rating among the major three rating agencies that dominate the market (the others are Fitch and Moody’s) since there is some evidence in the literature [40] that S&P acted as a rating setter during the recent crisis and that downgrade announcements of the specific agency carry increased importance for markets. In any case, we do not expect our findings to be driven by the agency choice due to the close correspondence of the three agencies [41] and the extremely high pairwise correlation coefficients found in our sample concerning them (over 0.970 in all cases).
The sovereign cost of debt is proxied by the yield to maturity of the ten-year zero-coupon sovereign benchmark bonds; if this is not available, the closest maturity is chosen. If such data were completely unavailable, we filled, wherever possible, the dataset using the JP Morgan Chase Emerging Markets Bond Index Global (EMBI Global), which tracks total returns for traded external debt instruments in emerging markets (definition from https://cbonds.com/glossary/emerging-markets-bond-index/, accessed on 25 December 2022). The cost of debt sample comprises 862 observations of sixty-one countries for a time span of 2001–2016 (on this occasion, there are 114 missing county-year observations).
The independent variables, and the focus of interest in this study, are ICT penetration and the extent of the shadow economy across countries. ICT penetration and usage among countries are measured by the NRI composite index (network readiness index). The index was not published for years 2017 and 2018 and was redesigned in 2019 by the Portulans Institute, losing its consistency. It was first published in 2002 (involving the year 2001) and aims to measure the multitude of ICT aspects that have an impact on economic development and society by assigning a score on a scale from 1 to 10, with the latter being the best possible grade. The index was, until 2016, published by the World Economic Forum, Cornell University, and INSEAD (The NRI, 2022), and therefore, despite some minor reviews, retained its consistency and suitability for use in a time-series framework. It should be noted, though, that concerning the year 2015, no assigned scores were published, and therefore we interpolated the missing values by using the inverse distance weighted method of non-missing values, with weights being reciprocals of the squared distance between values (since NRI scores do not change dramatically from year to year, this method allows for assigning more weight to the closest non-missing values). We expect higher values of the index to be associated with lower yields and better (lower) ratings.
The shadow economy estimates (% GDP) are those [25]. (To the best of our knowledge, these are the latest and most updated estimates for 2017). In conjunction with the last consistent, in a time-series framework, publication of the NRI index (2016), the years under study cannot be significantly expanded. We expect higher values to be associated with increased yields and higher (or worse) credit ratings. Moreover, considering, on the one hand, the plethora of means that ICT delivers to the governments of developing countries to provide basic services and digitize parts of a fragile and vulnerable to corruption public sector and, on the other hand, the inverse relationship between ICT and shadow economies that is found in the literature [14], we expect that improvements on ICT diffusion will alleviate the positive (increasing) effects of large shadow economies on sovereign ratings and debt rates.
Furthermore, we employ a set of key economic variables that have been spotted in relative literature [8,42,43] as determining the capacity and willingness of borrowers to service their debt [44] along with factors capturing global conditions such as risk sentiment (VIX) and liquidity (risk-free U.S. rate). We include the specific variable only in bond yield models because it is not commonly included in modeling sovereign ratings in the relative literature.
Moreover, we use a set of dummy variables (mostly time-invariant) in order to capture a country’s classification as an advanced or developing economy (advanced) (a definition taken by the Country Composition of World Economic Outlook Groups in 2012), eurozone membership (eurozone), a default after 1995 (dflt95), or common or civil origin of law (lgluk) (an abbreviation of the corresponding proxy binary variable). Countries with common law origin take the value of 1, zero otherwise, and regional effects (West/Latin-Carribean/East Europe/Asia-Pacific/Africa/Middle-East) (binary indicators for region indicator). See Table A5 of Appendix A for a complete presentation of sampled countries by stage of development and region. Additionally, a dummy variable proxies the period of extreme stress in global financial markets between 2007–2010. Definitions of numeric explanatory variables, sources, and expected impact signs are shown in Table A3 of Appendix A, and overall descriptive statistics are shown in Table A2 of Appendix A.
When assessing the determinants of the cost of debt, we employ ratings as an independent (when employing credit ratings as an independent variable, we prefer a synthetic proxy constructed as the simple average of the assigned ratings of S&P, Moody’s, and Fitch because there is no reason to believe that investors will not take under consideration, in a distinct but unknown to us ratio, all available information and therefore all assigned sovereign credit ratings by the three agencies, if of course available.) variable is driven by the “extra” information they might convey beyond economic fundamentals. Table A4 of Appendix A gives the Pearson correlation coefficients of dependent and explanatory variables. Notably, yields are mainly correlated (negatively) to ICT penetration and labor productivity and positively to assigned ratings, inflation, the shadow economy, and corruption. On the other hand, S&P ratings (and also a synthetic metric based on the average ratings of S&P, Moody’s, and Fitch) are strongly (negatively) correlated to ICT penetration, labor productivity, and credit to the private sector, while positively correlated to corruption, the informal economy, and inflation. ICT penetration is strongly (positively) correlated to credit to the private sector and labor productivity and negatively to corruption and informality, which are also strongly and positively correlated between them.
Before proceeding with the main analysis and in order to secure the robustness of our models, we test to find out whether the set of employed independent variables (including ratings; here we employ the average of the assigned ratings by the three agencies since it constitutes public information, since this piece of information is also available to market participants) is able to discern between groups of countries of different creditworthiness or if we encounter an omitted-variable bias. For that purpose, we employ hierarchical clustering, an alternative to the k-means clustering approach that has the advantage of not needing a pre-specification of the number of clusters. Before applying the approach, all numeric variables are collapsed to their country means and scaled. Binary factor variables are set to their modes. The algorithm works in a bottom-up manner (agglomerative clustering), meaning that each country is considered a leaf (a distinct cluster), and at every next step, the pair of clusters with the minimum between-cluster distance are merged (Ward’s method) until we end up with only one cluster (the root).
The dissimilarity between any two observations is measured by the parametric correlation distance, which is defined by subtracting the correlation coefficient from 1 and takes the following form:
The distances are squared before cluster updating [45]. The cluster dendrogram generated along with approximately unbiased “p-values” of clusters’ support, calculated by multiscale bootstrap resampling, can be seen in Figure 1.
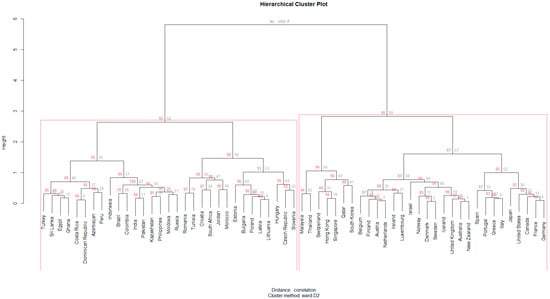
Figure 1.
Hierarchical cluster dendrogram. Notes: Values in red depict the approximately unbiased “p-values” calculated by multiscale bootstrap resampling. Cluster numbers in grey. Rectangles in red indicate the two main clusters supported by data (au > 95%). Conclusions about the proximity of two observations can be drawn only based on the height at which branches containing those two observations are first blended (bottom-up).
The two large groups (no. 56 and 57), generally corresponding to developing and developed countries, can be easily discerned and are strongly supported by the data (au >95%). However, this clustering is not very helpful in order to correctly identify the average expected cost of debt that a country will cope with, depending on its specific characteristics. Nevertheless, it can also be observed that with adequate confidence (au >= 94%), four distinct groups (no. 54, 55, 56, and 57) may be formed to provide us with quite a satisfactory clustering:
- ○
- Cluster 57: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Greece, Iceland, Ireland, Israel, Italy, Japan, Luxembourg, Netherlands, New Zealand, Norway, Portugal, Spain, Sweden, United Kingdom, United States.
- ○
- Cluster 54: Hong-Kong, Malaysia, Qatar, Singapore, South Korea, Switzerland, and Thailand.
- ○
- Cluster 56: Slovenia, Czech Republic, Estonia, South Africa, Croatia, Poland, Latvia, Hungary, Lithuania, Romania, Bulgaria, Tunisia, Jordan, and Morocco.
- ○
- Cluster 55: Azerbaijan, Brazil, Colombia, Costa Rica, Dominican Republic, Egypt, Ghana, India, Indonesia, Kazakhstan, Moldova, Pakistan, Peru, the Philippines, Russia, Sri Lanka, and Turkey.
As we can see, the first group refers to countries that are considered to belong to the “West” or have successfully adopted Western-type institutions (e.g., Japan, and Israel). The second cluster comprises highly dynamic Asian economies with skilled labor and semi-democratic institutions, along with Switzerland and Qatar. These two clusters are expected to be able to borrow with ease when needed. The third cluster consists mainly of ex-communist European countries rising rapidly along with African or Middle Eastern countries (South Africa, Tunisia, Jordan, and Morocco) that are more developed relative to their neighbors. This group is expected to attract investors through increased yields since it carries a higher risk than previous clusters. The last group is a mixture of South American, Eastern European, African, Asian, and Middle Eastern sovereigns that have a history of severe economic turbulence or defaults, and an unstable political environment and are obliged to cope with increased borrowing costs. Overall, the determinants seem to be able to distinguish, at least in broad terms, the different levels of credit risk depending on countries’ specific traits and permit us to consider the choice of independent variables as adequate.
4. Non-Parametric Analysis of Sovereign Credit Risk
When we have a dataset and need to answer questions using machine learning techniques, it is typical to use multiple approaches and evaluate their effectiveness, according to Boehmke and Greenwell [45]. A possible convergence of findings among different algorithms could lend us some confidence in our outcomes. Machine learning approaches are especially appropriate when dealing with complex situations [11] that lack a sound economic theory. The study (concerning empirical methods applied) that is closer to ours is that of Bennel et al. [44] (see also [46]) that applies several artificial neural networks on a 16-point (classes) scale of 1383 annual observations assigned by eleven rating agencies; they manage to achieve a correct classification rate of 42.4% or 67.3% if predictions within one notch of the true rating are taken as correct. We employ these rates as the benchmark for our models since other similar studies have artificially limited the number of classes and therefore are not comparable to the present study.
4.1. Classification Trees and Bagging on Credit Ratings
Classification trees partition a dataset through an iterative process that splits the data into homogeneous subgroups and then splits those subgroups (or branches) further until a certain criterion is met, a procedure known as binary recursive partitioning. Splitting the data randomly when constructing the train and the test set may cause data leakage since the time dimension would be ignored and we would try to forecast the past while we stand in the future, achieving an inflated rate of correct/near correct predictions. Therefore, we split our sample into two sequential periods: the first consists of years 2001–2013 (81.5% of total observations) and forms the training and validation set, and the second of years 2014–2016 (19.4% of total observations) and forms the testing set. Following a CART approach (classification and regression tree, developed by Breiman [47]), and after conducting a grid search in order to optimize the model’s parameters, we set the minimum number of observations that must exist in a node in order for a split to be attempted to 25, the maximum depth of any node to 9 (the root node counted as 0), and define that any split that does not improve fit by 0.01 will be pruned.
Figure 2 visualizes the generated classification tree that uses 24 final nodes and a depth of eight levels to achieve a 55.54% (computed as relative error*Root node error) correct classification rate concerning the training set and a rate of 48.2% on the testing set, which is quite satisfactory.
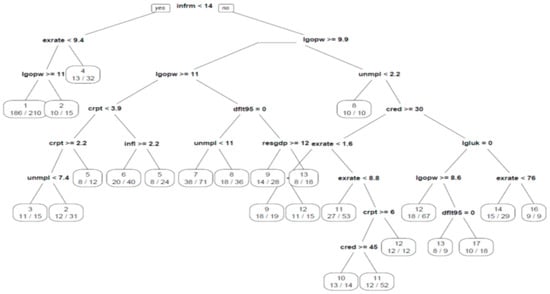
Figure 2.
S&P rating classification using a CART decision tree. The tree considers all available ratings. Notes: Numbers in nodes display the correct classification rate (correct classifications per number of observations in the node).
The default splitting criterion is the Gini index. (Alternatively, information gain can be used as the splitting criterion, but the classification rate does not improve substantially.) This is calculated by subtracting the sum of the squared probabilities of each class from one; therefore, it is defined as and equals zero in the case of perfect classification. As we can see in Figure 2, the size of the shadow economy (<14% of GDP) is the chosen feature basis of the root node. Given that a country confines the informal sector below 14% of GDP, if the local currency exchange rate to one US dollar is above 9.4 local units, the most probable anticipated assigned rate would be (AA-).
If, on the other hand, the local currency is stronger and, concurrently, output per worker equals or surpasses 59,784.14 constant 2010 USD per annum, the model predicts an AAA rating, otherwise an AA+. All branches of the presented tree can be read in the same way.
Additionally, to gain a deeper understanding of the factors influencing a model’s prediction (we note that a variable may score high without necessarily appearing in the tree [48]), we can measure the importance of the explanatory variables by summing the squared improvements across all internal nodes of the tree where each feature was selected as the partitioning variable, according to Boehmke and Greenwell [45]. To gain a deeper understanding of the factors influencing a model’s prediction, we can measure the importance of the explanatory variables by summing the squared improvements across all internal nodes of the tree where each feature was selected as the partitioning variable, according to Boehmke and Greenwell [45]. The relative importance of the explanatory variables of our tree classification model is shown in Figure 3. While the classification rate of our optimal classification tree is quite satisfactory for a classification problem concerning 20 classes, single-tree models are notorious for suffering from high variance, i.e., small changes in the training set might cause great alterations to the model.
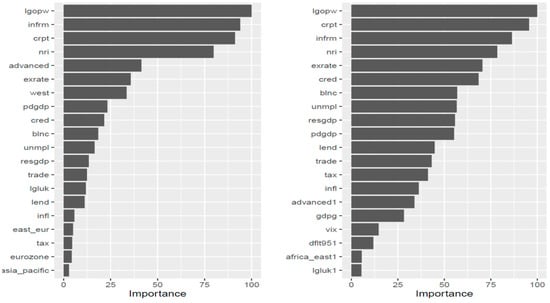
Figure 3.
Explanatory variables relative importance of S$P ratings single optimal classification tree (left) and bagging (right).
It has been proposed in the literature [49] that one way to overcome this deficiency is to average the outcomes of multiple models. Therefore, we use the proposed by Breimann [49] bagging (bagging stands for bootstrap aggregating) approach, which ultimately creates m bootstrap samples from the training set, and for each sample, a single, unpruned tree is trained while separate predictions from each tree are averaged in order to provide the finite predicted value.
This time, we repeat 10-fold cross-validation ten times in order to improve the estimation of the performance of our model. Following relative literature, the model’s performance improves significantly, not only concerning the cross-validation set, reaching a 70% correct classification rate, but more importantly, on the test set, achieving a rate of accuracy equal to 53.16%.
Relatively, the most important factors do not change dramatically, but we can discern that the CART method puts more emphasis on whether a country is considered advanced and whether it is a member of the “West”, while bagging relies more upon economic fundamentals.
Interestingly, ICT penetration and the size of the shadow economy are among the first four more important factors, with the most important being the workers’ productivity.
4.2. Classification Trees and Bagging on Bond Yields
Following the aforementioned methods, we split our sample into two sequential periods: the first consists of years 2001–2013 (78.8% of total observations) and forms the training and validating set, and the second of years 2014–2016 (21.2% of total observations) and forms the testing set. A ten-fold validation strategy is also implemented. A CART regression approach is similarly followed. After conducting a grid search in order to optimize the model’s parameters, we set the minimum number of observations that must exist in a node in order for a split to be attempted to 16, the maximum depth of any node to 12 (the root node counted as 0), and defined that any split that does not improve fit (overall R2) by 0.01 should be pruned. Figure 4 visualizes the classification tree that uses 12 nodes and a depth of three levels to achieve a training error of 2.44 (computed as relative error*Root node error) and a testing error of 2.824. The optimizing criterion is a reduction in the sum of the squares of the residuals (SSE).
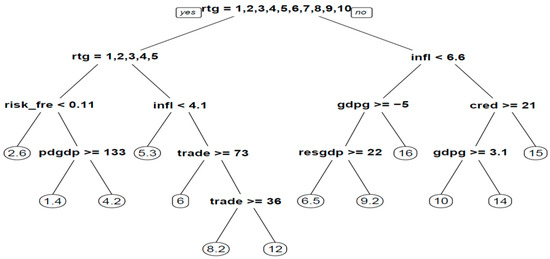
Figure 4.
Constructing a regression tree using the CART method concerning bond yields.
As we can see in the graph, the credit rating is the chosen feature basis of the root node, and countries that are assigned a rating between AAA and A+ while at the same time, the global risk-free rate is lower than 0.11% should expect, on average, a yield of 2.6%. If the risk-free rate is equal to or exceeds 0.11%, then the yield also depends on the public debt-to-GDP ratio.
If the assigned credit rating is between A and BBB-, i.e., still in investment grade with strong or adequate payment capacity, the predictions are further split based on inflation and the country’s openness to trade. On the other hand, if a country is assigned a non-investment grade, the predictions are split based on GDP growth and reserves to GDP or credit to the private sector and GDP growth.
The relative importance of the explanatory variables of our tree regression model is shown in Figure 5, along with a similar bagging model. As it is shown, the obvious most important feature (as expected) concerning the cart method is the assigned credit rating, followed by productivity per worker, ICT penetration, corruption, credit to the private sector, the magnitude of the informal economy, and inflation. The most noticeable difference between the two methods is that inflation and reserves relative to GDP are gaining importance with the bagging method.
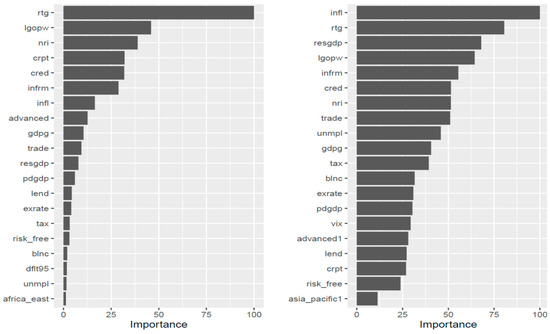
Figure 5.
Explanatory variable relative importance plot. Single optimal regression tree (left) and bagging (right) on bond yields.
ICT diffusion and the informal sector are still important drivers of sovereign yields in the bagging model. It can also be seen that the stage of development and the period of crisis (2007–2010) are not playing an important role in determining yields. We should note here that our bagging model fails to improve the test data error rate, which remains unchanged at 2.85.
4.3. Random Forests on Credit Ratings
According to Boehmke and Greenwell [45], although bagging regression trees can be seen as an improvement over a single tree model, which tends to have high variance, they still have the issue of tree correlation. A modification and remedy to this problem is the random forest method, which seeks to de-correlate the m-bootstrap sample trees by injecting randomness into the tree-growing process by limiting the candidate for split variables to a random subset. Furthermore, random forest models provide a method to approximate the test error without the need to withhold training data for validation purposes by utilizing the left-out data from the m-bootstrap samples, which are known as out of the bag (OOB) samples. Before actually running the model, a handful of tuning parameters was set through an extensive grid search. Concerning the number of variables randomly sampled as candidates at each split, the optimal number was set to 4, the number of trees to grow to 500, and the complexity of the trees, which is adjusted through the size of the nodes, to 1 (the smaller, the deeper); the OOB error rate for these parameters amounted to 27.29%. The accuracy rate of our model on the unseen (test) data increased slightly relative to the bagging model and reached a more than satisfactory 57.89% with a rather remarkable accuracy within one notch of 84.21%.
Clearly, the model finds difficulties in the area around the boundary of investing-non-investing grade predicting investing grade rating (BBB/9) for eight non-investing grade observations (see Table 1). An explanation could be that on this boundary, the assignment decision becomes even more subjective due to the profound implications.

Table 1.
Confusion matrix of random forest model.
For verification reasons, we present two plots of the variables’ importance (Figure 6): the one (left) based on the impurity measure, which is actually the Gini index for classification, and the permutation, which breaks any association between the variable of interest and the outcome by permuting the values of all observations concerning the specific variable, computes again the accuracy and then calculates the difference. The calculation is repeated for all the random forest model trees and averaged. It seems that the importance of the workers’ productivity is confirmed by the random forest model as well as by the size of the informal sector and corruption. ICT penetration appears to hold a moderate but still important place as a potential driver of credit ratings.
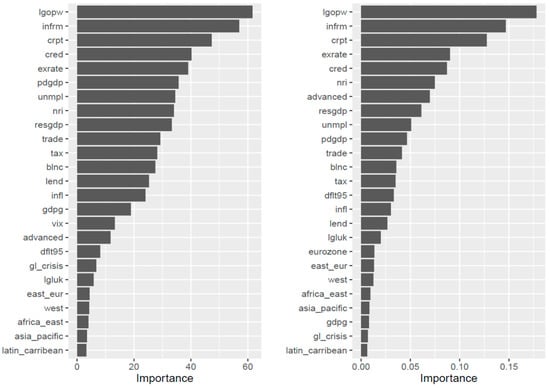
Figure 6.
Variable importance measures for the optimal random forest model based on impurity (left) and permutation (right).
In order to shed some light on the behavior of ICT penetration and the size of the informal sector, we plot their accumulated local effects (ALE) plots, which describe how features influence the predicted outcome on average [50]. The output here should be interpreted as the vector of the change of predicted probabilities, as the variable of interest varies, one for each response class (20 rating classes in our case).
Therefore, we choose to present the plots only for the assigned ratings equal to (AAA) and (BB+) (first non-investment grade) in order to check the impact of the two predictors at the crucial points when a sovereign spares no effort to be assigned the covetable triple (A) or to avoid being degraded to a non-investment grade (or the contrary).
Concerning the case of the assigned rating is equal to AAA (left plot in Figure 7), we can see that when the ICT value is below 4.5, a mild negative constant effect equal to 0.005 decreases the probability of being assigned the specific rating, while an improvement of ICT penetration beyond this value raises the probability of being assigned a rating of AAA by about 0.02 with a diminishing trend after the ICT penetration index value surpasses 5.5. Similarly, when the assigned rating equals BB+ (right plot in Figure 7) and the value of the ICT index is below 4, the effect is negative but diminishes as ICT penetration rises to a magnitude of about 0.01–0.03, and as soon as the index breaches the above limit, the effect becomes positive, reaching a maximum of 0.01 and then falling again.
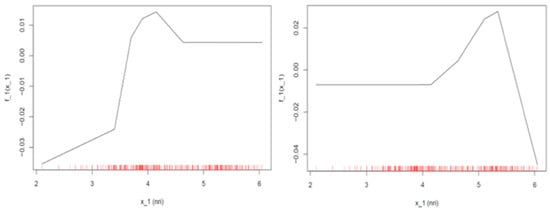
Figure 7.
ALE plots of ICT diffusion when ratings equal AAA (left) and BB+ (right) (random forest model). Note: The distribution of the independent determinant is depicted in red. If observations concerning specific areas of the model are limited, conclusions should be drawn with caution.
Similarly, concerning the impact of the size of the informal sector when the assigned rating equals AAA (left plot in Figure 8), we can discern that while the size of the informal sector remains under 10%, it has a positive impact of 0.1 to 0.15 on the probability of being assigned a rating of AAA, but as soon as the size exceeds that limit, the positive impact sharply decreases, and finally, after exceeding the ratio of 15% to GDP, the impact becomes negative.
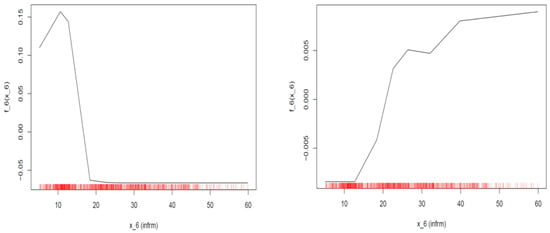
Figure 8.
ALE plots of the informal economy when ratings equal AAA (left) and BB+ (right) (random forest model).
On the other hand, when the assigned rating equals BB+, the plot (Figure 8) shows that for the area between values 10–22% of the shadow economy, the impact is slightly negative (−0.005–0.00), but when this limit is surpassed, the impact on the probability of being assigned a BB+ rating steadily increases (0.00–0.01).
Next, we consider the second-order effect of ICT penetration and the shadow economy (if any) on the prediction (Figure 9). The area of the plot that is formed when the ICT index is below 4.5 and the informal sector is under 10% will not be considered since the area is far from the data distribution; however, we can see that if the informal sector index ranges between 15–18%, a negative effect of magnitude 0.01–0.02 can be detected, while if the informal sector exceeds 20%, no additional effect is found. Moreover, we can see that if the ICT index is above 4.5 and at the same time the informal sector is confined below 15%, then the interaction of the two determinants adds another 0.005 to the probability of a sovereign being assigned a rating of AAA (lower right part of the plot). Nevertheless, if the informal sector exceeds 15% and the ICT index is larger than 4.5, the additional effect turns negative, with a magnitude ranging from 0.005 to 0.01.
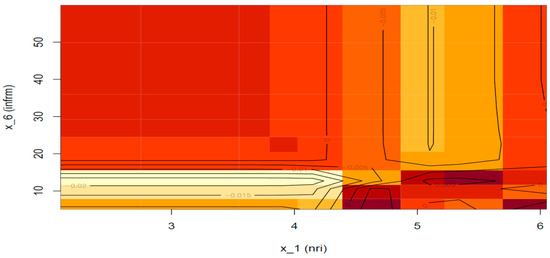
Figure 9.
ALE plot for the 2nd order effect of ICT penetration and informal sector random forest predictions when rating equals AAA. Note: The color red stands for positive effects (the darker, the stronger), and yellow for negative (the lighter, the stronger). In this plot, because impacts are mild, the red color on the left part of the graph stands for null.
Figure 10 shows the additional net effect of the interaction of the two features when the assigned ratings are equal (BB+), but fails to detect any. Similar to the above, we will abstain from any conclusion driven not only from the red area of the plot but also from the top right area (yellow) because both areas are far from the data distribution.
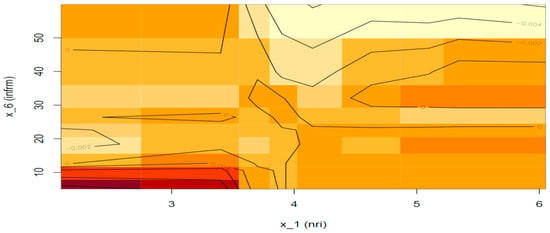
Figure 10.
ALE plot for the 2nd-order effect of ICT penetration and informal sector random forest predictions when rating equals BB+. Note: The color red stands for positive effects (the darker, the stronger) and yellow (the lighter, the stronger).
4.4. Random Forests on Bond Yields
First, we tune a number of hyperparameters in order to adjust them until the validation error stops improving by a certain ratio. Concerning the number of variables randomly sampled as candidates at each split, the optimal number is set to 9 and the number of trees grown to 300; too many trees may lead to overfitting. Our random forest models succeed in reducing the validation error to 2.27 and the testing error to 2.57 (RMSE), while a pseudo-R-squared metric, {1-mse/Var(ytm)} indicates that the variance explained equals 79.03%. Here (Figure 11) we provide two measures of variable importance after recording the prediction error for each tree: the average difference, normalized by the standard deviation of the differences, between the mean squared error of every validation set with each predictor being permuted and the average total decrease in node impurities from splitting on each variable.
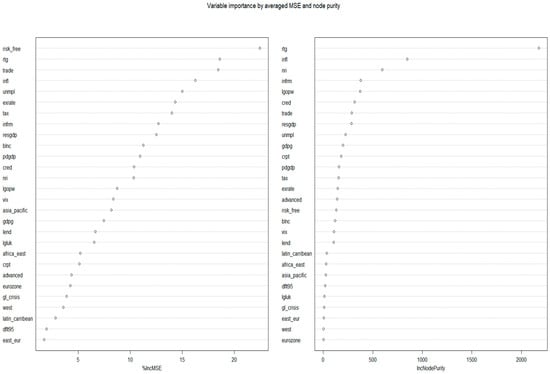
Figure 11.
Variable importance measures for the random forest optimal model. No other additional effect is found, while the positive (increasing) effects of the low left part of the plot are not taken into account since the area is far from the data distribution area.
It can be observed that the random forest model takes into account a larger number of determinants in relation to the previous models and considers especially the risk-free rate, credit ratings, trade openness, and inflation. Concerning ICT penetration and the size of the informal economy, they seem to play a modest but considerable role. The accumulated local effects (ALE) plots (Figure 12) based on the random forest model show that a low rate of ICT penetration (between 3 and 3.5) increases the sovereign yields by around 0.1–0.8 p.p., but with a sharp declining rate and after the variable takes a value of 4.0, no particular effect can be detected on the average prediction. When the variable exceeds the value of 5, then ICT penetration has a negative (decreasing) effect on yields by about 0.2 p.p. On the other hand, a small size of the informal sector has a negative effect on yields of around 0.2 p.p., but a larger informal sector that surpasses a ratio of 20% to GDP has a positive (increasing) impact on yields of about 0.2 p.p. to 0.4 p.p.
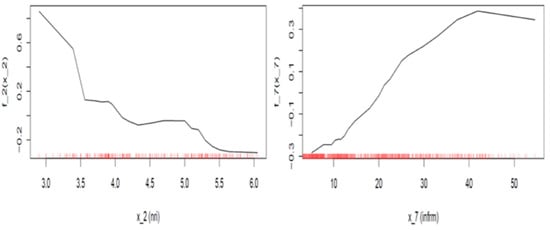
Figure 12.
ALE plots of ICT diffusion (left) and informal sector (right) (random forest model). Note: The distribution of the independent determinant is depicted in red. If observations concerning specific areas of the model are limited, conclusions should be drawn with caution.
Similarly, the accumulation effect plot (Figure 13) on the interaction of the ICT penetration and the size of the informal sector shows that an additional negative (decreasing) effect of a magnitude of 0.05 p.p. occurs when ICT penetration is very limited and the informal sector is medium-sized or when the informal sector skyrockets and the ICT penetration is mid-scaled (4.0–5.0).
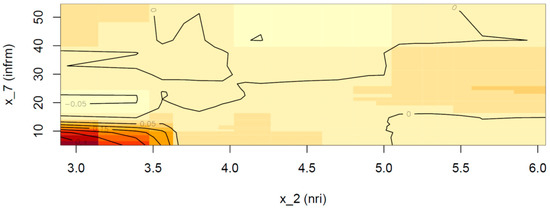
Figure 13.
ALE plot for the 2nd-order effect of ICT penetration and informal sector on random forest model predictions.
4.5. Gradient Boosting (We Do Not Present the Gradient Boosting Model for Sovereign Ratings Because It Failed to Deliver a Superior Classification Rate in Relation to the Random Forest Model.)
Instead of creating an ensemble of de-correlated trees such as random forests, gradient boosting builds, in an iterative fashion, an ensemble of shallow and weak trees. A weak classifier (tree) is one whose error is only slightly better than random guessing [51]. Usually, shallow trees are built with only 1–6 splits [45].), with each tree being an improvement of the previous since in every iteration the new base-learner is trained on the error learned so far [45]. The gradient boosting model is tuned by trial and error (a full grid search is computationally expensive in the case of a gradient boosting machine). The learning rate is set to 0.01, the number of iterations to 1040, the tree depth to 15, the minimum number of observations required in each terminal node to 9, the percent of training data to sample for each tree, and the percent of columns to sample for each tree to 80%.
The model further reduces the validation error relating to the previously presented models to 1.38 (RMSE), while the testing error drops as well to 2.41 (RMSE) with an R2 = 0.73. The variable importance plot (Figure 14) verifies that ICT penetration and the size of the informal sector are important drivers of the predictions of the gradient boosting model as well. By far, the model places a heavy weight on the assigned credit ratings. Measures of importance are computed based on the fractional contribution of each feature to the model based on the total gain of the corresponding feature’s splits. The ALE plots depicted in Figure 15 further refine our conclusions. It can be seen that the positive effect of ICT penetration (or better, its lack), when ranging between 3.2 and 3.5, declines rapidly and becomes negative (about 0.2 p.p.) as soon as the feature’s value exceeds 3.5. The plot detects turbulence in the range of 3.5 to 4 since the negative effect is not stable and quickly consolidates around zero until the ICT penetration value exceeds 5. Then the negative effect sharply reaches 0.2 p.p. and seems to stabilize. On the other hand, the negative (decreasing) effect of a very confined informal sector vanishes as soon as the ratio exceeds 20%, corroborating previous results. The effect becomes positive, and afterward, as the slow rate rises slowly, it increases rapidly and stabilizes around 1 p.p.
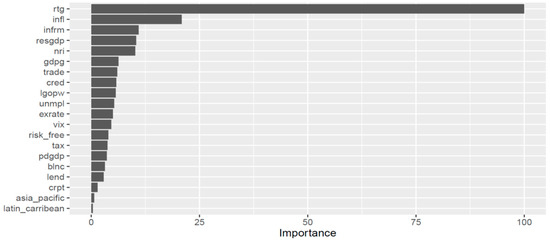
Figure 14.
Explanatory variable relative importance of the gradient boosting model concerning bond yields.
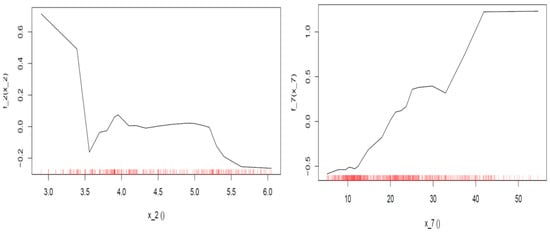
Figure 15.
ALE plots of ICT diffusion (left) and informal sector (right) (gradient boosting model). Note: The distribution of the independent determinant is depicted in red. If observations concerning specific areas of the model are limited, conclusions should be drawn with caution.
The accumulation effect plot (Figure 16) on the interaction of ICT penetration and the size of the informal sector is in line with previous findings and shows that an additional negative (decreasing) effect of a magnitude of 0.25 p.p. occurs when ICT penetration is very low and a medium informal sector accounting for 20–35% is present.
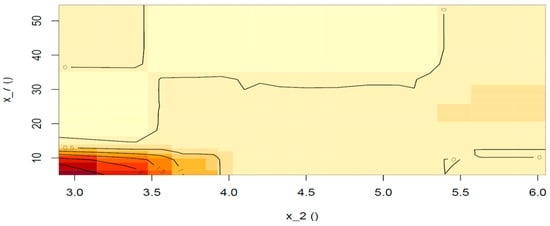
Figure 16.
ALE plot for the 2nd-order effect of ICT penetration and the informal sector on gradient boosting model predictions.
Moreover, a negative effect of the same magnitude (0.25 p.p.) can be seen for levels of ICT penetration between 3.5 and 5.5 in conjunction with a skyrocketing informal sector with a ratio over 40%. The area in red is, again, not taken into account.
5. Robustness Test
Rating agencies have often been accused of a pro-cyclical policy (meaning that rating standards are not consistent over the expansion and recession periods), responding with a considerable lag to shifts in sovereign credibility and therefore not acting as early warning systems to market participants as expected. Moreover, they are allegedly overreacting with abrupt downgrades in times of recession, exacerbating debt crises, remaining very cautious, or underreacting concerning upgrades during recovery phases or even for longer periods. In any case, the strong persistence and high level of inertia that sovereign ratings usually exhibit come as no surprise. The reason for this phenomenon can be traced back to an agency’s reputation mechanism [52], which seeks to restore their lost reputation due to warning failures by pushing them to excessive conservatism during and after crises. Stickiness may also exist, as it has been argued by agencies [53] because countries’ economic behavior during crises reveals new (negative) information that was not available beforehand. The conventional econometric approach, when analyzing panel data (datasets where the behavior of entities (countries concerning this study) is observed across time (years in this study)), is to apply fixed or random effects or a complete pooling modeling approach. Nonetheless, given the persistency of sovereign credit ratings, a growing trend in the relative literature is to account for this persistency by applying dynamic panel models [54], including in the set of independent variables the lags of the dependent. In the models presented in this study so far, we have not accounted for the time-series nature of our data nor for the persistence our dependent variables exhibit.
Considering the above, a machine learning approach, which is gaining recognition lately for efficient handling of such time-dynamic behavior based on recurrent artificial neural networks, is examined further down in this study in order to address the robustness of our findings when tackling these aspects. Moreover, in order to account for any possible irregularities arising from modeling the proxy of sovereign ratings by the standalone S&P ratings, we use as a dependent variable the synthetic measure of the simple average of the three most prominent agencies (S&P, Moody’s, and Fitch;. As a further check for validity, we exclude the synthetic measure of ratings from the set of independent variables of bond yield determinants that are fed to the first layer of the recurrent network to detect the behavior of the remaining features in the absence of a catch-all proxy as ratings.
An artificial neural network (ANN) is a nonlinear model that closely resembles the structure of a biological neural network. Artificial neural networks are made up of layers of nodes, each of which is connected to the others by nonlinear activation functions. Usually, the first layer of an artificial neural network is made up of explanatory variables. The explanatory variables in the middle layer undergo intermediate transformations. The nodes in the final layer are responsible for predicting the dependent variable. Each function is associated with a set of appropriate parameters called weights and biases. Training the neural net entails the optimization of these parameter values by minimizing a loss function that depends on the predicted dependent variable and its true values.
Recurrent neural networks (RNN) [55,56] are a special class of neural networks that are utilized in problems where input can be modeled as a temporal sequence. The main purpose of RNNs is to exploit the temporal relationship between input and output in order to improve their prediction accuracy. They have gained particular popularity in the domain of natural language, audio, or video processing and the demand for financial market predictions [55,57]. RRNs architecture evolved through the years so as to be able to overcome its initial limitations, such as being able to retain past events in memory for an extended time. Thus, new RNN architectures such as LSTM (long-short-term memory) and GRU (gated recurrent units) are proficient at modeling long-term sequence dependencies. LSTMs sophisticated cell units are able to recognize, “store and preserve” an important input in a long-term state. GRU units accomplish the same performance as the LSTM units but are, in general, faster to train.
In this study, a GRU recurrent neural network architecture has been put to the test with two appropriately prepared datasets. The first dataset consists of 28 features (including all the features plus one used in the previous methods as well as the synthetic measure of credit ratings for 65 countries over a period of 16 years). (Since in all our models we had excluded the risk-free rate as a determinant of the assigned credit ratings, in order to check for potential omitting bias, we included the specific feature in the set of independent variables when feeding the first layer of RNN. Nevertheless, the risk-free rate turns out to be the least important feature with negligible impact (see Figure 17) and therefore the omission of the variable does not insert any bias into our previous models.) It has been utilized to create a recurrent neural network that predicts the S&P credit ratings based on longitudinal data. Similarly, the second dataset consists of 28 features (including all but one of the features used in the previous methods as well as the bond yield values for 58 countries over periods from 6 to 16 years). (We exclude S&P ratings for the reasons mentioned earlier in the section.) and it has been utilized to create a recurrent neural network that predicts bond yields by exploring past patterns. The two datasets have been appropriately preprocessed. Regarding the credit ratings dataset, each of the 65 countries’ records has been broken into rolling 8-year windows, looking back 7 years to predict the year ahead. Similarly, the dataset concerning bond yields has been broken into rolling 6-year windows. Moreover, the datasets have been further split into training and testing datasets by country to avoid data leakage. The GRU architecture consists of a dense input layer followed by a gated recurrent unit layer, a dropout layer, and a final dense layer. The aforementioned GRU neural network has been implemented utilizing the APIs of Keras, Tensorflow, and the R language. Thus, all hyperparameters have also been tuned with the assistance of Keras Tuner for R. For the credit ratings dataset, the hyperparameters of GRU units, the GRU activation function, the GRU recurrent dropout, the dropout layer rate, and the optimizer learning rate were optimized using Adam, maximizing the accuracy metric (categorical cross entropy) on the validation set utilizing a random search algorithm. For the GRU network used in the bond yield dataset, the same scheme has been used; however, the Adam optimizer has been set to minimize the mean squared error on the validation set.
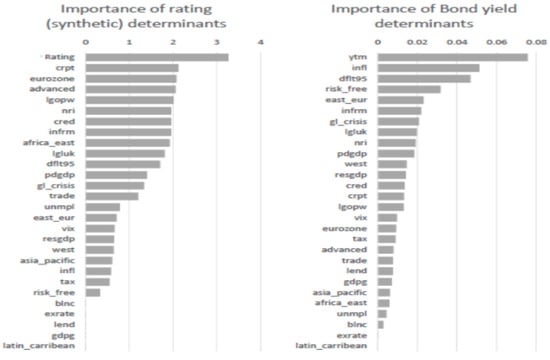
Figure 17.
Explanatory variables of relative importance for the GRU in credit ratings (left) and bond yields (right).
After hypertuning the RNN, the two models have been updated with the new hyperparameter values and then applied to the two datasets. For the bond yield dataset, the RNN performed exceptionally well, presenting an RMSE of 0.0601 on the test set. Figure 18 presents the original values versus the predicted values by the RNN on the test set. For the credit ratings dataset, the RNN produces a model achieving a more than satisfactory 52.99% accuracy rate on average, which is similar to the best accuracies achieved by our previous models, or 81% if classifying as correct, predictions within one notch of real values. This specification of correct classification has been widely used in the empirical literature due to the difficulty that neural networks present in determining the correct rating in adjacent categories [58].
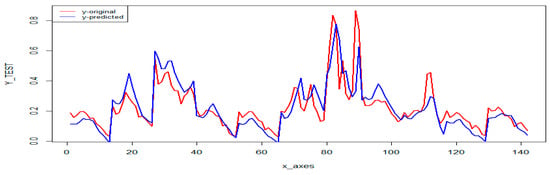
Figure 18.
Plot of GRU neural network performance over Bond yield test dataset.
Moreover, as Bennell et al. [44] have suggested, the method is equivalent to artificially creating meta-classes of evenly distributed observations by limiting the number of classification categories, a method that has also been extensively used in the literature (e.g., [11]).
In order to measure the importance of the features for both of the RNN model development, a permutation feature importance technique [59] has been applied to the test data sets. Next, each variable at a time is shuffled, and the model is utilized again to make new predictions. Afterwards, the root mean square difference between the original prediction and the prediction of the perturbed dataset is calculated. The process is repeated multiple times due to the stochastic nature of the methodologies used. The results of the permutation feature importance technique, presented in Figure 17, suggest that the ICT penetration rate and the size of the informal sector indeed play a considerable role in predicting risk ratings and sovereign debt rates, despite including lags of the dependent variables in our models or using a different metric as a proxy for the assigned ratings.
6. Discussion
Table 2 presents a summary of the 20 most significant variables obtained by employing different models on credit ratings. We first discuss the variable importance of models that exclude lags in ratings. The three models have a common set of variables in their top rankings, such as worker productivity, the size of the informal sector, and the level of corruption. ICT penetration is also considered important and is ranked sixth by the random forest model after the exchange rate and credit to the private sector. The ratings are expected to be affected by macroeconomic news, which is also observed in the analysis [60].

Table 2.
Variable importance by models employed predicting S&P ratings or average ratings of S&P, Moody’s, and Fitch.
The importance of lagged values in our RNN model appears to indicate persistence in credit ratings, as their score is twice as high as that of any other variable. (See Figure 17). Nevertheless, we cannot officially confirm inertia as conventionally done in the literature by testing if coefficients of lagged variables approach unity [61]. The levels of perceived corruption and productivity per worker continue to play an important role, along with credit to the private sector, the size of the informal sector, and ICT penetration, which more or less comprise the top-scoring variables. The obvious difference in the RNN model compared to the other three is the high importance of being a member of the eurozone or considered an advanced country, suggesting that these properties are valued by credit agencies beyond the usual information conveyed by the economic fundamentals.
As we have already seen in Section 3 through ALE plots, when ICT exceeds a value of 4.5, it begins to exert a moderate impact towards a better rating, while when ranging below 4.0, it exhibits an adverse effect.
The plots involving the size of the informal sector suggest that if the ratio ranges between 5 and 15%, the probability of a country attaining the characterization of a high-quality issuer increases significantly by 0.1. Nevertheless, as soon as the size exceeds the critical value of 15%, the effect becomes negative (degrading). The second-order effects detection plots suggest there is an additional small effect of about 0.005 in the probability of being assigned a top rating when the informal sector is detained below 15% and ICT penetration exceeds 4.5. Nevertheless, if, in this case, the shadow economy exceeds 15%, the interaction with a larger informal sector seems to have an adverse effect of around 0.01. Contrary to what was expected, we find no evidence that a larger ICT penetration (meaning above a certain rate) may deter the adverse effects of an expanded shadow economy on ratings.
Concerning yields, a comparison of the variable importance of the different models can be found in Table 3. The first three models that lack dependent variables lag and identify rather different sets; however, the ratings seem to be appraised by markets as a premium source of information since they are rated as one of the most important determinants after controlling for the economic fundamentals. Moreover, inflation seems to also play the role of an economic indicator and scores systematically high. Furthermore, findings confirm that, apart from country-specific fundamentals, global factors such as the VIX and the U.S. risk-free rate have an effect on debt rates. The informal sector and ICT usage are quite important factors across models, with the size of the shadow economy ranking a bit higher.

Table 3.
Variable importance by models employed predicting sovereign bond yields.
The RNN model suggests that, as the most important variable, the lags of the dependent variables have an importance factor that almost doubles relative to any other importance, showing that they also exhibit a rather sticky behavior. The role of inflation and the U.S. risk-free rate seem to be confirmed by the RNN model as well, while some other variables such as the history of defaults, the period of turbulence and economic crisis (2007–2010), and the origin of the law (common law considered safer for investors) seem to gain some importance.
The impact of ICT penetration and the size of the shadow economy are validated by our robustness model but in a more modest direction. The quantification of their impact through ALE plots is quite straightforward since all our models exhibit similar patterns.
When the ICT index ranges between 3.0 and 3.5, the effect is positive and varies from 0.2 to 0.4 p.p., indicating that technological laggards pay a premium. When ICT penetration is moderate (3.5–5), no effect may be discerned, and when referring to ICT pioneers (>5), the negative effect amounts to around 0.2 p.p.
Considering the informal sector when its size does not exceed 20%, a negative (decreasing) effect of around 0.1 to 0.3 p.p. is presented, while when the sector expands, the effect rapidly becomes positive, and when considering skyrocketing (>40%) shadow economies, the effect stabilizes to a rather considerable amount of 1.0 p.p. Concerning the second-order effects, an additional negative (decreasing) effect of a magnitude of 0.25 p.p. occurs when ICT penetration is substantially low (<3.5) in interaction with a medium informal sector accounting for 20–35%. Moreover, a negative effect of the same magnitude (0.25 p.p.) can be seen for a moderate ICT penetration (3.5–5.5) in interaction with a skyrocketing informal sector of a size above 40%. These findings are somewhat in line with our expectations but in a much more intuitive way. It seems that when referring to absolute laggards concerning ICT where governments fail to deliver even the basic services, a medium-sized shadow sector provides some prospects of employment [23] and income. On the other hand, moderate or even promising ICT penetration in interaction with a large informal sector seems to have a negative impact of about 0.25 p.p. on yields, probably signaling the appraisal of the investors to a government policy that strives to provide its people with all the benefits that a digital economy brings and motivate its citizens to return to (or enter) formality.
7. Conclusions and Policy Implications
The determinants of sovereign credit ratings and the rates paid on sovereign debt are still the subjects of much academic discussion. While economic fundamentals clearly play a significant role, additional factors have been proposed in the literature that could contribute to our understanding of the underlying mechanism. In this study, we introduce two factors that have received less attention but may have a significant impact on the economy and society: ICT penetration as a proxy for digital transformation and the informal sector, which remains part of every economy despite policies designed to eliminate it. In addition, to examine their effect on ratings and the cost of debt, as well as their possible combined effect, we use a series of machine learning techniques and employ state-of-the-art model-agnostic methods such as feature importance and accumulated local effects to better understand the relationships under scrutiny.
Our findings suggest that there is a clear, modest negative effect of ICT diffusion and usage on ratings and rates, with technological laggards paying a premium of 0.2 to 0.4 p.p. and pioneers paying a discount of about 0.2 p.p. Countries with modest ICT penetration do not enjoy any apparent direct effect; nevertheless, if they suffer from a high rate of the shadow economy, their commitment to digitization seems to be appraised by markets at a 0.25 p.p. discount.
In contrast, we discovered a positive relationship between the size of the informal economy and ratings as well as yields. Our research indicates that there is a threshold of approximately 15–20% that is deemed acceptable by both investors and agencies. Countries that manage to keep their shadow economies below this level increase their chances of obtaining a top rating by roughly 0.1. However, if this threshold is exceeded, the informal sector can have an adverse impact. Large shadow economies may be charged a premium of up to 1 percentage point by the markets. Notably, in the presence of poor ICT performance, a medium-sized shadow economy appears to be perceived by investors as a temporary economic safety valve.
Our results are consistent with some studies that suggest that ICT can be a significant determinant of ratings and the cost of debt [13]. However, we do not find evidence that ICT is the most important factor, as proposed by Bissoondoyal-Bheenick et al. [10] In addition, we confirmed that a shadow economy can have negative effects on sovereign risk when it exceeds a certain size, around 15–20%, which is in line with the findings of Markellos et al. [11], who suggested a similar threshold of 18%. Additionally, by presenting evidence that the informal sector of ICT laggards should not be eliminated before advancements in ICT take place, we indirectly support the findings of Ndoya et al. [62], who suggest that in some cases the underground economy presents a positive economic impact in African countries with low ICT penetration, and therefore a consolidation of ICT infrastructure in these countries could help curb the informal economy by including similar positive economic effects (absorption of unemployed workers, enhancement of entrepreneurial spirit, etc.).
The preceding discussion leads to a few policy implications. Firstly, countries can greatly benefit by keeping their shadow economies below 15–20%, which is the threshold for acceptable rates of informality set by both markets and agencies. Secondly, to take advantage of digitally transformed and interconnected economies, countries must invest heavily in ICT. Finally, if a country has a medium-sized shadow economy and low ICT penetration, it should prioritize improving its digital infrastructure before taking more aggressive measures to tackle the informal sector.
Author Contributions
Conceptualization, A.K., V.C. and D.P.; methodology, A.K., V.C. and D.P.; software, A.K., and V.C.; validation, A.K., V.C. and D.P.; formal analysis, A.K., V.C. and D.P.; investigation, A.K., V.C. and D.P.; resources, A.K.; data curation, A.K., V.C. and D.P.; writing—original draft preparation, A.K., V.C. and D.P.; writing—review and editing, A.K., and D.P.; visualization, A.K., V.C. and D.P.; supervision, D.P.; project administration, A.K., and D.P..; funding acquisition, D.P. All authors have read and agreed to the published version of the manuscript.
Funding
The publication of this paper has been partly supported by the University of Piraeus Research Center.
Data Availability Statement
Data upon request from the authors.
Acknowledgments
This work has been partly supported by the University of Piraeus Research Center.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Summary statistics.
Table A1.
Summary statistics.
| Numeric Variables | Binary Variables | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs | Mean | Std Dev | Min | Max | Freq. | Percent | Freq. | Percent | |||||
| ytm | 836 | 5.489 | 3.655 | −0.362 | 23.490 | Advanced | 0 | 560 | 53.85 | asia_pacific | 0 | 832 | 80 |
| nri | 1040 | 4.383 | 0.807 | 2.100 | 6.050 | 1 | 480 | 46.15 | 1 | 208 | 20 | ||
| blnc | 1040 | −0.111 | 7.827 | −29.824 | 38.304 | ||||||||
| exrate | 1040 | 235.598 | 1285.728 | 0.481 | 13,389.410 | Freq. | Percent | Freq. | Percent | ||||
| cred | 1040 | 76.344 | 49.311 | 0.000 | 308.978 | eurozone | 0 | 827 | 79.52 | africa_east | 0 | 896 | 86.15 |
| crpt | 1040 | 4.489 | 2.238 | 0.100 | 8.200 | 1 | 213 | 20.48 | 1 | 144 | 13.85 | ||
| infrm | 1040 | 23.529 | 11.806 | 5.100 | 59.900 | ||||||||
| lend | 1040 | −1.956 | 4.678 | −32.076 | 21.764 | Freq. | Percent | Freq. | Percent | ||||
| resgdp | 1040 | 17.793 | 18.061 | 0.343 | 120.840 | West | 0 | 688 | 66.15 | dflt95 | 0 | 771 | 74.13 |
| gdpg | 1040 | 3.398 | 3.871 | −14.839 | 34.466 | 1 | 352 | 33.85 | 1 | 269 | 25.87 | ||
| infl | 1040 | 4.246 | 4.878 | −4.876 | 54.246 | ||||||||
| pdgdp | 1040 | 54.383 | 35.604 | 0.059 | 236.394 | Freq. | Percent | Freq. | Percent | ||||
| tax | 1040 | 17.864 | 5.884 | 0.000 | 37.934 | latin_carribean | 0 | 896 | 86.15 | lgluk | 0 | 801 | 77.02 |
| unmpl | 1040 | 8.003 | 4.538 | 0.150 | 27.800 | 1 | 144 | 13.85 | 1 | 239 | 22.98 | ||
| trade | 1040 | 94.667 | 68.091 | 19.798 | 442.620 | ||||||||
| lgopw | 1040 | 10.339 | 1.136 | 7.778 | 12.477 | Freq. | Percent | Freq. | Percent | ||||
| vix | 1040 | 20.203 | 6.131 | 12.550 | 31.793 | east_eur | 0 | 848 | 81.54 | gl_crisis | 0 | 780 | 75 |
| risk_free | 1040 | 1.400 | 1.632 | 0.033 | 4.852 | 1 | 192 | 18.46 | 1 | 260 | 25 | ||

Table A2.
Descriptive statistics.
Table A2.
Descriptive statistics.
| Numeric Variables | Binary Variables | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs | Mean | Std Dev | Min | Max | Freq. | Percent | Freq. | Percent | |||||
| ytm | 836 | 5.489 | 3.655 | −0.362 | 23.490 | advanced | 0 | 560 | 53.85 | asia_pacific | 0 | 832 | 80 |
| nri | 1040 | 4.383 | 0.807 | 2.100 | 6.050 | 1 | 480 | 46.15 | 1 | 208 | 20 | ||
| blnc | 1040 | −0.111 | 7.827 | −29.824 | 38.304 | ||||||||
| exrate | 1040 | 235.598 | 1285.728 | 0.481 | 13,389.410 | Freq. | Percent | Freq. | Percent | ||||
| cred | 1040 | 76.344 | 49.311 | 0.000 | 308.978 | eurozone | 0 | 827 | 79.52 | africa_east | 0 | 896 | 86.15 |
| crpt | 1040 | 4.489 | 2.238 | 0.100 | 8.200 | 1 | 213 | 20.48 | 1 | 144 | 13.85 | ||
| infrm | 1040 | 23.529 | 11.806 | 5.100 | 59.900 | ||||||||
| lend | 1040 | −1.956 | 4.678 | −32.076 | 21.764 | Freq. | Percent | Freq. | Percent | ||||
| resgdp | 1040 | 17.793 | 18.061 | 0.343 | 120.840 | West | 0 | 688 | 66.15 | dflt95 | 0 | 771 | 74.13 |
| gdpg | 1040 | 3.398 | 3.871 | −14.839 | 34.466 | 1 | 352 | 33.85 | 1 | 269 | 25.87 | ||
| infl | 1040 | 4.246 | 4.878 | −4.876 | 54.246 | ||||||||
| pdgdp | 1040 | 54.383 | 35.604 | 0.059 | 236.394 | Freq. | Percent | Freq. | Percent | ||||
| tax | 1040 | 17.864 | 5.884 | 0.000 | 37.934 | latin_carribean | 0 | 896 | 86.15 | lgluk | 0 | 801 | 77.02 |
| unmpl | 1040 | 8.003 | 4.538 | 0.150 | 27.800 | 1 | 144 | 13.85 | 1 | 239 | 22.98 | ||
| trade | 1040 | 94.667 | 68.091 | 19.798 | 442.620 | ||||||||
| lgopw | 1040 | 10.339 | 1.136 | 7.778 | 12.477 | Freq. | Percent | Freq. | Percent | ||||
| vix | 1040 | 20.203 | 6.131 | 12.550 | 31.793 | east_eur | 0 | 848 | 81.54 | gl_crisis | 0 | 780 | 75 |
| risk_free | 1040 | 1.400 | 1.632 | 0.033 | 4.852 | 1 | 192 | 18.46 | 1 | 260 | 25 | ||

Table A3.
Definitions of (numeric) explanatory variables, data source, and expected sign.
Table A3.
Definitions of (numeric) explanatory variables, data source, and expected sign.
| Variable Abbreviation/ Variable Name | Definition | Source | Expected Impact |
|---|---|---|---|
| nri/Network Readiness Index | Published annually by World Economic Forum and INSEAD and ranges from 1 to 10 with higher values indicating a higher diffusion and use of ICTs. | The Global Information Reports | (−) |
| infrm/Shadow economy | Shadow economy estimates across countries/years. (% GDP) | [25] | (+) |
| blnc/Current Account Balance | The sum of trade balance (goods and services export fewer imports), net income from abroad, and net current transfers. A positive current account balance reflects a country’s net investment abroad while a negative current account balance reflects the foreign net investment to the country. (% GDP) | World Bank | (+/−) |
| exrate/Exchange Rates | Exchange rates as units of the local currency per US dollar | DataStream | |
| cred/Domestic credit to the private sector | Refers to financial resources provided to the private sector by financial corporations, such as through loans, purchases of non-equity securities, and trade credits, and other accounts receivable, that establish a claim for repayment. (% GDP) | World Bank | (+/−) |
| crpt/Corruption perception index | The CPI scores and ranks countries based on how corrupt a country’s public sector is perceived to be. It is a composite index, a combination of surveys and assessments of corruption, and is published annually, ranging from zero (highly corrupt) to ten (highly clean). Scale has been reversed to avoid the usual misconception that higher scores correspond to higher corruption. | Transparency International | (−) |
| lend/Net lending or borrowing | Refers to government surplus/deficit under Excessive Deficit Procedure, which is net lending (+)/net borrowing (−) of general government (as defined in ESA95), plus net streams of interest payments resulting from swaps arrangements and forward rate agreements. (% GDP) | World Bank/ DataStream | (+/−) |
| resgdp/Total reserves | Total reserves comprise holdings of monetary gold, special drawing rights, reserves of IMF members held by the IMF, and holdings of foreign exchange under the control of monetary authorities. The gold component of these reserves is valued at year-end (December 31) London prices. (% GDP) | World Bank/Own calculations | (+/−) |
| gdpg/Gross Domestic Product annual growth | GDP is the sum of gross value added by all resident producers in the economy plus any product taxes and minus any subsidies not included in the value of the products. It is expressed as a percentage that shows the rate of change from one year to the next. | World Bank | (−) |
| infl/inflation | As measured by the consumer price index. (%) | World Bank | (+) |
| pdgdp/Public debt | Total debt owned by any level of the Government. It consists of all liabilities that require payment or payments of interest and/or principal by the debtor to the creditor at a date or dates in the future. (% GDP) | IMF | (+) |
| tax/Tax revenues | Refers to compulsory transfers to the central government for public purposes. Certain compulsory transfers such as fines, penalties, and most social security contributions are excluded. (% GDP) | World Bank/ DataStream | (+/−) |
| unmpl/Unemployment | Refers to the share of the labor force that is without work but available for and seeking employment. (% of the total labor force) | World Bank | (+) |
| trade/Aggregate trade | Refers to the sum of imports and exports of goods and services. (% of GDP) | World Bank/Own calculations | (+/−) |
| lgopw/ | As measured by the output per worker expressed in constant 2010 US$. Natural log transformed. | International Labor Organization | (−) |
| vix/VIX index | Adjusted closing prices, year average. Natural log transformed. A benchmark index measuring the market’s expectation of future volatility. Sometimes called the investor fear gauge because it tends to rise during periods of increased anxiety in financial markets of steep market falls. | Yahoo finance | (+) |
| risk_free/US short-term yield curve. (included only in YTM models) | Three months US yield curve. The three-month U.S. Treasury bill is a useful proxy because the market considers there is virtually no chance of the U.S. government defaulting on its obligations. | US-Department of Treasury/Own calculations | (+) |

Table A4.
Pairwise correlation analysis among variables.
Table A4.
Pairwise correlation analysis among variables.
| ytm | avg_rtg | rtg_s&p | nri | blnc | exrate | cred | crpt | infrm | Lend | resgdp | gdpg | infl | pdgdp | tax | unmpl | TradwE e | lgopw | vix | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ytm | |||||||||||||||||||
| avg_rtg | 0.6918 * | ||||||||||||||||||
| rtg_s andp | 0.6940 * | 0.9933 * | |||||||||||||||||
| nri | −0.6384 * | −0.8076 * | −0.8137 * | ||||||||||||||||
| blnc | −0.3131 * | −0.3412 * | −0.3532 * | 0.4032 * | |||||||||||||||
| exrate | 0.1668 * | 0.1851 * | 0.1964 * | −0.1633 * | −0.0193 | ||||||||||||||
| cred | −0.4482 * | −0.5698 * | −0.5706 * | 0.6415 * | 0.1475 * | −0.1696 * | |||||||||||||
| crpt | 0.5641 * | 0.8439 * | 0.8485 * | −0.8831 * | −0.3330 * | 0.2133 * | −0.6209 * | ||||||||||||
| infrm | 0.5795 * | 0.7559 * | 0.7606 * | −0.7978 * | −0.2087 * | 0.0693 * | −0.5381 * | 0.8409 * | |||||||||||
| lend | −0.2293 * | −0.3154 * | −0.3134 * | 0.2722 * | 0.4328 * | 0.0312 | 0.0606 | −0.2587 * | −0.0836 * | ||||||||||
| resgdp | −0.1399 * | 0.0547 | 0.0406 | 0.0524 | 0.3575 * | −0.0414 | 0.1323 * | 0.0215 | 0.0883 * | 0.1920 * | |||||||||
| gdpg | 0.0637 | 0.1882 * | 0.1952 * | −0.2326 * | −0.049 | 0.1081 * | −0.2918 * | 0.2335 * | 0.2528 * | 0.2693 * | 0.1294 * | ||||||||
| infl | 0.6615 * | 0.4932 * | 0.5014 * | −0.4831 * | −0.3033 * | 0.1421 * | −0.3669 * | 0.4841 * | 0.4662 * | −0.0386 | −0.0473 | 0.2048 * | |||||||
| pdgdp | −0.1196 * | 0.0083 | 0.0021 | 0.1300 * | 0.0522 | −0.1089 * | 0.1547 * | −0.0945 * | −0.2055 * | −0.3962 * | −0.1284 * | −0.2705 * | −0.2486 * | ||||||
| tax | −0.1674 * | −0.2741 * | −0.2761 * | 0.2433 * | −0.1083 * | −0.1831 * | 0.2326 * | −0.3854 * | −0.2824 * | 0.1714 * | −0.2511 * | −0.1568 * | −0.1876 * | −0.0903 * | |||||
| unmpl | 0.3072 * | 0.4093 * | 0.4027 * | −0.3837 * | −0.3131 * | −0.0033 | −0.1450 * | 0.3122 * | 0.1898 * | −0.3441 * | −0.2232 * | −0.1528 * | 0.0337 | 0.1498 * | 0.1300 * | ||||
| trade | −0.2814 * | −0.2346 * | −0.2571 * | 0.2785 * | 0.4178 * | −0.1117 * | 0.1470 * | −0.2893 * | −0.2080 * | 0.2455 * | 0.6177 * | 0.0951 * | −0.1677 * | −0.1684 * | 0.0553 | −0.2294 * | |||
| lgopw | −0.6083 * | −0.8273 * | −0.8334 * | 0.8111 * | 0.3048 * | −0.2351 * | 0.5766 * | −0.8416 * | −0.8041 * | 0.2353 * | −0.1327 * | −0.3393 * | −0.5178 * | 0.1945 * | 0.4126 * | −0.1428 * | 0.2319 * | ||
| vix | 0.1481 * | −0.0487 | −0.0512 | −0.0296 | −0.0464 | −0.0212 | 0.034 | −0.0143 | 0.0005 | −0.1623 * | −0.0054 | −0.3351 * | 0.1311 * | −0.0461 | −0.0069 | −0.002 | −0.013 | 0.0122 | |
| risk_free | 0.0562 | −0.1260 * | −0.1213 * | −0.0177 | −0.0690 * | −0.01 | 0.0246 | −0.0624 | 0.0006 | 0.2601 * | −0.0816 * | 0.2882 * | 0.1106 * | −0.1447 * | 0.0950 * | −0.0938 * | 0.0139 | 0.0264 | −0.1854 * |
Note: * writing denotes statistically significant values at the 5 percent level (two-tailed tests). Listwise deletion when handling missing values.

Table A5.
Sampled Countries by development stage and region indicator.
Table A5.
Sampled Countries by development stage and region indicator.
| Development Stage | West | Latin_Carribean | East Europe | Asia Pacific | Africa Middle-East |
| Developing | Brazil | Bulgaria | Azerbaijan | Egypt | |
| Colombia | Croatia | India | Ghana | ||
| Costa Rica | Hungary | Indonesia | Jordan | ||
| Dominican Republic | Latvia | Kazakhstan | Morocco | ||
| El Salvador | Lithuania | Malaysia | Qatar | ||
| Jamaica | Moldova | Pakistan | South Africa | ||
| Nicaragua | Poland | Philippines | Tunisia | ||
| Peru | Romania | Sri Lanka | Turkey | ||
| Trinidad and Tobago | Russia | Thailand | |||
| Sum of developing countries: 35 | 0 | 9 | 9 | 9 | 8 |
| Advanced | Australia | Czech Republic | Hong Kong | Israel | |
| Austria | Estonia | Japan | |||
| Belgium | Slovenia | Singapore | |||
| Canada | South Korea | ||||
| Denmark | |||||
| Finland | |||||
| France | |||||
| Germany | |||||
| Greece | |||||
| Iceland | |||||
| Ireland | |||||
| Italy | |||||
| Luxembourg | |||||
| The Netherlands | |||||
| New Zealand | |||||
| Norway | |||||
| Portugal | |||||
| Spain | |||||
| Sweden | |||||
| Switzerland | |||||
| United Kingdom | |||||
| United States | |||||
| Sum of advanced countries: 30 | 22 | 0 | 3 | 4 | 1 |
| Total sum: 65 | 22 | 9 | 12 | 13 | 9 |
Note: Australia, New Zealand, Canada, the US, the UK, and the rest of the Western European countries, although not necessarily sharing geographic proximity, carry strong cultural and economic ties that permit financial spillovers and are grouped under the “West” label.
References
- Özmen, E.; Doğanay Yaşar, Ö. Emerging market sovereign bond spreads, credit ratings and global financial crisis. Econ. Model. 2016, 59, 93–101. [Google Scholar] [CrossRef]
- Afonso, A.; Arghyrou, M.; Kontonikas, A. The Determinants of Sovereign Bond Yield Spreads in the EMU; ECB Working Paper No 1781; European Central Bank: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Ferrucci, G. Empirical Determinants of Emerging Market Economies’ Sovereign Bond Spreads; Working Paper No 205; Bank of England: London, UK, 2003. [Google Scholar]
- Hill, P.; Bissoondoyal-Bheenick, E.; Faff, R. New evidence on sovereign to corporate credit rating spillovers. Int. Rev. Financ. Anal. 2018, 55, 209–225. [Google Scholar] [CrossRef]
- Kenourgios, D.; Umar, Z.; Lemonidi, P. On the effect of credit rating announcements on sovereign bonds: International evidence. Int. Econ. 2020, 163, 58–71. [Google Scholar] [CrossRef]
- Cavallo, E.; Powell, A.; Rigobon, R. Do credit rating agencies add value? Evidence from the sovereign rating business. Int. J. Financ. Econ. 2013, 18, 240–265. [Google Scholar] [CrossRef]
- Kaminsky, G.; Schmukler, S. Emerging Market Instability: Do Sovereign Ratings Affect Country Risk and Stock Returns. World Bank Econ. Rev. 2002, 16, 171–195. [Google Scholar] [CrossRef]
- Cantor, R.; Packer, F. Determinants and impact of sovereign credit ratings. Econ. Policy Rev. 1996, 2, 76–91. [Google Scholar]
- Elgin, C.; Uras, B.R. Public debt, sovereign default risk and shadow economy. J. Financ. Stab. 2013, 9, 628–640. [Google Scholar] [CrossRef]
- Bissoondoyal-Bheenick, E.; Brooks, R.; Yip, A.Y.N. Determinants of sovereign ratings: A comparison of case-based reasoning and ordered probit approaches. Glob. Financ. J. 2006, 17, 136–154. [Google Scholar] [CrossRef]
- Markellos, R.N.; Psychoyios, D.; Schneider, F. Sovereign debt markets in light of the shadow economy. Eur. J. Oper. Res. 2016, 252, 220–231. [Google Scholar] [CrossRef]
- Apergis, E.; Apergis, N. New evidence on corruption and government debt from a global country panel: A non-linear panel long-run approach. J. Econ. Stud. 2019, 46, 1009–1027. [Google Scholar] [CrossRef]
- Kotzinos, A.; Psychoyios, D.; Vlastakis, N. The impact of ICT diffusion on sovereign cost of debt. Int. J. Bank. Account. Financ. 2021, 12, 16–51. [Google Scholar] [CrossRef]
- Elgin, C. Internet usage and the shadow economy: Evidence form panel data. Econ. Syst. 2013, 37, 111–121. [Google Scholar] [CrossRef]
- Chacaltana, J.; Leung, V.; Lee, M. New Technologies and the Transition to Formality: The Trend Towards e-Formality; Employment Working Paper No. 247; International Labor Office: Geneva, Switzerland, 2018. [Google Scholar]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable; Independently Published: Munich, Germany, 2022. [Google Scholar]
- Psychoyios, D.; Missiou, O.; Dergiades, T. Energy based estimation of the shadow economy: The role of governance quality. Q. Rev. Econ. Financ. 2021, 80, 797–808. [Google Scholar] [CrossRef]
- Asea, P.K. The informal sector: Baby or bath water? A comment. Carnegie-Rochester Conf. Ser. Public Policy 1996, 45, 163–171. [Google Scholar] [CrossRef]
- Elgin, C.; Birinci, S. Growth and informality: A comprehensive panel data analysis. J. Appl. Econ. 2016, 19, 271–292. [Google Scholar] [CrossRef]
- Eilat, Y.; Zinnes, C. The shadow economy in transition countries: Friend or Foe? A policy perspective. World Dev. 2002, 30, 1233–1254. [Google Scholar] [CrossRef]
- Elgin, C.; Ayhan Kose, M.; Ohnsorge, F.; Yu, S. Understanding Informality. In Koç University-TUSIAD Economic Research Forum Working Papers 2114; Koc University-TUSIAD Economic Research Forum: Instabul, Turkey, 2021. [Google Scholar]
- Dau, L.A.; Cuervo-Cazurra, A. To formalize or not to formalize: Entrepreneurship and pro-market institutions. J. Bus. Ventur. 2014, 29, 668–686. [Google Scholar] [CrossRef]
- Gutiérrez-Romero, R. The Effects of Inequality on the Dynamics of the Informal Economy. In Proceedings of the IZA/WB conference, Bonn, Germany, 8–9 June 2007. [Google Scholar]
- Medina, L.; Schneider, F. Shedding Light on the Shadow Economy: A Global Database and the Interaction with the Official One; CESifo Working Paper, No. 7981; Center for Economic Studies and IFO Institute (CESifo): Munich, Germany, 2019. [Google Scholar]
- Ohnsorge, F.; Okawa, Y.; Yu, S. Lagging Behind: Informality and Development. In The Long Shadow of Informality: Challenges and Policies; Ohnsorge, F., Yu, S., Eds.; World Bank: Washington, DC, USA, 2022. [Google Scholar]
- Loayza, N.; Rigolini, J. Informal Employment: Safety Net or Growth Engine? World Dev. 2011, 39, 1503–1515. [Google Scholar] [CrossRef]
- Caruso, L. Digital innovation and the fourth industrial revolution: Epochal social changes? AI Soc. 2018, 33, 379–392. [Google Scholar] [CrossRef]
- Stiroh, K.J. Economic Impacts of Information Technology. In Encyclopedia of Information Systems; Hossein, B., Ed.; Elsevier: New York, NY, USA, 2003; pp. 1–14. [Google Scholar]
- Haacker, M.; Morsink, J. You Say You Want a Revolution. Information Technology and Growth, IMF Working Paper, WP/02/70, 2002. Available online: https://www.imf.org/en/Publications/WP/Issues/2016/12/30/You-Say-You-Want-A-Revolution-Information-Technology-and-Growth-15787 (accessed on 24 December 2022).
- Vu, K.; Hanafizadeh, P.; Bohlin, E. ICT as a driver of economic growth: A survey of the literature and directions for future research. Telecommun. Policy 2020, 44, 101922. [Google Scholar] [CrossRef]
- The World Development report. Digital dividends. A World Bank Group Flagship Report. 2016. Available online: https://www.worldbank.org/en/publication/wdr2016, (accessed on 24 December 2022).
- Joia, L.A.; dos Santos, R.P. ICT and Financial Inclusion in the Brazilian Amazon. In Electronic Government. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10428. [Google Scholar]
- Garcia-Murillo, M.; Velez-Ospina, A.J. The impact of ICTs on the informal economy. In Proceedings of the 20th ITS Biennial Conference, International Telecommunications Society, Rio de Janeiro, Brazil, 30 November–3 December 2014. [Google Scholar]
- Veiga, L.; Rohman, I. E-Government and the Shadow Economy: Evidence from across the Globe. In Proceedings of the Electronic Government: 16th IFIP WG 8.5 International Conference, EGOV 2017, St. Petersburg, Russia, 4–7 September 2017; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Elbahnasawy, N. Can e-government limit the scope of the informal economy? World Dev. 2021, 139, 105341. [Google Scholar] [CrossRef]
- Vorisek, D.; Kindberg-Hanlon, G.; Koh, W.C.; Okawa, Y.; Taskin, T.; Vashakmadze, E.; Ye, L.S. Informality in Emerging Market and Developing Economies: Regional Dimensions. In The Long Shadow of Informality: Challenges and Policies (205–254); The World Bank: Washington, DC, USA, 2022. [Google Scholar]
- Akitoby, B. Raising revenue. Financ. Dev. 2018, 55, 18–21. [Google Scholar]
- Berdiev, A.N.; Saunoris, J.W. Financial development and the shadow economy: A panel VAR analysis. Econ. Model. 2016, 57, 197–207. [Google Scholar] [CrossRef]
- Brooks, R.; Faff, R.; Hillier, D.; Hillier, J. The national market impact of sovereign rating changes. J. Bank. Financ. 2004, 28, 233–250. [Google Scholar] [CrossRef]
- Gibson, H.D.; Hall, S.G.; Tavlas, G.S. Self-fulfilling dynamics: The interactions of sovereign spreads, sovereign ratings and bank ratings during the euro financial crisis. J. Int. Money Financ. 2017, 73, 371–385. [Google Scholar] [CrossRef]
- Mellios, C.; Paget-Blanc, E. Which factors determine sovereign credit ratings? Eur. J. Financ. 2006, 12, 361–377. [Google Scholar] [CrossRef]
- Reusens, P.; Croux, C. Sovereign credit rating determinants: A comparison before and after the European debt crisis. J. Bank. Financ. 2017, 77, 108–121. [Google Scholar] [CrossRef]
- Bennell, J.A.; Crabbe, D.; Thomas, S.; Gwilym, O.A. Modelling sovereign credit ratings: Neural networks versus ordered probit. Expert Syst. Appl. 2006, 30, 415–425. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. Hands-On Machine Learning with R; Taylor and Francis: New York, NY, USA, 2020. [Google Scholar]
- Overes, B.H.L.; van der Wel, M. Modelling Sovereign Credit Ratings: Evaluating the Accuracy and Driving Factors using Machine Learning Techniques. Comput. Econ. 2022. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees, 1st ed.; Routledge: Abingdon, UK, 1984. [Google Scholar]
- Manasse, P.; Roubini, N. “Rules of thumb” for sovereign debt crises. J. Int. Econ. 2009, 78, 192–205. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach Learn 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Apley, D.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B R. Stat. Soc. 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- LeDell. useR! Machine Learning Tutorial. 2018. Available online: https://koalaverse.github.io/machine-learning-in-R/ (accessed on 24 December 2022).
- Ferri, G.; Liu, G.; Stiglitz, J. The Procyclical Role of Rating Agencies: Evidence from the East Asian Crisis. Econ. Notes 1999, 3, 335–355. [Google Scholar] [CrossRef]
- Monfort, B.; Mulder, C. Using Credit Ratings for Capital Requirements on Lending to Emerging Market Economies: Possible Impact of a New Basel Accord. IMF Working Paper No. 00/69, 2000. Available online: https://ssrn.com/abstract=879567 (accessed on 24 December 2022).
- Bellas, D.; Papaioannou, M.; Petrova, I. Determinants of Emerging Market Sovereign Bond Spreads: Fundamentals vs. Financial Stress. IMF Working Paper No. 10/281, 2010. Available online: https://ssrn.com/abstract=1751394 (accessed on 24 December 2022).
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. Int. J. Forecast. 2021, 1, 388–427. [Google Scholar] [CrossRef]
- Tölö, E. Predicting systemic financial crises with recurrent neural networks. J. Financ. Stab. 2020, 49, 100746. [Google Scholar] [CrossRef]
- Bandara, K.; Shi, P.; Bergmeir, C.; Hewamalage, H.; Tran, Q.; Seaman, B. Sales demand forecast in e-commerce using a long short-term memory neural network methodology. In Neural Information Processing (462–474); Gedeon, T., Wong, K.W., Lee, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 462–474. [Google Scholar]
- Surkan, A.J.; Singleton, J.C. Neural networks for bond rating improved by multiple hidden layers. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 2, pp. 157–162. [Google Scholar]
- Freeborough, W.; Terence, Z. Investigating Explainability Methods in Recurrent Neural Network Architectures for Financial Time Series Data. Appl. Sci. 2022, 12, 1427. [Google Scholar] [CrossRef]
- Mora, N. Sovereign credit ratings: Guilty beyond reasonable doubt? J. Bank. Financ. 2006, 30, 2041–2062. [Google Scholar] [CrossRef]
- Haque, N.U.L.; Kumar, M.S.; Mark, N.; Mathieson, D.J. The Economic Content of Indicators of Developing Country Creditworthiness. IMF Staff Pap. 1996, 43, 688–724. [Google Scholar] [CrossRef]
- Ndoya, H.; Okere, D.; Belomo, M.; Atangana, M. Does ICTs decrease the spread of informal economy in Africa. Telecommun. Policy 2023, 47, 102485. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).