Abstract
We present a generalised complex contagion model for describing behaviour and opinion spreading on social networks. Recurrent interactions between adjacent nodes and circular influence in loops in the network structure enable the modelling of influence spreading on the network scale. We have presented details of the model in our earlier studies. Here, we focus on the interpretation of the model and discuss its features by using conventional concepts in the literature. In addition, we discuss how the model can be extended to account for specific social phenomena in social networks. We demonstrate the differences between the results of our model and a simple contagion model. Results are provided for a small social network and a larger collaboration network. As an application of the model, we present a method for profiling individuals based on their out-centrality, in-centrality, and betweenness values in the social network structure. These measures have been defined consistently with our spreading model based on an influence spreading matrix. The influence spreading matrix captures the directed spreading probabilities between all node pairs in the network structure. Our results show that recurrent and circular influence has considerable effects on node centrality values and spreading probabilities in the network structure.
1. Introduction
Research on social networks is a growing field of study in network science [1], social sciences [2,3,4,5,6], and mathematics. The availability of user-provided content in online social media [7,8] makes the spreading of disinformation and fake news easier. Recently, methods of how disinformation circulates on social media have been investigated [9]. Disinformation can have severe implications for democratic processes and human rights [10]. These present-day phenomena underline the importance of studying mechanisms of opinion formation. Methods and models can help us better understand and manage these unwanted developments.
In social network analysis, the concept of scope is used to assess the convincing ability of a user toward other users on social platforms. Other concepts such as centrality, reliability, power, reputation, influence, trust, and diffusion can be seen as different aspects of scope. In [7], researchers have studied how the scope of a sentiment propagates in space and time in a social network. The authors present a general framework for extracting information about the scope of the sentiment of a user on topics of any subject.
Despite the richness of publications addressing social networks from many perspectives, there are still open questions about how to classify social interactions and how to model both static properties and dynamic effects on social networks. In the current literature, few studies consider complex contagion processes with loops [11]. Theories of interactions on social networks involve describing various processes from information to opinion and behaviour spreading [12,13,14,15]. Epidemic spreading is closely related to social contact networks [16,17,18,19,20]. Researchers have recognised that diverse approaches are needed for modelling network structures and different dynamic processes on social networks [21,22].
One categorisation into two classes, simple contagion and complex contagion, has been widely discussed in the literature [23,24,25]. Simple contagion refers to spreading processes induced by a single exposure to a contagious entity, while complex contagion demands multiple exposures for transmission [25]. Information and epidemic spreading are examples of processes where simple contagion models can be useful. Rumour and behaviour spreading are examples where complex contagion models are needed.
Some complex contagion models have been investigated in the literature. Non-Markovian network models have been proposed that account for higher-order interactions [26]. A recent study [27] suggests that higher-order interactions can change the collective dynamics of pairwise interactions. Mean-field theory approximates the original model by averaging over an independent variable of the model [28]. These models are intended for different applications, they do not consider global interactions, or they are not microscopic-level models.
Obviously, many real-world processes can not be identified as pure simple or complex contagions. There are processes which do not fit into either of the two categories [29]. More expressive and detailed definitions are needed to conceptualise, at least, typical or representative processes on social networks [30,31]. This is not an easy task due to the complex nature of human social behaviour.
Technically, simple contagion can be determined as a class of processes where only self-avoiding paths, or paths where each node only appears once, are allowed. However, many characteristics can still be different in this class; for example, rules for allowed or preferred paths, temporal distribution for spreading processes, effects of node and link attributes, collective network effects, etc. In the case of complex contagion, the current definition is even more problematic because many other complex processes exist in real life. One solution would be to call these all complex contagion processes and define sub-categories under this general concept.
In [32], network mechanisms have been categorised according to research tradition into two outcomes they are used to explain: social capital and social homogeneity (Table 2 in [32]). Both of these categories consist of two kinds of network models: flow model and bond model. Flows are what actually pass between nodes as they interact, such as ideas or goods; whereas, in a bond model network, links serve as bonds that align and coordinate action. Flow-based explanations of social homogeneity, or contagion, is the most studied theme in the literature [32].
In [32], links are categorised into two types: states and events. States have continuity over time. Examples of state-type ties include role-based, cognitive/perceptual, and affective relations. State-type ties have attributes such as strength, intensity, and duration. Event-type links have a discrete and transitory nature and can be counted over periods of time. Examples of event-type ties include e-mail exchanges, phone conversations, and transactions such as sales or treaties signed. The frequency of occurrence can be assigned to event-type links [32].
In a review article [12], opinion dynamics and empirical data are analysed as discrete or continuous depending on the nature of the state variables. In discrete models, the opinion of an individual is one of a finite number of possibilities, such as a political candidate, a choice of product, or a predefined answer in a survey. Continuous models, on the other hand, use real-valued state variables to capture the level of agreement with an opinion, attitude, or topic of interest [8,12,22].
Methods to identify important nodes in complex networks have been studied for static network structures [33,34,35] and dynamic spreading processes [36,37,38]. Many existing methods focus only on the local interaction of nodes but neglect the effects of far-away nodes. Conventional closeness centrality and betweenness centrality measures are based on counting the shortest paths between node pairs in the network [33,34]. Consequently, these methods can describe most real-world processes only approximately. To reconcile this issue, we propose in Section 2 a microscopic-level spreading model that considers all paths in the network, including recurrent and circular structures.
The outline of this article is as follows. In the Model Section 2, we have two subsections. In Section 2.1, we present the main mathematical formulas used in this work. We refer to our earlier work [39,40,41,42,43,44] for the pseudo algorithms of the model that are useful in computer implementations. In Section 2.2, we introduce our model’s microscopic features and their extensibility. In the Results Section 3.1, we present modelling results and their interpretation by using the concepts explained in the Introduction Section 1. In the out- and in-centrality measures Section 3.2.1 and in the Betweenness Section 3.2.2, these measures are demonstrated with a small social network. In Section 3.2.3 and in the Appendix A, a collaboration network is used to demonstrate the use of a larger network structure in the analysis. In the last Section, Section 3.2.4, we introduce a new application of our model to profile individuals in a social network. This study has two main contributions: First, we propose a new model for describing behaviour and opinion spreading on social networks. Second, we apply the proposed model for profiling individuals based on their out-centrality, in-centrality, and betweenness measures. The Conclusion Section 4 summarises the results and highlights the contributions of our work.
2. Model
In Section 2.1, we present the main mathematical ideas on how the spreading process is modelled by combining alternative paths of the network structure from source nodes to target nodes. Detailed algorithms are not reproduced here because they have been published in our earlier studies and the focus of this work is on the interpretation and application of the modelling framework. In Section 2.2, we provide information about the features and extensibility of our proposed model.
2.1. Mathematical Formulation
Our model describes a microscopic-level spreading mechanism, and it enables calculating spreading probabilities between all node pairs in the detailed network structure. Directed edges with individual weights for nodes and edges are considered in the model. The probability of influence spreading from a starting node through a path is the product of the weights of each edge and node on the path:
where is the probability of spreading through the path L of k edges and nodes, and and are the weight of the jth edge and node on the path, respectively. The probabilistic interpretation is that all attempts to spread along the path must be successful. The weight of the starting node is not included in the product because we assume that the spreading starts from the node with probability one. In this study, to demonstrate our model, we use the same link weights for all links in the network and all node weights are assumed to be one. When empirical data are available, these parameter values are set to their actual observed or evaluated probability values.
In our model, influence is spreading simultaneously through multiple paths in the network structure [39,40,41]. The method of spread is non-conserved; that is appropriate for describing the transitions of opinion spreading. We assume that the probabilities of influence spreading through different paths are independent.
The probability of spreading from a source node to target nodes is calculated by two paths at a time by using the well-known non-mutually exclusive formula of probability theory. We denote by the probability of influence spreading through path L. To calculate the probability of spreading through path or path , we use the probability for the longest common prefix (LCP) of the two paths. We denote the LCP by and its probability by . In the case where is empty—that is, there is no common prefix—we assign . The probability of spreading through or is
Equation (2) is used iteratively by repeatedly applying the equation to include more and more paths in the calculation. The probabilities for the paths are combined in the descending order of the lengths of the longest common prefixes. As the final result, we obtain the total probability of influence spreading from any one node to any other one through all possible paths of maximum length .
The algorithm calculates the probabilities of influence spreading from a node to all other nodes. This is repeated for every source node of the network, and an influence spreading matrix is formed. No restrictions are placed on breakthrough spreading through nodes. We have also developed an efficient algorithm [41] that does not have to store the paths in memory, making it very efficient even for larger networks.
The influence spreading matrix can be used in various applications for analysing social networks and their elements. Next, we present three different quantities [39,40], in-centrality, out-centrality, and betweenness centrality, that measure the importance of a node in a network. In the following, the set of nodes in the network is denoted by V. The in-centrality of node t is defined as
and the out-centrality of node s as
These quantities have a natural interpretation as expected values: the in-centrality is the expected number of nodes, from which influence will spread to it, and out-centrality is the expected amount of nodes influenced when the spreading is started from it. The in-centrality could represent, for example, how exposed an individual is to misinformation, and the out-centrality could represent the expected number of influenced individuals initiated by the source node.
We define betweenness centrality [39] for node s as the relative difference in the cohesion of the network when node s is removed from the network
where is the cohesion of the network
and is the cohesion of the network with node s removed
The betweenness centrality of a set of nodes can be defined similarly to the definition of the betweenness measure of a single node. The betweenness centrality could be used to find, for example, critical nodes that mediate information or influence between different parts of a network structure.
2.2. Microscopic Modelling and Extensibility
In our model describing influence spreading, connections between the nodes of a social network are modelled at a detailed level. We define the spreading ability of a node as the number of finally influenced nodes given that the spreading is initialised from the node [45]. Individual nodes and links have weights that are interpreted as probabilities of influence spreading through nodes and via links, respectively. Links are bi-directional, allowing different weights for both directions. In our earlier studies [20,39,40,41,42,44], we have presented how temporal spreading can be studied in the detailed network. Different models for the temporal distribution can be used, for example, Poisson distribution or e-mail forwarding distributions [40]. In addition, empirical temporal distributions can be used as input for the model.
Since the distribution is defined as a two-dimensional matrix as a function of time and path length, the method also enables studying functional dependence on the path length; for example, an extra factor for decreasing influence as a function of path length can be incorporated into the model. Our model is global in the sense that path lengths between 1 and 20 can be used. Longer path lengths are beyond the accuracy of typical computing environments. Local effects can be investigated by using smaller parameter values for . Most of the network models in the literature consider only local interactions [38] or they are not based on the microscopic structure of the network.
The key element in our model is the method of how different spreading paths are processed to achieve the combined effects (Algorithm 1 in [41]). An efficient computer algorithm implementing the path combining method is developed for calculating effects in larger networks (Algorithm 2 in [41]). We have developed computer programs to analyse network structures in various applications [20,43]. Details of the algorithms and computer running times can be found in [41,46].
Details of the model have been explained in our earlier work, including comparisons of the efficiency of different models in [41,42]. In this work, we focus on interpretations of the model in the context of social interactions. We discuss how our proposed model is related to other models in the literature and how our model can be extended to include rules in considering specific real-world processes.
In [25], complex contagions are characterised as events that require social affirmation from multiple sources. We propose a new model where all interactions are allowed between individuals in a social network, recurrent interactions between neighbouring nodes, and circular influence spreading through loops in the network structure. In the basic model, we do not deploy any additional rules for the spreading process. One advantage of the proposed microscopic-level model is that different rules of interactions can be easily incorporated into the model. For example, thresholds [19] for successful events or breakthrough effects through influenced nodes are included. Multiple states and corresponding transition probabilities can be defined for the nodes in the network structure. This can be compared with the traditional SIR and SEIR models [37] in the literature of epidemic-spreading models.
3. Results
In Section 3.1, we explain the characteristics of our proposed model by using the conventional concepts introduced in Section 1. Essential here is the interpretation of circular influence through loops and repetitive influence between neighbouring nodes in the network structure.
In Section 3.2, we demonstrate our model with a small social network structure and a larger collaboration network structure. We compare the results of complex and simple contagion models. In addition, we provide a novel node profiling method based on the magnitude of node centrality measures and the ratio of out- and in-centrality values.
3.1. Features and Interpretation of the Model
Clearly, our model describes complex contagion in the sense that multiple nodes and links are involved in the interactions. The model allows circular interactions or loops and recurrent interactions between adjacent nodes, but self-loops are not implemented in the current version of the computer program. We deduce that these features are characteristic of behaviour and opinion spreading in social interactions. Our model includes Centola’s complex contagion [25], but we have allowed influence spreading events to all connections in the network structure. This enables the modelling of influence spreading, or opinion formation, in the network. Other complex contagion models in the literature [26,27,28] lack these features, describe local interactions, are approximations, or are intended for other applications.
In addition, our methodology enables consistent definitions of in-centrality, out-centrality, and betweenness measures. In addition, community detection can be modelled with the same formalism [39,40]. We compare the results of our complex contagion model with a simple contagion model where only self-avoiding paths are allowed.
Both social homogeneity and social capital [32] can be modelled with our model by calculating network measures and assigning numerical values to network attributes or weights. As mentioned in Section 1, network mechanisms can be categorised as flow models and bond models. Our model is a flow model because it describes influence spreading as a spreading process. Modelling network bonds that align and coordinate actions is a subject for future study. Possible features of the model to be utilised include using link weights , setting initial values to node weights, and using unconventional distributions as temporal distributions.
Regarding categorisation into the event- or state-type [32] links, our model can be used for both types. Link weights can describe the strength, intensity, and duration of state-type links or the frequency of occurrence of event-type links. We have used this interpretation for link weights in our earlier study [47].
In addition, opinion dynamics [12] is described with continuous node state variables. Node states are probabilities of influence with values ranging between 0 and 1. The continuous node state value is interpreted as the level of agreement with an opinion, attitude, or topic of interest. Discrete node state variables can be defined by using a threshold for the continuous variable to indicate a state change from consideration to decision. If needed, new attributes can be assigned to nodes when more complex rules or more node states are required in the model.
3.2. Numerical Demonstrations
In our first example, we analyse a small real-world social network of 32 nodes [48]. From Figure 1, we can see that the network has a varied internal structure that can be useful in our demonstration. We have also used the same network for demonstrating community detection in [39].
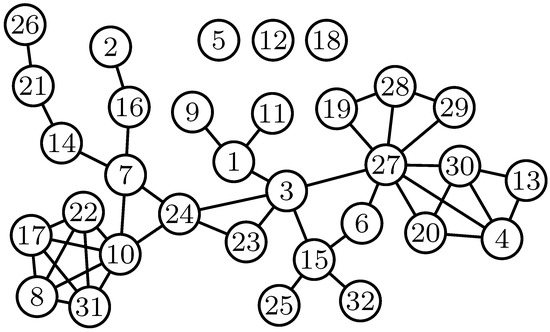
Figure 1.
The Dutch students’ social network [48].
3.2.1. Out- and In-Centrality Measures
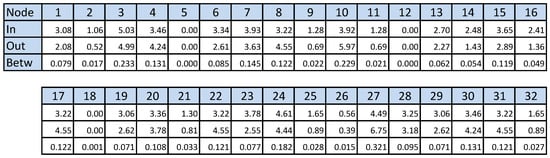
Figure 2, Figure 3, Figure 4 and Figure 5 show node-level out-centrality, and in-centrality values for link weights and , respectively. Albeit the original study has recorded different attribute values for the nodes in the Dutch students’ social network [48], we use the same link weights for all connections between the nodes. In this way, we can more clearly demonstrate the basic features of our model. In the actual analyses, both link and node weights should be taken into account. In our microscopic model, individual node and link weights are included in the calculation of the influence spreading matrix elements as explained in Section 3.1. We have kept nodes , and 18 to preserve the same numbering of nodes as in earlier works. In our definitions of centrality and betweenness measures, we have the convention that source nodes themselves do not contribute to these quantities.
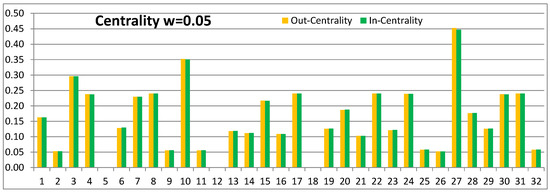
Figure 2.
Complex contagion .
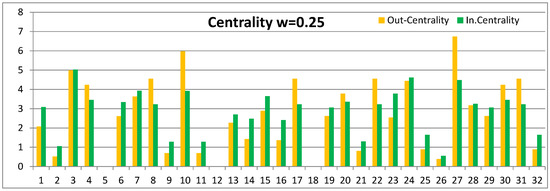
Figure 3.
Complex contagion .
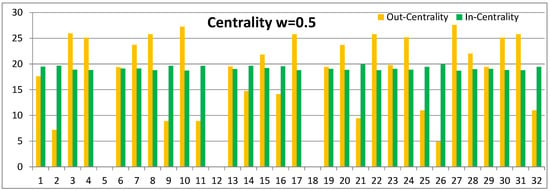
Figure 4.
Complex contagion .
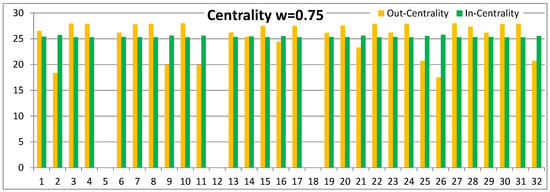
Figure 5.
Complex contagion .
The first, and obvious, observation from Figure 2 is that nodes in a central position in Figure 1 such as , and 3 have high out-centrality and in-centrality values. Figure 2 shows that the out-centrality and in-centrality values are almost equal in this case. This is explained by the fact that for low link weight values local interactions dominate because of the exponentially decreasing factor as a function of the path length L. As a consequence, the centrality values, and corresponding rankings of the nodes, are mainly determined by node degrees. Nodes , and 3 have degrees , and 5, respectively.
The interpretation is clear: The social influence of individuals with low influence spreading probability values, or low link weights, is limited to short distances in the social network structure. With increasing link weights, node-level out-centrality and in-centrality increase. This is because the probability of influence between neighbouring nodes increases and because of the longer range of influence. This is a non-linear process because the structure of the network affects the spreading process.
Less obvious is that the node rankings (and relative values) can change for higher values of link weights. This can happen because distant nodes with larger degrees have more influence on the spreading process. However, this is not the whole story. In our proposed model, recurrent interactions between neighbouring nodes and circular interactions in loops enhance these effects.
Recurrent and circular effects can change the relative importance or rankings of nodes when compared with simple contagion models. As we mentioned, with low link values only the links between the source node and neighbouring nodes are relevant. For this reason, the simple contagion model with self-avoiding paths provides similar results when link weights are small. Simple contagion results are shown in Figure 6, where we can see that node rankings are preserved when link weights are increased. This does not generally hold for our complex contagion model.
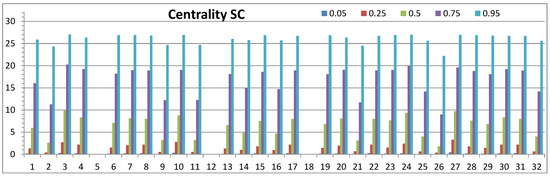
Figure 6.
Centrality values for link weight values and in the simple contagion model.
Before we investigate the dependence of node rankings on link weights, we notice from Figure 2, Figure 3, Figure 4 and Figure 5 that node-level in-centrality and out-centrality values are different for higher link weights. These values are similar for each node for low link weights (see Figure 2). Again, the reasoning is that only the links incident to the node have effects. Clearly, this holds only for undirectional and equally weighted links. In the complex contagion model for higher link weights, it depends on the network structure whether the out-centrality or the in-centrality value is higher for a node.
From Figure 3, we can see that with link weights , out-centrality values are higher for nodes and 31. These nodes are well-connected, and their neighbours typically have connections with each other. For node 3 with link weights , the out-centrality and in-centrality values are almost equal. This is a consequence of its different position in the network compared to nodes 10 and 27. Let us compare node 7 with nodes and 30. They all have four degrees, but the in-centrality of node 7 is higher than out-centrality for link weight . This can be explained by the lower local connectivity of node 7 compared to the other nodes. For node 7 with higher link weights, out-centrality is higher than in-centrality, as can be seen from Figure 4 and Figure 5. With higher link weights, distant well-connected nodes with loops enhance the influence of node 7 to other nodes. This phenomenon is not so important for in-centrality because the influence of distant nodes on node 7 are averaged over multiple source nodes from different distances and loops, on average, have weaker effects.
Nodes , and 3 dominate in Figure 2 as influential spreaders with low link weights; however, in Figure 4 with higher link weights, there are about ten nodes with similar capabilities. With higher link weights also node 3 has a higher out-centrality value than in-centrality value.
Figure 5 shows that both out-centrality and in-centrality values approach the number of nodes in the network or the number of nodes in a connected component in the network. In-centrality values are more even, but some peripheral nodes such as nodes and 32 still have relatively low out-centrality values.
The interpretation in the context of social networks is that an individual’s role as an influencer or an influenced person depends on the position in the social network structure. Often, however, a central person has both roles at the same time; only the dominant role can vary. The second result that the dominant role can change when the strength of social influence changes is a novel result of our influence spreading model that considers circular interactions at different distances. The third observation is that weakly connected and isolated individuals have low influence on other people but they may still be influenced by the larger social network.
Figure 6 shows centrality values with different link weights for nodes of Figure 1 in the simple contagion model with self-avoiding paths. In this model, recurrent and circular effects are not allowed. As a consequence, rankings are preserved with increasing link weights. With bi-directional and equally weighted networks, in-centrality and out-centrality values are equal and only the centrality values are presented.
This kind of simple contagion model can describe information spreading where the same piece of information is communicated only once between neighbouring individuals in the social network structure. Real-world contacts in social networks can have different types of interactions. Opinion formation, for example, can involve simultaneous simple contagion and complex contagion interactions. These kinds of spreading mechanisms can be described by models with breakthrough effects. We have proposed a unifying model [41] where the probability of a breakthrough event can be set between 0 and 1. The general model with breakthrough effects is beyond the scope of this study, but the general idea is to adjust the ratio between simple and complex contagion according to the modelled spreading process.
3.2.2. Betweenness Measure
Betweenness measures a node’s role as a mediator in the network structure. The definition of the traditional betweenness measure for node v is based on the total number of shortest paths and the number of shortest paths through node v. Paths where node v is an endpoint are not included in the calculation. There are versions for weighted networks and state-aware networks considering the states of the source and target nodes of each shortest path. Reviews of standard centrality and betweenness measures in the literature can be found in [33,35].
Our definition of the betweenness measure in Equation (5) is based on the same influence matrix as the in- and out-centrality measures in Equations (3) and (4) in Section 3.2. We have calculated the results for our example network in Figure 1 for the complex contagion model in Figure 7 and for the simple contagion model in Figure 8. As can be seen, the results are almost similar for the two models. There is a minor difference in the results, which are relatively larger in the complex contagion model in Figure 7 than in the simple contagion model in Figure 8. Altogether, the betweenness measure, as defined in Equation (5), is relatively less dependent on link weights than out- and in-centrality measures in Equations (3) and (4). For example, the ranking of nodes is almost independent of the link weight values.
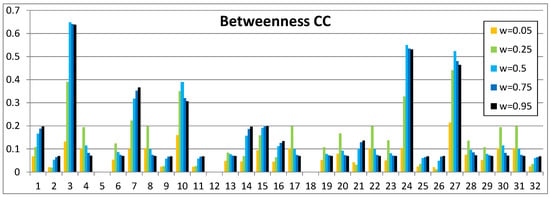
Figure 7.
Betweenness in the complex contagion (CC) model.
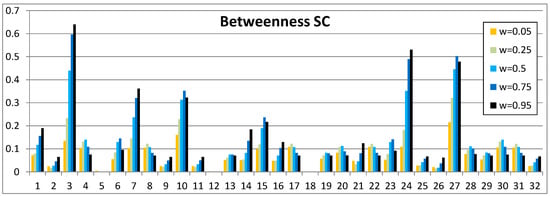
Figure 8.
Betweenness in the simple contagion (SC) model.
Node 27 has the highest betweenness value for low link weights, and it has also the highest out- and in-centrality values, as can be seen in Figure 2. This can be expected because in- and out-centrality values for low link weights are almost equal, and betweenness measures both incoming and outgoing effects. Node 3 has a high betweenness value and node 10 has a lower betweenness ranking with link weight , as can be seen from the table in Figure 9. In Figure 7, with high link weights, the betweenness value of node 3 is higher than the betweenness value of node 27. Node 24 has moderate centrality values, but it has high betweenness values, as can be expected from the network structure of Figure 1. Betweenness values may have a maximum value at some point in the range of .
Figure 9.
Rankings of out-centrality, in-centrality and betweenness values for the Dutch students’ network of Figure 1 (). Numerical values of the quantities are provided in Figure A2 in the Appendix A.
3.2.3. Demonstration with a Larger Network Structure
Next, we demonstrate our model results with the larger network structure of 4158 nodes and 13,422 bidirectional links in Figure 10. The data for the Collaboration network [49] have been gathered from the e-print arXiv. The network is based on collaborations between authors on manuscripts submitted to the General Relativity and Quantum Cosmology category. Nodes in Figure 10 represent authors, and edges are collaborations between them. A manuscript of k authors will result in a completely connected subgraph of k nodes.

Figure 10.
The largest connected component of the collaboration network [49].
Figure 11 shows out-centrality and in-centrality values calculated from the complex contagion model where the horizontal axis presents nodes arranged by the out-centrality values in ascending order. The results in Figure 11 illustrate the general features of the model and also some specific characteristics of the network structure. All figures show the different behaviour of out- and in-centrality. Typically, out-centrality values are increasing and in-centrality values are almost constant in most cases. For low link weights, out-centrality values are larger than in-centrality for the majority of nodes. This is reversed for high link weights: in this case.
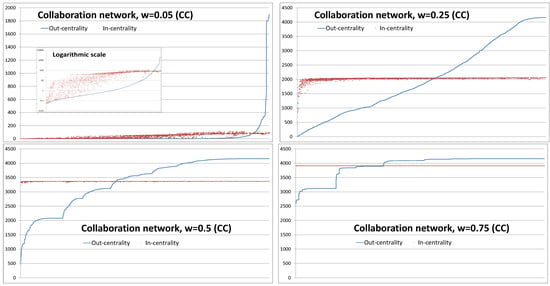
Figure 11.
Out- and in-centrality values with link weights , and . Nodes on the horizontal axes are arranged in the ascending order of out-centrality values.
With very low link weight values, in this network, out- and in-centrality values are approximately equal because only the links to neighbouring nodes have effects (see Figure A1 with ). Out-centrality reveals network structures more clearly. When link weights are , out-centrality values are low except for a set of nodes that are members of larger collaboration groups. With higher link weights, smaller collaboration groups also have effects on the curves.
In the Appendix Figure A1, we show an example of the effects of delimiting the path lengths . As expected, both out- and in-centrality values are lower than in the corresponding results with higher maximum path length values ( in Figure 11). Interesting structures are revealed in out-centrality values with high link weights. In this study, we do not investigate these results in more detail because they are outside the scope of this work. In Section 3.2.4, we present an example of how the proposed model can be used to examine different roles of individuals in a selected group of people according to their out-centrality, in-centrality, and betweenness values.
3.2.4. Profiling
As an application, we present how the out-centrality, in-centrality, and betweenness measures can be used to profile individuals. This is possible and consistent because all these measures are defined based on the same influence spreading matrix introduced in Section 2.1. First, we explain the idea with a small test network of Figure 12. The same network structure has been used in [34] to demonstrate conventional centrality measures and their inconsistencies.
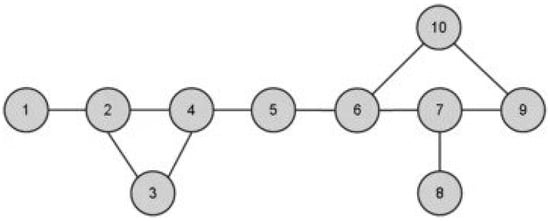
Figure 12.
Network structure for illustration of centrality measures and profiling of nodes [34].
Figure 13 shows centrality measure values for the complex contagion model with link weights , and . As we know from Section 3.2.1, the rankings of nodes in the simple contagion model are similar to the rankings in the complex contagion model with low link weights. Therefore, Figure 13a has the information for both models. On the other hand, in our profiling demonstration, we use only the complex contagion results because our novel idea is based on node-level differences in out- and in-centrality values.
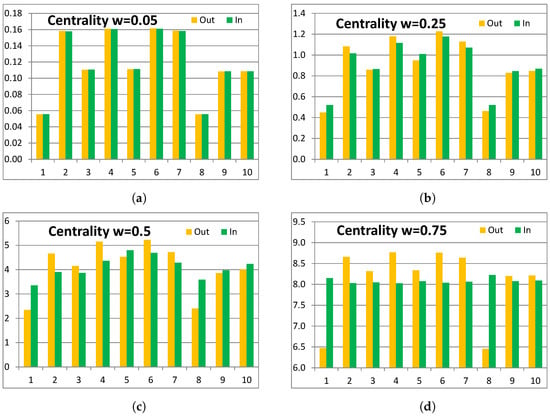
Figure 13.
Out- and in-centrality values for the test network of ten nodes in the complex contagion (CC) model. (a) Link weight (b) Link weight (c) Link weight (d) Link weight .
Figure 14a,b show the complex contagion and simple contagion betweenness results with different link weight values. In our analysis, we use only the complex contagion results because they are calculated from the same model as the out- and in-centrality results.
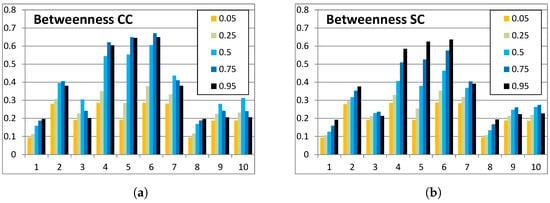
Figure 14.
Betweenness values for the test network of ten nodes for link weight values and . (a) complex contagion (CC) model. (b) simple contagion (SC) model.
As we have seen in Section 3.2.1 and Section 3.2.2, rankings and numerical values of out-centrality and in-centrality can change as a function of link weights. Usually, these variations can only change some details in our analysis. However, these details can be important in some specific real-world cases if a node is profiled differently. We take as our representative example in Figure 13b and Figure 14a.
In Figure 15, we demonstrate with the test network of Figure 12 how profiling could be performed. Detailed parameter values and classification can be designed for specific purposes and different network sizes.

Figure 15.
Profiles of the nodes in the test network of Figure 12 of ten nodes ().
We have used the following rules for the ‘Peripheral’, ‘Central’, and ‘Mediator’ roles:
- If the node’s ratio of the in-centrality to out-centrality is larger than , it is classified as ‘Peripheral’ [or as (Peripheral)].
- If the node’s out-centrality value is larger than , it is classified as ‘Central’ [or as (Central)].
- If the node’s betweenness value is larger than , it is classified as a ‘Mediator’ [or as (Mediator)]. (Sum of betweenness values is normalised to the same value as the out- and in-centrality sums)
Now, we use the above rules and identify the roles of the nodes in Figure 12. Nodes 1, , 5, 8, , and are ‘Peripheral’. Nodes 2, , 4, 5, 6, 7, , and are ‘Central’. Nodes 2, , 4, 5, 6, 7, , and are ‘Mediators’.
The idea is to group different combinations into classes. We can identify four classes, ignoring the parentheses. These are indicated by the brown, green, and blue colours in Figure 15. We could have a more detailed classification. For example, node 5 has strong roles as ‘Peripheral’, ‘Central’, and ‘Mediator’. By looking at Figure 12, we realise the special position of the node. Node’s roles as ‘Central’ and ‘Mediator’ are clear. Role ‘Peripheral’ is assigned to node 5 because its neighbours 4 and 6 are not connected with each other.
Next, we present an example of how profiling can be performed for a group in a larger network. We selected one node (Node 1 in the example) and its neighbours from the network structure of Figure 11. Then, we set node weights of these nodes and all the other node weights or . These values should be designed for the specific application at hand. In Figure 16a,b out-centrality, in-centrality, and betweenness values are shown for the seven nodes of the group.
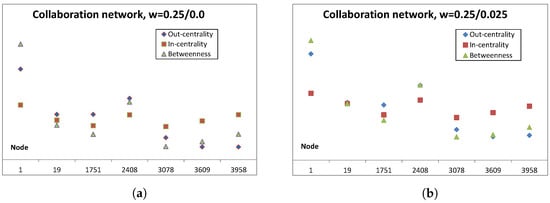
Figure 16.
Out-centrality, in-centrality and betweenness values of a set of connected nodes in the Collaboration network Figure 10. (Numerical values are normalised equally for the three measures). (a) Link weights of outsider nodes . (b) Link weights of outsider nodes .
Technically, the numerical values are normalised to have equal sums for the three measures. Out- and in-centrality sums for the entire network are equal but, in general, they are not equal for a subset of nodes of the network. As we have used node weights instead of link weights, the influence of each link originating from the group members has a weight , but the influence of each link from outside of the group has a weight of or . We can see that in this case, the results are almost similar for the two cases where we have used different weights for the nodes outside of the group. Again, this is not universally true as it depends on the network structure. The interpretation for using non-zero node or link weights is that the group is not isolated from the outside world but has interactions with others in the social network. Parameter values should be designed for the specific situation and type of social influence to be modelled. Based on the results in Figure 16, classifications such as those in Figure 17 can be produced.
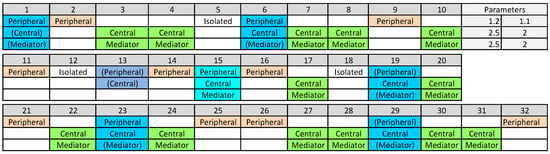
Figure 17.
Profiles of the nodes in the Dutch students’ social network of Figure 1 of 32 nodes ().
The method is based on the fact that out-centrality and in-centrality values for a node can be different even in the case of bidirectional equally weighted links. This is contrary to the simple contagion model with self-avoiding paths where the node-level out-centrality and in-centrality values are equal. Usually, these values are different for networks with directed and weighted links. Recurrent and circular effects in the influence spreading process have significant effects in the profiling results, as well as in the centrality and betweenness results.
4. Conclusions
We have highlighted the properties and interpretations of our influence spreading model proposed in our earlier studies [20,39,40,41,42,44]. Our model considers microscopic-level recurrent and circular effects in the influence spreading process on social networks. In the literature, the need for new models has been recognised and the concept of complex contagion [25], as opposed to simple contagion, has been introduced to point out this research gap. We used a version of a simple contagion model with self-avoiding paths to verify that our proposed model produces different results than the corresponding simple contagion model.
New out-centrality, in-centrality, and betweenness measures are defined consistently with the influence spreading model. The definitions are based on the influence spreading matrix of the model. We demonstrated these measures with a well-known social network of 32 Dutch students social network and a larger collaboration network. As a novel application, we presented ideas on how profiling could be performed by using our model and corresponding influence measures. The proposed method is based on the fact that the out-centrality and in-centrality values can be different.
The contributions of this study include discussing the interpretations of our spreading model in the context of behaviour and opinion spreading on social networks. The novelty of our model is how to consistently consider recurrent and circular interactions in the network structure. We demonstrated that the model with measures calculated from the influence spreading matrix generated from our model. In this study, we apply the proposed model for profiling individuals based on their out-centrality, in-centrality, and betweenness measures.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this article:
| CC | Complex Contagion |
| SC | Simple Contagion |
| LCP | Longest Common Prefix |
Appendix A
Here, we demonstrate the effects of limiting the maximum path length of the spreading process. In the example of Figure A1, the path lengths are limited to . Link weight values , and are used for all links in the network. The first figure illustrates that node-level out- and in-centrality values are approximately equal with low link values . With a slightly higher link weight value , out-centrality values are higher and increasing when the nodes on the horizontal axes are arranged in the order of ascending out-centrality values. For a small set of highly connected nodes, the out-centrality values are higher than i-centrality values. Limiting the values of L requires the use of higher link weights to have comparable spreading probabilities as with higher L. However, limiting L has complex effects caused by the complex structure of the network. For example, the network structure has an impact on both out-centrality and in-centrality results (see results in Figure A1).
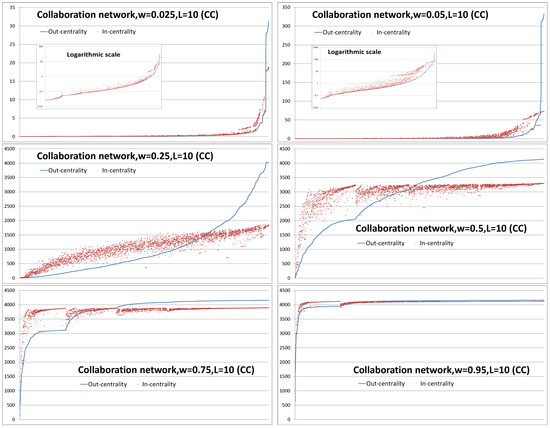
Figure A1.
Out- and in-centrality values with a maximum path length and link weights , and . Nodes on the horizontal axes are arranged in the ascending order of out-centrality values.
References
- Barabási, A.-L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; Free Press: New York, NY, USA, 2003; p. 576. [Google Scholar]
- Friedkin, N.E. Theoretical foundations for centrality measures. Am. J. Sociol. 1991, 96, 1478–1504. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Proskurnikov, A.V. Generalized Markovian Quantity Distribution Systems: Social Science Applications. Sociol. Sci. 2020, 7, 487–503. [Google Scholar] [CrossRef]
- Granovetter, M.S. The Strength of Weak Ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Burt, R.S. Structural Holes: The Social Structure of Competition; Harvard University Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Bonifazi, G.; Cauteruccio, F.; Corradini, E.; Marchetti, M.; Sciarretta, L.; Ursino, D.; Virgili, L. A Space-Time Framework for Sentiment Scope Analysis in Social Media. Big Data Cogn. Comput. 2022, 6, 130. [Google Scholar] [CrossRef]
- An, L.; Zhou, W.; Ou, M.; Li, G.; Yu, C.; Wang, X. Measuring and profiling the topical influence and sentiment contagion of public event stakeholders. Int. J. Inf. Manag. 2021, 58, 102327. [Google Scholar] [CrossRef]
- Diaz Ruiz, C.; Nilsson, T. Disinformation and Echo Chambers: How Disinformation Circulates on Social Media Through Identity-Driven Controversies. J. Public Policy Mark. 2023, 42, 18–35. [Google Scholar] [CrossRef]
- Wardle, C. A New World Disorder—Our willingness to share content without thinking is exploited to spread disinformation. Sci. Am. 2019, 2019, 82–86. [Google Scholar]
- Kirkley, A.; Cantwell, G.T.; Newman, M. Belief propagation for networks with loops. Sci. Adv. 2021, 7, eabf1211. [Google Scholar] [CrossRef]
- Fernandez Peralta, A.; Kertész, J.; Iñiguez, G. Opinion dynamics in social networks: From models to data. arXiv 2023, arXiv:2201.01322. [Google Scholar] [CrossRef]
- Perra, N.; Rocha, L.E. Modelling opinion dynamics in the age of algorithmic personalisation. Sci. Rep. 2019, 9, 7261. [Google Scholar] [CrossRef]
- Nguyen, V.X.; Xiao, G.; Xu, X.J.; Wu, Q.; Xia, C.Y. Dynamics of opinion formation under majority rules on complex social networks. Sci. Rep. 2020, 10, 456. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Zhang, L.; Huang, H. Social influence analysis: Models, methods, and evaluation. Engineering 2018, 4, 40–46. [Google Scholar] [CrossRef]
- Dudkina, E.; Bin, M.; Breen, J.; Crisostomi, E.; Ferraro, P.; Kirkland, S.; Marecek, J.; Murray-Smith, R.; Parisini, T.; Stone, L.; et al. A comparison of centrality measures and their role in controlling the spread in epidemic networks. Int. J. Control 2023, 1. [Google Scholar] [CrossRef]
- Kamp, C.; Moslonka-Lefebvre, M.; Alizon, S. Epidemic spread on weighted networks. PLoS Comput. Biol. 2013, 9, e1003352. [Google Scholar] [CrossRef]
- Feng, M.; Li, X.; Li, Y.; Li, Q. The impact of nodes of information dissemination on epidemic spreading in dynamic multiplex networks. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 043112. [Google Scholar] [CrossRef]
- Castellano, C.; Pastor-Satorras, R. Thresholds for epidemic spreading in networks. Phys. Rev. Lett. 2010, 105, 218701. [Google Scholar] [CrossRef]
- Kuikka, V. Modelling epidemic spreading in structured organisations. Phys. A Stat. Mech. Its Appl. 2022, 592, 126875. [Google Scholar] [CrossRef]
- Romero, D.M.; Meeder, B.; Kleinberg, J. Differences in the mechanics of information diffusion across topics: Idioms, political hashtags, and complex contagion on twitter. In Proceedings of the 20th International Conference on World Wide Web, WWW’11, Hyderabad, India, 28 March–1 April 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 695–704. [Google Scholar] [CrossRef]
- Hamzehei, A.; Jiang, S.; Koutra, D.; Wong, R.; Chen, F. Topic-based social influence measurement for social networks. Australas. J. Inf. Syst. 2017, 21. [Google Scholar] [CrossRef]
- Guilbeault, D.; Becker, J.; Centola, D. Complex Contagions: A Decade in Review. In Complex Spreading Phenomena in Social Systems: Influence and Contagion in Real-World Social Networks; Lehmann, S., Ahn, Y.Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–25. [Google Scholar] [CrossRef]
- Ghasemiesfeh, G.; Ebrahimi, R.; Gao, J. Complex Contagion and the Weakness of Long Ties in Social Networks: Revisited. In Proceedings of the Fourteenth ACM Conference on Electronic Commerce, EC’13, Philadelphia, PA, USA, 16–20 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 507–524. [Google Scholar] [CrossRef]
- Centola, D.; Macy, M. Complex contagions and the weakness of long ties. Am. J. Sociol. 2007, 113, 702–734. [Google Scholar] [CrossRef]
- Lambiotte, R.; Rosvall, M.; Scholtes, I. From networks to optimal higher-order models of complex systems. Nat. Phys. 2019, 15, 313–320. [Google Scholar] [CrossRef]
- Zhang, Y.; Lucas, M.; Battiston, F. Higher-order interactions shape collective dynamics differently in hypergraphs and simplicial complexes. Nat. Commun. 2023, 14, 1605. [Google Scholar] [CrossRef] [PubMed]
- Bick, C.; Goodfellow, M.; Laing, C.R.; Martens, E.A. Understanding the dynamics of biological and neural oscillator networks through exact mean-field reductions: A review. J. Math. Neurosci. 2020, 10, 9. [Google Scholar] [CrossRef] [PubMed]
- Min, B.; San Miguel, M. Competing contagion processes: Complex contagion triggered by simple contagion. Sci. Rep. 2018, 8, 10422. [Google Scholar] [CrossRef] [PubMed]
- Flache, A.; Mäs, M.; Feliciani, T.; Chattoe-Brown, E.; Deffuant, G.; Huet, S.; Lorenz, J. Models of social influence: Towards the next frontiers. J. Artif. Soc. Soc. Simul. 2017, 20. [Google Scholar] [CrossRef]
- Kozitsin, I.V. A general framework to link theory and empirics in opinion formation models. Sci. Rep. 2022, 12, 5543. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.P.; Halgin, D.S. On network theory. Organ. Sci. 2011, 22, 1168–1181. [Google Scholar] [CrossRef]
- Gómez, S. Centrality in Networks: Finding the Most Important Nodes. Bus. Consum. Anal. New Ideas 2019, 401–433. [Google Scholar] [CrossRef]
- Landherr, A.; Friedl, B.; Heidemann, J. A Critical Review of Centrality Measures in Social Networks. Bus. Inf. Syst. Eng. 2010, 2, 371–385. [Google Scholar] [CrossRef]
- Ronqui, J.R.F.; Travieso, G. Analyzing complex networks through correlations in centrality measurements. J. Stat. Mech. Theory Exp. 2015, 2015, P05030. [Google Scholar] [CrossRef]
- Lawyer, G. Understanding the influence of all nodes in a network. Sci. Rep. 2015, 5, 8665. [Google Scholar] [CrossRef]
- ÅžimÅŸek, A. Lexical sorting centrality to distinguish spreading abilities of nodes in complex networks under the Susceptible-Infectious-Recovered (SIR) model. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 4810–4820. [Google Scholar] [CrossRef]
- Zhu, X.; Huang, J. SpreadRank: A Novel Approach for Identifying Influential Spreaders in Complex Networks. Entropy 2023, 25, 637. [Google Scholar] [CrossRef] [PubMed]
- Kuikka, V. Influence spreading model used to analyse social networks and detect sub-communities. Comput. Soc. Netw. 2018, 5, 12–15. [Google Scholar] [CrossRef] [PubMed]
- Kuikka, V. Modelling community structure and temporal spreading on complex networks. Comput. Soc. Netw. 2021, 8, 13. [Google Scholar] [CrossRef]
- Kuikka, V.; Aalto, H.; Ijäs, M.; Kaski, K.K. Efficiency of algorithms for computing influence and information spreading on social networks. Algorithms 2022, 15, 262. [Google Scholar] [CrossRef]
- Kuikka, V.; Pham, M.A.A. Models of influence spreading on social networks. In Proceedings of the Complex Networks & Their Applications X; Benito, R.M., Cherifi, C., Cherifi, H., Moro, E., Rocha, L.M., Sales-Pardo, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 112–123. [Google Scholar] [CrossRef]
- Almiala, I.; Kuikka, V. Similarity of epidemic spreading and information network connectivity mechanisms demonstrated by analysis of two probabilistic models. AIMS Biophys. 2023, 10, 173–183. [Google Scholar] [CrossRef]
- Kuikka, V. Modelling Influence Spreading on Complex Networks. Ph.D. Thesis, School of Science, Aalto University, Espoo, Finland, 2022. [Google Scholar]
- Sun, Y.; Ma, L.; Zeng, A.; Wang, W.X. Spreading to localized targets in complex networks. Sci. Rep. 2016, 6, 38865. [Google Scholar] [CrossRef]
- Ijäs, M.; Levijoki, J.; Kuikka, V. Scalable Algorithm for Computing Influence Spreading Probabilities in Social Networks. In Proceedings of the 5th European Conference on Social Media, Limerick, Irland, 21–22 June 2018. [Google Scholar]
- Kuikka, V.; Monsivais, D.; Kaski, K.K. Influence spreading model in analysing ego-centric social networks. Phys. A Stat. Mech. Its Appl. 2022, 588, 126524. [Google Scholar] [CrossRef]
- Van de Bunt, G. Friends by Choice. An Actor-Oriented Statistical Network Model for Friendship Networks through Time. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 1999. [Google Scholar]
- Leskovec, J.; Krevl, A. SNAP Datasets: Stanford Large Network Dataset Collection. 2014. Available online: http://snap.stanford.edu/data (accessed on 1 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).