Crack Detection in an Aluminium Oxide Grinding Wheel by Impact Hammer Tests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Grinding Wheel Cracking
2.3. Ring Testing of Wheel
2.4. Impact Hammer Test Setup
2.5. Signal Processing
2.5.1. Displacement of the Wheel
2.5.2. Natural Frequency of the Grinding Wheel
3. Result
3.1. Ring Testing
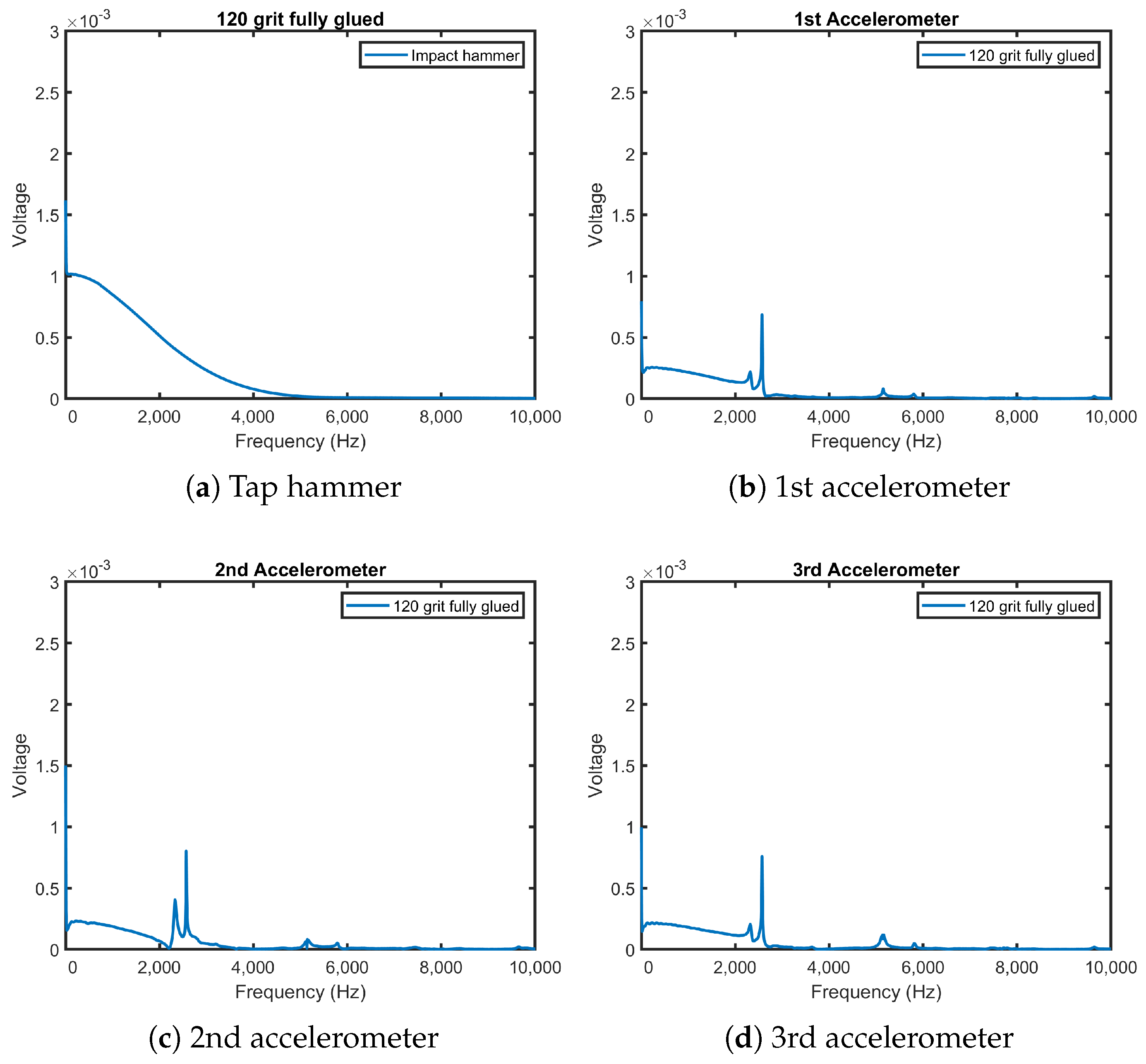
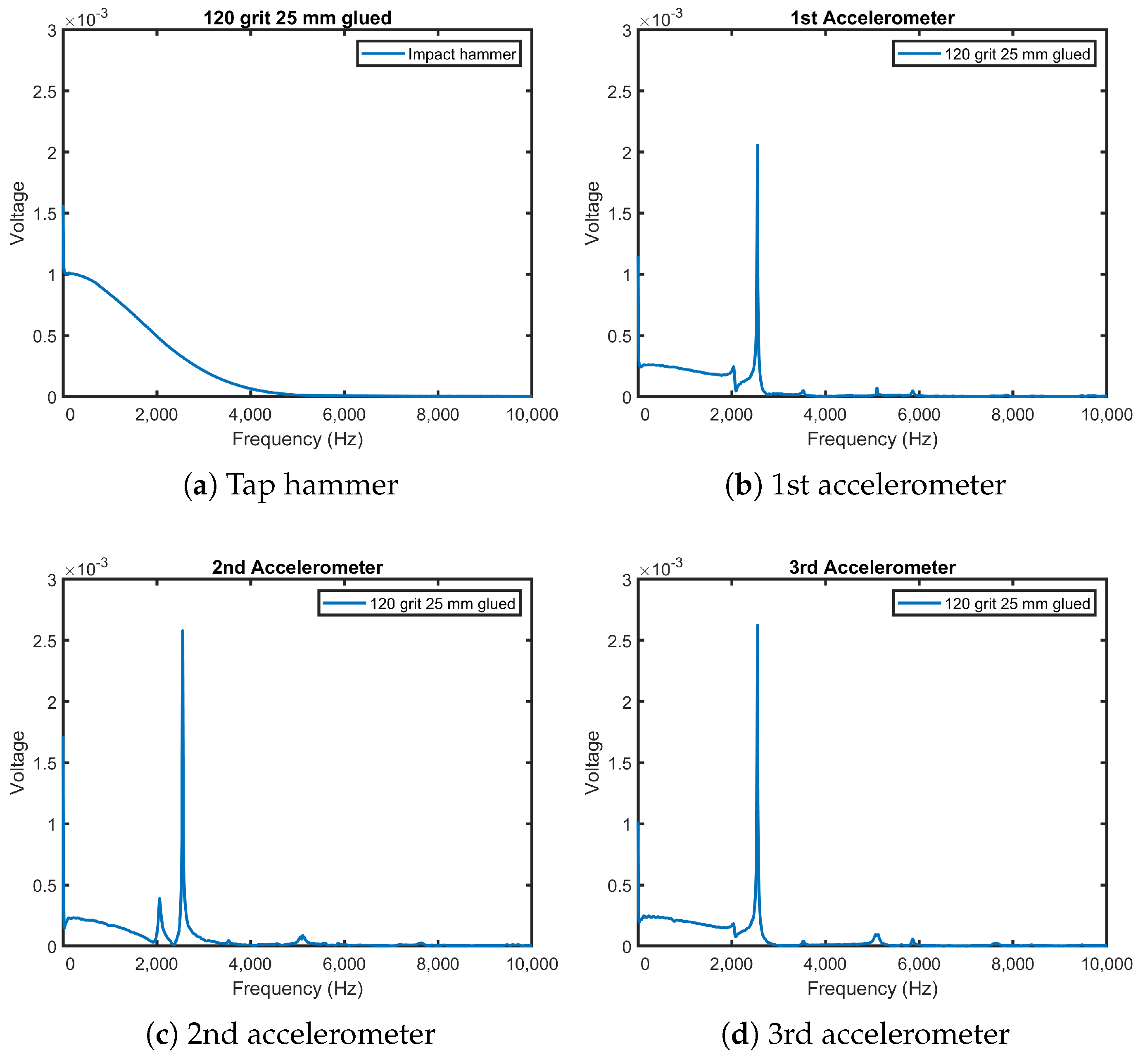
3.2. Impact Hammer Test
4. Conclusions
- Audible ring testing, using a screwdriver handle, did not indicate a distinguishable sound difference between undamaged grinding wheels and grinding wheels that had been broken and glued back together. In future studies, the acoustic emission method can be used to scientifically quantify the possible difference in sound signals between undamaged, damaged, and repaired wheels.
- Impact hammer tests of the undamaged 60- and 120-grit wheels showed that they had less displacement than repaired wheels. The average displacement of repaired wheel increased by more than fifty percent compared to undamaged wheel. It was also observed that the fully glued wheel had less deflection than one that was partially repaired. Moreover, the undamaged wheels had positive displacements, whereas the repaired wheels had negative displacements.
- The impact hammer test, using a tap hammer with accelerometers, can be used to detect repaired cracks in a bonded grinding wheel as the repaired cracks manifest as a drop in the natural vibration frequency of the wheel. This was evident by the 200 Hz drop in the detected natural frequency of the repaired wheel when compared to the undamaged wheel.
- The impact hammer test can be used to distinguish different grit sizes or wheel hardness of grinding wheels as they have different natural frequencies. This phenomenon was observed both in the natural frequency and displacement of the undamaged wheel. A future study could examine in more detail how tap testing can be used to identify different grit sizes or wheel bonding materials.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stephenson, D.A.; Agapiou, J.S. Metal Cutting Theory and Practice, 3rd ed.; CRC Press: New York, NY, USA, 2019; pp. 255–260. [Google Scholar]
- Oberg, E. Machinery’s Handbook: A Reference Book for the Mechanical Engineer, Designer, Manufacturing Engineer, Draftsman, Toolmaker, and Machinist, 29th ed.; Industrial Press: New York, NY, USA, 2012; pp. 1246–1248. [Google Scholar]
- 1926.303; Abrasive Wheels and Tools. Safety and Health Regulations for Construction. Occupational Safety & Health Administration (OSHA). U.S. Department of Labor: Washington DC, USA, 1926.
- Avitabile, P. Modal Testing: A Practitioner’s Guide, 1st ed.; Wiley: Hoboken, NJ, USA, 2018; pp. 6–89. [Google Scholar]
- Lee, C.S.; Kim, J.Y.; Kang, J. Development of the Natural Frequency Analysis System to Examine the Defects of Metal Parts. J. Sens. Sci. Technol. 2015, 24, 169–174. [Google Scholar] [CrossRef]
- Muhsin, J.J.; Salah, N.A.; Salah, K.M. Dynamic analysis of a rotating stepped shaft with and without defects. IOP Conf. Ser. Mater. Sci. Eng. 2020, 671, 012004. [Google Scholar]
- Tandon, K.N.; Begin, J. A study of variation in the natural frequency of steel castings containing porosity and inclusions. Appl. Acoust. 1990, 29, 219–227. [Google Scholar] [CrossRef]
- Kumar, N.M.S.; Kerur, M.R.H.; Khan, N.; Shashank, T.N. Vibration analysis of healthy and faulty gear of parallel shaft drive system. AIP Conf. Proc. 2022, 2463, 020055. [Google Scholar]
- Husain, M.A.; Al-shammari, M.A. Effect of Cracks on the Natural Frequency of Cylindrical Shell Structures. Eng. Technol. J. 2020, 38, 1808–1817. [Google Scholar] [CrossRef]
- Vader, S.S.; Raikar, V.A. Crack detection in composite cantilever beam by vibration analysis and numerical method. Int. Res. J. Eng. Technol. 2017, 4, 1776–1784. [Google Scholar]
- Capozucca, R. Vibration of CFRP cantilever beam with damage. Compos. Struct. 2014, 116, 211–222. [Google Scholar] [CrossRef]
- Wang, R.-J.; Shang, D.-G.; Li, L.-S.; Li, C.-S. Fatigue damage model based on the natural frequency changes for spot-welded joints. Int. J. Fatigue 2008, 30, 1047–1055. [Google Scholar] [CrossRef]
- Fiks, W.; Zora, A. Grinding wheels defects detection using natural vibration analysis. Diagnostyka 2009, 2, 50. [Google Scholar]
- Introduction to Shock. Vibration Response Spectra. Available online: https://endaq.com/pages/introduction-to-shock-vibration-response-spectra (accessed on 8 January 2022).
- Thong, Y.K.; Woolfson, M.S.; Crowe, J.A. Numerical double integration of acceleration measurements in noise. Measurement 2004, 36, 73–92. [Google Scholar] [CrossRef]
- Nussbaumer, H.J. The Fast Fourier Transform. In Fast Fourier Transform and Convolution Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 8–111. [Google Scholar]
- Montalvao, D. A review of vibration-based structural health monitoring with special emphasis on composite materials. Shock Vib. Dig. 2006, 38, 295–324. [Google Scholar] [CrossRef]
















| Outer diameter (mm) | 203.2 | 203.2 |
| Inner diameter (mm) | 25 | 25 |
| Grade | Medium | Fine |
| Abrasive grit size (line/25 mm) | 60 | 120 |
| Hardness | M | K |
| Thickness (mm) | 25 | 25 |
| Abrasive type | Brown aluminium oxide | White aluminum oxide |
| Porosity (structure) | 5 | 5 |
| Bond type | Vitrified | Vitrified |
| Absolute Maximum Displacement (mm) | |||||
|---|---|---|---|---|---|
| New 60-grit wheel | Accelerometers | Average | STDV | ||
| 1 | 2 | 3 | 0.0388 | 0.0115 | |
| 0.0445 | 0.0324 | 0.0396 | |||
| Fully glued 60-grit wheel | Accelerometers | Average | STDV | ||
| 1 | 2 | 3 | 0.0599 | 0.0140 | |
| 0.0718 | 0.0547 | 0.0532 | |||
| 25 mm glued 60-grit wheel | Accelerometers | Average | STDV | ||
| 1 | 2 | 3 | 0.0635 | 0.0145 | |
| 0.0752 | 0.0617 | 0.0536 | |||
| Absolute Maximum Displacement (mm) | |||||
|---|---|---|---|---|---|
| New 120-grit wheel | Accelerometer | Average | STDV | ||
| 1 | 2 | 3 | 0.0235 | 0.0143 | |
| 0.0292 | 0.0250 | 0.0164 | |||
| Fully glued 120-grit wheel | Accelerometer | Average | STDV | ||
| 1 | 2 | 3 | 0.0432 | 0.0224 | |
| 0.0508 | 0.0373 | 0.0416 | |||
| 25 mm glued 120-grit wheel | Accelerometer | Average | STDV | ||
| 1 | 2 | 3 | 0.0507 | 0.020 | |
| 0.0699 | 0.0478 | 0.0345 | |||
| Grinding Wheel | Increase in Displacement Compared to Undamaged Wheel (%) |
|---|---|
| 60-grit fully glued | 54 |
| 60-grit 25 mm glue | 64 |
| 120-grit fully glued | 84 |
| 120-grit 25 mm glue | 116 |
| Grinding Wheel | Primary and Average Natural Frequency (Hz) |
|---|---|
| New 60-grit wheel | 2920 |
| Fully glued 60 grit wheel | 2720 |
| 25 mm glued 60-grit wheel | 2470 |
| Grinding Wheel | Primary and Average Natural Frequency (Hz) |
|---|---|
| New 120-grit wheel | 2770 |
| Fully glued 120-grit wheel | 2570 |
| 25 mm glued 120-grit wheel | 2550 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Turcic, D.; Danks, D.; Wern, C. Crack Detection in an Aluminium Oxide Grinding Wheel by Impact Hammer Tests. Computation 2023, 11, 47. https://doi.org/10.3390/computation11030047
Lee Y, Turcic D, Danks D, Wern C. Crack Detection in an Aluminium Oxide Grinding Wheel by Impact Hammer Tests. Computation. 2023; 11(3):47. https://doi.org/10.3390/computation11030047
Chicago/Turabian StyleLee, Yubin, David Turcic, Dan Danks, and Chien Wern. 2023. "Crack Detection in an Aluminium Oxide Grinding Wheel by Impact Hammer Tests" Computation 11, no. 3: 47. https://doi.org/10.3390/computation11030047
APA StyleLee, Y., Turcic, D., Danks, D., & Wern, C. (2023). Crack Detection in an Aluminium Oxide Grinding Wheel by Impact Hammer Tests. Computation, 11(3), 47. https://doi.org/10.3390/computation11030047






