Abstract
We present results from ab initio, self-consistent calculations of electronic, transport, and bulk properties of cubic magnesium silicide (Mg2Si). We employed a local density approximation (LDA) potential to perform the computation, following the Bagayoko, Zhao, and Williams (BZW) method, as improved by Ekuma and Franklin (BZW-EF). The BZW-EF method guarantees the attainment of the ground state as well as the avoidance of over-complete basis sets. The ground state electronic energies, total and partial densities of states, effective masses, and the bulk modulus are investigated. As per the calculated band structures, cubic Mg2Si has an indirect band gap of 0.896 eV, from Γ to X, for the room temperature experimental lattice constant of 6.338 Å. This is in reasonable agreement with the experimental value of 0.8 eV, unlike previous ab initio DFT results of 0.5 eV or less. The predicted zero temperature band gap of 0.965 eV, from Γ to X, is obtained for the computationally determined equilibrium lattice constant of 6.218 Å. The calculated value of the bulk modulus of Mg2Si is 58.58 GPa, in excellent agreement with the experimental value of 57.03 ± 2 GPa.
1. Introduction and Motivation
Magnesium silicide (Mg2Si) has a face-centered cubic (FCC) antifluorite structure [1,2] with a room temperature lattice constant of 6.338 Å [3]. The compound is of particular interest to experimentalists and theorists because it crystallizes in the antifluorite structure, with only one molecular unit per primitive cell, unlike Zinc-blende or diamond structures. Mg2Si has received much attention as a potential high-performance thermoelectric material. As a result, the electrical, optical, and thermal properties of the material have been studied [1,3,4,5,6]. Mg2Si is an alternative solar cell material, as reported by Kato et al. [7]. It is also reported by Scouler [1] to show a high absorption coefficient of 3 × 105 cm−1 at 2.5 eV. Experimental measurements on the compound show that the material has a narrow, indirect band gap. Several experimental studies of Mg2Si have been carried out through Raman scattering [8], electro-reflectance measurements [9], reflectivity spectra [10], photo-emission spectroscopy [11], infrared reflectivity spectroscopy [12], and X-ray diffraction [13] in order to determine its physical properties and related parameters.
Heller and Danielson [14] measured the resistivity and Hall coefficient of Mg2Si single crystal and reported an indirect energy gap of 0.8 eV. Winkler [15] experimentally examined the semiconducting properties of polycrystalline n-type Mg2Si. His results include an indirect band gap of 0.77 eV. An infrared absorption spectrum experiment of n-type Mg2Si single crystal, carried out by Koenig et al. [16], obtained a 0.4 eV indirect band gap. The large difference between this value and the ones above, which are in general agreement, leads us to note that long tails of absorption spectra are known to result in significant uncertainties in the determination of band gaps. The accepted experimental gaps for the material are from 0.65 eV to 0.80 eV. Table 1 shows various experimental band gaps reported for Mg2Si.

Table 1.
Experimental measurements of the band gap of Mg2Si.
Numerous theoretical studies of Mg2Si have been performed. Some of them utilized ab-initio LDA or GGA potential in first-principles calculations.
Corkill et al. [18] investigated the structural and electronic properties of Mg2Si, utilizing the ab-initio pseudopotential approach within a local density approximation (LDA) potential. They reported an indirect band gap of 0.118 eV. Premlata and Sankar [18], using ab-initio density functional theory within the generalized gradient approximation (GGA), reported an indirect band gap of 0.42 eV. The density functional theory perturbation calculations of Boulet et al. [19] found an indirect band gap of 0.21 eV, from Γ-X. Imai [20] performed calculations of electronic proprieties and densities of states of Mg2Si, using the pseudopotential method, and reported an indirect band gap of 0.28 eV.
Other previous calculations of the band gap of Mg2Si are shown in Table 2. As per the content of this table, six previous calculations with an ab-initio LDA potential have produced indirect band gaps ranging from 0.11 eV to 0.53 eV. Seven previous ab-initio GGA calculations found band gap values between 0.19 eV and 0.42 eV. The generally accepted experimental band gap of Mg2Si is approximately between 0.65 eV and 0.80 eV. The table also shows a result from DFT calculations using a hybrid functional, and one from a Green function and dressed Coulomb approximation (GWA) calculations. We do not discuss the GW result, however, given that DFT is a totally different theory than GW. As for the hybrid functional result, it agrees with experiment, even though hybrid functional calculations have no predictive capabilities, given that their results depend on the values of the parameters employed in their construction.

Table 2.
Previous calculated band gaps of Mg2Si, mostly obtained with ab initio LDA or GGA potentials.
The previous ab-initio DFT results, in Table 2, are uniformly much smaller than the accepted experimental gap. This fact is a central motivation for our work. Additionally, an accurate theoretical description of electronic and related properties of the material could lead to the exploration of novel practical applications. A support for our motivation consists of the fact that previous applications of our computational methods have provided accurate descriptions and predictions of proprieties of semiconductors.
2. Computational Method
The computational details that permit the replication of this study follow. Mg2Si crystallizes into a stable face-centered cubic (FCC) antifluorite (anti-CaF2-type cF12) structure [2] (space group: , No. 225), with the two magnesium (Mg) atoms located at ± (1/4, 1/4, 1/4), and one silicon (Si) atom located at (0, 0, 0) Wyckoff positions. In this work, we performed first-principles full-potential DFT calculations for the electronic properties of Mg2Si, using the room temperature experimental lattice constant of 6.338 Å [2]. We employed the linear combination of atomic orbitals (LCAO) formalism in this work. We utilized a computational package based on density functional theory (DFT), developed at the Ames Laboratory of the United States Department of Energy (DOE), Ames, Iowa [30,31]. The LCAO formalism was implemented following the Bagayoko, Zhao, and Williams (BZW) method [32,33,34], as enhanced by Ekuma and Franklin (BZW-EF) [35,36,37,38,39].
We employed the local density approximation (LDA) potential of Ceperley and Alder [40] as parameterized by Vosko et al. [41]. As per the BZW-EF method, our self-consistent calculations began with a small basis set that can account for all the electrons in the system under study. Hence, this selected basis set is not smaller than the minimum basis set. The radial parts of the atomic wave functions were expanded in terms of Gaussian functions. The s and p orbitals for the cation Mg1+ were described with 22 even-tempered Gaussian functions with respective minimum and maximum exponents 0.34333 and 0.40013 × 105 for the atomic potential and 0.17830 and 0.11000 × 106 for the atomic wave functions. The self-consistent calculations for Mg1+ led to the total, core, and valence charges of 11.0000, 1.9999, and 9.0000, respectively. For Si2- the s and p orbitals were also described with 22 even-tempered Gaussian functions with respective minimum and maximum Gaussian exponents of 0.22100 and 0.58500 × 106, for the atomic potential, and 0.13557 and 0.44000 × 106, for the atomic functions. These Gaussian exponents led to the convergence of the atomic calculations with the total, core, and valence charges of 16.0003, 2.0003, and 13.9999, respectively. In the self-consistent iterative calculations, a mesh of 60 k points with proper weights in the irreducible Brillouin zone was used. The convergence for a given self-consistent calculation was reached after 60 iterations, when the difference between the potentials from two consecutive iterations was less than 2.0 × 10−4 Hartree. Further, for the self-consistent calculations of the electronic band structures, we used a total of 81 k points in the Brillouin zone.
Our ab initio, self-consistent calculations with the BZW-EF method began with a small basis set which was large enough to accommodate all the electrons in Mg2Si. The first self-consistent iterations, for Calculation I, were performed with this basis set. After augmenting the basis set of Calculation I with one orbital, we carried out self-consistent Calculation II. Then, we compared the occupied energies of Calculation I and Calculation II, graphically and numerically, with the Fermi energy set to zero. This comparison revealed that some occupied energies from Calculation II were lower than their corresponding values from Calculation I. This lowering of occupied energies shows that the basis set of Calculation I was not adequate for describing the true ground state of Mg2Si. With no certainty that Calculation II produced the ground state energies, we augmented its basis set by one orbital to perform Calculation III. Again, we compared the occupied energies from Calculations II and III. We continued this process until we found three consecutive calculations that produced the same occupied energies. These three calculations are the rigorous criterion that the occupied energies have reached their absolute minima, i.e., the ground state. Our verifiable attainment of the ground state, following a generalized minimization of the energy, is required by the second DFT theorem [38]. The first of these three consecutive calculations, with the smallest basis set, is the one providing the true DFT description of the material. The basis set of this calculations is called the optimal basis set. When self-consistency is reached with the optimal basis set, the resulting charge density is that of the ground state. The lowering of eigenvalues as the size of the basis set increases stems from the Rayleigh theorem for eigenvalues [37,38,39]. A crucial point consists of the fact that basis sets that are larger than the optimal one, and that contain the optimal one, lead to the same occupied energies, the same charge density, and the same Hamiltonian upon reaching self-consistency. Due to the differences in the sizes of the basis sets, some unoccupied energies are lowered by larger basis sets while the occupied energies do not change from their values obtained with the optimal basis set. Consequently, any unoccupied eigenvalue obtained with a large basis set containing the optimal one, and that is lower than its corresponding value produced with the optimal basis set, does not belong to the spectrum of the Hamiltonian, a unique functional of the charge density [37]. We note here that the referenced lowering of some unoccupied energies, while the occupied ones are unchanged, can explain the widespread underestimation of band gaps by DFT calculations that do not perform a generalized minimization as required by DFT. In the EF enhancement of the BZW method, orbitals are added as follows: for a principal quantum number n, the p, d, and f orbitals are added, if they were occupied in the neutral system, before the spherically symmetric s orbital. This counterintuitive approach recognizes the inherent polarization of the valence electrons shared by two or more ionic sites.
3. Results
We list below, in Table 3, orbitals involved in the description of the valence states of Mg1+ and Si2- in columns two and three, respectively. A superscript of zero signifies that the concerned orbital is empty. The total number of wave functions (with the number of orbitals for Mg1+counted twice for Mg2Si), and the obtained bandgaps from Γ to X and from Γ to K, for each calculation are also listed. As per the BZW-EF method, in going from one calculation to the next, one orbital is added to the basis set of the former. We see the progressive increase in the size of the basis set from one calculation to the next.

Table 3.
This table shows the successive additions of one orbital, from a calculation to the next, in performing density functional theory (DFT) studies of cubic Mg2Si, following the BZW-EF method. We utilized a local density approximation (LDA) potential and a room temperature experimental lattice constant of 6.338 Å. The indirect bandgap of Mg2Si in its natural, stable phase (cF12) is 0.896 eV.
The generalized minimization of the occupied energies requires the described successive calculations. The calculations stopped at VIII because Calculations VI, VII, and VIII produced identical occupied energies. Figure 1, Figure 2 and Figure 3 illustrate the referenced minimization. It is clearly visible in Figure 1 that the occupied bands from Calculation III, as a whole, are lower than those from Calculation II. Figure 2 shows that the occupied energies from Calculation V, as a whole, are slightly lower than those from Calculation IV. In contrast, the occupied energies of Calculations VI and VII are identical, as seen in Figure 3. The expression “as a whole” underscores the fact that the movement (i.e., lowered or not) of individual bands is not the focus, as it is the sum of all the occupied energies that represents the energy content of the Hamiltonian.
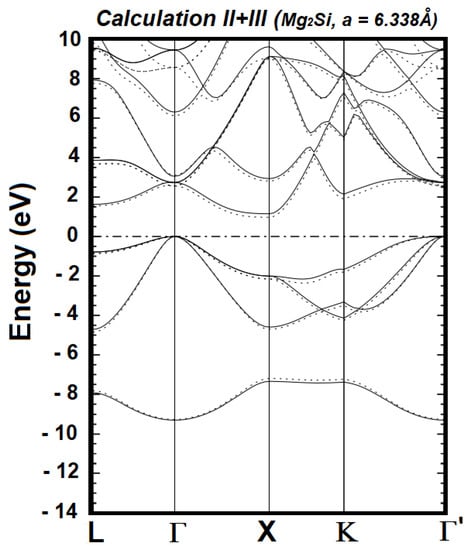
Figure 1.
Electronic energy bands of cubic Mg2Si from Calculation II (solid lines) and Calculation III (dotted lines), upon setting the Fermi level to zero; this level is indicated by the horizontal dashed-dotted line.
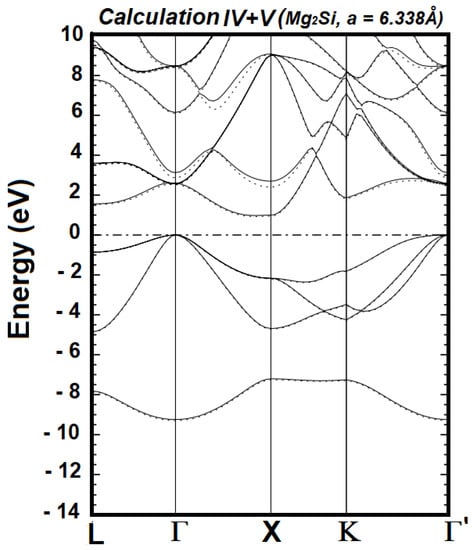
Figure 2.
Electronic energy bands of cubic Mg2Si from Calculation IV (solid lines) and Calculation V (dotted lines), upon setting the Fermi level to zero; this level is indicated by the horizontal dashed-dotted line.
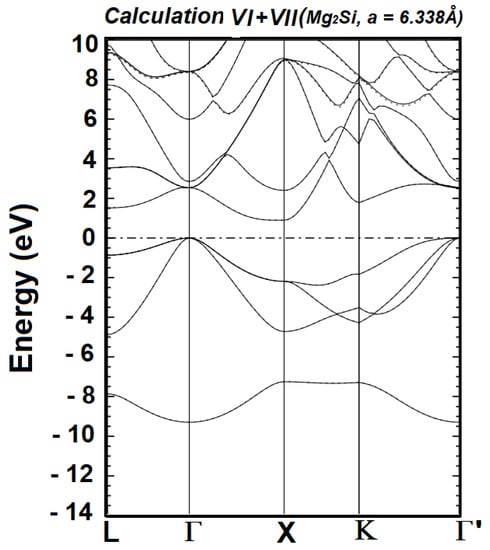
Figure 3.
Electronic band structure of cubic Mg2Si, obtained from Calculations VI (solid lines) and VII (dotted lines), for a room temperature experimental lattice constant of 6.338 Å, using the BZW-EF method. The Fermi level has been set to zero and its position is denoted by the horizontal dashed-dotted line. The calculated band gap, as obtained with the optimal basis set of Calculation VI, is from the Γ point to the X point, with a value of 0.896eV.
For all the eight calculations (I–VIII), the top of the valence band is located at the Γ point, as expected for a cubic structure, while the bottom of the conduction band is at the X point. Consequently, Mg2Si is an indirect band gap material. As illustrated above in Figure 1, Figure 2 and Figure 3, the occupied energies from Calculation VI have reached their absolute minimum values, i.e., the ground state. This assertion rests on the fact that the occupied energies from Calculation VIII are identical to those of VI and VII. The basis set for Calculation VI is the optimal basis set, i.e., the smallest basis set that leads to the ground state charge density upon reaching self-consistency. There exists a potentially infinite number of basis sets, obtained by augmenting the optimal basis set, and that lead to the ground state of the material. However, depending on the orbitals utilized to augment the optimal basis set, a given large basis set may lower some unoccupied energies from their values obtained with the optimal basis set. Such spuriously lowered, unoccupied energies no longer belong to the spectrum of the Hamiltonian, a unique functional of the ground state charge density—according to the second corollary to the first DFT theorem [37,38]. The calculated indirect band gap, obtained with the optimal basis set of Calculation VI, is 0.896 eV, from Γ to X points.
In Table 4, we list the calculated electronic energies of Mg2Si at some high-symmetry points (Γ, X, K, and L) in the Brillouin zone. The listed energies are obtained from the first-principles self-consistent calculations using the optimal basis set, i.e., in calculation VI. The listed energies in Table 4 can be used in detailed comparisons with future experimental measurements such as mid-IR infrared and X-ray spectroscopic measurements.

Table 4.
Calculated eigenvalues (in eV) at high-symmetry points for cubic Mg2Si, as obtained from Calculation VI, with the optimal basis. The room temperature experimental lattice constant is 6.338 Å.
Figure 4 shows the total electronic density of states (DOS) obtained from the bands produced using Calculation VI, with the optimal basis set, i.e., the basis set including the atomic orbitals 2s2 2p6 3s1 3p0 4p0 4s0 for Mg+ and 2s2 2p6 3s2 3p4 4p0 4s0 for Si2−. The embedded panel is the magnified DOS near the absorption edge, from −0.4 eV to 1.2 eV, with a 20-fold magnification. From the table of energies at high-symmetry points, the total width of the valence band is 9.295 eV. The width of the lowest laying valence band is 2.039 eV, while that of the group of upper valence bands is about 4.966 eV. Figure 5 shows the partial densities of states (pDOS) for the Mg-s and p, and Si-s and p states, respectively, derived from the ground state band structure in Figure 3. From the pDOS, it can be seen that the valence band of Mg2Si is mainly dominated by the Si-p and Mg-p states, in the vicinity of the Fermi level. The structure in the −7 eV to −9 eV is mainly from Si-s, with relatively tiny contributions from the Mg-p and s states. The group of upper valence bands is formed by a hybridization of Si-p, Mg-p, and Mg-s, with much smaller contributions from Si-s. The conduction bands, in the vicinity of the Fermi level, are mainly from a hybridization of Mg-s and p states.
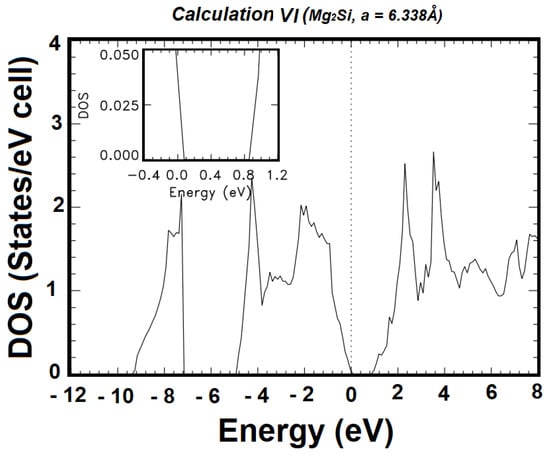
Figure 4.
Total density of states (DOS) of Mg2Si, as derived from the bands from Calculation VI, shown in Figure 3. The vertical dashed line indicates the position of the Fermi level. The insert panel is the magnified DOS near the band gap, with 20-fold magnification.
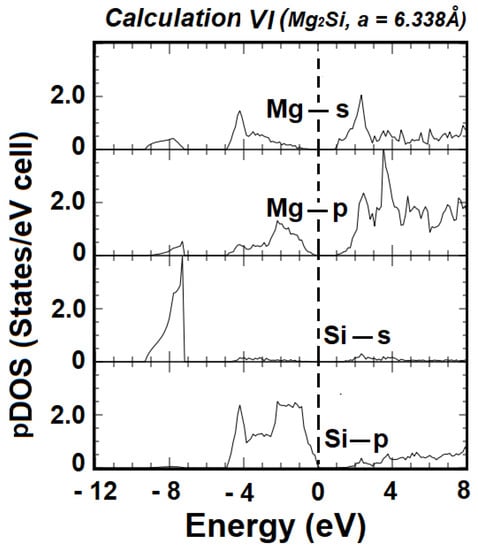
Figure 5.
Partial densities of states (pDOS) of Mg2Si, as derived from ground state band structure from Calculation VI. The vertical dashed line indicates the position of the Fermi level.
The transport properties of materials, including charge mobilities, require an accurate and detailed knowledge of effective masses. In the vicinities of the conduction band minimum and the valence band maxima at the Fermi level, the energy bands are fitted with polynomials using both the least squares approximation and Lagrange/Hermite interpolation polynomial scheme. At the extrema, the first derivatives of these polynomials with respect to the electron/hole momentum are zero. The second derivatives lead to the effective masses, in units of the electron mass (m0), as follows.
As per the content of Table 5, calculations of electron effective masses have been performed around the lowest conduction band at the X, L, and Γ points. The effective masses of the light and the two heavy holes at the top of the valence band at Γ have been calculated. These effective masses are shown in Table 5, for various directions, in units of the mass of the electron (mo). The effective masses of heavy hole 1 and heavy hole 2 are equal, except in the (Γ-K)110 direction. Their difference in this direction is due to the splitting of the bands in the (Γ-K)110 direction by the Coulomb crystal field. The calculated electron effective mass for antifluorite Mg2Si at the Γ point is 0.418 mo in the Γ to L direction, 0.211 mo in the Γ to X direction, and 0.247 mo in the G to K direction. It is anisotropic. The electron effective masses at the minimum of the conduction band at the X point are essentially anisotropic, with a longitudinal electron effective mass of 19.707 mo in the X to Γ direction, a transverse electron effective mass of 0.171 mo in the X to W direction, and a value of 0.176 mo in the X to K direction. The electron effective masses at the lowest conduction band at the L point are also essentially anisotropic, with a longitudinal electron effective mass of 3.420 mo in the L to Γ direction, a transverse electron effective mass of 0.161 mo in the L to K direction, and one of 0.173 mo in the L to W direction. The value of the heavy hole 1 effective mass is 0.838 mo in the Γ to L direction (Γ-L)111, 0.288 mo in the Γ to X direction (Γ-X)100, and 0.516 mo in the Γ to K direction (Γ-K)110. The heavy hole 2 effective mass in the (Γ-K)110 direction is 0.327 mo. The effective masses of the light hole are 0.106 mo in the (Γ-L)111 direction, 0.183 mo in the (Γ-X)100 direction, and 0.141 mo in the (Γ-K)110 direction. We expect future experiments to corroborate our predictions in the table below. When measurements are available, our findings generally agree with them, as was the case for zb-InAs and zb-BeS [42,43] where our calculated effective masses for the electron and for the holes are in agreement with the experiment.

Table 5.
Calculated effective masses for antifluorite Mg2Si in units of free electron mass (mo). me indicates an electron effective mass at the X, Γ and, L points; mhh and mlh represent the heavy and light hole effective masses, respectively.
Figure 6 exhibits the computed total energy as a function of the lattice constant. The minimum total energy lies at a lattice constant of 6.218 Å, which is our computed equilibrium lattice constant at zero Kelvin. The range of the lattice constant in which our total energy values were obtained is 6.10 Å to 6.38 Å. Our calculation of the bulk modulus first entailed a least squares fitting of the total energy curve in the vicinity of its minimum. The bulk modulus is obtained from the second derivative of this fit at the equilibrium lattice constant, i.e., B = V d2E/dV2. We found 58.58 GPa. This value is in agreement with the experimental finding [44] of 57.03 ± 2 GPa, while it is a little smaller than the theoretical finding of Corkill and Cohen [17] of 59.2 GPa.
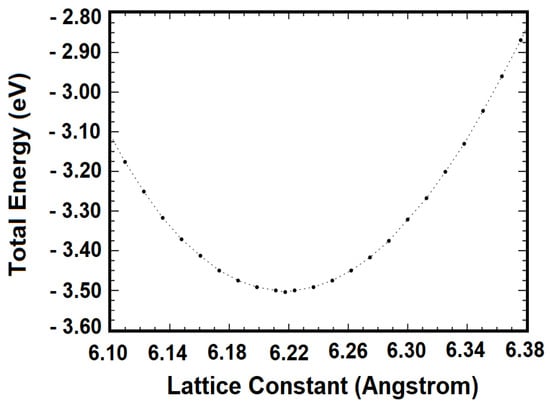
Figure 6.
The total energy versus the lattice constant for the cubic Mg2Si, obtained from calculations employing the optimal basis set at various lattice constants.
As noted above, the minimum of the total energy curve is at 6.218 Å, which is the predicted equilibrium lattice constant. With this lattice constant, we obtained 0.965 eV as the zero-temperature band gap of Mg2Si.
4. Discussion
Below, we compare our findings to those of previous density functional theory calculations. Given the lack of predictive capability of calculations with ad hoc potentials, as the results vary with the parameters employed in the construction of these potentials, we focus below on ab-initio DFT calculations with local density approximation (LDA) or generalized gradient approximation (GGA) potentials. The Green function and dressed Coulomb approximation (GWA) is not a DFT theory. For this reason, we do not compare our LDA results to GWA findings.
The six ab-initio LDA calculations in Table 1 led to band gaps between 0.118 eV and 0.53 eV. The seven ab-initio GGA computations produced gaps between 0.19 eV and 0.42 eV. Clearly, these previous ab-initio DFT calculations seriously underestimated the measured band gap around 0.8 eV. To the best of our knowledge, these calculations employed a single basis set to perform self-consistency iterations to arrive at a stationary state assumed to be the ground state. As amply discussed by Bagayoko [38,39], a stationary state, obtained with a single basis set, is one among an infinite number of such states. Hence, the chances for it be the ground state are practically zero. In contrast to these previous calculations, our DFT work entailed successive calculations with progressively augmented basis sets, up to three consecutive calculations that produce the same occupied energies. By virtue of the Rayleigh theorem for eigenvalues [37,38,39], as the size of the basis set is increased, a given eigenvalue is either decreased or stays the same if it has reached its absolute minimum. While the occupied energies from the three calculations are identical, there are differences between their unoccupied energies. It is the first of the three calculations that produces the DFT results for the material. The reasonable agreement between our calculated band gap of 0.896 eV and the experimental finding of 0.8 eV stems from the fact that our calculations employed the true ground state charge density, as required by the second DFT theorem. We recall that the optimal basis set, upon reaching self-consistency, produces the ground state charge density. Larger basis sets that contain the optimal basis set lead to the same occupied energies as the optimal basis set; they also lower some unoccupied energies from their values obtained with the optimal basis set. Needless to add, a lowering of the minimum of the conduction band, while the occupied bands do not change, can explain the widespread underestimation of band gaps by DFT calculations that do not perform the generalized minimization of the energy as described here. This process not only leads to the ground state, in a verifiable manner, but also avoids over-complete basis sets that can lead to the noted spurious lowering of some unoccupied energies.
In general, a lowering of unoccupied bands results in a decrease in their degree of flatness. A decrease in the degree of flatness around the conduction band minimum clearly leads to a decrease in the electron effective masses. Hence, the above lowering of unoccupied energies is a plausible explanation of the underestimation of the electron effective masses in a way that is linked to the underestimation of the band gap.
5. Conclusions
In summary, first-principles self-consistent calculations of electronic, transport, and bulk properties of cubic antifluorite magnesium silicide (Mg2Si), using a local density approximation (LDA) potential and the Bagayoko, Zhao, and Williams (BZW) method, as enhanced by Ekuma and Franklin (BZW-EF), have been performed. The BZW-EF method strictly adheres to the necessary conditions of validity of DFT calculations; it guarantees the verifiable attainment of the ground state and the avoidance of over-complete basis sets that can spuriously lower unoccupied energies. The calculated band structures show that Mg2Si has an indirect bandgap of 0.896 eV, from the Γ to X point. This value is in reasonable agreement with experimental data and is different from previously reported DFT results, which are uniformly smaller than the band gap of cubic Mg2Si. The calculated DOS and effective masses of the hole and electron will hopefully be confirmed by future experimental investigations on Mg2Si, as has been the case for several predictions of our group [38,39]. Our calculated bulk modulus value of 58.58 GPa is in excellent agreement with the experimentally determined value of 57.03 ± 2 GPa. The results from our computations will aid in the future design of optoelectronic devices.
Author Contributions
Conceptualization, D.B., A.D. and A.C.B.; methodology, D.B.; software, D.B.; validation, B.A.A., D.B. and Y.I.D. and Y.M.; formal analysis, Y.M. and D.B.; investigation, A.D., Y.I.D., B.A.A. and A.C.B.; writing—original draft preparation, A.D.; writing—review and editing, B.A.A., Y.M. and D.B.; supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.”
Funding
This research work was funded, in part, by the Cheikh Anta Diop University (UCAD) in Dakar, Senegal, the US Fulbright Fellowship Program, the US Department of Energy (DOE), National Nuclear Security Administration (NNSA) (Award No. DE-NA0003679), the National Science Foundation (NSF, Award no, 1503226DE), LaSPACE, and LONI-SUBR.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scouler, W.J. Optical Properties of Mg2Si, Mg2Ge, and Mg2Sn from 0.6 to 11.0 eV at 77 °K. Phys. Rev. 1969, 178, 1353–1357. [Google Scholar] [CrossRef]
- Borisenko, V.E. Semi-conducting Silicides. Springer Series in Material Science; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Morris, R.G.; Redin, R.D.; Danielson, G.C. Semiconducting Properties ofMg2Si Single Crystals. Phys. Rev. 1957, 1957, 1909–1915. [Google Scholar] [CrossRef]
- Zaitsev, V.K.; Fedorov, M.I.; Gurieva, E.A.; Eremin, I.S.; Konstantinov, P.P.; Samunin, A.Y.; Vedernikov, M.V. Highly effectiveMg2Si1−xSnxthermoelectrics. Phys. Rev. B 2006, 74, 045207. [Google Scholar] [CrossRef]
- Stella, A.; Brothers, A.D.; Hopkins, R.H.; Lynch, D.W. Pressure Coefficient of the Band Gap in Mg2Si, Mg2Ge, and Mg2Sn. Phys. Status Solidi (b) 1967, 23, 697–702. [Google Scholar] [CrossRef]
- Satyala, N.; Vashaee, D. Modeling of Thermoelectric Properties of Magnesium Silicide (Mg2Si). J. Electron. Mater. 2012, 41, 1785–1791. [Google Scholar] [CrossRef]
- Kato, T.; Sago, Y.; Fujiwara, H. Optoelectronic properties of Mg2Si semiconducting layers with high absorption coefficients. J. Appl. Phys. 2011, 110, 063723. [Google Scholar] [CrossRef]
- Buchenauer, C.J.; Cardona, M. Raman Scattering in Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. B 1971, 3, 2504–2507. [Google Scholar] [CrossRef]
- Vazquez, F.; Forman, R.A.; Cardona, M. Electroreflectance Measurements on Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. 1968, 176, 905–908. [Google Scholar] [CrossRef]
- Sobolev, V.V. Reflectivity spectra and energy band structure of Mg2X crystals. Phys. Status Solidi (b) 1972, 209, K209–K214. [Google Scholar] [CrossRef]
- Tejeda, J.; Cardona, M. Valence bands of theMg2X (X = Si, Ge, Sn ssemiconducting compounds. Phys. Rev. B 1976, 14, 2559–2568. [Google Scholar] [CrossRef]
- McWilliams, D.; Lynch, D.W. Infrared Reflectivities of Magnesium Silicide, Germanide, and Stannide. Phys. Rev. 1963, 130, 2248–2252. [Google Scholar] [CrossRef]
- Panke, D.; Wölfel, E. Die Verteilung der Valenzelektronen im Mg2Si. Z. Für Krist.-Cryst. Mater. 1969, 129, 28. [Google Scholar] [CrossRef]
- Heller, M.; Danielson, G. Seebeck effect in Mg2Si single crystals. J. Phys. Chem. Solids 1962, 23, 601–610. [Google Scholar] [CrossRef]
- Busch, G.; Winkler, U. Elektrische Eigenschaften Der Intermetallischen Verbindungen Mg2Si, Mg2Ge, Mg2Sn Und Mg2Pb. Physica 1954, 20, 1067–1072. [Google Scholar] [CrossRef]
- Koenig, P.; Lynch, D.W.; Danielson, G.C. Infrared absorption in magnesium silicide and magnesium germanide. J. Phys. Chem. Solids 1961, 20, 122–126. [Google Scholar] [CrossRef]
- Pandit, P.; Sanyal, S.P. First principles study of electronic, elastic and lattice dynamical properties of Mg2X (X = Si, Ge and Sn) compounds. Indian J. Pure Appl. Phys. 2011, 49, 692–697. [Google Scholar]
- Corkill, J.L.; Cohen, M.L. Structural, bonding, and electronic properties of IIA-IV antifluorite compounds. Phys. Rev. B 1993, 48, 17138–17144. [Google Scholar] [CrossRef]
- Boulet, P.; Verstraete, M.; Crocombette, J.-P.; Briki, M.; Record, M.-C. Electronic properties of the Mg2Si thermoelectric material investigated by linear-response density-functional theory. Comput. Mater. Sci. 2011, 50, 847–851. [Google Scholar] [CrossRef]
- Imai, Y.; Watanabe, A.; Mukaida, M. Electronic structures of semiconducting alkaline-earth metal silicides. J. Alloy. Compd. 2003, 358, 257–263. [Google Scholar] [CrossRef]
- Arnaud, B.; Alouani, M. Electron-hole excitations inMg2SiandMg2Gecompounds. Phys. Rev. B 2001, 64, 0332021–0332024. [Google Scholar] [CrossRef]
- Mars, K.; Ihou-Mouko, H.; Pont, G.; Tobola, J.; Scherrer, H. Thermoelectric Properties and Electronic Structure of Bi- and Ag-Doped Mg2Si1−x Ge x Compounds. J. Electron. Mater. 2009, 38, 1360–1364. [Google Scholar] [CrossRef]
- Au-Yang, M.Y.; Cohen, M.L. Electronic Structure and Optical Properties of Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. 1969, 178, 1358–1364. [Google Scholar] [CrossRef]
- Aymerich, F.; Mula, G. Pseudopotential band structures of Mg2Si, Mg2Ge, Mg2Sn, and of the solid solution Mg2(Ge, Sn). Phys. Status Solidi (b) 1970, 42, 697–704. [Google Scholar] [CrossRef]
- Balout, H.; Boulet, P.; Record, M.-C. Electronic and transport properties of Mg2Si under isotropic strains. Intermetallics 2014, 50, 8–13. [Google Scholar] [CrossRef]
- Krivosheeva, A.V.; Kholod, A.N.; Shaposhnikov, V.L.; Krivosheev, A.E.; Borisenko, V.E. Band structure of Mg2Si and Mg2Ge semiconducting compounds with a strained crystal lattice. Semiconductors 2002, 36, 496–500. [Google Scholar] [CrossRef]
- Fan, W.H.; Chen, R.X.; De Han, P.; Meng, Q.S. First-Principle Study of Electronic Structures of Y-Doped Mg2Si. Mater. Sci. Forum 2011, 689, 102–107. [Google Scholar]
- Chen, Q.; Xie, Q. First-principles calculations on the electronic structure and optical properties of Mg2Si epitaxial on Si (111). Phys. Procedia 2011, 11, 134–137. [Google Scholar] [CrossRef]
- Ryu, B.; Park, S.; Choi, E.-A.; de Boor, J.; Ziolkowski, P.; Chung, J.; Park, S.D. Hybrid-Functional and Quasi-Particle Calculations of Band Structures of Mg2Si, Mg2Ge, and Mg2Sn. J. Korean Phys. Soc. 2019, 75, 144–152. [Google Scholar] [CrossRef]
- Feibelman, P.J.; Appelbaum, J.A.; Hamann, D.R. Electronic structure of a Ti (0001) film. Phys. Rev. B 1979, 20, 1433–1443. [Google Scholar] [CrossRef]
- Harmon, B.N.; Weber, W.; Hamann, D.R. Total-energy calculations for Si with a first-principles linear-combination-of-atomic-orbitals method. Phys. Rev. B 1982, 25, 1109–1115. [Google Scholar] [CrossRef]
- Franklin, L.; Ekuma, C.; Zhao, G.; Bagayoko, D. Density functional theory description of electronic properties of wurtzite zinc oxide. J. Phys. Chem. Solids 2013, 74, 729–736. [Google Scholar] [CrossRef]
- Bagayoko, D.; Franklin, L.; Zhao, G.L. Predictions of electronic, structural, and elastic properties of cubic InN. J. Appl. Phys. 2004, 96, 4297–4301. [Google Scholar] [CrossRef]
- Bagayoko, D.; Zhao, G.L.; Fan, J.D.; Wang, J.T. Ab initio calculations of the electronic structure and optical properties of ferroelectric tetragonal. J. Phys. Condens. Matter 1998, 10, 5645–5655. [Google Scholar] [CrossRef]
- Ekuma, C.; Franklin, L.; Zhao, G.L.; Wang, J.T.; Bagayoko, D. Local density approximation description of electronic properties of wurtzite cadmium sulfide (w-CdS). Can. J. Phys. 2011, 89, 319–324. [Google Scholar] [CrossRef]
- Ayirizia, B.A.; Malozovsky, Y.; Franklin, L.; Bhandari, U.; Bagayoko, D. Ab-Initio Self-Consistent Density Functional Theory Description of Rock-Salt Magnesium Selenide (MgSe). Mater. Sci. Appl. 2020, 11, 401–414. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding the Relativistic Generalization of Density Functional Theory (DFT) and Completing It in Practice. J. Mod. Phys. 2016, 07, 911–919. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Bagayoko, D. Comprendre La Théorie De La Fonctionnelle De La Densité Et La Completer Dans La Pratique. In Proceedings of the Malian Symposium of Applied Sciences (MSAS), Bamako, Mali, 3–8 August 2014; pp. 251–258. [Google Scholar]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Vosko, N.M.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Diakite, Y.I.; Malozovsky, Y.; Bamba, C.O.; Franklin, L.; Bagayoko, D. First Principle Calculation of Accurate Electronic and Related Properties of Zinc Blende Indium Arsenide (zb-InAs). Materials 2022, 15, 3690. [Google Scholar] [CrossRef]
- Ayirizia, B.A.; Brumfield, J.S.; Malozovsky, Y.; Bagayoko, D. Ground State Properties of the Wide Band Gap Semiconductor Beryllium Sulfide (BeS). Materials 2021, 14, 6128. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Zou, B.; Zhu, P.; Gao, C.; Li, Y.; Liu, D.; Wang, K.; Lei, W.; Cui, Q.; Zou, G. In situ X-ray observation of phase transitions in Mg2Si under high pressure. Solid State Commun. 2009, 149, 689–692. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).