On Volatility Transmission between Gold and Silver Markets: Evidence from A Long-Term Historical Period

Abstract

Several studies estimate the volatility spillover effects between gold and silver returns, but none of them used the implied volatility to evaluate the long-term relationship between these two metal markets. Our paper aims to fill this gap in the existing literature. This paper investigates the long-term volatility transmission between gold and silver; by using GARCH and VAR modelling, it finds that the volatility transmission from gold to silver is unidirectional. Volatility strategies using options can be designed to take advantage of this especially in times where the volatility transmission is not captured by the markets. Additionally, the results appear to be useful for gaining better portfolio diversification benefits. Investors, for instance, could use the results of this study for making proper investment decisions during the period of economic down-turns or inflation surges.

1. Introduction

Investigating the volatility spillover effects among different types of markets such as commodities and stocks is of crucial importance for understanding the financial distress transmission channel throughout different segmentations of the economy. The volatility informational content is essential for pricing different type of assets and for the development of risk management practices and strategies. This necessity is pronounced the last period which is characterized by extended volatility regimes on several commodities due to the energy crisis and drives many investors to precious metals that is assumed to be a safe heaven. It is astonishing to notice that the conditional volatility context accounts for the flow of information on time series and for the persistence of the volatility process, which is useful for asset pricing models, volatility transmission models, effective risk management, optimal portfolio selection and investment decisions, and volatility strategies.

There is an extensive use of gold and silver by investors either for yield enhancement, portfolio diversification, speculation, or inflation hedger. The instruments are ranging from physical form to futures, options, or swaps. In the investment process the inclusion of both metals depends on the correlation between them and the way the one affects the other not only on the directional but also on the volatility level. It is well known that both gold and silver have many commercial uses but also due to their monetary history, people still consider them as natural anti-inflationary protection (especially gold) and store of value. For gold, this is at least evident from the fact that central banks are storing gold and commercial banks weigh their gold assets as risk free. Furthermore, in periods of geopolitical and financial uncertainty, there is a tendency for the investors to resort to these precious metals (and especially gold).

Gold and silver represent a portion (even a small one) of every well-diversified portfolio due to the perceived negative correlation with other assets and the anticipation that they will serve as a hedge in case of inflation. Strategies that include gold and silver try to profit either from their price spread (using cash or futures) or by their volatility relationship by using options. The relationship between the two markets have been extensively studied and although signs of long-term relationship are found, this relationship has been found to be time and state dependent.

This paper, utilizes precious metals’ data and applies conditional volatility models (GARCH framework) during a long period, spanning from 1982 to 2021, in order to investigate the potential spillover effects of the commodities that have attracted investors interest especially during non-tranquil periods. The well-established GARCH framework for almost half a century has been preferred as a solid and easily interpreted econometric tool which offers robust results under a parsimonious scheme. Moreover, this paper aims to detect potential shocks on volatility of the precious metals along with the spillover effects between them. Notable articles exploring the volatility dynamics of precious metals and energy markets include [1,2,3].

Among these articles, Escribano and Granger [1] studied the long-term relationships of gold and silver by using cointegration techniques and although they found evidence of cointegration, they also found signs of separations. Ciner [4] found evidence that the long-term relationship between the gold and silver market has disappeared and they should be treated as separate markets and not used as a substitute in hedging strategies. Lycey and Tully [5], by studying their relationship during a period of 25 years ending in 2002, showed through the use of cointegration techniques that the long-term relationship of gold and silver is stable, although this relationship broke in 1990s.

Batten et al. [6] studied the dynamic of the relationship between gold and silver by investigating the spread of future contracts and by using the Hurst coefficient, they found out significant arbitrage possibilities between the two markets. Schweikert [7] by applying quantile cointegration found that the long-term relationship between gold and silver is state-dependent: a strong response of silver prices to gold pieces when silver prices are relatively high and a strong response of gold prices to silver pieces when gold prices are relatively high. This makes statistical arbitrage between the two markets based on a stable long-term relationship very risky. Liu and Su [8] examined the dynamic causality between the returns of gold and silver in the China market by using a rolling widow bootstrap approach and found out that gold significantly affected the solver in multiple periods between 2006 and 2017 but not vice versa. Sami [9] revisited the long-term relationship between gold and silver by using data from the Indian market from 1978 to 2019 and found robust evidence of a stable, long-term relationship between the two markets, implying the use of the one as a hedger of the other and few benefits of the inclusion of both in a portfolio for risk diversification reasons. Moreover, they find that their long-term stable relationship has not broken in India, suggesting that local factors may affect this relationship. Kayal et al. [10] showed, using extreme valued estimators and the Expected Lifetime Short measure of risk, that for medium-term investments, gold is more preferred than silver because gold is more mean reverting whereas silver is more time persistent in periods of low and high prices.

The study of the volatility and correlation dependence between the two markets gives significant insight how turbulence in one market affects the other and how investment strategies that profit from volatility should be designed. Although empirical results cannot exclude the bidirectionality of volatilities between the two markets, the unidirectional from gold to silver seems to be clearer, which the results of this paper confirm. Zhu et al. [11] studied the quantile behavior of cointegration between silver and gold by employing the quantile autoregressive distributed lag model. They found that the silver price changes are more sensitive to gold price changes, and this become stronger when the prices of silver are too high or too low. Similarly, Bouri and Jalkh [12], by using a copula-based quantile regression, studied the option-implied volatilities of gold and silver and showed extreme tail dependency in low and upper quantiles. Moreover, they found that the silver implied volatility can be used to predict the next day’s probability of gold implied volatility. They concluded that volatility spread trading can be very risky due to string tail dependency.

Finally, the leading effect of gold volatility to other markets has been recently explored. Ewing and Malik [13], by using bivariate GARCH models, found significant evidence of transmission of volatility between gold and oil markets when structural breaks in variance are ignored, implying that intermarket hedging and option trading between the two markets is possible. Mensi et al. [14], by employing DCC and DCC-GARCH, studied the volatility transmission between crude oil and four precious metals including gold and silver. They found out that the volatility transmission and the correlation between oil and the four precious metals are time varying in periods of economic uncertainty and that the inclusion of oil and precious metals in a portfolio increases the diversification benefits and reduces the downside risk. Farid et al. [15] studied the patterns of volatility connectedness across equities and commodities using high frequency data and found that gold and stocks are the two largest contributors of volatility shocks. Iqbal, Najaf, et al. [16], using a dataset comprising 12 implied volatility indices, demonstrated that the identity of transmitters and receivers of volatility shocks differ between normal and high volatility states. Yaya et al. [17] studied the returns and volatility spillovers from the bitcoin market to the gold and silver markets. Our findings show strong price persistence with bitcoin posing the highest volatility, whereas silver poses the lowest volatility persistence. Finally, Cui, Moyang, et al. [18] found that in the long run, oil and gold price volatility positively affect the gold prices, whereas the effect of silver price volatility on gold prices is negative in the long run.

As presented above, the literature is divided on the direction of volatility transmission between gold and silver. The empirical results of this paper, using long-term data, support the unidirectional (from gold to silver) volatility transmission. Moreso, the duration of the effect is the same by using either weekly or monthly data—approximately 10 months (or 40 weeks). This paves the way for designing volatility strategies that profit from volatility transmissions but are not yet captured by the market, as is seen in option markets.

2. Data

In order to explore the volatility transmission between precious metals, we recruit data from both spot and futures markets during the period from August 1982 to November 2021. Due to the use of monthly and weekly data, information contained in smaller time frames is not captured. On the other hand, high-frequency data contain increased noise which is difficult to filter out. Moreover, the volatility of the gold and silver usually included in many investment portfolios may be masked due their use as a portfolio risk diversification constituent. In this way, the volatility transmission mechanism between them may be distorted.

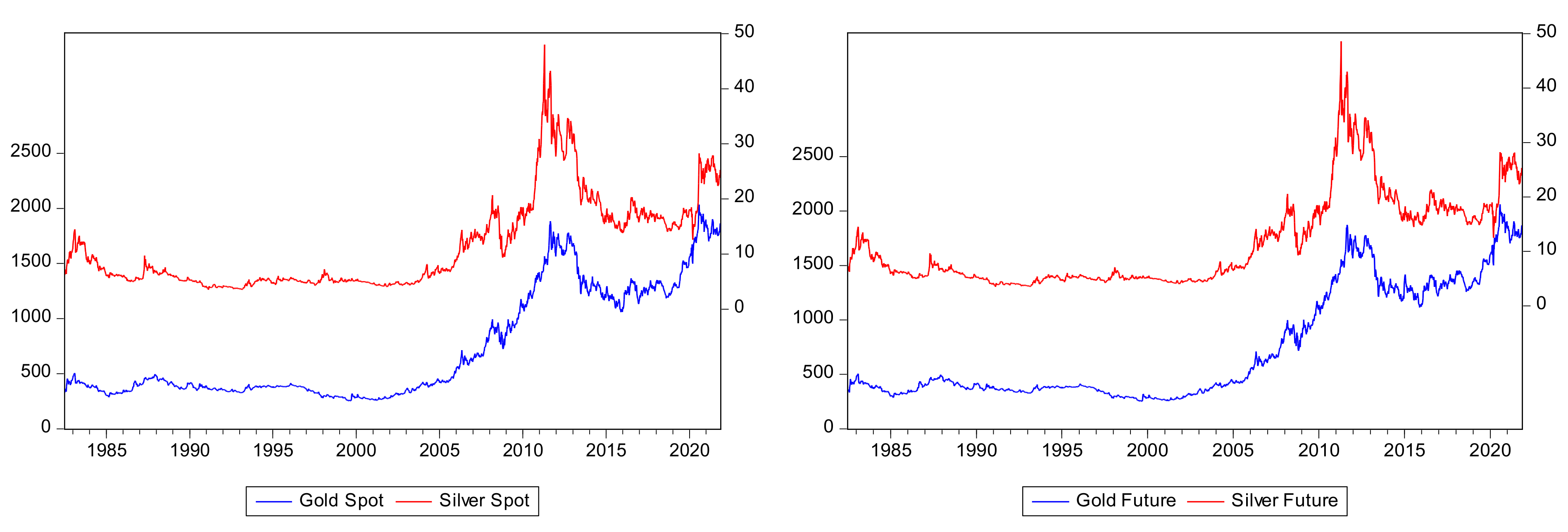
The sample size was chosen to account for many crises and shocks in markets. Period and frequency were chosen based on the fact that investors have a long-term investment horizon. Investing for the long-term can help investors to minimize their portfolio risk and at the same time enables them to enhance their returns through compounding. These two aspects provide a strong argument for continuing to hold investments over the long run. A total of 2054 weekly and 451 monthly observations have been used. Prices for gold and silver are shown in Figure 1.

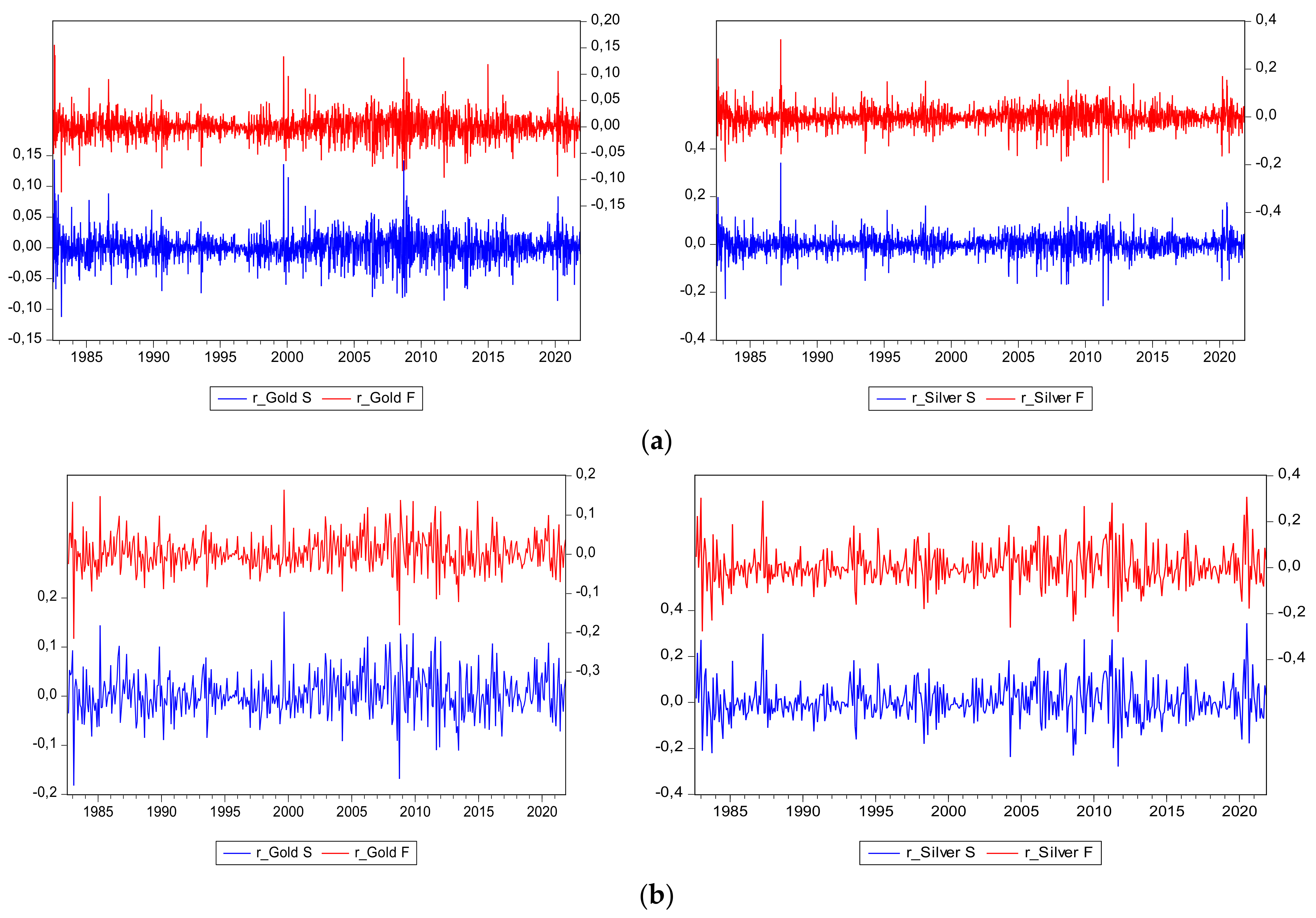
As we can see both markets show similar patterns and trends although the silver spikes seem to be more pronounced. The return in the two markets have been calculated as $\left(X_2-X_1\right)/X_1$, where $X_i$ is the price of the commodity (spot or future) in the i period.

Returns are shown in Figure 2:

As we see from Figure 2, the weekly and monthly returns for both spot and futures contract show general stationary behavior. We can also observe some volatility clustering, especially during the turmoil periods like in the 80s, 1990, 2001, 2007–2010, 2013–2015, and the COVID-19 era from 2019 onwards.

The statistics for spot and futures are shown in

Table 1. Descriptive statistics and unit root test results.

Commodity		Mean	Standard Deviation	Skewness	Kurtosis	t-Stat b
Gold Spot	Weekly	0.001084	0.022102	0.263215	7.091533	−45.21 a
	Monthly	0.004180	0.044637	0.142168	4.260140	−24.73 a
Future	Weekly	0.001073	0.022608	0.281340	7.678274	−47.01 a
	Monthly	0.004251	0.045629	0.051799	4.826097	−24.37 a
Silver Spot	Weekly	0.001465	0.039816	−0.050100	9.277886	−28.53 a
	Monthly	0.005745	0.082517	0.386634	4.438367	−18.77 a
Future	Weekly	0.001501	0.040847	−0.094558	9.055247	−29.02 a
	Monthly	0.005913	0.083809	0.294785	4.466175	−45.21 a

^a Statistical significance at 5%. ^b Unit Root Test (Augmented Dickey-Fuller).

:

According to the descriptive statistics of Table 1, there is evidence that the return is higher in monthly data implying that the holding period of one month should be preferred whereas unconditional volatility of futures market is higher than that of spot market. A similar pattern exhibits the volatility of monthly data which is higher than that of the weekly data. Additionally, the distributional form of the data is leptokurtic and positively skewed in all cases except when dealing with silver market (spot and futures) and the weekly frequency.

Tests for the presence of unit root are performed by conducting the Augmented Dickey–Fuller (ADF) unit root test assuming no linear trend in the data generation process. However, after plotting the data, we have identified that our series appear to be trended. Therefore, the tests were performed using a linear time trend and an intercept. The ADF (four lags) test statistics indicate that none of the level series are stationary processes; whereas, for the differenced series, the hypothesis of a unit root is rejected at a 5% level, suggesting that the differenced series are stationary processes. The test results are reported in Table 1.

3. Methodology and Empirical Results

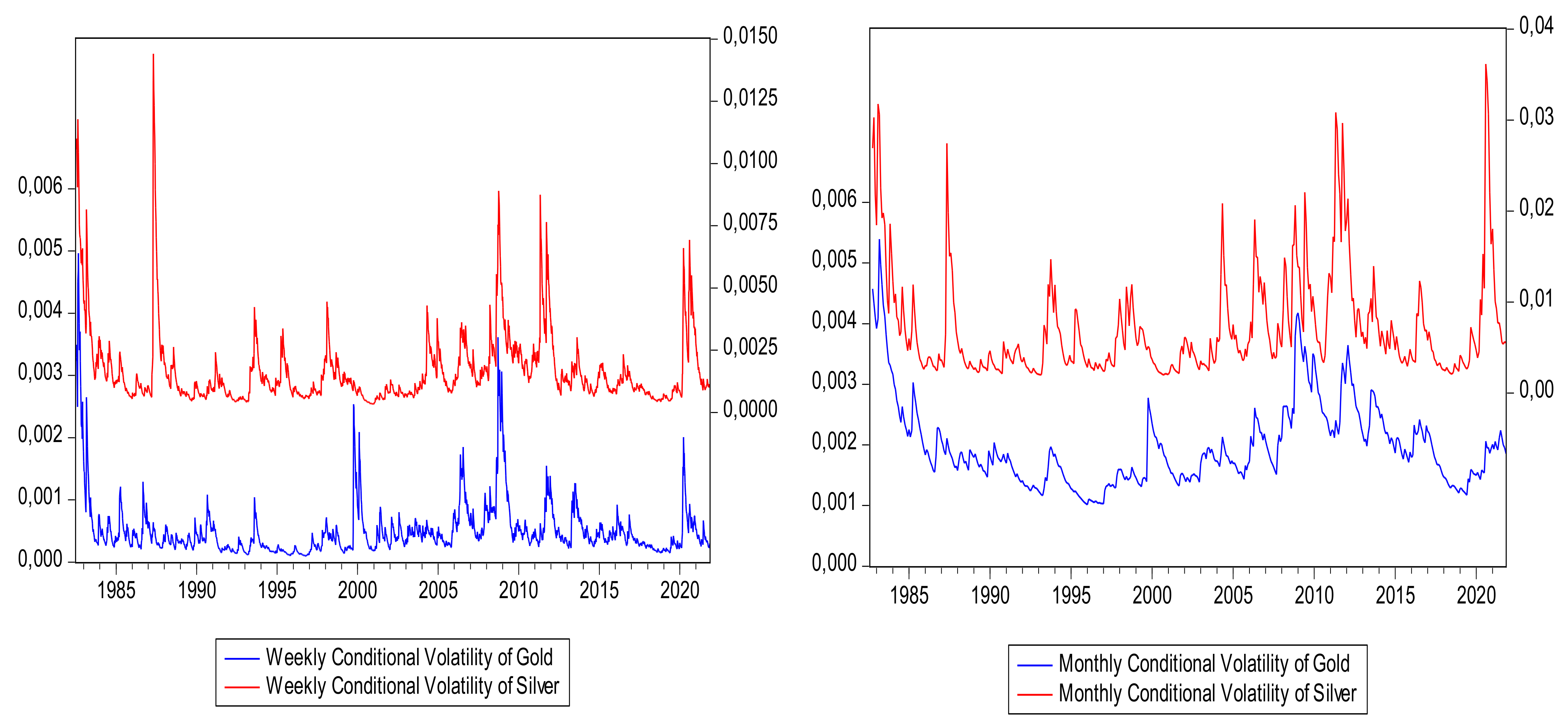
Following Bollerslev [19], the conditional volatility series are obtained by using Garch (1, 1) with innovations as t-distributed on weekly and monthly gold and silver prices. The conditional volatilities series are shown in Figure 3.

As we can see from the Figure 3, the conditional volatility of gold and silver on weekly and monthly level exhibit the same pattern of behavior, although it seems that the volatility spike of gold precedes those of the silver implying a volatility transfer mechanism between the two markets. Moreover, we can see that there does not seem to be a major long-term trend in volatility in both markets, although local volatility trends may appear that can last from two to three years.

The volatility transmission mechanism is explored via the impulse response analysis through the VAR model estimation

$$Y\left(t\right)=C+{{\displaystyle \sum }}_{i=1}^{n}A\left(i\right)Y\left(t-m\right)+v\left(t\right)$$

(1)

where Y(t) is the column vector of the conditional volatilities of gold and the conditional volatilities of silver, C is the constant component, A(i) are the coefficient matrices v(t) is the random error vector and m is the optimal lag length (under Schwartz and Hann–Quinn information criteria). v(t) is uncorrelated with the past of Y(t). The weekly and monthly results are shown in Figure 4 and Figure 5, respectively.

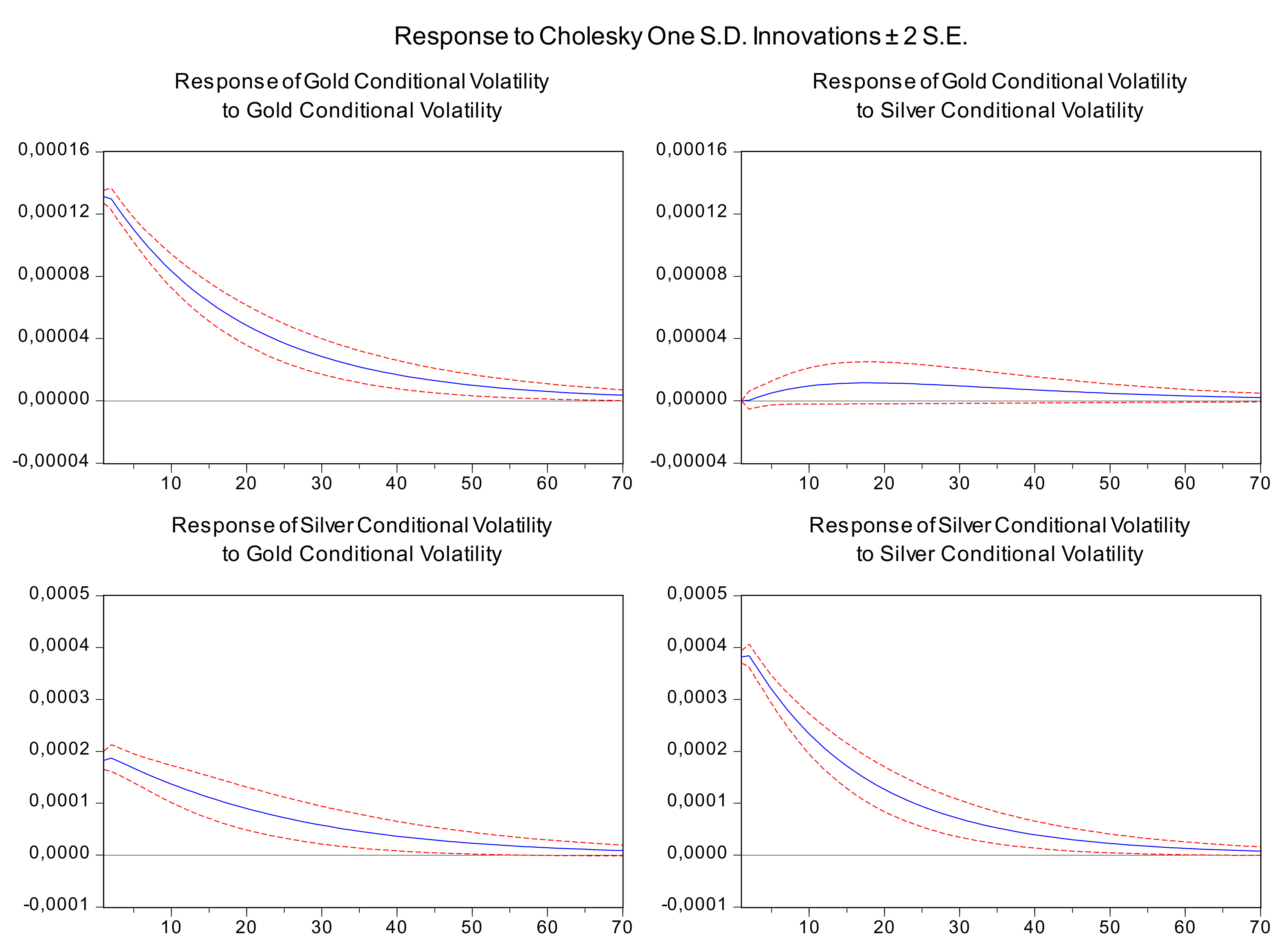
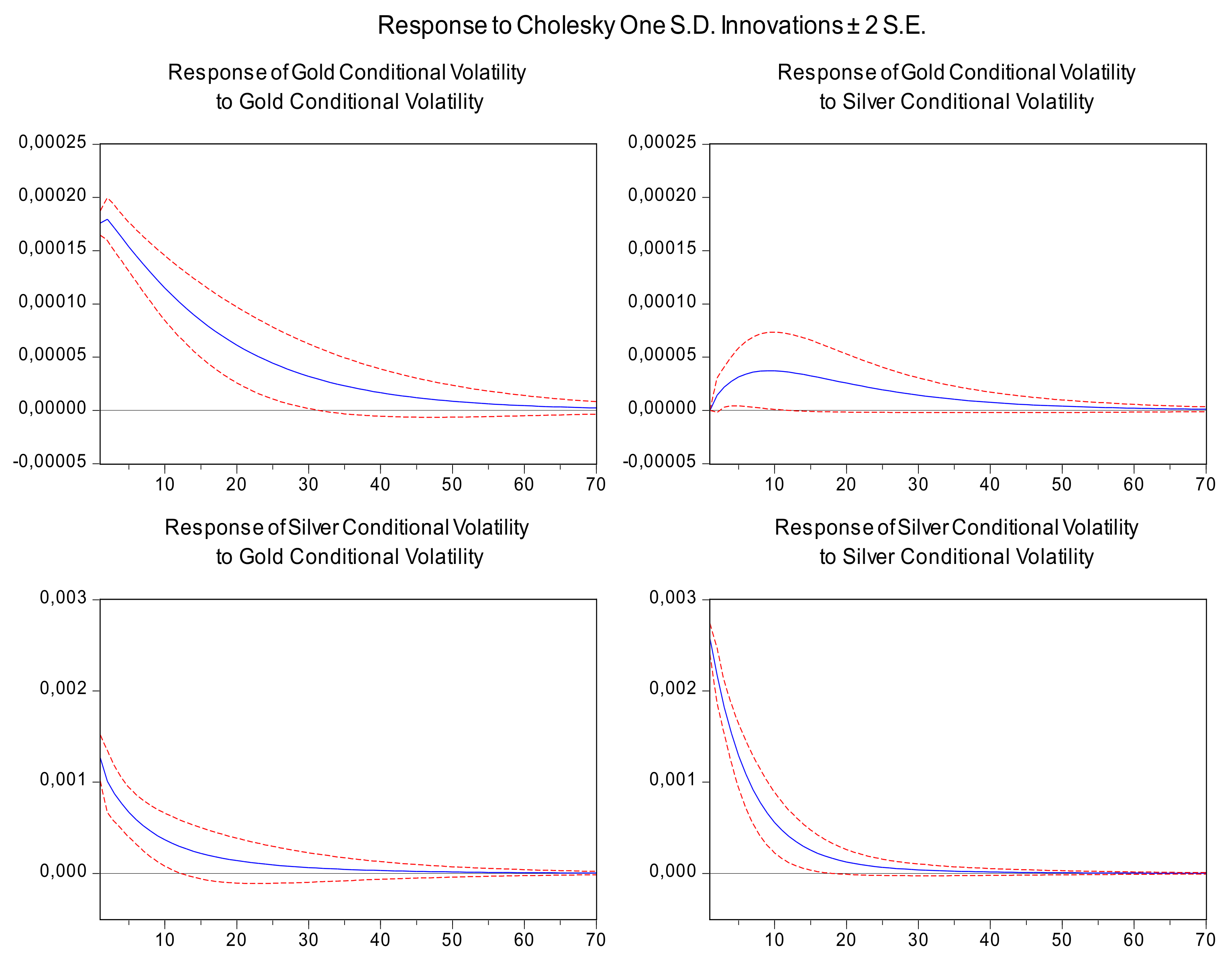
As is shown in Figure 4, there is a strong volatility transmission from gold to silver that can last up to 40 weeks (fourth panel clockwise). Although it exists, the volatility from silver to gold is much weaker (second panel clockwise). This result is also confirmed on a monthly basis (Figure 5). The effect of gold volatility now is approximately 10 periods (months) (fourth panel clockwise), which is approximately equivalent to 40 weekly periods. Further, the monthly results confirm that the effect of the volatility shock to silver are mildly transmitted to gold (second panel clockwise), supporting the part of the literature findings for unidirectional transfer mechanism of volatility from gold to silver. Investors could exploit the 10-month effect on the volatility of silver by the gold volatility by designing appropriate option strategies and extracting the vega from these strategies to their advantages. In this way, directional or pure volatility strategies can be designed on silver using the gold volatility, as the observation variable. Moreover, these strategies will be articular profitable in times when gold volatility is increased but silver volatility remains subdued.

4. Conclusions

This paper, by using GARCH and VAR modelling, adds to the majority of the relevant literature that volatility transmission is unidirectional from gold to silver. It also specified the duration of the shock as approximately 10 months (or 40 weeks). The findings of our empirical research have interesting implications for policy makers and institutional and individual investors. The former should be aware that during non-tranquil periods, the so-called sift-to-safe heaven options might result in high volatility transmission to precious metals and thus take necessary action to dampen this effect, i.e., by imposing higher fees to enter the market which would potentially prevent contagion risk during periods of economic downturns or crises. Regarding the investor’s perspective, this paper should motivate them to enhance their efforts to apply volatility strategies on precious metals and consider diversifying away from potential idiosyncratic components of risk. Future research could explore the methodology on specific periods (i.e., bull or bear) and examine the behavior of conditional volatilities particular towards the end of them. The methodology could be enhanced further by incorporating other assets (financial, real estate, etc.) and examine the results on a portfolio basis. Finally, during the last years, inclusion of commodities has been dramatically increased by institutional investors (state funds, pension funds, etc.). Metals (and in particular gold and silver) are portfolio constituents with hopefully positive risk diversification effects. Extensions of this research could include the study of the effect of metals’ volatility transmission mechanism on the portfolio volatility and its ability to locate low portfolio risk areas.