Modeling of 2R Planar Dumbbell Stacker Robot Locomotion Using Force Control for Gripper Dexterous Manipulation
Abstract
:1. Introduction
- Mechanical Structure Analysis;
- Gripper Design;
- Kinematics;
- Dynamics;
- Model-based Control of Robot Dynamical Interaction with Environment;
- Contact Forces Set;
- Trajectory Set.
2. Materials and Methods
- Euler–Newton formulation: to describe the bodies of the rigid dynamic, it is an effective way for complex systems and is used to assemble the equation of the motion using the algorithms;
- Lagrangian formulation: using the kinetic and potential energy of the robot, it is effective for simple systems with few bodies that have a degree of freedom.
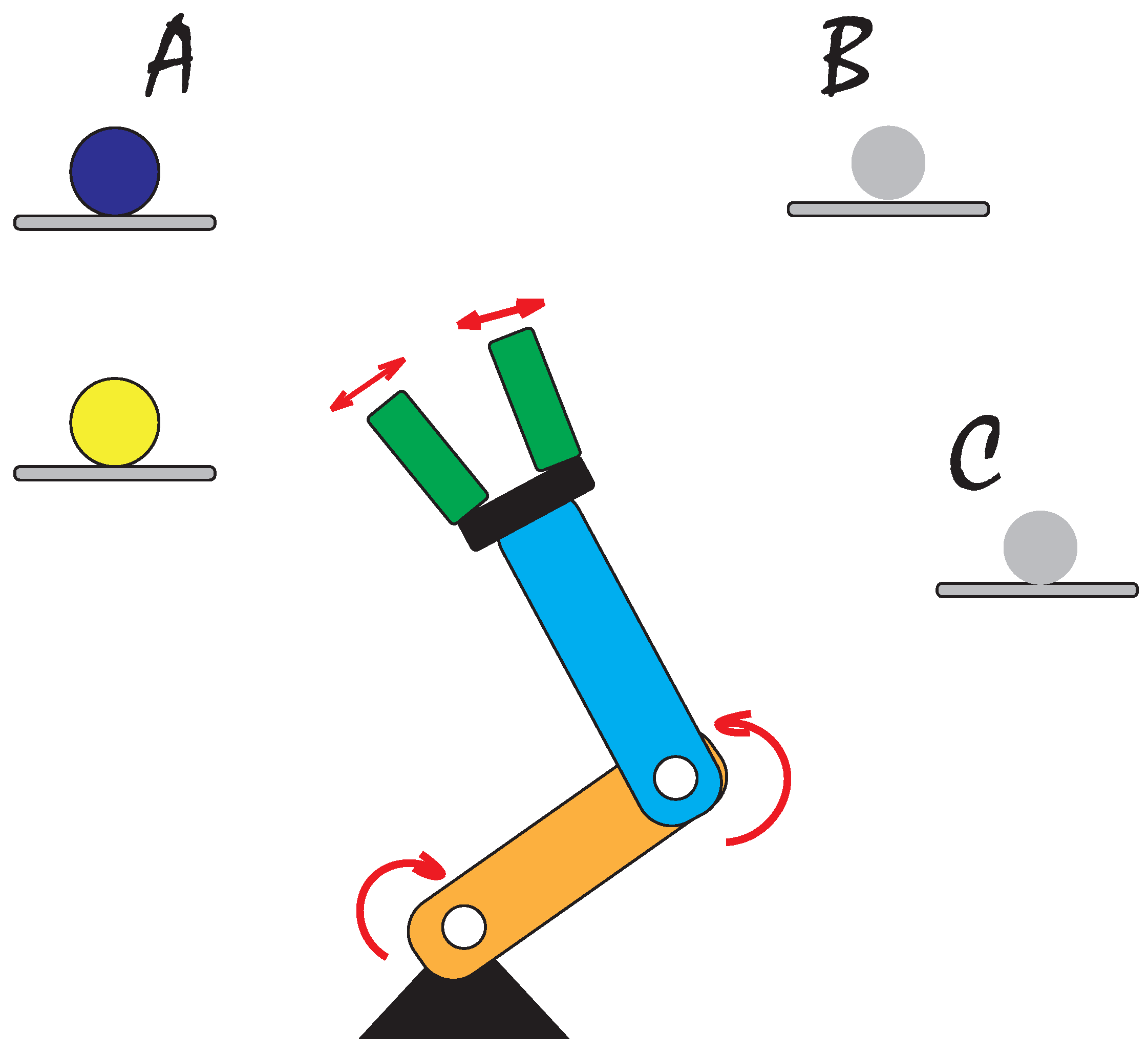
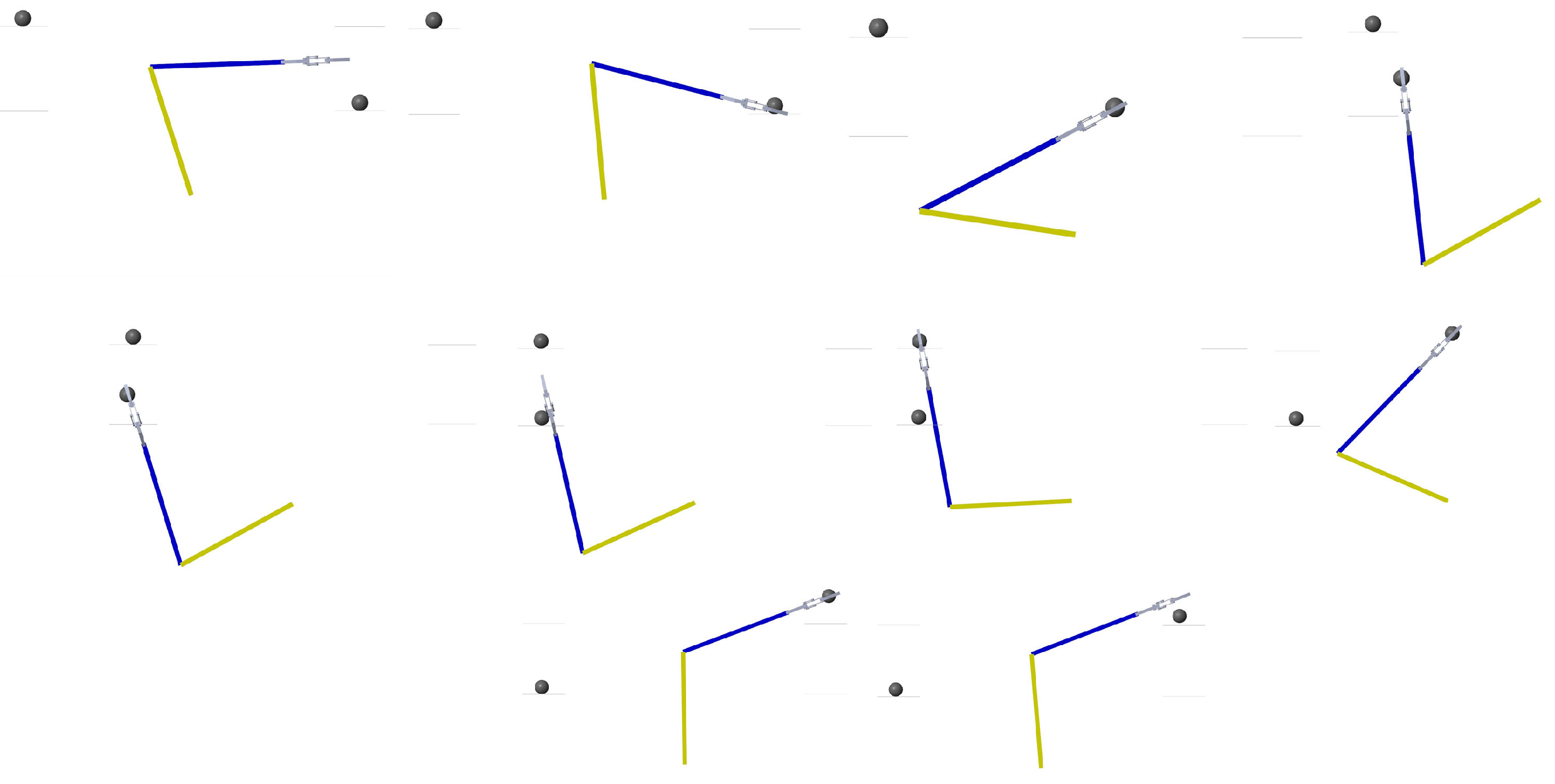
2.1. Mechanical Structure
2.2. Forward Kinematics
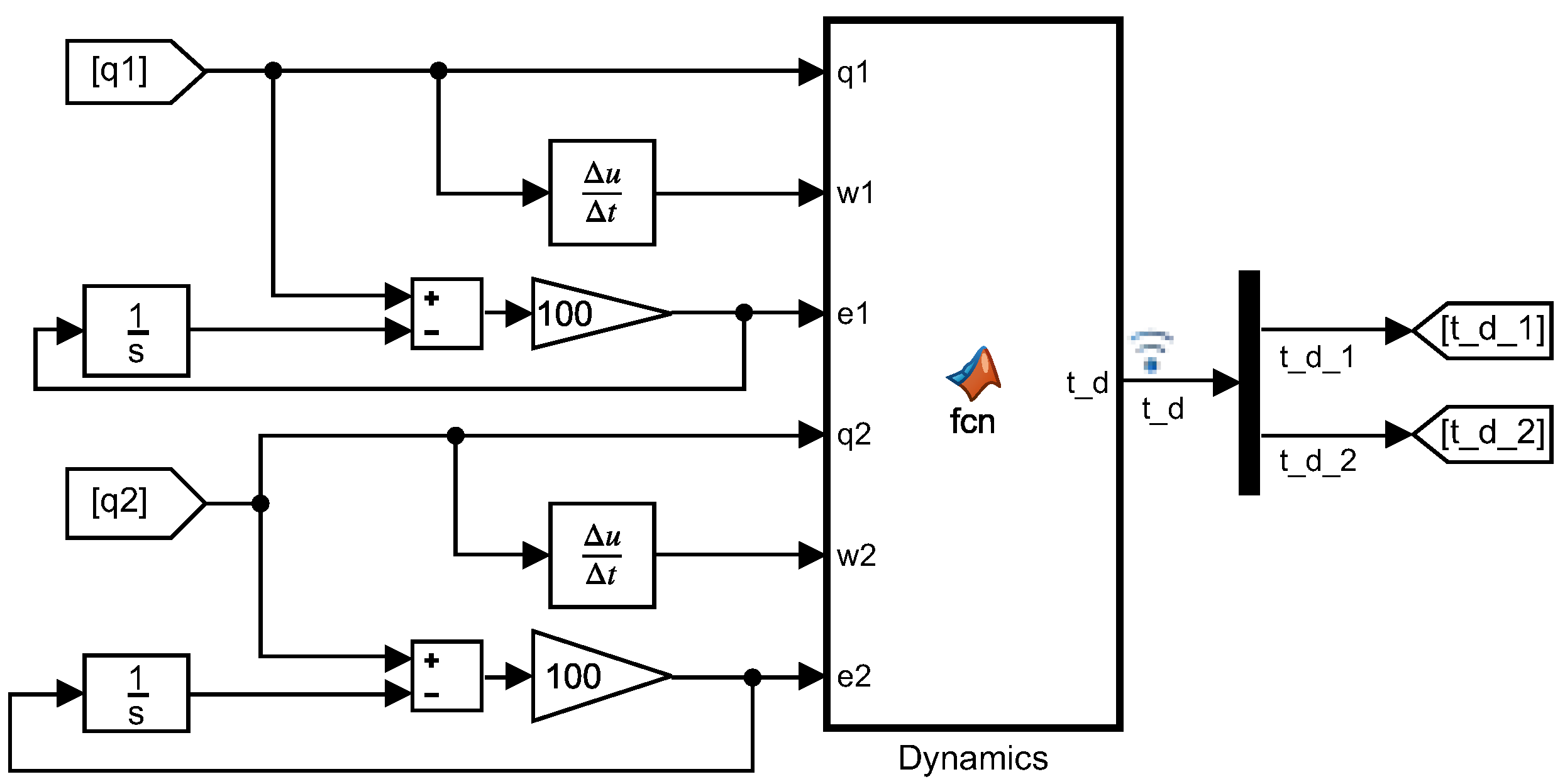
2.3. Robot Dynamics
2.4. Robot Control
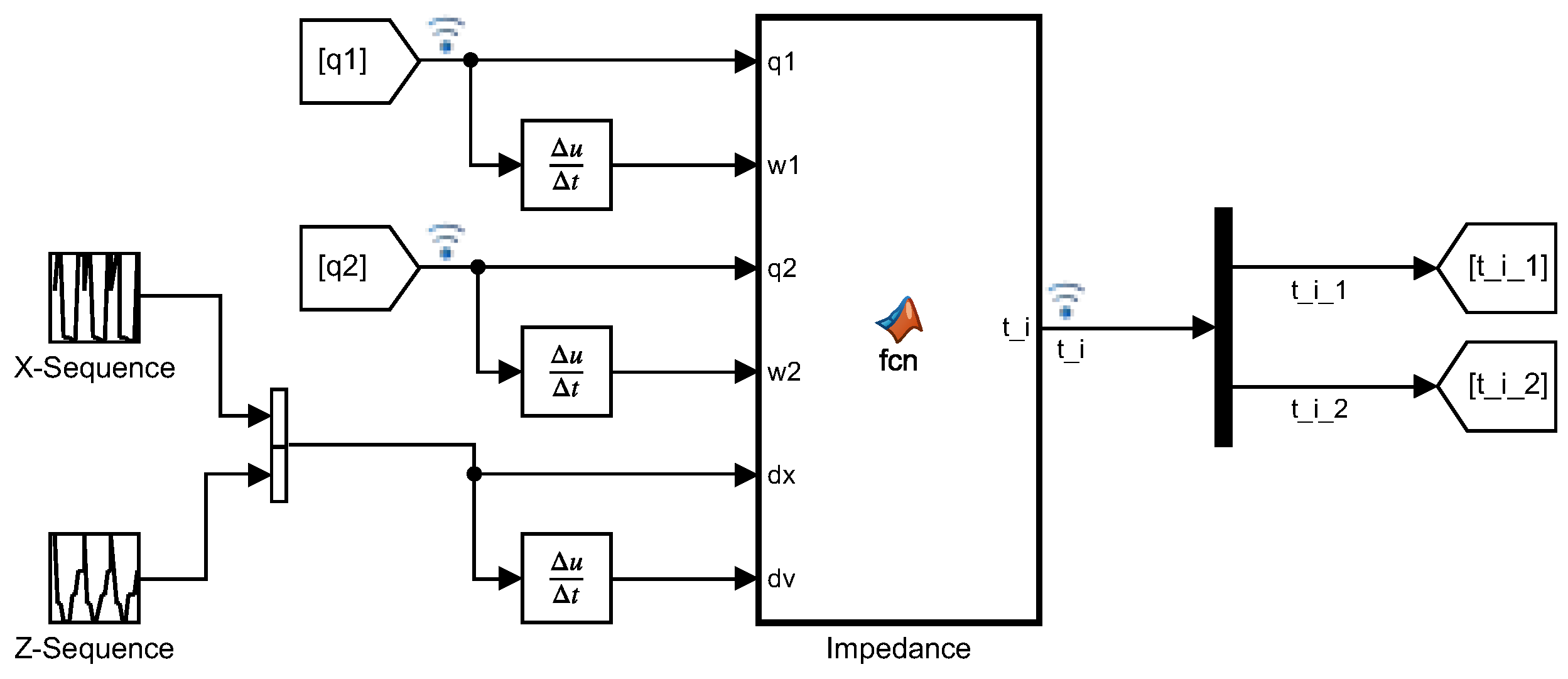
2.5. Impedance Control
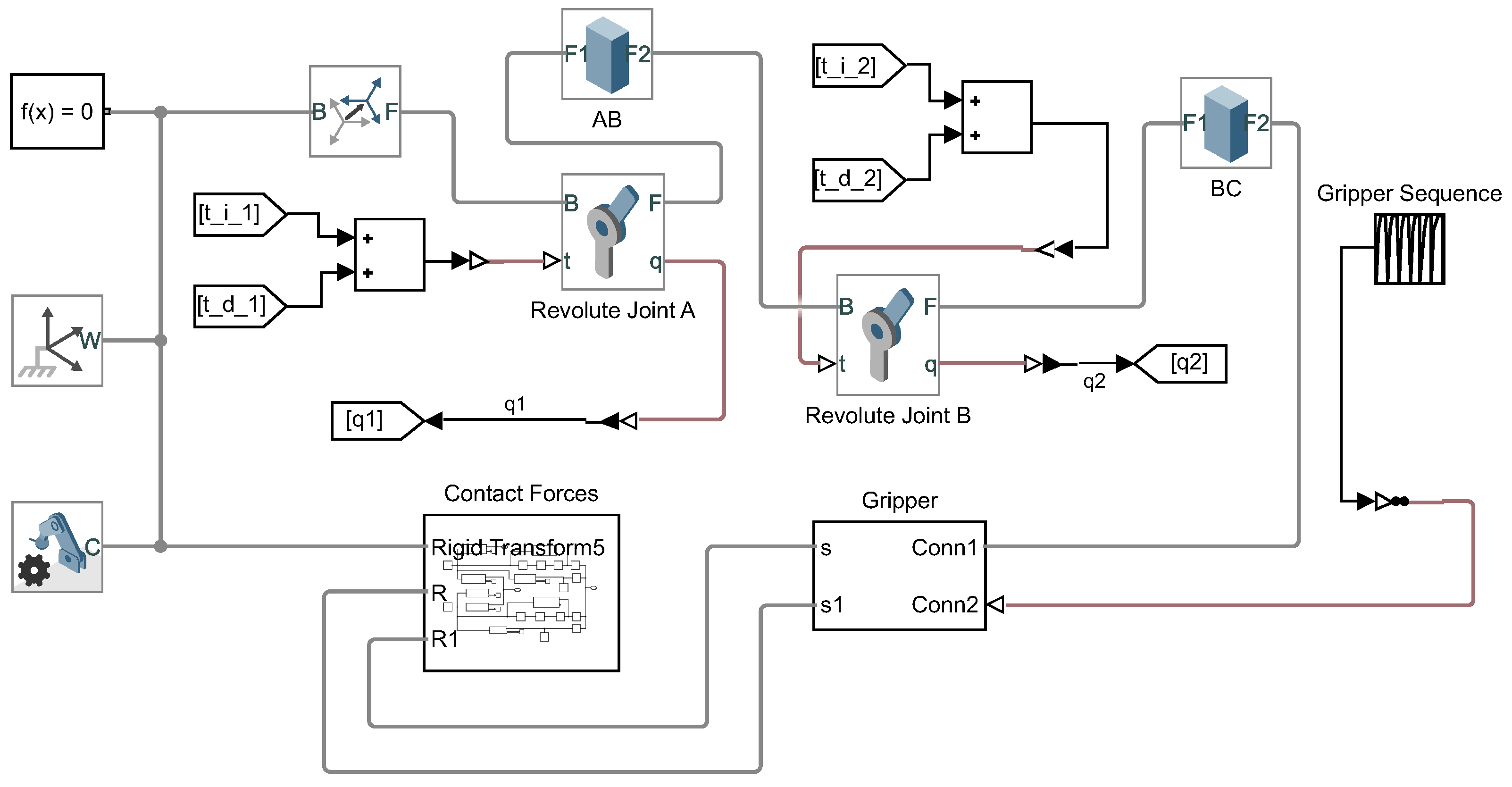
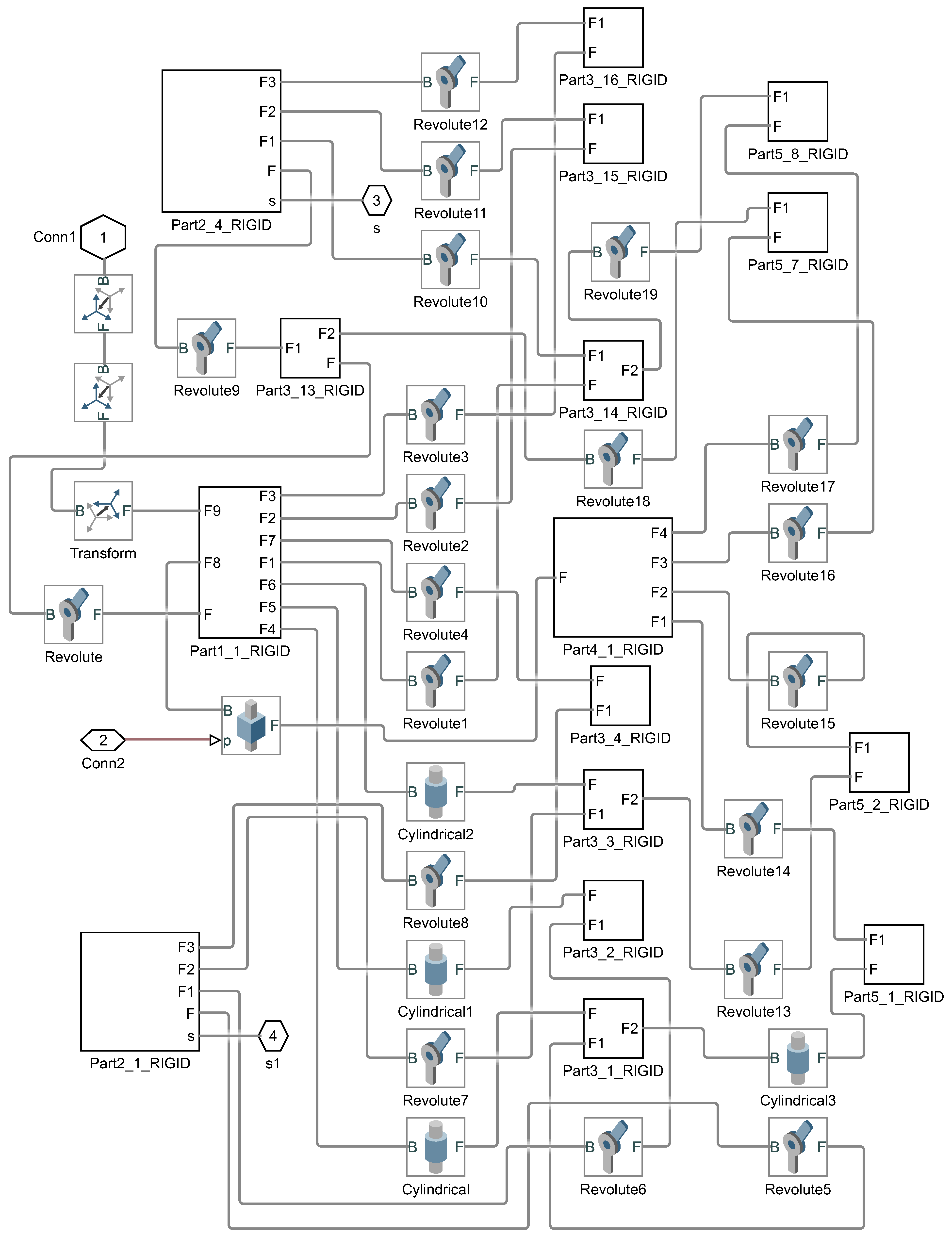
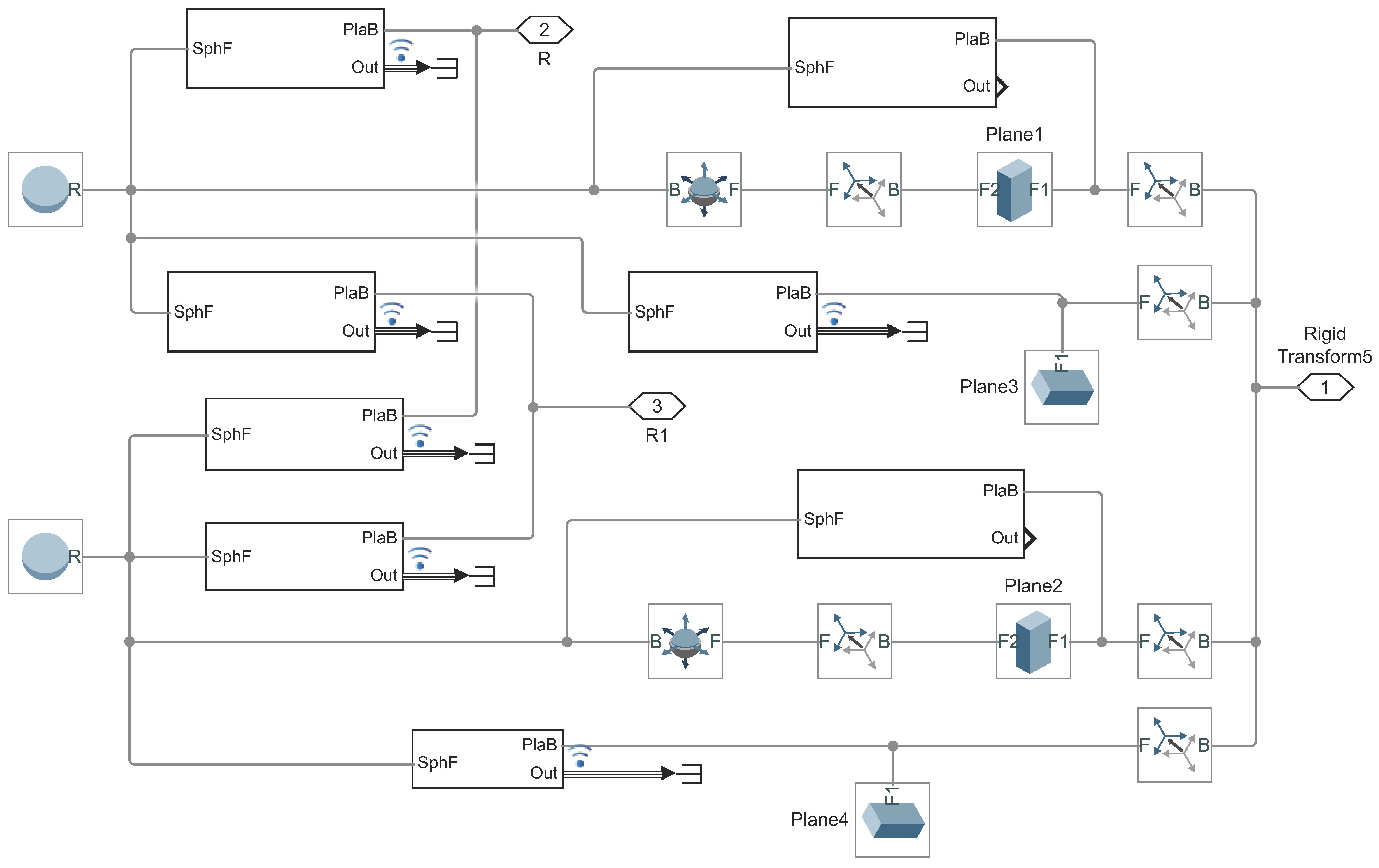
2.6. Simulink Model
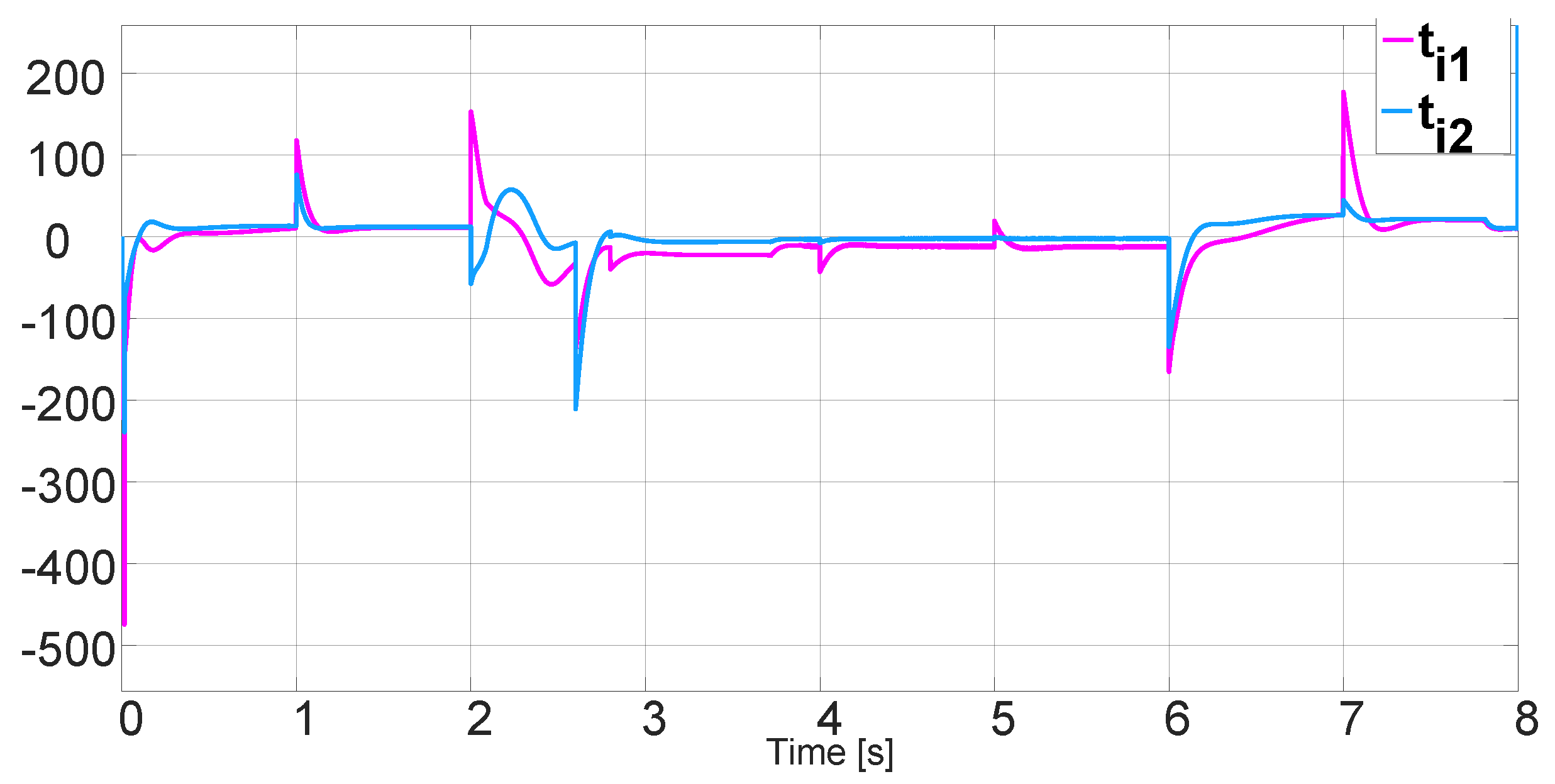
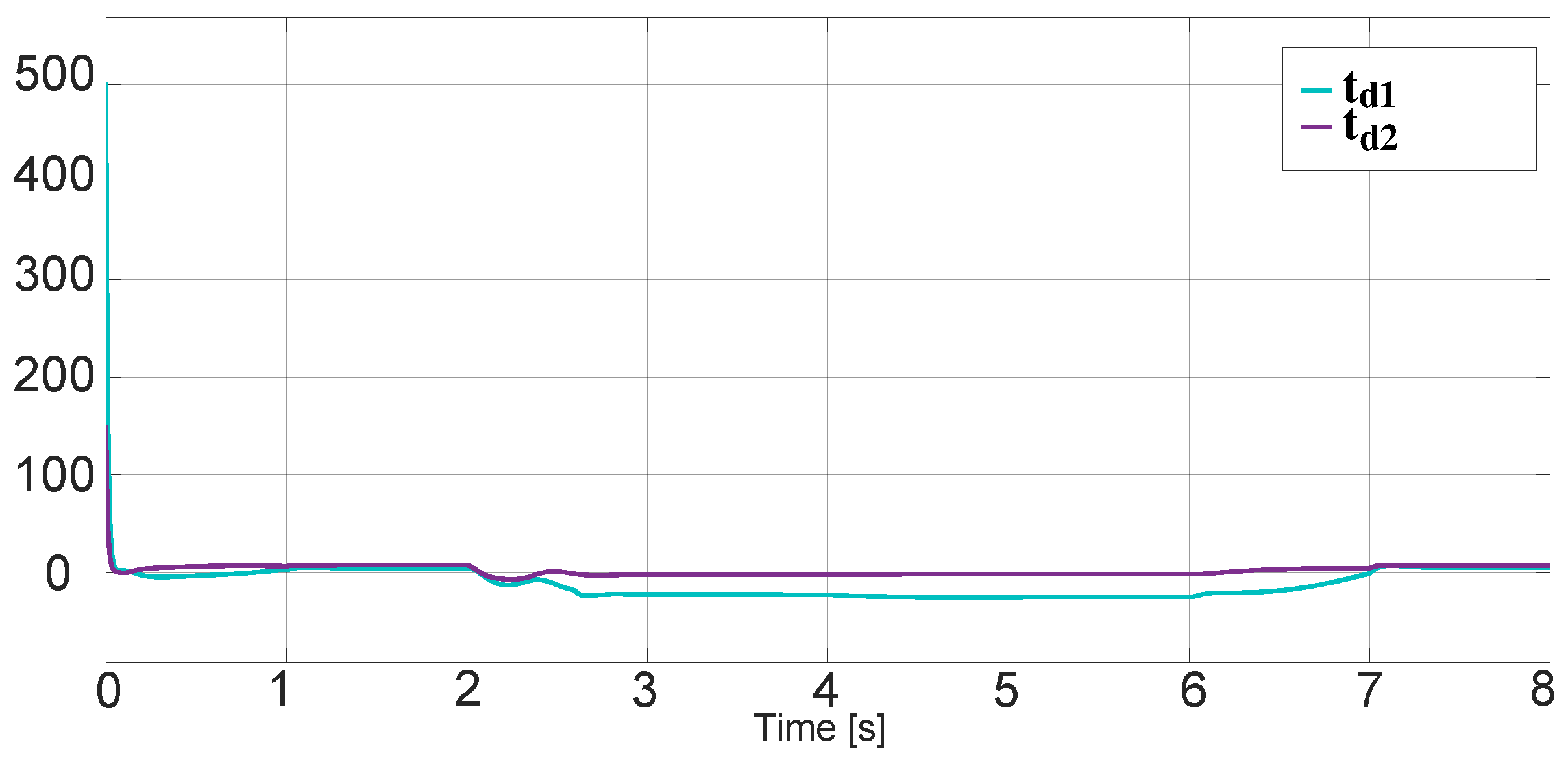
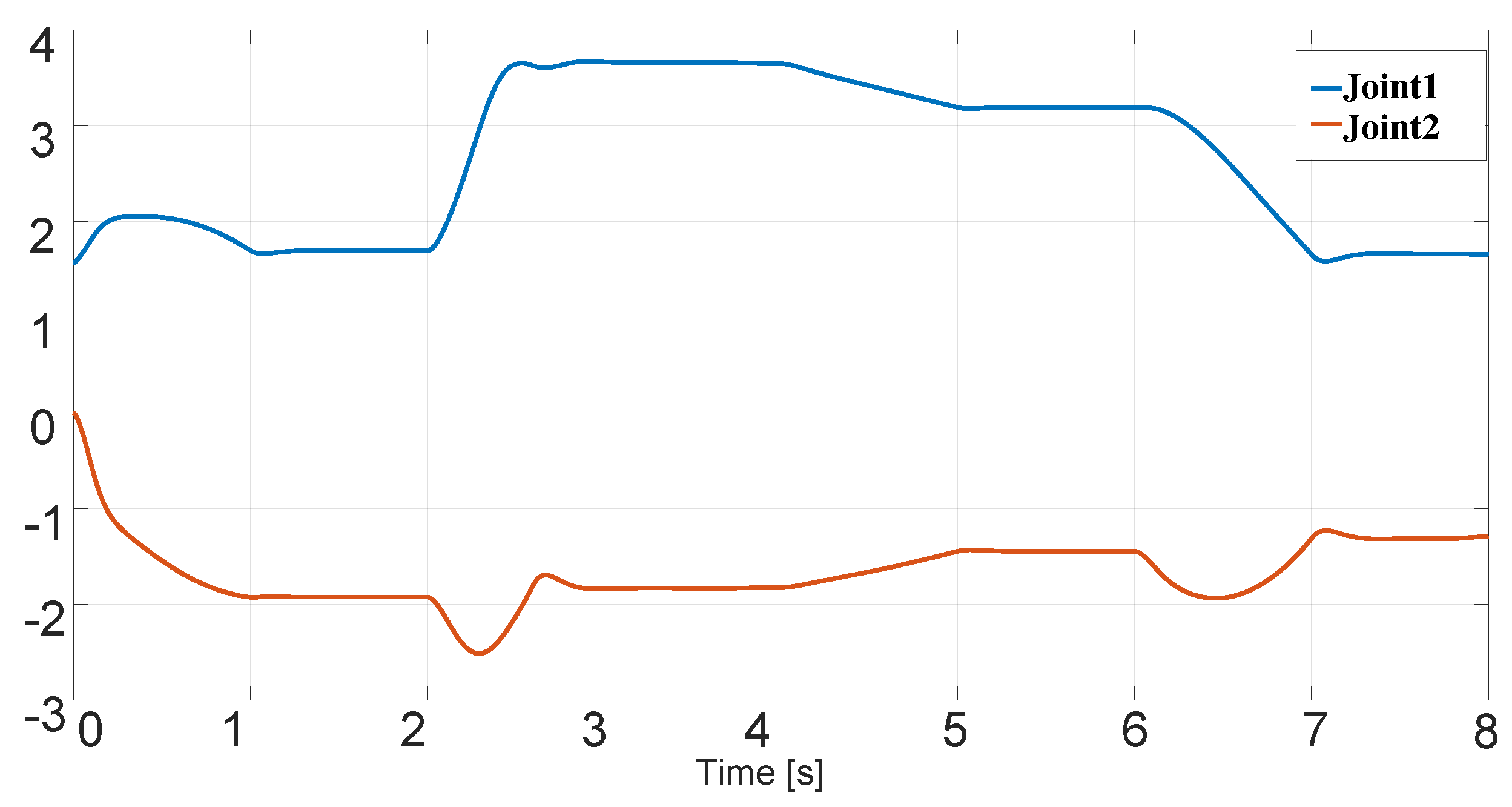
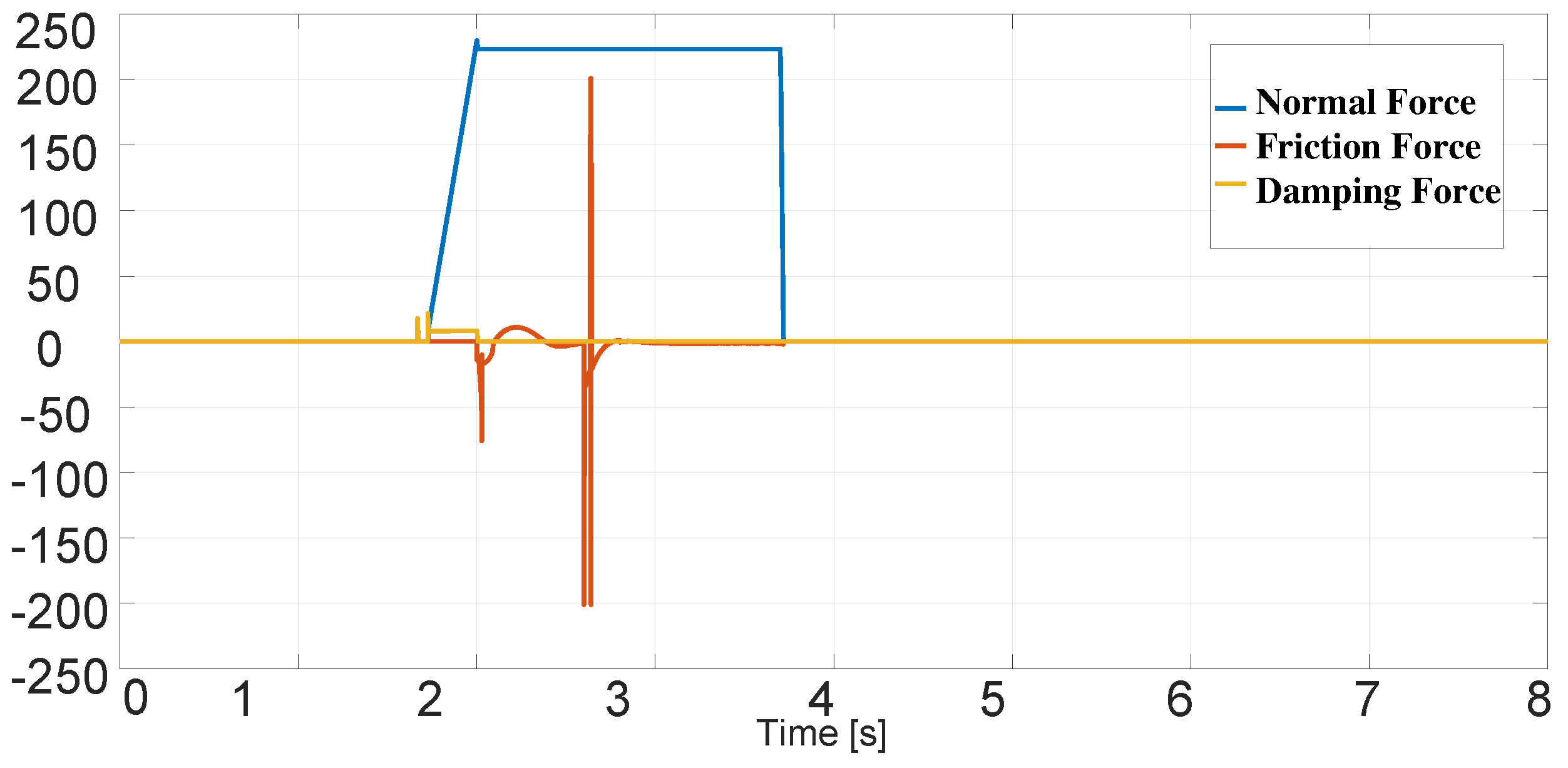
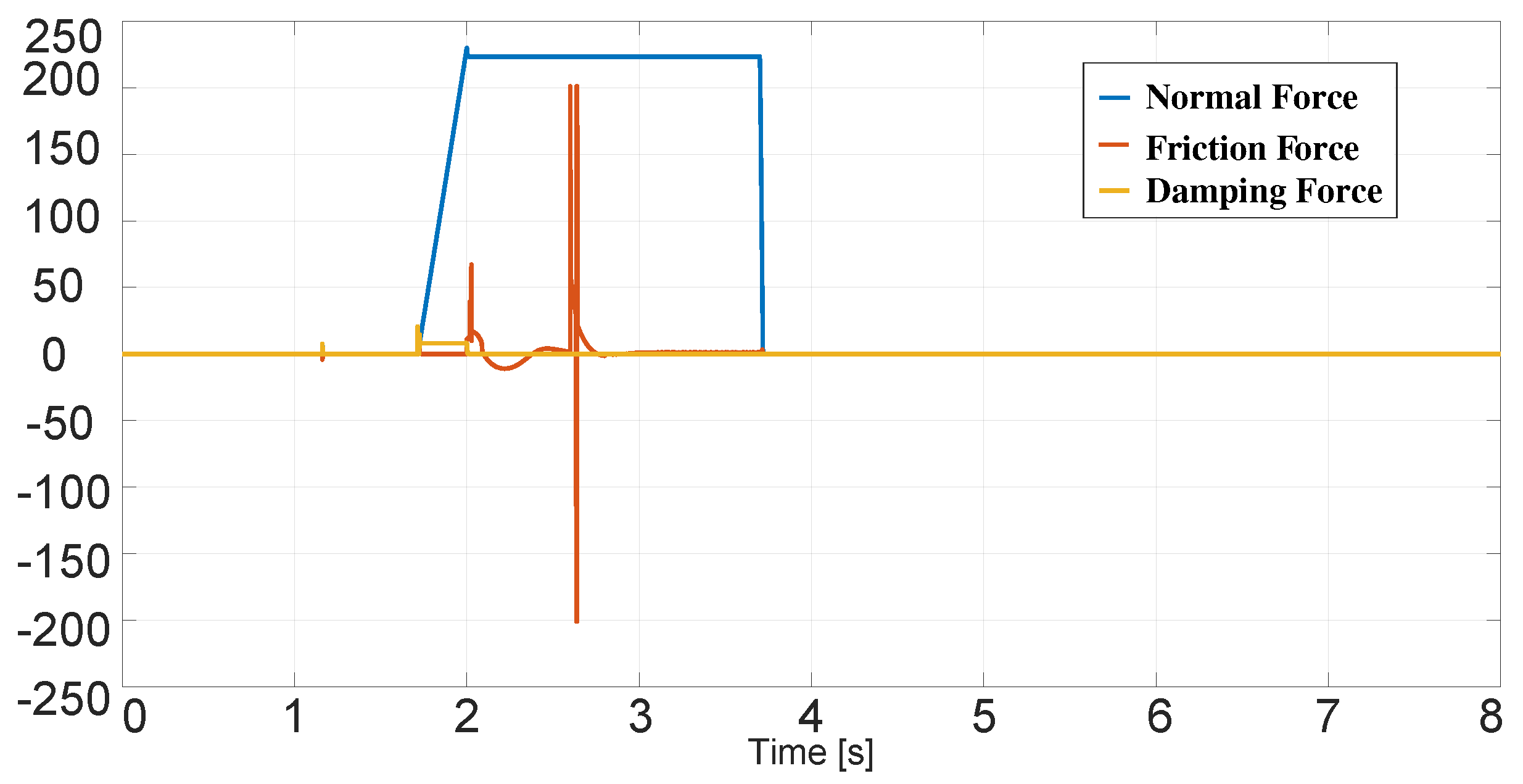
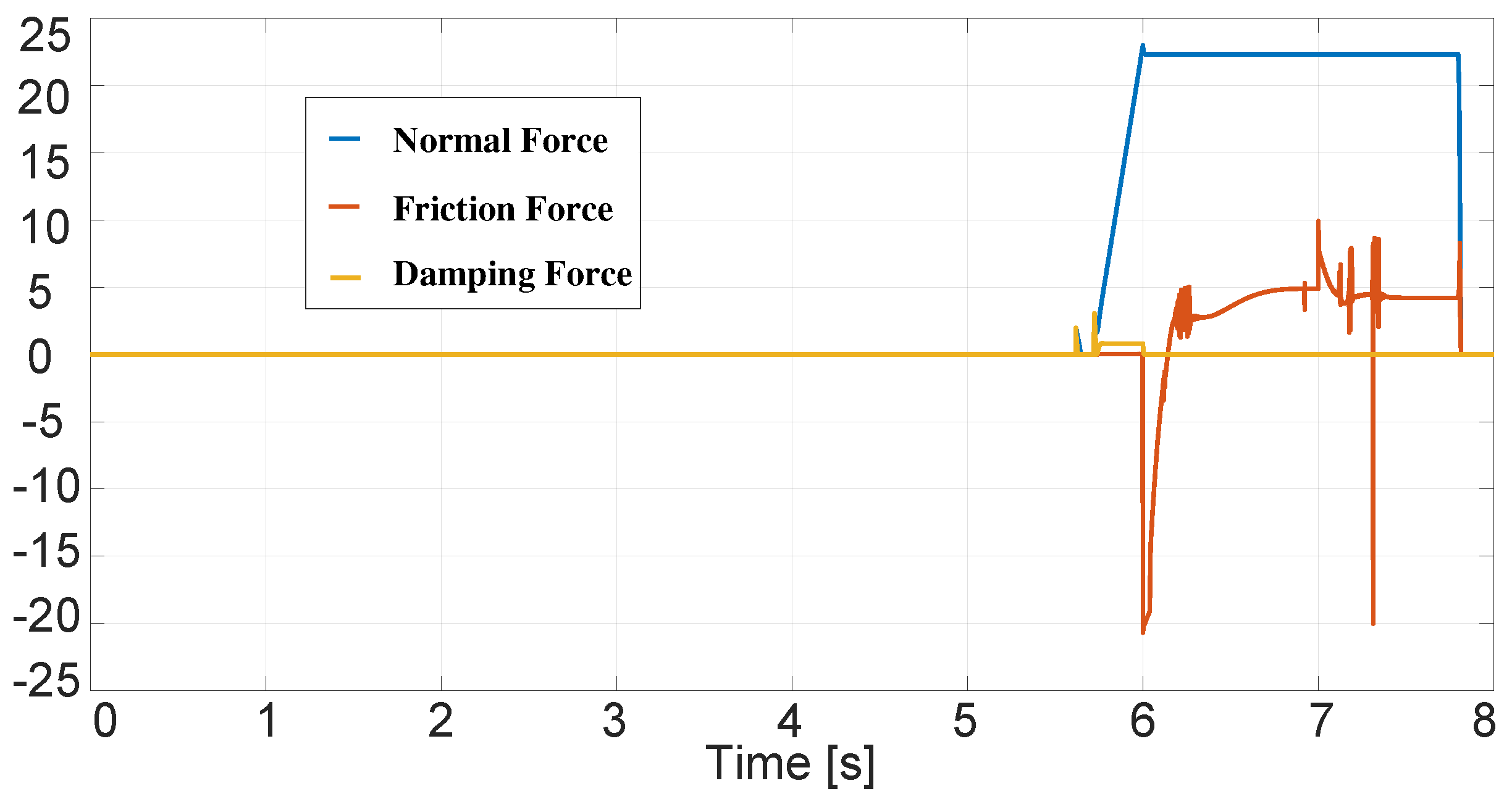
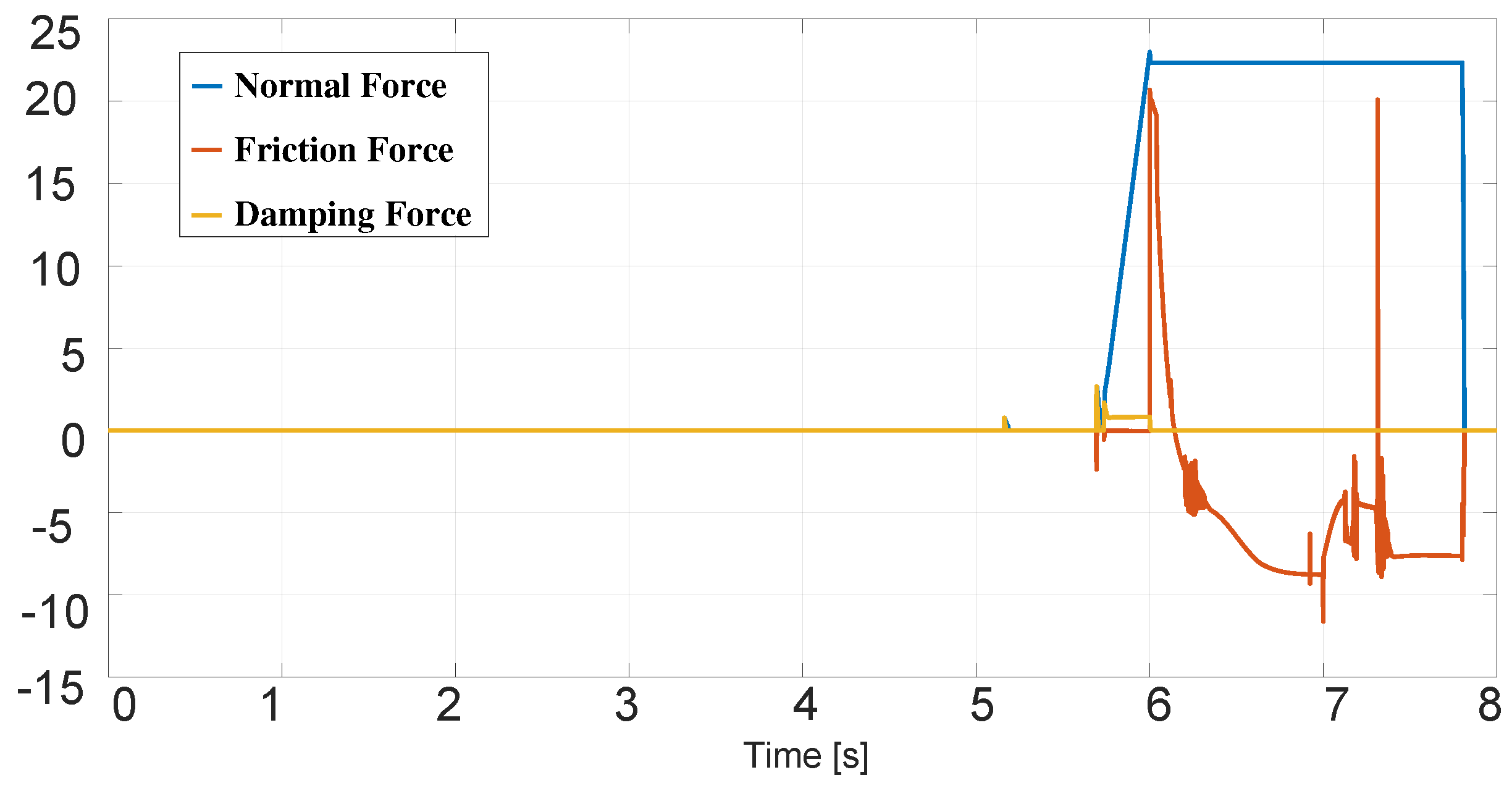
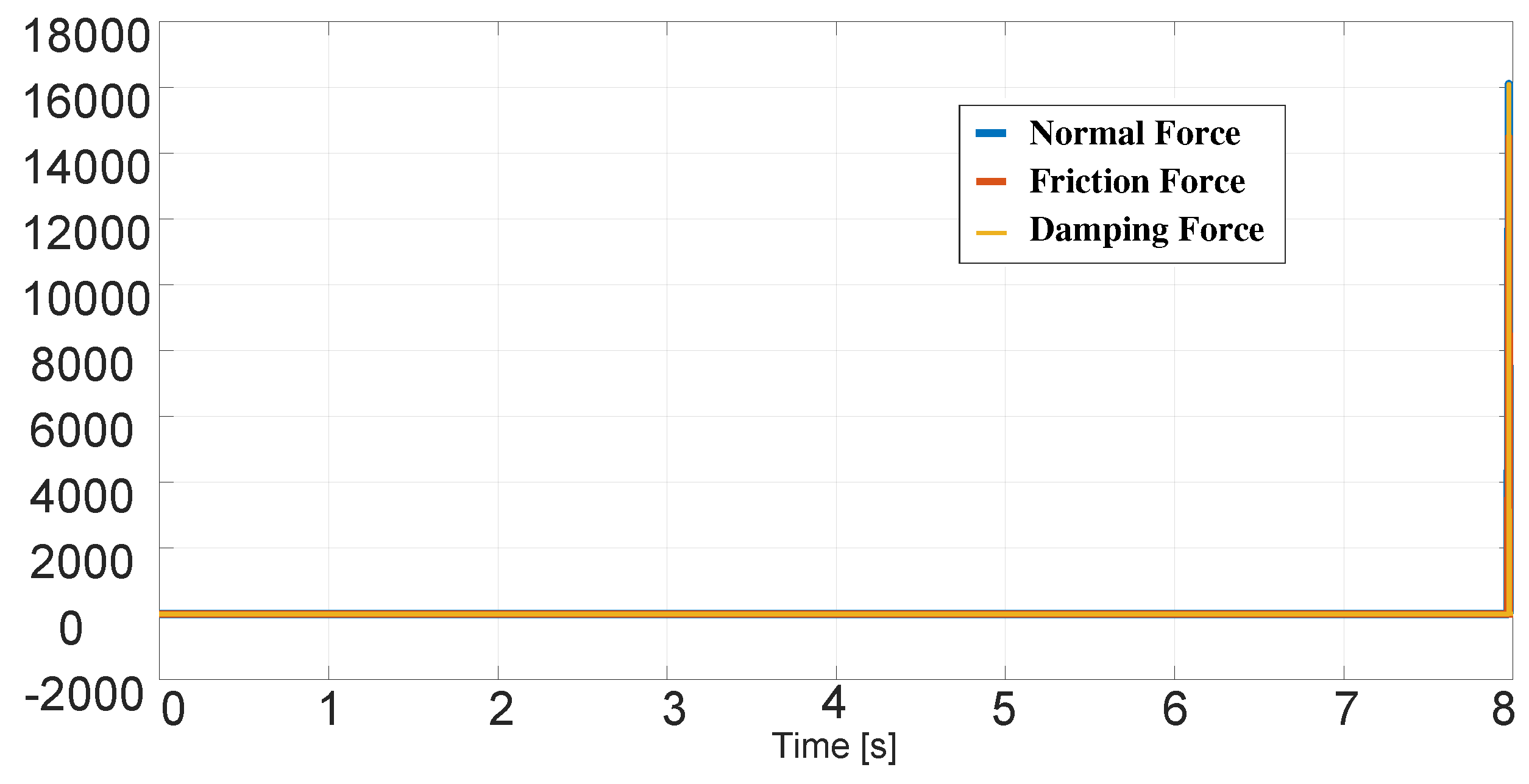
3. Results and Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bruno Siciliano and Oussama Khatib. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Khalil, W.; Dombre, E. Modeling, Identification and Control of Robots; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Borisov, I.I.; Kolyubin, S.A.; Bobtsov, A.A. Static force analysis of a finger mechanism for a versatile gripper. In Proceedings of the International Conference Cyber-Physical Systems and Control (CPSC 2019), St. Petersburg, Russia, 10–12 June 2019; pp. 308–324. [Google Scholar]
- Borisov, I.I.; Borisov, O.I.; Gromov, V.S.; Vlasov, S.M.; Dobriborsci, D.; Kolyubin, S.A. Design of versatile gripper with robust control. IFAC-PapersOnLine 2018, 51, 56–61. [Google Scholar] [CrossRef]
- Artemov, K.; Kolyubin, S.; Stramigioli, S. Multi-Stage Energy-Aware Motion Control with Exteroception-Defined Dynamic Safety Metric. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 9290–9296. [Google Scholar] [CrossRef]
- Zanchettin, A.M.; Ceriani, N.M.; Rocco, P.; Ding, H.; Matthias, B. Safety in human-robot collaborative manufacturing environments: Metrics and control. IEEE Trans. Autom. Sci. Eng. 2016, 13, 882–893. [Google Scholar] [CrossRef] [Green Version]
- Brunssen, S.; Hueber, S.; Wohlmuth, B. Contact dynamics with lagrange multipliers. In IUTAM Bookseries, Proceedings of the IUTAM Symposium on Computational Methods in Contact Mechanics, Hannover, Germany, 5–8 November 2006; Springer: Dordrecht, The Netherlands, 2007; pp. 17–32. [Google Scholar]
- Hogan, N. Impedance control: An approach to manipulation. In Proceedings of the 1984 American Control Conference, San Diego, CA, USA, 6–8 June 1984; pp. 304–313. [Google Scholar]
- Raiola, G.; Cardenas, C.A.; Tadele, T.S.; de Vries, T.; Stramigioli, S. Development of a Safety- and Energy-Aware Impedance Controller for Collaborative Robots. IEEE Robot. Autom. Lett. 2018, 3, 1237–1244. [Google Scholar] [CrossRef] [Green Version]
- Bohan, L.; Yue, Z.; Xinying, Z.; Guangshang, Z. Research on Position-Based Impedance Control in Cartesian Space of Robot Manipulators. In Proceedings of the 2019 2nd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 22–24 November 2019; pp. 549–551. [Google Scholar] [CrossRef]
- Gerlagh, B.; Califano, F.; Stramigioli, S.; Roozing, W. Energy-aware adaptive impedance control using offline task-based optimization. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021; pp. 187–194. [Google Scholar] [CrossRef]
- Kondratyev, S.; Cruypeninck, L.; Tsareva, A. Lower Extremity Exoskeleton Simulation Model with Variable Stiffness Actuation for Vertical Locomotion. In Proceedings of the 2021 3rd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russia, 10–12 November 2021; pp. 1178–1183. [Google Scholar] [CrossRef]
- Romano, D.; Benelli, G.; Kavallieratos, N.G.; Athanassiou, C.G.; Canale, A.; Stefanini, C. Beetle-robot hybrid interaction: Sex, lateralization and mating experience modulate behavioural responses to robotic cues in the larger grain borer Prostephanus truncatus (Horn). Biol. Cybern. 2020, 114, 473–483. [Google Scholar] [CrossRef] [PubMed]
- Güntürkün, O.; Ströckens, F.; Ocklenburg, S. Brain lateralization: A comparative perspective. Physiol. Rev. 2020, 100, 1019–1063. [Google Scholar] [CrossRef] [PubMed]
- Romano, D.; Donati, E.; Canale, A.; Messing, R.H.; Benelli, G.; Stefanini, C. Lateralized courtship in a parasitic wasp. Laterality Asymmetries Body Brain Cogn. 2016, 21, 243–254. [Google Scholar] [CrossRef] [PubMed]
- Cogan, G.B.; Thesen, T.; Carlson, C.; Doyle, W.; Devinsky, O.; Pesaran, B. Sensory-motor transformations for speech occur bilaterally. Nature 2014, 507, 94–98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuo, P.; DeBacker, J.; Deshpande, A.D. Design of robotic fingers with human-like passive parallel compliance. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2562–2567. [Google Scholar]
- Gil, C.R.; Calvo, H.; Sossa, H. Learning an efficient Gait Cycle of a Biped Robot Based on Reinforcement Learning and Artificial Neural Networks. Appl. Sci. 2019, 9, 502. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Armendáriz, M.A.; Calvo, H. Visual SLAM and Obstacle Avoidance in Real Time for Mobile Robots Navigation. In Proceedings of the Mechatronics, Electronics and Automotive Engineering, Cuernavaca, Mexico, 18–21 November 2014; pp. 44–49. [Google Scholar]
- Lawhorn, R.; Susanibar, S.; Lu, L.; Wang, C. Polymorphic robot learning for dynamic and contact-rich handling of soft-rigid objects. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 596–601. [Google Scholar]
- Dong, Y.; Ren, T.; Wu, D.; Chen, K. Compliance Control for Robot Manipulation in Contact with a Varied Environment Based on a New Joint Torque Controller. J. Intell. Robot. Syst. 2020, 99, 79–90. [Google Scholar] [CrossRef]

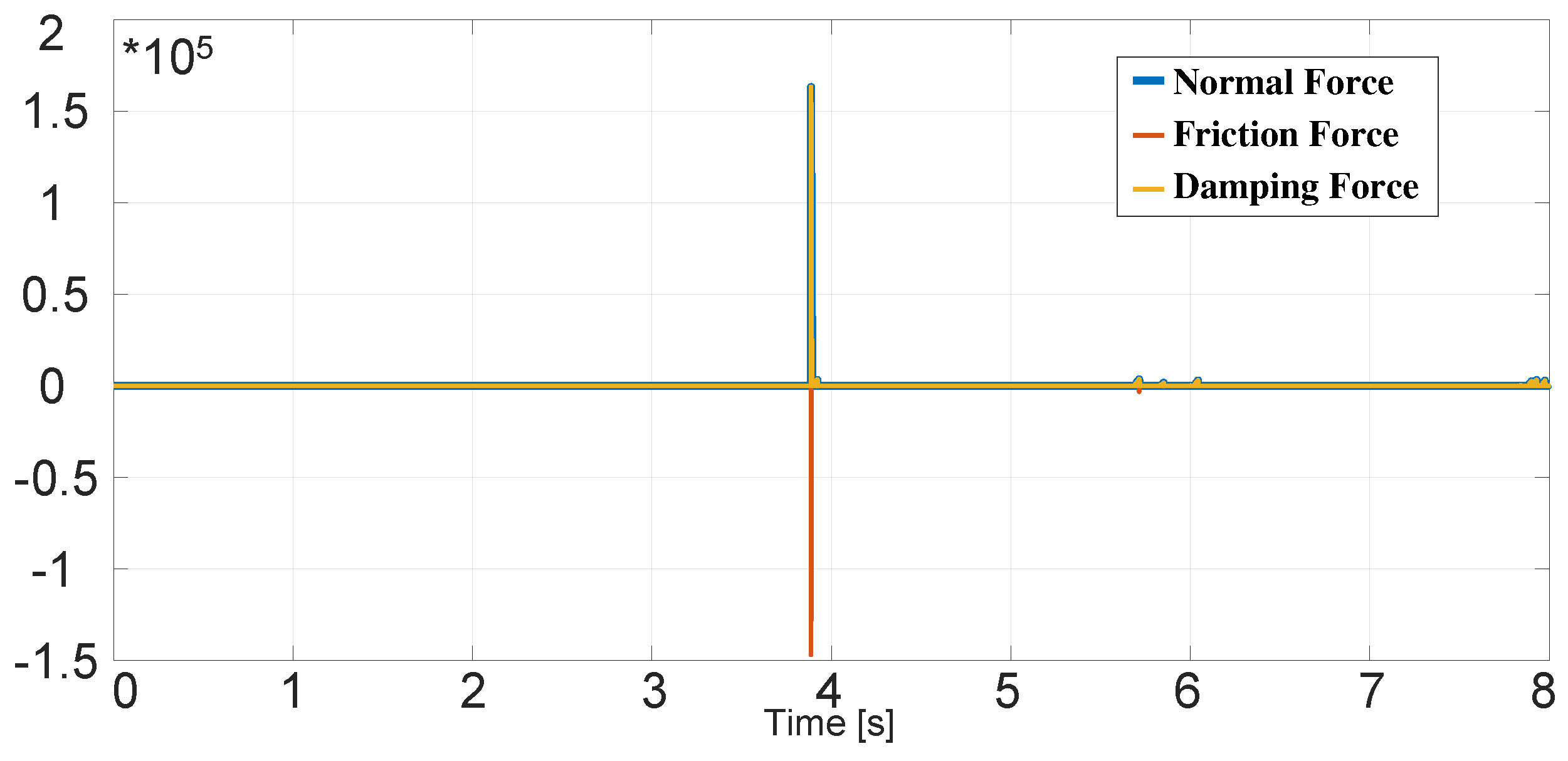
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondratev, S.; Meshcheryakov, V. Modeling of 2R Planar Dumbbell Stacker Robot Locomotion Using Force Control for Gripper Dexterous Manipulation. Computation 2022, 10, 143. https://doi.org/10.3390/computation10090143
Kondratev S, Meshcheryakov V. Modeling of 2R Planar Dumbbell Stacker Robot Locomotion Using Force Control for Gripper Dexterous Manipulation. Computation. 2022; 10(9):143. https://doi.org/10.3390/computation10090143
Chicago/Turabian StyleKondratev, Sergei, and Victor Meshcheryakov. 2022. "Modeling of 2R Planar Dumbbell Stacker Robot Locomotion Using Force Control for Gripper Dexterous Manipulation" Computation 10, no. 9: 143. https://doi.org/10.3390/computation10090143
APA StyleKondratev, S., & Meshcheryakov, V. (2022). Modeling of 2R Planar Dumbbell Stacker Robot Locomotion Using Force Control for Gripper Dexterous Manipulation. Computation, 10(9), 143. https://doi.org/10.3390/computation10090143





