Abstract
In addition to a wide range of socio-economic impacts, traffic congestion during the era of the COVID-19 pandemic has been identified as a critical issue to be addressed. In urban neighborhoods, the timespan of traffic congestion hazard (HTC) after the curfew lift is subjected to the commuters’ decisions about home-to-shopping center departures. The decision for departing early or late for shopping depends on both the internal (commuter related) and external (shopping center related) factors. The present study developed a practical methodology to assess the HTC period after the curfew timings. An online questionnaire survey was conducted to appraise the commuters’ perception about departure time and to assess the impact of eight internal (family size, involvement in other activities, nature of job, education level, age, number of vehicles, number of children, and availability of personal driver) and three external (availability of shopping center of choice in near vicinity, distance to shopping center, and size of the city) factors on their decision. With an acceptable 20% response rate, Chi-square and Cramer’s V tests ascertained family size and involvement in other activities as the most significant internal factors and availability of shopping center of choice as the primary external factor. Age, number of children, and size of the city influenced to some extent the commuters’ decisions about early or delayed departure. Large associations were found for most of the factors, except education level and availability of drivers in a household. Fuzzy synthetic evaluation (FSE) first segregated the commuters’ responses over a four level-rating system: no delay (0), short delay (1), moderate delay (3), and long delay (5). Subsequently, the hierarchical bottom-up aggregation effectively determined the period of highest traffic congestion. Logical study findings revealed that most (about 65%) of the commuters depart for shopping within 15 min after the curfew lift, so HTC in the early part (the first one hour) of the no curfew period needs attention. The traffic regulatory agencies can use the proposed approach with basic socio-demographic data of an urban neighborhood’s residents to identify the HTC period and implement effective traffic management strategies accordingly.
1. Introduction
On December 2019, the authorities in Wuhan City (Hubei Province of China), reported the novel coronavirus disease COVID-19 epidemic. This disease is resulted from acute respiratory syndrome SARS-CoV-2 [1]. Since then, the COVID-19 has attracted global attention because of the affirmed risk of human-to-human transmission [2]. On 11 March 2019, the World Health Organization (WHO) announced COVID-19 as a global pandemic [3]. As of January 2022, over 352 million people have been affected by COVID-19 (SARS-CoV-2), and around 5.6 million affected have died. The United States, with over 7 million cases and 889,000 deaths, is on the top of the global counts, followed by India with more than 39 million cases (490,000 deaths) and Brazil with over 24 million cases (623,000 deaths) [4]. The COVID-19 pandemic not only infected people and took lives; it significantly disrupted all types of socioeconomic activities around the globe [5]. The fear of the virus itself, governmental restrictions, and curfew timings have restricted the movement of citizens for business, education, recreation, and religious activities.
The COVID-19 pandemic situation posed new inquiries to traffic engineers and planners. The pandemic situation demands contemporary transportation planning approaches to deal with changing mobility and activity habits [6]. The situation also demands regional specific planning, keeping in view the exclusive socio-economic and environmental characteristics of the region [7]. Particularly in the early stage, many countries adopted varying strategies to attenuate the socioeconomic and health impacts of the COVID-19 pandemic on their communities. The Kingdom of Saudi Arabia (KSA) among many other countries also implemented precautionary measures to prevent the transmission of the COVID-19 infection to protect the health of citizens and residents of the Kingdom. One of these measures is forcing partial and total public curfews on certain cities. A complete public curfew was enforced on large cities with high transmission rates of COVID-19 such as Riyadh, while a partial public curfew was imposed on the relatively smaller regions with low spread rate of COVID-19 such as the Qassim Region.
Despite the fact the public curfew policies are important in the age of COVID-19, studying the impact of such policies on transportation systems has yet to be considered. Large cities with overcrowded populations such as Riyadh City, KSA, continue to suffer from congested roads. In the efforts to mitigate day-to day traffic congestion, different traffic management strategies have been developed and implemented. For example, during rush hours, the traffic department in Riyadh City controls the entrances and the exits on main roads to regulate traffic flows and thus mitigate possible congestion. Such policies may not be adequate during public curfews. Immediately after lifting a curfew, people rush to the roadways to arrange their necessities on one side. On the other hand, some people delay their shopping trips to avoid that early congestion and contribute to traffic congestion in the last part prior to curfew. Recently, certain cities in Saudi Arabia have adopted a partial curfew policy. The question of interest is whether there would be a sudden traffic congestion after a public curfew is lifted or higher congestion subject to the later part of the no-curfew duration. Information on possible traffic congestion in response to different curfew policies will help the decision-makers in evaluating the potential congestion hazard, revising and modifying the curfew durations, and anticipating the congested road sections so that the public may be advised to avoid such roads during certain times.
Traffic congestion occurs when too many vehicles use common main streets and service points with limited capacity, which can potentially lead to an increase in traffic flow and impact commuter’s travel time [8]. The adoption of imposing partial public curfews in cities resulted in high traffic congestion on the main streets, particularly around shopping areas, right after a curfew is lifted. For instance, the population of Riyadh City is approximately under 5 million with about 985,000 vehicles flooding the city main streets daily [9]. Since post-curfew traffic may adversely impact main streets, it is of great importance to measure the impacts of different curfew policies on traffic flows. To anticipate the effect of the public curfew policies on the urban traffic system in Saudi Arabia, it is important to understand different factors that affect the commuter decision about early or delayed post-curfew departure to shopping areas. This would be of high importance in supporting decision-making and giving more useful insights on the implementation of suitable public curfew policies.
Since the beginning of the pandemic, several studies have been conducted on the impacts of COVID-19 on urban traffic and transportation systems. Bucsky [10] investigated the changes in traffic behavior in Hungary during the COVID-19 pandemic and found significant changes in travel mode and decline in public transit users by almost 80%, while car usage increased to 65% in response to the spread of the disease. This was supported by Jenelius and Cebecauer [11], who found almost a 60% decrease in public transit users in Sweden during the COVID-19 outbreak. Abdullah et al. [12] developed a binary logistic model to assess commuters’ travel mode choices (public and private) during the pandemic and identified gender, income, job type, education level, vehicle ownership, and safety precautions as important influencing factors. Other researchers reported the impact of COVID-19 on consumer travel behavior. Consumer grocery trips right after curfew (which was referred to as panic buying) was observed to increase during the COVD-19 pandemic compared to other types of shopping and leisure activities [13,14,15,16,17]. The type of shopping was reported to be dependent on the curfew duration and restrictions. The impact of the COVID-19 pandemic on both traffic volume and car accidents was studied by Katrakazas et al. [15] using tracking technologies in Greece and Saudi Arabia. Their study showed a reduction in travel volume with an almost 41% reduction in car accidents. Similar findings were observed by Saladie et al. [16], who found a 63% reduction in travel volume along with 74% decline in car accidents in Spain during the year of 2020. In some of the European countries such as Sweden, Germany, and Austria, the public preferred travelling for short distances compared to long distances. Furthermore, the number of people travelling to commercial areas and city centers decreased in response to the lockdowns and COVID-19 restrictions in those countries [18,19].
While the above studies focused on the impact of the COVID-19 pandemic on changes in public travel modes and transportation safety, limited studies exist on the COVID-19 impact on traffic congestion. Huang et al. [20] conducted a data-driven analysis of travel behavior during the pandemic in China. Various factors were found to influence the travel behavior and traffic congestion, such as means of transportation, distance, and location. Muley et al. [21] studied the impact of staged and sequential COVID-19 preventive measures on traffic mobility in several intersections in Qatar. Their study found that although the volumes were significantly reduced to almost 30%, traffic patterns were similar before and after the implementation of the measures. Moreover, traffic violations and accidents showed a drop of 73% and 37%, respectively, 56t as a response to the preventive measures. Recently, Xu et al. [22] investigated the changes in traffic patterns before and during the COVID-19 pandemic in Shanghai, China. Their study found that the central areas were more affected by the travel restrictions during the pandemic compared to suburban areas, in which a decrease in the traffic congestion was observed. An analytical framework was proposed based on the traffic characteristics and areas to help with policy decision-making of urban road transportation systems during the pandemic. Loo and Huang [23] studied the changes in traffic congestion patterns due to the enforced curfew in Hong Kong by calculating a congestion index. Their study showed that under the curfew law, morning peak-hour congestion was reduced with a significant drop in congestion index in the central areas and urban cores.
Like other countries, after the nationwide spread of the COVID-19 outbreak in Saudi Arabia, partial and total public curfew policies were adopted to mitigate the transmission rate of the virus. From the review of the literature, while the majorities of the studies focused on the impact of COVID-19 on travel modes and car accidents, none of the past studies have identified the factors that affect the commuter decision about early or delayed post-curfew departure to shopping areas and city centers. Hence, it is difficult for the cities’ transportation ministries to identify the high congestion periods during the time of no curfew and subsequently plan and implement traffic management strategies.
To the best of our knowledge, no methodology in the literature assesses traffic congestion during the no curfew period based on socio-demographic data of an urban neighborhood’s residents. To avoid traffic congestion, the present study primarily aimed to investigate the commuter’s decision of home-to-shopping center departure (HSD) after a public curfew is lifted. Primary objectives of the study are to: (i) assess the impact of different internal (commuter) and external (shopping center) factors affecting traffic congestion through interview-based surveys, (ii) perform statistical analysis to establish the significance of the factors on the departure delay decision, and (iii) develop a multicriteria analysis-based approach to come up with the traffic congestion hazard period within the no curfew timing. The results of this study are intended to support decision makers in anticipating possible traffic congestion due to different curfew strategies and developing or reviewing appropriate traffic management strategies accordingly.
2. Materials and Methods
2.1. Traffic Congestion Hazard Evaluation Framework
Figure 1 presents the traffic congestion hazard evaluation framework developed in the present study. First, potential internal (commuter related) and external (shopping center related) departure delay factors (DF) were identified through published literature and expert opinion in brainstorming sessions. Internal factors cover commuters’ household and socioeconomic characteristics (e.g., age, education, and family size), while external factors are associated with the type (commuter’s choice), location (distance from commuter’s residence) of the shopping area, and the size of the commuter’s city. Subsequently, a questionnaire survey was developed that encompassed all the factors and the departure delay duration (DD) in the form of dichotomous or multiple-choice questions. After securing ethics approval from the funding agency, the online version of the questionnaire survey was distributed to around 300 participants. The sample size selection process considered participants with different age groups, family sizes, job sectors, and education levels, residing in cities of different sizes (small, medium, and large). Details for city size classification are given in the subsequent sections. Third, the responses received were statistically analyzed using Chi-square and Cramer’s V tests to establish the association between the DF and DD. Fuzzy set theory has been recognized in dealing with imprecise and subjective judgment [24,25] and was found as an appropriate approach for the linguistic nature of available data in the present study. Hence, spatial variations of traffic congestion during the no-curfew interval were assessed using fuzzy synthetic evaluation (FSE).
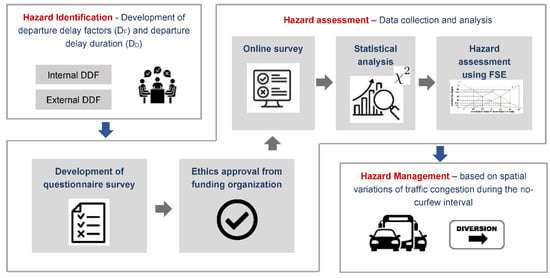
Figure 1.
Vignette of Traffic Congestion Hazard Evaluation Framework.
2.2. Development of Departure Delay Factors and Questionnaire Survey
After the implementation of curfew, traffic congestion was recognized in the central cities of almost all the provinces across KSA. Adopting a partial curfew policy may exacerbate the problem of congested roads in large cities such as Riyadh City, capital of Saudi Arabia. Nevertheless, shopping areas in small- to medium-sized cities also face traffic congestion prone to post-curfew traffic. Although large cities like Riyadh, with a population of around 7.4 million, are more prone to congestion, capital cities of other provinces also face the similar issues during the no-curfew period. The cities of Buraydah, with a population of around 0.7 million, and Madinah, with 1.52 million, were classified as medium-sized cities, while Hail City, with a population of 407,000, was classified as a small sized-city [26,27].
To determine the post-curfew traffic congestion problem in shopping areas, the response of commuters’ departure times after curfew is lifted needs to be known. In order to understand the commuter perception of delaying the post-curfew departure time, different internal and external DDF and expected DD were identified. Subsequently, both the DF and DD were translated into a survey format, which was approved by the ethics department at Qassim University, Saudi Arabia. Table 1 presents the DF, DD, and the corresponding questions asked from the commuters. The online questionnaire survey was sent to varying people living in Riyadh, Buraydah, Madinah, and Hail cities using an online questionnaire. Each observation in the travel survey represents the perception of one commuter of how long he (or she) delayed their departure based on the internal factors. The survey targeted individual households commuting from their houses between 6:00–10:00 am, the no-curfew period.

Table 1.
Internal and external factors for evaluating commuter home-to-shopping center departure delay after COVID-19 curfew timings.
A random sampling approach was used to select a representative sample. First, common characteristics (internal factors) were identified such as family size (1.1 in Table 1), job type (1.3), age (1.4), and education level (1.5). Particular to the COVID-19 situation, these characteristics were used in a study on the COVID-19 impact on transportation mode selection [12]. Second, characteristics (DF) specific to the present study, such as involvement in activities (1.2), number of vehicles (1.6), and number of children (1.7), and availability of driver (1.8) were identified using expert opinion and personal observations. Finally, recent studies were consulted to identify the characteristics (external factors) affecting traffic congestion in urban areas, such as size of city [28] and distance and type of shopping center [29].
In Table 1, we tried to capture the commuter’s personal household related aspects through the internal DF. The last column of the table presents the related questions asked from the commuter. For example, the households with many family members may decide for a longer delay to their home-to-shopping center departure (HSD). Similarly, older commuters or the families with more children may also delay their departures for grocery shopping. Generally, people working in the private sector are busier and may delay their trips. Availability of more than one car and a driver can also relax an individual, which delays HSD. We also thought that external factors, such as shopping center of choice (e.g., convenient store, medium-sized market, and supermarket) and its availability in the near vicinity, can also influence the commuter’s decision and thus included them in the questionnaire. Finally, the information regarding the departure delay duration was also gathered through the questions mentioned in the last column.
2.3. Statistical Analysis
The data collected through the questionnaire provided the information regarding both the DF and DD. Statistical analysis of the collected data was performed to estimate the percentage frequencies of all the DF for different DD (long, moderate, and short delay). Before using this data to the proposed model for identifying the peak congestion period, the Chi-square independence test established the level of association (weak, moderate, or strong) between the DF and DD. An example of the null and alternative hypothesis for family size is given in the following.
H0:
The null hypothesis: Family size of the commuter is a perfectly independent factor and does not affect the home-to-shopping center departure delay.
Ha:
The alternative hypothesis: Family size of the commuter is a dependent factor and somehow affects the home-to-shopping center departure delay.
Similar hypotheses were applicable for the remaining DD. The Chi-square method is based on expected frequencies at which the null hypothesis holds. The expected frequencies for all the DF against the given DD were calculated using the following relationship [30]:
where eij denotes the expected frequency, oi and oj presents the marginal column and row frequencies respectively, and N is the total number of responses.
As the oi and oj differ, the residuals were estimated as:
A larger rij value (absolute) denotes that there is a large difference between the observed responses and the null hypothesis. Subsequently, all the residuals were added to estimate the chi-square test statistic as:
In the next step, the independence of the variables in the given population, in terms of p-value, was estimated for a given and degree of freedom using the following equation.
where i and j are the number of rows and column (categories) in the contingency table.
To reject the null hypothesis of independence, the calculated chi-squared values were compared with the critical values from the chi-squared distribution at p < 0.05. The critical values are 3.84, 5.99, 7.82, 9.49, 11.07, and 12.59 with corresponding df of 1, 2, 3, 4, 5, and 6. The chi-square values higher than the critical values reject the null hypothesis of independence.
As the performance of the chi-square test depends on an adequately large sample size, the significance estimated by this test does not inform the degree of effect. Therefore, the effect size can give the magnitude of effect. The strength of association between the DF and DD was estimated using the effect size (ES) of the chi-square test for each DF using Cramér’s V, which essentially is a kind of Pearson correlation for categorical variables as used in the present study. It was determined by:
where n is the total number of responses, dividing by the number, and taking the square root. Cohen [31] presented the interpretation of effect size using the Cramér’s V method. For the df of 5 or higher, the fields have small association if ES < 0.04, medium association if 0.04 < ES ≤ 0.13, and large association if ES > 0.22 [31].
2.4. Traffic Congestion Hazard Period Assessment
To identify the time segment with the highest congestion during the no-curfew interval, the following assumptions were established through the brainstorming sessions supported by practical observations in Saudi Arabia and news reporting by electronic and print media during the era of COVID-19 curfews around the globe:
- Commuters with immediate (no delay) departures contributed to traffic congestion in the earliest time segment of the no-curfew period.
- Commuters with shortly (<15 min) delayed departures contributed to traffic congestion in the early-middle time segment of the no-curfew period.
- Commuter with moderately (15–30 min) delayed departures contributed to traffic congestion in the middle time segment of the no-curfew period.
- Commuters with long (>30 min) delayed departures contributed to traffic congestion in the last time segment of the no-curfew period.
The statistical analysis in the previous section established the linkage between the DF and DD. The information obtained from survey responses was aggregated using the multicriteria evaluation model to identify the time segment with the highest traffic congestion hazard. The hierarchical-based Fuzzy Synthetic Evaluation (FSE) approach presented in Figure 2 aggregated the information in the form of DF. The step-by-step procedure given in the following was modified from Zhao et al. [25]:
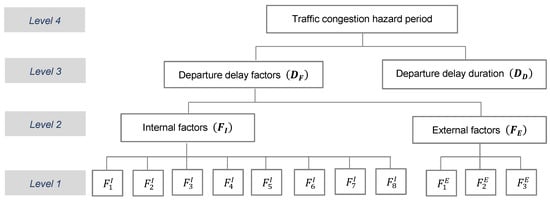
Figure 2.
Hierarchical-based Fuzzy Synthetic Evaluation approach for assessing traffic congestion period. Details of internal and external factors shown at level 1 are given in Table 1.
Levels 1 and 2: Estimate the impact of internal and external factors on departure delay
The impact for each internal factor (FI) was obtained from the questionnaire survey given in Table 1. The UoD linguistically defines a four level-rating (Sj = 0, 1, 3, 5) to evaluate the impact as no delay (0), short delay (1), moderate delay (3), and long delay (5). The term essentially describes the degree of association of each factor to these levels. The following equation describes this step in the matrix form:
where represents the internal factor (i = 1, 2, …, n) and n is the total number of internal factors.
The impact of each internal factor () was calculated by the following equation:
To calculate the overall impact of internal factors at level 2 of Figure 2, the importance weight of each internal factor was estimated using the following equation:
The FSE method aggregates the weighted matrix given in Equation (7) and the evaluation matrix given in Equation (6) and presents the results in the form of the following equation to estimate the membership functions for each internal factor, where i = 1, 2, …, t:
Knowing the membership functions of t number of factors’ groups at level 2, the overall impact of internal factors () can be estimated as:
Similarly, the overall impact of external factors () was estimated as:
Levels 3 and 4: Calculate the overall impact of departure delay factors and departure delay duration on the traffic congestion hazard period
To estimate the impact of DF and DD on traffic congestion hazard period, their respective importance weights were estimated using the following equation:
where are the importance weights of the two sub-groups ( and ) of departure delay factors, t represents the number of groups (q = 2), and i denotes the number of factors under (k = 8) and (k = 3).
Furthermore,
Similarly,
and the impact of departure delay duration (DD) at level 3 can be estimated as:
Finally, the impact of DF was aggregated with the DD at level 4 to estimate the traffic congestion hazard period (HTC) as:
3. Results
3.1. Survey Responses
The online survey was sent to around 250 respondents in June 2020. After the asked time to return the questionnaire, a satisfactory response rate of 20% was received from 50 participants residing in the four provinces of the country [32]. As the survey responses provided the opinion of the participants about both the departure delay and delay duration, statistical analysis estimated the percent frequencies for all the DF against different DD. Figure 3a–k presents the stacked bar charts for all the internal and external departure delay factors as given in Table 1. Figure 3a shows that overall, the small-sized families with less than 10 persons had lesser tendency to delay the HSD, while 80% of the large-sized families with more than 10 persons delayed their HSD for over 30 min. As per Figure 3b, the respondents busy in some work at home mostly delayed their departure, i.e., 40% of the busy persons delayed their departure for over 30 min. It was also found that people who work in the private sector (usually busy schedule of possible online working) delay their shopping visits (Figure 3c). The results revealed that 80% of the respondents working in non-profit organizations did not delay their HSD, while only 43% of public sector employees departed immediately after the curfew lift.
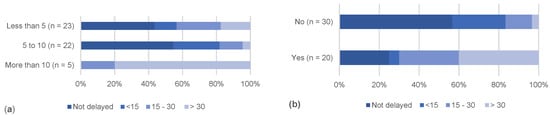
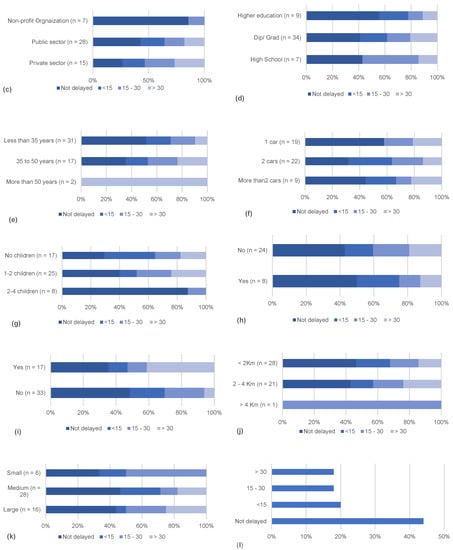
Figure 3.
Stacked bar charts showing percentage frequencies for each departure delay factor for each departure delay duration: (a) family size, (b) involvement in other activities, (c) nature of job, (d) education level, (e) age, (f) number of vehicles, (g) number of children, (h) availability of driver, (i) availability of shopping center of choice, (j) distance to shopping center, and (k) size of the city; (l) percentage distribution of departure delay.
Figure 3d illustrates that highly educated people have a general tendency to go early for shopping after lifting of curfew period. Around 80% of the highly educated respondents reported their departure within 15 min after the curfew lift. It can be seen in Figure 3e that around 55% of people older than 35 years of age delay their HSD more than 15 min in comparison to 30% of younger respondents. In Figure 3f, commuters having more than one vehicle have more leisure to delay their shopping visits. Around 60% of people with one car immediately depart after the curfew timing, while around 70% of owners with two vehicles leave after 15 min. Larger families with more children are generally busy and delay their HSD (see Figure 3g). For instance, around 90% families with more than two children do not immediately depart to shop. Availability of driver is another factor that can delay the home to shopping area departure. Figure 3h shows that 40% of households with drivers delayed their trips for more than 15 min in comparison to 26% of households with no drivers.
Figure 3i shows that the commuters (65%) who do not reside nearby the shopping center of their choice usually delay their HSD, because by delaying their trip they might face less traffic. Likewise, longer distance to the shopping center of commuters’ choice also leads to HSD delay, as illustrated in Figure 3j. Figure 3k reveals that the citizens of smaller cities leave for shopping within 30 min after the lift of curfew period. Finally, Figure 3l displays that 44% of the commuters did not delay their shopping visits, while 18% of them delayed their trips for more than 30 min. The distribution of departure delay shown in Figure 3l and the impacts of different factors described in Figure 3a–k demand a more detailed methodology to identify the potential period with highest traffic congestion.
3.2. Statistical Analysis
Prior to applying the survey findings to assess the traffic congestion hazard period (HTC) using the hierarchical framework presented in Figure 2, the level of association between the DF and DD was established using the Chi-square independence test. The null and alternate hypothesis were established between all the internal and external departure delay factors and departure delay duration. An example for family size is given in Section 2.3. Table 2 presents the rationale to develop the null and alternative hypothesis for all the departure delay factors. The table also presents the results of Chi-square tests, which are described in the following section.

Table 2.
Hypothesis and the level of association between DF and DD.
Due to space limitations, the detailed calculations for establishing the association between family size and DD are not given here. First, the obtained data was populated in the contingency table that shows the observed frequency of responses. Table 3 displays the information as percentages for better understanding and was used to develop Figure 3. There are three family size categories and four departure delay categories. The data clearly shows that 44% of the respondents did not delay HSD, while 38% delayed their shopping trips for more than 15 min. The table also shows that 80% of the commuters with family size larger than 10 delayed their HSD for more than 30 min.

Table 3.
Observed percentage frequencies for family size (n = 50).
The subsequent step establishes the expected frequencies, which are essentially the frequencies we expect in the observed data if the null hypothesis holds. The expected frequencies calculated using Equation (1) are given in Table 4. Next, the residuals as the difference between the observed and expected frequencies were determined using Equation (2). Table 5 shows the Chi-square values for each cell of the contingency table determined from Equation (3). The final value (sum of the columns’ total of Table 5) was found to be 18.8. Equation (4) estimated the degree of freedom (df = 6), which informs the probability of finding . Finally, the scale of association between the groups was found using Equation (5). Chi-square values for df = 6 and p-value < 0.05 showed that only two internal factors (family size and involvement in other activities) and one external factor (availability of shopping center of choice) significantly depend on departure delay duration with Chi-squared values higher than the critical values. However, with the small number of responses (n = 50), Cramer’s V test established the magnitude of effect for all the internal and external factors. Table 2 presents that all the factors have a large magnitude of effect, except education level and presence of driver in a household. Hence, all the selected factors were used for assessing the HTC with the help of the FSE methodology described in Section 2.4.

Table 4.
Expected frequencies for perfectly independent variables.

Table 5.
Contingency table showing calculated Chi-square values.
3.3. Assessment of Traffic Congestion Hazard Period
Equation (6) calculated the degree of association of each factor (internal of external) to the four-level-rating (Sj = 0, 1, 3, 5) as described in Section 2.4. The term for family size was calculated as:
The impact of family size was estimated using Equation (7) as:
Similarly, for all the internal factors were calculated.
Importance weights of all the internal factor were estimated to calculate the overall impact of internal factors at level 2 of Figure 2, using Equation (8):
Similarly, the weights of all the internal and external factors were calculated.
Subsequently, to apply FSE, Equation (10) estimated the membership functions for internal factors:
Similarly, the membership functions for external factors were estimated as:
Then, with known membership functions of t number of factors’ groups at level 2, the overall impact of each group ( and was estimated using Equations (11) and (12):
At level 4, the impacts of DF and DD on HTC were aggregated by estimating their respective importance weights using Equation (13):
and
and
Similarly,
Finally, the impacts of DF and DD were aggregated to estimate the traffic congestion hazard period (HTC) using Equation (19) as:
4. Discussion
The methodology developed in the present research contains two primary phases. The first phase identifies internal and external factors encompassing socio-economic variables of the commuters residing in small, medium, and large cities which can affect departure (early or late) decision. All the internal and external factors were identified through literature and expert opinion during brain storming sessions. The results illustrated in Section 3.1 highlights some important characteristics of the commuters during pandemic restrictions. Man-Keun et al. [33] investigated the impact of family size on grocery shopping and found that large-sized households prefer large discount stores even if not located in the near vicinity. Preparing for grocery shopping for large families also takes much longer in comparison to small families in order to find several missing items to meet the needs of family members [34]. Age, education level, and job type play an important role in decisions to commute after curfew lift. Their findings are in line with a recent past study on selection of traffic modes during COVID-19 by Abdullah et al. [12]. While evaluating the impact of job sector on commuter departure decision, it was also reported that private sector employees remained busier than public sector ones due to a faster transition and technical support in the private sector during the COVID-19 pandemic [35].
The study considered size of the city as a factor contributing to traffic congestion after curfew lift. High congestion has always been associated with larger cities [36]; nevertheless, ever-increasing population, inadequate capacity of streets, and mixed land uses pose diverse impacts of traffic in smaller cities as well, such as high accident frequencies in urban centers [28]. The findings of the present study revealed that departure patterns in small- and medium-sized cities are almost consistent with those in large cities during the COVID-19 period. Another reason for such findings is that the small- and medium-sized cities in this study are also capital cities of their respective provinces, with all the types of commercial, public, and residential land uses as large cities. Statistical analysis established that almost all the factors have large magnitude of effect, except education level and presence of driver in a household.
The past studies effectively employed FSE for risk assessment based on human perception and uncertain expert judgment. Akter et al. [37] used FSE and Intergovernmental Panel on Climate Change (IPCC) methods to develop risk assessment maps. They found that FSE eliminated the uncertainties associated with expert judgment in different IPCC methods and generated one risk map for a known hazard domain. Zhao et al. [28] used the FSE approach for risk assessment of green building projects in Singapore. Their approach aggregated the likelihood of occurrence and risk criticality of risk factors. They used a questionnaire survey method to interview experienced (over 10 years) project managers to ascertain the risks involved in green building projects. Their approach was modified for traffic hazard assessment in the present research. Same values of DF and DD affirm the computational accuracy of the proposed approach. Based on the UoD defined prior to conducting the commuter survey, the calculated HTC value of 1.64 ascertains the highest congestion after 20 min of curfew lift, where “0” corresponds to immediate home-to-shopping center departure right after the curfew lift; “1” to a departure within 15 min; “3” to a delay between 15 and 30 min; and “5” to a departure delay of more than 30 min.
Figure 4 illustrates a theoretical display of the highest traffic congestion hazard period due to home-to-shopping center departure delay by commuters. Based on the questionnaire survey, the findings of this study show that 44% of the people depart as soon as the curfew lifts. Without much delay, an additional 20% of commuters leave their homes (within 15 min of the lift) for shopping that further increase the traffic congestion on the urban roads and streets. In the next 15 min (between 15 and 30 min after the lift), almost 82% of the total commuters have left their homes for shopping. The remaining 18% of commuters, who leave their homes after half an hour, are assumed to have a mindset of using the last part of the no curfew period. The behavior of the commuters illustrated in Figure 4 directs to the traffic congestion hazard in the early part of the no curfew period. The figure also shows that around 60% to 80% of the residents in an area occupy the capacity of urban streets and parking areas during his period. As per Figure 4, the highest possible congestion can be expected after half an hour of curfew lift to the end of the first hour. Responsible traffic agencies can adopt appropriate traffic management measures during this part of the day during a pandemic. The measures may include the following actions by a traffic regulatory agency [38]: reducing the need and length of a trip, promoting nonmotorized and public transport, promoting carpooling, shifting peak-hour travel, and diverting travel from congested locations. For the specific scenario of traffic in Saudi Arabia, the last two measures seem more practical.
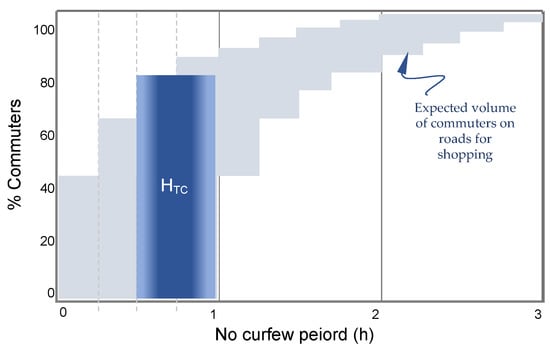
Figure 4.
A theoretical illustration of highest traffic congestion period after COVID-19 curfew timings. Assumed no curfew period is 3 h based on 2021 no curfew timings in Saudi Arabia.
Modern transport system models (TSM) integrated with traditional approaches can evaluate the potential effects of traffic demand variations during COVID-19. For instance, floating car data can be used in TSM supported with big data for travel demand analysis [39]. Using the proposed methodology, the regulators can use socio-demographic data to identify the traffic congestion hazard period after the curfew timing. The data regarding the internal or external factors with higher significance and large effect size should be given importance. Interestingly, such internal DF need simple and easily available data from the General Authority of Statistics in Saudi Arabia, such as family size, nature of job, age of the commuter, and number of children in a household. The only important external factor is availability of shopping center of choice in the near vicinity. As most of the cities in Saudi Arabia possess similar cultural practices, layouts of urban streets, and types of shopping centers, the percentages found in the present research can be used to assess these factors. Accordingly, the traffic regulators can identify the highest congestion period in an urban setting during the pandemic era.
The subjective organization of the proposed traffic congestion hazard assessment framework during pandemics’ curfew periods is a limitation of the present study. Future studies following a similar approach using larger data sets can establish the credibility of the objective source basis and a practical reference value of the methods used.
5. Conclusions
Traffic congestion is evident after curfew lifting during the era of the COVID-19 pandemic. In an urban neighborhood, a congestion episode depends on the percentage of commuters leaving for home-to-shopping centers over the span of the no curfew period. The study found that departing early or delaying the shopping trip depends on certain internal (commuter related) and external (shopping related) factors. Among internal factors, family size and business (involvement in other activities) were found to be the most significant factors affecting the departure delay, while availability of shopping center of choice significantly affected the decision amongst the external factors. Age, number of children, and size of the city also influenced the commuters’ decision about delaying the departure. Commuters’ departure patterns in the small- and medium-sized cities (capitals of respective provinces) were found to be consistent with large cities during the COVID-19 period, primarily due to similar commercial, public, and residential activities.
Chi-square and Cramer’s V tests established the statistical significance of the association between the departure delay factors and the departure delay duration. Chi-square values widely ranged between 0.8 and 18.8 for internal factors and from 5.1 to 9.5 for external factors. Cramers’ V established large associations for most of the factors, except education level and availability of driver in a household. Fuzzy synthetic evaluation (FSE) can effectively ascertain the period of highest traffic congestion based on the commuters’ responses. The study revealed that traffic congestion hazard in the early part (precisely the second half of the first hour) after the curfew lift needs particular attention of the traffic regulatory agencies. Future studies can validate the findings of the present research by implementing the proposed approach in different areas and conducting traffic monitoring studies after the curfew lift during pandemics.
Author Contributions
M.A. (Majed Alinizzi), funding, supervision, conceptualization, and writing—review and editing; H.H., conceptualization, methodology, analysis, validation, and writing-original draft preparation, M.A. (Mohammad Alresheedi), data collection, methodology, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research, Qassim University, grant No. 10014-qec-2020-1-1-L.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the shareable data is given in the main text.
Acknowledgments
The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, for the financial support of this research under the number (10014-qec-2020-1-1-L) during the academic year 1440 AH/2020 AD.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wu, F.; Zhao, S.; Yu, B.; Chen, Y.; Wang, W.; Song, Z.; Hu, Y.; Tao, Z.; Tian, J.; Pei, Y.; et al. A new coronavirus associated with human respiratory disease in China. Nature 2020, 579, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Jiang, A.; Gong, L.; Luo, L.; Guo, W.; Li, C.; Zheng, J.; Li, C.; Yang, B.; Zeng, J. Temperature significant change COVID-19 transmission in 429 cities. medRxiv 2020. [Google Scholar] [CrossRef]
- WHO. WHO Characterizes COVID-19 as a Pandemic; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Worldometer. Available online: https://www.worldometers.info/coronavirus/#countriesm (accessed on 24 January 2022).
- Kim, K. Impacts of COVID-19 on transportation: Summary and synthesis of interdisciplinary research. Trans. Res. Interdiscip. Perspect. 2021, 9, 100305. [Google Scholar] [CrossRef] [PubMed]
- Cartenì, A.; Henke, I. Transportation Planning, Mobility Habits and Sustainable Development in the Era of COVID-19 Pandemic. Sustainability 2022, 14, 2968. [Google Scholar] [CrossRef]
- Russo, F.; Corrado, R. Regional transport plans: From direction role denied to common rules identified. Sustainability 2021, 13, 9052. [Google Scholar] [CrossRef]
- Khawagi, W. The problem of traffic congestion in Saudi Arabia. Int. J. Sci. Eng. Res. 2017, 8, 1632–1638. [Google Scholar]
- Majhad, H.; Bramantoro, A.; Syamsuddin, I.; Yunianta, A.; Basori, A.; Prabuwono, A.; Barukab, O. A traffic congestion framework for smart Riyadh City based on IoT services. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 2018. [Google Scholar] [CrossRef][Green Version]
- Bucsky, P. Modal share changes due to COVID-19: The case of Budapest. Transport. Res. Interdiscip. Perspect. 2020, 8, 100141. [Google Scholar] [CrossRef] [PubMed]
- Jenelius, E.; Cebecauer, M. Impacts of COVID-19 on public transport ridership in Sweden: Analysis of ticket validations, sales and passenger counts. Transp. Res. Interdiscip. Perspect. 2020, 8, 100242. [Google Scholar] [PubMed]
- Abdullah, M.; Ali, N.; Javid, M.A.; Dias, C.; Campisi, T. Public transport versus solo travel mode choices during the COVID-19 pandemic: Self-reported evidence from a developing country. Transp. Eng. 2021, 5, 100078. [Google Scholar] [CrossRef]
- Parady, G.; Tanaguchi, A.; Takami, K. Travel behavior changes during the COVID-19 pandemic in Japan: Analyzing the effects of risk perception and social influence on going-out self-restriction. Transp. Res. Interdiscip. Perspect. 2020, 7, 100181. [Google Scholar] [CrossRef]
- Abdullah, M.; Dias, C.; Muley, D.; Shahin, M.d. Exploring the impacts of COVID-19 on travel behavior and mode preferences. Transp. Res. Interdiscip. Perspect. 2020, 8, 100255. [Google Scholar] [CrossRef] [PubMed]
- Katrakazas, C.; Michelaraki, E.; Sekadakis, M.; Yannis, G. A descriptive analysis of the effect of the COVID-19 pandemic on driving behavior and road safety. Transp. Res. Interdiscip. Perspect. 2020, 7, 100186. [Google Scholar] [CrossRef] [PubMed]
- Saladie, O.; Bustamante, E.; Gutierrez, A. COVID-19 lockdown and reduction of traffic accidents in Tarragona province, Spain. Transp. Res. Interdiscip. Perspect. 2020, 8, 1000218. [Google Scholar] [CrossRef] [PubMed]
- Loske, D. The impact of COVID-19 on transport volume and freight capacity dynamics: An empirical analysis in German food retail logistics. Transp. Res. Interdiscip. Perspect. 2020, 6, 100165. [Google Scholar] [CrossRef]
- Dahlberg, M.; Edin, P.-A.; Grönqvist, E.; Lyhagen, J.; Östh, J.; Siretskiy, A.; Toger, M. Effects of the COVID-19 Pandemic on Population Mobility under Mild Policies: Causal Evidence from Sweden. arXiv 2020, arXiv:2004.09087. [Google Scholar] [CrossRef]
- Heiler, G.; Reisch, T.; Hurt, J.; Forghani, M.; Omani, A.; Hanbury, A.; Karimipour, F. Country-wide mobility changes observed using mobile phone data during COVID-19 pandemic. In Proceedings of the 2020 IEEE International Conference on Big Data, Atlanta, GA, USA, 10–13 December 2020. [Google Scholar]
- Huang, J.; Wang, H.; Fan, M.; Zhuo, A.; Sun, Y.; Li, Y. Understanding the impact of the COVID-19 pandemic on transportation-related behaviors with human mobility data. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 3443–3450. [Google Scholar]
- Muley, D.; Ghanim, M.; Mohammad, A.; Kharbeche, M. Quantifying the impact of COVID-19 preventive measures on traffic in the State of Qatar. Transp. Policy 2021, 103, 45–59. [Google Scholar] [CrossRef]
- Xu, P.; Li, W.; Hu, X.; Wu, H.; Li, J. Spatiotemporal analysis of urban road congestion during and post COVID-19 pandemic in Shanghai, China. Transp. Res. Interdiscip. Perspect. 2022, 13, 100555. [Google Scholar] [CrossRef]
- Loo, B.; Huang, Z. Spatio-temporal variations of traffic congestion under work from home (WFH) arrangements: Lessons learned from COVID-19. Cities 2022, 124, 103610. [Google Scholar] [CrossRef] [PubMed]
- Alinizzi, M.; Haider, H.; Almoshaogeh, M.; Alharbi, F.; Alogla, S.M.; Al-Saadi, G.A. Sustainability Assessment of Construction Technologies for Large Pipelines on Urban Highways: Scenario Analysis using Fuzzy QFD. Sustainability 2020, 12, 2648. [Google Scholar] [CrossRef]
- Zhao, X.; Hwang, B.G.; Gao, Y. A fuzzy synthetic evaluation approach for risk assessment: A case of Singapore’s green projects. J. Clean. Product. 2016, 115, 203–213. [Google Scholar] [CrossRef]
- Saudi Ministry of Health. Available online: https://www.moh.gov.sa (accessed on 5 January 2022).
- Saudi Ministry of Interior. Available online: https://www.moi.gov.sa (accessed on 5 January 2022).
- Wang, M.; Debbage, N. Urban morphology and traffic congestion: Longitudinal evidence from US cities. Comput. Environ. Urban Syst. 2021, 89, 101676. [Google Scholar] [CrossRef]
- Hawkins-Mofokeng, R.; Tlapana, T.; Ssemugooma, D.K. Effects of Traffic Congestion on Shopping Location Choice in the Greater eThekwini Region. J. Bus. Manag. Rev. 2022, 3, 372–386. [Google Scholar] [CrossRef]
- SPSS Tutorials. Available online: https://www.spss-tutorials.com/chi-square-independence-test/ (accessed on 10 February 2022).
- Cohen, J. Statistical Power and Analysis for the Behavioral Sciences, 2nd ed.; Hisdale, N.J., Ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988; pp. 79–80. [Google Scholar]
- Visser, P.S.; Krosnick, J.A.; Marquette, J.; Curtin, M. Mail surveys for election forecasting? An evaluation of the Columbus Dispatch poll. Public Opin. Q. 1996, 60, 181–227. [Google Scholar] [CrossRef]
- ManKeun, K.; Lee, Y.; Kim, S. The influence of household types on food and grocery store choices. J. Rural Dev. 2018, 41, 89–121. [Google Scholar]
- Thomson, E. Family Size Preferences, International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 805–808. [Google Scholar]
- Deloitte, Perspectives-Working from Home during the Coronavirus Crisis Is Far Less Common among Public Authorities than in the Private Sector. Available online: https://www2.deloitte.com/ch/en/pages/public-sector/articles/working-from-home-during-coronavirus-less-common-among-public-authorities.html (accessed on 27 July 2022).
- Chang, Y.S.; Lee, Y.J.; Choi, S.S.B. Is there more traffic congestion in larger cities?—Scaling analysis of the 101 largest US urban centers. Transp. Policy 2017, 59, 54–63. [Google Scholar] [CrossRef]
- Akter, M.; Momtaz, J.; Rubaiya, K.; Dewan, S.K.; Anisul, H.; Munsur, R.; Mashfiqus, S. Risk assessment based on fuzzy synthetic evaluation method. Sci. Total Environ. 2019, 658, 818–829. [Google Scholar] [CrossRef] [PubMed]
- Strickland, S.G.; Berman, W. Congestion Control and Demand Management, Public Road-Winter; Federal Highway Administration: Washington, DC, USA, 1995; Volume 58.
- Croce, A.; Musolino, G.; Rindone, C.; Vitetta, A. Estimation of travel demand models with limited information: Floating car data for parameters’ calibration. Sustainability 2021, 16, 8838. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).