Calibration Methods of a Portable Polarizing System for Monitoring Optically Inhomogeneous Media

Abstract

Theoretical aspects of methods for calibrating Stokes polarimeters are considered. The prospects and opportunities for implementing the presented methods for calibrating portable polarization systems used in biology and medicine are determined. Based on a comparative analysis, a method for calibrating a portable Stokes polarimeter for medical applications is proposed. The chosen method provides the smallest error in measuring the parameters of the Stokes vector for calculating the parameters of optical anisotropy and researching the polarization properties of biological tissues. A series of experimental research and statistical analysis of the spatial distributions of the polarization parameters of the calibration sample was carried out to use the results for forming the instrument matrix of the developed Stokes polarimeter during calibration.

1. Introduction

Currently, optoelectronic systems are being actively developed to research the phenomena that accompany the propagation of optical radiation in inhomogeneous media, the refractive index of which is not constant but depends on the coordinates.

Such systems are most in demand in biology and medicine for working with biological media, which are complex and heterogeneous complexes belonging to the class of highly scattering turbid media. At the same time, polarization systems are widely used, as they demonstrate the possibility of localization and visualization of structural inhomogeneities of biological tissues at different depths from tens of micrometers to several centimeters.

In biological and medical research, practical methods of polarization mapping of biological tissues are used, based on general approximations, such as the Mueller–Stokes formalism [1,2,3].

The implementation of polarization methods not only for scientific research but also for solving the problems of operational diagnostics of the state of biological tissues calls for the development of portable systems that use the achievements of modern technologies to miniaturize the operating schemes of devices and visualize measurement results. The active development of smartphone production technologies makes it possible to use their capabilities in the development of portable polarization systems for various biomedical applications [4,5,6,7,8].

Portable polarization systems are most in demand for monitoring the surface structures of biological tissues and media in dermatology, as well as for diagnostic imaging using a smartphone as an attachment [5,6]. The use of portable optoelectronic systems to minimize the invasiveness of procedures in endoscopy, microscopy, and surgery has also been reported [7,8].

Ensuring the required accuracy in estimating the polarization characteristics of radiation at the output of an optically inhomogeneous media is associated with solving the hardware problems of taking into account specific polarization distortions inherent in two main schemes for obtaining polarization readings: serial or parallel. In a sequential scheme, during the exposure of the Stokes image, at least four polarizers based on wide-aperture film polaroids must move in front of a single objective [9,10]. In a parallel scheme, in the presence of one objective, it is necessary to use beam splitters or increase the number of independent identical optoelectronic measuring channels [11,12].

The problems of minimizing hardware errors and weight and size characteristics of portable systems can now be drastically reduced due to the advent of micro polarizers—Metallic Nanowire Polarization Filters formed directly on the photosensitive elements of CMOS photodetectors [13].

In addition, to minimize errors in optoelectronic paths of portable polarization systems, it is important to use various calibration methods. Recently, various methods have been developed for calibrating polarimeters depending on the construction scheme [14,15,16,17,18,19,20].

Previously, the effect of errors of polarimeter scheme elements, consisting of a polarizer and a rotating retarder, on the measured parameters of an object was considered [17,18]. During the calibration of the scheme, four values of the optimal rotation angle (−45°, 0°, 30°, 60°) were obtained for a polarizer with a standard quarter-wave phase plate, at which the influence of errors on the parameters of the object under research is minimal [16].

For polarization measurements based on dividing the input radiation intensity by amplitude, calibration schemes are implemented that consist of one fixed polarizer and two variable retarders. At the same time, to equalize the noise, the authors of [19,20] proposed a system of two liquid-crystal adjustable retarders with a variable delay and fixed angular positions, which are set at 22.5° and 45°, as a fixed linear polarizer. A set of optimal deceleration values is also set, for example −158° and 50.6°. Other configurations are also possible, which are described in detail in [16].

The results of experimental research on polarimeter errors are known [21,22]. In this research, a system of two-phase retarders was used as a fixed linear polarizer. In these studies, four combinations of optimal azimuths of anisotropic axes were found, for example −20.3° and −41.14°. However, the resulting configurations did not allow us to fully take into account the systematic error to a sufficient extent. The advantage of this polarimeter calibration method is the reduction in measurement time due to the simultaneous measurement of four intensities. In addition, random and systematic errors are reduced and evenly distributed across the four channels of the system.

Previously, we developed a scheme for a portable four-channel Stokes polarimeter for monitoring blood hematocrit [23]. The scheme is based on the amplitude separation of the radiation scattered by the sample and can be used as a prefix to a smartphone. An important criterion for the efficiency of the system, in this case, is the possibility of obtaining information about a biological object with the maximum exclusion of the influence of the elements of the receiving channel on the values of the measured polarization parameters of the output radiation. Therefore, it is necessary to develop a method for calibrating the polarimeter, which will allow one to take into account the systematic components of the measurement error.

All the methods discussed above provide for the optimization of the design parameters of one of the polarization elements of the scheme. This is impractical concerning multi-channel portable polarizing systems. Therefore, it is necessary to search for calibration methods that will allow taking into account all the systematic errors of multichannel polarimeters in a single instrument matrix of the system.

The purpose of this research is an analytical review of methods for calibrating multichannel polarization schemes of optoelectronic attachments that operate in conjunction with a smartphone visualization system, and the technical implementation of the chosen method for a previously developed four-channel Stokes polarimeter.

2. Analysis of Calibration Methods

Polarimetry of diffusely scattering media, including biological tissues, can be divided into two categories: Stokes polarimetry and Mueller polarimetry. The corresponding optical design schemes can be divided into Stokes and Mueller polarimeters.

Stokes polarimeters are used to analyze the passage of partially polarized radiation through the investigated depolarizing optically inhomogeneous media and make it possible to determine their parameters based on revealing the dependence of the anisotropy parameters of the media on the measured output radiation polarization parameters.

Mueller polarimeters are used to analyze the polarization properties of optically inhomogeneous media based on the determination of the Mueller matrix of an object, which contains all information about the optical parameters of its surface and internal structure [24].

Stokes polarimeters are of greatest interest because the measurement procedure is easily automated, and the processing of parameter measurements takes much less time than the Mueller polarimeter scheme: this fact is very important for portable optoelectronic systems used to monitor optically inhomogeneous media.

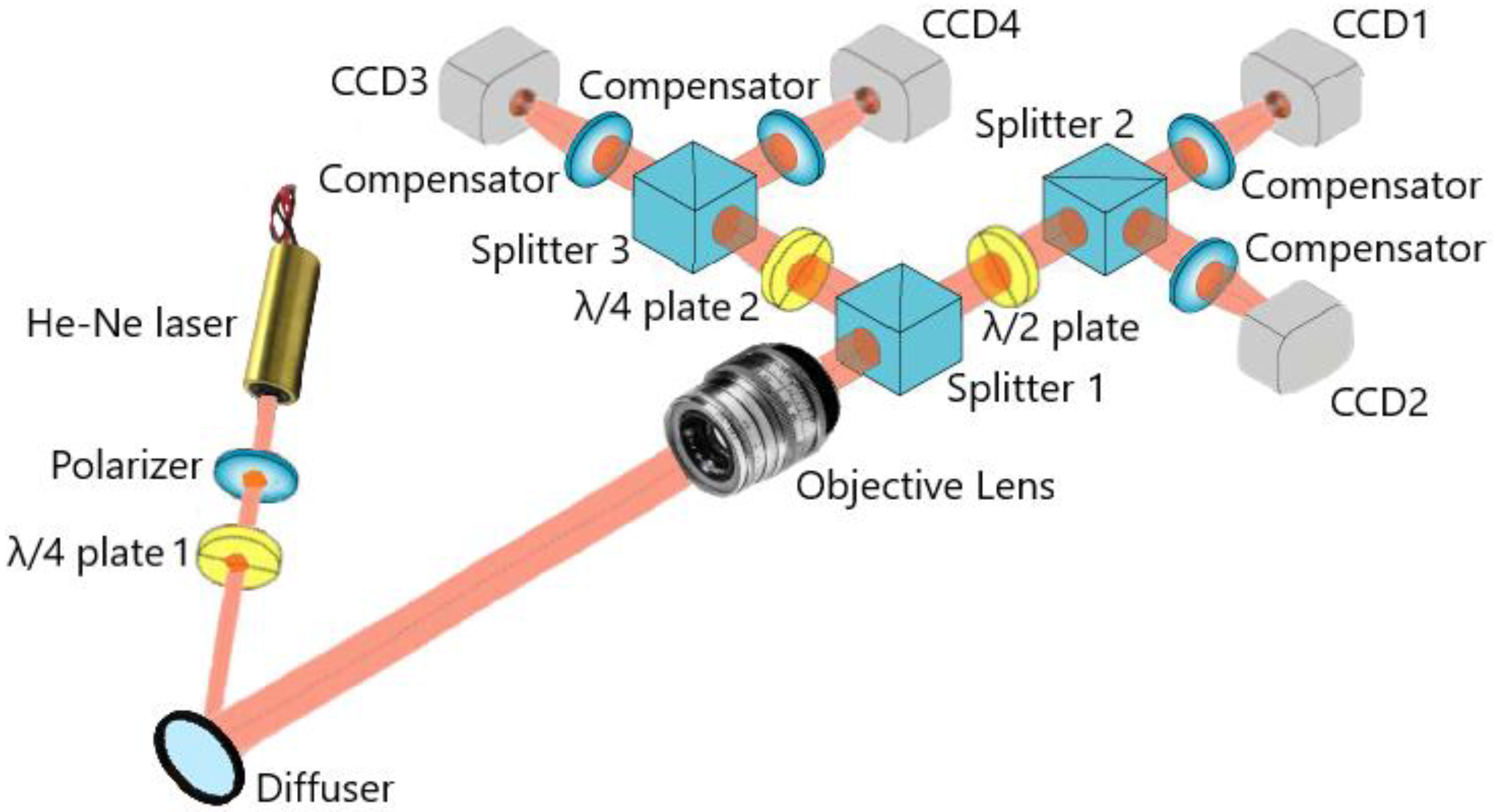
Figure 1 shows the calibration scheme of the developed portable four-channel Stokes polarimeter for non-invasive monitoring of blood hematocrit. The proposed optical scheme is universal for calibrating four-channel polarization systems based on the spatial separation of the input radiation intensity in amplitude [11,12,25,26].

The scheme consists of a helium-neon laser, a polarizer, two quarter-wave $\left(\lambda /4\right)$ phase plates, a diffuser, an objective lens, a half-wave $\left(\lambda /2\right)$ phase plate, one partially polarizing beam splitter (splitter 1), two polarizing beam splitters (splitter 2, splitter 3), four compensators, and four CCD-matrices.

The scheme of the Stoke polarimeter contains transmitting and four-channel receiving units. The transmitting unit consists of a source of coherent optical radiation that passes through a polarizer and quarter-wave phase plate 1 to form a given state of polarization of the radiation affecting the object. A diffuser with known optical parameters (transmission coefficient 0.2, reflection coefficient 0.4, absorption coefficient 0.04) is used as an object for calibration. The radiation scattered by the object enters the entrance pupil of the objective lens of the receiving unit.

Next, the objective lens converts the brightness distribution of the radiation scattered by the object into irradiance distributions on matrix analyzers of photodetectors (CCD1, CCD2, CCD3, CCD4) of four receiving channels. Separation of radiation by intensity is performed by polarization beam splitters.

Information about the intensity distribution of all pixels of digital images is recorded in separate files and transmitted via optical communication to the LI-NANO-CB microprocessor manufactured by Leopard Imaging for joint processing. The received intensity data arrays in the microprocessor are automatically processed using specially developed software. This launches commands for converting information about the intensity into parameters of the full Stokes vector and calculating the parameters of the radiation polarization state from it. Then the processed data arrays are converted into digital images and displayed on the information visualization device (smartphone screen), which is connected to the microprocessor using a MicroUSB/USB Type-A cable.

In the quasi-monochromatic approximation, the transmitting properties of a polarization system can be described by a linear transformation whose operator is characteristic of the system and does not depend on the incident radiation. The specified operator corresponds to the instrument matrix of the entire system.

Thanks to the linear transformation, with the help of one device matrix, it is possible to describe the action of a single element, as well as the actions of several series-connected elements.

To transform the radiation polarization parameters in the optical scheme without distortion, the action of the polarimeter can be represented by a unit matrix. However, as a rule, the measured parameters are systematically different from the actual ones. Then, knowing the instrumental matrix of the system, which characterizes the systematic operation of the polarimeter, this error is easily eliminated by inverse transformation.

Having determined the instrument matrix of the receiving optical unit of the system, it is possible to obtain a functional relationship between the unknown parameters of the Stokes vector of the scattered radiation and the measured electrical signals proportional to the intensity distribution on the matrix receivers.

The first of the considered methods for calibrating Stokes polarimeters is developed by launching a series of known radiation polarization states in the direction of a calibration sample with given optical parameters.

The orientation of the anisotropic axes of the optical elements of the transmitting channel is changed to sequentially introduce a set of known polarization states, which are described by the Stokes vector $Sq$ (1) [26]:

$$Sq=\left[\begin{array}{c}1\\ {cos}^2\left(\mathsf{\theta }\right)+{sin}^2\left(\mathsf{\theta }\right)·cos\mathsf{\delta }\\ \begin{array}{c}sin\left(\mathsf{\theta }\right)·cos\left(\mathsf{\theta }\right)·\left(1-cos\mathsf{\delta }\right)\\ sin\left(\mathsf{\theta }\right)·sin\mathsf{\delta }\end{array}\end{array}\right]·i_{0,x,y}.$$

(1)

With different orientations of the anisotropic axes of the polarizing filters, a set of N-images is obtained at the output of each receiving channel. The relationship between the parameters of the spatial distribution of the known polarization states $s_{ij}$ ($i$ = 1, 2, 3; $j$ = 1, 2, …, N) of the input radiation and the measured irradiance of each pixel of the image $b_{ij}$ ($i$ = 0, 1, 2, 3; $j$ = 1, 2, …, N) with coordinates (x, y) can be represented by the following matrix equation [26]:

$$[\begin{array}{cccc}{b}_{00}& b_{01}& \cdots & b_{0N}\\ b_{10}& \cdots & b_{11}& \cdots & b_{1N}\\ b_{20}& b_{21}& \cdots & b_{2N}\\ b_{30}& b_{31}& \cdots & b_{3N}\end{array}{]}_{x,y}=[\begin{array}{cccc}{a}_{00}& a_{01}& a_{02}& a_{03}\\ a_{10}& a_{11}& a_{12}& a_{13}\\ a_{20}& a_{21}& a_{22}& a_{23}\\ a_{30}& a_{31}& a_{32}& a_{33}\end{array}{]}_{x,y}·[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ s_{1,0}& s_{1,1}& s_{1,2}& \cdots & s_{1,N}\\ s_{2,0}& s_{2,1}& s_{2,2}& \cdots & s_{2,N}\\ s_{3,0}& s_{3,1}& s_{3,2}& \cdots & s_{3,N}\end{array}]·i_{0,x,y}.$$

(2)

It can be written in a simplified form:

$$B_{x,y}=A_{x,y}·S·i_{0,x,y},$$

(3)

where $A_{x,y}$ is the instrument matrix of the system, which is the same for all image pixels in the paraxial approximation; $S$ is the total Stokes vector of radiation at the input to the receiving unit of the polarimeter; $i_{0,x,y}$ is an electrical signal taken from each pixel with coordinates $\left(x, y\right)$, proportional to the irradiance on its surface; $B_{x,y}$ is the irradiance matrix of each pixel in the image.

Next, the instrument matrix of the system is calculated using Equation (4) below or by determining the Mueller matrices for each channel of the four-channel system and then substituting the first rows of the Mueller matrices into the instrument matrix of the system [26]:

$$A_{x,y}={\left(S^T·S\right)}^{-1}·S^T·B_{x,y}·i_{0,x,y}.$$

(4)

Thus, the presented polarimeter calibration method allows us to obtain the final real instrument matrix of the system for all image pixels, taking into account the measurement errors of the Stokes vector parameters and the degree of radiation polarization. Calculations performed by this method showed that the specified error is several percent [26]. To achieve such an accuracy, the set of calibration Stokes vectors must be chosen so that the instrument matrix of the polarimeter is not singular.

The second of the considered methods for calibrating Stokes polarimeters is to use an arbitrary set of linearly independent calibration vectors. To do this, the vector of the corresponding current responses of photodetectors $I_k={\left(I_{0k}, I_{1k}, I_{2k}, I_{3k}\right)}^T$. Then the classical matrix equation describing the operation of the Stokes polarimeter $\left(I=A·S\right)$ is rewritten in the following form (5) [27,28,29,30]

$$I_k=A·S_k,\left(k=0,\dots ,3\right),$$

(5)

where $A=\left[a_{ij}\right]$ is the instrument matrix of the system.

The calibration problem is to represent the instrument matrix $A$ and its relative error $\mathsf{\delta }A=\left|\left|\Delta A\right|\right|/\left|\left|A\right|\right|$ in the Euclidean norm through the vectors $S,I,$ and the errors of their measurement $\mathsf{\delta }S$, $\mathsf{\delta }I$. There are two ways of solving this problem.

The first way consists of the initial formation of block-diagonal matrices of the sixteenth order for an arbitrary set of Stokes vectors $S$, as well as for the instrument $A$ and current $I$ matrices of each channel of the receiving unit. In this case, the block-diagonal matrices $a$ and $i$ (corresponding to matrices $A$ and $I$) contain columns formed by rows of matrices $A$ and $I$. Then the classical matrix equation of the Stokes polarimeter is represented as a linear combination of equations, and the condition for calculating the condition number is determined [28,29,30]:

$$\mathsf{\delta }a\le \frac{{\nu }_s}{1-{\nu }_s·\mathsf{\delta }s}\left(\mathsf{\delta }s+\mathsf{\delta }\mathit{i}\right),$$

(6)

where ${\nu }_s$ is the condition number of the block-diagonal matrix $s$.

Then, by determining the relative error of the instrument matrix $\mathsf{\delta }a=\mathsf{\delta }A$, the relative error of the Stokes vector $\mathsf{\delta }s=\mathsf{\delta }S$, and the relative error of the characteristic matrix of the polarimeter $\mathsf{\delta }\mathit{i}=\mathsf{\delta }I$, the condition number can be calculated as follows (7) [28,29]:

$${\nu }_s=\left|\right|\mathit{s}\left|\right|·\left|\right|{\mathit{s}}^{-1}\left|\right|=2\left|\right|\mathit{S}\left|\right|·2\left|\right|{\mathit{S}}^{-1}\left|\right|=4{\nu }_S.$$

(7)

Replacing the obtained values into Formula (6) we can calculate the desired relative error for the instrument matrix of the system [28,29]:

$$\mathsf{\delta }A\le \frac{4·{\nu }_S}{1-{\nu }_S·\mathsf{\delta }S}·\left(\mathsf{\delta }I+\mathsf{\delta }S\right).$$

(8)

The second way to obtain the solution consists in writing the classical equation for the Stokes polarimeter in perturbed form, taking into account the absolute errors for the current matrix $I$, the polarimeter instrument matrix $A,$ and the Stokes vector $S$. Assuming that the final matrix, which is the sum of the Stokes vector and its absolute error, is nondegenerate, we can use the properties of the norm described in [28] to calculate the relative error of the polarimeter instrument matrix [28,29,30]:

$$\mathsf{\delta }A\le \frac{{\nu }_S}{1-{\nu }_S·\mathsf{\delta }S}·\left(\mathsf{\delta }I+\mathsf{\delta }S\right).$$

(9)

Thus, the estimate of the relative error of the instrumental matrix of the Stokes polarimeter, obtained by inequality (9), even if we assume $\mathsf{\delta }I=\mathsf{\delta }S=0$, is four times smaller than the estimate obtained by solving inequalities (6)–(8). The reason is that the estimate by inequality (6) is obtained under the condition that perturbations are independent of all elements of the sixteenth-order block-diagonal matrix $s$ for the Stokes vector, which does not correspond to the real operating conditions of the system. Therefore, using inequality (9), we obtain an error estimate up to small values of the second order.

There is also a well-known method for calibrating Stokes polarimeters, which consists in using a certain normalized set of linearly independent calibration vectors to determine the condition number of the Stokes vector $S$ (10) [29]:

$$S_k=\left(1,S_{1k}{S}_{2k},S_{3k}\right),S_{1k}+S_{2k}+S_{3k}=1.$$

(10)

However, such an orthogonal system does not exist, because the absolute value of the determinant, composed of vectors $S_k$, is equal in absolute value to six times the volume of a three-dimensional pyramid, which is inscribed in a three-dimensional sphere of unit radius centered at the origin [31]. In this regard, the coordinates of the tetrahedron vertices are corrected so that the tetrahedron vertex is on the OZ axis, at the point with coordinates $\left(0,0,1\right)$. Then the matrix $S\left(\mathsf{\phi }\right)$ composed of the normalized set of Stokes gauge vectors $S_k$ takes the following form (11) [31]:

$$S\left(\phi \right)=\left[\begin{array}{cccc}1& 1& 1& 1\\ 0& \frac{2\sqrt{2}}{3}cos\mathsf{\phi }& \frac{2\sqrt{2}}{3}cos\left(\mathsf{\phi }+\frac{2\pi }{3}\right)& \frac{2\sqrt{2}}{3}cos\left(\mathsf{\phi }+\frac{4\pi }{3}\right)\\ 0& \frac{2\sqrt{2}}{3}sin\mathsf{\phi }& \frac{2\sqrt{2}}{3}sin\left(\mathsf{\phi }+\frac{2\pi }{3}\right)& \frac{2\sqrt{2}}{3}sin\left(\mathsf{\phi }+\frac{4\pi }{3}\right)\\ 1& -\frac{1}{3}& -\frac{1}{3}& -\frac{1}{3}\end{array}\right],$$

(11)

where $\mathsf{\phi }$ is the angle between the positive direction of the OX axis and the radius vector.

Regardless of the angle $\mathsf{\phi }$, for the Euclidean norm of the matrix $S\left(\mathsf{\phi }\right)$ and its determinant, we obtain the following Equation (12) [31]:

$$\left|\right|S\left(\mathsf{\phi }\right)\left|\right|=2\sqrt{2},\left|S\left(\mathsf{\phi }\right)\right|=\frac{16\sqrt{3}}{9}.$$

(12)

The inverse matrix $S{\left(\mathsf{\phi }\right)}^{-1}$ can be found analytically. Then the condition number ${\nu }_S$ of the matrix $S\left(\mathsf{\phi }\right)$ does not depend on the angle between the positive direction of the OX axis and the radius vector and is equal to ${\nu }_S=||S\left(\mathsf{\phi }\right)\left||·|\right|\mathit{S}{\left(\mathsf{\phi }\right)}^{-1}\left|\left|=\left|\left|S\right|\right|·\right|\right|S^{-1}||={\nu }_S=2\sqrt{5}$.

Thus, in the research of biological objects with a complex optically inhomogeneous structure, the most preferred method is calibration, which is carried out by launching a series of known states of radiation polarization in the direction of a calibration sample with specified optical parameters. Compared with the second method, it is completely focused on working with real scheme elements. Compared with the third method, it does not require the formation of an ideal orthogonal system of Stokes calibration vectors.

To apply the chosen calibration method to the developed scheme of a four-channel Stokes polarimeter [23], it is necessary to first determine the polarization parameters of the calibration sample (diffuser) to make appropriate corrections when determining the instrumental matrix of the receiving channel of the system.

In this regard, experimental research on the polarization properties of the optical radiation diffuser and their statistical analysis was carried out.

3. Experimental Investigation

A series of experimental research was conducted on a setup formed according to the scheme of a single-channel polarimeter based on a sequential change in the parameters of polarizing filters a finite number of times.

The transmitting channel of the setup consists of an optical radiation source—a helium-neon laser (He-Ne) with a wavelength of $0.63 \mathsf{\mu }\mathrm{m}$, a polarizer, and a quarter-wave phase plate. The radiation that has passed through the transmitting channel and scattered from the sample enters the receiving channel, passes through the quarter-wave phase plate and the analyzer, and is focused by the objective lens in the plane of the photosensitive area of the matrix photodetector (CMOS-matrix). A quarter-wave phase plate is introduced in the course of the radiation scattered by the sample only to detect circularly polarized radiation.

The scheme is based on the analysis of intensity distributions of the radiation scattered by the calibration sample (diffuser) on the matrix field of the photodetector at known states of the polarization filters of the transmitting channel and the receiving channel of visualization. According to the method for measuring the parameters of the Stokes vector, six files were recorded: $I_{0°}$, $I_{90°}$, $I_{45°}$, $I_{-45°}$, $I_r$, $I_l$, each of them contains information related to the spatial distribution of radiation intensity in the image plane [23,27]. Next, the parameters of the Stokes vector were calculated and complex polarization analysis of the radiation at the output of the calibration sample was performed [23,27].

$$S=\left(\begin{array}{c}{S}_0\\ S_1\\ \begin{array}{c}{S}_2\\ S_3\end{array}\end{array}\right)=\left(\begin{array}{c}{I}_{0°}+I_{90°}\\ I_{0°}-I_{90°}\\ \begin{array}{c}{I}_{45°}-I_{-45°}\\ I_r-I_l\end{array}\end{array}\right);$$

(13)

$$P=\frac{\sqrt{S_1{}^2+S_2{}^2+S_3{}^2}}{S_0};\mathsf{\alpha }=\frac{1}{2}·\mathrm{arctg}\left(\frac{S_2}{S_1}\right);\mathsf{\beta }=\sqrt{\frac{S_0-\sqrt{S_1{}^2+S_2{}^2}}{S_0+\sqrt{S_1{}^2+S_2{}^2}}},$$

(14)

where $P$ is the polarization degree, $\mathsf{\alpha }$ is the azimuth, and $\mathsf{\beta }$ is the ellipticity of the radiation ellipse.

The investigation of the mechanisms of optically anisotropic absorption and phase modulation of polarized radiation by the sample under investigation was carried out based on determining its 4 × 4 Mueller matrix [32,33,34]:

$$M=\left[\begin{array}{cccc}{M}_{11}& M_{12}& M_{13}& M_{14}\\ M_{21}& M_{22}& M_{23}& M_{24}\\ M_{31}& M_{32}& M_{33}& M_{34}\\ M_{41}& M_{42}& M_{43}& M_{44}\end{array}\right].$$

(15)

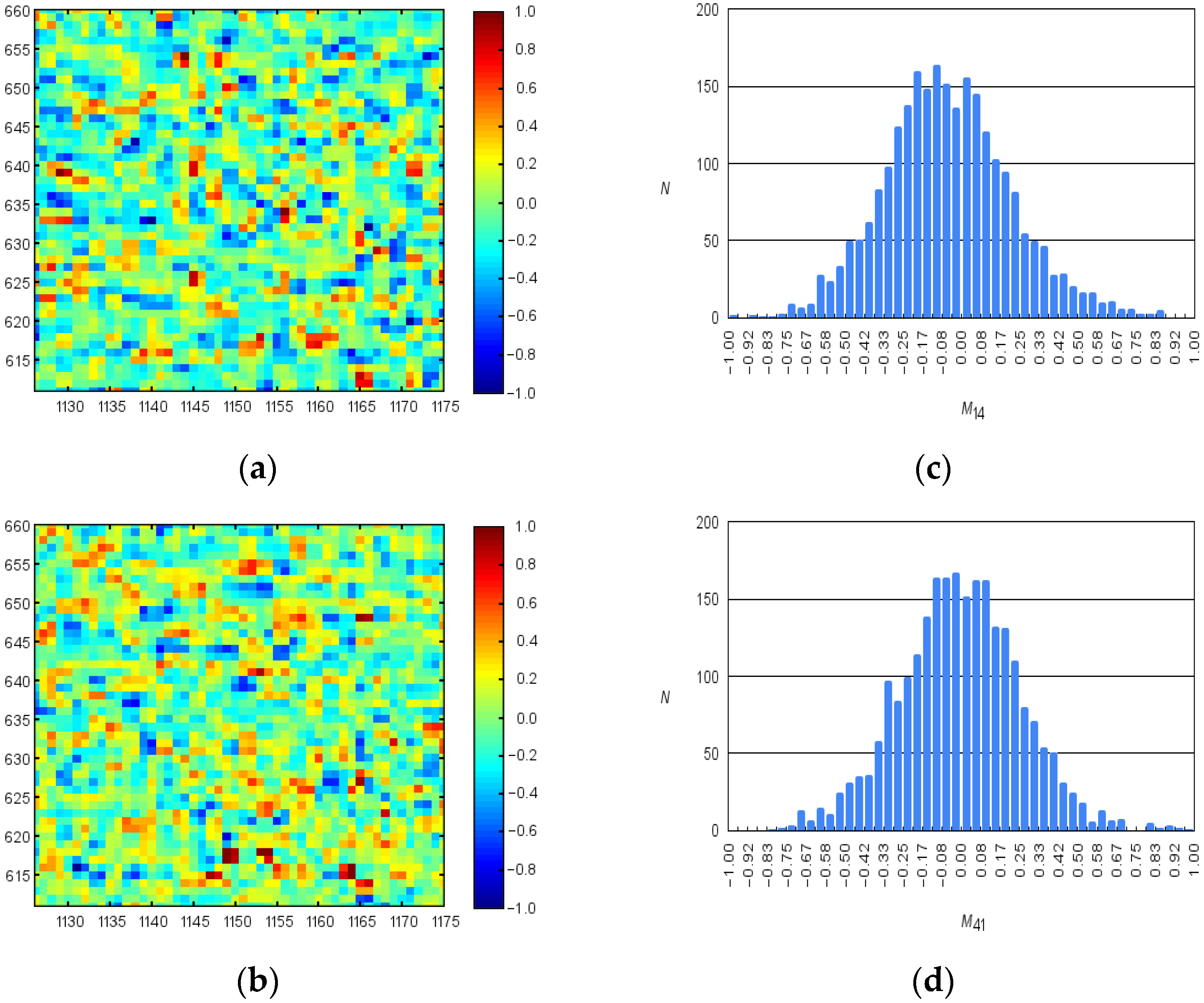
The elements of the matrix depend on the scattering angle, wavelength, and geometric and optical parameters of scattering centers. $M_{11}$ is the quantity that is measured when the incident light is not polarized; its dependence on the scattering angle is the phase function of the scattered light. $M_{12}$ characterizes the degree of linear polarization of scattered light. $M_{22}$ shows the proportion of depolarized light in the total scattered radiation (concerning a biological sample, a measure of the nonsphericity of scattering particles can be estimated). $M_{34}$ characterizes the transformation of 45° obliquely polarized incident light into circularly polarized scattered light (which is unique to various biological systems). The difference between $M_{33}$ and $M_{44}$ is a good measure of the nonsphericity of scattering particles.

However, the practical use of the entire Mueller matrix is difficult. The reason for this is the azimuthal dependence of most matrix elements—in the general case, 12 out of 16 elements change when the spatial position of the object of investigation relative to the axis of incidence of radiation changes. The following elements of the Mueller matrix turn out to be azimuthally stable, independent of the angle of rotation of the object of investigation: $M_{11}$, $M_{14}$, $M_{41}$, $M_{44}$ [35,36].

When the Mueller matrix is normalized, the first invariant $M_{11}$ is always equal to one, and the fourth invariant $M_{44}$ contains information about the radiation parameters at the output of the sample when its input is exposed to circularly polarized radiation. Since the value of the $M_{44}$ invariant is negligibly small for biological structures, and the errors in its determination are large, it can be in this case further disregarded.

Therefore, to research the polarization properties of biological samples, it suffices to determine two invariants of the Mueller matrix $M_{14}$ and $M_{41}$, which characterize the processes of transformation of the researched media of circularly polarized radiation into linearly polarized radiation and the transformation of the linearly polarized radiation into circularly polarized radiation, respectively [30,32].

According to the method of experimental determination of the Mueller matrix of the optical media [30,32], the coordinate distributions of the radiation intensity were measured, which are necessary for calculating the elements of the sample matrix $M_{14}$, $M_{14}$, invariant to its spatial orientation.

As a result, the coordinate distributions of the parameters of the Stokes vector of the radiation scattered by the sample, the elements of the Mueller matrix of the surface structure of the diffuser, the polarization degree, azimuth, and ellipticity of the radiation ellipse, as well as their histograms, were obtained.

4. Experimental Results

The vector calculations were carried out using the MATLAB software package.

Since slight movements of the optical elements of the instrument are possible during the measurements, increasing the measurement error, the obtained images were combined based on calculating the position of their energy centers.

Next, a statistical analysis of the spatial distributions of the measured radiation parameters characterizing the polarization properties of the diffuser was carried out.

The obtained coordinate distributions and histograms of the parameters of the Stokes vector and the polarization state of the output radiation are shown in Figure 2 and Figure 3.

Coordinate intensity distributions and histograms of two invariants of the diffuser surface structure matrix $\left(M_{14}, M_{41}\right)$ were obtained, providing azimuthally stable information about the optically anisotropic properties of the object under investigation Figure 4.

The boundaries of the error intervals for measuring the parameters of the Stokes vector (${\delta }_{S_1}, {\delta }_{S_2}, {\delta }_{S_3}$), polarization degree (${\delta }_P$), azimuth (${\delta }_{\mathsf{\alpha }}$) and ellipticity of the radiation ellipse (${\delta }_{\mathsf{\beta }}$) with a set probability of 0.95 are determined by calculation by formulas for indirect measurements:

$${\delta }_{S_1}=\pm K_{S_1}·\sqrt{w·\frac{\Delta I_{0°}{}^2+\Delta I_{90°}{}^2}{{\left(I_{0°}-I_{90°}\right)}^2}·\left(\frac{{\delta }_1{}^2}{K_1{}^2}+\frac{{\delta }_2{}^2}{K_2{}^2}\right)+\frac{{\delta }_3{}^2}{K_3{}^2}+\frac{{\delta }_4{}^2}{K_4{}^2}};$$

(16)

$${\delta }_{S_2}=\pm K_{S_2}·\sqrt{w·\frac{\Delta I_{45°}{}^2+\Delta I_{-45°}{}^2}{{\left(I_{45°}-I_{-45°}\right)}^2}·\left(\frac{{\delta }_1{}^2}{K_1{}^2}+\frac{{\delta }_2{}^2}{K_2{}^2}\right)+\frac{{\delta }_3{}^2}{K_3{}^2}+\frac{{\delta }_4{}^2}{K_4{}^2}};$$

(17)

$${\delta }_{S_3}=\pm K_{S_3}·\sqrt{w·\frac{\Delta I_r{}^2+\Delta I_l{}^2}{{\left(I_r-I_l\right)}^2}·\left(\frac{{\delta }_1{}^2}{K_1{}^2}+\frac{{\delta }_2{}^2}{K_2{}^2}\right)+\frac{{\delta }_3{}^2}{K_3{}^2}+\frac{{\delta }_4{}^2}{K_4{}^2}+\frac{{\delta }_5{}^2}{K_5{}^2}};$$

(18)

$${\delta }_P=\pm K_P·\sqrt{\frac{S_1{}^4·\frac{{\delta }_{S_1}{}^2}{K_{S_1}{}^2}+S_2{}^4·\frac{{\delta }_{S_2}{}^2}{K_{S_2}{}^2}+S_3{}^4·\frac{{\delta }_{S_3}{}^2}{K_{S_3}{}^2}}{{\left(S_1{}^2+S_2{}^2+S_3{}^2\right)}^2}+\frac{\Delta I_{0°}{}^2+\Delta I_{90°}{}^2}{{\left(I_{0°}-I_{90°}\right)}^2}·\left(\frac{{\delta }_1{}^2}{K_1{}^2}+\frac{{\delta }_2{}^2}{K_2{}^2}\right)};$$

(19)

$${\delta }_{\mathsf{\alpha }}=\pm K_{\mathsf{\alpha }}·\frac{S_2}{2·S_1·\mathsf{\alpha }·\left(1+\frac{S_2{}^2}{S_1{}^2}\right)}·\sqrt{\frac{{\delta }_{S_1}{}^2}{K_{S_1}{}^2}+\frac{{\delta }_{S_2}{}^2}{K_{S_2}{}^2}};$$

(20)

$${\delta }_{\mathsf{\beta }}=\pm K_{\mathsf{\beta }}·\frac{S_0}{\mathsf{\beta }·\left(S_0+\sqrt{S_1{}^2+S_2{}^2}\right)}·\sqrt{\frac{S_1{}^4·\frac{{\delta }_{S_1}{}^2}{K_{S_1}{}^2}+S_2{}^4·\frac{{\delta }_{S_2}{}^2}{K_{S_2}{}^2}}{S_1{}^2+S_2{}^2}+\left(S_1{}^2+S_2{}^2\right)·\left(\frac{{\delta }_1{}^2}{K_1{}^2}+\frac{{\delta }_2{}^2}{K_2{}^2}\right)},$$

(21)

where $w$ is the coefficient that takes into account the systematic errors of the means for measuring the radiation intensity, since when measuring $I_{0°}$, $I_{90°}$, $I_{45°}$, $I_{-45°}$, $I_r$, $I_l$ the same instance of the measuring instrument is used, $w\le 0.5$; ${\delta }_1$ is measurement instrument error $\pm 8$%; ${\delta }_2$ is the error due to the inaccuracy of the analyzer scale graduation $\pm 1$%; ${\delta }_3$ is the error introduced by the diffuser $\pm 3$%; ${\delta }_4$ is the error due to the instability of the energy (power) of laser radiation during measurements $\pm 3$%; ${\delta }_5$ is the error introduced by the phase plate $\pm 5$%; $K_{S_1}$, $K_{S_2}$, $K_{S_3}$, $K_P$, $K_{\mathsf{\alpha }}$, $K_{\mathsf{\beta }}$, $K_1$, $K_2$, $K_3$, $K_4$, $K_5$ are coefficients depending on the distribution of total, and partial errors and the established probability with which these errors are determined; $K_1=K_2=K_3=K_5=1.73$ for a uniform distribution law; $K_{S_1}=K_{S_2}=K_{S_3}=K_P=K_{\mathsf{\alpha }}=K_{\mathsf{\beta }}=1.96$ for the normal distribution law; $K_4=3$; $\Delta I_{0°}$, $\Delta I_{90°}$, $\Delta I_{45°}$, $I_{-45°}$, $\Delta I_r$, $\Delta I_l$ is the variance of measurement of the radiation intensity.

As a result of calculations using the formulas presented above, the boundaries of the error intervals are determined for measuring the parameters of the Stokes vector (${\delta }_{S_1}=\pm 3$%, ${\delta }_{S_2}=\pm 11$%, ${\delta }_{S_3}=\pm 8$%), the polarization degree (${\delta }_P=\pm 10$%), azimuth (${\delta }_{\mathsf{\alpha }}=\pm 10$%) and ellipticity of the radiation ellipse (${\delta }_{\mathsf{\beta }}=\pm 7$%).

5. Discussion

Analysis of received results was produced within the framework of the statistical approach: the set $Z_i$ statistical moments of the 1st–4th order of the coordinate distributions of the investigated polarization parameters [37]:

$$Z_1=\frac{1}{N}{{\displaystyle \sum }}_{j=1}^N{q}_j,Z_2=\sqrt{\frac{1}{N-1}{{\displaystyle \sum }}_{j=1}^N{\left(q_j-Z_1\right)}^2},$$

(22)

$$Z_3=\frac{1}{Z_2{}^3}\frac{1}{N}{{\displaystyle \sum }}_{j=1}^N{\left(q_j-Z_1\right)}^3,Z_4=\frac{1}{Z_2{}^4}\frac{1}{N}{{\displaystyle \sum }}_{j=1}^N{\left(q_j-Z_1\right)}^4,$$

(23)

where $N=m·n$ is the number of pixels in the CMOS sensor; $q_j$ is the numerical value of the parameter in the distribution cell.

Table 1. Statistical moments of coordinate distributions of polarization parameters of a sample.

Parameter	$S_1$	$S_2$	$S_3$	$P$	$\mathsf{\alpha }$	$\mathsf{\beta }$	$M_{14}$	$M_{41}$
Moment
$Z_1$	−0.056	−0.019	−0.018	0.40	−0.020	−0.024	−0.057	−0.003
$Z_2$	0.37	0.45	0.10	0.23	0.45	0.15	0.28	0.27
$Z_3$	0.078	−1.93	−0.48	0.33	0.090	−0.24	0.30	0.29
$Z_4$	3.20	33.03	7.73	2.59	1.86	8.14	3.69	4.53

shows the results of calculating the average value $\left(Z_1\right)$, variance $\left(Z_2\right)$, skewness $\left(Z_3\right)$, and kurtosis $\left(Z_4\right)$ for the obtained coordinate distributions of the Stokes vector parameters, polarization state parameters, and two invariants of the diffuser matrix.

The skewness of the distributions is due to the uneven placement of the acquired data on both sides of the modal value of the parameter. In this case, the distributions of the ellipticity of the radiation ellipse $\mathsf{\beta }$ and parameters of the Stokes vectors $S_2$ and $S_3$ have negative skewness, that is, the number of the acquired data is greater to the left of the mode, and the distributions of the remaining parameters have positive skewness, that is, the number of the acquired data is greater to the right of the mode.

The kurtosis of the distributions S₁ and M₁₄ are close to three, which corresponds to a distribution close to the normal one. Although the kurtosis for parameter P is also close to three, this distribution cannot be interpreted as close to normal due to the presence of an outlier in the histogram near-zero (Figure 3d). The distribution of azimuth $\mathsf{\alpha }$ is close to uniform, which is confirmed by the type of histogram shown in Figure 3e and its kurtosis value of 1.86 (for a uniform distribution, the kurtosis is 1.8). In this case, most of the options for the sets of parameters $S_2, S_3, \mathsf{\beta }$, and $M_{41}$ are concentrated around the arithmetic mean and the frequency distributions are represented by a peaked curve, which is expressed by large values of kurtosis.

Because the statistical moments of the third and fourth order differ significantly for different polarization radiation parameters, the selected radiation parameters and the moments of their coordinate distributions are the most informative diagnostic indicators in a comparative analysis of the properties of optically inhomogeneous, including biological samples.

6. Conclusions

An analytical review of calibration methods for multichannel polarization schemes of optoelectronic attachments operating in conjunction with a smartphone visualization system made it possible to establish that for such systems used in the medical field, the first calibration method is the most preferable. It is carried out by launching a known set of calibration vectors and consists in determining a single instrument matrix of the system, which will take into account all the components of systematic measurement errors.

As a result of the technical implementation of the chosen calibration method for the previously developed four-channel Stokes polarimeter and statistical analysis, the statistical moments of the coordinate distributions of the Stokes vector parameters, the polarization states parameters of the output radiation, and the azimuthally stable invariants of the Mueller matrix of the diffuser subsurface structure were determined. The obtained numerical values provide information about the polarization properties of the researched calibration sample and can be used to form a single instrumental matrix of the system. In addition, significant differences in the statistical moments of the third and fourth orders were revealed for all considered distributions of the parameters of polarized radiation, which allow using them as informative parameters for a comparative analysis of the properties of optically inhomogeneous and biological media.

The boundaries of the error intervals for measuring the parameters of the Stokes vector, the polarization degree, azimuth, and ellipticity of the radiation ellipse obtained without the use of the chosen calibration method indicate the need to introduce appropriate corrections into the single instrumental matrix of the receiving channel of the developed four-channel Stokes polarimeter for non-invasive monitoring of blood hematocrit. Such an approach will make it possible to reduce the systematic error introduced by real scheme elements as compared with the error of 3–5% obtained by the classical method of precision calculation for commercially available polarizing elements.