1. Introduction
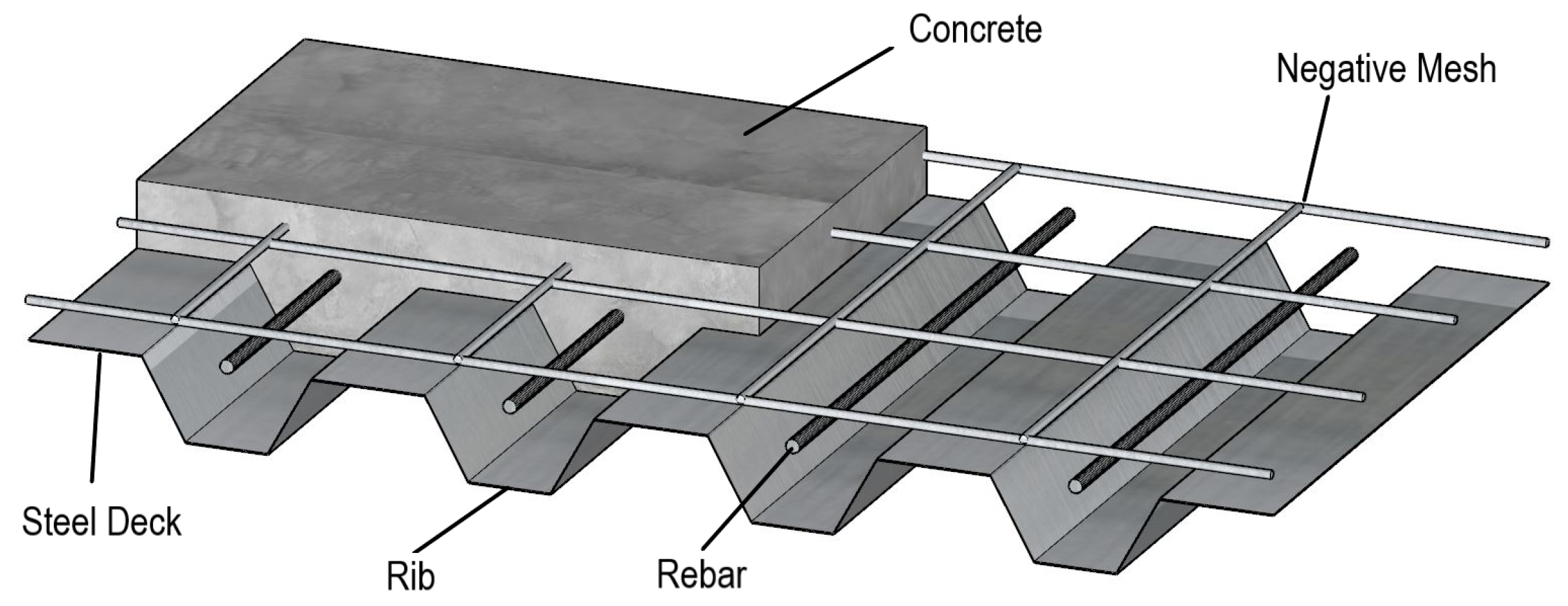
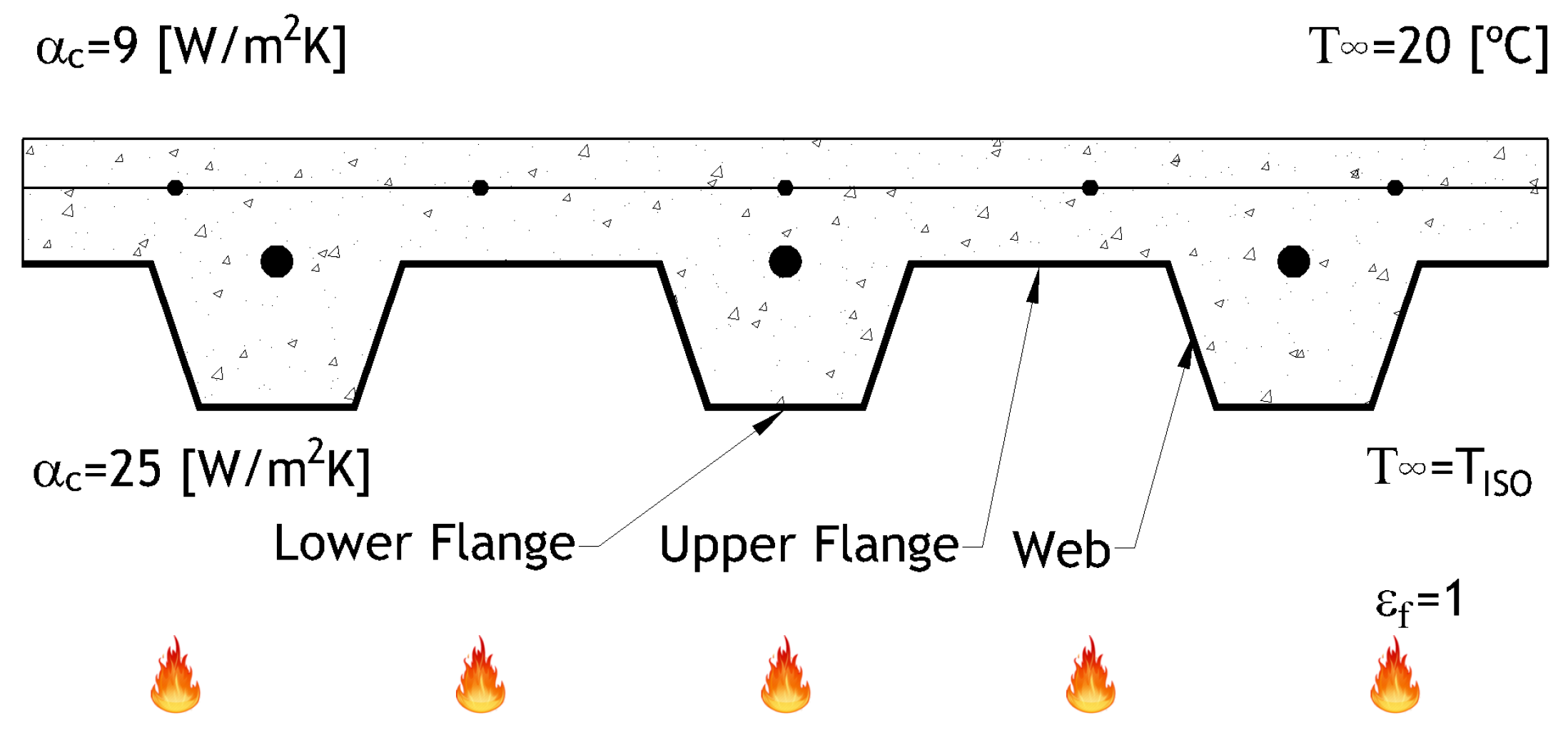
Steel–concrete composite slabs are made of a profiled steel deck, which can be used as a permanent formwork, and reinforced concrete. Normally, the concrete is reinforced with an anti-crack mesh positioned on the upper part and individual reinforcement bars in the ribs (see
Figure 1). These construction elements offer some advantages for the structures, such as reducing the dead weight while speeding up the construction process. The use of composite slabs in buildings has become very popular in North America since 1960. However, as there was insufficient information on structural safety in Europe, this element type has became popular after 1980. The overall thickness of the slab usually varies between 100 and 170 mm. The thickness and geometry of the steel deck depends on the manufacturer of the steel deck profiles and usually includes a zinc layer on the exposed surface to increase the corrosion resistance [
1].
Besides being exposed to a corrosive environment, the composite slabs may suffer considerable damage when exposed to fire, as the steel elements responsible for the bending strength of the composite slabs are significantly affected by elevated temperatures. It is therefore necessary to carry out a thermal analysis prior to the static analysis to ensure that this building element is fire resistant in accordance with the regulations and standards. The fire resistance of composite slabs with a steel deck is usually determined by standard fire tests, considering the ability to sustain the load (R), the thermal insulation (I), and the integrity (E). In order to demonstrate the fire resistance according to the fire ratings of the European standard EN 13501-2 [
2], the element must be able to prevent large deformations or rates of deformation for the case of load-bearing (R) and also provide thermal insulation that limits the temperature rise on the unexposed side (I). Finally, the composite slabs must contain the fire from below and prevent the passage of flames and hot gases through cracks or holes, keeping the integrity criterion (E). This last criterion is usually verified by considering the presence of the steel deck.
This paper is concerned with the calculation of the temperature of composite slabs under a standard, ISO-834 fire [
3], in particular the temperature evolution at the components of the steel deck (upper flange, web, lower flange) and the reinforcing bars. An accurate and reliable method to determine the temperature field in these components is required, in particular to determine the load-bearing criterion (R), as these temperatures have a direct influence on the reduction factors for the steel and concrete strength and, consequently, on the bending resistance of the slabs.
Among the different methods to determine the fire resistance of a composite slab, the development of standard experimental fire tests is the most expensive and time consuming. Alternatively, Annex D of EN 1994-1-2 [
4] provides the guidelines to determine the fire resistance based on the simplified calculation method. This method is based on studies conducted a long time ago and is currently outdated. The third method is to simulate the experimental fire tests computationally using numerical methods. Computer simulations are of great importance in this field because they allow a reliable and realistic description of the physical phenomena, including the effects of different fire scenarios, such as natural fires. In addition, computer simulations are less expensive and faster than conducting experimental tests.
The year 1983 was very important for the spread of composite slabs in Europe as an alternative and functional building method. In that year, the European Convention for Constructional Steelwork ECCS [
5] published the design rules for composite concrete slabs with a steel deck exposed to a standard fire. According to this document, explicit fire design is not required for composite slabs when the fire requirements are less than or equal to 30 min, and for other fire ratings, the calculation methods are based on conservative approximations for a safer design procedure. This technical guide has been developed to provide structural safety in accordance with the fire resistance classes specified in ISO 834-1 [
3] without the need for experimental testing. This document should only be used if the composite slab has been safely designed for room temperature.
Hamerlinck developed some mathematical models for estimating the fire resistance of composite slabs. In 1990, he proposed a numerical procedure comprising thermal models for cross-section analysis and a structural analysis model for composite slabs. In his paper published in 1991 [
1], Hamerlinck described in detail all the methods for carrying out numerical and experimental studies regarding the thermal and mechanical behaviour of reinforced composite slabs under fire. The experimental programme took into account the most important parameters for fire resistance, and a new computer programme was developed to allow simulations with low computational cost (low processing time). It was concluded that the two-dimensional model developed gave satisfactory results, although it did not take into account the three-dimensional thermal effects. The current standards are still based on his work.
In 1998, Both [
6] introduced an easy-to-use calculation rule in order to give more insight into the fire behaviour and failure mechanisms of continuous composite slabs. The numerical models were validated against the results of experimental tests conducted by the author and other researchers. The numerical models were created using the multi-purpose finite element programme DIANA, originally developed at TNO Building and Construction Research. The 2D and 3D thermal models of the composite slab were developed. The authors concluded that the thermal model was capable of describing the two- and three-dimensional heat flow in composite slabs during fire exposure and that the assessment rules for fire resistance, which at that time were specified in Eurocode 4, could be significantly improved.
In recent years, a wide range of thermal and structural models have been developed in various finite element software programmes to predict the structural and thermal behaviour of steel–concrete composite slabs under fire conditions. In 2018, Piloto et al. [
7] analysed the fire resistance of composite concrete slabs with a profiled steel deck, in this case also with a steel mesh on the top, including reinforcing bars between the ribs. The main objective of this study was to develop two-dimensional numerical models using the Matlab and ANSYS programmes to evaluate the fire resistance of different composite slab configurations according to the insulation criterion. For the development of this research, the fire resistance criterion for insulation (I) was evaluated using numerical and simple calculation methods and then validated using experimental fire tests. The results obtained by the authors allowed proving that the fire resistance (I) increases with the concrete thickness for both calculation methods. However, when using the numerical method, the simulation predicts a lower fire resistance (I) compared to the basic standards, thus ensuring a higher structural safety with this method. Therefore, a new and better approach has been proposed that considers a quadratic variation between the fire resistance and the effective thickness of the composite slab. For the first time, the authors [
8] decided to consider an air gap between the steel deck and the concrete topping. This innovation considers the implicit model of the detachment between the steel deck and the concrete, which has been demonstrated in many experimental fire tests.
In 2019, Jian Jiang et al. [
9] from the National Institute of Standards and Technology (NIST) conducted a numerical investigation on various parameters that may affect the fire resistance of composite slabs with respect to the thermal insulation criterion (I). A set of 54 composite slabs was selected for the numerical analysis, which were developed using the finite element software LS-DYNA. A 2D high-fidelity thermal model of the symmetrical part of the cross-section of the composite slab was used. The concrete thickness and moisture content were found to be the parameters that most influenced the fire resistance. An improved algebraic expression for the calculation of the fire resistance was proposed that explicitly takes into account the moisture content of the concrete. The formulation is applicable to an extended range of geometries compared to the limitations of the calculation method in the current version of Eurocode 4.
Recently, full-scale 3D numerical models have been developed by Paulo Piloto and his team to evaluate the thermal behaviour of a series of composite slabs with different geometries under the action of different types of standard fires. In [
10,
11,
12], 3D finite element models were developed to perform thermal analyses based on the insulation criterion (I), and in [
11,
13], a coupled thermal and mechanical model was applied to perform mechanical analyses based on the load-bearing criterion (R). The thermal models were implemented using Matlab or ANSYS software, and the mechanical model was developed using ANSYS only. In both cases, three-dimensional finite elements were used.
In 2021, Bolina et al. [
14] determined the temperature analysis of steel–concrete slabs exposed to a standard fire. The main objective of this investigation was to develop a comparison of the temperature evolution in the cross-section through different methods: experimental, numerical, and simplified. The authors conducted eight full-scale fire tests, which were used to validate the numerical models developed with the ABAQUS software. The numerical results were compared with the analytical results obtained from Eurocode 1994-1-2 [
4]. The authors found a good agreement between the simplified method and the other methods (numerical and experimental) only for the steel deck temperature, but not for the concrete, the reinforcing bars (positive and negative), and the thermal insulation. Therefore, a new approximation was developed to determine the temperature in the rebars, including new factors to evaluate the performance of the thermal insulation.
In the present paper, which is an improved version of the conference paper [
15], the authors improve the analytical temperature calculation method, following the simplified calculation method in Annex D of Eurocode 1994 1-2. This analytical method allows the calculation of temperatures in different composite slab components (lower and upper flange, web and reinforcing bars) for different fire ratings. A correct estimation of these temperatures is of great importance for the design of the slabs according to the load-bearing criterion. Since the temperatures affect the mechanical properties of the slabs, incorrect temperature values can lead to unsafe design. A parametric study is carried out to analyse the thermal behaviour of composite slabs as a function of concrete thickness. The temperature distribution along the composite slabs of normal and lightweight concrete (NWC and LWC) was determined using four different types of composite slabs selected to represent two different steel deck geometries, trapezoidal and re-entrant. The composite slabs were subjected to the thermal effects of a standard fire exposure from below.
The full-scale tests were simulated with three-dimensional finite elements using the Matlab Partial Differential Equations Toolbox (PDE Toolbox) [
16]. The discrete composite slab models consist of different physical subdomains with different thermal properties corresponding to the components of the slab such as concrete, steel deck, and reinforcing bars. In addition, an air gap, with constant thickness, is included between the steel deck and the bottom surface of the concrete, to simulate the separation effect of both materials (debonding). Effectively, the thermal contact resistance in the joint boundary of layers is an important parameter that is not considered by most of authors [
17]. This air gap model is introduced to simulate a similar thermal contact resistance.
The thermal models are validated with results from experimental tests found in the literature [
7,
8]. The thermal analysis on the steel deck components and on the reinforcing bars is evaluated in every composite slab with different concrete thicknesses
. The numerical results are compared with the simplified method from Annex D of Eurocode 1994-1-2. Finally, the results of all simulations developed for the parametric study are used to propose a new formula for the analytical estimation of the temperature of the four slab components. The coefficients of the new proposal are obtained by fitting this proposal to the numerical data using a non-linear least-squares method. It is important to mention that the proposed analytical method avoids unsafe temperature predictions resulting from the use of the simplified method, currently proposed by the standards.
This article is structured as follows.
Section 2 introduces the thermal problem to be solved. The methodology used to solve it numerically is presented in
Section 3.
Section 4 is devoted to the simplified method provided by the standard for calculating the temperatures in the composite slab components. A new proposal for this simplified method, based on the numerical results obtained with the finite element calculation model, is presented in
Section 5. This section also includes the validation of the model with experimental results available in the literature and a brief analysis of its computational performance. The article ends with the presentation of some final considerations in
Section 6. In order to increase the readability of this paper, nomenclature has been defined in
Table 1.
3. Numerical Solution through Finite Element Method
In thermal problems, the finite element mesh is generally used to model solids in which conduction is the predominant heat transfer method, and the radiation and convection are imposed through boundary conditions. To perform a thermal analysis on composite slabs, Equation (
1) is discretised by finite elements inside the physical sub-domains, corresponding to different materials.
Figure 7 presents the generated mesh, produced by the Matlab PDE Toolbox, for each composite slab.
Equation (
1) is solved by the finite elements method (FEM), based on the weak-form Galerkin model, using the weighted residual method, thus leading to the energy matrix formulae:
where
is the capacitance matrix,
is the vector of the time derivatives of the nodal temperatures,
is the conductivity matrix, and
is the vector of the thermal loads (for details, see, for instance, [
23]). The vector of the thermal loads
includes the boundary conditions. The solution of the first-order non-linear system of ordinary differential equations given by Equation (
8), considering
and the boundary conditions, enables determining the temperature at each node of the finite element mesh, illustrated in
Figure 7, over the time interval
.
Computational Solution with Matlab
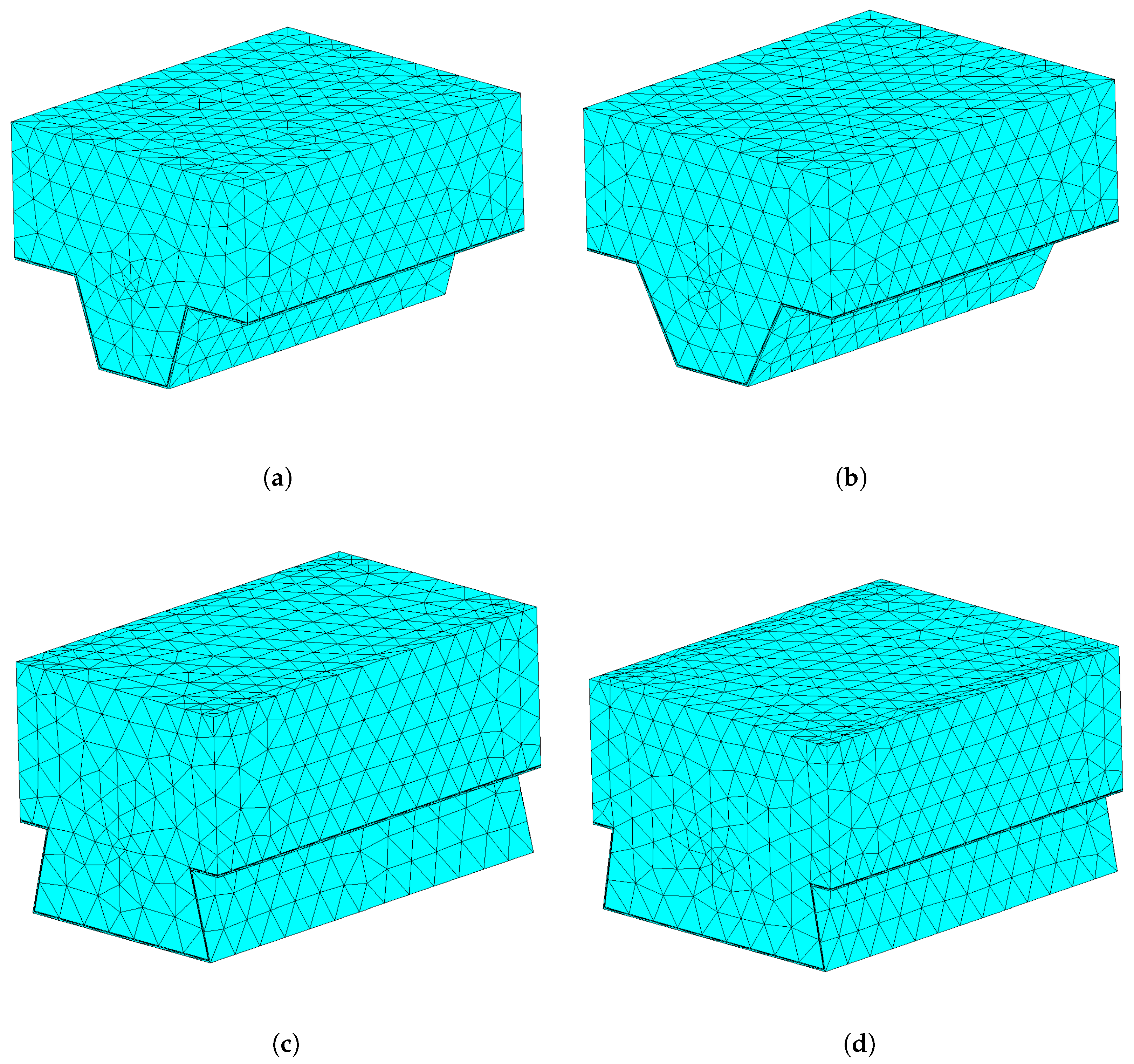
The Matlab (R2021a) PDE Toolbox was used to solve the non-linear transient thermal problem. The finite element model of the composite slab, created with Matlab, uses the tetrahedral finite element type. This finite element is defined by four nodes and uses linear interpolating functions. The finite element mesh includes the five sub-domains: concrete, steel deck, rebar, anti-crack mesh, and air gap. Thus, three different materials are used (concrete, steel, and air). Additionally, two different types of concrete are considered: NWC and LWC.
The minimum finite element mesh size length changes according to each composite slab profile.
Figure 7 depicts the finite element mesh of the models, the element size being selected by a convergence test of the results, which means that the size of the mesh was adjusted until the relative error in nodal temperature calculations reached the maximum value of
in the worst scenario.
The solution method used by the Matlab PDE Toolbox is incremental in time and iterative in each time step due to the non-linear thermal properties of the material. Equation (
8) is converted to
where
. The solution of Equation (
9) is achieved by the built-in function ode15s [
24]. The solution method implemented in this function is based on the discretisation of the time derivative by numerical differentiation formulas (NDFs) of orders 1 to 5. The accuracy of the solution can be explicitly controlled through the absolute or relative tolerance parameters. The absolute tolerance is a threshold parameter, below which the value of the solution component is disregarded. This property determines the accuracy when the solution approaches zero. The relative tolerance is a measure of the error relative to the size of each solution component (for more details, see [
16]). In this paper, the absolute tolerance is set to
and the relative tolerance is set to
. In each time step, the non-linear system of algebraic equations is solved through the Gauss–Newton method, whose stopping criterion can be monitored by means of the maximal number of iterations (25), the residual tolerance (
), and the minimum damping of search direction (
).
4. Simplified Calculation Method
The simplified calculation method used for the load-bearing criterion (R) presented in Eurocode EN1994-1-2 [
4] can be applied to simply supported composite slabs when exposed to an ISO-834 standard fire [
3].
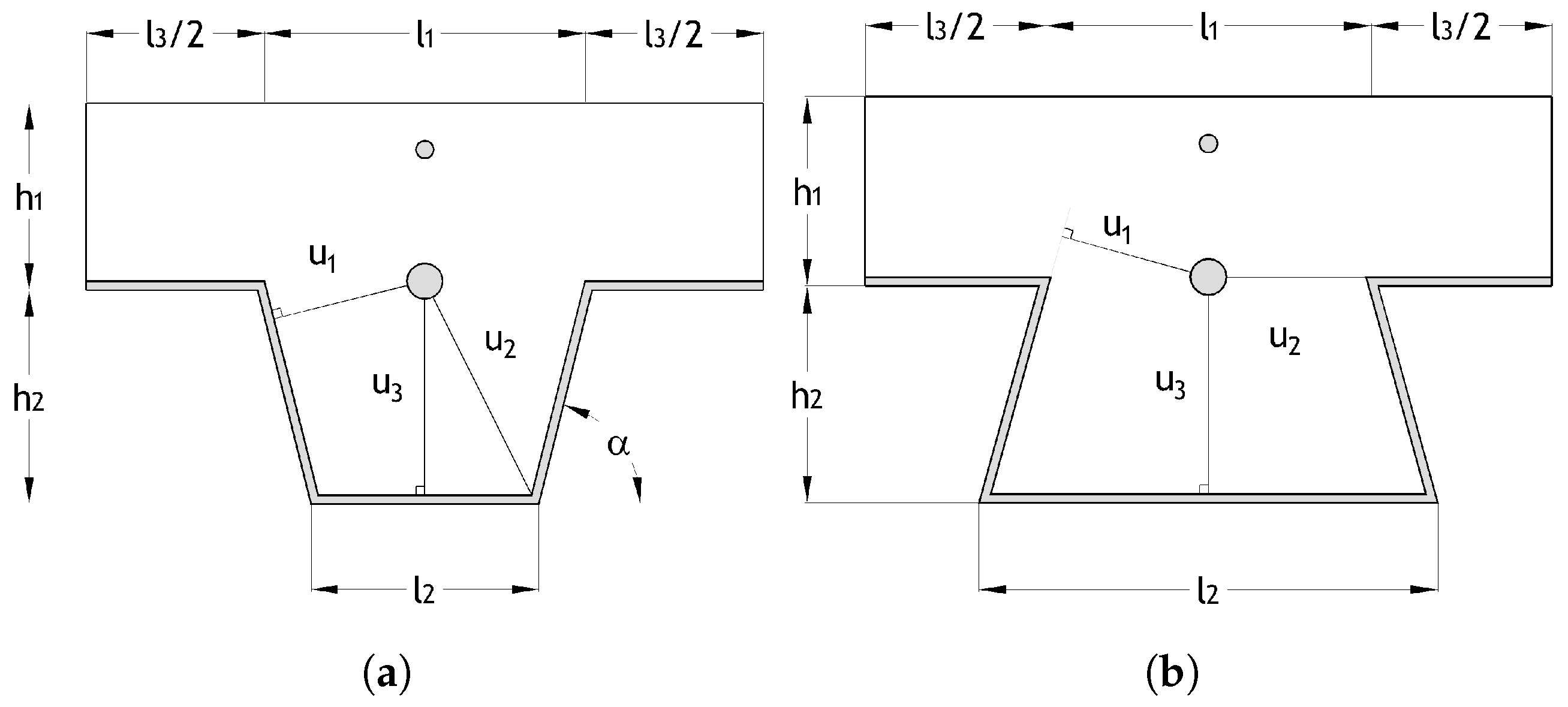
In order to calculate the bending moment resistance of the composite slab (sagging moment), this standard requires the temperature calculation for each steel deck component (upper flange, web, and lower flange), for each required fire rating, according to the formula
and also for the rebar component
by the formula
where the temperatures
and
are given in °C. The parameter
is dimensionless and represents the view factor of the steel deck component (upper flange only), given by Equation (
3);
is the distance within the ribs (see
Figure 6);
represents the distance from the middle of the rebar to the lower flange in mm (see
Figure 6); the
z-factor represents the position of the rebar concerning the slab rib given by
in mm
;
represents the angle between the web component of the steel deck and the horizontal direction in degrees (°) (see
Figure 6);
is the ratio between the concrete volume and the exposed area per meter of rib length of the steel deck, given in mm, and its calculation is performed through
The terms
and
represent the empirical coefficients given by Eurocode EN1994-1-2 [
4], which depend on the type of concrete used (NWC or LWC) and on the standard fire rating, which must be verified.
Equations (
12) and (
13) enable estimating the temperatures that affect the reduction strength coefficients in all the slab components and, consequently, an accurate estimation of the load-bearing resistance criteria. The load-bearing resistance criteria (R) will be based on the reduction coefficients applied to the yield strength of each component.
5. Validation, Parametric Analysis, and New Proposal
After the validation of the numerical model, a parametric study was conducted to analyse the influence of the concrete thickness
on the temperature of each component, used to determine the fire resistance of composite slabs according to the load-bearing criterion (R). As mentioned before, the load-bearing resistance depends on the temperatures in the steel deck components and rebar. A simplified calculation method is proposed by Eurocode EN1994-1-2 [
4]. Unfortunately, this model has not been modified for a long time and, according to the authors, needs to be improved. The proposed methodology is based on the numerical solution of the non-linear and incremental thermal analysis, presented in the previous section, for different thicknesses of the concrete topping (
), comparing the results with the simplified solution method.
5.1. Validation of the Computational Model
Measuring the errors of numerical against experimental results is of paramount importance in order to assess the performance of the computational model. As shown by Chai and Draxler [
25], assessing the accuracy of the predicted values is best done using various metrics. Three metrics are especially useful when trying to assess the performance of a computational model. The simplest of those metrics is the bias, given by
where
n is the number of values,
is a numerical value, and
is the corresponding experimental value. As its name suggests, bias measures the bias of the model, which is simply the average error compared to the experimental. However, it does not really show the behaviour of the error. It is useful to determine if the computational model makes predictions that are lower or higher than the reference value (experimental), but it is not enough in itself to really know how well the model performs. It only shows the systematic error of the model.
Thus, complementary to the bias, the root-mean-squared error (RMSE) is also used:
The RMSE is useful because the squared terms give a higher weight to higher errors. Thus, the RMSE will be higher if the model makes predictions that are far from the reference, even if these erroneous predictions are few in number.
To complement the bias and RMSE metrics, the standard deviation of the error (SDE) may also be considered. The SDE simply corresponds to
Considering the bias as a basic indicator of the systematic error in a prediction, then the SDE is the equivalent indicator of the random error.
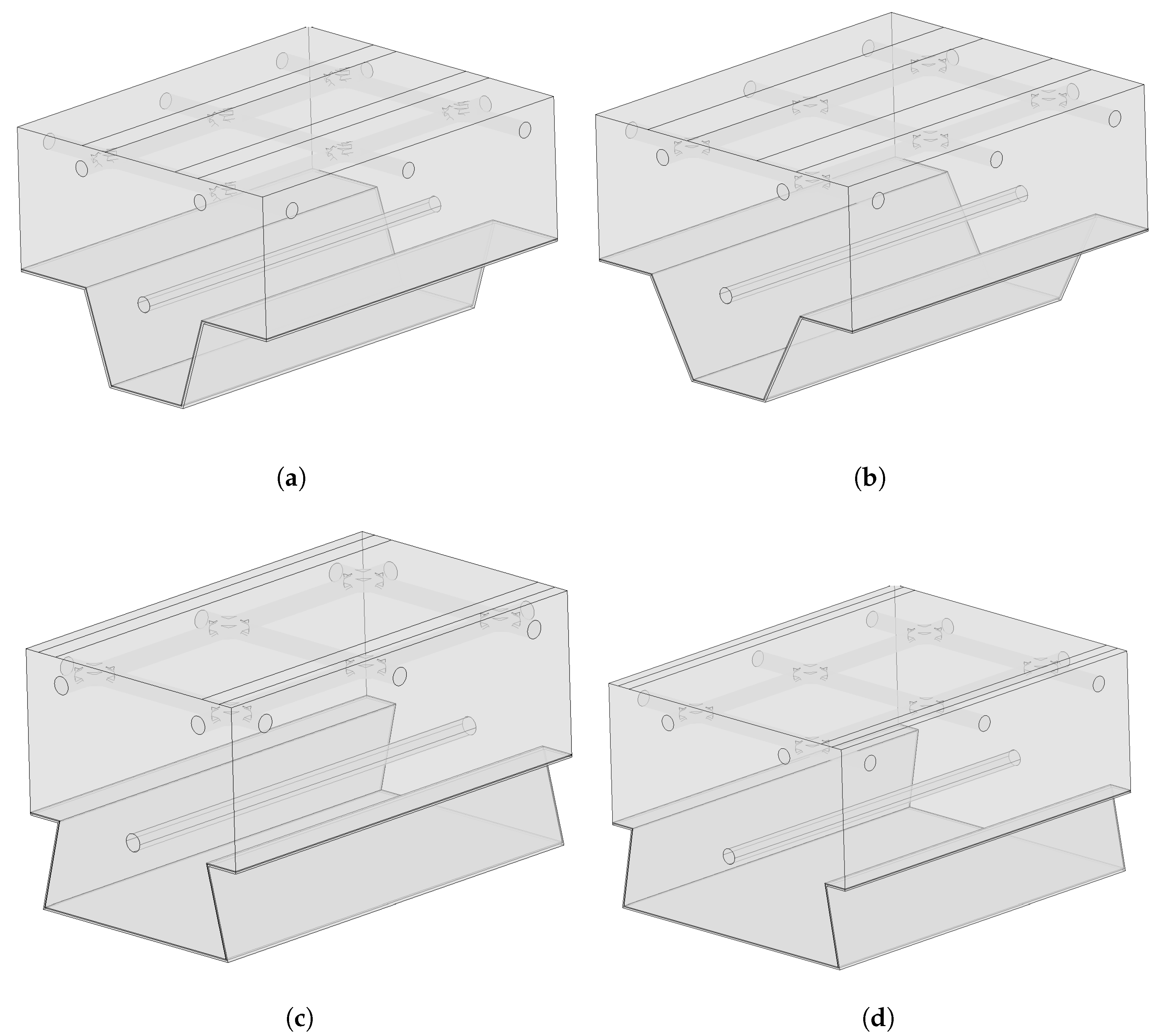
Unfortunately, there are no experimental results in the literature with the four slabs that are investigated in this work (see
Figure 2). Therefore, the finite element computational model was validated with the experimental results published by Lim and Wade [
26] and Piloto et al. [
7]. The results published by Lim and Wade [
26] correspond to test number 4, obtained on a composite slab with a clear span of 3160 mm wide by 4160 mm long, with normal-weight concrete with siliceous aggregates and the moisture content of 5.6% by weight; the initial bulk temperature was 13
C. The results published by Piloto et al. [
7] correspond to test number 1, obtained on a slab with a clear span of 985 mm wide by 916.8 mm long; normal-weight concrete was used, and the moisture content was approximately 3.0% by weight; the initial bulk temperature amounted to 20
C.
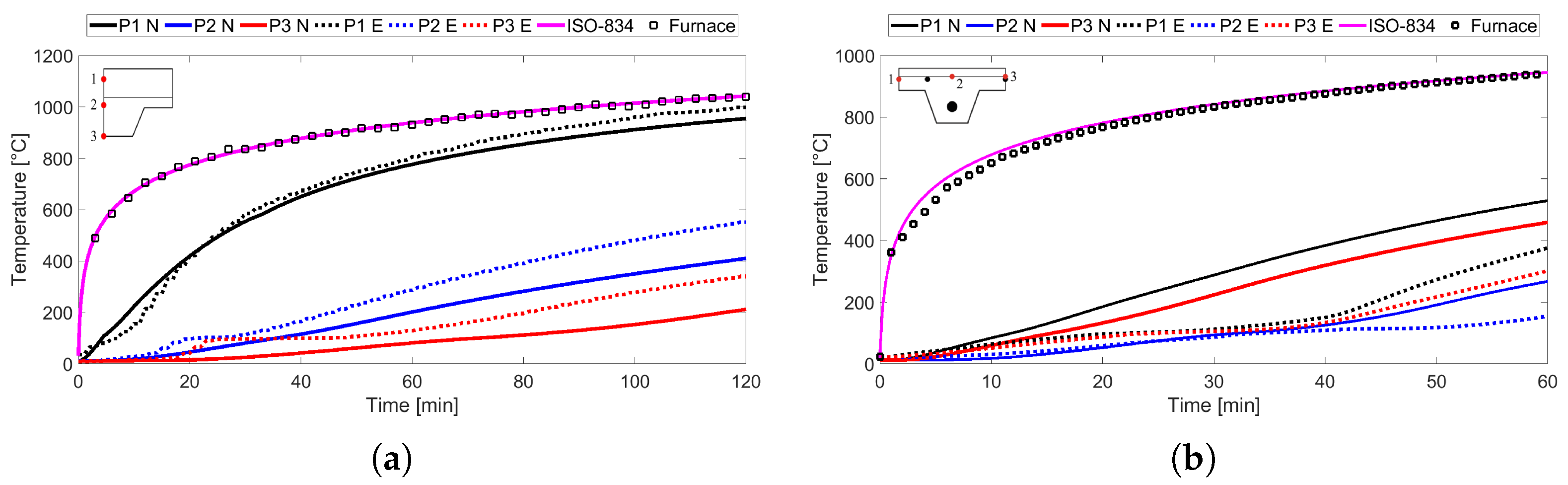
The values of the validation errors obtained with different air gap values are presented in
Table 2, for the temperatures obtained at three points of the slab: P1, P2, and P3 (see the left-upper corner of
Figure 8). In the case of Lim and Wade [
26], the points are located at the middle of the rib, respectively, at distances of 20, 70, and 130 mm from the top. In the case of Piloto et al. [
7], P1 and P3 are located in the middle of the upper flange, at distances of 20 and 15 mm, respectively, from the top; P2 is located in the middle of the rib at a distance of 15 mm from the top.
From the validation with the experimental results of Lim and Wade [
26] presented in
Table 2, one can see, in the case of P1, that the global reduction of the errors is achieved with an air gap of 0.5 mm, while for points P2 and P3, this reduction is not achieved; on the contrary, the errors increase with the increase of the air gap size.
Figure 8a depicts the evolution of the experimental and numerical temperatures in points P1, P2, and P3 along the first 120 min after the beginning of the fire, for the case of an air gap of 0.5 mm. Additionally, the bulk temperature corresponding to the standard fire ISO 834, given by Equation (
5), and the furnace temperature, registered during the experiment, are also included.
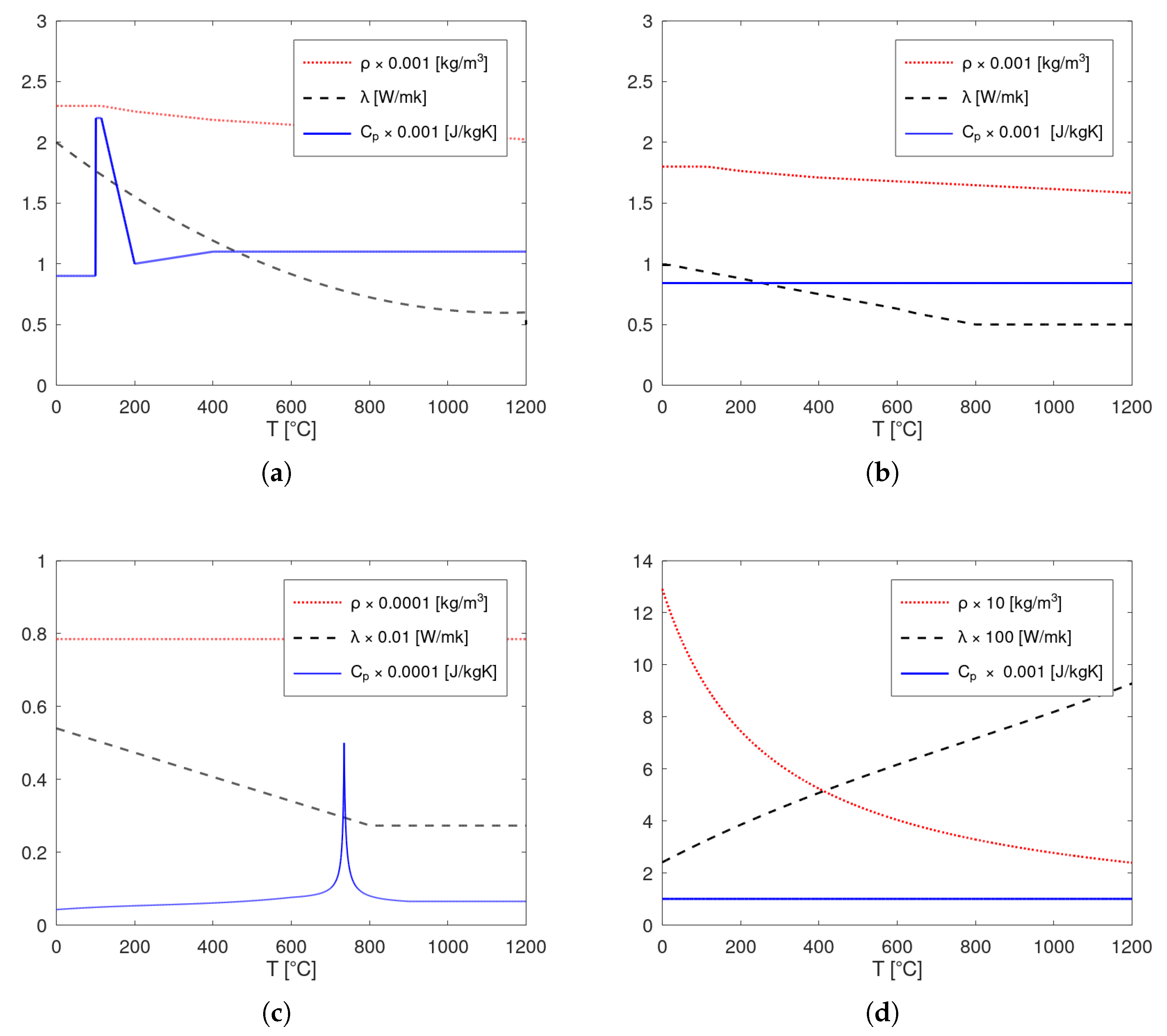
For the experimental results depicted in
Figure 8, one can see a plateau at about 100
C. This is due to moisture evaporation in the concrete. This phenomenon translates into a sudden rise in the specific heat (illustrated in
Figure 4a) and has the immediate consequence of a decrease in the rate of temperature increase. The results of the numerical simulations do not present this pronounced plateau, probably because localised moisture concentrations in the tests were higher than the uniform moisture content introduced in the thermal models for each slab.
From the validation with the experimental results of Piloto et al. [
7] presented in
Table 2, it can be observed that, in general, the errors decrease with the increase of the air gap.
Figure 8b depicts the experimental and numerical temperatures in points P1, P2, and P3 along the first 120 min after the beginning of the fire, for the case of an air gap of 0.5 mm, along with the bulk and furnace temperatures.
From the results of the validation presented in
Table 2 and
Figure 8, one cannot conclude that there exists an optimal air gap. The experimental results are highly influenced by the concrete thermal properties, such as the moisture content, which influences, in particular, the specific heat. For these reasons, an air gap of 0.5 mm, greater than zero, but not too thick, was chosen.
5.2. Parametric Analysis
A parametric analysis was developed to determine the influence of the concrete thickness
on the temperature field, used to determine the fire resistance of composite slabs and the ability to sustain the load (R). A total of 40 numerical simulations were carried out, using an air gap of 0.5 mm, in agreement with the reasons previously discussed. The computational simulations took into account
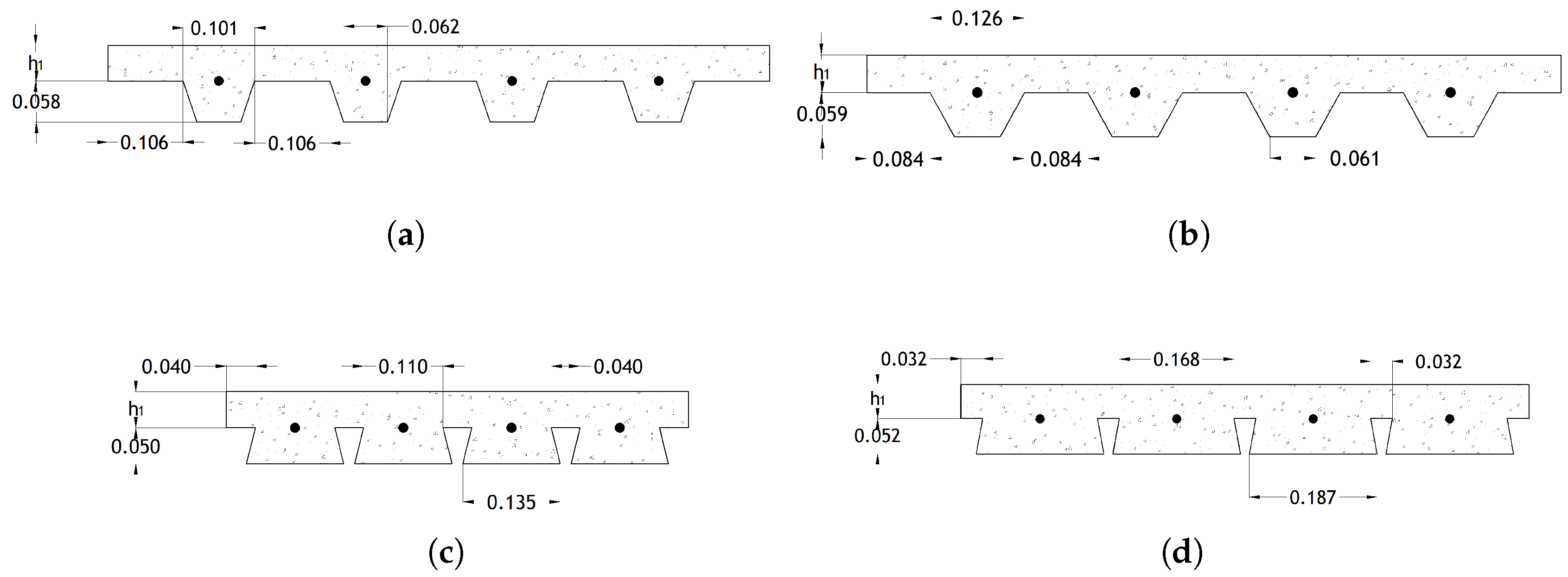
values equal to 60, 70, 90, 110, and 125 mm for the two trapezoidal steel deck geometries (see
Figure 2a,b) and
values equal to 50, 70, 90, 110, and 125 mm for the two re-entrant steel deck geometries (see
Figure 2c,d). All simulations were developed for NWC and LWC.
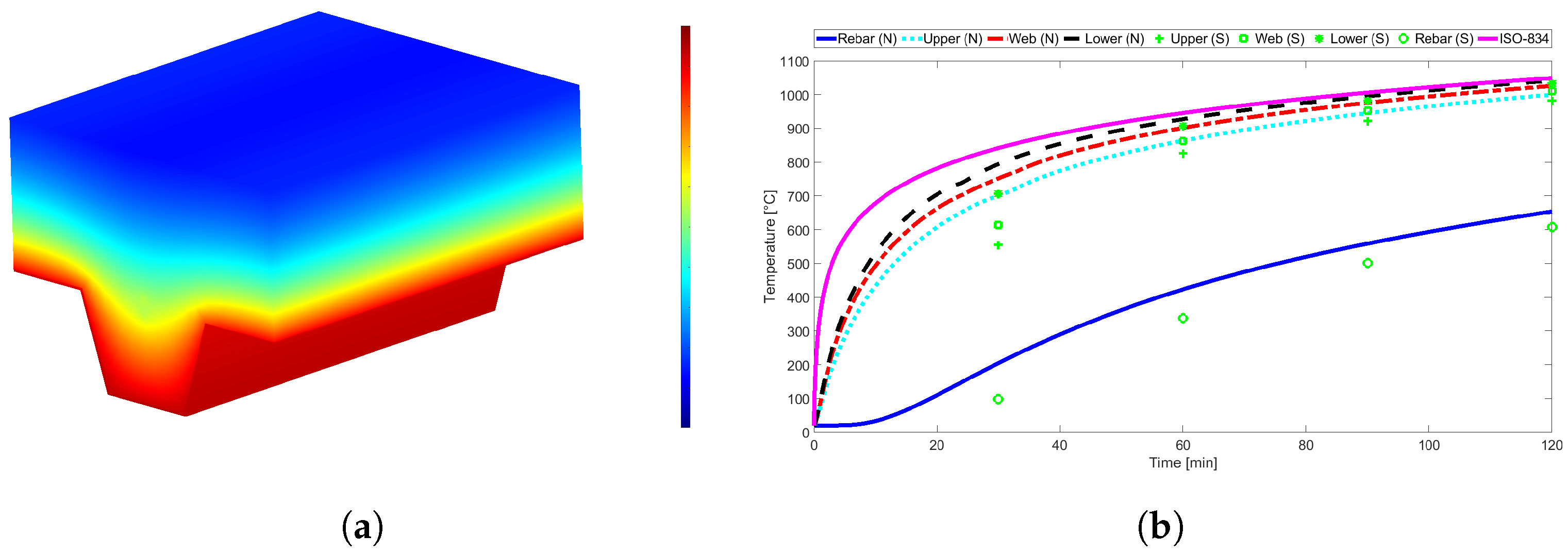
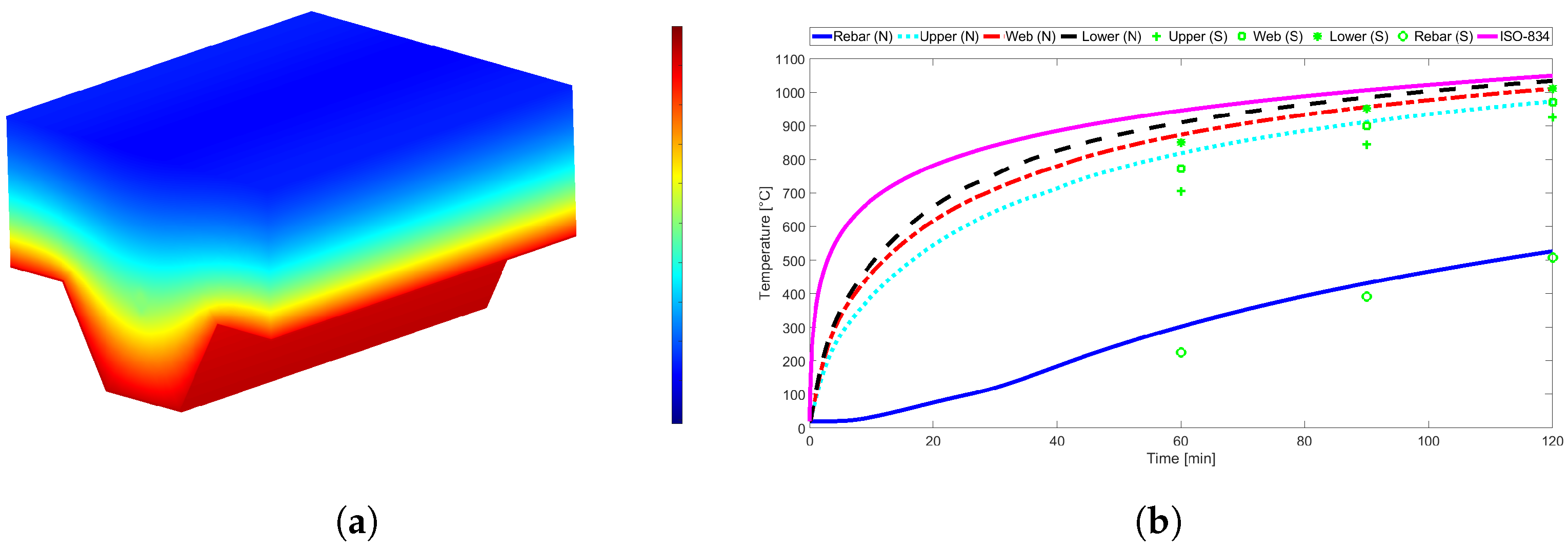
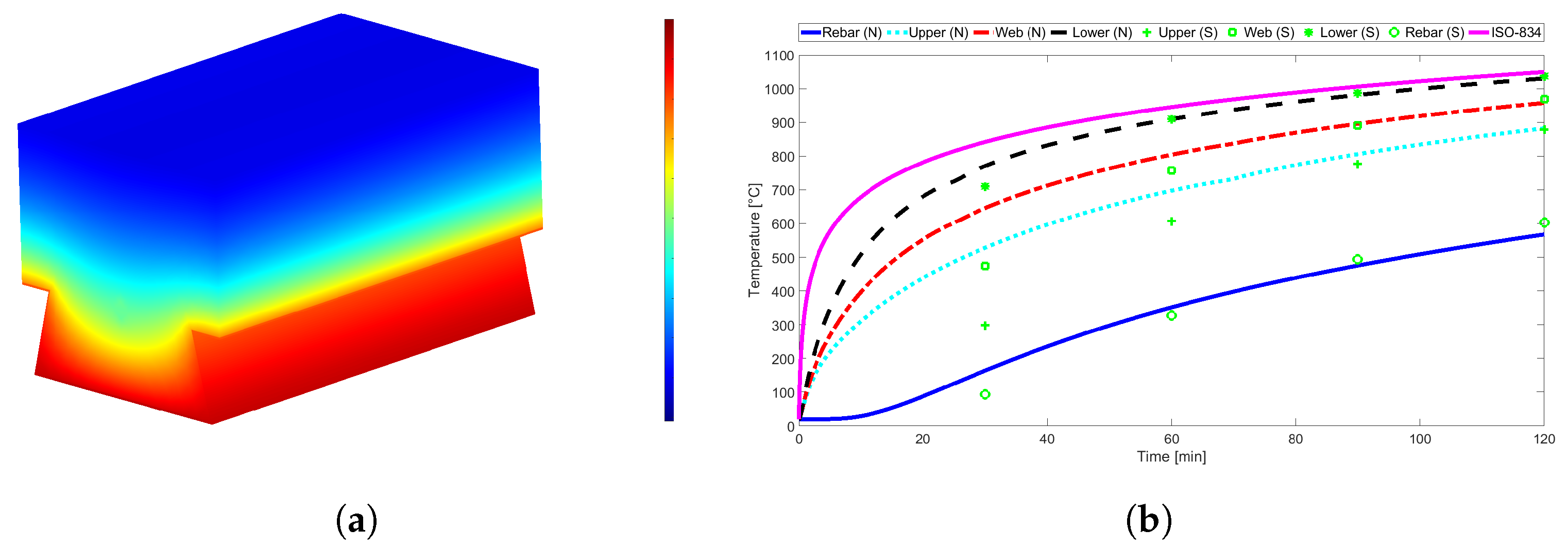
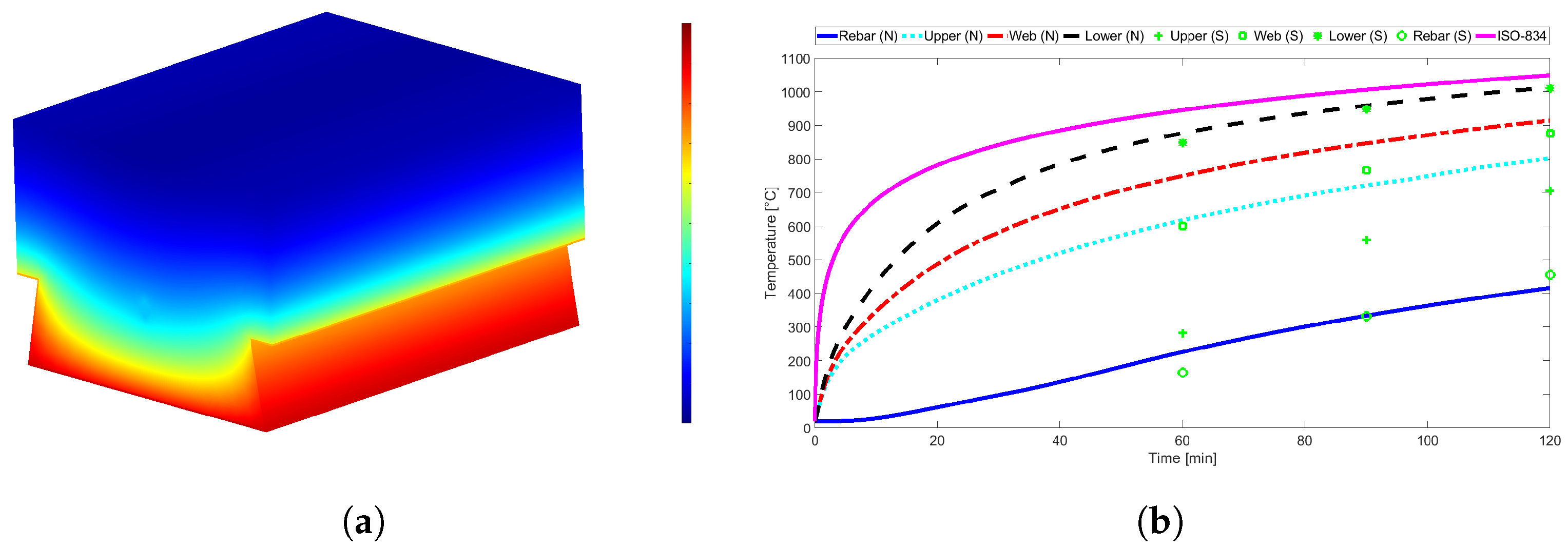
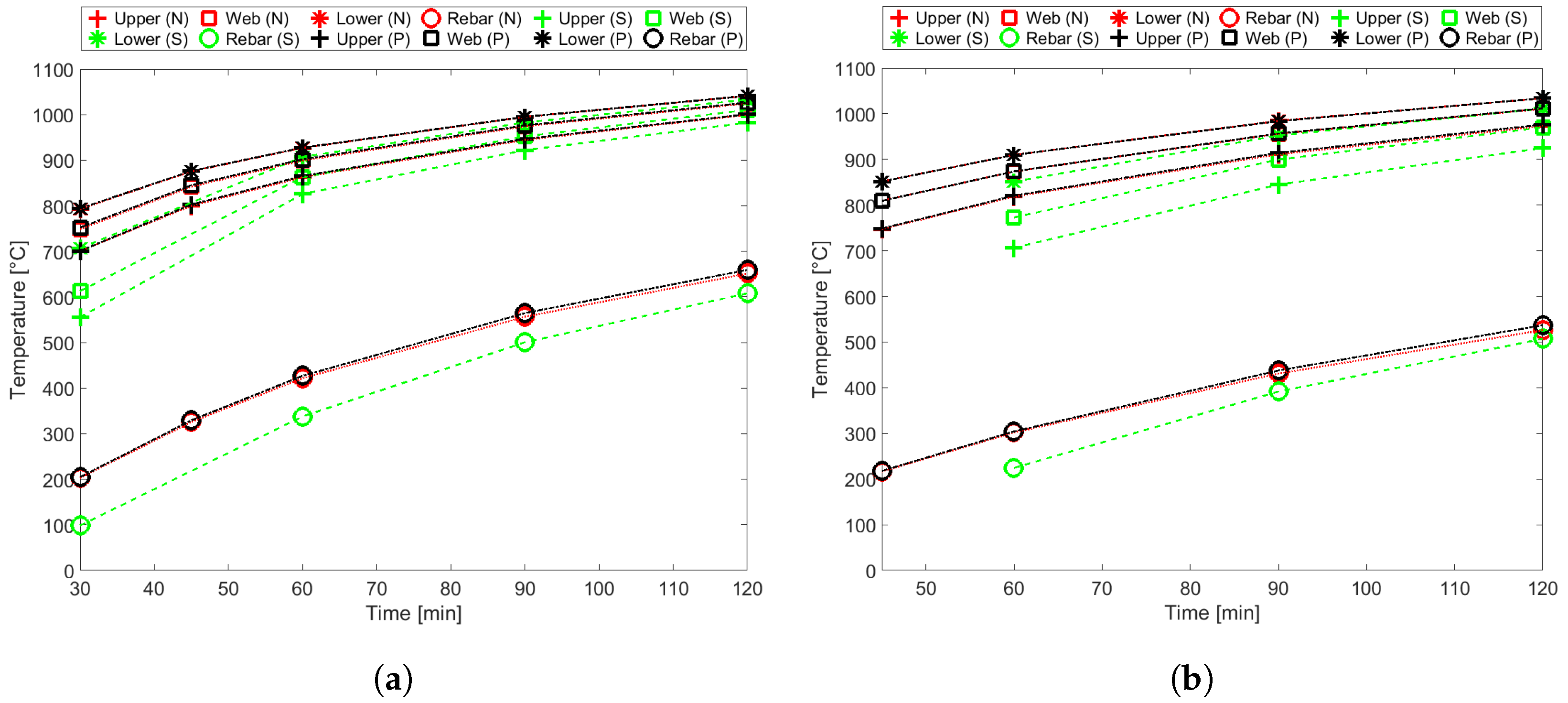
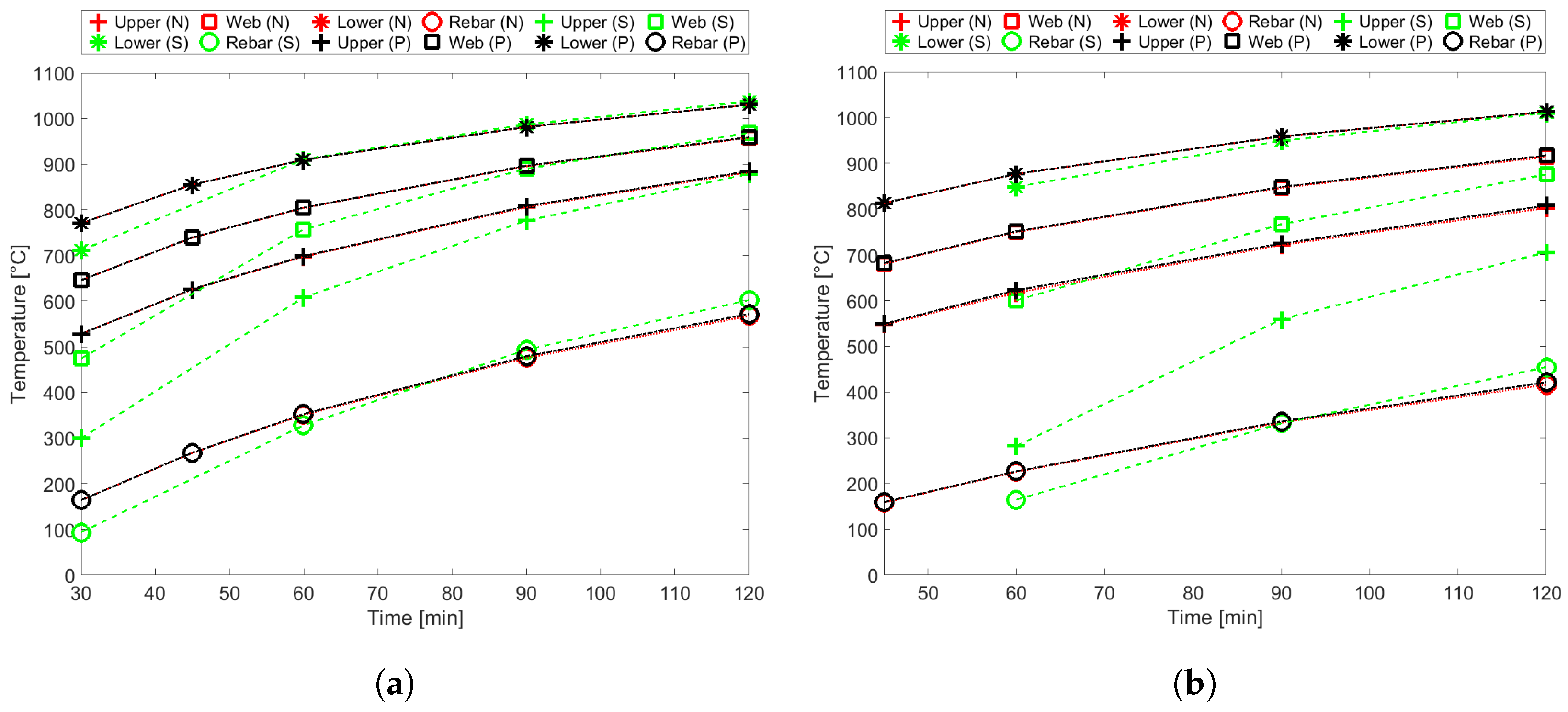
Figure 9,
Figure 10,
Figure 11 and
Figure 12 show the temperature field inside the composite slab after 120 min and the time evolution of the average temperatures, determined by numerical simulation (N), in the three components of the steel deck and in the rebar. For comparison, the values calculated using the simplified method (S), given by Equations (
10) and (
11), are also included. In the case of NWC, the standard EN-1994-1-2 provides only the fire rating for 60, 90, and 120 min, because it is considered that, if the slab project is well made for the room temperature, it is able to resist fire for at least 30 min. According to the same standard, when the slab is made of LWC, it will require the fire analysis for 30 min. Additionally, the
given by Equation (
5) is also depicted in these figures.
Figure 9 shows the thermal behaviour of the trapezoidal Confraplus 60 slab with
mm using LWC.
Figure 10 shows the thermal behaviour of the trapezoidal Polydeck 59S slab with
mm using NWC.
Figure 11 presents the thermal behaviour of the re-entrant Multideck 50 slab with
mm using LWC.
Figure 12 presents the thermal behaviour of the re-entrant Bondeck slab with
mm using NWC. One can see that, in general, the temperatures predicted by the simplified calculation method are below the numerical results. This is especially true for the fire ratings of 30 and 60 min, in the case of the Multideck 50, and for the fire rating of 60 min, in the case of the Polideck 59S geometry. It is also noted that the temperature in the rebar is higher when LWC is used instead of NWC. It can also be noted that the temperatures of the trapezoidal slabs are usually higher than the temperatures of the re-entrant slabs.
5.3. Computational Times
The computational simulations were performed on a Linux system, running in a machine with a 16-core AMD EPYC 7351 CPU and 64 GB of RAM, with a Matlab code purely sequentially. The computational times related to the simulation of the thermal effects, caused by a standard fire over 120 min, are shown in
Table 3. These times were obtained in the four slabs with thickness
mm. The anti-crack mesh is located 19 mm from the top. The space between each bar of the anti-crack mesh is 50 mm, and the diameter of each bar is 4 mm.
The results presented in
Table 3 show that the computational times of the simulations with NWC are much higher than the times obtained with LWC. This is due to the thermal properties of the LWC, which vary more linearly with temperature than the properties of NWC (see
Figure 4), creating fewer convergence problems in the numerical integration scheme. It is also observed that the slabs with the re-entrant geometry present longer computation times. This is due to the fact that they present a larger volume, whose modelling implies the use of a greater number of finite elements.
Another important observation is that the use of the anti-crack mesh increases the computation times substantially. The reason is the refinement of the mesh and the consecutive increase in the number of nodes where it is necessary to estimate the temperature. However, this increase in time is not justified, as the estimation of temperatures in the slab components is not improved.
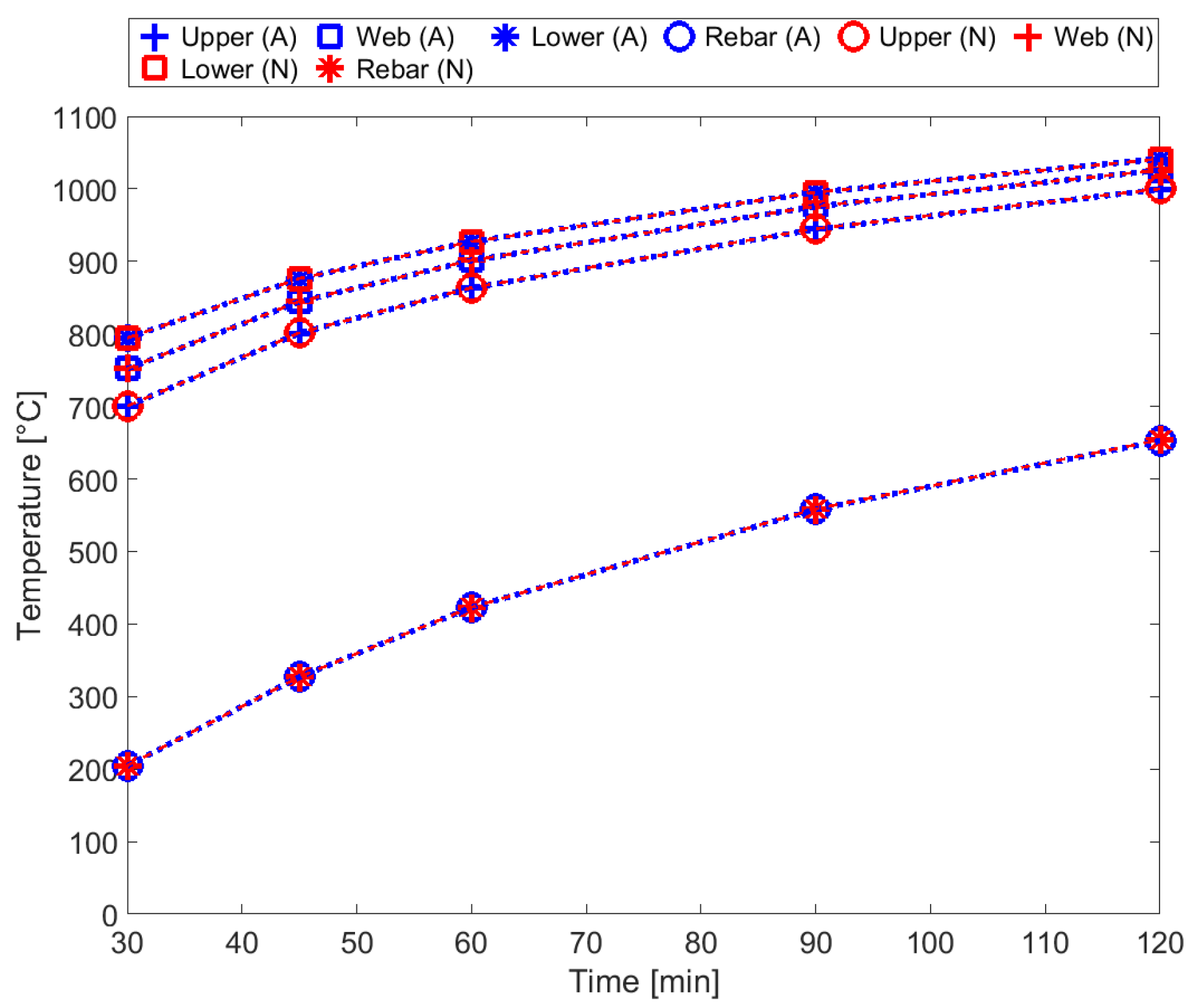
Figure 13 compares the numerical temperatures, obtained after 30, 45, 60, 90, and 120 min, with (A) and without (N) anti-crack mesh in the Confraplus 60 slab. The temperatures obtained with and without the anti-crack mesh are superposed, which means they are almost the same.
5.4. New Calculation Proposal
Based on the numerical results, new coefficients
and
are proposed for the simplified calculation model. In addition, the original models, given by Equations (
10) and (
11), were modified by including a new term that depends on
, in order to take into account the effect on the temperatures for the thickness of the concrete topping. The thickness
is explicitly included in the mathematical model multiplied by coefficient
, in the case of the steel deck temperatures, and by
, in the case of the rebar temperature. Thus, the new proposal for the steel deck temperature is
and for the rebar is
The coefficients for these new proposed methods were determined by fitting the mathematical models, represented by Equations (
17) and (
18), to the numerical results obtained with the parametric analysis when changing the
dimension, applied on two different types of concrete and the four different composite slab geometries. The coefficients were determined using the non-linear least-squares method. This method consists of minimising the sum of the squared deviations between the temperatures obtained with Equation (
17) or (
18) and those obtained through numerical simulations. This sum was minimised using the generalised reduced gradient (GRG) non-linear solver [
27].
The determined coefficients used for the calculation of temperatures at the steel deck components, through Equation (
17), are presented in
Table 4. For the calculation of the temperatures at the rebar, through Equation (
18), the proposed coefficients are presented in
Table 5. It is worth mentioning that in addition to the standard fire ratings of 60, 90, and 120 min for NWC and 30, 60, 90, and 120 min for LWC, the new proposal also comprises the coefficients for the fire rating of 45 min. This fire rating may also be regarded for the fire classification of construction products and building elements, when using also the separating function.
Analysing the new coefficients presented in
Table 4 and
Table 5, it appears that increasing
leads to small reductions in temperatures on the steel deck components and on the rebar since
and
are generally small in magnitude. However, in the case of rebar,
has a greater effect, especially for longer fire resistance ratings.
5.5. Comparison of Results
This subsection presents the differences between the results proposed by the simplified model (S) presented in Eurocode 1994-1-2 [
4], the numeric results (N), and the new calculation proposal (P). This comparison is presented in the following graphs.
Figure 14a establishes this comparison for each steel deck component and the rebar for LWC, while
Figure 14b plays the same role for NWC, where both slabs have a trapezoidal profile.
Figure 15 establishes the same comparison in the case of the two slabs with re-entrant profiles.
The results depicted in
Figure 14 and
Figure 15 show that the new proposal fits very well with the proposed numerical results. It was observed also that the temperatures estimated by the simplified model are always lower than the numerical temperatures. The differences are most noticed for the lower fire ratings, especially in the case of steel deck components. The numerical temperatures on the rebar are relatively close to the temperatures estimated by the simplified model, especially for the slabs with the re-entrant geometry.
When compared with the actual version of the Eurocode 1994-1-2 model, the new proposal contributes to improving the temperature estimation according to each fire rating time. For both types of concrete (NWC and LWC), the new proposal matches very well with the numerical results. It is also possible to verify that the simplified model, proposed by the current version of the Eurocode, predicted much lower temperatures than the numerical results, mainly for the case of steel deck components and for the lowest fire ratings. The new proposal decreases the difference between the expected temperatures and the numerical simulation results, by more than 100 C, especially for low fire ratings. In the case of the rebar, the difference between the temperatures is smaller, especially for the slabs with the re-entrant geometry.
6. Final Considerations
In this paper, a realistic computational model, based on 3D finite elements, was developed to determine the thermal behaviour of composite slabs under standard fire conditions. This model takes into account the various sub-domains of the composite slab, their respective thermal properties, and the debonding effect of the steel deck. The results of the numerical simulations enabled us to determine the temperatures for different slab geometries and compare them with the ones provided by the simplified calculation model presented in Eurocode EN1994-1-2. The proposed model aims to include some effects that the current version of the Eurocode neglects, such as the debonding effect between the steel deck and concrete and the thickness of the concrete topping.
The computational model is reliable and allows thermal simulations on composite slabs to be carried out in a not very long time. However, these computational times can be reduced, without loss of the quality of the results, by simplifying the physical model. It thus constitutes an efficient alternative to carrying out experimental tests, which are very demanding and expensive.
In order to improve the current simplified method, new analytical formulae were proposed to determine the temperature in the steel deck components and in the rebars, based on the numerical results. The new proposal includes, with respect to the current model of the Eurocode, an additional term to account for the effect of the concrete thickness (). The new coefficients were determined by fitting the new proposal to the numerical results by non-linear least squares.
The new proposal provides an improvement of the temperature estimation that affects the reduction coefficients in all the slab components. In the cases of low fire ratings, the new formulae decrease the difference between the expected temperatures and the numerical simulation results, by more than 100 C. The use of this new proposal enables accurate estimation of the load-bearing resistance criteria and, consequently, the safer design of composite slabs.