Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer
Abstract
:1. Introduction
2. Criteria for Basis Set Optimization and Contraction Scheme: Size and Composition
3. Computational Details
4. Results and Discussion
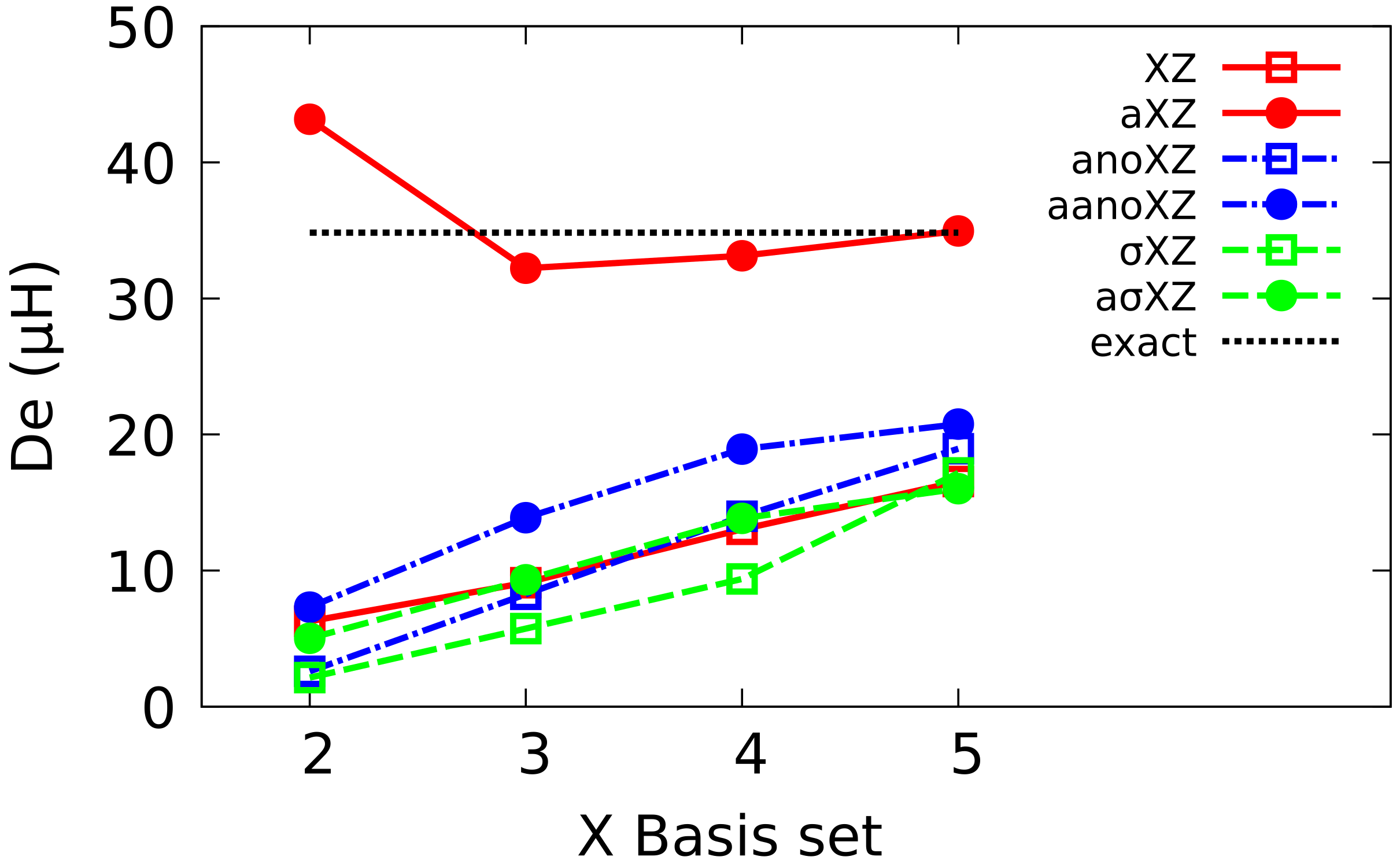
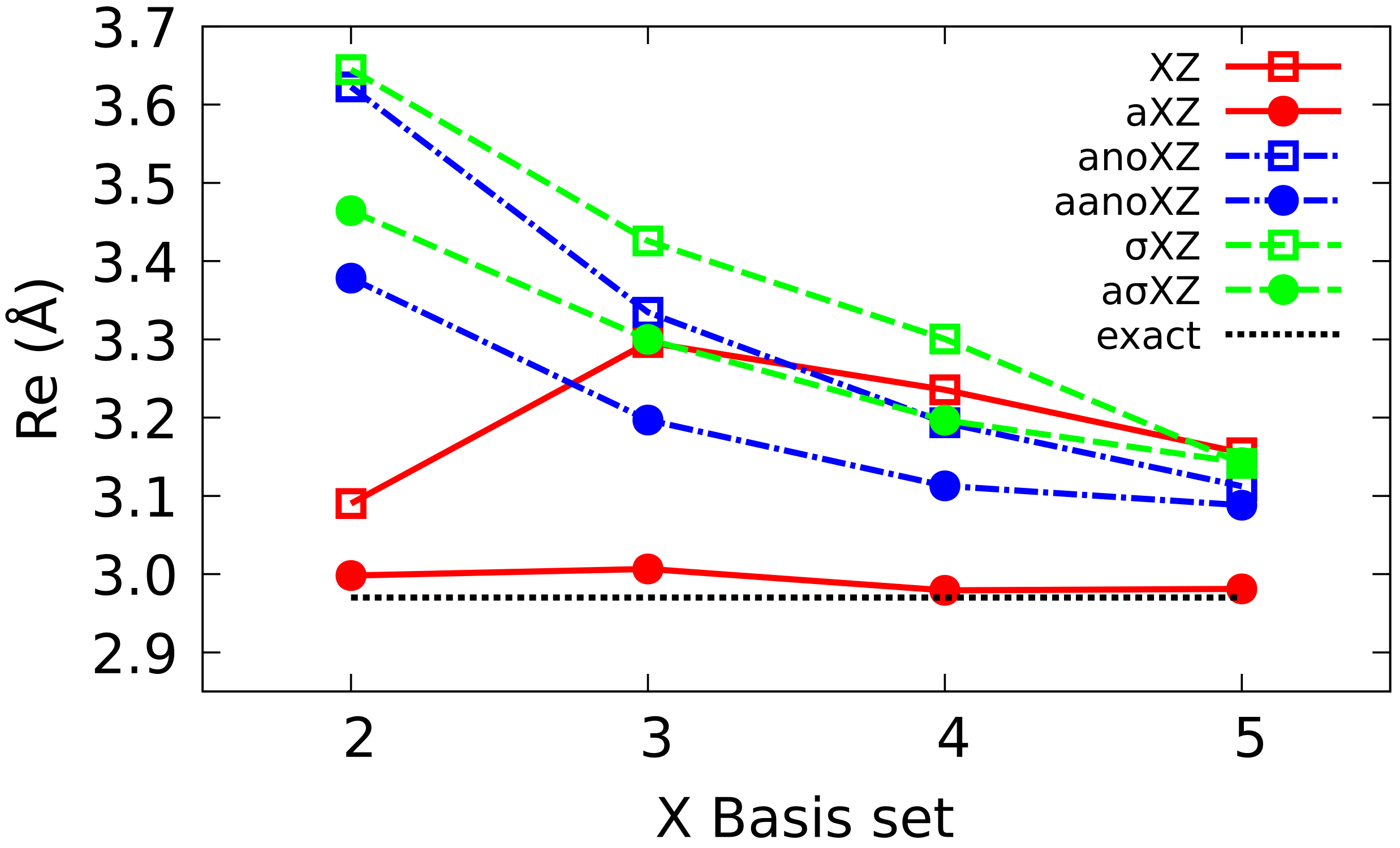
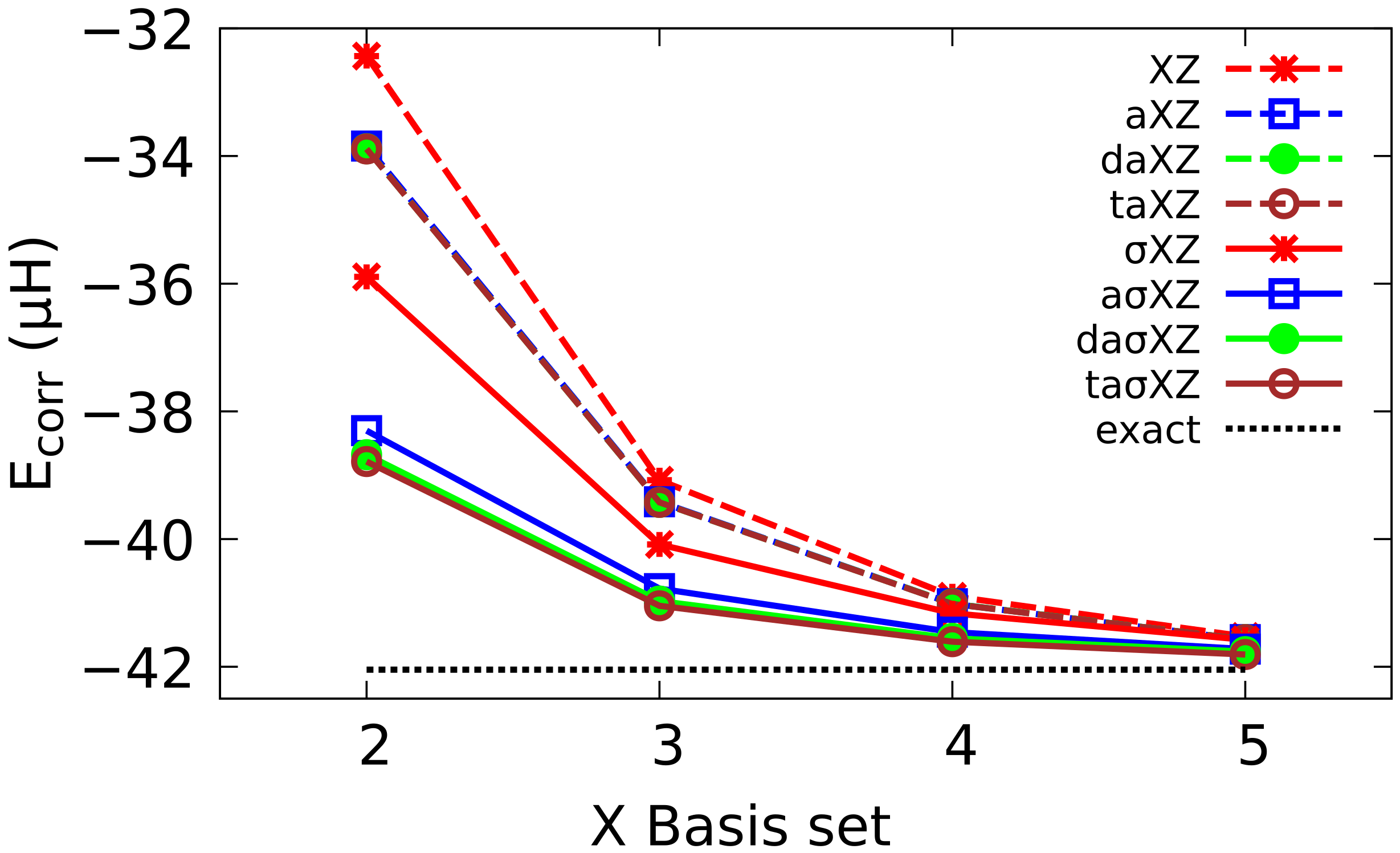
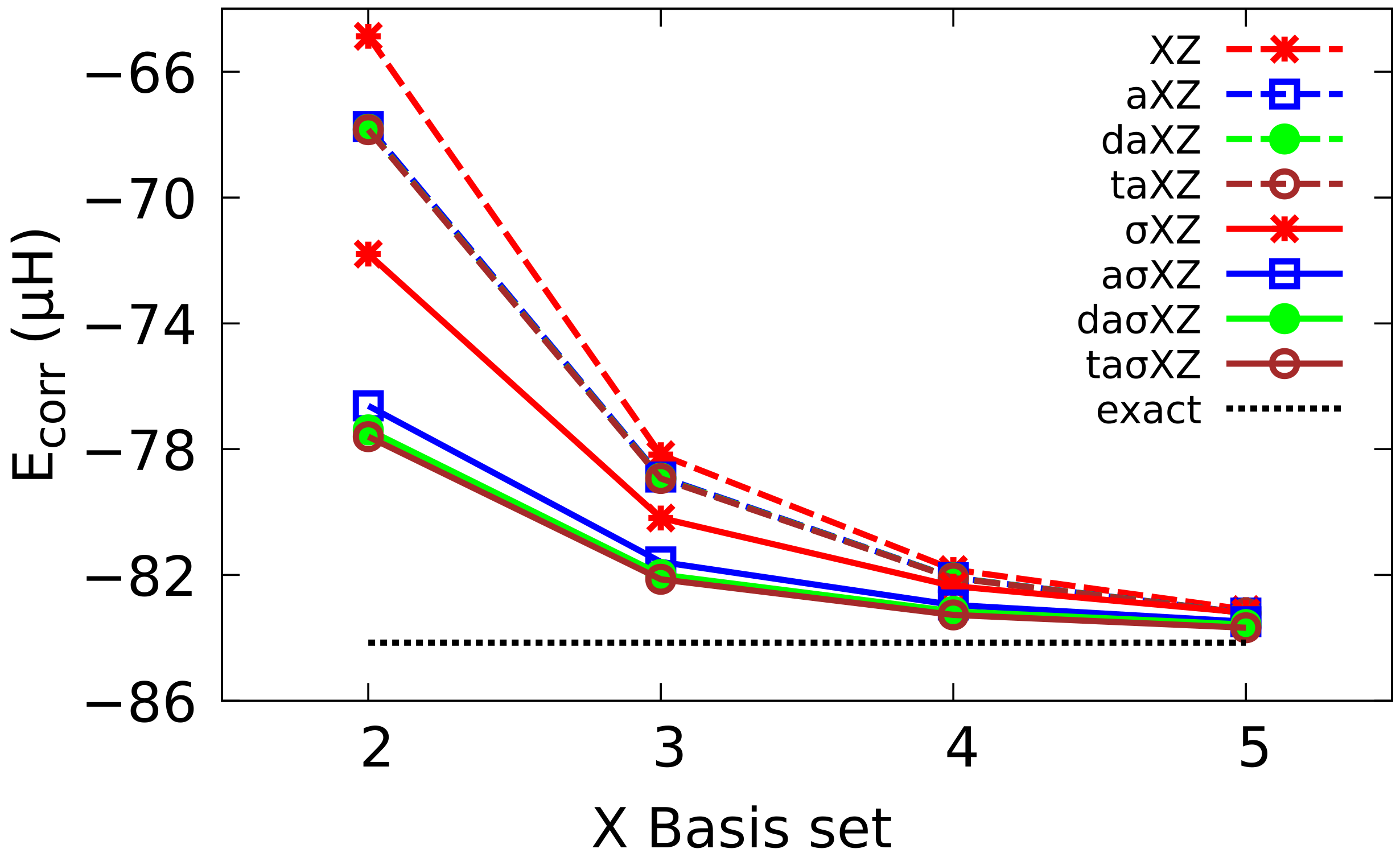
4.1. Sigma Basis Sets vs. Dunning and ANO Basis Sets
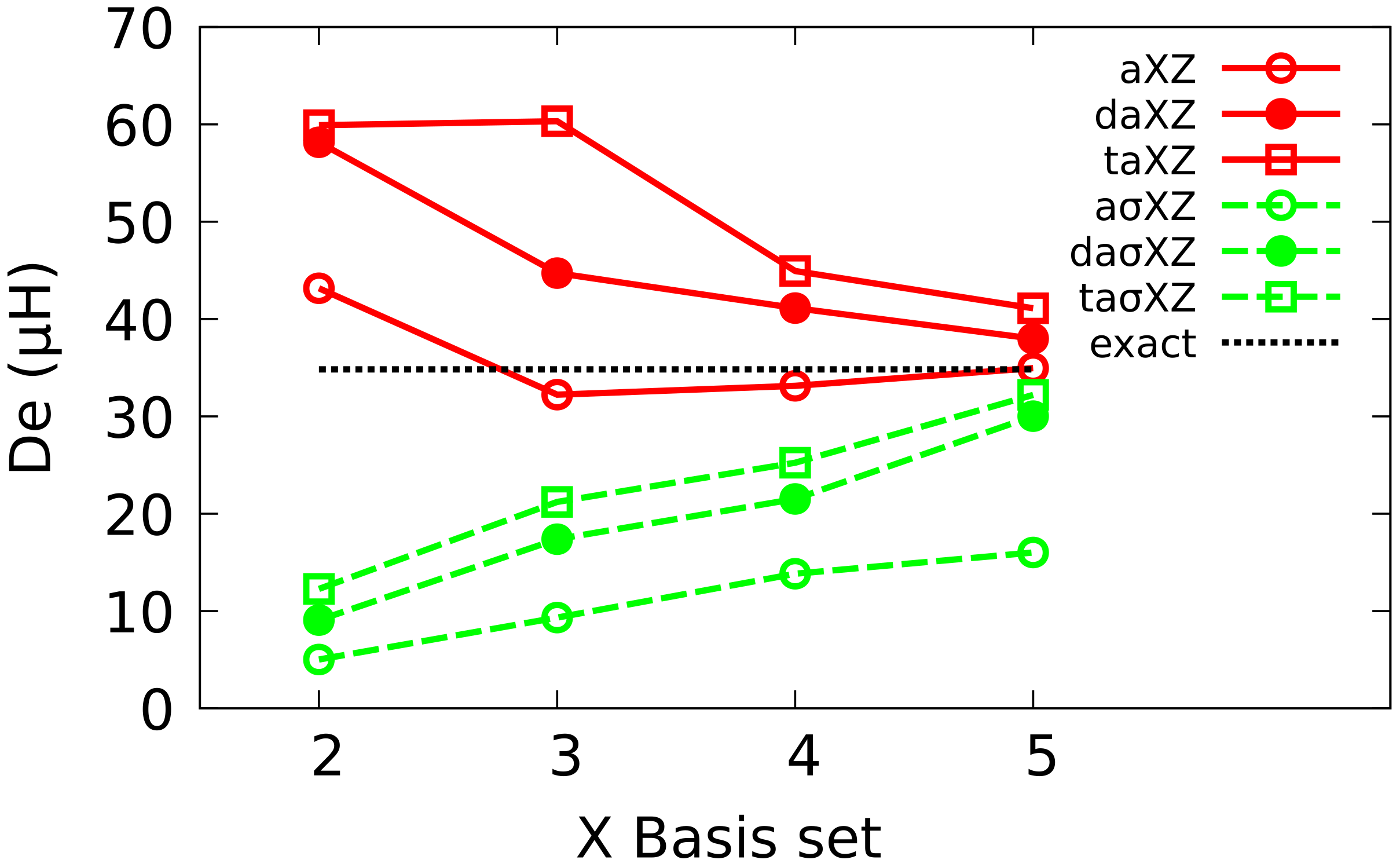
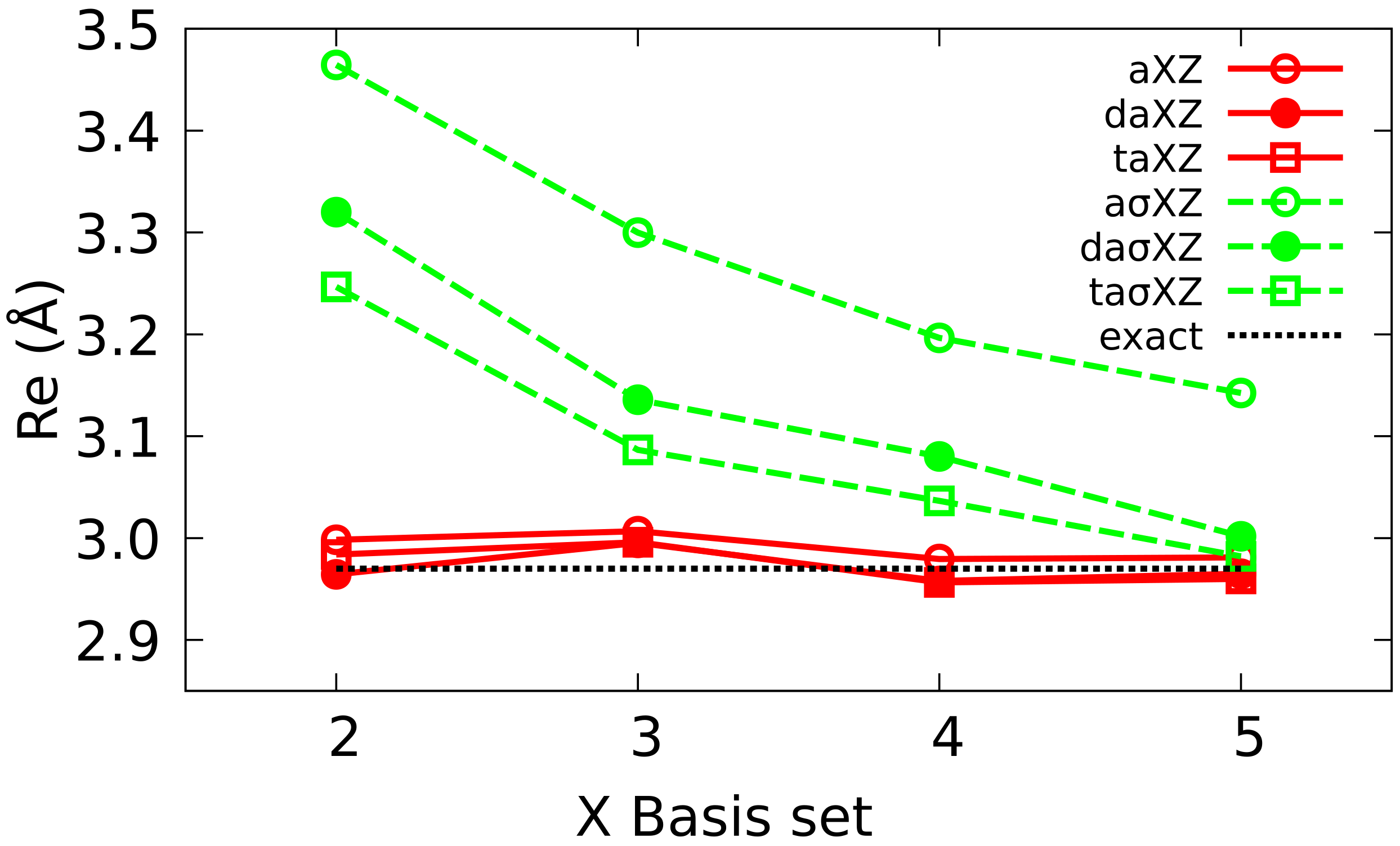
4.2. Multiple Augmented Basis Sets
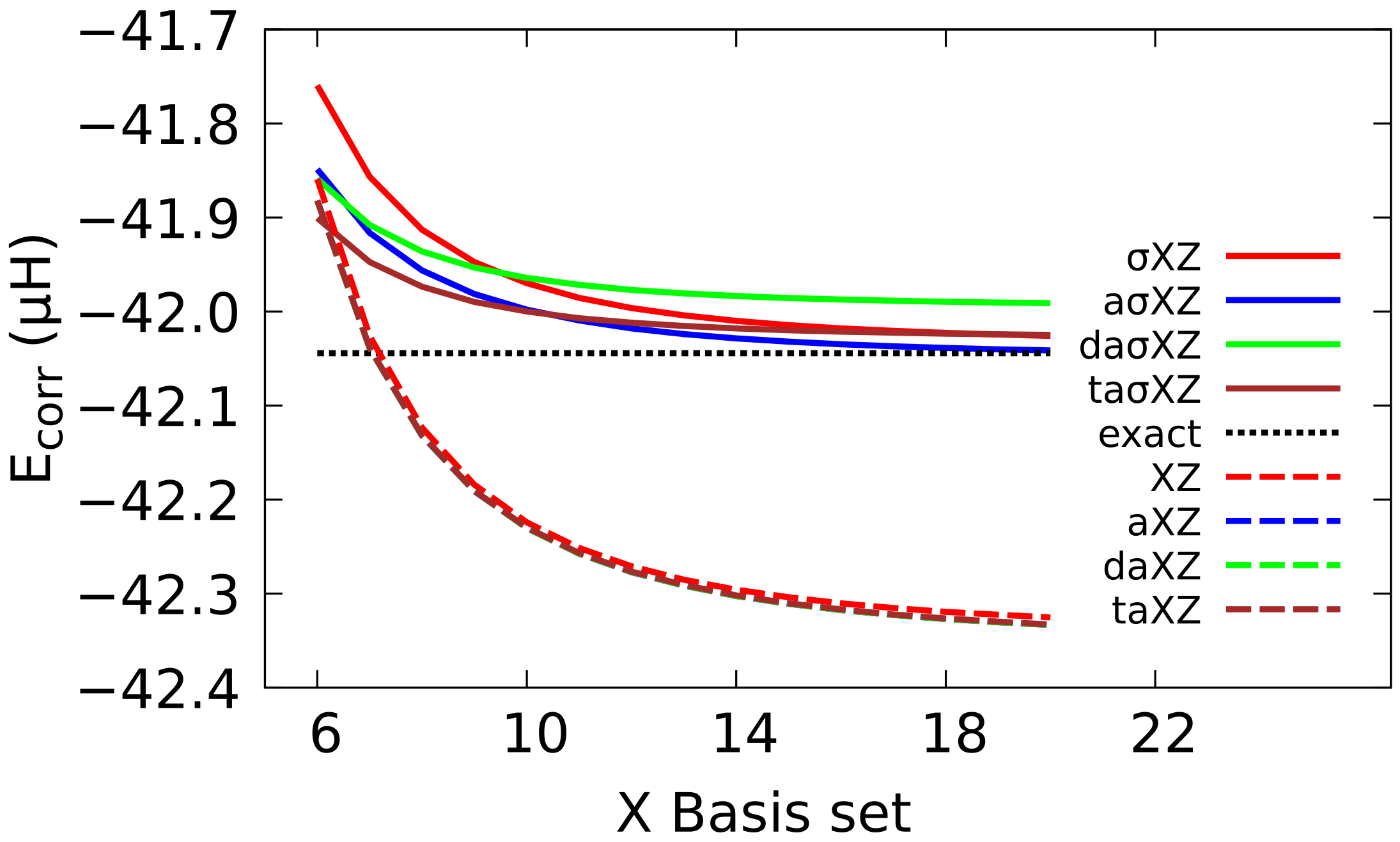
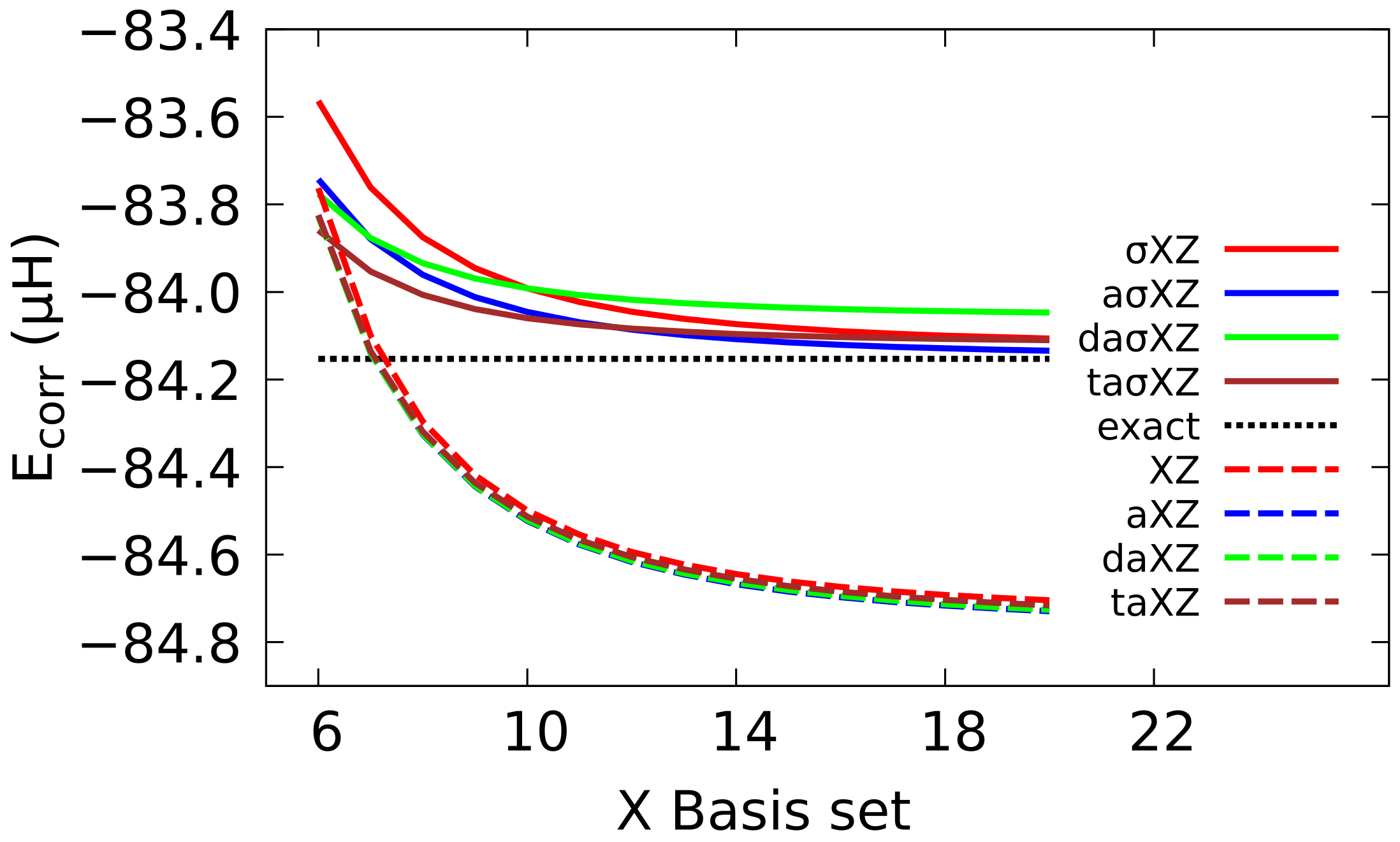
4.3. Extrapolation to CBS
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANO | Atomic Natural Orbitals |
| aANO | Augmented ANO |
| aXZ | aug-cc-pVXZ |
| aBS | Augmented Sigma Basis Set |
| BED | Best Available Equilibrium Distance of He |
| BS | Basis set(s) |
| BSSE | Basis Set Superposition Error |
| CBS | Complete Basis Set |
| CC | Coupled Clusters |
| CCSD(T) | Coupled Clusters Singles Doubles (Triples) |
| CISD | Configuration Interactions Singles and Doubles |
| CP | Cunterpoise |
| daXZ | aug-aug-cc-pVXZ |
| daBS | Double Augmented Sigma Basis Set |
| FCI | Full Configuration Interaction |
| HF | Hartree-Fock |
| MP | Möller-Plesset |
| MR-ACPF | Multi-Reference Averaged Coupled-Pair Functional |
| MRCI | Multi-Reference Configuration Interaction |
| SAPT | Symmetry-Adapted Intermolecular Perturbation Theory |
| BS | Sigma Basis Set |
| taXZ | aug-aug-aug-cc-pVXZ |
| taBS | Triple Augmented Sigma Basis Set |
| vdW | van der Waals |
| XZ | cc-pVXZ |
References
- Riley, K.E.; Pitoňák, M.; Jurečka, P.; Hobza, P. Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories. Chem. Rev. 2010, 110, 5023–5063. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. Exchange-hole dipole moment and the dispersion interaction revisited. J. Chem. Phys. 2007, 127, 154108. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la Roza, A.; Johnson, E.R. Van der Waals interactions in solids using the exchange-hole dipole moment model. J. Chem. Phys. 2012, 136, 174109. [Google Scholar] [CrossRef] [PubMed]
- Tantardini, C.; Michalchuk, A.A.L.; Samtsevich, A.; Rota, C.; Kvashnin, A.G. The Volumetric Source Function: Looking Inside van der Waals Interactions. Sci. Rep. 2020, 10, 7816. [Google Scholar] [CrossRef] [PubMed]
- Laschuk, E.F.; Martins, M.M.; Evangelisti, S. Ab initio potentials for weakly interacting systems: Homonuclear rare gas dimers. Int. J. Quantum Chem. 2003, 95, 303–312. [Google Scholar] [CrossRef]
- Sheng, X.; Toennies, J.P.; Tang, K.T. Conformal Analytical Potential for All the Rare Gas Dimers over the Full Range of Internuclear Distances. Phys. Rev. Lett. 2020, 125, 253402. [Google Scholar] [CrossRef] [PubMed]
- Van Mourik, T.; van Lenthe, J.H. Benchmark full configuration interaction calculations on the helium dimer. J. Chem. Phys. 1995, 102, 7479–7483. [Google Scholar] [CrossRef] [Green Version]
- Van Mourik, T.; Dunning, T.H., Jr. A new ab initio potential energy curve for the helium dimer. J. Chem. Phys. 1999, 111, 9248–9258. [Google Scholar] [CrossRef]
- Van Mourik, T.; Wilson, A.K.; Dunning, T.H., Jr. Benchmark calculations with correlated molecular wavefunctions. XIII. Potential energy curves for He2, Ne2 and Ar2 using correlation consistent basis sets through augmented sextuple zeta. Mol. Phys. 1999, 96, 529–547. [Google Scholar] [CrossRef]
- Korona, T.; Williams, H.L.; Bukowski, R.; Jeziorski, B.; Szalewicz, K. Helium dimer potential from symmetry-adapted perturbation theory calculations using large Gaussian geminal and orbital basis sets. J. Chem. Phys. 1997, 106, 5109–5122. [Google Scholar] [CrossRef]
- Cybulski, S.M.; Toczyłowski, R.R. Ground state potential energy curves for He2, Ne2, Ar2, He–Ne, He–Ar, and Ne–Ar: A coupled-cluster study. J. Chem. Phys. 1999, 111, 10520–10528. [Google Scholar] [CrossRef]
- Gdanitz, R.J. Accurately solving the electronic Schrödinger equation of atoms and molecules using explicitly correlated (r12-)MR-CI IV. The helium dimer (He2). Mol. Phys. 1999, 96, 1423–1434. [Google Scholar]
- Gdanitz, R.J. Accurately solving the electronic Schrödinger equation of atoms and molecules by extrapolating to the basis set limit. I. The helium dimer (He2). J. Chem. Phys. 2000, 113, 5145–5153. [Google Scholar] [CrossRef]
- Gdanitz, R.J. Accurately solving the electronic Schrödinger equation of atoms and molecules using explicitly correlated (r12-) MR-CI. VI. The helium dimer (He2) revisited. Mol. Phys. 2001, 99, 923–930. [Google Scholar] [CrossRef]
- Van de Bovenkamp, J.; van Duijneveldt, F.B. MRCI calculations on the helium dimer employing an interaction optimized basis set. J. Chem. Phys. 1999, 110, 11141–11151. [Google Scholar] [CrossRef]
- Klopper, W. A critical note on extrapolated helium pair potentials. J. Chem. Phys. 2001, 115, 761–765. [Google Scholar] [CrossRef]
- Anderson, J.B. Comment on “An exact quantum Monte Carlo calculation of the helium–helium intermolecular potential” [J. Chem. Phys. 115, 4546 (2001)]. J. Chem. Phys. 2004, 120, 9886–9887. [Google Scholar] [CrossRef] [Green Version]
- Komasa, J. Exponentially correlated Gaussian functions in variational calculations. Momentum space properties of the ground state helium dimer. J. Chem. Phys. 2001, 115, 158–165. [Google Scholar] [CrossRef] [Green Version]
- Cencek, W.; Jeziorska, M.; Bukowski, R.; Jaszuński, M.; Jeziorski, B.; Szalewicz, K. Helium Dimer Interaction Energies from Gaussian Geminal and Orbital Calculations. J. Phys. Chem. A 2004, 108, 3211–3224. [Google Scholar] [CrossRef]
- Patkowski, K.; Cencek, W.; Jeziorska, M.; Jeziorski, B.; Szalewicz, K. Accurate pair interaction energies for helium from supermolecular Gaussian geminal calculations. J. Phys. Chem. A 2007, 111, 7611–7623. [Google Scholar] [CrossRef]
- Gutowski, M.; Lenthe, J.V.; Verbeek, J.; Van Duijneveldt, F.; Chałasinski, G. The basis set superposition error in correlated electronic structure calculations. Chem. Phys. Lett. 1986, 124, 370–375. [Google Scholar] [CrossRef]
- Varandas, A. Can extrapolation to the basis set limit be an alternative to the counterpoise correction? A study on the helium dimer. Theor. Chem. Acc. 2008, 119, 511–521. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Idaboy, J.R.; Galano, A. Counterpoise corrected interaction energies are not systematically better than uncorrected ones: Comparison with CCSD(T) CBS extrapolated values. Theor. Chem. Acc. 2010, 126, 75–85. [Google Scholar] [CrossRef]
- Sheng, X.W.; Mentel, L.; Gritsenko, O.V.; Baerends, E.J. Counterpoise correction is not useful for short and Van der Waals distances but may be useful at long range. J. Comput. Chem. 2011, 32, 2896–2901. [Google Scholar] [CrossRef] [PubMed]
- Varandas, A.J.C. Extrapolation to the Complete Basis Set Limit without Counterpoise. The Pair Potential of Helium Revisited. J. Phys. Chem. A 2010, 114, 8505–8516. [Google Scholar] [CrossRef] [PubMed]
- Cencek, W.; Przybytek, M.; Komasa, J.; Mehl, J.B.; Jeziorski, B.; Szalewicz, K. Effects of adiabatic, relativistic, and quantum electrodynamics interactions on the pair potential and thermophysical properties of helium. J. Chem. Phys. 2012, 136, 224303. [Google Scholar] [CrossRef]
- Luo, F.; Giese, C.F.; Gentry, W.R. Direct measurement of the size of the helium dimer. J. Chem. Phys. 1996, 104, 1151–1154. [Google Scholar] [CrossRef]
- García de la Vega, J.M.; Miguel, B.; Ramírez, G. Single-exponent Slater function expansions for lithium to neon atoms. J. Phys. B 1996, 29, 5273–5282. [Google Scholar] [CrossRef]
- Koga, T.; García de la Vega, J.M.; Miguel, B. Double-zeta Slater-type basis sets with noninteger principal quantum numbers and common exponents. Chem. Phys. Lett. 1998, 283, 97–101. [Google Scholar] [CrossRef]
- Miguel, B.; Koga, T.; García de la Vega, J.M. Double- and triple-zeta Slater-type basis sets with common exponents. Theor. Chem. Acc. 2000, 104, 167–171. [Google Scholar] [CrossRef]
- Ema, I.; García de la Vega, J.M.; Ramírez, G.; López, R.; Rico, J.F.; Meissner, H.; Paldus, J. Polarized basis sets of Slater-type orbitals: H to Ne atoms. J. Comput. Chem. 2003, 24, 859–868. [Google Scholar] [CrossRef] [PubMed]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef] [Green Version]
- Woon, D.E. Benchmark calculations with correlated molecular wave functions. V. The determination of accurate ab initio intermolecular potentials for He2, Ne2, and Ar2. J. Chem. Phys. 1994, 100, 2838–2850. [Google Scholar] [CrossRef]
- Almlöf, J.; Taylor, P.R. Atomic natural orbital (ANO) basis sets for quantum chemical calculations. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1991; Volume 22, pp. 301–373. [Google Scholar]
- Neese, F.; Valeev, E.F. Revisiting the atomic natural orbital approach for basis sets: Robust systematic basis sets for explicitly correlated and conventional correlated ab initio methods? J. Chem. Theory Comput. 2011, 7, 33–43. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO. A Package of Ab Initio Programs. Version 2012.1. 2012. Available online: https://www.molpro.net/ (accessed on 19 April 2022).
- Bunge, C.F.; Barrientos, J.A.; Bunge, A.V.; Cogordan, J.A. Hartree-Fock and Roothaan-Hartree-Fock energies for the ground states of He through Xe. Phys. Rev. A 1992, 46, 3691–3696. [Google Scholar] [CrossRef]
- Bunge, C.; Barrientos, J.; Bunge, A. Roothaan-Hartree-Fock Ground-State Atomic Wave Functions: Slater-Type Orbital Expansions and Expectation Values for Z = 2-54. Atom. Data Nucl. Data Tables 1993, 53, 113–162. [Google Scholar] [CrossRef]
- Nakashima, H.; Nakatsuji, H. Solving the Schrödinger equation for helium atom and its isoelectronic ions with the free iterative complement interaction (ICI) method. J. Chem. Phys. 2007, 127, 224104. [Google Scholar] [CrossRef] [Green Version]
- Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. [Google Scholar] [CrossRef]
| Basis Sets | # Exponentials | # | Primitives | # | Contracted |
|---|---|---|---|---|---|
| DZ | 5 | 7 | (4s, 1p) | 5 | [2s, 1p] |
| TZ | 8 | 16 | (5s, 2p, 1d) | 14 | [3s, 2p, 1d] |
| QZ | 12 | 32 | (6s, 3p, 2d, 1f) | 30 | [4s, 3p, 2d, 1f] |
| 5Z | 17 | 57 | (7s, 4p, 3d, 2f, 1g) | 55 | [5s, 4p, 3d, 2f, 1g] |
| anoDZ | 15 | 25 | (10s, 5p) | 5 | [2s, 1p] |
| anoTZ | 19 | 45 | (10s, 5p, 4d) | 14 | [3s, 2p, 1d] |
| anoQZ | 23 | 66 | (10s, 5p, 4d, 3f) | 30 | [4s, 3p, 2d, 1f] |
| ano5Z | 25 | 84 | (10s, 5p, 4d, 3f, 2g) | 55 | [5s, 4p, 3d, 2f, 1g] |
| DZ | 10 | 19 | (10s, 3p) | 5 | [2s, 1p] |
| TZ | 10 | 37 | (10s, 4p, 3d) | 14 | [3s, 2p, 1d] |
| QZ | 10 | 66 | (10s, 5p, 4d, 3f) | 30 | [4s, 3p, 2d, 1f] |
| 5Z | 10 | 108 | (10s, 6p, 5d, 4f, 3g) | 55 | [5s, 4p, 3d, 2f, 1g] |
| aDZ | 7 | 11 | (5s, 2p) | 9 | [3s, 2p] |
| aTZ | 11 | 25 | (6s, 3p, 2d) | 23 | [4s, 3p, 2d] |
| aQZ | 16 | 48 | (7s, 4p, 3d, 2f) | 46 | [5s, 4p, 3d, 2f] |
| a5Z | 22 | 82 | (8s, 5p, 4d, 3f, 2g) | 80 | [6s, 5p, 4d, 3f, 2g] |
| aanoDZ | 15 | 25 | (10s, 5p) | 9 | [3s, 2p] |
| aanoTZ | 19 | 45 | (10s, 5p, 4d) | 23 | [4s, 3p, 2d] |
| aanoQZ | 23 | 66 | (10s, 5p, 4d, 3f) | 46 | [5s, 4p, 3d, 2f] |
| aano5Z | 25 | 84 | (10s, 5p, 4d, 3f, 2g) | 80 | [6s, 5p, 4d, 3f, 2g] |
| aDZ | 11 | 23 | (11s, 4p) | 9 | [3s, 2p] |
| aTZ | 11 | 46 | (11s, 5p, 4d) | 23 | [4s, 3p, 2d] |
| aQZ | 11 | 82 | (11s, 6p, 5d, 4f) | 46 | [5s, 4p, 3d, 2f] |
| a5Z | 11 | 133 | (11s, 7p, 6d, 5f, 4g) | 80 | [6s, 5p, 4d, 3f, 2g] |
| He Atom | He Dimer | D(H) | R(Å) | |||||
|---|---|---|---|---|---|---|---|---|
| HF | FCI | HF | FCI | HF | FCI | HF | FCI | |
| DZ | −2.85516048 | −2.88759483 | −5.71032241 | −5.77519594 | 1.47 | 6.28 | 3.209 | 3.090 |
| TZ | −2.86115334 | −2.90023217 | −5.72230756 | −5.80047345 | 0.87 | 9.11 | 3.637 | 3.296 |
| QZ | −2.86151423 | −2.90241088 | −5.72302886 | −5.80483479 | 0.40 | 13.03 | 3.806 | 3.236 |
| 5Z | −2.86162483 | −2.90315188 | −5.72324982 | −5.80632032 | 0.15 | 16.55 | 4.005 | 3.155 |
| anoDZ | −2.86165583 | −2.89748229 | — | −5.79496717 | — | 2.60 | — | 3.623 |
| anoTZ | −2.86166988 | −2.90170267 | — | −5.80341360 | — | 8.26 | — | 3.335 |
| anoQZ | −2.86167139 | −2.90282021 | — | −5.80565442 | — | 13.99 | — | 3.194 |
| ano5Z | −2.86167205 | −2.90324192 | — | −5.80650279 | — | 18.95 | — | 3.112 |
| DZ | −2.86166454 | −2.89755779 | — | −5.79511772 | — | 2.13 | — | 3.645 |
| TZ | −2.86166897 | −2.90175275 | — | −5.80351122 | — | 5.73 | — | 3.426 |
| QZ | −2.86167087 | −2.90283439 | — | −5.80567817 | — | 9.39 | — | 3.301 |
| 5Z | −2.86167106 | −2.90324791 | — | −5.80651300 | — | 17.17 | — | 3.141 |
| aDZ | −2.85570467 | −2.88954849 | −5.71141075 | −5.77914013 | 1.41 | 43.16 | 3.417 | 2.998 |
| aTZ | −2.86118343 | −2.90059792 | −5.72236734 | −5.80122808 | 0.49 | 32.22 | 3.806 | 3.007 |
| aQZ | −2.86152200 | −2.90253360 | −5.72304429 | −5.80510033 | 0.30 | 33.13 | 4.057 | 2.979 |
| a5Z | −2.86162693 | −2.90320053 | −5.72325393 | −5.80643456 | 0.07 | 34.96 | 4.131 | 2.981 |
| aanoDZ | −2.86166988 | −2.89996594 | — | −5.79993919 | — | 7.31 | — | 3.378 |
| aanoTZ | −2.86167139 | −2.90245288 | — | −5.80490575 | — | 13.88 | — | 3.197 |
| aanoQZ | −2.86167205 | −2.90312610 | — | −5.80627113 | — | 18.93 | — | 3.113 |
| aano5Z | −2.86167282 | −2.90339507 | — | −5.80681090 | — | 20.76 | — | 3.088 |
| aDZ | −2.86167614 | −2.89997789 | — | −5.79996081 | — | 5.02 | — | 3.464 |
| aTZ | −2.86167722 | −2.90245411 | — | −5.80491755 | — | 9.33 | — | 3.300 |
| aQZ | −2.86167716 | −2.90313545 | — | −5.80628469 | — | 13.84 | — | 3.197 |
| a5Z | −2.86167707 | −2.90340070 | — | −5.80681741 | — | 16.02 | — | 3.143 |
| Basis Sets | # Exponentials | # | Primitives | # | Contracted |
|---|---|---|---|---|---|
| daDZ | 9 | 15 | (6s, 3p) | 13 | [4s, 3p] |
| daTZ | 14 | 34 | (7s, 4p, 3d) | 32 | [5s, 4p, 3d] |
| daQZ | 20 | 64 | (8s, 5p, 4d, 3f) | 62 | [6s, 5p, 4d, 3f] |
| da5Z | 27 | 107 | (9s, 6p, 5d, 4f, 3g) | 105 | [7s, 6p, 5d, 4f, 3g] |
| daDZ | 12 | 27 | (12s, 5p) | 13 | [4s, 3p] |
| daTZ | 12 | 55 | (12s, 6p, 5d) | 32 | [5s, 4p, 3d] |
| daQZ | 12 | 98 | (12s, 7p, 6d, 5f) | 62 | [6s, 5p, 4d, 3f] |
| da5Z | 12 | 158 | (12s, 8p, 7d, 6f, 5g) | 105 | [7s, 6p, 5d, 4f, 3g] |
| taDZ | 11 | 19 | (7s, 4p) | 17 | [5s, 4p] |
| taTZ | 17 | 43 | (8s, 5p, 4d) | 41 | [6s, 5p, 4d] |
| taQZ | 24 | 80 | (9s, 6p, 5d, 4f) | 78 | [7s, 6p, 5d, 4f] |
| ta5Z | 32 | 132 | (10s, 7p, 6d, 5f, 4g) | 130 | [8s, 7p, 6d, 5f, 4g] |
| taDZ | 13 | 31 | (13s, 6p) | 17 | [5s, 4p] |
| taTZ | 13 | 64 | (13s, 7p, 6d) | 41 | [6s, 5p, 4d] |
| taQZ | 13 | 114 | (13s, 8p, 7d, 6f) | 78 | [7s, 6p, 5d, 4f] |
| ta5Z | 13 | 183 | (13s, 9p, 8d, 7f, 6g) | 130 | [8s, 7p, 6d, 5f, 4g] |
| He Atom | He Dimer | D(H) | R(Å) | |||||
|---|---|---|---|---|---|---|---|---|
| HF | FCI | HF | FCI | HF | FCI | HF | FCI | |
| daDZ | −2.85570939 | −2.88959436 | −5.71142686 | −5.77924689 | 8.09 | 58.17 | 3.288 | 2.964 |
| daTZ | −2.86118387 | −2.90060812 | −5.72237146 | −5.80126097 | 3.72 | 44.72 | 3.837 | 2.995 |
| daQZ | −2.86152234 | −2.90253661 | −5.72304596 | −5.80511435 | 1.28 | 41.13 | 4.045 | 2.958 |
| da5Z | −2.86162717 | −2.90320194 | −5.72325487 | −5.80644187 | 0.52 | 37.98 | 3.882 | 2.965 |
| daDZ | −2.86167803 | −2.90035561 | — | −5.80072031 | — | 9.08 | — | 3.320 |
| daTZ | −2.86167821 | −2.90265038 | — | −5.80531813 | — | 17.37 | — | 3.136 |
| daQZ | −2.86167822 | −2.90323388 | — | −5.80648926 | — | 21.52 | — | 3.080 |
| da5Z | −2.86167816 | −2.90343963 | — | −5.80690928 | — | 30.02 | — | 3.002 |
| taDZ | −2.85571146 | −2.88960188 | −5.71143417 | −5.77926374 | 11.22 | 59.92 | 3.351 | 2.984 |
| taTZ | −2.86118406 | −2.90061002 | −5.72237488 | −5.80128012 | 6.76 | 60.33 | 3.654 | 2.996 |
| taQZ | −2.86152247 | −2.90253721 | −5.72304861 | −5.80511936 | 3.67 | 44.93 | 3.973 | 2.957 |
| ta5Z | −2.86162726 | −2.90320225 | −5.72325624 | −5.80644560 | 1.72 | 41.10 | 3.850 | 2.960 |
| taDZ | −2.86167928 | −2.90046500 | — | −5.80094227 | — | 12.26 | — | 3.247 |
| taTZ | −2.86167885 | −2.90272428 | — | −5.80546977 | — | 21.21 | — | 3.087 |
| taQZ | −2.86167886 | −2.90328593 | — | −5.80659710 | — | 25.24 | — | 3.037 |
| ta5Z | −2.86167829 | −2.90344482 | — | −5.80692585 | — | 32.21 | — | 2.982 |
| He Atom | He Dimer | |||
|---|---|---|---|---|
| Limit | 0.0420444 | 0.0841528 | ||
| BS | Dunning | Sigma | Dunning | Sigma |
| DZ | −0.0324343 | −0.0358932 | −0.0648756 | −0.0717958 |
| TZ | −0.0390788 | −0.0400838 | −0.0781781 | −0.0801879 |
| QZ | −0.0408967 | −0.0411635 | −0.0818256 | −0.0823559 |
| 5Z | −0.0415271 | −0.0415768 | −0.0830947 | −0.0831955 |
| CBS a | −0.0423430 | −0.0420352 | −0.0847403 | −0.0841253 |
| aDZ | −0.0338438 | −0.0383018 | −0.0677448 | −0.0766221 |
| aTZ | −0.0394145 | −0.0407769 | −0.0788879 | −0.0815831 |
| aQZ | −0.0410116 | −0.0414583 | −0.0820829 | −0.0829540 |
| a5Z | −0.0415736 | −0.0417231 | −0.0832083 | −0.0834887 |
| CBS a | −0.0423532 | −0.0420496 | −0.0847687 | −0.0841510 |
| daDZ | −0.0338850 | −0.0386776 | −0.0678307 | −0.0773832 |
| daTZ | −0.0394242 | −0.0409722 | −0.0789168 | −0.0819873 |
| daQZ | −0.0410143 | −0.0415557 | −0.0820937 | −0.0831597 |
| da5Z | −0.0415748 | −0.0417615 | −0.0832142 | −0.0835811 |
| CBS a | −0.0423531 | −0.0419952 | −0.0847654 | −0.0840554 |
| taDZ | −0.0338904 | −0.0385857 | −0.0678420 | −0.0776054 |
| taTZ | −0.0394260 | −0.0410454 | −0.0789302 | −0.0821388 |
| taQZ | −0.0410147 | −0.0416071 | −0.0820963 | −0.0832671 |
| ta5Z | −0.0415750 | −0.0418099 | −0.0832159 | −0.0836765 |
| CBS a | −0.0423526 | −0.0420285 | −0.0847545 | −0.0841117 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ema, I.; Ramírez, G.; López, R.; García de la Vega, J.M. Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer. Computation 2022, 10, 65. https://doi.org/10.3390/computation10050065
Ema I, Ramírez G, López R, García de la Vega JM. Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer. Computation. 2022; 10(5):65. https://doi.org/10.3390/computation10050065
Chicago/Turabian StyleEma, Ignacio, Guillermo Ramírez, Rafael López, and José Manuel García de la Vega. 2022. "Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer" Computation 10, no. 5: 65. https://doi.org/10.3390/computation10050065
APA StyleEma, I., Ramírez, G., López, R., & García de la Vega, J. M. (2022). Generation of Basis Sets for Accurate Molecular Calculations: Application to Helium Atom and Dimer. Computation, 10(5), 65. https://doi.org/10.3390/computation10050065






