Abstract
Quantum embedding is a divide and conquer strategy that aims at solving the electronic Schrödinger equation of sizeable molecules or extended systems. We establish in the present work a clearer and in-principle-exact connection between density matrix embedding theory (DMET) and density-functional theory (DFT) within the simple but nontrivial one-dimensional Hubbard model. For that purpose, we use our recent reformulation of single-impurity DMET as a Householder transformed density-matrix functional embedding theory (Ht-DMFET). On the basis of well-identified density-functional approximations, a self-consistent local potential functional embedding theory (LPFET) is formulated and implemented. Combining both LPFET and DMET numerical results with our formally exact density-functional embedding theory reveals that a single statically embedded impurity can in principle describe the density-driven Mott–Hubbard transition, provided that a complementary density-functional correlation potential (which is neglected in both DMET and LPFET) exhibits a derivative discontinuity (DD) at half filling. The extension of LPFET to multiple impurities (which would enable to circumvent the modeling of DDs) and its generalization to quantum chemical Hamiltonians are left for future work.
1. Introduction
Kohn–Sham density-functional theory (KS-DFT) [1] has become over the last two decades the method of choice for computational chemistry and physics studies, essentially because it often provides a relatively accurate description of the electronic structure of large molecular or extended systems at a low computational cost. The major simplification of the electronic structure problem in KS-DFT lies in the fact that the ground-state energy is evaluated, in principle exactly, from a non-interacting single-configuration wave function, which is simply referred to as the KS determinant. The latter is obviously not the exact solution to the Schrödinger equation. However, its density matches the exact interacting ground-state density, so that the Hartree-exchange-correlation (Hxc) energy of the physical system, which is induced by the electronic repulsion, can be recovered from an appropriate (in principle exact and universal) Hxc density functional. Despite the success of KS-DFT, standard density-functional approximations still fail in describing strongly correlated electrons. To overcome this issue, various strategies have been explored and improved over the years, both in condensed matter physics [2,3,4,5,6,7] and quantum chemistry [8]. Note that, in the latter case, in-principle-exact multi-determinantal extensions of DFT based on the adiabatic connection formalism have been developed [9,10,11,12]. In these approaches, the KS system is only referred to in the design of density-functional approximations. In practice, a single (partially-interacting) many-body wave function is calculated self-consistently and the complement to the partial interaction energy is described with an appropriate density functional (which differs from the conventional xc one). In other words, there is no KS construction in the actual calculation. Some of these concepts have been reused in the study of model lattice Hamiltonians [12,13]. A similar strategy will be adopted in the present work, with an important difference though. The reduced-in-size correlated density-functional many-body wave function that we will introduce will be extracted from a quantum embedding theory where the KS determinant of the full system is a key ingredient that must be evaluated explicitly.
Quantum embedding theory [14] is at first sight a completely different approach to the strong electron correlation problem. Interestingly, some of its implementations, like the density matrix embedding theory (DMET) [15,16,17,18,19,20,21,22,23], rely on a reference Slater determinant that is computed for the full system. This is also the case in practical embedding calculations based on the exact factorization formalism [24,25]. Unlike the well-established dynamical mean-field theory (DMFT) [26,27,28,29,30], which relies on the one-electron Green’s function, DMET is a static theory of ground electronic states. Most importantly, the bath, in which a fragment of the original system (referred to as impurity when it is a single localized orbital) is embedded, is drastically reduced in size in DMET. As a result, the “impurity+bath” embedding cluster can be accurately (if not exactly) described with wave function-based quantum chemical methods. The authors have shown recently that the Schmidt decomposition of the reference Slater determinant, which is central in DMET, can be recast into a (one-electron reduced) density-matrix functional Householder transformation [31], which is much simpler to implement. This approach, in which the bath orbitals can in principle be correlated directly through the density matrix [31], is referred to as Householder transformed density matrix functional embedding theory (Ht-DMFET). Since the seminal work of Knizia and Chan on DMET [15], various connections with DMFT and related approaches have been established [32,33,34,35,36,37]. Connections with DFT have been less explored, and only at the approximate level of theory. We can refer to the density embedding theory (DET) of Bulik et al. [38], which is a simplified version of DMET where only the diagonal elements of the embedded density matrix are mapped onto the reference Slater determinant of the full system. More recently, Senjean [39] combined DFT for lattices [40,41] with DMET, and Mordovina et al. [42] (see also Ref. [43]) proposed a self-consistent density-functional embedding (SDE), where the KS determinant is explicitly used as the reference wave function in the DMET algorithm.
In the present work, an in-principle-exact combination of KS-DFT with DMET is derived for the one-dimensional (1D) Hubbard lattice, as a proof of concept. For that purpose, we use the density-matrix functional Householder transformation introduced recently by the authors [31]. On the basis of well-identified density-functional approximations, we propose and implement a local potential functional embedding theory (LPFET) where the Hxc potential is evaluated self-consistently in the lattice by “learning” from the embedding cluster at each iteration of the optimization process. LPFET can be seen as a flavor of KS-DFT where no density functional is actually used.
The paper is organized as follows. After a short introduction to the 1D Hubbard model in Section 2.1, a detailed review of Ht-DMFET is presented in Section 2.2, for clarity and completeness. An exact density-functional reformulation of the theory is then proposed in Section 2.3. The resulting approximate LPFET and its comparison with SDE are detailed in Section 2.4 and Section 2.5, respectively. The LPFET algorithm is summarized in Section 3. Results obtained for a 1000-site Hubbard ring are presented and discussed in Section 4. The conclusion and perspectives are finally given in Section 5.
2. Theory
2.1. One-Dimensional Hubbard Lattice
By analogy with Ref. [31], various quantum embedding strategies will be discussed in the following within the simple but nontrivial uniform 1D Hubbard model. The corresponding lattice Hamiltonian (for a L-site ring) reads as
where the hopping operator (written in second quantization),
with parameter t, is the analog for lattices of the kinetic energy operator. For convenience, we will systematically use periodic boundary conditions, i.e., . On-site repulsions are only taken into account in the two-electron repulsion operator , i.e.,
where , U is the parameter that controls the strength of the interaction, and is a site occupation operator for spin . Since the lattice is uniform, the local external potential (which would correspond to the nuclear potential in a conventional quantum chemical calculation) operator is proportional to the electron counting operator (see the last term on the right-hand side of Equation (1)),
The uniform value of the external potential can be rewritten as
where the chemical potential controls the number of electrons N or, equivalently, the uniform density in the lattice. In this case, is actually a (zero-temperature) grand canonical Hamiltonian. For convenience, we rewrite the hopping operator as follows,
where
and . From now on the bounds in the summations over the full lattice will be dropped, for simplicity:
Note that the quantum embedding strategies discussed in the present work can be extended to more general (quantum chemical, in particular) Hamiltonians [20]. For that purpose, the true ab initio Hamiltonian should be written in a localized molecular orbital basis, thus leading to the more general Hamiltonian expression,
where and are the (kinetic and nuclear attraction) one-electron and two-electron repulsion integrals, respectively. Using a localized orbital basis allows for the decomposition of the molecule under study into fragments that can be embedded afterward [20]. In the following, we will work with the simpler Hamiltonian of Equation (1), as a proof of concept.
2.2. Review of Ht-DMFET
For the sake of clarity and completeness, a review of Ht-DMFET [31] is presented in the following subsections. Various ingredients (operators and reduced quantities) that will be used later on in Section 2.3 in the derivation of a formally exact density-functional embedding theory (which is the main outcome of this work) are introduced. Real algebra will be used. For simplicity, we focus on the embedding of a single impurity. A multiple-impurity extension of the theory can be obtained from a block Householder transformation [31,44]. Unlike in the exact reformulation of the theory which is proposed in the following Section 2.3 and where the chemical potential controls the density of the uniform lattice, the total number of electrons will be fixed to the value N in the present section. In other words, the uniform density is set to and is an arbitrary constant (that could be set to zero).
2.2.1. Exact Non-Interacting Embedding
Let us first consider the particular case of a non-interacting () lattice for which Ht-DMFET is exact [31]. As it will be applied later on (in Section 2.3) to the auxiliary KS lattice, it is important to highlight the key features of the non-interacting embedding. Following Ref. [31], we label as one of the localized (lattice site in the present case) spin-orbital [we denote the vacuum state of second quantization] that, ultimately, will become the so-called embedded impurity. The ingredient that is central in Ht-DMFET is the (one-electron reduced) density matrix of the full system in the lattice representation, i.e.,
where we restrict ourselves to closed-shell singlet ground states , for simplicity. Note that
is the uniform lattice filling per spin. Since the full lattice will always be described with a single Slater determinant in the following, the density matrix will always be idempotent. The latter is used to construct the Householder unitary transformation which, once it has been applied to the one-electron lattice space, defines the so-called bath spin-orbital with which the impurity will ultimately be exclusively entangled. More explicitly, the Householder transformation matrix
where is the identity matrix, is a functional of the density matrix, i.e.,
where the density-matrix-functional Householder vector components read as [31]
with
and
Note that, in the extreme case of a two-site lattice, the denominator in Equations (15) and (16) is still well defined and it does not vanish. Indeed, by construction (see Equation (17)),
in this case, thus leading to . Note also that is hermitian and unitary, i.e., and
The bath spin-orbital is then constructed as follows in second quantization,
where, according to Equations (12) and (14),
More generally, the entire lattice space can be Householder-transformed as follows,
and the back transformation simply reads as
We stress that the impurity is invariant under the Householder transformation, i.e.,
and, according to the Appendix A, the Householder-transformed density matrix elements involving the impurity can be simplified as follows,
As readily seen from Equations (15) and (26), the matrix element introduced in Equation (17) is in fact the bath-impurity element of the density matrix in the Householder representation:
If we denote
the full Householder-transformed density matrix, we do readily see from Equations (16) and (26) that the impurity is exclusively entangled with the bath, i.e.,
by construction [31]. As inherits the idempotency of through the unitary Householder transformation, we deduce from Equation (29) that
or, equivalently,
thus leading to (see Equation (29))
and
Equations (32) and (33) simply indicate that, by construction [31], the bath is itself entangled exclusively with the impurity, and the Householder “impurity+bath” cluster, which is disconnected from its environment, contains exactly two electrons (one per spin). Therefore, the Householder cluster sector of the density matrix can be described exactly by a two-electron Slater determinant :
Note that, in the Householder representation, the lattice ground-state determinant reads as , where the cluster’s determinant is disentangled from the core one . Once the cluster’s block of the density matrix has been diagonalized, we obtain the sole occupied orbital that overlaps with the impurity, exactly like in DMET [20]. In other words, for non-interacting (or mean-field-like descriptions of) electrons, the Ht-DMFET construction of the bath is equivalent (although simpler) to that of DMET. We refer the reader to Ref. [31] for a more detailed comparison of the two approaches.
2.2.2. Non-Interacting Embedding Hamiltonian
As the Householder cluster is strictly disconnected from its environment in the non-interacting case, it is exactly described by the two-electron ground state of the Householder-transformed hopping operator (that we refer to as kinetic energy operator from now on, like in DFT for lattices [13,41]) on projected onto the cluster [31], i.e.,
where, according to Equations (6) and (24),
For convenience, we will separate in the physical per-site kinetic energy operator (see Equation (2)),
from the correction induced (within the cluster) by the Householder transformation:
Note that, since , can be expressed more explicitly as follows,
thus leading to
where we used Equations (12) and (22), as well as the fact that and . Note that, when no Householder transformation is performed (i.e., when for ), the bath site simply corresponds to the nearest neighbor () of the impurity in the lattice (see Equation (22)) and, as readily seen from Equations (38) and (40), the non-interacting cluster’s Hamiltonian reduces to .
Unlike in the interacting case, which is discussed in Section 2.2.3, it is unnecessary to introduce an additional potential on the embedded impurity in order to ensure that it reproduces the correct lattice filling. Indeed, according to Equations (11), (14), (26), (28) and (34),
This constraint is automatically fulfilled when Householder transforming the kinetic energy operator of the full lattice, thanks to the local potential contribution on the bath (see the last term on the right-hand side of Equation (40)). Interestingly, the true (non-interacting in this case) per-site energy of the lattice can be determined solely from . Indeed, according to Equation (10), the per-site kinetic energy can be evaluated from the lattice ground-state wave function as follows,
When rewritten in the Householder representation, Equation (42) gives (see Equations (24), (29) and (34))
where we used Equation (25) and the fact that , since is constructed within the cluster. We finally recover from Equation (43) the following equality [31],
which drastically (and exactly) simplifies the evaluation of non-interacting energies for lattices.
2.2.3. Approximate Interacting Embedding
The simplest (approximate) extension of Ht-DMFET to interacting electrons consists in introducing the on-impurity-site two-electron repulsion operator into the non-interacting Householder cluster’s Hamiltonian of Equation (35), by analogy with DMET [15,31]. In such a (standard) scheme, the interaction is treated on top of the non-interacting embedding. Unlike in the non-interacting case, it is necessary to introduce a chemical potential on the embedded impurity in order to ensure that it reproduces the correct lattice filling [31], i.e.,
where the two-electron cluster’s ground-state wave function fulfills the following interacting Schrödinger equation:
The physical per-site energy (from which we remove the chemical potential contribution) is then evaluated as follows:
Let us stress that, in Ht-DMFET, the cluster is designed from a single determinantal (non-interacting in the present case) lattice wave function, like in regular DMET calculations [20]. In other words, the Householder transformation is constructed from an idempotent density matrix. Moreover, the interacting cluster is described as a closed (two-electron) subsystem. As shown for small Hubbard rings, the exact interacting cluster is in principle an open subsystem [31]. It rigorously contains two electrons only at half filling, as a consequence of the hole-particle symmetry of the Hubbard lattice Hamiltonian [31].
Note finally that, if we Householder transform the two-electron repulsion operator of the full lattice, one can in principle take into account its complete projection onto the cluster. It means that the interaction on the bath site could be added to the Hamiltonian in Equation (46). For simplicity, we will focus in the following on the (so-called) non-interacting bath formulation of the theory, which is described by Equation (46). Let us finally mention that, in the present single-impurity embedding, DMET, DET, and Ht-DMFET are equivalent [31].
2.3. Exact Density-Functional Embedding
We will show in the following that, once it has been merged with KS-DFT, Ht-DMFET can be made formally exact. For clarity, we start with reviewing briefly KS-DFT for lattice Hamiltonians in Section 2.3.1. A multi-determinantal extension of the theory based on the interacting Householder cluster’s wave function is then proposed in Section 2.3.2.
2.3.1. KS-DFT for Uniform Lattices
According to the Hohenberg–Kohn (HK) variational principle [45], which is applied in this work to lattice Hamiltonians [41], the ground-state energy of the full lattice can be determined as follows,
where the HK density functional reads as
and is the lattice ground state with uniform density profile . Strictly speaking, is a function of the site occupation n, hence the name site occupation functional theory often given to DFT for lattices [13,41]. Note that the ground-state energy E is in fact a (zero-temperature) grand canonical energy since a change in uniform density n induces a change in the number of electrons. In the thermodynamic and limit, with fixed to n, one can in principle describe continuous variations in n with a pure-state wave function . The derivations that follow will be based on this assumption. If we introduce the per-site analog of the HK functional,
and use the notation of Equation (5), then Equation (48) becomes
and the minimizing density fulfills the following stationarity condition:
In the conventional KS formulation of DFT, the per-site HK functional is decomposed as follows,
where
is the (per-site) analog for lattices of the non-interacting kinetic energy functional, and the Hxc density functional reads as [41]
where is the exact (per-site) correlation energy functional of the interacting lattice. The (normalized) density-functional lattice KS determinant fulfills the (non-interacting) KS equation
so that (see Equation (54))
since . Thus, we recover from Equations (52) and (53) the well-known relation between the physical and KS chemical potentials:
where the density-functional Hxc potential reads as with
Note that the exact non-interacting density-functional chemical potential can be expressed analytically as follows [40]:
Capelle and coworkers [40,41] have designed a local density approximation (LDA) to on the basis of exact Bethe Ansatz (BA) solutions [46] (the functional is usually referred to as BALDA).
Unlike in conventional ab initio DFT, the Hxc functional of lattice Hamiltonians is not truly universal in the sense that it is universal for a given choice of (hopping) one-electron and two-electron repulsion operators. In other words, the Hxc functional does not depend on the (possibly non-uniform) one-electron local potential operator , which is the analog for lattices of the nuclear potential in molecules, but it is t- and U-dependent and, in the present case, it should be designed specifically for the 1D Hubbard model. Even though BALDA can be extended to higher dimensions [47], there is no general strategy for constructing (localized) orbital-occupation functional approximations, thus preventing direct applications to quantum chemistry [12], for example. Turning ultimately to a potential-functional theory, as proposed in Section 2.4, is appealing in this respect. With this change of paradigm, which is the second key result of the paper, the Hxc energy and potential become implicit functionals of the density, and they can be evaluated from a (few-electron) correlated wave function through a quantum embedding procedure.
2.3.2. Density-Functional Interacting Cluster
We propose in this section an alternative formulation of DFT based on the interacting Householder cluster introduced in Section 2.2.3. For that purpose, we consider the following exact decomposition,
where the Householder cluster HK functional
is evaluated from the two-electron cluster density-functional wave function , and is the complementary correlation density functional that describes the missing correlation effects of the interacting bath and the Householder cluster’s environment on the embedded impurity [31]. Note that, according to Section 2.2.3, fulfills the following Schrödinger-like equation,
where (we use the same notations as in Section 2.2.3)
and
The dependence in n of the (projected-onto-the-cluster) Householder-transformed kinetic energy operator comes from the fact that the KS lattice density matrix (on which the Householder transformation is based) is, like the KS determinant of the lattice, a functional of the uniform density n. On the other hand, for a given uniform lattice density n, the local potential is adjusted on the embedded impurity such that the interacting cluster reproduces n, i.e.,
Interestingly, on the basis of the two decompositions in Equations (53), (61) and (62), we can relate the exact Hxc functional to the density-functional Householder cluster as follows,
where, as shown in Equation (44), the per-site non-interacting kinetic energy can be determined exactly from the two-electron cluster’s part of the KS lattice determinant , i.e.,
thus leading to the final expression
Note that, according to Equations (35) and (38), fulfills the KS-like equation
where the Householder transformation ensures that (see Equation (41)).
We will now establish a clearer connection between the KS lattice system and the Householder cluster via the evaluation of the Hxc density-functional potential in the lattice. According to Equations (59) and (69), the latter can be expressed as follows,
or, equivalently (see Equations (63), (66) and (70)),
If we introduce the following bi-functional of the density,
which can be interpreted as a kinetic correlation energy induced within the density-functional cluster by the Householder transformation and the interaction on the impurity, we obtain the final exact expression
which is the first key result of this paper.
Before turning Equation (74) into a practical self-consistent embedding method (see Section 2.4), let us briefly discuss its physical meaning and connection with Ht-DMFET. As pointed out in Section 2.2.1, the (density-functional) operator is an auxiliary correction to the true per-site kinetic energy operator which originates from the Householder-transformation-based embedding of the impurity. It is not physical and its impact on the impurity chemical potential , which is determined in the presence of in the cluster’s Hamiltonian (see Equations (63)–(65)), should be removed when evaluating the Hxc potential of the true lattice, hence the minus sign in front of the second term on the right-hand side of Equation (74). Finally, the complementary correlation potential is in charge of recovering the electron correlation effects that were lost when considering an (impurity-only) interacting cluster that is disconnected from its environment [31]. We should stress at this point that, in Ht-DMFET (which is equivalent to DMET or DET when a single impurity is embedded [31]), the following density-functional approximation is made:
so that the physical density-functional chemical potential is evaluated as follows [31],
Interestingly, even though it is never computed explicitly in this context, the corresponding (approximate) Hxc potential simply reads as
or, equivalently (see Equations (74) and (75)),
Therefore, Ht-DMFET can be seen as an approximate formulation of KS-DFT where the Hxc potential is determined solely from the density-functional Householder cluster. As illustrated in Figure 9 of Ref. [31], the approximation of Equation (75) leads, for example, to a substantial underestimation of the per-site energy, except in the vicinity of half filling where the energy is overestimated. Describing the electron repulsion in the bath (not considered in the present work, for simplicity) lowers the energy even further, thus leading to accurate results only at half filling, because of error cancellations [31]. Most importantly, Equation (75) implies that Ht-DMFET neglects the fluctuations in the electron number within the Householder cluster (see Equations (61)–(63)). Consequently, as further discussed in Ref. [31] and Section 4, Ht-DMFET is unable to describe the opening of the gap at half filling.
2.4. Local Potential Functional Embedding Theory
Until now the Householder transformation has been described as a functional of the uniform density n or, more precisely, as a functional of the KS density matrix, which is itself a functional of the density. If we opt for a potential-functional reformulation of the theory, as suggested in the following, the Householder transformation becomes a functional of the KS chemical potential instead, and, consequently, the Householder correction to the per-site kinetic energy operator within the cluster (see Equation (65)) is also a functional of :
Similarly, the interacting cluster’s wave function becomes a bi-functional of the KS and interacting embedded impurity chemical potentials:
In the exact theory, for a given chemical potential value in the true interacting lattice, both the KS lattice and the embedded impurity reproduce the interacting lattice density , i.e.,
where
and
with, according to Equation (74),
The density constraint of Equation (81) combined with Equation (84) allows for an in-principle-exact evaluation of the Hxc potential . Most importantly, these two equations can be used for designing an alternative (and self-consistent) embedding strategy on the basis of well-identified density-functional approximations. Indeed, in Ht-DMFET, the second term on the right-hand side of Equation (84) is simply dropped, for simplicity (see Equation (75)). If, in addition, we neglect the Householder kinetic correlation density-bi-functional potential correction [last term on the right-hand side of Equation (84)], we obtain from Equation (81) the following self-consistent equation,
from which an approximation to the Hxc potential can be determined. Equation (85) is the second main result of this paper. Since is now the to-be-optimized quantity on which the embedding fully relies, we refer to the approach as local potential functional embedding theory (LPFET), in which the key density-functional approximation that is made reads as
The approach is graphically summarized in Figure 1.
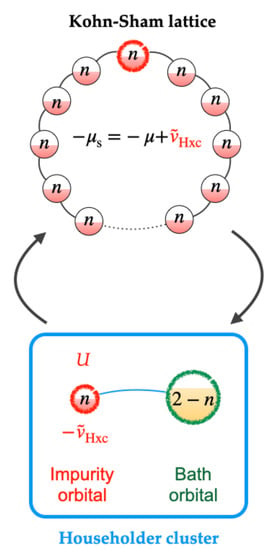
Figure 1.
Graphical representation of the LPFET procedure. Note that the same Hxc potential is used in the KS lattice and the embedding Householder cluster. It is optimized self-consistently in order to fulfill the density constraint of Equation (85). See text for further details.
In order to verify that the first HK theorem [45] still holds at the LPFET level of approximation, let us assume that two chemical potentials and lead to the same density. If so, the converged Hxc potentials should differ by , so that both calculations give the same KS chemical potential value (see Equation (58)). According to Equations (85) and (86), it would imply that two different values of the interacting embedded impurity chemical potential can give the same density, which is impossible [31,48]. Therefore, when convergence is reached in Equation (85), we can generate an approximate map
and compute approximate per-site energies as follows,
since the approximation in Equation (75) is also used in LPFET, as discussed above.
Note that Ht-DMFET (which is equivalent to DMET in the present context) and LPFET use the same per-site energy expression (see Equation (47)), which is a functional of the interacting cluster’s wave function. In both approaches, the latter and the non-interacting lattice share the same density. Therefore, if the per-site energy or the double occupation were plotted as functions of the (converged) lattice filling n, as it is usually done in the literature [15], both methods would give exactly the same results. The reason is that, at convergence of the LPFET algorithm, the density constraint of Equation (85) should be fulfilled, exactly like in Ht-DMFET (see Equations (45) and (46)). However, if properties were plotted as functions of the chemical potential value in the true interacting lattice, LPFET and Ht-DMFET would give different results, simply because the densities obtained (for a given value) with the two methods would be different. Indeed, as shown in Section 2.3.2, Ht-DMFET can be viewed as an approximation to KS-DFT where the Hxc density-functional potential of Equation (78) is employed. As readily seen from Equation (86), the LPFET and Ht-DMFET Hxc potentials differ by the Householder kinetic correlation potential (which is neglected in LPFET). If the corresponding KS densities were the same then the Hxc potential, the Householder transformation, and, therefore, the chemical potential on the interacting embedded impurity would be the same, which is impossible according to Equations (78) and (86). In summary, differences in properties between LPFET and Ht-DMFET are directly related to differences in density. This is the reason why, in order to compare the two methods, we will restrict ourselves to the computation of chemical-potential-density maps (see Section 4).
2.5. Comparison with SDE
At this point we should stress that LPFET is very similar to the SDE approach of Mordovina et al. [42]. The major difference between SDE and LPFET (in addition to the fact that LPFET has a clear connection with a formally exact density-functional embedding theory based on the Householder transformation) is that no KS construction is made within the cluster. Instead, the Hxc potential is directly updated in the KS lattice, on the basis of the correlated embedded impurity density. This becomes even more clear when rewriting Equation (85) as follows,
where is the inverse of the non-interacting chemical-potential-density map. A practical advantage of such a procedure (which remains feasible since the full system is treated at the non-interacting KS level only) lies in the fact that the KS construction within the cluster is automatically (and exactly) generated by the Householder transformation, once the density has been updated in the KS lattice (see Equation (41) and the comment that follows). Most importantly, the density in the KS lattice and the density of the non-interacting KS embedded impurity (which, unlike the embedded interacting impurity, is not used in the actual calculation) will match at each iteration of the Hxc potential optimization process, as it should when convergence is reached. If, at a given iteration, the KS construction were made directly within the cluster, there would always be a “delay” in density between the KS lattice and the KS cluster, which would only disappear at convergence. Note that, when the latter is reached, the (approximate) Hxc potential of the lattice should match the one extracted from the cluster, which is defined in SDE as the difference between the KS cluster Hamiltonian and the one-electron part of the interacting cluster’s Hamiltonian [42], both reproducing the density of the KS lattice. Therefore, according to Equations (64), (65) and (70), the converged Hxc potential will simply correspond to the chemical potential on the interacting embedded impurity, exactly like in LPFET (see Equation (86)).
Note finally that the simplest implementation of LPFET, as suggested by Equation (89), can be formally summarized as follows:
A complete description of the algorithm is given in the next section.
3. LPFET Algorithm
The LPFET approach introduced in Section 2.4 aims at computing the interacting chemical-potential-density map through the self-consistent optimization of the uniform Hxc potential. A schematics of the algorithm is provided in Figure 2. It can be summarized as follows.
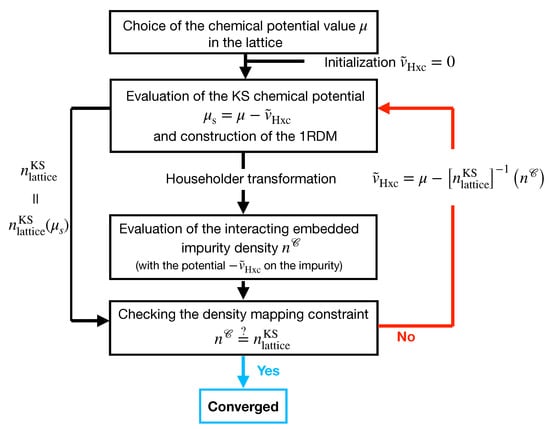
Figure 2.
Schematics of the LPFET algorithm. The (one-electron reduced) density matrix of the KS lattice is referred to as the 1RDM. See text for further details.
- We start by diagonalizing the one-electron Hamiltonian (i.e., the hopping in the present case) matrix (see Equation (7)). Thus, we obtain the “molecular” spin-orbitals and their corresponding energies. We fix the chemical potential of the interacting lattice to some value and (arbitrarily) initialize the Hxc potential to . Therefore, at the zeroth iteration, the KS chemical potential equals .
- We occupy all the molecular spin-orbitals with energies below and construct the corresponding density matrix (in the lattice representation). The latter provides the uniform KS density (denoted in Figure 2) and the embedding Householder cluster Hamiltonian (see Equation (46)) in which the impurity chemical potential is set to (see Equation (86)).
- We solve the interacting Schrödinger equation for the two-electron Householder cluster and deduce the occupation of the embedded impurity (which is denoted in Figure 2). This can be done analytically since the Householder cluster is an asymmetric Hubbard dimer [31].
- We verify that the density in the KS lattice and the occupation of the interacting embedded impurity match (a convergence threshold has been set to 10). If this is the case, the calculation has converged and is interpreted as (an approximation to) the density in the true interacting lattice. If the two densities do not match, the Hxc potential is adjusted in the KS lattice such that the latter reproduces (see Equation (90)) or, equivalently, such that the KS lattice contains electrons. We then return to step 2.
4. Results and Discussion
In the following, LPFET is applied to a uniform Hubbard ring with a large L = 1000 number of sites in order to approach the thermodynamic limit. Periodic boundary conditions have been used. The hopping parameter is set to t = 1. As explained at the end of Section 2.4, plotting Ht-DMFET (which is equivalent to DMET or DET in the present single embedded impurity case) and LPFET properties such as the per-site energy or the double occupation as functions of the (converged) lattice filling n would give exactly the same results. We refer the reader to Ref. [31] for a detailed analysis of the Ht-DMFET scheme and its performance. On the other hand, the two methods are expected to give different chemical-potential-density maps since they rely on different density-functional approximations (see Equations (78) and (86)). We focus in the following on the self-consistent computation of this map at the LPFET level of theory. Comparison will be made with Ht-DMFET and the exact BA results.
As illustrated by the strongly correlated results of Figure 3 and Figure 4, the LPFET self-consistency loop converges smoothly in few iterations. The same observation is made in weaker correlation regimes (not shown). The deviation in density between the KS lattice and the embedded impurity is drastically reduced after the first iteration (see Figure 3). This is also reflected in the large variation of the Hxc potential from the zeroth to the first iteration (see Figure 4). It originates from the fact that, at the zeroth iteration, the Hxc potential is set to zero in the lattice while, in the embedding Householder cluster, the interaction on the impurity site is “turned on”. As shown in Figure 3, the occupation of the interacting embedded impurity is already at the zeroth iteration a good estimate of the self-consistently converged density. A few additional iterations are needed to refine the result.
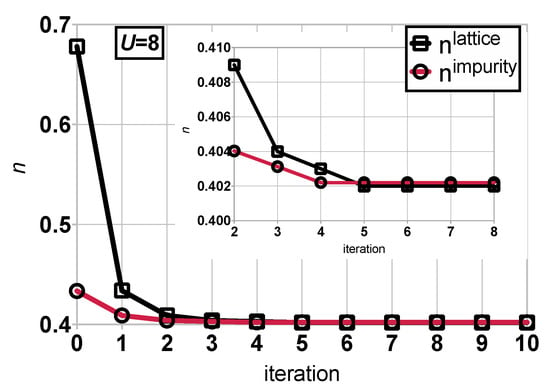
Figure 3.
Comparison of the KS lattice and embedded impurity densities at each iteration of the LPFET calculation. The interaction strength and chemical potential values are set to and , respectively. As shown in the inset, convergence is reached after five iterations.
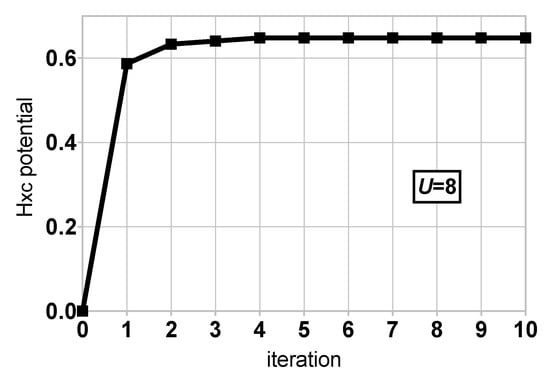
Figure 4.
Convergence of the LPFET Hxc potential for and .
The converged LPFET densities are plotted in Figure 5 as functions of the chemical potential in various correlation regimes. The non-interacting curve describes the KS lattice at the zeroth iteration of the LPFET calculation. Thus, we can visualize, as U deviates from zero, how much the KS lattice learns from the interacting two-electron Householder cluster. LPFET is actually quite accurate (even more than Ht-DMFET, probably because of error cancellations) in the low filling regime. Even though LPFET deviates from Ht-DMFET when electron correlation is strong, as expected, their chemical-potential-density maps are quite similar. This is an indication that neglecting the Householder kinetic correlation potential contribution to the Hxc potential, as done in LPFET, is not a crude approximation, even in the strongly correlated regime. As expected [15,31], LPFET and Ht-DMFET poorly perform when approaching half filling. Like the well-established single-site DMFT (see Figure 7 of Ref. [5]), they are unable to describe the density-driven Mott–Hubbard transition (i.e., the opening of the gap). As discussed in Ref. [31], this might be related to the fact that, in the exact theory, the Householder cluster is not disconnected from its environment and it contains a fractional number of electrons, away from half filling, unlike in the (approximate) Ht-DMFET and LPFET schemes. In the language of KS-DFT, modeling the gap opening is equivalent to modeling the derivative discontinuity in the density-functional correlation potential at half filling. As clearly shown in Figure 6, Ht-DMFET and LPFET do not reproduce this feature. In the language of the exact density-functional embedding theory derived in Section 2.3, both Ht-DMFET and LPFET approximations neglect the complementary density-functional correlation energy that is induced by the interacting bath and the environment of the (closed) density-functional Householder cluster. As readily seen from Equation (74), it should be possible to describe the density-driven Mott–Hubbard transition with a single statically embedded impurity, provided that we can model the derivative discontinuity in at half filling. This is obviously a challenging task that is usually bypassed by embedding more impurities [15,31]. The implementation of a multiple-impurity LPFET as well as its generalization to higher-dimension lattice or quantum chemical Hamiltonians is left for future work.
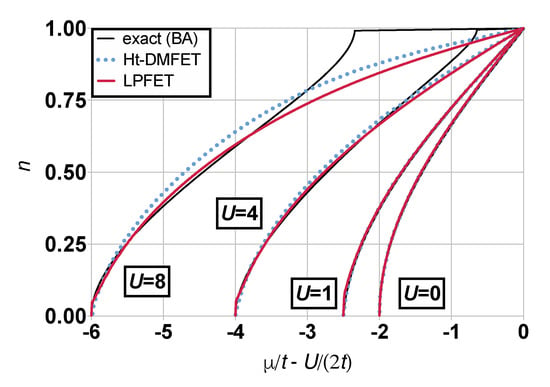
Figure 5.
Converged LPFET densities (red solid lines) plotted as functions of the chemical potential in various correlation regimes. Comparison is made with the exact BA (black solid lines) and Ht-DMFET (blue dotted lines) results. In the latter case, the chemical potential is evaluated via the numerical differentiation of the density-functional Ht-DMFET per-site energy (see Equations (62) and (76)). The non-interacting () chemical-potential-density map (see Equation (60)) is shown for analysis purposes.
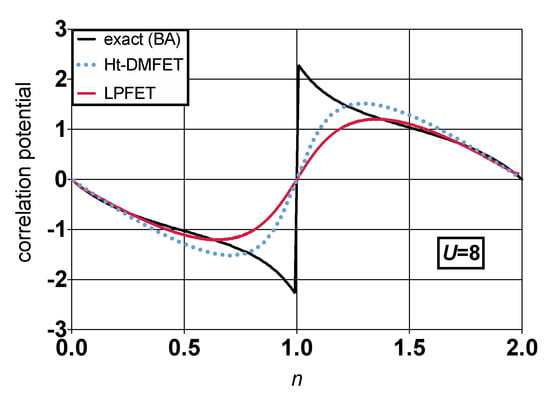
Figure 6.
Correlation potential plotted as a function of the lattice filling n at the Ht-DMFET (blue dashed line) and LPFET (red solid line) levels of approximation for . Comparison is made with the exact BA correlation potential (black solid line).
5. Conclusions and Perspectives
An in-principle-exact density-functional reformulation of the recently proposed Householder transformed density matrix functional embedding theory (Ht-DMFET) [31] has been derived for the uniform 1D Hubbard Hamiltonian with a single embedded impurity. On that basis, an approximate local potential functional embedding theory (LPFET) has been proposed and implemented. Ht-DMFET, which is equivalent to DMET or DET in the particular case of a single impurity, is reinterpreted in this context as an approximation to DFT where the complementary density-functional correlation energy induced by the interacting bath and the environment of the (closed) embedding “impurity+bath” cluster is neglected. LPFET neglects, in addition, the kinetic correlation effects induced by the Householder transformation on the impurity chemical potential. We have shown that combining the two approximations is equivalent to approximating the latter potential with the Hxc potential of the full lattice. Thus, an approximate Hxc potential can be determined self-consistently for a given choice of external (chemical in the present case) potential in the true interacting lattice. The self-consistency loop, which does not exist in regular single-impurity DMET or DET [36], emerges naturally in LPFET from the exact density constraint, i.e., by forcing the KS lattice and interacting embedded impurity densities to match. In this context, the energy becomes a functional of the Hxc potential. In this respect, LPFET can be seen as a flavor of KS-DFT where no density functional is used. LPFET is very similar to SDE [42]. The two approaches essentially differ in the optimization of the potential. In LPFET, no KS construction is made within the embedding cluster, unlike in SDE. Instead, the Hxc potential is directly updated in the lattice. As a result, the KS cluster (which is not used in the actual calculation) can be automatically generated with the correct density by applying the Householder transformation to the KS lattice Hamiltonian.
LPFET and Ht-DMFET chemical-potential-density maps have been computed for a 1000-site Hubbard ring. Noticeable differences appear in the strongly correlated regime. LPFET is more accurate than Ht-DMFET in the low filling regime, probably because of error cancellations. As expected from previous works [15,31], their performance deteriorates as we approach half filling. It appears that, in the language of density-functional embedding theory, it should be possible to describe the density-driven Mott–Hubbard transition (i.e., the opening of the gap), provided that the complementary correlation potential exhibits a derivative discontinuity at half filling. Since the latter is neglected in both methods, the gap opening is not reproduced. The missing correlation effects might be recovered by applying a multi-reference Görling–Levy-type perturbation theory on top of the correlated cluster calculation [31]. Extending LPFET to multiple impurities by means of a block Householder transformation is another viable strategy [31]. Work is currently in progress in these directions. Note that, like DMET or SDE, LPFET is in principle applicable to quantum chemical Hamiltonians written in a localized molecular orbital basis. A general computational implementation of the theory will be presented in a forthcoming paper and the code will be made available on that occasion.
Author Contributions
Conceptualization, E.F. and M.S.; methodology, E.F.; software, S.S.; validation, E.F., S.S. and M.S.; formal analysis, E.F. and S.S.; investigation, E.F. and S.S.; resources, S.S.; data curation, S.S.; writing—original draft preparation, E.F. and S.S.; writing—review and editing, E.F., S.S. and M.S.; visualization, E.F. and S.S.; supervision, E.F.; project administration, E.F.; funding acquisition, E.F. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
LabEx CSC (grant number: ANR-10-LABX-0026-CSC) and ANR (grant numbers: ANR-19-CE29-0002 DESCARTES and ANR-19-CE07-0024-02 CoLab).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors thank Saad Yalouz (for his comments on the manuscript and many fruitful discussions) as well as Thomas Baker and Martin Rafael Gulin for stimulating discussions.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Appendix A. Simplification of Density Matrix Elements in the Householder Representation
References
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Lichtenstein, A.I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA +U method. J. Phys. Condens. Matter 1997, 9, 767–808. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Poteryaev, A.I.; Korotin, M.A.; Anokhin, A.O.; Kotliar, G. First-principles calculations of the electronic structure and spectra of strongly correlated systems: Dynamical mean-field theory. J. Phys. Condens. Matter 1997, 9, 7359–7367. [Google Scholar] [CrossRef]
- Lichtenstein, A.I.; Katsnelson, M.I. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 1998, 57, 6884–6895. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef]
- Haule, K. Exact Double Counting in Combining the Dynamical Mean Field Theory and the Density Functional Theory. Phys. Rev. Lett. 2015, 115, 196403. [Google Scholar] [CrossRef]
- Requist, R.; Gross, E.K.U. Model Hamiltonian for strongly correlated systems: Systematic, self-consistent, and unique construction. Phys. Rev. B 2019, 99, 125114. [Google Scholar] [CrossRef]
- Ghosh, S.; Verma, P.; Cramer, C.J.; Gagliardi, L.; Truhlar, D.G. Combining Wave Function Methods with Density Functional Theory for Excited States. Chem. Rev. 2018, 118, 7249–7292. [Google Scholar] [CrossRef]
- Savin, A. Recent Developments and Applications of Modern Density Functional Theory; Elsevier: Amsterdam, The Netherlands, 1996; p. 327. [Google Scholar]
- Toulouse, J.; Colonna, F.; Savin, A. Long-range–short-range separation of the electron-electron interaction in density-functional theory. Phys. Rev. A 2004, 70, 062505. [Google Scholar] [CrossRef]
- Sharkas, K.; Toulouse, J.; Savin, A. Double-hybrid density-functional theory made rigorous. J. Chem. Phys. 2011, 134, 064113. [Google Scholar] [CrossRef]
- Fromager, E. On the exact formulation of multi-configuration density-functional theory: Electron density versus orbitals occupation. Mol. Phys. 2015, 113, 419–434. [Google Scholar] [CrossRef]
- Senjean, B.; Nakatani, N.; Tsuchiizu, M.; Fromager, E. Site-occupation embedding theory using Bethe ansatz local density approximations. Phys. Rev. B 2018, 97, 235105. [Google Scholar] [CrossRef]
- Wasserman, A.; Pavanello, M. Quantum embedding electronic structure methods. Int. J. Quantum Chem. 2020, 120, e26495. [Google Scholar] [CrossRef]
- Knizia, G.; Chan, G.K.L. Density Matrix Embedding: A Simple Alternative to Dynamical Mean-Field Theory. Phys. Rev. Lett. 2012, 109, 186404. [Google Scholar] [CrossRef] [PubMed]
- Knizia, G.; Chan, G. Density matrix embedding: A strong-coupling quantum embedding theory. J. Chem. Theory Comput. 2013, 9, 1428–1432. [Google Scholar] [CrossRef] [PubMed]
- Tsuchimochi, T.; Welborn, M.; Van Voorhis, T. Density matrix embedding in an antisymmetrized geminal power bath. J. Chem. Phys. 2015, 143, 024107. [Google Scholar] [CrossRef] [PubMed]
- Welborn, M.; Tsuchimochi, T.; Van Voorhis, T. Bootstrap embedding: An internally consistent fragment-based method. J. Chem. Phys. 2016, 145, 074102. [Google Scholar] [CrossRef]
- Sun, Q.; Chan, G.K.L. Quantum Embedding Theories. Accounts Chem. Res. 2016, 49, 2705–2712. [Google Scholar] [CrossRef]
- Wouters, S.; Jiménez-Hoyos, C.A.; Sun, Q.; Chan, G.K.L. A Practical Guide to Density Matrix Embedding Theory in Quantum Chemistry. J. Chem. Theory Comput. 2016, 12, 2706–2719. [Google Scholar] [CrossRef]
- Wu, X.; Cui, Z.H.; Tong, Y.; Lindsey, M.; Chan, G.K.L.; Lin, L. Projected density matrix embedding theory with applications to the two-dimensional Hubbard model. J. Chem. Phys. 2019, 151, 064108. [Google Scholar] [CrossRef]
- Cui, Z.H.; Zhu, T.; Chan, G.K.L. Efficient Implementation of Ab Initio Quantum Embedding in Periodic Systems: Density Matrix Embedding Theory. J. Chem. Theory Comput. 2020, 16, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Faulstich, F.M.; Kim, R.; Cui, Z.H.; Wen, Z.; Kin-Lic Chan, G.; Lin, L. Pure State v-Representability of Density Matrix Embedding Theory. J. Chem. Theory Comput. 2022, 18, 851–864. [Google Scholar] [CrossRef] [PubMed]
- Lacombe, L.; Maitra, N.T. Embedding via the Exact Factorization Approach. Phys. Rev. Lett. 2020, 124, 206401. [Google Scholar] [CrossRef]
- Requist, R.; Gross, E.K.U. Fock-Space Embedding Theory: Application to Strongly Correlated Topological Phases. Phys. Rev. Lett. 2021, 127, 116401. [Google Scholar] [CrossRef] [PubMed]
- Georges, A.; Kotliar, G. Hubbard model in infinite dimensions. Phys. Rev. B 1992, 45, 6479–6483. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Kotliar, G.; Vollhardt, D. Strongly Correlated Materials: Insights From Dynamical Mean-Field Theory. Phys. Today 2004, 57, 53–59. [Google Scholar] [CrossRef]
- Held, K. Electronic structure calculations using dynamical mean field theory. Adv. Phys. 2007, 56, 829–926. [Google Scholar] [CrossRef]
- Zgid, D.; Chan, G.K.L. Dynamical mean-field theory from a quantum chemical perspective. J. Chem. Phys. 2011, 134, 094115. [Google Scholar] [CrossRef]
- Sekaran, S.; Tsuchiizu, M.; Saubanère, M.; Fromager, E. Householder-transformed density matrix functional embedding theory. Phys. Rev. B 2021, 104, 035121. [Google Scholar] [CrossRef]
- Ayral, T.; Lee, T.H.; Kotliar, G. Dynamical mean-field theory, density-matrix embedding theory, and rotationally invariant slave bosons: A unified perspective. Phys. Rev. B 2017, 96, 235139. [Google Scholar] [CrossRef]
- Lee, T.H.; Ayral, T.; Yao, Y.X.; Lanata, N.; Kotliar, G. Rotationally invariant slave-boson and density matrix embedding theory: Unified framework and comparative study on the one-dimensional and two-dimensional Hubbard model. Phys. Rev. B 2019, 99, 115129. [Google Scholar] [CrossRef]
- Fertitta, E.; Booth, G.H. Rigorous wave function embedding with dynamical fluctuations. Phys. Rev. B 2018, 98, 235132. [Google Scholar] [CrossRef]
- Fertitta, E.; Booth, G.H. Energy-weighted density matrix embedding of open correlated chemical fragments. J. Chem. Phys. 2019, 151, 014115. [Google Scholar] [CrossRef] [PubMed]
- Sriluckshmy, P.V.; Nusspickel, M.; Fertitta, E.; Booth, G.H. Fully algebraic and self-consistent effective dynamics in a static quantum embedding. Phys. Rev. B 2021, 103, 085131. [Google Scholar] [CrossRef]
- Lee, T.H.; Lanatà, N.; Kim, M.; Kotliar, G. Efficient Slave-Boson Approach for Multiorbital Two-Particle Response Functions and Superconductivity. Phys. Rev. X 2021, 11, 041040. [Google Scholar] [CrossRef]
- Bulik, I.W.; Scuseria, G.E.; Dukelsky, J. Density matrix embedding from broken symmetry lattice mean fields. Phys. Rev. B 2014, 89, 035140. [Google Scholar] [CrossRef]
- Senjean, B. Projected site-occupation embedding theory. Phys. Rev. B 2019, 100, 035136. [Google Scholar] [CrossRef]
- Lima, N.A.; Silva, M.F.; Oliveira, L.N.; Capelle, K. Density Functionals Not Based on the Electron Gas: Local-Density Approximation for a Luttinger Liquid. Phys. Rev. Lett. 2003, 90, 146402. [Google Scholar] [CrossRef]
- Capelle, K.; Campo, V.L. Density functionals and model Hamiltonians: Pillars of many-particle physics. Phys. Rep. 2013, 528, 91–159. [Google Scholar] [CrossRef]
- Mordovina, U.; Reinhard, T.E.; Theophilou, I.; Appel, H.; Rubio, A. Self-Consistent Density-Functional Embedding: A Novel Approach for Density-Functional Approximations. J. Chem. Theory Comput. 2019, 15, 5209–5220. [Google Scholar] [CrossRef] [PubMed]
- Theophilou, I.; Reinhard, T.E.; Rubio, A.; Ruggenthaler, M. Approximations based on density-matrix embedding theory for density-functional theories. Electron. Struct. 2021, 3, 035001. [Google Scholar] [CrossRef]
- Rotella, F.; Zambettakis, I. Block Householder transformation for parallel QR factorization. Appl. Math. Lett. 1999, 12, 29–34. [Google Scholar] [CrossRef][Green Version]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension. Phys. Rev. Lett. 1968, 20, 1445–1448. [Google Scholar] [CrossRef]
- Vilela, L.N.P.; Capelle, K.; Oliveira, L.N.; Campo, V.L. Approximate expression for the ground-state energy of the two- and three-dimensional Hubbard model at arbitrary filling obtained from dimensional scaling. J. Phys. Condens. Matter 2019, 31, 455601. [Google Scholar] [CrossRef]
- Senjean, B.; Tsuchiizu, M.; Robert, V.; Fromager, E. Local density approximation in site-occupation embedding theory. Mol. Phys. 2017, 115, 48–62. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).