An Alternative Methodology to Compute the Geometric Tortuosity in 2D Porous Media Using the A-Star Pathfinding Algorithm
Abstract
:1. Introduction
2. Materials and Methods
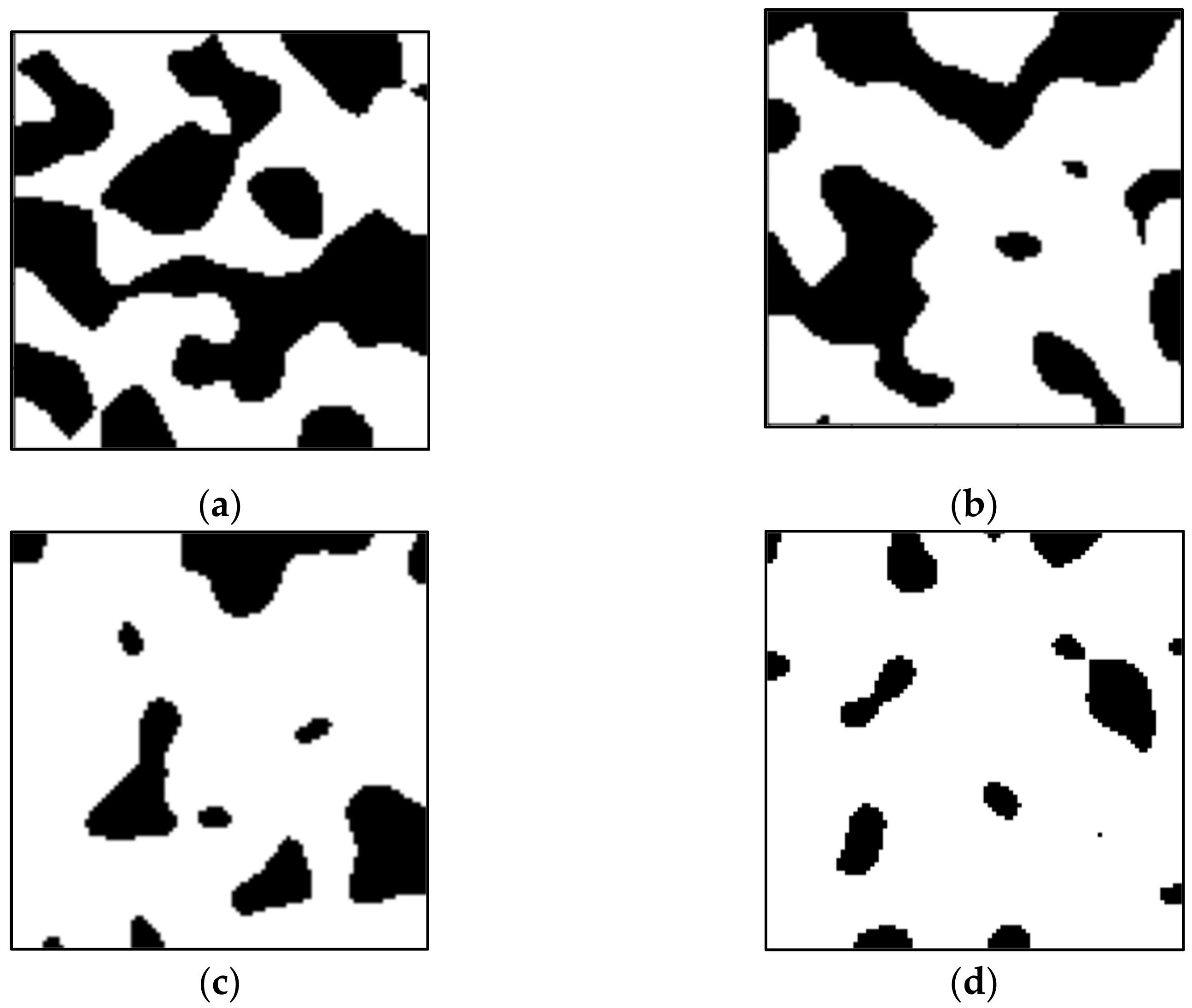
2.1. Porous Media Generation
2.2. Porous Media Selection
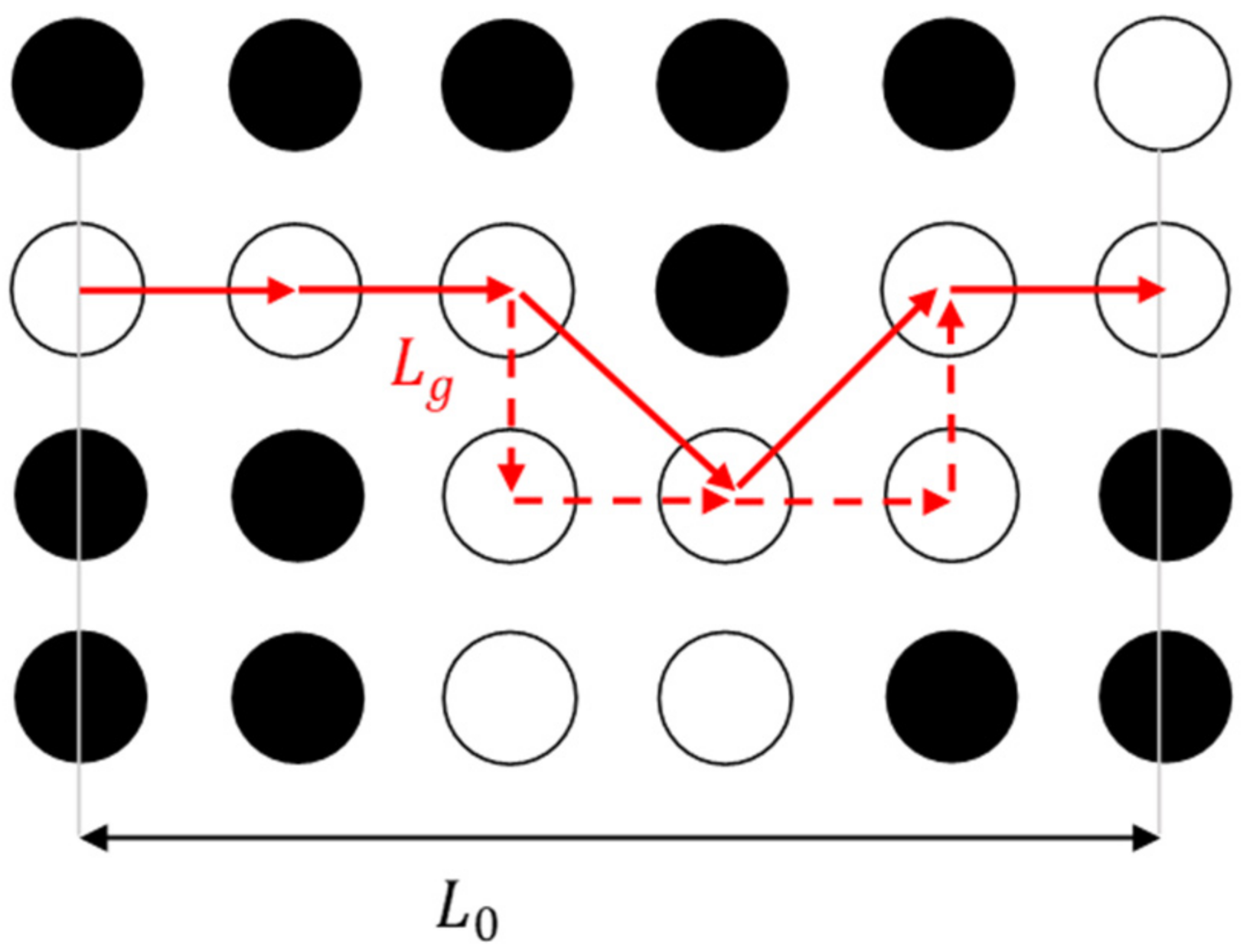
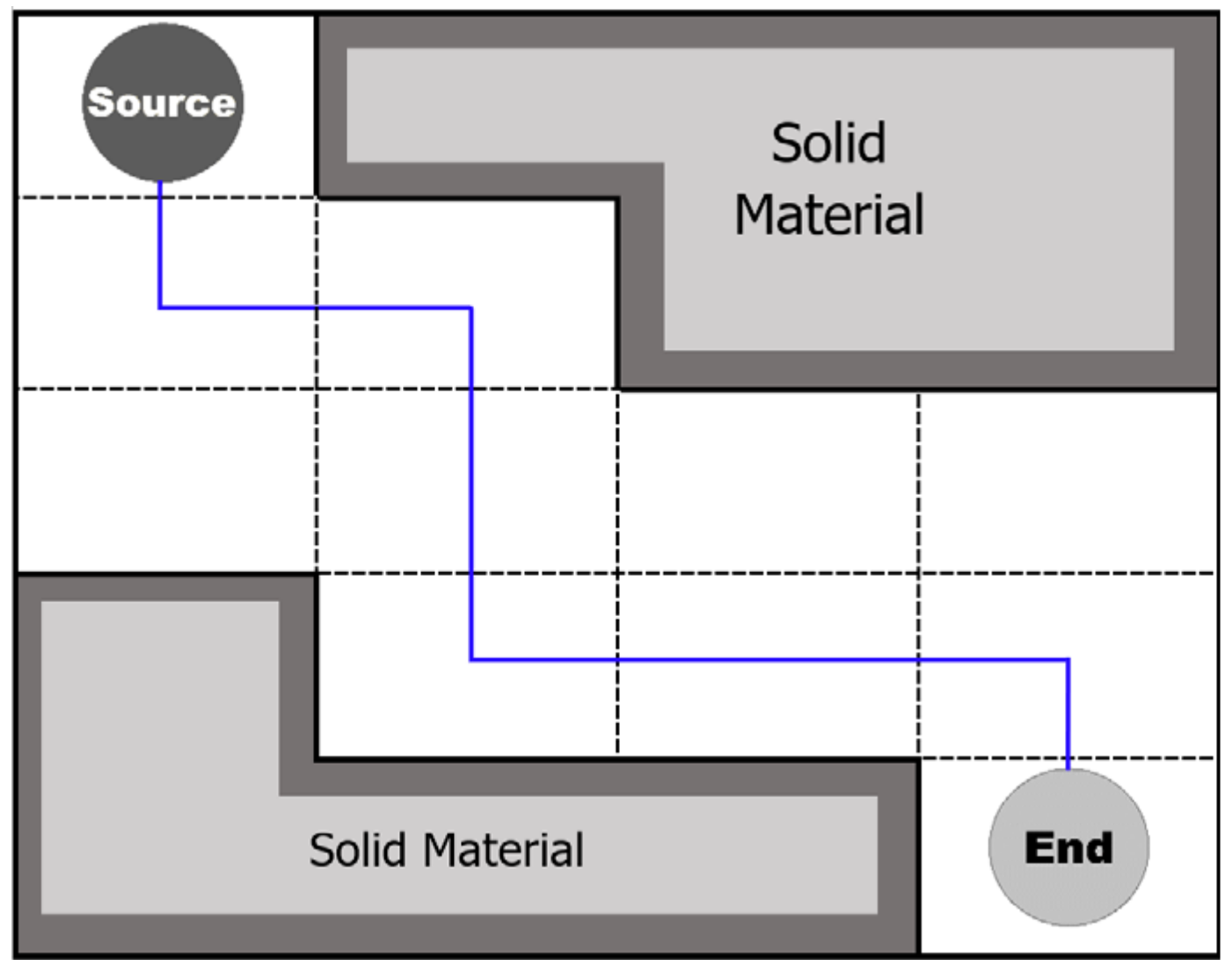
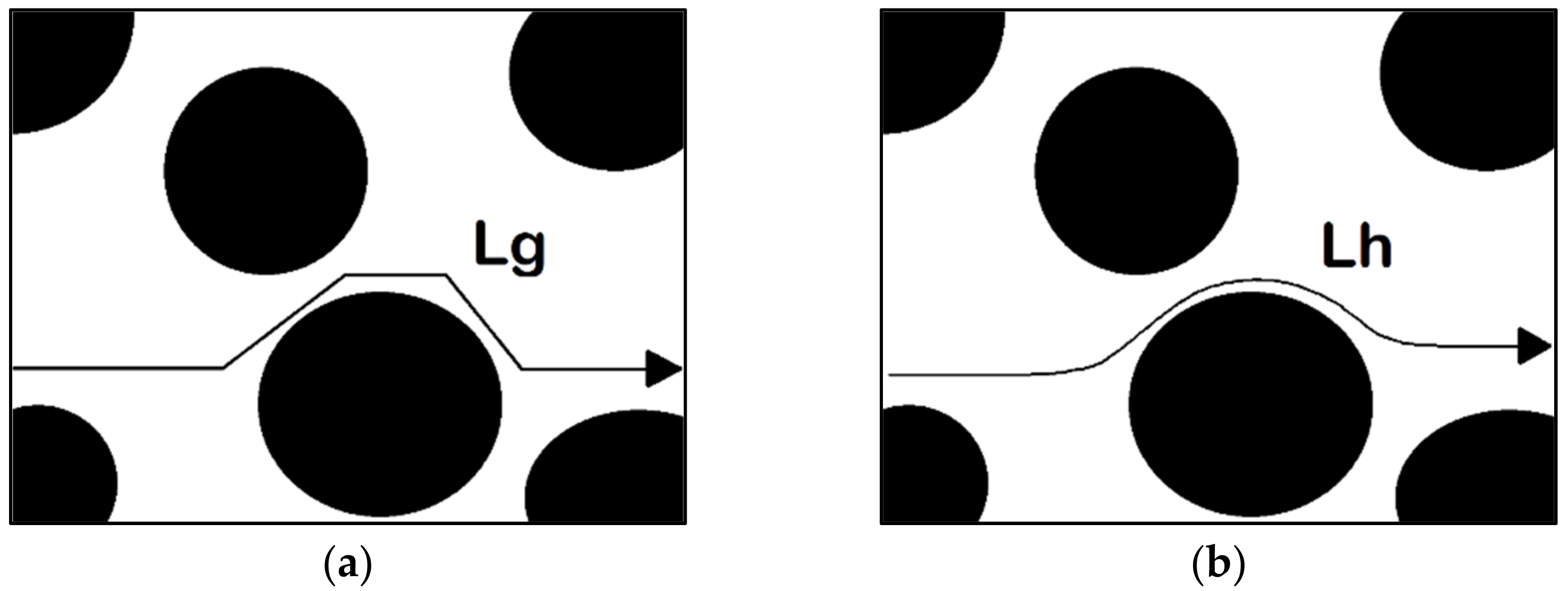
2.3. Geometric Path
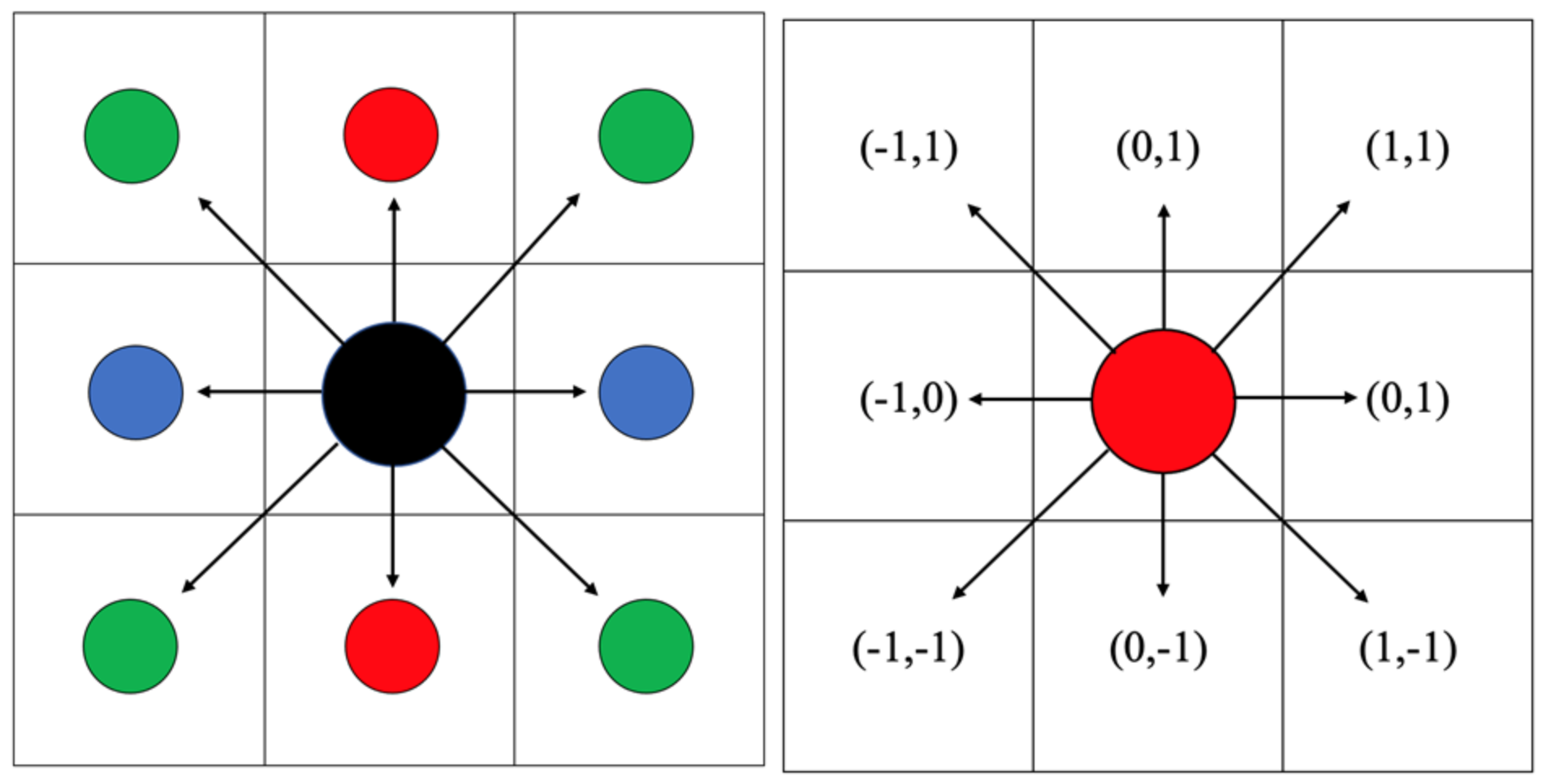
2.4. A-Star Algorithm
2.5. Geometric Tortuosity
2.6. Tortuosity Path
2.7. Other Algorithms
3. Results and Discussion
3.1. Generated Porous Media
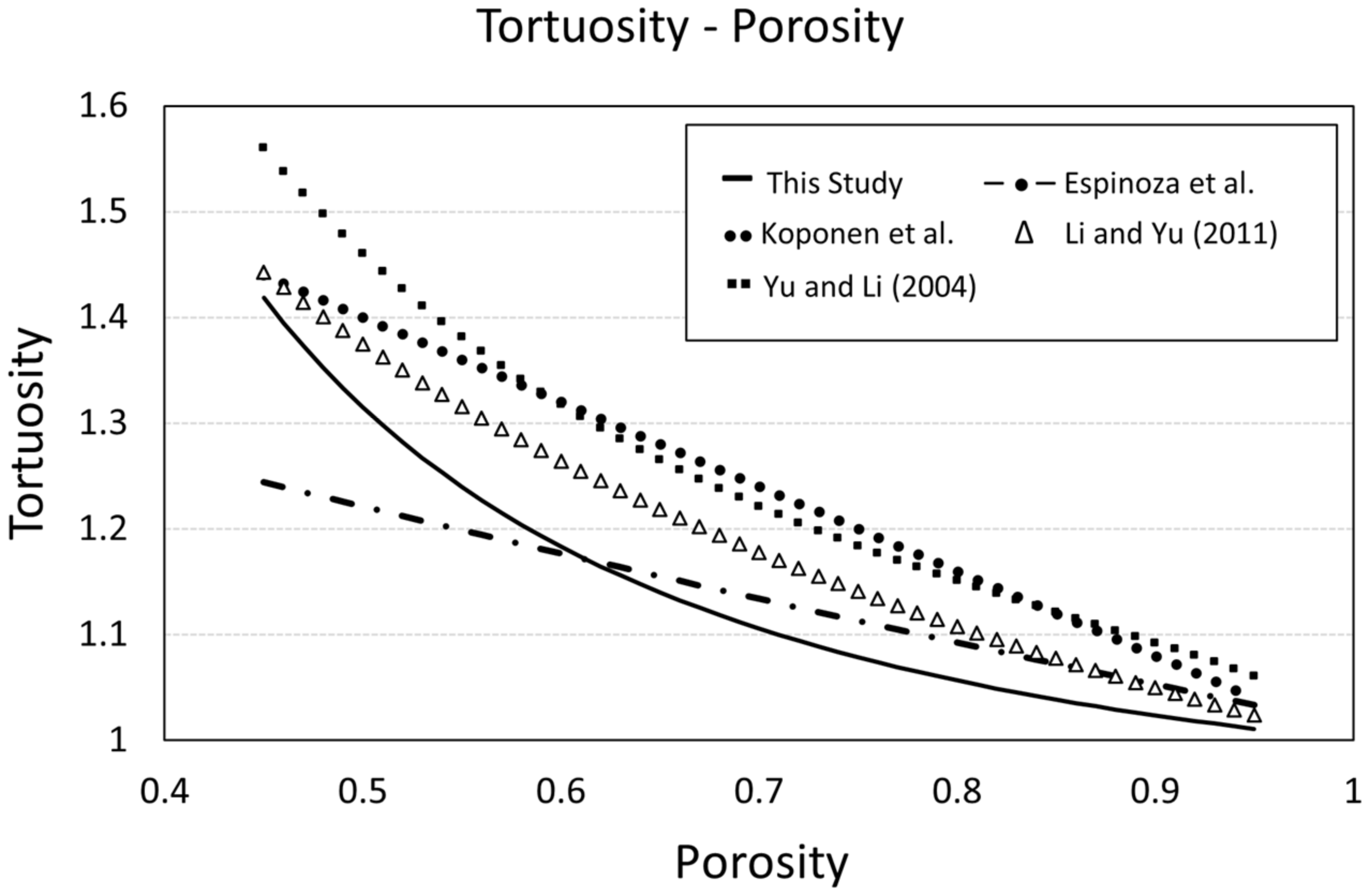
3.2. Tortuosity–Porosity Correlations
3.3. Hydraulic Tortuosity vs. Geometric Tortuosity
3.4. Geometric Tortuosity (A-Star) vs. Other Algorithms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determination of the Number of Samples
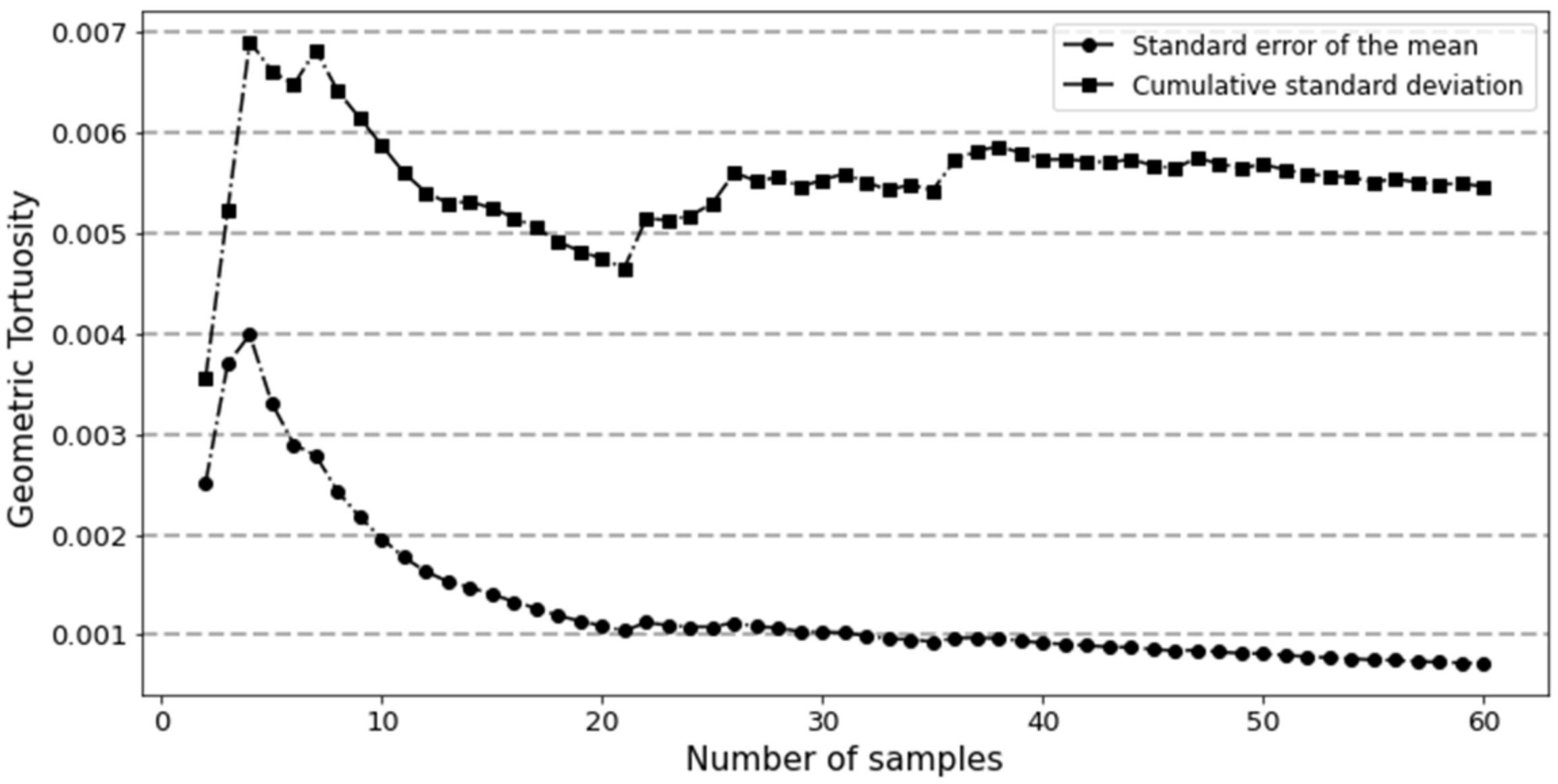


References
- Fu, J.; Thomas, H.R.; Li, C. Tortuosity of porous media: Image analysis and physical simulation. Earth-Sci. Rev. 2021, 212, 1–52. [Google Scholar] [CrossRef]
- Valdés-Parada, F.J.; Porter, M.L.; Wood, B.D. The Role of Tortuosity in Upscaling. Transp. Porous Media 2011, 88, 1–30. [Google Scholar] [CrossRef]
- Friedman, S.P. Critical path analysis of the relationship between permeability and electrical conductivity of three-dimensional pore networks. Water Resour. Res. 1998, 34, 1703–1710. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in Porous Media: A Critical Review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Zhang, X.; Knackstedt, M.A. Direct simulation of electrical and hydraulic tortuosity in porous solids. Geophys. Res. Lett. 1995, 22, 2333–2336. [Google Scholar] [CrossRef]
- Encalada, Á.; Barzola-Monteses, J.; Espinoza-Andaluz, M. A Permeability–Throat Diameter Correlation for a Medium Generated with Delaunay Tessellation and Voronoi Algorithm. Transp. Porous Media 2020, 132, 201–217. [Google Scholar] [CrossRef]
- Ciurică, S.; Lopez-Sublet, M.; Loeys, B.L.; Radhouani, I.; Natarajan, N.; Vikkula, M.; Maas, A.H.E.M.; Adlam, D.; Persu, A. Arterial Tortuosity Novel Implications for an Old Phenotype. Australas. Phys. Eng. Sci. Med. 2019, 73, 951–960. [Google Scholar] [CrossRef]
- Espinoza-Andaluz, M.; Andersson, M.; Sundén, B. Computational time and domain size analysis of porous media flows using the lattice Boltzmann method. Comput. Math. Appl. 2017, 74, 26–34. [Google Scholar] [CrossRef]
- Encalada-Dávila, Á.; Espinoza-Andaluz, M.; Barzola-Monteses, J.; Li, S.; Andersson, M. Transport Parameter Correlations for Digitally Created PEFC Gas Diffusion Layers Using OpenPNM. Processes 2021, 9, 1141. [Google Scholar] [CrossRef]
- Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. Engineering route planning algorithms. In Algorithmics of Large and Complex Networks; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5515 LNCS, pp. 117–139. [Google Scholar] [CrossRef] [Green Version]
- Storandt, S. Contraction hierarchies on grid graphs. In Annual Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8077 LNAI, pp. 236–247. [Google Scholar] [CrossRef]
- Bast, H.; Funke, S.; Matijevic, D.; Sanders, P.; Schultes, D. In transit to constant time shortest-path queries in road networks. In Proceedings of the Ninth Workshop on Algorithm Engineering and Experiments (ALENEX), New Orleans, LA, USA, 6 January 2007; pp. 46–59. [Google Scholar] [CrossRef] [Green Version]
- Rios, L.H.O.; Chaimowicz, L. A survey and classification of A* based best-first heuristic search algorithms. In Brazilian Symposium on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6404 LNAI, pp. 253–262. [Google Scholar] [CrossRef] [Green Version]
- Rusell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Davis, E., Edwards, D.D., Forsyth, D., Hay, N.J., Malik, J.M., Mittal, V., Sahami, M., Thrun, S., Eds.; Pearson Education: London, UK, 2010; ISBN 9780136042594. [Google Scholar]
- Stenzel, O.; Pecho, O.; Holzer, L.; Neumann, M.; Schmidt, V. Predicting Effective Conductivities Based on Geometric Microstructure Characteristics. AIChE J. 2016, 62, 1834–1843. [Google Scholar] [CrossRef]
- Shanti, N.O.; Chan, V.W.L.; Stock, S.R.; De Carlo, F.; Thornton, K.; Faber, K.T. X-ray micro-computed tomography and tortuosity calculations of percolating pore networks. Acta Mater. 2014, 71, 126–135. [Google Scholar] [CrossRef]
- Taiwo, O.O.; Finegan, D.P.; Eastwood, D.S.; Fife, J.L.; Brown, L.D.; Darr, J.A.; Lee, P.D.; Brett, D.J.L.; Shearing, P.R. Comparison of three-dimensional analysis and stereological techniques for quantifying lithium-ion battery electrode microstructures. J. Microsc. 2016, 263, 280–292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zharbossyn, A.; Berkinova, Z.; Boribayeva, A.; Yermukhambetova, A.; Golman, B. Analysis of tortuosity in compacts of ternary mixtures of spherical particles. Materials 2020, 13, 4487. [Google Scholar] [CrossRef] [PubMed]
- Tjaden, B.; Brett, D.J.L.; Shearing, P.R. Tortuosity in electrochemical devices: A review of calculation approaches. Int. Mater. Rev. 2018, 63, 47–67. [Google Scholar] [CrossRef] [Green Version]
- Lotito, V.; Zambelli, T. Pattern detection in colloidal assembly: A mosaic of analysis techniques. Adv. Colloid Interface Sci. 2020, 284, 102252. [Google Scholar] [CrossRef] [PubMed]
- Lotito, V.; Zambelli, T. A journey through the landscapes of small particles in binary colloidal assemblies: Unveiling structural transitions from isolated particles to clusters upon variation in composition. Nanomaterials 2019, 9, 921. [Google Scholar] [CrossRef] [Green Version]
- Lotito, V.; Zambelli, T. Playing with sizes and shapes of colloidal particles via dry etching methods. Adv. Colloid Interface Sci. 2022, 299, 102538. [Google Scholar] [CrossRef]
- Lotito, V.; Karlušić, M.; Jakšić, M.; Luketić, K.T.; Müller, U.; Zambelli, T.; Fazinić, S. Shape deformation in ion beam irradiated colloidal monolayers: An AFM investigation. Nanomaterials 2020, 10, 453. [Google Scholar] [CrossRef] [Green Version]
- Slotte, P.A.; Berg, C.F.; Khanamiri, H.H. Predicting Resistivity and Permeability of Porous Media Using Minkowski Functionals. Transp. Porous Media 2020, 131, 705–722. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Miyazawa, M.; Okamoto, A.; Shimizu, H.; Obayashi, I.; Hiraoka, Y.; Tsuji, T.; Kang, P.K.; Ito, T. Inferring fracture forming processes by characterizing fracture network patterns with persistent homology. Comput. Geosci. 2020, 143, 104550. [Google Scholar] [CrossRef]
- Gostick, J.; Khan, Z.; Tranter, T.; Kok, M.; Agnaou, M.; Sadeghi, M.; Jervis, R. PoreSpy: A Python Toolkit for Quantitative Analysis of Porous Media Images. J. Open Source Softw. 2019, 4, 1296. [Google Scholar] [CrossRef]
- Wu, M.; Liu, J.; Lv, X.; Shi, D.; Zhu, Z. A Study on Homogenization Equations of Fractal Porous Media. J. Geophys. Eng. 2018, 15, 2388–2398. [Google Scholar] [CrossRef] [Green Version]
- Gunathilake, T.M.S.U.; Ching, Y.C.; Ching, K.Y.; Chuah, C.H.; Abdullah, L.C. Biomedical and microbiological applications of bio-based porous materials: A review. Polymers 2017, 9, 160. [Google Scholar] [CrossRef] [PubMed]
- Simaafrookhteh, S.; Shakeri, M.; Baniassadi, M.; Sahraei, A.A. Microstructure Reconstruction and Characterization of the Porous GDLs for PEMFC Based on Fibers Orientation Distribution. Fuel Cells 2018, 18, 160–172. [Google Scholar] [CrossRef]
- Espinoza, M.; Sunden, B.; Andersson, M.; Yuan, J. Analysis of Porosity and Tortuosity in a 2D Selected Region of Solid Oxide Fuel Cell Cathode Using the Lattice Boltzmann Method. ECS Trans. 2015, 65, 59–73. [Google Scholar] [CrossRef] [Green Version]
- Espinoza-Andaluz, M.; Velasco-Galarza, V.; Romero-Vera, A. On hydraulic tortuosity variations due to morphological considerations in 2D porous media by using the Lattice Boltzmann method. Math. Comput. Simul. 2020, 169, 74–87. [Google Scholar] [CrossRef]
- de Carvalho, T.P.; Morvan, H.P.; Hargreaves, D.M.; Oun, H.; Kennedy, A. Pore-Scale Numerical Investigation of Pressure Drop Behaviour Across Open-Cell Metal Foams. Transp. Porous Media 2017, 117, 311–336. [Google Scholar] [CrossRef] [Green Version]
- Grigoriev, M.; Khafizov, A.; Kokhan, V.; Asadchikov, V. Robust technique for representative volume element identification in noisy microtomography images of porous materials based on pores morphology and their spatial distribution. In Proceedings of the Thirteenth International Conference on Machine Vision. International Society for Optics and Photonics, Rome, Italy, 2–6 November 2020. [Google Scholar] [CrossRef]
- Ezzatabadipour, M.; Zahedi, H. A Novel Method for Streamline-Based Tortuosity Calculation and Investigation of Obstacles Shape Effect on Tortuosity in Porous Media with Random Elliptical Obstacles Using Lattice Boltzmann Method. Transp. Porous Media 2021, 136, 103–124. [Google Scholar] [CrossRef]
- Ferguson, D.; Likhachev, M.; Stentz, A. A guide to heuristic-based path planning. In Proceedings of the International Workshop on Planning under Uncertainty for Autonomous Systems, International Conference on Automated Planning and Scheduling (ICAPS), Monterey, CA, USA, 5–10 June 2005; pp. 1–10. [Google Scholar]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An Improved A-star algorithm considering water current, traffic separation and berthing for vessel path planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef] [Green Version]
- Espinoza, M.; Sundén, B.; Andersson, M. Pore-Scale Analysis of Diffusion Transport Parameters in Digitally Reconstructed SOFC Anodes with Gradient Porosity in the Main Flow Direction. ECS Trans. 2017, 78, 2785–2796. [Google Scholar] [CrossRef] [Green Version]
- Mohamad, A.A. Lattice Boltzmann Method, 2nd ed.; Springer: London, UK, 2019; ISBN 978-1-4471-7422-6. [Google Scholar]
- Cooper, S.J.; Kishimoto, M.; Tariq, F.; Bradley, R.S.; Marquis, A.J.; Brandon, N.P.; Kilner, J.A.; Shearing, P.R. Microstructural Analysis of an LSCF Cathode Using In Situ Tomography and Simulation. ECS Trans. 2013, 57, 2671–2678. [Google Scholar] [CrossRef]
- Shen, L.; Chen, Z. Critical review of the impact of tortuosity on diffusion. Chem. Eng. Sci. 2007, 62, 3748–3755. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Tortuous flow in porous media. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1996, 54, 406–410. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.M.; Li, J.H. A geometry model for tortuosity of flow path in porous media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar] [CrossRef]
- Li, J.H.; Yu, B.M. Tortuosity of flow paths through a Sierpinski carpet. Chin. Phys. Lett. 2011, 28, 3–6. [Google Scholar] [CrossRef]
- Ritter, F.E.; Schoelles, M.J.; Quigley, K.S.; Klein, L.C. Determining the Number of Simulation Runs: Treating Simulations as Theories by Not Sampling Their Behavior. In Human-in-the-Loop Simulations Methods Pract; Springer: London, UK, 2011; pp. 97–116. [Google Scholar]






| Empirical Correlation for τ | Coefficient of Determination | Type |
|---|---|---|
| 0.9975 | Power | |
| 0.9969 | Exponential | |
| 0.9888 | Polynomial |
| Correlation for τ | Structure | Reference | |
|---|---|---|---|
| Randomly placed fully overlapping rectangles | Koponen et al. (1996) | [41] | |
| Square shaped particles | Yu and Li (2004) | [42] | |
| Sierpinski carpet | Li and Yu (2011) | [43] | |
| Circle-shaped particles | Espinoza et al. (2019) | [31] |
| Pathfinding Methods | Tortuosity τ | Relative Deviation (%) |
|---|---|---|
| This study | 1.2747 | - |
| Pore centroid | 1.3831 | 8.503 |
| Skeleton (PoreSpy) | 1.4109 | 10.685 |
| Dijkstra | 1.3213 | 3.655 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinoza-Andaluz, M.; Pagalo, J.; Ávila, J.; Barzola-Monteses, J. An Alternative Methodology to Compute the Geometric Tortuosity in 2D Porous Media Using the A-Star Pathfinding Algorithm. Computation 2022, 10, 59. https://doi.org/10.3390/computation10040059
Espinoza-Andaluz M, Pagalo J, Ávila J, Barzola-Monteses J. An Alternative Methodology to Compute the Geometric Tortuosity in 2D Porous Media Using the A-Star Pathfinding Algorithm. Computation. 2022; 10(4):59. https://doi.org/10.3390/computation10040059
Chicago/Turabian StyleEspinoza-Andaluz, Mayken, Javier Pagalo, Joseph Ávila, and Julio Barzola-Monteses. 2022. "An Alternative Methodology to Compute the Geometric Tortuosity in 2D Porous Media Using the A-Star Pathfinding Algorithm" Computation 10, no. 4: 59. https://doi.org/10.3390/computation10040059
APA StyleEspinoza-Andaluz, M., Pagalo, J., Ávila, J., & Barzola-Monteses, J. (2022). An Alternative Methodology to Compute the Geometric Tortuosity in 2D Porous Media Using the A-Star Pathfinding Algorithm. Computation, 10(4), 59. https://doi.org/10.3390/computation10040059








